Línea de contorno

Una línea de contorno (también isolínea , isopleta , isocuanta o isaritma ) de una función de dos variables es una curva a lo largo de la cual la función tiene un valor constante, de modo que la curva une puntos de igual valor. ^{[1] [2]} Es una sección plana del gráfico tridimensional de la función paralela al plano . De manera más general, una línea de contorno para una función de dos variables es una curva que une puntos donde la función tiene el mismo valor particular. ^[2]${\displaystyle f(x,y)}$${\estilo de visualización (x,y)}$

En cartografía , una línea de contorno (a menudo simplemente llamada "contorno") une puntos de igual elevación (altura) por encima de un nivel dado, como el nivel medio del mar . ^[3] Un mapa de contorno es un mapa ilustrado con líneas de contorno, por ejemplo un mapa topográfico , que muestra así valles y colinas, y la inclinación o suavidad de las pendientes. ^[4] El intervalo de contorno de un mapa de contorno es la diferencia de elevación entre líneas de contorno sucesivas. ^[5]

El gradiente de la función siempre es perpendicular a las curvas de nivel. Cuando las curvas están muy próximas entre sí, la magnitud del gradiente es grande: la variación es pronunciada. Un conjunto de niveles es una generalización de una curva de nivel para funciones de cualquier número de variables.

Las líneas de contorno son líneas curvas, rectas o una mezcla de ambas líneas en un mapa que describen la intersección de una superficie real o hipotética con uno o más planos horizontales. La configuración de estas líneas de contorno permite a los lectores de mapas inferir el gradiente relativo de un parámetro y estimar ese parámetro en lugares específicos. Las líneas de contorno pueden trazarse en un modelo tridimensional visible de la superficie , como cuando un fotogrametrista que ve un modelo estereoscópico traza contornos de elevación, o interpolarse a partir de las elevaciones de superficie estimadas , como cuando un programa de computadora traza contornos a través de una red de puntos de observación de centroides de área. En el último caso, el método de interpolación afecta la confiabilidad de las isolíneas individuales y su representación de la pendiente , los hoyos y los picos. ^[6]

La idea de las líneas que unen puntos de igual valor fue redescubierta varias veces. La isóbata (línea de contorno de profundidad constante) más antigua que se conoce se encuentra en un mapa del río Spaarne , cerca de Haarlem , fechado en 1584, obra del holandés Pieter Bruinsz. ^[7] En 1701, Edmond Halley utilizó dichas líneas (isógonos) en un gráfico de variación magnética. ^[8] El ingeniero holandés Nicholas Cruquius dibujó el lecho del río Merwede con líneas de igual profundidad (isóbatas) a intervalos de 1 braza en 1727, y Philippe Buache las utilizó a intervalos de 10 brazas en un mapa del Canal de la Mancha que se preparó en 1737 y se publicó en 1752. Tales líneas se utilizaron para describir una superficie terrestre (líneas de contorno) en un mapa del Ducado de Módena y Reggio por Domenico Vandelli en 1746, y fueron estudiadas teóricamente por Ducarla en 1771, y Charles Hutton las utilizó en el experimento de Schiehallion . En 1791, un mapa de Francia por JL Dupain-Triel utilizó líneas de contorno a intervalos de 20 metros, sombreados, alturas puntuales y una sección vertical. En 1801, el jefe del Cuerpo de Ingenieros de Francia, Haxo , utilizó líneas de contorno a una escala mayor de 1:500 en un plano de sus proyectos para Rocca d'Anfo , ahora en el norte de Italia, bajo el mando de Napoleón . ^{[9] [10] [11]}

Hacia 1843, cuando el Ordnance Survey comenzó a registrar regularmente las curvas de nivel en Gran Bretaña e Irlanda , ya se utilizaban de forma generalizada en los países europeos. Las isóbatas no se utilizaron de forma rutinaria en las cartas náuticas hasta las de Rusia a partir de 1834 y las de Gran Bretaña a partir de 1838. ^{[9] [12] [13]}

A medida que se inventaron diferentes usos de la técnica de forma independiente, los cartógrafos comenzaron a reconocer un tema común y debatieron cómo llamar a estas "líneas de igual valor" en general. La palabra isograma (del griego antiguo ἴσος (isos)  'igual' y γράμμα (gramma)  'escritura, dibujo') fue propuesta por Francis Galton en 1889 para las líneas que indican igualdad de alguna condición física o cantidad, ^[14] aunque isograma también puede referirse a una palabra sin una letra repetida . En 1944, John K. Wright todavía prefería isograma , pero nunca alcanzó un uso amplio. A principios del siglo XX, la isopleta ( πλῆθος , plethos , 'cantidad') se utilizaba en 1911 en los Estados Unidos, mientras que la isaritma ( ἀριθμός , arithmos , 'número') se había vuelto común en Europa. También surgieron alternativas adicionales, incluida la isolínea híbrida griego-inglesa y la línea isométrica ( μέτρον , metron , 'medida'). A pesar de los intentos de seleccionar un único estándar, todas estas alternativas han sobrevivido hasta el presente. ^{[15] [16]}

Cuando los mapas con curvas de nivel se hicieron comunes, la idea se extendió a otras aplicaciones. Tal vez las últimas en desarrollarse sean los mapas de curvas de nivel de la calidad del aire y la contaminación acústica , que aparecieron por primera vez en los Estados Unidos aproximadamente en 1970, en gran medida como resultado de la legislación nacional que exigía la delimitación espacial de estos parámetros.

Las curvas de nivel suelen recibir nombres específicos que comienzan con " iso- " según la naturaleza de la variable que se representa en el mapa, aunque en muchos casos la frase "curva de nivel" es la más utilizada. Los nombres específicos son más comunes en meteorología, donde se pueden ver simultáneamente varios mapas con diferentes variables. El prefijo "' iso- " se puede reemplazar por " isallo- " para especificar una curva de nivel que conecta puntos donde una variable cambia al mismo ritmo durante un período de tiempo determinado.

Un isógono (del griego antiguo γωνία (gonia)  'ángulo') es una línea de contorno para una variable que mide la dirección. En meteorología y en geomagnética, el término isógono tiene significados específicos que se describen a continuación. Una isoclina ( κλίνειν , klinein , 'inclinarse o inclinarse') es una línea que une puntos con la misma pendiente. En dinámica de poblaciones y en geomagnética, los términos isoclina y línea isoclínica tienen significados específicos que se describen a continuación.

Una curva de puntos equidistantes es un conjunto de puntos que se encuentran todos a la misma distancia de un punto , una línea o una polilínea determinados . En este caso, la función cuyo valor se mantiene constante a lo largo de una línea de contorno es una función de distancia .

En 1944, John K. Wright propuso que el término isopleta se utilizara para las líneas de contorno que representan una variable que no se puede medir en un punto, sino que debe calcularse a partir de datos recopilados sobre un área, a diferencia de las líneas isométricas para variables que se pueden medir en un punto; desde entonces, esta distinción se ha seguido en general. ^{[16] [17]} Un ejemplo de isopleta es la densidad de población , que se puede calcular dividiendo la población de un distrito censal por la superficie de ese distrito. Se supone que cada valor calculado es el valor de la variable en el centro del área, y luego se pueden dibujar isopletas mediante un proceso de interpolación . La idea de un mapa de isopletas se puede comparar con la de un mapa de coropletas . ^{[18] [19]}

En meteorología, la palabra isopleta se utiliza para cualquier tipo de línea de contorno. ^[20]

Las curvas de nivel meteorológicas se basan en la interpolación de los datos puntuales recibidos de las estaciones meteorológicas y los satélites meteorológicos . Las estaciones meteorológicas rara vez se encuentran exactamente en una curva de nivel (cuando lo están, esto indica una medición exactamente igual al valor de la curva de nivel). En cambio, las líneas se dibujan para aproximar lo mejor posible las ubicaciones de los valores exactos, en función de los puntos de información dispersos disponibles.

Los mapas de contorno meteorológicos pueden presentar datos recopilados, como la presión del aire real en un momento determinado, o datos generalizados, como la presión promedio durante un período de tiempo, o datos pronosticados, como la presión del aire prevista en algún momento en el futuro.

Los diagramas termodinámicos utilizan múltiples conjuntos de contornos superpuestos (incluidas isobaras e isotermas) para presentar una imagen de los principales factores termodinámicos en un sistema meteorológico.

Una isobara (del griego antiguo βάρος (baros)  'peso') es una línea de presión igual o constante en un gráfico, diagrama o mapa; una isopleta o línea de contorno de presión. Más exactamente, las isobaras son líneas dibujadas en un mapa que unen lugares de igual presión atmosférica promedio reducida al nivel del mar durante un período de tiempo específico. En meteorología , las presiones barométricas mostradas se reducen al nivel del mar , no las presiones superficiales en las ubicaciones del mapa. ^[21] La distribución de isobaras está estrechamente relacionada con la magnitud y la dirección del campo de viento , y se puede utilizar para predecir patrones climáticos futuros. Las isobaras se utilizan comúnmente en los informes meteorológicos de televisión.

Las isalobaras son líneas que unen puntos de igual cambio de presión durante un intervalo de tiempo específico. ^[22] Estas se pueden dividir en analobaras , líneas que unen puntos de igual aumento de presión durante un intervalo de tiempo específico, ^[23] y katalobaras , líneas que unen puntos de igual disminución de presión. ^[24] En general, los sistemas meteorológicos se mueven a lo largo de un eje que une centros isalobáricos altos y bajos. ^[25] Los gradientes isalobáricos son componentes importantes del viento ya que aumentan o disminuyen el viento geostrófico .

Una isopicna es una línea de densidad constante. Una isoaltura o isohipsa es una línea de altura geopotencial constante en un mapa de superficie de presión constante. La isohipsa y la isoaltura se conocen simplemente como líneas que muestran la misma presión en un mapa.

Una isoterma (del griego antiguo θέρμη (thermē)  'calor') es una línea que une puntos de un mapa que tienen la misma temperatura . Por lo tanto, todos los puntos por los que pasa una isoterma tienen la misma o iguales temperaturas en el momento indicado. ^{[26] [2]} Una isoterma a 0 °C se llama nivel de congelación . El término lignes isothermes (o lignes d'égale chaleur) fue acuñado por el geógrafo y naturalista prusiano Alexander von Humboldt , quien como parte de su investigación sobre la distribución geográfica de las plantas publicó el primer mapa de isotermas en París, en 1817. ^{[27] [28]}

Una isoquema es una línea de igual temperatura media de invierno, y una isotérea es una línea de igual temperatura media de verano.

Un isohelo ( ἥλιος , helios , 'Sol') es una línea de radiación solar igual o constante .

Una isogeoterma es una línea de igual temperatura debajo de la superficie de la Tierra.

Una isoyeta o línea isoyética (del griego antiguo ὑετός (huetos)  'lluvia') es una línea en un mapa que une los puntos con la misma cantidad de lluvia en un período determinado. Un mapa con isoyetas se llama mapa isoyético .

Una isohume es una línea de humedad relativa constante , mientras que una isodroterma (del griego antiguo δρόσος (drosos)  'rocío' y θέρμη (therme)  'calor') es una línea de punto de rocío igual o constante .

Una isonefa es una línea que indica una cobertura de nubes igual .

Una isocalaz es una línea de frecuencia constante de tormentas de granizo , y un isobronte es una línea trazada a través de puntos geográficos en los que ocurrió simultáneamente una fase dada de actividad de tormenta eléctrica.

La capa de nieve se muestra frecuentemente como un mapa de líneas de contorno.

Una isotaca (del griego antiguo ταχύς (tachus)  'rápido') es una línea que une puntos con una velocidad del viento constante . En meteorología, el término isógono se refiere a una línea con una dirección del viento constante.

Una línea isopéctica denota fechas iguales de formación de hielo cada invierno, y una isotac denota fechas iguales de descongelación.

Las curvas de nivel son uno de los métodos más comunes que se utilizan para indicar la elevación o altitud y la profundidad en los mapas . A partir de estas curvas de nivel, se puede determinar una idea del terreno general . Se utilizan en una variedad de escalas, desde dibujos de ingeniería y planos arquitectónicos a gran escala, pasando por mapas topográficos y cartas batimétricas , hasta mapas a escala continental.

"Línea de contorno" es el uso más común en cartografía , pero también se utilizan isobatas para profundidades submarinas en mapas batimétricos e isohipsas para elevaciones.

En cartografía, el intervalo de curvas de nivel es la diferencia de elevación entre curvas de nivel adyacentes. El intervalo de curvas de nivel debe ser el mismo en un mismo mapa. Cuando se calcula como una relación con la escala del mapa, se puede obtener una idea de la pendiente del terreno.

Hay varias reglas a tener en cuenta al interpretar las curvas de nivel del terreno:

• Regla de las V : las V puntiagudas suelen estar en valles fluviales, con el canal de drenaje pasando por la punta de la V, y esta apuntando hacia aguas arriba. Esto es consecuencia de la erosión .
• Regla de Os : los bucles cerrados normalmente son cuesta arriba en el interior y cuesta abajo en el exterior, y el bucle más interno es el área más alta. Si, en cambio, un bucle representa una depresión, algunos mapas lo indican mediante líneas cortas llamadas rayados que son perpendiculares al contorno y apuntan en la dirección de la depresión. ^[29] (El concepto es similar al de rayados utilizados en los mapas de rayados, pero distinto ).
• Espaciamiento de las curvas de nivel : las curvas de nivel cercanas indican una pendiente pronunciada; las curvas de nivel distantes, una pendiente suave. La unión de dos o más curvas de nivel indica un acantilado. Contando el número de curvas de nivel que cruzan un segmento de un arroyo , se puede aproximar el gradiente del arroyo .

Por supuesto, para determinar las diferencias de elevación entre dos puntos, se debe conocer el intervalo de contorno, o la distancia en altitud entre dos líneas de contorno adyacentes, y esto normalmente se indica en la clave del mapa. Por lo general, los intervalos de contorno son consistentes en todo el mapa, pero hay excepciones. A veces, hay contornos intermedios en áreas más planas; estas pueden ser líneas discontinuas o punteadas en la mitad del intervalo de contorno indicado. Cuando se utilizan contornos con tintes hipsométricos en un mapa de pequeña escala que incluye montañas y áreas bajas más planas, es común tener intervalos más pequeños en elevaciones más bajas para que se muestren los detalles en todas las áreas. Por el contrario, para una isla que consiste en una meseta rodeada de acantilados escarpados, es posible utilizar intervalos más pequeños a medida que aumenta la altura. ^[30]

Un mapa isopotencial es una medida del potencial electrostático en el espacio, a menudo representado en dos dimensiones con las cargas electrostáticas que inducen ese potencial eléctrico . El término línea equipotencial o línea isopotencial se refiere a una curva de potencial eléctrico constante . Si cruzar una línea equipotencial representa un potencial ascendente o descendente se infiere de las etiquetas en las cargas. En tres dimensiones, las superficies equipotenciales se pueden representar con una sección transversal bidimensional, que muestra líneas equipotenciales en la intersección de las superficies y la sección transversal.

El término matemático general conjunto de niveles se utiliza a menudo para describir la colección completa de puntos que tienen un potencial particular, especialmente en el espacio de dimensiones superiores.

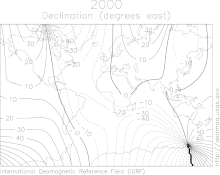
En el estudio del campo magnético de la Tierra , el término isógono o línea isogónica se refiere a una línea de declinación magnética constante , la variación del norte magnético con respecto al norte geográfico. Una línea agónica se traza a través de puntos de declinación magnética cero. Una línea isopórica se refiere a una línea de variación anual constante de la declinación magnética. ^[31]

Una línea isoclínica conecta puntos de igual inclinación magnética , y una línea aclínica es la línea isoclínica de inclinación magnética cero.

Una línea isodinámica (de δύναμις o dynamis , que significa 'poder') conecta puntos con la misma intensidad de fuerza magnética.

Además de la profundidad del océano, los oceanógrafos utilizan las curvas de nivel para describir fenómenos variables difusos, de forma muy similar a como lo hacen los meteorólogos con los fenómenos atmosféricos. En particular, las isobatitermas son líneas que muestran profundidades de agua con la misma temperatura, las isohalinas muestran líneas de igual salinidad oceánica y las isopicnas son superficies con la misma densidad de agua.

En geología estructural , sedimentología , estratigrafía y geología económica se representan diversos datos geológicos como mapas de contorno . Los mapas de contorno se utilizan para mostrar la superficie subterránea de los estratos geológicos , las superficies de fallas (especialmente fallas inversas de ángulo bajo ) y las discordancias . Los mapas de isopacas utilizan isopacas (líneas de igual espesor) para ilustrar las variaciones en el espesor de las unidades geológicas.

Al hablar de contaminación, los mapas de densidad pueden ser muy útiles para indicar fuentes y áreas de mayor contaminación. Los mapas de contorno son especialmente útiles para formas difusas o escalas de contaminación. La precipitación ácida se indica en mapas con isobelios . Algunas de las aplicaciones más extendidas de los mapas de contorno de la ciencia ambiental implican el mapeo del ruido ambiental (donde las líneas de igual nivel de presión sonora se denotan como isobelios ^[32] ), la contaminación del aire , la contaminación del suelo , la contaminación térmica y la contaminación de las aguas subterráneas . Mediante la plantación y el arado en contorno , la tasa de escorrentía de agua y, por lo tanto, la erosión del suelo se pueden reducir sustancialmente; esto es especialmente importante en las zonas ribereñas .

Una isopleta es un contorno isopleta que conecta áreas de diversidad biológica comparable. Por lo general, la variable es el número de especies de un género o familia determinado que se encuentran en una región. Los mapas de isopletas se utilizan para mostrar patrones y tendencias de distribución, como centros de diversidad. ^[33]

En economía , las curvas de nivel se pueden utilizar para describir características que varían cuantitativamente en el espacio. Una isócrona muestra líneas de tiempo de conducción o tiempo de viaje equivalente a una ubicación determinada y se utiliza en la generación de mapas de isócronas . Una isócrona muestra los costos de transporte equivalentes desde la fuente de una materia prima, y ​​una isodapana muestra el costo equivalente del tiempo de viaje.

Las curvas de nivel también se utilizan para mostrar información no geográfica en economía. Las curvas de indiferencia (como se muestra a la izquierda) se utilizan para mostrar paquetes de bienes a los que una persona asignaría la misma utilidad. Una isocuanta (en la imagen de la derecha) es una curva de igual cantidad de producción para combinaciones alternativas de usos de insumos , y una curva de isocosto (también en la imagen de la derecha) muestra usos alternativos que tienen costos de producción iguales.

En la ciencia política se utiliza un método análogo para comprender las coaliciones (por ejemplo, el diagrama en el trabajo de Laver y Shepsle ^[34] ).

En dinámica de poblaciones , una isoclina muestra el conjunto de tamaños de población en los que la tasa de cambio, o derivada parcial, de una población en un par de poblaciones que interactúan es cero.

En estadística, las líneas de isodensidad ^[35] o isodensanas son líneas que unen puntos con el mismo valor de una densidad de probabilidad . Las isodensanas se utilizan para mostrar distribuciones bivariadas . Por ejemplo, para una distribución elíptica bivariada, las líneas de isodensidad son elipses .

Diversos tipos de gráficos en termodinámica , ingeniería y otras ciencias utilizan isobaras (presión constante), isotermas (temperatura constante), isocoras (volumen específico constante) u otros tipos de isolíneas, aunque estos gráficos no suelen estar relacionados con mapas. Estas isolíneas son útiles para representar más de dos dimensiones (o cantidades) en gráficos bidimensionales. Algunos ejemplos comunes en termodinámica son algunos tipos de diagramas de fases .

Las isoclinas se utilizan para resolver ecuaciones diferenciales ordinarias .

Al interpretar imágenes de radar , un isodop es una línea de igual velocidad Doppler y un isoeco es una línea de igual reflectividad de radar.

En el caso de los contornos híbridos se representan gráficamente las energías de los orbitales híbridos y las energías de los orbitales atómicos puros. El gráfico obtenido se denomina contorno híbrido.

• isochasma :ocurrencia equivalente de auroras
• isócor : volumen
• isodosis : dosis absorbida de radiación
• isofeno : eventos biológicos que ocurren por coincidencia, como la floración de las plantas.
• isofota : iluminancia
• Telefonía móvil: potencia recibida del móvil y área de cobertura celular

• Encontrar límites de conjuntos de niveles después de la segmentación de imágenes
  • Detección de bordes
  • Método de nivelación
  • Trazado de límites
• Modelo de contorno activo

Para maximizar la legibilidad de los mapas de contorno, hay varias opciones de diseño disponibles para el creador del mapa, principalmente el grosor de la línea, el color de la línea , el tipo de línea y el método de marcado numérico.

El grosor de la línea es simplemente la oscuridad o el grosor de la línea utilizada. Esta elección se realiza en función de la forma menos intrusiva de las curvas de nivel que permitan al lector descifrar la información de fondo del mapa. Si hay poco o ningún contenido en el mapa base, las curvas de nivel pueden dibujarse con un grosor relativamente grueso. Además, para muchas formas de curvas de nivel, como los mapas topográficos, es habitual variar el grosor y/o el color de la línea, de modo que se produzca una característica de línea diferente para ciertos valores numéricos. Por ejemplo, en el mapa topográfico anterior, las elevaciones pares de cien pies se muestran con un grosor diferente al de los intervalos de veinte pies.

El color de las líneas se puede elegir entre una cantidad de pigmentos que se adapten a la presentación. A veces, se utiliza un brillo o lustre además del color para diferenciar las líneas de contorno del mapa base . El color de las líneas se puede variar para mostrar otra información.

El tipo de línea se refiere a si la línea de contorno básica es sólida, discontinua, punteada o discontinua en algún otro patrón para crear el efecto deseado. Las líneas punteadas o discontinuas se utilizan a menudo cuando el mapa base subyacente transmite información muy importante (o difícil de leer). Los tipos de línea discontinua se utilizan cuando se infiere la ubicación de la línea de contorno.

El marcado numérico es la forma de indicar los valores aritméticos de las curvas de nivel. Esto se puede hacer colocando números a lo largo de algunas de las curvas de nivel, generalmente mediante interpolación para las líneas intermedias. Alternativamente, se puede generar una clave de mapa que asocie las curvas de nivel con sus valores.

Si las líneas de contorno no están etiquetadas numéricamente y las líneas adyacentes tienen el mismo estilo (con el mismo grosor, color y tipo), entonces la dirección del gradiente no se puede determinar a partir de las líneas de contorno solamente. Sin embargo, si las líneas de contorno pasan por tres o más estilos, entonces la dirección del gradiente se puede determinar a partir de las líneas. La orientación de las etiquetas de texto numéricas se usa a menudo para indicar la dirección de la pendiente.

Por lo general, las líneas de contorno se dibujan en una vista en planta, o como un observador en el espacio vería la superficie de la Tierra: en forma de mapa ordinario. Sin embargo, algunos parámetros a menudo se pueden mostrar en una vista de perfil que muestra un perfil vertical del parámetro mapeado. Algunos de los parámetros más comunes mapeados en perfil son las concentraciones de contaminantes del aire y los niveles de sonido . En cada uno de esos casos, puede ser importante analizar (las concentraciones de contaminantes del aire o los niveles de sonido) a diferentes alturas para determinar la calidad del aire o los efectos del ruido en la salud de las personas a diferentes alturas, por ejemplo, que viven en diferentes niveles de piso de un apartamento urbano. En la actualidad, tanto los mapas de contorno en planta como en vista de perfil se utilizan en estudios de contaminación del aire y contaminación acústica .

Las etiquetas son un componente fundamental de los mapas de elevación. Un mapa de curvas de nivel correctamente etiquetado ayuda al lector a interpretar rápidamente la forma del terreno. Si los números se colocan cerca unos de otros, significa que el terreno es empinado. Las etiquetas deben colocarse a lo largo de una línea ligeramente curva que "apunte" a la cumbre o al nadir, desde varias direcciones si es posible, lo que facilita la identificación visual de la cumbre o el nadir. ^{[36] [37]} Las etiquetas de curvas de nivel se pueden orientar de modo que el lector mire hacia arriba cuando lea la etiqueta.

El etiquetado manual de mapas de contorno es un proceso que requiere mucho tiempo, sin embargo, existen algunos sistemas de software que pueden realizar el trabajo de forma automática y de acuerdo con las convenciones cartográficas, denominado colocación automática de etiquetas .

Wikimedia Commons alberga una categoría multimedia sobre Líneas de contorno .

• El frontisterio de Forthright