Orden de 5 mosaicos cuadrados
| Orden de 5 mosaicos cuadrados | |
|---|---|
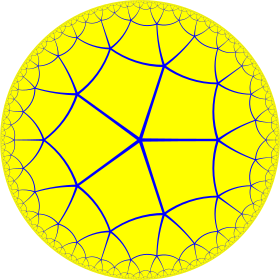 Modelo de disco de Poincaré del plano hiperbólico | |
| Tipo | Teselación regular hiperbólica |
| Configuración de vértice | 4 5 |
| Símbolo de Schläfli | {4,5} |
| Símbolo de Wythoff | 5 | 4 2 |
| Diagrama de Coxeter |      |
| Grupo de simetría | [5,4], (*542) |
| Dual | Orden 4: mosaico pentagonal |
| Propiedades | Vértice-transitivo , arista-transitivo , cara-transitivo |
En geometría , el mosaico cuadrado de orden 5 es un mosaico regular del plano hiperbólico . Tiene el símbolo de Schläfli {4,5}.
Poliedros relacionados y teselación
| Esférico | Teselación hiperbólica | |||||||
|---|---|---|---|---|---|---|---|---|
 {2,5}      |  {3,5}      |  {4,5}      |  {5,5}      |  {6,5}      |  {7,5}      |  {8,5}      | ... |  {∞,5}      |
Este teselado está relacionado topológicamente como parte de una secuencia de poliedros regulares y teselados con figura de vértice (4 n ).
| * n 42 mutación de simetría de teselaciones regulares: {4, n } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Esférico | Euclidiano | Hiperbólica compacta | Paracompacto | ||||||||
 {4,3}      |  {4,4}      |  {4,5}      |  {4,6}      |  {4,7}      |  {4,8} ...      |  {4,∞}      | |||||
| Azulejos pentagonales/cuadrados uniformes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simetría: [5,4], (*542) | [5,4] + , (542) | [5 + ,4], (5*2) | [5,4,1 + ], (*552) | ||||||||
     |      |      |      |      |      |      |      |      |      | ||
 |  |  |  |  |  |  |  |  |  | ||
| {5,4} | t{5,4} | r{5,4} | 2t{5,4}=t{4,5} | 2r{5,4}={4,5} | rr{5,4} | tr{5,4} | sr{5,4} | s{5,4} | h{4,5} | ||
| Duelos uniformes | |||||||||||
     |      |      |      |      |      |      |      |      |      | ||
 |  |  |  |  |  |  |  |  | |||
| V54 | V4.10.10 | V4.5.4.5 | V5.8.8 | V4 5 | V4.4.5.4 | V4.8.10 | V3.3.4.3.5 | V3.3.5.3.5 | V5 5 | ||
Esta teselación hiperbólica está relacionada con un poliedro semirregular infinito oblicuo con la misma figura de vértice en el espacio tridimensional euclidiano.
Referencias
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Capítulo 19, Las teselaciones hiperbólicas de Arquímedes)
- "Capítulo 10: Panales regulares en el espacio hiperbólico". La belleza de la geometría: doce ensayos . Publicaciones de Dover. 1999. ISBN 0-486-40919-8. Número de serie LCCN 99035678.
Véase también
- Azulejos cuadrados
- Teselación uniforme en el plano hiperbólico
- Lista de politopos regulares
- Triacontaedro rómbico medial
Enlaces externos
- Weisstein, Eric W. "Teselación hiperbólica". MathWorld .
- Weisstein, Eric W. "Disco hiperbólico de Poincaré". MathWorld .
- Galería de mosaicos hiperbólicos y esféricos
- KaleidoTile 3: Software educativo para crear mosaicos esféricos, planos e hiperbólicos
- Teselaciones planas hiperbólicas, Don Hatch


