Material granular

Física de la materia condensada
Fases Transición de fase PCC
States of matter Solid Liquid Gas Plasma Bose–Einstein condensate Bose gas Fermionic condensate Fermi gas Fermi liquid Supersolid Superfluidity Luttinger liquid Time crystal
Phase phenomena Order parameter Phase transition QCP
Electronic phases Electronic band structure Plasma Insulator Mott insulator Semiconductor Semimetal Conductor Superconductor Thermoelectric Piezoelectric Ferroelectric Topological insulator Spin gapless semiconductor
Electronic phenomena Quantum Hall effect Spin Hall effect Kondo effect
Magnetic phases Diamagnet Superdiamagnet Paramagnet Superparamagnet Ferromagnet Antiferromagnet Metamagnet Spin glass
Quasiparticles Phonon Exciton Plasmon Polariton Polaron Magnon Roton
Soft matter Amorphous solid Colloid Granular material Liquid crystal Polymer
Scientists Van der Waals Onnes von Laue Bragg Debye Bloch Onsager Mott Peierls Landau Luttinger Anderson Van Vleck Hubbard Shockley Bardeen Cooper Schrieffer Josephson Louis Néel Esaki Giaever Kohn Kadanoff Fisher Wilson von Klitzing Binnig Rohrer Bednorz Müller Laughlin Störmer Yang Tsui Abrikosov Ginzburg Leggett Parisi Wetterich Perdew
Physics portal  Category
v t e

Un material granular es un conglomerado de partículas macroscópicas sólidas discretas que se caracteriza por una pérdida de energía siempre que las partículas interactúan (el ejemplo más común sería la fricción cuando los granos chocan). ^[1] Los constituyentes que componen el material granular son lo suficientemente grandes como para que no estén sujetos a fluctuaciones de movimiento térmico. Por lo tanto, el límite de tamaño inferior para los granos en material granular es de aproximadamente 1 μm . En el límite de tamaño superior, la física de los materiales granulares se puede aplicar a los témpanos de hielo donde los granos individuales son icebergs y a los cinturones de asteroides del Sistema Solar donde los granos individuales son asteroides .

Algunos ejemplos de materiales granulares son la nieve , las nueces , el carbón , la arena , el arroz , el café , los copos de maíz , la sal y las bolas de cojinetes . Por lo tanto, la investigación sobre materiales granulares es directamente aplicable y se remonta al menos a Charles-Augustin de Coulomb , cuya ley de fricción se estableció originalmente para materiales granulares. ^[2] Los materiales granulares son comercialmente importantes en aplicaciones tan diversas como la industria farmacéutica , la agricultura y la producción de energía .

Los polvos son una clase especial de material granular debido a su pequeño tamaño de partícula, lo que los hace más cohesivos y más fácilmente suspendidos en un gas .

El militar y físico brigadier Ralph Alger Bagnold fue uno de los pioneros de la física de la materia granular y su libro The Physics of Blown Sand and Desert Dunes ^[3] sigue siendo una referencia importante hasta el día de hoy. Según el científico de materiales Patrick Richard, "los materiales granulares son omnipresentes en la naturaleza y son el segundo material más manipulado en la industria (el primero es el agua )". ^[4]

En cierto sentido, los materiales granulares no constituyen una fase única de la materia , sino que tienen características que recuerdan a los sólidos , líquidos o gases, dependiendo de la energía promedio por grano. Sin embargo, en cada uno de estos estados, los materiales granulares también presentan propiedades que son únicas. ^[5]

Los materiales granulares también presentan una amplia gama de comportamientos de formación de patrones cuando se excitan (por ejemplo, se los vibra o se los deja fluir). Como tal, los materiales granulares bajo excitación pueden considerarse un ejemplo de un sistema complejo . También muestran inestabilidades basadas en fluidos y fenómenos como el efecto Magnus . ^[6]

La materia granular es un sistema compuesto por muchas partículas macroscópicas. Las partículas microscópicas (átomos/moléculas) se describen (en mecánica clásica) por todos los grados de libertad del sistema. Las partículas macroscópicas se describen solo por los grados de libertad del movimiento de cada partícula como un cuerpo rígido . En cada partícula hay muchos grados de libertad internos. Consideremos una colisión inelástica entre dos partículas: la energía de la velocidad como cuerpo rígido se transfiere a los grados de libertad internos microscópicos. Obtenemos " Disipación ": generación de calor irreversible. El resultado es que sin un impulso externo, eventualmente todas las partículas dejarán de moverse. En las partículas macroscópicas, las fluctuaciones térmicas son irrelevantes.

Cuando una materia es diluida y dinámica (impulsada) entonces se denomina gas granular y domina el fenómeno de disipación.

Cuando una materia es densa y estática entonces se denomina sólido granular y predomina el fenómeno de atasco.

Cuando la densidad es intermedia entonces se denomina líquido granular .

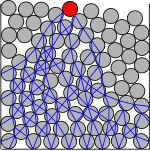
Coulomb consideró las fuerzas internas entre partículas granulares como un proceso de fricción y propuso la ley de fricción, según la cual la fuerza de fricción de las partículas sólidas es proporcional a la presión normal entre ellas y el coeficiente de fricción estática es mayor que el coeficiente de fricción cinética. Estudió el colapso de montones de arena y encontró empíricamente dos ángulos críticos: el ángulo estable máximo y el ángulo mínimo de reposo . Cuando la pendiente del montón de arena alcanza el ángulo estable máximo, las partículas de arena en la superficie del montón comienzan a caer. El proceso se detiene cuando el ángulo de inclinación de la superficie es igual al ángulo de reposo. La diferencia entre estos dos ángulos, , es el ángulo de Bagnold, que es una medida de la histéresis de los materiales granulares. Este fenómeno se debe a las cadenas de fuerza : la tensión en un sólido granular no se distribuye uniformemente, sino que se conduce a lo largo de las llamadas cadenas de fuerza , que son redes de granos que descansan unos sobre otros. Entre estas cadenas hay regiones de baja tensión cuyos granos están protegidos de los efectos de los granos superiores mediante bóvedas y arqueos . Cuando la tensión de corte alcanza un valor determinado, las cadenas de fuerza pueden romperse y las partículas que se encuentran en los extremos de las cadenas sobre la superficie comienzan a deslizarse. Luego, se forman nuevas cadenas de fuerza hasta que la tensión de corte es menor que el valor crítico y, de esta manera, la pila de arena mantiene un ángulo de reposo constante. ^[7]${\displaystyle \theta _{m}}$ ${\displaystyle \theta _{r}}$${\displaystyle \Delta \theta =\theta _{m}-\theta _{r}}$

En 1895, H. A. Janssen descubrió que en un cilindro vertical lleno de partículas, la presión medida en la base del cilindro no depende de la altura del relleno, a diferencia de los fluidos newtonianos en reposo que siguen la ley de Stevin . Janssen propuso un modelo simplificado con los siguientes supuestos:

1) La presión vertical, , es constante en el plano horizontal;${\displaystyle \sigma _{zz}}$

2) La presión horizontal, , es proporcional a la presión vertical , donde es constante en el espacio;${\displaystyle \sigma _{rr}}$${\displaystyle \sigma _{zz}}$${\displaystyle K={\frac {\sigma _{rr}}{\sigma _{zz}}}}$

3) El coeficiente estático de fricción de la pared sostiene la carga vertical en el contacto con la pared;${\displaystyle \mu ={\frac {\sigma _{rz}}{\sigma _{rr}}}}$

4) La densidad del material es constante en todas las profundidades.

La presión en el material granular se describe entonces en una ley diferente, que explica la saturación: donde y es el radio del cilindro, y en la parte superior del silo .$${\displaystyle p(z)=p_{\infty }[1-\exp(-z/\lambda )]}$$${\displaystyle \lambda ={\frac {R}{2\mu K}}}$${\displaystyle R}$${\displaystyle z=0}$

La ecuación de presión dada no tiene en cuenta las condiciones de contorno, como la relación entre el tamaño de las partículas y el radio del silo. Dado que no se puede medir la tensión interna del material, las especulaciones de Janssen no se han verificado mediante ningún experimento directo.

A principios de la década de 1960, Rowe estudió el efecto de la dilatación sobre la resistencia al corte en pruebas de corte y propuso una relación entre ellos.

Las propiedades mecánicas del ensamblaje de partículas monodispersas en 2D pueden analizarse en función del volumen elemental representativo , con longitudes típicas, , en direcciones vertical y horizontal respectivamente. Las características geométricas del sistema se describen mediante y la variable , que describe el ángulo cuando los puntos de contacto comienzan el proceso de deslizamiento. Denote por la dirección vertical, que es la dirección del esfuerzo principal mayor, y por la dirección horizontal, que es la dirección del esfuerzo principal menor.${\displaystyle \ell _{1},\ell _{2}}$${\displaystyle \alpha =\arctan({\frac {\ell _{1}}{\ell _{2}}})}$${\displaystyle \beta }$${\displaystyle \sigma _{11}}$${\displaystyle \sigma _{22}}$

Entonces, la tensión en el límite se puede expresar como la fuerza concentrada que soportan las partículas individuales. Bajo carga biaxial con tensión uniforme y, por lo tanto , .${\displaystyle \sigma _{12}=\sigma _{21}=0}$${\displaystyle F_{12}=F_{21}=0}$

En estado de equilibrio:

$${\displaystyle {\frac {F_{11}}{F_{22}}}={\frac {\sigma _{11}\ell _{2}}{\sigma _{22}\ell _{1}}}=\tan(\theta +\beta )}$$

donde , el ángulo de fricción, es el ángulo entre la fuerza de contacto y la dirección normal del contacto.${\displaystyle \theta }$

${\displaystyle \theta _{\mu }}$, que describe el ángulo en el que, si la fuerza tangencial cae dentro del cono de fricción, las partículas permanecerían estables. Está determinado por el coeficiente de fricción , por lo que . Una vez que se aplica tensión al sistema , aumenta gradualmente mientras que permanece sin cambios. Cuando entonces las partículas comenzarán a deslizarse, lo que provocará un cambio en la estructura del sistema y la creación de nuevas cadenas de fuerza. , los desplazamientos horizontal y vertical respectivamente satisfacen:${\displaystyle \mu =tg\phi _{u}}$${\displaystyle \theta \leq \theta _{\mu }}$${\displaystyle \theta }$${\displaystyle \alpha ,\beta }$${\displaystyle \theta \geq \theta _{\mu }}$${\displaystyle \Delta _{1},\Delta _{2}}$

$${\displaystyle {\frac {\dot {\Delta _{2}}}{\dot {\Delta _{1}}}}={\frac {{\dot {\varepsilon _{22}}}\ell _{2}}{{\dot {\varepsilon _{11}}}\ell _{1}}}=-\tan \beta }$$

Si el material granular se endurece de tal manera que los contactos entre los granos se vuelven muy poco frecuentes, el material entra en un estado gaseoso. En consecuencia, se puede definir una temperatura granular igual a la raíz cuadrada media de las fluctuaciones de la velocidad del grano que es análoga a la temperatura termodinámica . A diferencia de los gases convencionales, los materiales granulares tenderán a agruparse y aglutinarse debido a la naturaleza disipativa de las colisiones entre granos. Esta agrupación tiene algunas consecuencias interesantes. Por ejemplo, si una caja parcialmente particionada de materiales granulares se agita vigorosamente, con el tiempo los granos tenderán a acumularse en una de las particiones en lugar de distribuirse uniformemente en ambas particiones como sucedería en un gas convencional. Este efecto, conocido como el demonio de Maxwell granular , no viola ningún principio de la termodinámica ya que se pierde energía constantemente del sistema en el proceso.

Consideremos partículas, partícula que tiene energía . A una tasa constante por unidad de tiempo, elija aleatoriamente dos partículas con energías y calcule la suma . Ahora, distribuya aleatoriamente la energía total entre las dos partículas: elija aleatoriamente de modo que la primera partícula, después de la colisión, tenga energía , y la segunda .${\displaystyle N}$${\displaystyle i}$${\displaystyle \varepsilon _{i}}$${\displaystyle i,j}$${\displaystyle \varepsilon _{i},\varepsilon _{j}}$${\displaystyle \varepsilon _{i}+\varepsilon _{j}}$${\displaystyle z\in \left[0,1\right]}$${\displaystyle z\left(\varepsilon _{i}+\varepsilon _{j}\right)}$${\displaystyle \left(1-z\right)\left(\varepsilon _{i}+\varepsilon _{j}\right)}$

La ecuación de evolución estocástica : donde es la tasa de colisión, se elige aleatoriamente de (distribución uniforme) y j es un índice también elegido aleatoriamente de una distribución uniforme. La energía promedio por partícula:$${\displaystyle \varepsilon _{i}(t+dt)={\begin{cases}\varepsilon _{i}(t)&probability:\,1-\Gamma dt\\z\left(\varepsilon _{i}(t)+\varepsilon _{j}(t)\right)&probability:\,\Gamma dt\end{cases}}}$$${\displaystyle \Gamma }$${\displaystyle z}$${\displaystyle \left[0,1\right]}$$${\displaystyle {\begin{aligned}\left\langle \varepsilon (t+dt)\right\rangle &=\left(1-\Gamma dt\right)\left\langle \varepsilon (t)\right\rangle +\Gamma dt\cdot \left\langle z\right\rangle \left(\left\langle \varepsilon _{i}\right\rangle +\left\langle \varepsilon _{j}\right\rangle \right)\\&=\left(1-\Gamma dt\right)\left\langle \varepsilon (t)\right\rangle +\Gamma dt\cdot {\dfrac {1}{2}}\left(\left\langle \varepsilon (t)\right\rangle +\left\langle \varepsilon (t)\right\rangle \right)\\&=\left\langle \varepsilon (t)\right\rangle \end{aligned}}}$$

El segundo momento:

${\displaystyle {\begin{aligned}\left\langle \varepsilon ^{2}(t+dt)\right\rangle &=\left(1-\Gamma dt\right)\left\langle \varepsilon ^{2}(t)\right\rangle +\Gamma dt\cdot \left\langle z^{2}\right\rangle \left\langle \varepsilon _{i}^{2}+2\varepsilon _{i}\varepsilon _{j}+\varepsilon _{j}^{2}\right\rangle \\&=\left(1-\Gamma dt\right)\left\langle \varepsilon ^{2}(t)\right\rangle +\Gamma dt\cdot {\dfrac {1}{3}}\left(2\left\langle \varepsilon ^{2}(t)\right\rangle +2\left\langle \varepsilon (t)\right\rangle ^{2}\right)\end{aligned}}}$

Ahora la derivada temporal del segundo momento:

${\displaystyle {\dfrac {d\left\langle \varepsilon ^{2}\right\rangle }{dt}}=lim_{dt\rightarrow 0}{\dfrac {\left\langle \varepsilon ^{2}(t+dt)\right\rangle -\left\langle \varepsilon ^{2}(t)\right\rangle }{dt}}=-{\dfrac {\Gamma }{3}}\left\langle \varepsilon ^{2}\right\rangle +{\dfrac {2\Gamma }{3}}\left\langle \varepsilon \right\rangle ^{2}}$

En estado estacionario:

${\displaystyle {\dfrac {d\left\langle \varepsilon ^{2}\right\rangle }{dt}}=0\Rightarrow \left\langle \varepsilon ^{2}\right\rangle =2\left\langle \varepsilon \right\rangle ^{2}}$

Resolviendo la ecuación diferencial para el segundo momento:

${\displaystyle \left\langle \varepsilon ^{2}\right\rangle -2\left\langle \varepsilon \right\rangle ^{2}=\left(\left\langle \varepsilon ^{2}(0)\right\rangle -2\left\langle \varepsilon (0)\right\rangle ^{2}\right)e^{-{\frac {\Gamma }{3}}t}}$

Sin embargo, en lugar de caracterizar los momentos, podemos resolver analíticamente la distribución de energía, a partir de la función generadora de momentos. Consideremos la transformada de Laplace : .${\displaystyle g(\lambda )=\left\langle e^{-\lambda \varepsilon }\right\rangle =\int _{0}^{\infty }e^{-\lambda \varepsilon }\rho (\varepsilon )d\varepsilon }$

Dónde , y${\displaystyle g(0)=1}$${\displaystyle {\dfrac {dg}{d\lambda }}=-\int _{0}^{\infty }\varepsilon e^{-\lambda \varepsilon }\rho (\varepsilon )d\varepsilon =-\left\langle \varepsilon \right\rangle }$

La derivada n:

${\displaystyle {\dfrac {d^{n}g}{d\lambda ^{n}}}=\left(-1\right)^{n}\int _{0}^{\infty }\varepsilon ^{n}e^{-\lambda \varepsilon }\rho (\varepsilon )d\varepsilon =\left\langle \varepsilon ^{n}\right\rangle }$

ahora:

${\displaystyle e^{-\lambda \varepsilon _{i}(t+dt)}={\begin{cases}e^{-\lambda \varepsilon _{i}(t)}&1-\Gamma t\\e^{-\lambda z\left(\varepsilon _{i}(t)+\varepsilon _{j}(t)\right)}&\Gamma t\end{cases}}}$

${\displaystyle \left\langle e^{-\lambda \varepsilon \left(t+dt\right)}\right\rangle =\left(1-\Gamma dt\right)\left\langle e^{-\lambda \varepsilon _{i}(t)}\right\rangle +\Gamma dt\left\langle e^{-\lambda z\left(\varepsilon _{i}(t)+\varepsilon _{j}(t)\right)}\right\rangle }$

${\displaystyle g\left(\lambda ,t+dt\right)=\left(1-\Gamma dt\right)g\left(\lambda ,t\right)+\Gamma dt\int _{0}^{1}{\underset {=g^{2}(\lambda z,t)}{\underbrace {\left\langle e^{-\lambda z\varepsilon _{i}(t)}\right\rangle \left\langle e^{-\lambda z\varepsilon _{j}(t)}\right\rangle } }}dz}$

Resolviendo con cambio de variables :${\displaystyle g(\lambda )}$${\displaystyle \delta =\lambda z}$

${\displaystyle \lambda g(\lambda )=\int _{0}^{\lambda }g^{2}(\delta )d\delta \Rightarrow \lambda g'(\lambda )+g(\lambda )=g^{2}(\lambda )\Rightarrow g(\lambda )={\dfrac {1}{\lambda T+1}}}$

Demostraremos que ( Distribución de Boltzmann ) tomamos su transformada de Laplace y calculamos la función generadora:${\displaystyle \rho (\varepsilon )={\dfrac {1}{T}}e^{-{\frac {\varepsilon }{T}}}}$

${\displaystyle \int _{0}^{\infty }{\dfrac {1}{T}}e^{-{\frac {\varepsilon }{T}}}\cdot e^{-\lambda \varepsilon }d\varepsilon ={\dfrac {1}{T}}\int _{0}^{\infty }e^{-\left(\lambda +{\frac {1}{T}}\right)\varepsilon }d\varepsilon =-{\dfrac {1}{T\left(\lambda +{\frac {1}{T}}\right)}}e^{-\left(\lambda +{\frac {1}{T}}\right)\varepsilon }|_{0}^{\infty }={\dfrac {1}{\lambda T+1}}=g(\lambda )}$

Se sabe que los sistemas granulares presentan atascos y experimentan una transición de atasco que se considera una transición de fase termodinámica a un estado atascado. ^[8] La transición es de una fase similar a un fluido a una fase similar a un sólido y está controlada por la temperatura, , la fracción de volumen , y la tensión de corte, . El diagrama de fase normal de la transición vítrea está en el plano y se divide en una región de estado atascado y un estado líquido no atascado por una línea de transición. El diagrama de fase para la materia granular se encuentra en el plano, y la curva de tensión crítica divide la fase de estado en la región atascada\no atascada, que corresponde a los sólidos\líquidos granulares respectivamente. Para el sistema granular isótropo atascado, cuando se reduce alrededor de un cierto punto, , los módulos de volumen y de corte se acercan a 0. El punto corresponde a la fracción de volumen crítica . Defina la distancia al punto , la fracción de volumen crítica, . Se encontró empíricamente que el comportamiento de los sistemas granulares cerca del punto se asemeja a una transición de segundo orden : el módulo volumétrico muestra una escala de ley de potencia con y hay algunas longitudes características divergentes cuando se acerca a cero. ^[7] Si bien es constante para un sistema infinito, para un sistema finito los efectos de contorno dan como resultado una distribución de en algún rango.${\displaystyle T}$${\displaystyle \phi }$${\displaystyle \Sigma }$${\displaystyle \phi ^{-1}-T}$${\displaystyle \phi ^{-1}-\Sigma }$${\displaystyle \Sigma (\phi )}$${\displaystyle \phi }$${\displaystyle J}$${\displaystyle J}$${\displaystyle \phi _{c}}$${\displaystyle J}$${\displaystyle \Delta \phi \equiv \phi -\phi _{c}}$${\displaystyle J}$${\displaystyle \Delta \phi }$${\displaystyle \Delta \phi }$${\displaystyle \phi _{c}}$${\displaystyle \phi _{c}}$

El algoritmo de interferencia de Lubachevsky-Stillinger permite producir configuraciones granulares bloqueadas simuladas. ^[9]

La materia granular excitada es un sistema rico en formación de patrones. Algunos de los comportamientos de formación de patrones observados en materiales granulares son:

• La separación o segregación de granos diferentes bajo vibración y flujo. Un ejemplo de esto es el llamado efecto de la nuez de Brasil ^[10], donde las nueces de Brasil suben a la parte superior de un paquete de nueces mixtas cuando se agitan. La causa de este efecto es que, cuando se agitan, los materiales granulares (y algunos otros) se mueven en un patrón circular. Algunos materiales más grandes (nueces de Brasil) se atascan mientras bajan por el círculo y, por lo tanto, permanecen en la parte superior.
• La formación de patrones superficiales o volumétricos estructurados en capas granulares vibradas. ^[11] Estos patrones incluyen, entre otros, rayas, cuadrados y hexágonos. Se cree que estos patrones se forman por excitaciones fundamentales de la superficie conocidas como oscilos . La formación de estructuras volumétricas ordenadas en materiales granulares se conoce como cristalización granular e implica una transición de un empaquetamiento aleatorio de partículas a un empaquetamiento ordenado, como un empaquetamiento compacto hexagonal o cúbico centrado en el cuerpo. Esto se observa más comúnmente en materiales granulares con distribuciones de tamaño estrechas y morfología de grano uniforme. ^[11]
• La formación de ondulaciones de arena , dunas y láminas de arena.

Se ha podido reproducir algunos de los comportamientos de formación de patrones en simulaciones por computadora. ^{[12] [13]} Hay dos enfoques computacionales principales para tales simulaciones, la basada en pasos de tiempo y la basada en eventos , siendo la primera la más eficiente para una mayor densidad del material y los movimientos de una menor intensidad, y la segunda para una menor densidad del material y los movimientos de una mayor intensidad.

Algunas arenas de playa, como las de la playa Squeaky Beach , que tiene el nombre apropiado de playa , emiten chirridos cuando se camina sobre ellas. Se sabe que algunas dunas del desierto emiten ruidos durante avalanchas o cuando su superficie se altera de alguna otra manera. Los materiales granulados que se descargan de los silos producen emisiones acústicas fuertes en un proceso conocido como bocinazo de los silos.

La granulación es el acto o proceso mediante el cual las partículas de polvo primarias se adhieren para formar entidades multipartículas más grandes llamadas gránulos.

Cuando el agua u otros líquidos se enfrían con la suficiente lentitud, las moléculas ubicadas aleatoriamente se reorganizan y los cristales sólidos emergen y crecen. Un proceso de cristalización similar puede ocurrir en materiales granulares empaquetados aleatoriamente. A diferencia de la eliminación de energía mediante enfriamiento, la cristalización en material granular se logra mediante un impulso externo. Se ha observado que el ordenamiento o cristalización de materiales granulares ocurre en materia granular periódicamente cizallada y vibrada. ^[11] A diferencia de los sistemas moleculares, las posiciones de las partículas individuales se pueden rastrear en el experimento. ^[14] Las simulaciones por computadora para un sistema de granos esféricos revelan que la cristalización homogénea emerge en una fracción de volumen . ^[15] Las simulaciones por computadora identifican los ingredientes mínimos necesarios para la cristalización granular. En particular, la gravedad y la fricción no son necesarias.${\displaystyle \phi =0.646\pm 0.001}$

Existen varios métodos disponibles para modelar materiales granulares . La mayoría de estos métodos consisten en métodos estadísticos mediante los cuales se extraen y utilizan varias propiedades estadísticas, derivadas de datos puntuales o de una imagen, para generar modelos estocásticos del medio granular. Una revisión reciente y completa de dichos métodos está disponible en Tahmasebi y otros (2017). ^[16] Otra alternativa para construir un paquete de partículas granulares que se ha presentado recientemente se basa en el algoritmo de conjunto de niveles mediante el cual se puede capturar y reproducir la forma real de la partícula a través de las estadísticas extraídas para la morfología de las partículas. ^[17]

• Agregado (compuesto)
• Materia frágil
• Paquete cerrado aleatorio
• Licuefacción del suelo
• Polvo de metal
• Partículas
• Pasta (reología)
• Reología μ(I) : un modelo de la reología de un flujo granular.
• Dilatancia (material granular)

• Fundamentos de la tecnología de partículas – libro gratuito
• Lu, Kevin; et al. (noviembre de 2007). "Debilitamiento por cizallamiento del régimen de transición para flujo granular". J. Fluid Mech. 587 : 347–372. Bibcode :2007JFM...587..347L. doi :10.1017/S0022112007007331. S2CID  30744277.
• Mester, L., La nueva teoría físico-mecánica de los materiales granulares. 2009, Homonnai, ISBN 978-963-8343-87-1 
• Pareschi, L., Russo, G., Toscani, G., Modelado y numérica de sistemas disipativos cinéticos, Nova Science Publishers, Nueva York, 2006.