Grados de libertad (física y química)
Este artículo necesita citas adicionales para su verificación . ( noviembre de 2009 ) |
En física y química , un grado de libertad es un parámetro físico independiente en la parametrización elegida de un sistema físico . Más formalmente, dada una parametrización de un sistema físico, el número de grados de libertad es el número más pequeño de parámetros cuyos valores deben conocerse para que siempre sea posible determinar los valores de todos los parámetros en la parametrización elegida. En este caso, cualquier conjunto de tales parámetros se denomina grados de libertad .
La ubicación de una partícula en el espacio tridimensional requiere tres coordenadas de posición . De manera similar, la dirección y la velocidad a la que se mueve una partícula se pueden describir en términos de tres componentes de velocidad, cada uno en referencia a las tres dimensiones del espacio. Entonces, si la evolución temporal del sistema es determinista (donde el estado en un instante determina de manera única su posición y velocidad pasadas y futuras en función del tiempo), dicho sistema tiene seis grados de libertad. [ cita requerida ] Si el movimiento de la partícula está restringido a un número menor de dimensiones (por ejemplo, la partícula debe moverse a lo largo de un cable o sobre una superficie fija), entonces el sistema tiene menos de seis grados de libertad. Por otro lado, un sistema con un objeto extendido que puede rotar o vibrar puede tener más de seis grados de libertad.
En la mecánica clásica , el estado de una partícula puntual en un momento dado se describe a menudo con coordenadas de posición y velocidad en el formalismo lagrangiano , o con coordenadas de posición y momento en el formalismo hamiltoniano .
En mecánica estadística , un grado de libertad es un número escalar único que describe el microestado de un sistema. [1] La especificación de todos los microestados de un sistema es un punto en el espacio de fases del sistema .
En el modelo de cadena ideal 3D en química, son necesarios dos ángulos para describir la orientación de cada monómero.
A menudo resulta útil especificar grados de libertad cuadráticos, que son los grados de libertad que contribuyen en una función cuadrática a la energía del sistema.
Dependiendo de lo que se esté contando, hay varias formas diferentes de definir los grados de libertad, cada una con un valor diferente. [2]
Grados de libertad termodinámicos de los gases
| Imágenes externas | |
|---|---|
 https://chem.libretexts.org/@api/deki/files/9669/h2ovibrations.gif?revision=1 https://chem.libretexts.org/@api/deki/files/9669/h2ovibrations.gif?revision=1 | |
 https://chem.libretexts.org/@api/deki/files/9668/co2vibrations.gif?revision=1 https://chem.libretexts.org/@api/deki/files/9668/co2vibrations.gif?revision=1 |
Según el teorema de equipartición , la energía interna por mol de gas es igual a c v T , donde T es la temperatura absoluta y el calor específico a volumen constante es c v = (f)(R/2). R = 8,314 J/(K mol) es la constante universal de los gases y "f" es el número de grados de libertad termodinámicos (cuadráticos), que cuentan la cantidad de formas en las que puede existir energía.
Cualquier átomo o molécula tiene tres grados de libertad asociados al movimiento de traslación (energía cinética) del centro de masas con respecto a los ejes x, y y z. Estos son los únicos grados de libertad para una especie monoatómica, como los átomos de los gases nobles .
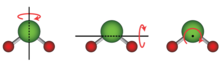
En el caso de una estructura formada por dos o más átomos, toda la estructura también tiene energía cinética rotacional, donde toda la estructura gira alrededor de un eje. Una molécula lineal , donde todos los átomos se encuentran a lo largo de un solo eje, como cualquier molécula diatómica y algunas otras moléculas como el dióxido de carbono (CO 2 ), tiene dos grados de libertad rotacional, porque puede girar alrededor de cualquiera de los dos ejes perpendiculares al eje molecular. Una molécula no lineal, donde los átomos no se encuentran a lo largo de un solo eje, como el agua (H 2 O), tiene tres grados de libertad rotacional, porque puede girar alrededor de cualquiera de los tres ejes perpendiculares. En casos especiales, como las moléculas grandes adsorbidas, los grados de libertad rotacional pueden limitarse a solo uno. [3]
Una estructura que consta de dos o más átomos también tiene energía vibracional, donde los átomos individuales se mueven uno con respecto al otro. Una molécula diatómica tiene un modo de vibración molecular : los dos átomos oscilan de un lado a otro con el enlace químico entre ellos actuando como un resorte. Una molécula con N átomos tiene modos más complicados de vibración molecular , con 3 N − 5 modos vibracionales para una molécula lineal y 3 N − 6 modos para una molécula no lineal. [4] Como ejemplos específicos, la molécula lineal de CO 2 tiene 4 modos de oscilación, [5] y la molécula de agua no lineal tiene 3 modos de oscilación [6] Cada modo vibracional tiene dos términos de energía: la energía cinética de los átomos en movimiento y la energía potencial del enlace químico tipo resorte. Por lo tanto, el número de términos de energía vibracional es 2(3 N − 5) modos para una molécula lineal y es 2(3 N − 6) modos para una molécula no lineal.
Tanto el modo rotacional como el vibracional están cuantificados, lo que requiere una temperatura mínima para activarse. [7] La " temperatura rotacional " para activar los grados de libertad rotacionales es menor de 100 K para muchos gases. Para N 2 y O 2 , es menor de 3 K. [1] La " temperatura vibracional " necesaria para una vibración sustancial está entre 10 3 K y 10 4 K, 3521 K para N 2 y 2156 K para O 2 . [1] Las temperaturas atmosféricas típicas no son lo suficientemente altas para activar la vibración en N 2 y O 2 , que comprenden la mayor parte de la atmósfera. (Véase la siguiente figura.) Sin embargo, los gases de efecto invernadero mucho menos abundantes mantienen la troposfera caliente mediante la absorción de infrarrojos de la superficie de la Tierra, lo que excita sus modos vibracionales. [8] Gran parte de esta energía se reirradia de nuevo a la superficie en el infrarrojo a través del " efecto invernadero ".
Como la temperatura ambiente (≈298 K) es superior a la temperatura rotacional típica pero inferior a la temperatura vibracional típica, solo los grados de libertad traslacional y rotacional contribuyen, en cantidades iguales, a la relación de capacidad térmica . Por eso γ ≈ 5/3 para gases monoatómicos y γ ≈ 7/5 paragases diatómicos a temperatura ambiente. [1]

Como el aire está dominado por gases diatómicos (el nitrógeno y el oxígeno contribuyen en un 99 %), su energía interna molar es cercana a c v T = (5/2) R T , determinada por los 5 grados de libertad que exhiben los gases diatómicos. [ cita requerida ] [11] [ referencia circular ] Vea el gráfico a la derecha. Para 140 K < T < 380 K, c v difiere de (5/2) R d en menos del 1 %. Solo a temperaturas muy superiores a las de la troposfera y la estratosfera algunas moléculas tienen suficiente energía para activar los modos vibracionales de N 2 y O 2 . El calor específico a volumen constante, c v , aumenta lentamente hacia (7/2) R a medida que la temperatura aumenta por encima de T = 400 K, donde c v es 1,3 % superior a (5/2) R d = 717,5 J/(K kg).
| Monatomic | Moléculas lineales | Moléculas no lineales | |
|---|---|---|---|
| Traducción ( x , y , z ) | 3 | 3 | 3 |
| Rotación ( x , y , z ) | 0 | 2 | 3 |
| Vibración (alta temperatura) | 0 | 2 (3 N − 5) | 2 (3 N - 6) |
Contar el número mínimo de coordenadas para especificar una posición
También se pueden contar los grados de libertad utilizando el número mínimo de coordenadas necesarias para especificar una posición. Esto se hace de la siguiente manera:
- Para una partícula individual necesitamos 2 coordenadas en un plano 2D para especificar su posición y 3 coordenadas en un espacio 3D. Por lo tanto, su grado de libertad en un espacio 3D es 3.
- Para un cuerpo que consta de 2 partículas (por ejemplo, una molécula diatómica) en un espacio tridimensional con distancia constante entre ellas (digamos d), podemos demostrar (a continuación) que sus grados de libertad son 5.
Digamos que una partícula en este cuerpo tiene coordenadas ( x 1 , y 1 , z 1 ) y la otra tiene coordenadas ( x 2 , y 2 , z 2 ) con z 2 desconocida. Aplicación de la fórmula para la distancia entre dos coordenadas
da como resultado una ecuación con una incógnita, en la que podemos resolver z 2 . Una de x 1 , x 2 , y 1 , y 2 , z 1 o z 2 puede ser una incógnita.
Contrariamente al teorema de equipartición clásico , a temperatura ambiente, el movimiento vibracional de las moléculas normalmente hace contribuciones insignificantes a la capacidad térmica . Esto se debe a que estos grados de libertad están congelados porque el espaciamiento entre los valores propios de energía excede la energía correspondiente a las temperaturas ambiente ( k B T ). [1]
Grados de libertad independientes
El conjunto de grados de libertad X 1 , ... , X N de un sistema es independiente si la energía asociada al conjunto se puede escribir en la siguiente forma:
donde E i es una función de la única variable X i .
Ejemplo: si X 1 y X 2 son dos grados de libertad y E es la energía asociada:
- Si , entonces los dos grados de libertad son independientes.
- Si , entonces los dos grados de libertad no son independientes. El término que implica el producto de X 1 y X 2 es un término de acoplamiento que describe una interacción entre los dos grados de libertad.
Para i de 1 a N , el valor del i- ésimo grado de libertad Xi se distribuye según la distribución de Boltzmann . Su función de densidad de probabilidad es la siguiente :
- ,
En esta sección y a lo largo del artículo los paréntesis indican la media de la cantidad que encierran.
La energía interna del sistema es la suma de las energías promedio asociadas a cada uno de los grados de libertad:
Grados de libertad cuadráticos
Un grado de libertad Xi es cuadrático si los términos de energía asociados con este grado de libertad se pueden escribir como
- ,
donde Y es una combinación lineal de otros grados de libertad cuadráticos.
Ejemplo: si X 1 y X 2 son dos grados de libertad y E es la energía asociada:
- Si , entonces los dos grados de libertad no son independientes ni cuadráticos.
- Si , entonces los dos grados de libertad son independientes y no cuadráticos.
- Si , entonces los dos grados de libertad no son independientes sino cuadráticos.
- Si , entonces los dos grados de libertad son independientes y cuadráticos.
Por ejemplo, en la mecánica newtoniana , la dinámica de un sistema de grados de libertad cuadráticos está controlada por un conjunto de ecuaciones diferenciales lineales homogéneas con coeficientes constantes .
Grado de libertad cuadrático e independiente
X 1 , ... , X N son grados de libertad cuadráticos e independientes si la energía asociada a un microestado del sistema que representan se puede escribir como:
Teorema de equipartición
En el límite clásico de la mecánica estadística , en equilibrio termodinámico , la energía interna de un sistema de N grados de libertad cuadráticos e independientes es:
Aquí, la energía media asociada con un grado de libertad es:
Como los grados de libertad son independientes, la energía interna del sistema es igual a la suma de la energía media asociada a cada grado de libertad, lo que demuestra el resultado.
Generalizaciones
La descripción del estado de un sistema como un punto en su espacio de fases, aunque matemáticamente conveniente, se considera fundamentalmente inexacta. En mecánica cuántica , los grados de libertad del movimiento se sustituyen por el concepto de función de onda , y los operadores que corresponden a otros grados de libertad tienen espectros discretos . Por ejemplo, el operador de momento angular intrínseco (que corresponde a la libertad rotacional) para un electrón o un fotón tiene solo dos valores propios . Esta discreción se hace evidente cuando la acción tiene un orden de magnitud de la constante de Planck , y se pueden distinguir grados de libertad individuales.
Referencias
- ^ abcde Reif, F. (2009). Fundamentos de física estadística y térmica . Long Grove, IL: Waveland Press, Inc. pág. 51. ISBN 978-1-57766-612-7.
- ^ "Química física: ¿Un gas diatómico tiene uno o dos grados de libertad vibracional?".
- ^ Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Estabilización de adsorbatos grandes mediante entropía rotacional: un estudio STM de temperatura variable con resolución temporal". ChemPhysChem . 14 (1): 162–9. doi :10.1002/cphc.201200531. PMID 23047526. S2CID 36848079.
- ^ Vibración molecular [ fuente generada por el usuario ]
- ^ Para ver los dibujos, consulte http://www.colby.edu/chemistry/PChem/notes/NormalModesText.pdf
- ^ Para ver los dibujos, consulte https://sites.cns.utexas.edu/jones_ch431/normal-modes-vibration
- ^ Sección 12-7 (págs. 376-379) de Sears y Salinger, 1975: Termodinámica, teoría cinética y termodinámica estadística. Tercera edición. Addison-Wesley Publishing Co.
- ^ "Las moléculas vibran". Centro de Educación Científica de la UCAR . Archivado desde el original el 10 de octubre de 2014. Consultado el 19 de enero de 2021 .
- ^ "Aire - Calor específico vs. Temperatura a presión constante".
- ^ Gatley, DP, S. Herrmann, H.-J. Kretzshmar, 2008: Una masa molar del siglo XXI para aire seco. HVAC&R Research, vol. 14, págs. 655-662.
- ^ Teorema de equipartición#Gases diatómicos
















