Capacidad

Símbolos comunes	do
Unidad SI	faradio
Otras unidades	μF, nF, pF
En unidades base del SI	F = A 2 s 4 kg −1 m −2
Derivaciones de otras magnitudes	C = carga / voltaje
Dimensión	${\displaystyle {\mathsf {L}}^{-2}{\mathsf {M}}^{-1}{\mathsf {T}}^{4}{\mathsf {I}}^{2}}$

Artículos sobre
Electromagnetismo
Electricidad Magnetismo Óptica Historia Computacional Libros de texto Fenómenos
Electrostática Densidad de carga Conductor Ley de Coulomb Electreto Carga eléctrica Dipolo eléctrico Campo eléctrico Flujo eléctrico Potencial eléctrico Descarga electrostática Inducción electrostática Ley de Gauss Insulator Permittivity Polarization Potential energy Static electricity Triboelectricity
Magnetostatics Ampère law Biot–Savart law Gauss magnetic law Magnetic dipole Magnetic field Magnetic flux Magnetic scalar potential Magnetic vector potential Magnetization Permeability Right-hand rule
Electrodynamics Bremsstrahlung Cyclotron radiation Displacement current Eddy current Electromagnetic field Electromagnetic induction Electromagnetic pulse Electromagnetic radiation Faraday law Jefimenko equations Larmor formula Lenz law Liénard–Wiechert potential London equations Lorentz force Maxwell equations Maxwell tensor Poynting vector Synchrotron radiation
Electrical network Alternating current Capacitance Current density Direct current Electric current Electric power Electrolysis Electromotive force Impedance Inductance Joule heating Kirchhoff laws Network analysis Ohm law Parallel circuit Resistance Resonant cavities Series circuit Voltage Watt Waveguides
Magnetic circuit AC motor DC motor Electric machine Electric motor Gyrator–capacitor Induction motor Linear motor Magnetomotive force Permeance Reluctance (complex) Reluctance (real) Rotor Stator Transformer
Covariant formulation Electromagnetic tensor Electromagnetism and special relativity Four-current Four-potential Mathematical descriptions Maxwell equations in curved spacetime Relativistic electromagnetism Stress–energy tensor
Scientists Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Helmholtz Henry Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Poisson Poynting Ritchie Savart Singer Steinmetz Tesla Thomson Volta Weber Wiechert
v t e

La capacitancia es la capacidad de un objeto o dispositivo material para almacenar carga eléctrica . Se mide por la carga en respuesta a una diferencia en el potencial eléctrico , expresada como la relación de esas cantidades. Comúnmente se reconocen dos nociones estrechamente relacionadas de capacitancia: autocapacitancia y capacitancia mutua . ^{[1] : 237–238} Un objeto que puede cargarse eléctricamente exhibe autocapacitancia, para la cual se mide el potencial eléctrico entre el objeto y tierra. La capacitancia mutua se mide entre dos componentes y es particularmente importante en el funcionamiento del capacitor , un componente electrónico lineal elemental diseñado para agregar capacitancia a un circuito eléctrico .

La capacitancia entre dos conductores depende únicamente de la geometría, de la superficie opuesta de los conductores y de la distancia entre ellos, y de la permitividad de cualquier material dieléctrico que haya entre ellos. En el caso de muchos materiales dieléctricos, la permitividad y, por lo tanto, la capacitancia, son independientes de la diferencia de potencial entre los conductores y de la carga total que soportan.

La unidad SI de capacitancia es el faradio (símbolo: F), llamado así en honor al físico inglés Michael Faraday . ^[2] Un capacitor de 1 faradio, cuando se carga con 1 culombio de carga eléctrica, tiene una diferencia de potencial de 1 voltio entre sus placas. ^[3] El recíproco de la capacitancia se llama elastancia .

Al hablar de circuitos eléctricos, el término capacitancia suele ser una forma abreviada de referirse a la capacitancia mutua entre dos conductores adyacentes, como las dos placas de un condensador. Sin embargo, cada conductor aislado también presenta capacitancia, aquí denominada autocapacitancia . Se mide por la cantidad de carga eléctrica que debe añadirse a un conductor aislado para aumentar su potencial eléctrico en una unidad de medida, por ejemplo, un voltio . ^[4] El punto de referencia para este potencial es una esfera conductora hueca teórica, de radio infinito, con el conductor centrado dentro de esta esfera.

La autocapacidad de un conductor se define por la relación entre la carga y el potencial eléctrico: donde$${\displaystyle C={\frac {q}{V}},}$$

• ${\textstyle q}$¿Se mantiene la carga?
• ${\textstyle V={\frac {1}{4\pi \varepsilon _{0}}}\int {\frac {\sigma }{r}}\,dS}$es el potencial eléctrico,
• ${\textstyle \sigma }$es la densidad de carga superficial,
• ${\textstyle dS}$es un elemento infinitesimal de área en la superficie del conductor, sobre el cual se integra la densidad de carga superficial,
• ${\textstyle r}$es la longitud desde un punto fijo M en el conductor,${\textstyle dS}$
• ${\displaystyle \varepsilon _{0}}$es la permitividad del vacío .

Utilizando este método, la autocapacidad de una esfera conductora de radio en el espacio libre (es decir, lejos de cualquier otra distribución de carga) es: ^[2]${\textstyle R}$$${\displaystyle C=4\pi \varepsilon _{0}R.}$$

Los valores de ejemplo de autocapacidad son:

• para la "placa" superior de un generador de van de Graaff , típicamente una esfera de 20 cm de radio: 22,24 pF,
• el planeta Tierra : alrededor de 710 μF. ^[5]

La capacitancia entre espiras de una bobina se denomina a veces capacitancia propia ^[6] , pero se trata de un fenómeno diferente. En realidad, se trata de una capacitancia mutua entre las espiras individuales de la bobina y es una forma de capacitancia parásita o parásita . Esta capacitancia propia es un factor importante a tener en cuenta en frecuencias altas: cambia la impedancia de la bobina y da lugar a una resonancia paralela . En muchas aplicaciones, este es un efecto indeseable y establece un límite de frecuencia superior para el funcionamiento correcto del circuito. ^{[ cita requerida ]}

Una forma común es el condensador de placas paralelas , que consta de dos placas conductoras aisladas entre sí, generalmente envueltas en un material dieléctrico . En un condensador de placas paralelas, la capacitancia es casi proporcional al área de superficie de las placas conductoras e inversamente proporcional a la distancia de separación entre las placas.

Si las cargas en las placas son y , y da el voltaje entre las placas, entonces la capacitancia está dada por que da la relación voltaje/ corriente donde es la tasa instantánea de cambio de voltaje, y es la tasa instantánea de cambio de la capacitancia. Para la mayoría de las aplicaciones, el cambio en la capacitancia a lo largo del tiempo es insignificante, por lo que la fórmula se reduce a:${\textstyle +q}$${\textstyle -q}$${\textstyle V}$${\textstyle C}$$${\displaystyle C={\frac {q}{V}},}$$$${\displaystyle i(t)=C{\frac {dv(t)}{dt}}+V{\frac {dC}{dt}},}$$${\textstyle {\frac {dv(t)}{dt}}}$${\textstyle {\frac {dC}{dt}}}$$${\displaystyle i(t)=C{\frac {dv(t)}{dt}},}$$

La energía almacenada en un condensador se obtiene integrando el trabajo :${\textstyle W}$$${\displaystyle W_{\text{charging}}={\frac {1}{2}}CV^{2}.}$$

La discusión anterior se limita al caso de dos placas conductoras, aunque de tamaño y forma arbitrarios. La definición no se aplica cuando hay más de dos placas cargadas, o cuando la carga neta en las dos placas no es cero. Para manejar este caso, James Clerk Maxwell introdujo sus coeficientes de potencial . Si a tres conductores (casi ideales) se les dan cargas , entonces el voltaje en el conductor 1 está dado por y de manera similar para los otros voltajes. Hermann von Helmholtz y Sir William Thomson demostraron que los coeficientes de potencial son simétricos, de modo que , etc. Por lo tanto, el sistema puede describirse mediante una colección de coeficientes conocidos como la matriz de elastancia o matriz de capacitancia recíproca , que se define como:${\displaystyle C=Q/V}$${\displaystyle Q_{1},Q_{2},Q_{3}}$$${\displaystyle V_{1}=P_{11}Q_{1}+P_{12}Q_{2}+P_{13}Q_{3},}$$${\displaystyle P_{12}=P_{21}}$$${\displaystyle P_{ij}={\frac {\partial V_{i}}{\partial Q_{j}}}.}$$

A partir de esto, la capacitancia mutua entre dos objetos se puede definir ^[7] resolviendo la carga total y utilizando .${\displaystyle C_{m}}$${\textstyle Q}$${\displaystyle C_{m}=Q/V}$

$${\displaystyle C_{m}={\frac {1}{(P_{11}+P_{22})-(P_{12}+P_{21})}}.}$$

Dado que ningún dispositivo real tiene cargas perfectamente iguales y opuestas en cada una de las dos "placas", es la capacitancia mutua la que se informa en los capacitores.

El conjunto de coeficientes se conoce como matriz de capacitancia , ^{[8] [9] [10]} y es la inversa de la matriz de elastancia.${\displaystyle C_{ij}={\frac {\partial Q_{i}}{\partial V_{j}}}}$

La capacidad de la mayoría de los condensadores utilizados en circuitos electrónicos es generalmente varios órdenes de magnitud menor que el faradio . Las unidades de capacidad más comunes son el microfaradio (μF), el nanofaradio (nF), el picofaradio (pF) y, en microcircuitos, el femtofaradio (fF). Algunas aplicaciones también utilizan supercondensadores que pueden ser mucho más grandes, hasta cientos de faradios, y los elementos capacitivos parásitos pueden ser menores que un femtofaradio. Los textos históricos utilizan otros submúltiplos obsoletos del faradio, como "mf" y "mfd" para el microfaradio (μF); "mmf", "mmfd", "pfd", "μμF" para el picofaradio (pF). ^{[11] [12]}

La capacitancia se puede calcular si se conocen la geometría de los conductores y las propiedades dieléctricas del aislante entre los conductores. La capacitancia es proporcional al área de superposición e inversamente proporcional a la separación entre las láminas conductoras. Cuanto más próximas estén las láminas entre sí, mayor será la capacitancia.

Un ejemplo es la capacitancia de un capacitor construido con dos placas paralelas, ambas de área separadas por una distancia . Si es suficientemente pequeña con respecto a la cuerda más pequeña de , se cumple, con un alto nivel de precisión:${\textstyle A}$${\textstyle d}$${\textstyle d}$${\textstyle A}$$${\displaystyle \ C=\varepsilon {\frac {A}{d}};}$$

$${\displaystyle \varepsilon =\varepsilon _{0}\varepsilon _{r},}$$

dónde

• ${\textstyle C}$es la capacitancia, en faradios;
• ${\textstyle A}$es el área de superposición de las dos placas, en metros cuadrados;
• ${\textstyle \varepsilon _{0}}$es la constante eléctrica ( );${\textstyle \varepsilon _{0}\approx 8.854\times 10^{-12}~\mathrm {F{\cdot }m^{-1}} }$
• ${\textstyle \varepsilon _{r}}$es la permitividad relativa (también constante dieléctrica) del material entre las placas (${\textstyle \varepsilon _{r}\approx 1}$ para el aire); y
• ${\textstyle d}$es la separación entre las placas, en metros.

La ecuación es una buena aproximación si d es pequeño en comparación con las otras dimensiones de las placas, de modo que el campo eléctrico en el área del capacitor es uniforme y el llamado campo de franja alrededor de la periferia proporciona solo una pequeña contribución a la capacitancia.

Combinando la ecuación de capacitancia con la ecuación anterior para la energía almacenada en un capacitor, para un capacitor de placa plana la energía almacenada es: donde es la energía, en julios; es la capacitancia, en faradios; y es el voltaje, en voltios.$${\displaystyle W_{\text{stored}}={\frac {1}{2}}CV^{2}={\frac {1}{2}}\varepsilon {\frac {A}{d}}V^{2}.}$$${\textstyle W}$${\textstyle C}$${\textstyle V}$

Dos conductores adyacentes pueden funcionar como un capacitor, aunque la capacitancia es pequeña a menos que los conductores estén cerca uno del otro por largas distancias o en un área grande. Esta capacitancia (a menudo no deseada) se llama capacitancia parásita o parásita. La capacitancia parásita puede permitir que las señales se filtren entre circuitos que de otro modo estarían aislados (un efecto llamado diafonía ) y puede ser un factor limitante para el funcionamiento adecuado de los circuitos a alta frecuencia .

La capacitancia parásita entre la entrada y la salida en los circuitos amplificadores puede ser problemática porque puede formar un camino para la retroalimentación , lo que puede causar inestabilidad y oscilación parásita en el amplificador. A menudo es conveniente para fines analíticos reemplazar esta capacitancia con una combinación de una capacitancia de entrada a tierra y una capacitancia de salida a tierra; la configuración original, incluida la capacitancia de entrada a salida, a menudo se conoce como configuración pi. El teorema de Miller se puede utilizar para efectuar este reemplazo: establece que, si la relación de ganancia de dos nodos es1/K⁠ , entonces una impedancia de Z que conecta los dos nodos se puede reemplazar con una ⁠O/1 −  K⁠ impedancia entre el primer nodo y tierra y una ⁠KZ/K  -1⁠ impedancia entre el segundo nodo y tierra. Dado que la impedancia varía inversamente con la capacitancia, la capacitancia del entrenudo, C , se reemplaza por una capacitancia de KC desde la entrada hasta tierra y una capacitancia de ⁠( K  -1) C/K⁠ de salida a tierra. Cuando la ganancia de entrada a salida es muy grande, la impedancia equivalente de entrada a tierra es muy pequeña, mientras que la impedancia de salida a tierra es esencialmente igual a la impedancia original (de entrada a salida).

Calcular la capacidad de un sistema equivale a resolver la ecuación de Laplace con un potencial constante en la superficie bidimensional de los conductores insertados en el espacio tridimensional. Esto se simplifica mediante simetrías. No existe solución en términos de funciones elementales en casos más complicados.${\textstyle \nabla ^{2}\varphi =0}$${\textstyle \varphi }$

En situaciones de planos, se pueden utilizar funciones analíticas para mapear diferentes geometrías entre sí. Véase también mapeo de Schwarz-Christoffel .

Capacitancia de sistemas simples

Tipo	Capacidad	Diagrama y definiciones
Condensador de placas paralelas	${\displaystyle \ {\mathcal {C}}={\frac {\ \varepsilon A\ }{d}}\ }$	${\textstyle \varepsilon }$: Permitividad
Cilindros concéntricos	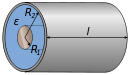${\displaystyle \ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\ \ln \left(R_{2}/R_{1}\right)\ }}\ }$	${\textstyle \varepsilon }$: Permitividad
Cilindros excéntricos [13]	${\displaystyle \ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\ \operatorname {arcosh} \left({\frac {R_{1}^{2}+R_{2}^{2}-d^{2}}{2R_{1}R_{2}}}\right)\ }}\ }$	${\textstyle \varepsilon }$: Permitividad ${\textstyle R_{1}}$: Radio exterior ${\textstyle R_{2}}$: Radio interior ${\textstyle d}$:Distancia entre centros ${\textstyle \ell }$:Longitud del cable
Par de cables paralelos [14]	${\displaystyle \ {\mathcal {C}}={\frac {\pi \varepsilon \ell }{\ \operatorname {arcosh} \left({\frac {d}{2a}}\right)\ }}={\frac {\pi \varepsilon \ell }{\ \ln \left({\frac {d}{\ 2a\ }}+{\sqrt {{\frac {d^{2}}{\ 4a^{2}\ }}-1\ }}\right)\ }}\ }$
Cable paralelo a la pared [14]	${\displaystyle \ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\ \operatorname {arcosh} \left({\frac {d}{a}}\right)\ }}={\frac {2\pi \varepsilon \ell }{\ \ln \left({\frac {\ d\ }{a}}+{\sqrt {{\frac {\ d^{2}\ }{a^{2}}}-1\ }}\right)\ }}\ }$	${\textstyle a}$: Radio del cable ${\textstyle d}$: Distancia,${\textstyle d>a}$ ${\textstyle \ell }$:Longitud del cable
Dos tiras paralelas coplanares [15]	${\displaystyle \ {\mathcal {C}}=\varepsilon \ell \ {\frac {\ K\left({\sqrt {1-k^{2}\ }}\right)\ }{K\left(k\right)}}\ }$	${\textstyle d}$: Distancia ${\textstyle \ell }$: Longitud ${\textstyle w_{1},w_{2}}$: Ancho de la tira ${\textstyle \ k_{1}=\left({\tfrac {\ 2w_{1}\ }{d}}+1\right)^{-1}\ }$ ${\displaystyle \ k_{2}=\left({\tfrac {\ 2w_{2}\ }{d}}+1\right)^{-1}\ }$${\displaystyle \ k={\sqrt {k_{1}\ k_{2}\ }}\ }$ ${\textstyle K}$: Integral elíptica completa de primer tipo
Esferas concéntricas	${\displaystyle \ {\mathcal {C}}={\frac {4\pi \varepsilon }{\ {\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\ }}\ }$	${\textstyle \varepsilon }$: Permitividad
Dos esferas, radio igual [16] [17]	${\displaystyle {\begin{aligned}\ {\mathcal {C}}\ =&\ {}2\pi \varepsilon a\ \sum _{n=1}^{\infty }{\frac {\sinh \left(\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}{\sinh \left(n\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}}\\={}&{}2\pi \varepsilon a\left[1+{\frac {1}{2D}}+{\frac {1}{4D^{2}}}+{\frac {1}{8D^{3}}}+{\frac {1}{8D^{4}}}+{\frac {3}{32D^{5}}}+{\mathcal {O}}\left({\frac {1}{D^{6}}}\right)\right]\\={}&{}2\pi \varepsilon a\left[\ln 2+\gamma -{\frac {1}{2}}\ln \left(2D-2\right)+{\mathcal {O}}\left(2D-2\right)\right]\\={}&{}2\pi \varepsilon a\,{\frac {\sqrt {D^{2}-1}}{\log(q)}}\left[\psi _{q}\left(1+{\frac {i\pi }{\log(q)}}\right)-i\pi -\psi _{q}(1)\right]\end{aligned}}\ }$	${\textstyle a}$: Radio ${\textstyle d}$: Distancia,${\textstyle d>2a}$ ${\textstyle D=d/2a,D>1}$ ${\textstyle \gamma }$: La constante de Euler ${\displaystyle q=D+{\sqrt {D^{2}-1}}}$ ${\displaystyle \psi _{q}(z)={\frac {\partial _{z}\Gamma _{q}(z)}{\Gamma _{q}(z)}}}$:la función q-digamma ${\displaystyle \Gamma _{q}(z)}$:la función q-gamma [18] Véase también Series hipergeométricas básicas .
Esfera delante de la pared [16]	${\displaystyle \ {\mathcal {C}}=4\pi \varepsilon a\sum _{n=1}^{\infty }{\frac {\sinh \left(\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}{\sinh \left(n\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}}\ }$	${\displaystyle \ a\ }$: Radio ${\displaystyle \ d\ }$: Distancia,${\displaystyle d>a}$ ${\displaystyle D=d/a}$
Esfera	${\displaystyle \ {\mathcal {C}}=4\pi \varepsilon a\ }$	${\displaystyle a}$: Radio
Disco circular [19]	${\displaystyle \ {\mathcal {C}}=8\varepsilon a\ }$	${\displaystyle a}$: Radio
Alambre recto delgado, longitud finita [20] [21] [22]	${\displaystyle \ {\mathcal {C}}={\frac {2\pi \varepsilon \ell }{\Lambda }}\left[1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left(1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right)+{\mathcal {O}}\left({\frac {1}{\Lambda ^{3}}}\right)\right]\ }$	${\displaystyle a}$: Radio del cable ${\displaystyle \ell }$: Longitud ${\displaystyle \ \Lambda =\ln \left(\ell /a\right)\ }$

La energía (medida en julios ) almacenada en un condensador es igual al trabajo necesario para empujar las cargas hacia el condensador, es decir, para cargarlo. Considere un condensador de capacidad C , que contiene una carga + q en una placa y − q en la otra. Mover un pequeño elemento de carga d q de una placa a la otra contra la diferencia de potencial V = q / C requiere el trabajo d W : donde W es el trabajo medido en julios, q es la carga medida en culombios y C es la capacitancia, medida en faradios.$${\displaystyle \mathrm {d} W={\frac {q}{C}}\,\mathrm {d} q,}$$

La energía almacenada en un capacitor se obtiene integrando esta ecuación. Para empezar con una capacitancia sin carga ( q = 0 ) y mover la carga de una placa a la otra hasta que las placas tengan carga + Q y − Q se requiere el trabajo W :$${\displaystyle W_{\text{charging}}=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q={\frac {1}{2}}{\frac {Q^{2}}{C}}={\frac {1}{2}}QV={\frac {1}{2}}CV^{2}=W_{\text{stored}}.}$$

La capacitancia de los capacitores dieléctricos a escala nanométrica, como los puntos cuánticos, puede diferir de las formulaciones convencionales de capacitores más grandes. En particular, la diferencia de potencial electrostático que experimentan los electrones en los capacitores convencionales está bien definida espacialmente y fijada por la forma y el tamaño de los electrodos metálicos, además de la cantidad estadísticamente grande de electrones presentes en los capacitores convencionales. Sin embargo, en los capacitores a escala nanométrica, los potenciales electrostáticos que experimentan los electrones están determinados por la cantidad y las ubicaciones de todos los electrones que contribuyen a las propiedades electrónicas del dispositivo. En tales dispositivos, la cantidad de electrones puede ser muy pequeña, por lo que la distribución espacial resultante de las superficies equipotenciales dentro del dispositivo es extremadamente compleja.

La capacitancia de un dispositivo de un solo electrón conectado o "cerrado" es el doble de la capacitancia de un dispositivo de un solo electrón no conectado o "abierto". ^[23] Este hecho puede atribuirse más fundamentalmente a la energía almacenada en el dispositivo de un solo electrón cuya energía de interacción de "polarización directa" puede dividirse equitativamente entre la interacción del electrón con la carga polarizada en el propio dispositivo debido a la presencia del electrón y la cantidad de energía potencial requerida para formar la carga polarizada en el dispositivo (la interacción de las cargas en el material dieléctrico del dispositivo con el potencial debido al electrón). ^[24]

La derivación de una "capacidad cuántica" de un dispositivo de pocos electrones implica el potencial químico termodinámico de un sistema de N partículas dado por$${\displaystyle \mu (N)=U(N)-U(N-1),}$$

cuyos términos de energía pueden obtenerse como soluciones de la ecuación de Schrödinger. La definición de capacitancia, con la diferencia de potencial$${\displaystyle {1 \over C}\equiv {\Delta V \over \Delta Q},}$$$${\displaystyle \Delta V={\Delta \mu \, \over e}={\mu (N+\Delta N)-\mu (N) \over e}}$$

puede aplicarse al dispositivo con la adición o eliminación de electrones individuales, y$${\displaystyle \Delta N=1}$$$${\displaystyle \Delta Q=e.}$$

La "capacidad cuántica" del dispositivo es entonces ^[25]$${\displaystyle C_{Q}(N)={\frac {e^{2}}{\mu (N+1)-\mu (N)}}={\frac {e^{2}}{E(N)}}.}$$

Esta expresión de "capacitancia cuántica" puede escribirse como que difiere de la expresión convencional descrita en la introducción donde , la energía potencial electrostática almacenada, por un factor de ⁠$${\displaystyle C_{Q}(N)={e^{2} \over U(N)},}$$${\displaystyle W_{\text{stored}}=U}$$${\displaystyle C={Q^{2} \over 2U},}$$1/2⁠ con .${\displaystyle Q=Ne}$

Sin embargo, en el marco de las interacciones electrostáticas puramente clásicas, la aparición del factor de ⁠1/2⁠ es el resultado de la integración en la formulación convencional que involucra el trabajo realizado al cargar un capacitor,$${\displaystyle W_{\text{charging}}=U=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q,}$$

lo cual es apropiado ya que para sistemas que involucran muchos electrones o electrodos metálicos, pero en sistemas de pocos electrones, . La integral generalmente se convierte en una suma. Se pueden combinar trivialmente las expresiones de capacitancia y energía de interacción electrostática para obtener${\displaystyle \mathrm {d} q=0}$${\displaystyle \mathrm {d} q\to \Delta \,Q=e}$$${\displaystyle Q=CV}$$$${\displaystyle U=QV,}$$$${\displaystyle C=Q{1 \over V}=Q{Q \over U}={Q^{2} \over U},}$$

que es similar a la capacitancia cuántica. En la literatura se informa sobre una derivación más rigurosa. ^[26] En particular, para sortear los desafíos matemáticos de las superficies equipotenciales espacialmente complejas dentro del dispositivo, se utiliza en la derivación un potencial electrostático promedio experimentado por cada electrón.

Las diferencias matemáticas aparentes pueden entenderse de manera más fundamental. La energía potencial, , de un dispositivo aislado (autocapacidad) es el doble de la almacenada en un dispositivo "conectado" en el límite inferior . A medida que aumenta, . ^[24] Por lo tanto, la expresión general de la capacitancia es${\displaystyle U(N)}$${\displaystyle N=1}$${\displaystyle N}$${\displaystyle U(N)\to U}$$${\displaystyle C(N)={(Ne)^{2} \over U(N)}.}$$

En los dispositivos a escala nanométrica, como los puntos cuánticos, el "condensador" suele ser un componente aislado o parcialmente aislado dentro del dispositivo. Las principales diferencias entre los condensadores a escala nanométrica y los condensadores macroscópicos (convencionales) son la cantidad de electrones en exceso (portadores de carga, o electrones, que contribuyen al comportamiento electrónico del dispositivo) y la forma y el tamaño de los electrodos metálicos. En los dispositivos a escala nanométrica, los nanocables que consisten en átomos de metal normalmente no presentan las mismas propiedades conductoras que sus contrapartes macroscópicas o de material a granel.

En dispositivos electrónicos y semiconductores, la corriente transitoria o dependiente de la frecuencia entre terminales contiene componentes tanto de conducción como de desplazamiento. La corriente de conducción está relacionada con los portadores de carga en movimiento (electrones, huecos, iones, etc.), mientras que la corriente de desplazamiento es causada por un campo eléctrico variable en el tiempo. El transporte de portadores se ve afectado por campos eléctricos y por una serie de fenómenos físicos, como la deriva y difusión de portadores, el atrapamiento, la inyección, los efectos relacionados con el contacto, la ionización por impacto, etc. Como resultado, la admitancia del dispositivo depende de la frecuencia y no es aplicable una fórmula electrostática simple para la capacitancia. Una definición más general de capacitancia, que abarca la fórmula electrostática, es: ^[27] donde es la admitancia del dispositivo y es la frecuencia angular.${\displaystyle C=q/V,}$$${\displaystyle C={\frac {\operatorname {Im} (Y(\omega ))}{\omega }},}$$${\displaystyle Y(\omega )}$${\displaystyle \omega }$

En general, la capacitancia es una función de la frecuencia. A frecuencias altas, la capacitancia se acerca a un valor constante, igual a la capacitancia "geométrica", determinada por la geometría de los terminales y el contenido dieléctrico del dispositivo. Un artículo de Steven Laux ^[27] presenta una revisión de las técnicas numéricas para el cálculo de la capacitancia. En particular, la capacitancia se puede calcular mediante una transformada de Fourier de una corriente transitoria en respuesta a una excitación de voltaje escalonada:$${\displaystyle C(\omega )={\frac {1}{\Delta V}}\int _{0}^{\infty }[i(t)-i(\infty )]\cos(\omega t)dt.}$$

Por lo general, la capacitancia en los dispositivos semiconductores es positiva. Sin embargo, en algunos dispositivos y bajo ciertas condiciones (temperatura, voltajes aplicados, frecuencia, etc.), la capacitancia puede volverse negativa. Se ha propuesto que el comportamiento no monótono de la corriente transitoria en respuesta a una excitación escalonada es el mecanismo de la capacitancia negativa. ^[28] La capacitancia negativa se ha demostrado y explorado en muchos tipos diferentes de dispositivos semiconductores. ^[29]

Un medidor de capacidad es un equipo de prueba electrónico que se utiliza para medir la capacidad, principalmente de capacitores discretos . Para la mayoría de los propósitos y en la mayoría de los casos, el capacitor debe estar desconectado del circuito .

Muchos voltímetros digitales (DVM ) tienen una función de medición de capacitancia. Estos suelen funcionar cargando y descargando el condensador bajo prueba con una corriente conocida y midiendo la velocidad de aumento del voltaje resultante ; cuanto más lenta sea la velocidad de aumento, mayor será la capacitancia. Los DVM suelen poder medir capacitancias desde nanofaradios hasta unos pocos cientos de microfaradios, pero no son inusuales los rangos más amplios. También es posible medir la capacitancia haciendo pasar una corriente alterna de alta frecuencia conocida a través del dispositivo bajo prueba y midiendo el voltaje resultante a través de ella (no funciona para condensadores polarizados).

Los instrumentos más sofisticados utilizan otras técnicas, como la inserción del condensador bajo prueba en un circuito de puente . Al variar los valores de las otras patas del puente (para equilibrar el puente), se determina el valor del condensador desconocido. Este método de uso indirecto de la medición de la capacitancia garantiza una mayor precisión. Mediante el uso de conexiones Kelvin y otras técnicas de diseño cuidadosas, estos instrumentos suelen poder medir condensadores en un rango que va desde picofaradios hasta faradios.

• Medios relacionados con Capacitancia en Wikimedia Commons