Desintegración radiactiva
| Física nuclear |
|---|
 |
La desintegración radiactiva (también conocida como desintegración nuclear , radiactividad , desintegración radiactiva o desintegración nuclear ) es el proceso por el cual un núcleo atómico inestable pierde energía por radiación . Un material que contiene núcleos inestables se considera radiactivo . Tres de los tipos de desintegración más comunes son la desintegración alfa , beta y gamma . La fuerza débil es el mecanismo responsable de la desintegración beta, mientras que los otros dos están regidos por las fuerzas electromagnética y nuclear . [1]
La desintegración radiactiva es un proceso aleatorio a nivel de átomos individuales. Según la teoría cuántica , es imposible predecir cuándo se desintegrará un átomo en particular, independientemente de cuánto tiempo haya existido el átomo. [2] [3] [4] Sin embargo, para un número significativo de átomos idénticos, la tasa de desintegración general se puede expresar como una constante de desintegración o como una vida media . Las vidas medias de los átomos radiactivos tienen un rango enorme: desde casi instantáneas hasta mucho más largas que la edad del universo .
El núcleo en descomposición se denomina radionúclido progenitor (o radioisótopo progenitor ) y el proceso produce al menos un nucleido hijo . A excepción de la desintegración gamma o la conversión interna a partir de un estado nuclear excitado , la desintegración es una transmutación nuclear que da como resultado un nucleido hijo que contiene un número diferente de protones o neutrones (o ambos). Cuando cambia el número de protones, se crea un átomo de un elemento químico diferente.
Existen 28 elementos químicos naturales en la Tierra que son radiactivos, que consisten en 35 radionucleidos (siete elementos tienen dos radionucleidos diferentes cada uno) que datan de antes del momento de formación del Sistema Solar . Estos 35 se conocen como radionucleidos primordiales . Ejemplos bien conocidos son el uranio y el torio , pero también se incluyen radioisótopos naturales de larga vida, como el potasio-40 . Cada uno de los radionucleidos primordiales pesados participa en una de las cuatro cadenas de desintegración .
Historia del descubrimiento

La radiactividad fue descubierta en 1896 por los científicos Henri Becquerel y Marie Curie , mientras trabajaban con materiales fosforescentes . [5] [6] [7] [8] [9] Estos materiales brillan en la oscuridad después de la exposición a la luz, y Becquerel sospechó que el brillo producido en los tubos de rayos catódicos por los rayos X podría estar asociado con la fosforescencia. Envolvió una placa fotográfica en papel negro y colocó varias sales fosforescentes sobre ella. Todos los resultados fueron negativos hasta que utilizó sales de uranio . Las sales de uranio causaron un ennegrecimiento de la placa a pesar de que la placa estaba envuelta en papel negro. Estas radiaciones recibieron el nombre de "rayos Becquerel".
Pronto se hizo evidente que el ennegrecimiento de la placa no tenía nada que ver con la fosforescencia, ya que el ennegrecimiento también lo producían las sales de uranio no fosforescentes y el uranio metálico. A partir de estos experimentos quedó claro que existía una forma de radiación invisible que podía atravesar el papel y que hacía que la placa reaccionara como si estuviera expuesta a la luz.
Al principio, parecía que la nueva radiación era similar a los rayos X, descubiertos recientemente. Investigaciones posteriores de Becquerel, Ernest Rutherford , Paul Villard , Pierre Curie , Marie Curie y otros demostraron que esta forma de radiactividad era significativamente más complicada. Rutherford fue el primero en darse cuenta de que todos esos elementos se desintegran de acuerdo con la misma fórmula matemática exponencial. Rutherford y su alumno Frederick Soddy fueron los primeros en darse cuenta de que muchos procesos de desintegración daban como resultado la transmutación de un elemento en otro. Posteriormente, se formuló la ley de desplazamiento radiactivo de Fajans y Soddy para describir los productos de la desintegración alfa y beta . [10] [11]
Los primeros investigadores descubrieron también que muchos otros elementos químicos , además del uranio, tienen isótopos radiactivos. Una búsqueda sistemática de la radiactividad total en los minerales de uranio también guió a Pierre y Marie Curie a aislar dos nuevos elementos: el polonio y el radio . A excepción de la radiactividad del radio, la similitud química del radio con el bario hizo que estos dos elementos fueran difíciles de distinguir.
El estudio de la radiactividad por parte de Marie y Pierre Curie es un factor importante en la ciencia y la medicina. Después de que su investigación sobre los rayos de Becquerel los llevó al descubrimiento del radio y el polonio, acuñaron el término "radiactividad" [12] para definir la emisión de radiación ionizante por parte de algunos elementos pesados. [13] (Más tarde, el término se generalizó a todos los elementos). Su investigación sobre los rayos penetrantes en el uranio y el descubrimiento del radio iniciaron una era de uso del radio para el tratamiento del cáncer. Su exploración del radio podría considerarse como el primer uso pacífico de la energía nuclear y el comienzo de la medicina nuclear moderna . [12]
Peligros tempranos para la salud

Los peligros de las radiaciones ionizantes debidas a la radiactividad y a los rayos X no fueron reconocidos inmediatamente.
Rayos X
El descubrimiento de los rayos X por Wilhelm Röntgen en 1895 dio lugar a una experimentación generalizada por parte de científicos, médicos e inventores. Muchas personas comenzaron a contar historias de quemaduras, pérdida de cabello y cosas peores en revistas técnicas ya en 1896. En febrero de ese año, el profesor Daniel y el doctor Dudley de la Universidad de Vanderbilt realizaron un experimento que implicaba tomarle rayos X a la cabeza a Dudley y que dio como resultado la pérdida de cabello. Un informe del doctor HD Hawks, sobre las graves quemaduras que sufrió en la mano y el pecho en una demostración de rayos X, fue el primero de muchos otros informes en Electrical Review . [14]
Otros experimentadores, entre ellos Elihu Thomson y Nikola Tesla , también informaron de quemaduras. Thomson expuso deliberadamente un dedo a un tubo de rayos X durante un período de tiempo y sufrió dolor, hinchazón y ampollas. [15] A veces se culpaba a otros efectos, incluidos los rayos ultravioleta y el ozono, por el daño, [16] y muchos médicos seguían afirmando que no había ningún efecto por la exposición a los rayos X. [15]
A pesar de ello, se llevaron a cabo algunas investigaciones sistemáticas sobre los riesgos y, ya en 1902, William Herbert Rollins escribió, casi con desesperación, que sus advertencias sobre los peligros que entrañaba el uso descuidado de los rayos X no estaban siendo atendidas, ni por la industria ni por sus colegas. Para entonces, Rollins había demostrado que los rayos X podían matar a los animales de experimentación, podían provocar el aborto de una cobaya preñada y podían matar a un feto. También destacó que "los animales varían en su susceptibilidad a la acción externa de la luz X" y advirtió que se debían tener en cuenta estas diferencias cuando se tratara a los pacientes con rayos X. [ cita requerida ]
Sustancias radiactivas
Sin embargo, los efectos biológicos de la radiación debida a las sustancias radiactivas eran menos fáciles de medir. Esto dio la oportunidad a muchos médicos y corporaciones de comercializar sustancias radiactivas como medicamentos patentados . Algunos ejemplos fueron los tratamientos con enemas de radio y las aguas que contenían radio para beber como tónicos. Marie Curie protestó contra este tipo de tratamiento, advirtiendo que "el radio es peligroso en manos inexpertas". [17] Curie murió más tarde de anemia aplásica , probablemente causada por la exposición a la radiación ionizante. En la década de 1930, después de una serie de casos de necrosis ósea y muerte de entusiastas del tratamiento con radio, los productos medicinales que contenían radio habían sido retirados en gran medida del mercado ( curanderismo radiactivo ).
Protección radiológica
Sólo un año después del descubrimiento de los rayos X por parte de Röntgen , el ingeniero estadounidense Wolfram Fuchs (1896) dio lo que probablemente sea el primer consejo de protección, pero no fue hasta 1925 cuando se celebró el primer Congreso Internacional de Radiología (CIR) y se consideró establecer estándares internacionales de protección. Los efectos de la radiación sobre los genes, incluido el efecto del riesgo de cáncer, se reconocieron mucho más tarde. En 1927, Hermann Joseph Müller publicó una investigación que demostraba los efectos genéticos y, en 1946, recibió el Premio Nobel de Fisiología o Medicina por sus hallazgos.
El segundo ICR se celebró en Estocolmo en 1928 y propuso la adopción de la unidad Röntgen , y se formó el Comité Internacional de Protección de los Rayos X y el Radio (IXRPC). Rolf Sievert fue nombrado presidente, pero una fuerza impulsora fue George Kaye, del Laboratorio Nacional de Física británico . El comité se reunió en 1931, 1934 y 1937.
Después de la Segunda Guerra Mundial , el aumento de la gama y la cantidad de sustancias radiactivas que se manejaban como resultado de los programas nucleares militares y civiles condujo a que grandes grupos de trabajadores ocupacionales y el público en general estuvieran potencialmente expuestos a niveles nocivos de radiación ionizante. Esto se tuvo en cuenta en la primera ICR de posguerra convocada en Londres en 1950, cuando nació la actual Comisión Internacional de Protección Radiológica (CIPR). [18] Desde entonces, la CIPR ha desarrollado el actual sistema internacional de protección radiológica, que abarca todos los aspectos de los peligros de la radiación.
En 2020, Hauptmann y otros 15 investigadores internacionales de ocho naciones (entre ellos: Institutos de Bioestadística, Investigación de Registros, Centros de Epidemiología del Cáncer, Epidemiología de la Radiación, y también el Instituto Nacional del Cáncer de EE. UU. (NCI), la Agencia Internacional para la Investigación del Cáncer (IARC) y la Fundación para la Investigación de los Efectos de la Radiación de Hiroshima ) estudiaron definitivamente a través de un metaanálisis los daños resultantes de las "bajas dosis" que han afectado a los supervivientes de los bombardeos atómicos de Hiroshima y Nagasaki y también en numerosos accidentes en plantas nucleares ocurridos. Estos científicos informaron, en JNCI Monographs: Epidemiological Studies of Low Dose Ionizing Radiation and Cancer Risk , que los nuevos estudios epidemiológicos respaldan directamente los riesgos excesivos de cáncer por radiación ionizante de dosis baja. [19] En 2021, el investigador italiano Sebastiano Venturi informó las primeras correlaciones entre el radiocesio y el cáncer de páncreas con el papel del cesio en la biología, en la pancreatitis y en la diabetes de origen pancreático. [20]
Unidades

La unidad de actividad radiactiva del Sistema Internacional de Unidades (SI) es el becquerel (Bq), llamado así en honor al científico Henri Becquerel . Un Bq se define como una transformación (o desintegración o desintegración) por segundo.
Una unidad más antigua de radiactividad es el curie , Ci, que originalmente se definió como "la cantidad o masa de emanación de radio en equilibrio con un gramo de radio (elemento)". [21] Hoy, el curie se define como3,7 × 10 10 desintegraciones por segundo, por lo que 1 curie (Ci) =3,7 × 10 10 Bq . Para fines de protección radiológica, aunque la Comisión Reguladora Nuclear de los Estados Unidos permite el uso de la unidad curie junto con las unidades del SI, [22] las directivas de la Unión Europea sobre unidades de medida europeas exigieron que su uso para "fines de salud pública" se eliminara gradualmente antes del 31 de diciembre de 1985. [23]
Los efectos de la radiación ionizante a menudo se miden en unidades de gray para daños mecánicos o sievert para daños a los tejidos.
Tipos
This section needs additional citations for verification. (May 2023) |
La desintegración radiactiva produce una reducción de la masa en reposo sumada , una vez que la energía liberada (la energía de desintegración ) ha escapado de alguna manera. Aunque la energía de desintegración a veces se define como asociada con la diferencia entre la masa de los productos nucleidos originales y la masa de los productos de desintegración, esto es cierto solo para las mediciones de masa en reposo, donde se ha eliminado algo de energía del sistema del producto. Esto es cierto porque la energía de desintegración siempre debe llevar masa con ella, donde sea que aparezca (ver masa en relatividad especial ) de acuerdo con la fórmula E = mc 2 . La energía de desintegración se libera inicialmente como la energía de los fotones emitidos más la energía cinética de las partículas masivas emitidas (es decir, partículas que tienen masa en reposo). Si estas partículas llegan al equilibrio térmico con su entorno y los fotones son absorbidos, entonces la energía de desintegración se transforma en energía térmica, que conserva su masa.
Por lo tanto, la energía de desintegración permanece asociada a una cierta medida de la masa del sistema de desintegración, llamada masa invariante , que no cambia durante la desintegración, aunque la energía de desintegración se distribuye entre las partículas de desintegración. La energía de los fotones, la energía cinética de las partículas emitidas y, más tarde, la energía térmica de la materia circundante, contribuyen todas a la masa invariante del sistema. Por lo tanto, mientras que la suma de las masas en reposo de las partículas no se conserva en la desintegración radiactiva, la masa del sistema y la masa invariante del sistema (y también la energía total del sistema) se conservan a lo largo de cualquier proceso de desintegración. Esta es una reformulación de las leyes equivalentes de conservación de la energía y conservación de la masa .
Desintegración alfa, beta y gamma
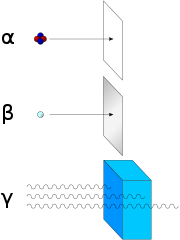
Los primeros investigadores descubrieron que un campo eléctrico o magnético podía dividir las emisiones radiactivas en tres tipos de rayos. Los rayos recibieron los nombres de alfa , beta y gamma, en orden creciente de su capacidad para penetrar la materia. La desintegración alfa se observa solo en elementos más pesados de número atómico 52 ( telurio ) y mayores, con la excepción del berilio-8 (que se desintegra en dos partículas alfa). Los otros dos tipos de desintegración se observan en todos los elementos. El plomo, de número atómico 82, es el elemento más pesado que tiene isótopos estables (hasta el límite de medición) a la desintegración radiactiva. La desintegración radiactiva se observa en todos los isótopos de todos los elementos de número atómico 83 ( bismuto ) o mayores. El bismuto-209 , sin embargo, es solo muy ligeramente radiactivo, con una vida media mayor que la edad del universo; los radioisótopos con vidas medias extremadamente largas se consideran efectivamente estables para fines prácticos.
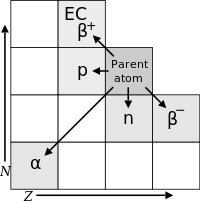
Al analizar la naturaleza de los productos de la desintegración, era obvio, a partir de la dirección de las fuerzas electromagnéticas aplicadas a las radiaciones por los campos magnéticos y eléctricos externos, que las partículas alfa tenían una carga positiva, las partículas beta una carga negativa y los rayos gamma eran neutros. A partir de la magnitud de la desviación, estaba claro que las partículas alfa eran mucho más masivas que las partículas beta . El paso de partículas alfa a través de una ventana de vidrio muy delgada y su atrapamiento en un tubo de descarga permitió a los investigadores estudiar el espectro de emisión de las partículas capturadas y, en última instancia, demostró que las partículas alfa son núcleos de helio . Otros experimentos mostraron que la radiación beta, resultante de la desintegración y los rayos catódicos , eran electrones de alta velocidad . Del mismo modo, se descubrió que la radiación gamma y los rayos X eran radiación electromagnética de alta energía .
También se empezó a estudiar la relación entre los tipos de desintegración: por ejemplo, la desintegración gamma se asociaba casi siempre a otros tipos de desintegración y se producía aproximadamente al mismo tiempo o después. Se descubrió que la desintegración gamma, como fenómeno independiente y con su propia vida media (ahora denominada transición isomérica ), en la radiactividad natural era el resultado de la desintegración gamma de isómeros nucleares metaestables excitados , que a su vez se creaban a partir de otros tipos de desintegración. Aunque las radiaciones alfa, beta y gamma eran las más comunes, con el tiempo se descubrieron otros tipos de emisión. Poco después del descubrimiento del positrón en los productos de rayos cósmicos, se descubrió que el mismo proceso que opera en la desintegración beta clásica también puede producir positrones ( emisión de positrones ), junto con neutrinos (la desintegración beta clásica produce antineutrinos).
Captura de electrones
En la captura de electrones, se descubrió que algunos nucleidos ricos en protones capturaban sus propios electrones atómicos en lugar de emitir positrones y, posteriormente, estos nucleidos emiten solo un neutrino y un rayo gamma desde el núcleo excitado (y a menudo también electrones Auger y rayos X característicos , como resultado de la reordenación de los electrones para llenar el lugar del electrón capturado faltante). Estos tipos de desintegración implican la captura nuclear de electrones o la emisión de electrones o positrones y, por lo tanto, actúan para mover un núcleo hacia la proporción de neutrones a protones que tiene la menor energía para un número total dado de nucleones . Esto, en consecuencia, produce un núcleo más estable (de menor energía).
Un proceso hipotético de captura de positrones, análogo a la captura de electrones, es teóricamente posible en átomos de antimateria, pero no se ha observado, ya que no se encuentran disponibles experimentalmente átomos de antimateria complejos más allá del antihelio . [24] Tal desintegración requeriría átomos de antimateria al menos tan complejos como el berilio-7 , que es el isótopo más ligero conocido de la materia normal, para sufrir una desintegración por captura de electrones. [25]
Emisión de nucleones
Poco después del descubrimiento del neutrón en 1932, Enrico Fermi se dio cuenta de que ciertas reacciones raras de desintegración beta producen inmediatamente neutrones como una partícula de desintegración adicional, la llamada emisión de neutrones retardada en beta . La emisión de neutrones suele ocurrir a partir de núcleos que están en un estado excitado, como el 17 O* excitado producido a partir de la desintegración beta del 17 N. El proceso de emisión de neutrones en sí está controlado por la fuerza nuclear y, por lo tanto, es extremadamente rápido, a veces denominado "casi instantáneo". Finalmente, se observó la emisión aislada de protones en algunos elementos. También se descubrió que algunos elementos pesados pueden sufrir fisión espontánea en productos que varían en composición. En un fenómeno llamado desintegración en cúmulos , se descubrió que combinaciones específicas de neutrones y protones distintos de las partículas alfa (núcleos de helio) se emitían espontáneamente desde los átomos.
Tipos de descomposición más exóticos
Se ha descubierto que otros tipos de desintegración radiactiva emiten partículas que ya se habían visto, pero a través de mecanismos diferentes. Un ejemplo es la conversión interna , que produce una emisión inicial de electrones y, a menudo, otras emisiones características de rayos X y electrones Auger , aunque el proceso de conversión interna no implica ni desintegración beta ni gamma. No se emite un neutrino y ninguno de los electrones y fotones emitidos se origina en el núcleo, aunque la energía para emitirlos todos se origina allí. La desintegración por conversión interna, al igual que la desintegración gamma de transición isomérica y la emisión de neutrones, implica la liberación de energía por parte de un nucleido excitado, sin la transmutación de un elemento en otro.
Se conocen eventos raros que involucran una combinación de dos eventos de tipo de desintegración beta que ocurren simultáneamente (ver más abajo). Se permite que ocurra cualquier proceso de desintegración que no viole las leyes de conservación de la energía o del momento (y quizás otras leyes de conservación de partículas), aunque no todos han sido detectados. Un ejemplo interesante que se analiza en una sección final es la desintegración beta en estado ligado del renio-187 . En este proceso, la desintegración del electrón beta del nucleido original no está acompañada por la emisión de electrones beta, porque la partícula beta ha sido capturada en la capa K del átomo emisor. Se emite un antineutrino, como en todas las desintegraciones beta negativas.
Si las circunstancias energéticas son favorables, un radionúclido determinado puede sufrir muchos tipos de desintegración en competencia, con algunos átomos desintegrándose por una vía y otros desintegrándose por otra. Un ejemplo es el cobre-64 , que tiene 29 protones y 35 neutrones, y que se desintegra con una vida media de12.7004(13) horas. [26] Este isótopo tiene un protón desapareado y un neutrón desapareado, por lo que tanto el protón como el neutrón pueden desintegrarse en la otra partícula, que tiene isospín opuesto . Este nucleido en particular (aunque no todos los nucleidos en esta situación) tiene más probabilidades de desintegrarse a través de la desintegración beta plus (61,52(26) % [26] ) que a través de la captura de electrones (38,48(26) % [26] ). Los estados de energía excitados resultantes de estas desintegraciones que no terminan en un estado de energía fundamental, también producen una conversión interna posterior y una desintegración gamma en casi el 0,5% del tiempo.
Lista de modos de decaimiento
| Modo | Nombre | Acción | Cambios en el núcleo |
|---|---|---|---|
| emisión alfa | Una partícula alfa ( A = 4, Z = 2) emitida desde el núcleo | ( A -4, Z -2) |
| emisión de protones | Un protón expulsado del núcleo | ( A -1, Z -1) |
| Emisión de 2 protones | Dos protones expulsados del núcleo simultáneamente | ( A -2, Z -2) |
| emisión de neutrones | Un neutrón expulsado del núcleo | ( A - 1, Z ) |
| Emisión de 2 neutrones | Dos neutrones expulsados del núcleo simultáneamente | ( A - 2, Z ) |
| captura de electrones | Un núcleo captura un electrón en órbita y emite un neutrino; el núcleo hijo queda en un estado inestable excitado. | ( A , Z − 1) |
| emisión de positrones | Un protón nuclear se convierte en un neutrón al emitir un positrón y un neutrino electrónico. | ( A , Z − 1) |
| emisión de positrones | En NUBASE2020, ß + se refiere a la tasa combinada de captura de electrones (ε) y emisión de positrones (e + ): ß + = ε+ e + | ( A , Z − 1) |
| β − desintegración | Un núcleo emite un electrón y un antineutrino electrónico. | ( A , Z +1) |
| doble desintegración β − | Un núcleo emite dos electrones y dos antineutrinos. | ( A , Z +2) |
| doble desintegración β + | Un núcleo emite dos positrones y dos neutrinos. | ( A , Z − 2) |
| emisión de neutrones retardada β − | Un núcleo se desintegra por emisión β − a un estado excitado, que luego emite un neutrón. | ( A -1, Z +1) |
| Emisión de 2 neutrones con retardo β | Un núcleo se desintegra por emisión β − a un estado excitado, que luego emite dos neutrones. | ( A -2, Z +1) |
| Emisión de 3 neutrones con retardo β | Un núcleo se desintegra por emisión β − a un estado excitado, que luego emite tres neutrones. | ( A -3, Z +1) |
| Emisión de protones retardada β + | Un núcleo se desintegra por emisión β + a un estado excitado, que luego emite un protón. | ( A -1, Z -2) |
| Emisión retardada de 2 protones β + | Un núcleo se desintegra por emisión β + a un estado excitado, que luego emite dos protones. | ( A -2, Z -3) |
| Emisión retardada de 3 protones β + | Un núcleo se desintegra por emisión β + a un estado excitado, que luego emite tres protones. | ( A -3, Z -4) |
| β − -emisión alfa retardada | Un núcleo se desintegra por emisión β − a un estado excitado, que luego emite una partícula α | ( A -4, Z -1) |
| Emisión alfa retardada β + | Un núcleo se desintegra por emisión β + a un estado excitado, que luego emite una partícula a | ( A -4, Z -3) |
| Emisión de deuterón retardada β − | Un núcleo se desintegra por emisión β − a un estado excitado, que luego emite un deuterón. | ( A - 2, Z ) |
| Emisión de tritones β − retardada | Un núcleo se desintegra por emisión β − a un estado excitado, que luego emite un tritón. | ( A - 3, Z ) |
| desintegración del racimo | Un núcleo emite un tipo específico de núcleo más pequeño ( A 1 , Z 1 ) que es más grande que una partícula alfa (por ejemplo, 14 C, 24 Ne) | ( UN - UN 1 , Z - Z 1 ) & ( UN 1 , Z 1 ) |
| transición interna (isomérica) | Un núcleo en estado metaestable cae a un estado de energía más bajo al emitir un fotón o expulsar un electrón. | ( A , Z ) |
| fisión espontánea | Un núcleo se desintegra en dos o más núcleos más pequeños y otras partículas, todas las cuales pueden variar con cada desintegración. | variable |
| β + -fisión retardada | Un núcleo se desintegra por emisión β + a un estado excitado, que luego sufre fisión espontánea. | β+ y variables |
| β − -fisión retardada | Un núcleo se desintegra por emisión β − a un estado excitado, que luego sufre fisión espontánea. | β − y variable |
Cadenas de desintegración y modos múltiples
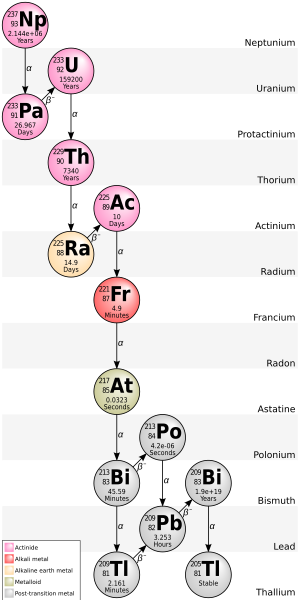
El nucleido hijo de un evento de desintegración también puede ser inestable (radiactivo). En este caso, también se desintegrará, produciendo radiación. El segundo nucleido hijo resultante también puede ser radiactivo. Esto puede dar lugar a una secuencia de varios eventos de desintegración denominados cadena de desintegración (consulte este artículo para obtener detalles específicos de las cadenas de desintegración naturales importantes). Finalmente, se produce un nucleido estable. Cualquier nucleido hijo que sea el resultado de una desintegración alfa también dará lugar a la creación de átomos de helio.
Algunos radionucleidos pueden tener varias vías de desintegración diferentes. Por ejemplo,El 35,94(6) % [26] del bismuto-212 se desintegra, mediante emisión alfa, en talio-208 mientrasEl 64,06(6) % [26] del bismuto-212 se desintegra, mediante emisión beta, en polonio-212 . Tanto el talio-208 como el polonio-212 son productos radiactivos derivados del bismuto-212, y ambos se desintegran directamente en plomo-208 estable .
Ocurrencia y aplicaciones
Según la teoría del Big Bang , los isótopos estables de los tres elementos más ligeros ( H , He y trazas de Li ) se produjeron muy poco después del surgimiento del universo, en un proceso llamado nucleosíntesis del Big Bang . Estos nucleidos estables más ligeros (incluido el deuterio ) sobreviven hasta hoy, pero cualquier isótopo radiactivo de los elementos ligeros producidos en el Big Bang (como el tritio ) se ha desintegrado hace mucho tiempo. Los isótopos de elementos más pesados que el boro no se produjeron en absoluto en el Big Bang, y estos primeros cinco elementos no tienen radioisótopos de larga duración. Por lo tanto, todos los núcleos radiactivos son, por lo tanto, relativamente jóvenes con respecto al nacimiento del universo, habiéndose formado más tarde en varios otros tipos de nucleosíntesis en estrellas (en particular, supernovas ), y también durante las interacciones en curso entre isótopos estables y partículas energéticas. Por ejemplo, el carbono-14 , un nucleido radiactivo con una vida media de solo5700(30) años, [26] se produce constantemente en la atmósfera superior de la Tierra debido a las interacciones entre los rayos cósmicos y el nitrógeno.
Los nucleidos que se producen por desintegración radiactiva se denominan nucleidos radiogénicos , ya sean estables o no. Existen nucleidos radiogénicos estables que se formaron a partir de radionucleidos extintos de vida corta en el Sistema Solar primitivo. [27] [28] La presencia adicional de estos nucleidos radiogénicos estables (como el xenón-129 a partir del yodo-129 extinto ) en el contexto de nucleidos estables primordiales se puede inferir por varios medios.
La desintegración radiactiva se ha utilizado en la técnica del marcaje radioisotópico , que se utiliza para rastrear el paso de una sustancia química a través de un sistema complejo (como un organismo vivo ). Se sintetiza una muestra de la sustancia con una alta concentración de átomos inestables. La presencia de la sustancia en una u otra parte del sistema se determina detectando las ubicaciones de los eventos de desintegración.
Partiendo de la premisa de que la desintegración radiactiva es verdaderamente aleatoria (y no meramente caótica ), se ha utilizado en generadores de números aleatorios de hardware . Como no se cree que el proceso varíe significativamente en su mecanismo a lo largo del tiempo, también es una herramienta valiosa para estimar las edades absolutas de ciertos materiales. En el caso de los materiales geológicos, los radioisótopos y algunos de sus productos de desintegración quedan atrapados cuando una roca se solidifica, y pueden utilizarse posteriormente (sujeto a muchas salvedades bien conocidas) para estimar la fecha de la solidificación. Estas incluyen la comprobación de los resultados de varios procesos simultáneos y sus productos entre sí, dentro de la misma muestra. De manera similar, y también sujeta a salvedades, se puede estimar la tasa de formación del carbono-14 en varias eras, la fecha de formación de la materia orgánica dentro de un período determinado relacionado con la vida media del isótopo, porque el carbono-14 queda atrapado cuando la materia orgánica crece e incorpora el nuevo carbono-14 del aire. Posteriormente, la cantidad de carbono-14 en la materia orgánica disminuye de acuerdo con procesos de descomposición que también pueden comprobarse independientemente por otros medios (como, por ejemplo, comprobando el carbono-14 en los anillos de los árboles individuales).
Efecto Szilard-Chalmers
El efecto Szilard-Chalmers es la ruptura de un enlace químico como resultado de una energía cinética impartida por la desintegración radiactiva. Funciona mediante la absorción de neutrones por un átomo y la posterior emisión de rayos gamma, a menudo con cantidades significativas de energía cinética. Esta energía cinética, por la tercera ley de Newton , empuja hacia atrás al átomo en desintegración, lo que hace que se mueva con suficiente velocidad para romper un enlace químico. [29] Este efecto se puede utilizar para separar isótopos por medios químicos.
El efecto Szilard-Chalmers fue descubierto en 1934 por Leó Szilárd y Thomas A. Chalmers. [30] Observaron que después del bombardeo con neutrones, la ruptura de un enlace en el yoduro de etilo líquido permitía eliminar el yodo radiactivo. [31]
Orígenes de los nucleidos radiactivos
Los nucleidos radiactivos primordiales que se encuentran en la Tierra son residuos de antiguas explosiones de supernovas que ocurrieron antes de la formación del Sistema Solar . Son la fracción de radionucleidos que sobrevivieron desde ese momento, a través de la formación de la nebulosa solar primordial, a través de la acreción planetaria y hasta el momento actual. Los radionucleidos radiogénicos de vida corta que se producen naturalmente y que se encuentran en las rocas actuales son los hijos de esos nucleidos radiactivos primordiales. Otra fuente menor de nucleidos radiactivos naturales son los nucleidos cosmogénicos , que se forman por el bombardeo de rayos cósmicos de material en la atmósfera o la corteza terrestre . La desintegración de los radionucleidos en las rocas del manto y la corteza terrestres contribuye significativamente al balance de calor interno de la Tierra .
Procesos agregados
Si bien el proceso subyacente de la desintegración radiactiva es subatómico, históricamente y en la mayoría de los casos prácticos se da en materiales a granel con cantidades muy grandes de átomos. En esta sección se analizan modelos que vinculan los eventos a nivel atómico con las observaciones en conjunto.
Terminología
La tasa de desintegración , o actividad , de una sustancia radiactiva se caracteriza por los siguientes parámetros independientes del tiempo:
- La vida media , t 1/2 , es el tiempo que tarda la actividad de una cantidad determinada de una sustancia radiactiva en decaer a la mitad de su valor inicial.
- La constante de desintegración , λ " lambda ", es el recíproco de la vida media (en s −1 ), a veces denominada simplemente tasa de desintegración .
- La vida media , τ " tau ", es la vida media (1/ e vida) de una partícula radiactiva antes de la desintegración.
Aunque se trata de constantes, están asociadas al comportamiento estadístico de poblaciones de átomos. En consecuencia, las predicciones que utilizan estas constantes son menos precisas para muestras minúsculas de átomos.
En principio, una vida media, una tercera vida o incluso una vida (1/√2) podrían usarse exactamente de la misma manera que la vida media; pero la vida media y la vida media t 1/2 se han adoptado como tiempos estándar asociados con la descomposición exponencial.
Estos parámetros pueden estar relacionados con los siguientes parámetros dependientes del tiempo:
- La actividad total (o simplemente actividad ), A , es el número de desintegraciones por unidad de tiempo de una muestra radiactiva.
- Número de partículas , N , en la muestra.
- La actividad específica , a , es el número de desintegraciones por unidad de tiempo por cantidad de sustancia de la muestra en el tiempo establecido en cero ( t = 0 ). La "cantidad de sustancia" puede ser la masa, el volumen o los moles de la muestra inicial.
Estos se relacionan de la siguiente manera:
donde N 0 es la cantidad inicial de sustancia activa, sustancia que tiene el mismo porcentaje de partículas inestables que cuando se formó la sustancia.
Supuestos
Las matemáticas de la desintegración radiactiva dependen de un supuesto clave: el núcleo de un radionúclido no tiene "memoria" ni forma de traducir su historia a su comportamiento actual. Un núcleo no "envejece" con el paso del tiempo. Por lo tanto, la probabilidad de que se descomponga no aumenta con el tiempo, sino que permanece constante, sin importar cuánto tiempo haya existido el núcleo. Esta probabilidad constante puede variar mucho entre un tipo de núcleo y otro, lo que da lugar a las distintas tasas de desintegración observadas. Sin embargo, sea cual sea la probabilidad, no cambia con el tiempo. Esto contrasta marcadamente con los objetos complejos que sí muestran envejecimiento, como los automóviles y los seres humanos. Estos sistemas envejecidos tienen una probabilidad de desintegración por unidad de tiempo que aumenta desde el momento en que comienzan su existencia.
Los procesos agregados, como la desintegración radiactiva de un conjunto de átomos, para los cuales la probabilidad de realización de un solo evento es muy pequeña pero en los cuales el número de porciones de tiempo es tan grande que hay, no obstante, una tasa razonable de eventos, se modelan mediante la distribución de Poisson , que es discreta. La desintegración radiactiva y las reacciones de partículas nucleares son dos ejemplos de tales procesos agregados. [32] Las matemáticas de los procesos de Poisson se reducen a la ley de desintegración exponencial , que describe el comportamiento estadístico de un gran número de núcleos, en lugar de un núcleo individual. En el siguiente formalismo, el número de núcleos o la población de núcleos N , es por supuesto una variable discreta (un número natural ), pero para cualquier muestra física N es tan grande que puede ser tratado como una variable continua. El cálculo diferencial se utiliza para modelar el comportamiento de la desintegración nuclear.
Proceso de una sola desintegración
Consideremos el caso de un nucleido A que se desintegra en otro B mediante algún proceso A → B (emisión de otras partículas, como neutrinos electrónicos) .
no
miy los electrones e − como en la desintegración beta , son irrelevantes en lo que sigue). La desintegración de un núcleo inestable es completamente aleatoria en el tiempo, por lo que es imposible predecir cuándo se desintegrará un átomo en particular. Sin embargo, es igualmente probable que se desintegra en cualquier instante en el tiempo. Por lo tanto, dada una muestra de un radioisótopo particular, el número de eventos de desintegración −d N que se espera que ocurran en un pequeño intervalo de tiempo d t es proporcional al número de átomos presentes N , es decir [33]
Los radionucleidos particulares se desintegran a diferentes velocidades, por lo que cada uno tiene su propia constante de desintegración λ . La desintegración esperada −d N / N es proporcional a un incremento de tiempo, d t :
El signo negativo indica que N disminuye a medida que aumenta el tiempo, ya que los eventos de desintegración se suceden uno tras otro. La solución de esta ecuación diferencial de primer orden es la función :
donde N 0 es el valor de N en el tiempo t = 0, con la constante de decaimiento expresada como λ [33]
Tenemos desde siempre t :
donde N total es el número constante de partículas a lo largo del proceso de desintegración, que es igual al número inicial de nucleidos A ya que ésta es la sustancia inicial.
Si el número de núcleos A no desintegrados es:
entonces el número de núcleos de B (es decir, el número de núcleos de A desintegrados ) es
El número de desintegraciones observadas en un intervalo dado obedece a la estadística de Poisson . Si el número promedio de desintegraciones es ⟨ N ⟩ , la probabilidad de un número dado de desintegraciones N es [33]
Procesos de desintegración en cadena
Cadena de dos desintegraciones
Ahora consideremos el caso de una cadena de dos desintegraciones: un nucleido A que se desintegra en otro B mediante un proceso, luego B que se desintegra en otro C mediante un segundo proceso, es decir, A → B → C . La ecuación anterior no se puede aplicar a la cadena de desintegración, pero se puede generalizar de la siguiente manera. Dado que A se desintegra en B , luego B se desintegra en C , la actividad de A se suma al número total de nucleidos B en la muestra actual, antes de que esos nucleidos B se desintegran y reducen el número de nucleidos que conducen a la muestra posterior. En otras palabras, el número de núcleos de segunda generación B aumenta como resultado de la desintegración de los núcleos de primera generación de A , y disminuye como resultado de su propia desintegración en los núcleos de tercera generación C . [34] La suma de estos dos términos da la ley para una cadena de desintegración de dos nucleidos:
La tasa de cambio de N B , es decir d N B /d t , está relacionada con los cambios en las cantidades de A y B , N B puede aumentar a medida que B se produce a partir de A y disminuir a medida que B produce C .
Reescribiendo utilizando los resultados anteriores:
Los subíndices simplemente se refieren a los respectivos nucleidos, es decir , N A es el número de nucleidos del tipo A ; N A 0 es el número inicial de nucleidos del tipo A ; λ A es la constante de desintegración de A – y de manera similar para el nucleido B. Resolviendo esta ecuación para N B se obtiene:
En el caso en que B sea un nucleido estable ( λ B = 0), esta ecuación se reduce a la solución anterior:
como se muestra arriba para una desintegración. La solución se puede encontrar mediante el método del factor de integración , donde el factor de integración es e λ B t . Este caso es quizás el más útil ya que puede derivar tanto la ecuación de una desintegración (arriba) como la ecuación para cadenas de múltiples desintegraciones (abajo) de manera más directa.
Cadena de cualquier número de desintegraciones
Para el caso general de cualquier número de desintegraciones consecutivas en una cadena de desintegración, es decir A 1 → A 2 ··· → A i ··· → A D , donde D es el número de desintegraciones e i es un índice ficticio ( i = 1, 2, 3, ..., D ), cada población de nucleidos se puede encontrar en términos de la población anterior. En este caso N 2 = 0 , N 3 = 0 , ..., N D = 0 . Utilizando el resultado anterior en una forma recursiva:
La solución general del problema recursivo viene dada por las ecuaciones de Bateman : [35]
Varios productos
En todos los ejemplos anteriores, el nucleido inicial se desintegra en un solo producto. [36] Consideremos el caso de un nucleido inicial que puede desintegrarse en cualquiera de los dos productos, es decir, A → B y A → C en paralelo. Por ejemplo, en una muestra de potasio-40 , el 89,3% de los núcleos se desintegran en calcio-40 y el 10,7% en argón-40 . Para todo el tiempo t tenemos :
que es constante, ya que el número total de nucleidos permanece constante. Derivando con respecto al tiempo:
definiendo la constante de desintegración total λ en términos de la suma de las constantes de desintegración parcial λ B y λ C :
Resolviendo esta ecuación para N A :
donde N A 0 es el número inicial de nucleidos A. Al medir la producción de un nucleido, solo se puede observar la constante de desintegración total λ . Las constantes de desintegración λ B y λ C determinan la probabilidad de que la desintegración dé como resultado los productos B o C de la siguiente manera:
porque la fracción λ B / λ de núcleos se desintegra en B mientras que la fracción λ C / λ de núcleos se desintegra en C.
Corolarios de las leyes
Las ecuaciones anteriores también se pueden escribir utilizando cantidades relacionadas con el número de partículas de nucleido N en una muestra;
- La actividad: A = λN .
- La cantidad de sustancia : n = N / N A .
- La masa : m = Mn = MN / N A .
donde N A =6.022 140 76 × 10 23 mol −1 [ 37] es la constante de Avogadro , M es la masa molar de la sustancia en kg/mol y la cantidad de la sustancia n está en moles .
Tiempo de decaimiento: definiciones y relaciones
Constante de tiempo y vida media
Para la solución de una desintegración A → B :
La ecuación indica que la constante de desintegración λ tiene unidades de t −1 y, por lo tanto, también puede representarse como 1/ τ , donde τ es un tiempo característico del proceso llamado constante de tiempo .
En un proceso de desintegración radiactiva, esta constante de tiempo es también la vida media de los átomos en desintegración. Cada átomo "vive" durante una cantidad finita de tiempo antes de desintegrarse, y se puede demostrar que esta vida media es la media aritmética de las vidas de todos los átomos, y que es τ , que a su vez está relacionada con la constante de desintegración de la siguiente manera:
Esta forma también es válida para dos procesos de desintegración simultánea A → B + C , insertando los valores equivalentes de las constantes de desintegración (como se indica arriba)
En la solución de descomposición se produce:

Vida media
Un parámetro más comúnmente utilizado es la vida media T 1/2 . Dada una muestra de un radionúclido en particular, la vida media es el tiempo que tarda la mitad de los átomos del radionúclido en desintegrarse. Para el caso de reacciones nucleares de una sola desintegración:
La vida media está relacionada con la constante de desintegración de la siguiente manera: establezca N = N 0 /2 y t = T 1/2 para obtener
Esta relación entre la vida media y la constante de desintegración muestra que las sustancias altamente radiactivas se gastan rápidamente, mientras que las que irradian débilmente duran más. Las vidas medias de los radionucleidos conocidos varían en casi 54 órdenes de magnitud, desde más de2,25(9) × 10 24 años (6,9 × 10 31 seg) para el nucleido casi estable 128 Te ,8,6(6) × 10 −23 segundos para el nucleido altamente inestable 5 H . [26]
El factor de ln(2) en las relaciones anteriores resulta del hecho de que el concepto de "vida media" es simplemente una forma de seleccionar una base diferente a la base natural e para la expresión de la vida media. La constante de tiempo τ es la vida media e −1 , el tiempo hasta que solo queda 1/ e , aproximadamente el 36,8%, en lugar del 50% en la vida media de un radionúclido. Por lo tanto, τ es más largo que t 1/2 . Se puede demostrar que la siguiente ecuación es válida:
Como la desintegración radiactiva es exponencial con una probabilidad constante, cada proceso podría describirse fácilmente con un período de tiempo constante diferente que (por ejemplo) diera su "vida (1/3)" (cuánto tiempo hasta que quede solo 1/3) o su "vida (1/10)" (un período de tiempo hasta que quede solo el 10%), y así sucesivamente. Por lo tanto, la elección de τ y t 1/2 como tiempos marcadores es solo por conveniencia y por convención. Reflejan un principio fundamental solo en la medida en que muestran que la misma proporción de una sustancia radiactiva dada se desintegrará durante cualquier período de tiempo que se elija.
Matemáticamente, la n- ésima vida para la situación anterior se encontraría de la misma manera que antes: estableciendo N = N 0 /n , t = T 1/ n y sustituyendo en la solución de desintegración para obtener
Ejemplo para el carbono-14
El carbono-14 tiene una vida media de5700(30) años [26] y una tasa de desintegración de 14 desintegraciones por minuto (dpm) por gramo de carbono natural.
Si se descubre que un artefacto tiene una radiactividad de 4 dpm por gramo de su C actual, podemos encontrar la edad aproximada del objeto utilizando la ecuación anterior:
dónde:
Cambios en las tasas
Se sabe que los modos de desintegración radiactiva de captura de electrones y conversión interna son ligeramente sensibles a los efectos químicos y ambientales que cambian la estructura electrónica del átomo, lo que a su vez afecta la presencia de electrones 1s y 2s que participan en el proceso de desintegración. Un pequeño número de nucleidos se ven afectados. [38] Por ejemplo, los enlaces químicos pueden afectar la tasa de captura de electrones en un pequeño grado (en general, menos del 1%) dependiendo de la proximidad de los electrones al núcleo. En 7Be , se ha observado una diferencia del 0,9% entre las vidas medias en entornos metálicos y aislantes. [39] Este efecto relativamente grande se debe a que el berilio es un átomo pequeño cuyos electrones de valencia están en orbitales atómicos 2s , que están sujetos a la captura de electrones en 7Be porque (como todos los orbitales atómicos s en todos los átomos) penetran naturalmente en el núcleo.
En 1992, Jung et al. del grupo de investigación de iones pesados de Darmstadt observaron una desintegración β − acelerada del 163 Dy 66+ . Aunque el 163 Dy neutro es un isótopo estable, el 163 Dy 66+ completamente ionizado sufre una desintegración β − en las capas K y L para formar el 163 Ho 66+ con una vida media de 47 días. [40]
El renio-187 es otro ejemplo espectacular. El 187 Re normalmente sufre una desintegración beta a 187 Os con una vida media de 41,6 × 10 9 años, [41] pero estudios que utilizan átomos de 187 Re completamente ionizados (núcleos desnudos) han descubierto que esta puede disminuir a solo 32,9 años. [42] Esto se atribuye a la " desintegración β − del estado ligado " del átomo completamente ionizado: el electrón se emite a la "capa K" ( orbital atómico 1s ), lo que no puede ocurrir para átomos neutros en los que todos los estados ligados de baja altitud están ocupados. [43]
Varios experimentos han demostrado que las tasas de desintegración de otros tipos de radioisótopos artificiales y naturales no se ven afectadas, con un alto grado de precisión, por condiciones externas como la temperatura, la presión, el entorno químico y los campos eléctricos, magnéticos o gravitacionales. [44] La comparación de experimentos de laboratorio durante el último siglo, estudios del reactor nuclear natural Oklo (que ejemplificó los efectos de los neutrones térmicos en la desintegración nuclear) y observaciones astrofísicas de las desintegraciones de luminosidad de supernovas distantes (que ocurrieron muy lejos, por lo que la luz ha tardado mucho tiempo en llegar hasta nosotros), por ejemplo, indican firmemente que las tasas de desintegración no perturbadas han sido constantes (al menos dentro de las limitaciones de pequeños errores experimentales) también como función del tiempo. [ cita requerida ]
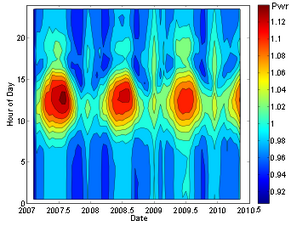
Resultados recientes sugieren la posibilidad de que las tasas de desintegración puedan tener una dependencia débil de factores ambientales. Se ha sugerido que las mediciones de las tasas de desintegración de silicio-32 , manganeso-54 y radio-226 exhiben pequeñas variaciones estacionales (del orden del 0,1%). [45] [46] [47] Sin embargo, dichas mediciones son altamente susceptibles a errores sistemáticos, y un artículo posterior [48] no ha encontrado evidencia de tales correlaciones en otros siete isótopos ( 22 Na, 44 Ti, 108 Ag, 121 Sn, 133 Ba, 241 Am, 238 Pu), y establece límites superiores al tamaño de dichos efectos. Se informó una vez que la desintegración del radón-222 exhibía grandes variaciones estacionales de un 4% de pico a pico (ver gráfico), [49] que se propuso que estaban relacionadas con la actividad de erupciones solares o la distancia al Sol, pero un análisis detallado de los defectos de diseño del experimento, junto con comparaciones con otros experimentos mucho más estrictos y controlados sistemáticamente, refutan esta afirmación. [50]
Anomalía GSI
Una serie inesperada de resultados experimentales para la tasa de desintegración de iones radiactivos pesados altamente cargados que circulan en un anillo de almacenamiento ha provocado una actividad teórica en un esfuerzo por encontrar una explicación convincente. Se ha descubierto que las tasas de desintegración débil de dos especies radiactivas con vidas medias de aproximadamente 40 s y 200 s tienen una modulación oscilatoria significativa , con un período de aproximadamente 7 s. [51] El fenómeno observado se conoce como la anomalía GSI , ya que el anillo de almacenamiento es una instalación en el Centro GSI Helmholtz para la Investigación de Iones Pesados en Darmstadt , Alemania . Como el proceso de desintegración produce un neutrino electrónico , algunas de las explicaciones propuestas para la oscilación de velocidad observada invocan propiedades de neutrinos. Las ideas iniciales relacionadas con la oscilación del sabor se encontraron con escepticismo. [52] Una propuesta más reciente involucra diferencias de masa entre los estados propios de masa de los neutrinos . [53]
Procesos nucleares
Se considera que un nucleido "existe" si tiene una vida media mayor que 2x10 -14 s. Este es un límite arbitrario; las vidas medias más cortas se consideran resonancias, como un sistema que experimenta una reacción nuclear. Esta escala de tiempo es característica de la interacción fuerte que crea la fuerza nuclear . Se considera que solo los nucleidos se desintegran y producen radiactividad. [54] : 568
Los nucleidos pueden ser estables o inestables. Los nucleidos inestables se desintegran, posiblemente en varios pasos, hasta que se vuelven estables. Se conocen 256 nucleidos estables. El número de nucleidos inestables descubiertos ha aumentado, y en 2006 se conocían unos 3000. [54]
Las formas más comunes y, por lo tanto, históricamente más importantes de desintegración radiactiva natural implican la emisión de partículas alfa, partículas beta y rayos gamma. Cada una de ellas corresponde a una interacción fundamental predominantemente responsable de la radiactividad: [55] : 142
- desintegración alfa -> interacción fuerte ,
- desintegración beta -> interacción débil ,
- desintegración gamma -> electromagnetismo .
En la desintegración alfa, una partícula que contiene dos protones y dos neutrones, equivalente a un núcleo de He, se desprende del núcleo original. El proceso representa una competencia entre la repulsión electromagnética entre los protones en el núcleo y la fuerza nuclear atractiva , un residuo de la interacción fuerte. La partícula alfa es un núcleo especialmente fuertemente unido, lo que le ayuda a ganar la competencia con más frecuencia. [56] : 872 Sin embargo, algunos núcleos se rompen o se fisionan en partículas más grandes y los núcleos artificiales se desintegran con la emisión de protones simples, protones dobles y otras combinaciones. [54]
La desintegración beta transforma un neutrón en un protón o viceversa. Cuando un neutrón dentro de un nucleido padre se desintegra en un protón, se forma un electrón, un antineutrino y un nucleido con un número atómico alto. Cuando un protón en un nucleido padre se transforma en un neutrón, se forma un positrón , un neutrino y un nucleido con un número atómico más bajo. Estos cambios son una manifestación directa de la interacción débil. [56] : 874
La desintegración gamma se parece a otros tipos de emisión electromagnética: corresponde a transiciones entre un estado cuántico excitado y un estado de energía más bajo. Cualquiera de los mecanismos de desintegración de partículas suele dejar a la hija en un estado excitado, que luego se desintegra mediante emisión gamma. [56] : 876
Otras formas de desintegración incluyen la emisión de neutrones , la captura de electrones , la conversión interna y la desintegración en cúmulos . [57]
Señales de advertencia de peligro
- El símbolo del trébol se utiliza para advertir de la presencia de material radiactivo o radiación ionizante.
- Símbolo de peligro de radiactividad ISO 2007 destinado a fuentes de categorías 1, 2 y 3 del OIEA definidas como fuentes peligrosas capaces de causar la muerte o lesiones graves [58]
- Una de las varias señales de clasificación de transporte de mercancías peligrosas para materiales radiactivos
Véase también
- Actínidos en el medio ambiente
- Radiación de fondo
- Desastre de Chernóbil
- Delitos relacionados con sustancias radiactivas
- Cadena de desintegración
- Corrección de la descomposición
- Refugio antiatómico
- contador Geiger
- Radiactividad inducida
- Listas de desastres nucleares e incidentes radiactivos
- Consejo Nacional de Medidas y Protección Radiológica
- Ingeniería nuclear
- Farmacia nuclear
- Física nuclear
- Energía nuclear
- Reacción nuclear en cadena
- Desintegración de partículas
- Proceso de Poisson
- Radioterapia
- Contaminación radiactiva
- La radiactividad en la biología
- Datación radiométrica
- Estocástico
- Equilibrio transitorio
 Portal de tecnología nuclear
Portal de tecnología nuclear Portal de física
Portal de física
Notas
Referencias
- ^ "Radioactividad: fuerzas débiles". Radioactividad . EDP Sciences. Archivado desde el original el 12 de agosto de 2021 . Consultado el 4 de marzo de 2020 .
- ^ Stabin, Michael G. (2007). "3". En Stabin, Michael G (ed.). Protección radiológica y dosimetría: una introducción a la física de la salud . Springer . doi :10.1007/978-0-387-49983-3. ISBN . 978-0-387-49982-6.
- ^ Best, Lara; Rodrigues, George; Velker, Vikram (2013). "1.3". Introducción y revisión de la oncología radioterápica . Demos Medical Publishing . ISBN 978-1-62070-004-4.
- ^ Loveland, W.; Morrissey, D.; Seaborg, GT (2006). Química nuclear moderna . Wiley-Interscience. p. 57. Bibcode :2005mnc..book.....L. ISBN 978-0-471-11532-8.
- ^ Mould, Richard F. (1995). Un siglo de rayos X y radiactividad en medicina: con énfasis en los registros fotográficos de los primeros años (Reimpresión con correcciones menores). Bristol: Inst. of Physics Publ. p. 12. ISBN 978-0-7503-0224-1.
- ^ Henri Becquerel (1896). "Sur les radiaciones emitidas por fosforescencia". Cuentas Rendus . 122 : 420–421.
- ↑ Comptes Rendus 122 : 420 (1896), traducido por Carmen Giunta. Consultado el 12 de abril de 2021.
- ^ Henri Becquerel (1896). "Sobre las radiaciones invisibles emitidas por los cuerpos fosforescentes". Cuentas Rendus . 122 : 501–503.
- ↑ Comptes Rendus 122 : 501–503 (1896), traducido por Carmen Giunta. Consultado el 12 de abril de 2021.
- ^ Kasimir Fajans, "Transformaciones radiactivas y sistema periódico de los elementos". Berichte der Deutschen Chemischen Gesellschaft , nr. 46, 1913, págs. 422–439
- ^ Frederick Soddy, "Los elementos de radio y la ley periódica", Chem. News, Nr. 107, 1913, págs. 97-99
- ^ ab L'Annunziata, Michael F. (2007). Radiactividad: Introducción e historia . Ámsterdam, Países Bajos: Elsevier Science. p. 2. ISBN 9780080548883.
- ^ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). Química general (8.ª ed.). Prentice Hall. pág. 1025. ISBN 0-13-014329-4.
- ^ Sansare, K.; Khanna, V.; Karjodkar, F. (2011). "Víctimas tempranas de los rayos X: un tributo y la percepción actual". Radiología dentomaxilofacial . 40 (2): 123–125. doi :10.1259/dmfr/73488299. ISSN 0250-832X. PMC 3520298 . PMID 21239576.
- ^ ab "Ronald L. Kathern y Paul L. Ziemer, Los primeros cincuenta años de protección radiológica, physics.isu.edu". Archivado desde el original el 12 de septiembre de 2017. Consultado el 25 de noviembre de 2013 .
- ^ Hrabak, M.; Padovan, RS; Kralik, M.; Ozretic, D.; Potocki, K. (julio de 2008). "Nikola Tesla y el descubrimiento de los rayos X". RadioGraphics . 28 (4): 1189–92. doi : 10.1148/rg.284075206 . PMID 18635636.
- ^ Rentetzi, Maria (7 de noviembre de 2017). «Marie Curie y los peligros del radio». Physics Today (11): 30676. Bibcode :2017PhT..2017k0676R. doi :10.1063/PT.6.4.20171107a . Consultado el 3 de mayo de 2022 .
- ^ Clarke, RH; J. Valentin (2009). "La historia de la ICRP y la evolución de sus políticas" (PDF) . Anales de la ICRP . Publicación de la ICRP 109. 39 (1): 75–110. doi :10.1016/j.icrp.2009.07.009. S2CID 71278114 . Consultado el 12 de mayo de 2012 .
- ^ Daniels, M.; et al. (2020). "Estudios epidemiológicos de radiación ionizante de dosis baja y cáncer: evaluación resumida del sesgo y metanálisis". J Natl Cancer Inst Monogr . 56 (1 de julio): 188–200. doi :10.1093/jncimonographs/lgaa010. ISSN 1434-6001. PMC 8454205. PMID 32657347 .
- ^ Venturi, Sebastiano (enero de 2021). "El cesio en la biología, el cáncer de páncreas y la controversia sobre los daños causados por la exposición a la radiación alta y baja: aspectos científicos, ambientales, geopolíticos y económicos". Revista internacional de investigación ambiental y salud pública . 18 (17): 8934. doi : 10.3390/ijerph18178934 . PMC 8431133 . PMID 34501532.
 El texto fue copiado de esta fuente, que está disponible bajo una Licencia Creative Commons Atribución 4.0 Internacional.
El texto fue copiado de esta fuente, que está disponible bajo una Licencia Creative Commons Atribución 4.0 Internacional. - ^ Rutherford, Ernest (6 de octubre de 1910). «Nomenclatura y estándares del radio». Nature . 84 (2136): 430–431. Bibcode :1910Natur..84..430R. doi : 10.1038/084430a0 .
- ^ 10 CFR 20.1005. Comisión Reguladora Nuclear de Estados Unidos. 2009.
- ^ Consejo de las Comunidades Europeas (21 de diciembre de 1979). «Directiva 80/181/CEE del Consejo, de 20 de diciembre de 1979, relativa a la aproximación de las legislaciones de los Estados miembros sobre las unidades de medida y a la derogación de la Directiva 71/354/CEE» . Consultado el 19 de mayo de 2012 .
- ^ "Desintegración radiactiva". chemed.chem.purdue.edu . Consultado el 5 de mayo de 2022 .
- ^ «CH103 – Capítulo 3: Radiactividad y química nuclear – Química» . Consultado el 5 de julio de 2022 .
- ^ abcdefghi Kondev, FG; Wang, M.; Huang, WJ; Naimi, S.; Audi, G. (2021). "La evaluación NUBASE2020 de las propiedades nucleares" (PDF) . Chinese Physics C . 45 (3): 030001. doi :10.1088/1674-1137/abddae.
- ^ Clayton, Donald D. (1983). Principios de evolución estelar y nucleosíntesis (2.ª ed.). University of Chicago Press. pág. 75. ISBN 978-0-226-10953-4.
- ^ Bolt, BA; Packard, RE; Price, PB (2007). "John H. Reynolds, Physics: Berkeley". Universidad de California, Berkeley . Consultado el 1 de octubre de 2007 .
- ^ "Efecto Szilard-Chalmers - Oxford Reference". oxfordreference.com . Consultado el 27 de diciembre de 2019 .
- ^ Szilard, Leó; Chalmers, Thomas A. (1934). "Separación química del elemento radiactivo de su isótopo bombardeado en el efecto Fermi". Nature . 134 (3386): 462. Bibcode :1934Natur.134..462S. doi : 10.1038/134462b0 . S2CID 4129460.
- ^ Harbottle, Garman; Sutin, Norman (1 de enero de 1959), Emeléus, HJ; Sharpe, AG (eds.), La reacción de Szilard-Chalmers en sólidos, Advances in Inorganic Chemistry and Radiochemistry, vol. 1, Academic Press, págs. 267–314, doi :10.1016/S0065-2792(08)60256-3, ISBN 9780120236015, consultado el 19 de marzo de 2020
- ^ Leo, William R. (1992). "Cap. 4". Estadística y tratamiento de datos experimentales (Técnicas para experimentos de física nuclear y de partículas, ed.). Springer-Verlag.
- ^ abc Patel, SB (2000). Física nuclear: una introducción . Nueva Delhi: New Age International. págs. 62-72. ISBN 978-81-224-0125-7.
- ^ Introducción a la física nuclear, KS Krane, 1988, John Wiley & Sons Inc, ISBN 978-0-471-80553-3
- ^ Cetnar, Jerzy (mayo de 2006). "Solución general de ecuaciones de Bateman para transmutaciones nucleares". Anales de energía nuclear . 33 (7): 640–645. Bibcode :2006AnNuE..33..640C. doi :10.1016/j.anucene.2006.02.004.
- ^ KS Krane (1988). Introducción a la física nuclear . John Wiley & Sons Inc., pág. 164. ISBN 978-0-471-80553-3.
- ^ "Valor CODATA 2022: constante de Avogadro". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Mayo de 2024. Consultado el 18 de mayo de 2024 .
- ^ Emery, GT (diciembre de 1972). "Perturbación de las tasas de desintegración nuclear". Revista anual de ciencia nuclear . 22 (1): 165–202. Código Bibliográfico :1972ARNPS..22..165E. doi :10.1146/annurev.ns.22.120172.001121. ISSN 0066-4243 . Consultado el 23 de febrero de 2022 .
- ^ Wang, B.; et al. (2006). "Cambio de la vida media de captura de electrones del 7Be en entornos metálicos". The European Physical Journal A . 28 (3): 375–377. Bibcode :2006EPJA...28..375W. doi :10.1140/epja/i2006-10068-x. ISSN 1434-6001. S2CID 121883028.
- ^ Jung, M.; et al. (1992). "Primera observación de la desintegración β − en estado ligado ". Physical Review Letters . 69 (15): 2164–2167. Bibcode :1992PhRvL..69.2164J. doi :10.1103/PhysRevLett.69.2164. ISSN 0031-9007. PMID 10046415.
- ^ Smoliar, MI; Walker, RJ; Morgan, JW (1996). "Edades Re-Os de meteoritos de hierro de los grupos IIA, IIIA, IVA y IVB". Science . 271 (5252): 1099–1102. Bibcode :1996Sci...271.1099S. doi :10.1126/science.271.5252.1099. S2CID 96376008.
- ^ Bosch, F.; et al. (1996). "Observación de la desintegración beta-menos en estado ligado de 187 Re: 187 Re– 187 Os Cosmochronometry completamente ionizado". Physical Review Letters . 77 (26): 5190–5193. Bibcode :1996PhRvL..77.5190B. doi :10.1103/PhysRevLett.77.5190. PMID 10062738.
- ^ Bosch, F.; et al. (1996). "Observación de la desintegración β en estado ligado de átomos completamente ionizados de 187 Re: 187 Re- 187 Os Cosmochronometry". Physical Review Letters . 77 (26): 5190–5193. Bibcode :1996PhRvL..77.5190B. doi :10.1103/PhysRevLett.77.5190. PMID 10062738.
- ^ Emery, GT (1972). "Perturbación de las tasas de desintegración nuclear". Revista anual de ciencia nuclear . 22 (1): 165–202. Código Bibliográfico :1972ARNPS..22..165E. doi : 10.1146/annurev.ns.22.120172.001121 .
- ^ "El misterio de la desintegración nuclear variable". Physics World . 2 de octubre de 2008.
- ^ Jenkins, Jere H.; Fischbach, Ephraim (2009). "Perturbación de las tasas de desintegración nuclear durante la llamarada solar del 13 de diciembre de 2006". Astroparticle Physics . 31 (6): 407–411. arXiv : 0808.3156 . Bibcode :2009APh....31..407J. doi :10.1016/j.astropartphys.2009.04.005. S2CID 118863334.
- ^ Jenkins, JH; Fischbach, Ephraim; Buncher, John B.; Gruenwald, John T.; Krause, Dennis E.; Mattes, Joshua J. (2009). "Evidencia de correlaciones entre las tasas de desintegración nuclear y la distancia Tierra-Sol". Astroparticle Physics . 32 (1): 42–46. arXiv : 0808.3283 . Bibcode :2009APh....32...42J. doi :10.1016/j.astropartphys.2009.05.004. S2CID 119113836.
- ^ Norman, EB; Browne, Edgardo; Shugart, Howard A.; Joshi, Tenzing H.; Firestone, Richard B. (2009). "Evidencia contra las correlaciones entre las tasas de desintegración nuclear y la distancia Tierra-Sol" (PDF) . Astroparticle Physics . 31 (2): 135–137. arXiv : 0810.3265 . Bibcode :2009APh....31..135N. doi :10.1016/j.astropartphys.2008.12.004. S2CID 7051382. Archivado desde el original (PDF) el 29 de junio de 2010 . Consultado el 23 de septiembre de 2009 .
- ^ Sturrock, PA; Steinitz, G.; Fischbach, E.; Javorsek, D.; Jenkins, JH (2012). "Análisis de la radiación gamma de una fuente de radón: indicaciones de una influencia solar". Astroparticle Physics . 36 (1): 18–25. arXiv : 1205.0205 . Bibcode :2012APh....36...18S. doi :10.1016/j.astropartphys.2012.04.009. ISSN 0927-6505. S2CID 119163371.
- ^ Pommé, S.; Lutter, G.; Marouli, M.; Kossert, K.; Nähle, O. (1 de enero de 2018). "Sobre la afirmación de modulaciones en la desintegración del radón y su asociación con la rotación solar". Astroparticle Physics . 97 : 38–45. Bibcode :2018APh....97...38P. doi : 10.1016/j.astropartphys.2017.10.011 . ISSN 0927-6505.
- ^ Kienle P, Bosch F, Bühler P, Faestermanna T, Litvinov Yu.A., Winckler N, et al. (2013). "Medición de alta resolución de la captura electrónica orbital modulada en el tiempo y de la desintegración β + de iones de 142 Pm 60+ similares al hidrógeno ". Physics Letters B . 726 (4–5): 638–645. arXiv : 1309.7294 . Código Bibliográfico :2013PhLB..726..638K. doi : 10.1016/j.physletb.2013.09.033. ISSN 0370-2693. S2CID 55085840.
- ^ Giunti, Carlo (2009). "La anomalía temporal GSI: hechos y ficción". Física nuclear B: suplementos de actas . 188 : 43–45. arXiv : 0812.1887 . Código Bibliográfico : 2009NuPhS.188...43G. doi : 10.1016/j.nuclphysbps.2009.02.009. ISSN 0920-5632. S2CID 10196271.
- ^ Gal, Avraham (2016). "Señales de neutrinos en experimentos de captura de electrones en anillos de almacenamiento". Symmetry . 8 (6): 49. arXiv : 1407.1789 . Bibcode :2016Symm....8...49G. doi : 10.3390/sym8060049 . ISSN 2073-8994. S2CID 14287612.
- ^ abc Pfützner, M.; Karny, M.; Grigorenko, LV; Riisager, K. (30 de abril de 2012). "Desintegraciones radiactivas en los límites de la estabilidad nuclear". Reseñas de Física Moderna . 84 (2): 567–619. doi :10.1103/RevModPhys.84.567. ISSN 0034-6861.
- ^ Pais, Abraham (2002). Inward bound: de materia y fuerzas en el mundo físico (edición reimpresa). Oxford: Clarendon Press [ua] ISBN 978-0-19-851997-3.
- ^ abc Ohanian, Hans C. (1994). Principios de física (1.ª ed.). Nueva York: WW Norton. ISBN 978-0-393-95773-0.OCLC 1311044116 .
- ^ "Otros tipos de desintegración radiactiva". Agencia Australiana de Protección Radiológica y Seguridad Nuclear .
- ^ Comunicado de prensa del OIEA, febrero de 2007
Enlaces externos
- Búsqueda de datos nucleares de Lund/LBNL: contiene información tabulada sobre los tipos y energías de desintegración radiactiva.
- Nomenclatura de la química nuclear
- Actividad específica y temas relacionados.
- El gráfico en tiempo real de los nucleidos – OIEA
- Diagrama interactivo de nucleidos Archivado el 10 de octubre de 2018 en Wayback Machine
- Sitio web de educación pública de la Sociedad de Física de la Salud
- Beach, Chandler B., ed. (1914). . ). Chicago: FE Compton and Co.
- Bibliografía comentada sobre radiactividad de la Biblioteca digital Alsos para cuestiones nucleares Archivado el 7 de octubre de 2010 en Wayback Machine.
- Aplicación Java estocástica sobre la desintegración de átomos radiactivos Archivado el 13 de agosto de 2011 en Wayback Machine por Wolfgang Bauer
- Simulación flash estocástica de la desintegración de átomos radiactivos por David M. Harrison
- "Henri Becquerel: El descubrimiento de la radiactividad", artículos de Becquerel de 1896 en línea y analizados en BibNum [haga clic en 'descargar' para la versión en inglés] .
- "Radioactive change", artículo de Rutherford & Soddy (1903), disponible en línea y analizado en Bibnum [haga clic en 'descargar' para la versión en inglés]



![{\displaystyle {\begin{aligned}t_{1/2}&={\frac {\ln(2)}{\lambda }}=\tau \ln(2)\\[2pt]A&=-{\ frac {\mathrm {d} N}{\mathrm {d} t}}=\lambda N={\frac {\ln(2)}{t_{1/2}}}N\\[2pt]S_{ A}a_{0}&=-{\frac {\mathrm {d} N}{\mathrm {d} t}}{\bigg |}_{t=0}=\lambda N_{0}\end{ alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08fd79adb91a3896db0855d30c72096055431cbf)










![{\displaystyle \lim _{\lambda _{B}\rightarrow 0}\left[{\frac {N_{A0}\lambda _{A}}{\lambda _{B}-\lambda _{A}}}\left(e^{-\lambda _{A}t}-e^{-\lambda _{B}t}\right)\right]={\frac {N_{A0}\lambda _{A}}{0-\lambda _{A}}}\left(e^{-\lambda _{A}t}-1\right)=N_{A0}\left(1-e^{-\lambda _{A}t}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/982ae50245eea1305c63a7b97be54ea1e2a19ccf)

![{\displaystyle {\begin{aligned}N_{D}&={\frac {N_{1}(0)}{\lambda _{D}}}\sum _{i=1}^{D}\lambda _{i}c_{i}e^{-\lambda _{i}t}\\[3pt]c_{i}&=\prod _{j=1,i\neq j}^{D}{\frac {\lambda _{j}}{\lambda _{j}-\lambda _{i}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd85cd77b00707ebf272a4cb25d5b2768e2ab39)
















![Símbolo de peligro de radiactividad ISO 2007 destinado a fuentes de categorías 1, 2 y 3 del OIEA definidas como fuentes peligrosas capaces de causar la muerte o lesiones graves[58]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/35/Logo_iso_radiation.svg/120px-Logo_iso_radiation.svg.png)


