Desintegración beta

β−
desintegración en un núcleo atómico (se omite el antineutrino que la acompaña). El recuadro muestra la desintegración beta de un neutrón libre. Ninguna de estas representaciones muestra el neutrón virtual intermedio.
Yo−
bosón.
| Física nuclear |
|---|
 |
En física nuclear , la desintegración beta (β-decaimiento) es un tipo de desintegración radiactiva en la que un núcleo atómico emite una partícula beta ( electrón o positrón de energía rápida ), transformándose en una isobara de ese nucleido. Por ejemplo, la desintegración beta de un neutrón lo transforma en un protón mediante la emisión de un electrón acompañado de un antineutrino ; o, a la inversa, un protón se convierte en un neutrón mediante la emisión de un positrón con un neutrino en lo que se denomina emisión de positrones . Ni la partícula beta ni su (anti-)neutrino asociado existían dentro del núcleo antes de la desintegración beta, sino que se crean en el proceso de desintegración. Mediante este proceso, los átomos inestables obtienen una proporción más estable de protones a neutrones . La probabilidad de que un nucleido se desintegra debido a la desintegración beta y otras formas de desintegración está determinada por su energía de enlace nuclear . Las energías de enlace de todos los nucleidos existentes forman lo que se denomina la banda nuclear o valle de estabilidad . [1] Para que la emisión de electrones o positrones sea energéticamente posible, la liberación de energía (ver más abajo) o el valor Q debe ser positivo.
La desintegración beta es una consecuencia de la fuerza débil , que se caracteriza por tiempos de desintegración relativamente largos. Los nucleones están compuestos de quarks up y quarks down [2] y la fuerza débil permite que un quark cambie su sabor mediante la emisión de un bosón W que conduce a la creación de un par electrón/antineutrino o positrón/neutrino. Por ejemplo, un neutrón, compuesto de dos quarks down y un quark up, se desintegra en un protón compuesto de un quark down y dos quarks up.
La captura de electrones se incluye a veces como un tipo de desintegración beta, [3] porque el proceso nuclear básico, mediado por la fuerza débil, es el mismo. En la captura de electrones, un electrón atómico interno es capturado por un protón en el núcleo, transformándolo en un neutrón, y se libera un neutrino electrónico .
Descripción
Los dos tipos de desintegración beta se conocen como beta menos y beta más . En la desintegración beta menos (β − ), un neutrón se convierte en un protón y el proceso crea un electrón y un antineutrino electrónico ; mientras que en la desintegración beta más (β + ), un protón se convierte en un neutrón y el proceso crea un positrón y un neutrino electrónico. La desintegración β + también se conoce como emisión de positrones . [4]
La desintegración beta conserva un número cuántico conocido como número leptónico , o el número de electrones y sus neutrinos asociados (otros leptones son las partículas muónicas y tau ). Estas partículas tienen un número leptónico +1, mientras que sus antipartículas tienen un número leptónico -1. Como un protón o neutrón tiene un número leptónico cero, la desintegración β + (un positrón o antielectrón) debe ir acompañada de un neutrino electrónico, mientras que la desintegración β- ( un electrón) debe ir acompañada de un antineutrino electrónico.
Un ejemplo de emisión de electrones (desintegración β − ) es la desintegración del carbono-14 en nitrógeno-14, con una vida media de unos 5.730 años:
- 14
6do
→14
7norte
+
mi−
+
no
mi
En esta forma de desintegración, el elemento original se convierte en un nuevo elemento químico en un proceso conocido como transmutación nuclear . Este nuevo elemento tiene un número másico A inalterado , pero un número atómico Z que aumenta en uno. Como en todas las desintegraciones nucleares, el elemento en desintegración (en este caso14
6do
) se conoce como el nucleido padre mientras que el elemento resultante (en este caso14
7norte
) se conoce como el nucleido hijo .
Otro ejemplo es la descomposición del hidrógeno-3 ( tritio ) en helio-3, con una vida media de aproximadamente 12,3 años:
- 3
1yo
→3
2Él
+
mi−
+
no
mi
Un ejemplo de emisión de positrones (desintegración β + ) es la desintegración del magnesio-23 en sodio-23 con una vida media de aproximadamente 11,3 s:
- 23
12Mg
→23
11N / A
+
mi+
+
no
mi
La desintegración β + también produce transmutación nuclear, y el elemento resultante tiene un número atómico que se reduce en uno.

El espectro beta, o distribución de valores de energía para las partículas beta, es continuo. La energía total del proceso de desintegración se divide entre el electrón, el antineutrino y el nucleido en retroceso. En la figura de la derecha, se muestra un ejemplo de un electrón con 0,40 MeV de energía de la desintegración beta de 210 Bi. En este ejemplo, la energía total de desintegración es 1,16 MeV, por lo que el antineutrino tiene la energía restante: 1,16 MeV − 0,40 MeV = 0,76 MeV . Un electrón en el extremo derecho de la curva tendría la máxima energía cinética posible, dejando que la energía del neutrino fuera solo su pequeña masa en reposo.
Historia
Descubrimiento y caracterización inicial
La radiactividad fue descubierta en 1896 por Henri Becquerel en el uranio , y posteriormente observada por Marie y Pierre Curie en el torio y en los nuevos elementos polonio y radio . En 1899, Ernest Rutherford separó las emisiones radiactivas en dos tipos: alfa y beta (ahora beta menos), basándose en la penetración de objetos y la capacidad de causar ionización. Los rayos alfa podían ser detenidos por hojas delgadas de papel o aluminio, mientras que los rayos beta podían penetrar varios milímetros de aluminio. En 1900, Paul Villard identificó un tipo de radiación aún más penetrante, que Rutherford identificó como un tipo fundamentalmente nuevo en 1903 y denominó rayos gamma . Alfa, beta y gamma son las primeras tres letras del alfabeto griego .
En 1900, Becquerel midió la relación masa-carga ( m / e ) de las partículas beta mediante el método de J. J. Thomson utilizado para estudiar los rayos catódicos e identificar el electrón. Descubrió que la relación m / e de una partícula beta es la misma que la del electrón de Thomson, y por lo tanto sugirió que la partícula beta es, de hecho, un electrón. [5]
En 1901, Rutherford y Frederick Soddy demostraron que la radiactividad alfa y beta implica la transmutación de átomos en átomos de otros elementos químicos. En 1913, después de que se conocieran los productos de desintegraciones más radiactivas, Soddy y Kazimierz Fajans propusieron de forma independiente su ley de desplazamiento radiactivo , que establece que beta (es decir,
β−
) la emisión de un elemento produce otro elemento un lugar a la derecha en la tabla periódica , mientras que la emisión alfa produce un elemento dos lugares a la izquierda.
Neutrinos
El estudio de la desintegración beta proporcionó la primera evidencia física de la existencia del neutrino . Tanto en la desintegración alfa como en la gamma, la partícula alfa o gamma resultante tiene una distribución de energía estrecha , ya que la partícula transporta la energía de la diferencia entre los estados nucleares inicial y final. Sin embargo, la distribución de energía cinética, o espectro, de las partículas beta medida por Lise Meitner y Otto Hahn en 1911 y por Jean Danysz en 1913 mostró múltiples líneas sobre un fondo difuso. Estas mediciones ofrecieron el primer indicio de que las partículas beta tienen un espectro continuo. [6] En 1914, James Chadwick utilizó un espectrómetro magnético con uno de los nuevos contadores de Hans Geiger para realizar mediciones más precisas que mostraron que el espectro era continuo. [6] [7] La distribución de energías de las partículas beta estaba en aparente contradicción con la ley de conservación de la energía . Si la desintegración beta fuera simplemente emisión de electrones como se suponía en ese momento, entonces la energía del electrón emitido debería tener un valor particular, bien definido. [8] Sin embargo, en el caso de la desintegración beta, la amplia distribución de energías observada sugería que se perdía energía en el proceso de desintegración beta. Este espectro fue desconcertante durante muchos años.
Un segundo problema está relacionado con la conservación del momento angular . Los espectros de bandas moleculares mostraron que el espín nuclear del nitrógeno-14 es 1 (es decir, igual a la constante de Planck reducida ) y, de manera más general, que el espín es integral para núcleos de número de masa par y semientero para núcleos de número de masa impar. Esto se explicó más tarde mediante el modelo protón-neutrón del núcleo . [8] La desintegración beta deja el número de masa sin cambios, por lo que el cambio de espín nuclear debe ser un número entero. Sin embargo, el espín del electrón es 1/2, por lo tanto, el momento angular no se conservaría si la desintegración beta fuera simplemente emisión de electrones.
Entre 1920 y 1927, Charles Drummond Ellis (junto con Chadwick y sus colegas) estableció además que el espectro de desintegración beta es continuo. En 1933, Ellis y Nevill Mott obtuvieron pruebas sólidas de que el espectro beta tiene un límite superior efectivo en energía. Niels Bohr había sugerido que el espectro beta podría explicarse si la conservación de la energía fuera cierta solo en un sentido estadístico, por lo que este principio podría violarse en cualquier desintegración dada. [8] : 27 Sin embargo, el límite superior en energías beta determinado por Ellis y Mott descartó esa noción. Ahora, el problema de cómo explicar la variabilidad de la energía en los productos de desintegración beta conocidos, así como la conservación del momento y el momento angular en el proceso, se agudizó.
En una famosa carta escrita en 1930, Wolfgang Pauli intentó resolver el enigma de la energía de las partículas beta sugiriendo que, además de electrones y protones, los núcleos atómicos también contenían una partícula neutra extremadamente ligera, a la que llamó neutrón. Sugirió que este "neutrón" también se emitía durante la desintegración beta (lo que explicaba la energía, el momento y el momento angular que faltaban), pero simplemente aún no se había observado. En 1931, Enrico Fermi rebautizó el "neutrón" de Pauli como "neutrino" ('pequeño neutro' en italiano). En 1933, Fermi publicó su histórica teoría de la desintegración beta , donde aplicó los principios de la mecánica cuántica a las partículas de materia, suponiendo que pueden crearse y aniquilarse, al igual que los cuantos de luz en las transiciones atómicas. Por lo tanto, según Fermi, los neutrinos se crean en el proceso de desintegración beta, en lugar de estar contenidos en el núcleo; lo mismo sucede con los electrones. La interacción de los neutrinos con la materia era tan débil que detectarlos supuso un gran desafío experimental. Se obtuvieron más pruebas indirectas de la existencia de los neutrinos observando el retroceso de los núcleos que emitían una partícula de este tipo después de absorber un electrón. Los neutrinos fueron finalmente detectados directamente en 1956 por los físicos estadounidenses Clyde Cowan y Frederick Reines en el experimento de neutrinos de Cowan-Reines . [9] Las propiedades de los neutrinos fueron (con algunas modificaciones menores) las predichas por Pauli y Fermi.
β+
Desintegración y captura de electrones
En 1934, Frédéric e Irène Joliot-Curie bombardearon aluminio con partículas alfa para provocar la reacción nuclear.4
2Él
+ 27
13Alabama
→30
15PAG
+ 1
0norte
, y observó que el isótopo del producto30
15PAG
emite un positrón idéntico a los que se encuentran en los rayos cósmicos (descubiertos por Carl David Anderson en 1932). Este fue el primer ejemplo de
β+
desintegración ( emisión de positrones ), a la que denominaron radiactividad artificial .30
15PAG
es un nucleido de vida corta que no existe en la naturaleza. En reconocimiento a su descubrimiento, la pareja recibió el Premio Nobel de Química en 1935. [10]
La teoría de la captura de electrones fue discutida por primera vez por Gian-Carlo Wick en un artículo de 1934, y luego desarrollada por Hideki Yukawa y otros. La captura de electrones K fue observada por primera vez en 1937 por Luis Alvarez , en el nucleido 48 V. [11] [12] [13] Alvarez continuó estudiando la captura de electrones en 67 Ga y otros nucleidos. [11] [14] [15]
No conservación de la paridad
En 1956, Tsung-Dao Lee y Chen Ning Yang notaron que no había evidencia de que la paridad se conservara en interacciones débiles, por lo que postularon que esta simetría podría no conservarse mediante la fuerza débil. Esbozaron el diseño de un experimento para probar la conservación de la paridad en el laboratorio. [16] Más tarde ese año, Chien-Shiung Wu y sus colaboradores llevaron a cabo el experimento de Wu que mostraba una desintegración beta asimétrica de60
Co
a bajas temperaturas, lo que demostró que la paridad no se conserva en la desintegración beta. [17] [18] Este sorprendente resultado desmintió las suposiciones que se habían mantenido durante mucho tiempo sobre la paridad y la fuerza débil. En reconocimiento a su trabajo teórico, Lee y Yang recibieron el Premio Nobel de Física en 1957. Sin embargo, Wu, que era mujer, no recibió el premio Nobel. [19]
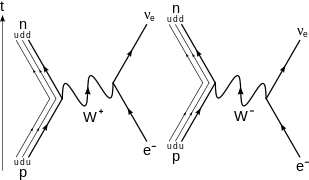
β−decadencia

β−
desintegración de un neutrón en un protón , un electrón y un antineutrino electrónico a través de un intermediario
Yo−
bosón . Para diagramas de orden superior, véase [20] [21]
En
β−
desintegración, la interacción débil convierte un núcleo atómico en un núcleo con número atómico aumentado en uno, mientras emite un electrón (
mi−
) y un antineutrino electrónico (
no
mi).
β−
La desintegración ocurre generalmente en núcleos ricos en neutrones. [22] La ecuación genérica es:
- A-
Zincógnita
→A-
Z +1INCÓGNITA'
+
mi−
+
no
mi[1]
donde A y Z son el número másico y el número atómico del núcleo en desintegración, y X y X′ son los elementos iniciales y finales, respectivamente.
Otro ejemplo es cuando el neutrón libre (1
0norte
) se desintegra por
β−
desintegrarse en un protón (
pag
):
norte
→
pag
+
mi−
+
no
mi.
En el nivel fundamental (como se muestra en el diagrama de Feynman a la derecha), esto es causado por la conversión de la carga negativa ( − 1/3 e ) quark down al ( + ) cargado positivamente2/3 e ) quark up por emisión de un
Yo−
bosón ; el
Yo−
El bosón posteriormente se desintegra en un electrón y un antineutrino electrónico:
d
→
tú
+
mi−
+
no
mi.
β+decadencia

β+
desintegración de un protón en un neutrón , un positrón y un neutrino electrónico a través de un intermediario
Yo+
bosón
En
β+
desintegración o emisión de positrones, la interacción débil convierte un núcleo atómico en un núcleo con número atómico disminuido en uno, mientras emite un positrón (
mi+
) y un neutrino electrónico (
no
mi).
β+
La desintegración ocurre generalmente en núcleos ricos en protones. La ecuación genérica es:
- A-
Zincógnita
→A
Z −1INCÓGNITA'
+
mi+
+
no
mi[1]
Esto puede considerarse como la desintegración de un protón dentro del núcleo en un neutrón:
- p → n +
mi+
+
no
mi[1]
Sin embargo,
β+
La desintegración no puede ocurrir en un protón aislado porque requiere energía, debido a que la masa del neutrón es mayor que la masa del protón.
β+
La desintegración sólo puede ocurrir dentro de los núcleos cuando el núcleo hijo tiene una mayor energía de enlace (y por lo tanto una energía total menor) que el núcleo madre. La diferencia entre estas energías se refleja en la reacción de conversión de un protón en un neutrón, un positrón y un neutrino y en la energía cinética de estas partículas. Este proceso es opuesto a la desintegración beta negativa, en el sentido de que la interacción débil convierte un protón en un neutrón al convertir un quark up en un quark down, lo que da como resultado la emisión de un
Yo+
o la absorción de una
Yo−
. Cuando un
Yo+
Se emite un bosón, que se desintegra en un positrón y un neutrino electrónico :
tú
→
d
+
mi+
+
no
mi.
Captura de electrones (captura K/captura L)
En todos los casos en que
β+
La desintegración (emisión de positrones) de un núcleo se permite energéticamente, por lo que también se permite la captura de electrones . Se trata de un proceso durante el cual un núcleo captura uno de sus electrones atómicos, lo que da lugar a la emisión de un neutrino:
- A-
Zincógnita
+
mi−
→A
Z −1INCÓGNITA'
+
no
mi
Un ejemplo de captura de electrones es uno de los modos de desintegración del criptón-81 en bromo-81 :
- 81
36Kr
+
mi−
→81
35Es
+
no
mi
Todos los neutrinos emitidos tienen la misma energía. En los núcleos ricos en protones, donde la diferencia de energía entre el estado inicial y el final es menor que 2 m e c 2 ,
β+
La desintegración no es energéticamente posible y la captura de electrones es el único modo de desintegración. [23]
Si el electrón capturado proviene de la capa más interna del átomo, la capa K , que tiene la mayor probabilidad de interactuar con el núcleo, el proceso se llama captura K. [24] Si proviene de la capa L, el proceso se llama captura L, etc.
La captura de electrones es un proceso de desintegración que compite (simultáneamente) para todos los núcleos que pueden sufrir desintegración β + . Sin embargo, lo inverso no es cierto: la captura de electrones es el único tipo de desintegración que se permite en los nucleidos ricos en protones que no tienen suficiente energía para emitir un positrón y un neutrino. [23]
Transmutación nuclear
Si el protón y el neutrón forman parte de un núcleo atómico , los procesos de desintegración descritos anteriormente transmutan un elemento químico en otro. Por ejemplo:
137
55Cs
→ 137
56Licenciado en Letras
+
mi−
+
no
mi(desintegración beta negativa) 22
11N / A
→ 22
10Nordeste
+
mi+
+
no
mi(beta más desintegración) 22
11N / A
+
mi−
→ 22
10Nordeste
+
no
mi(captura de electrones)
La desintegración beta no cambia el número ( A ) de nucleones en el núcleo, sino que cambia solamente su carga Z . Por lo tanto, se puede introducir el conjunto de todos los nucleidos con el mismo A ; estos nucleidos isobáricos pueden convertirse entre sí a través de la desintegración beta. Para un A dado hay uno que es más estable. Se dice que es beta estable, porque presenta un mínimo local del exceso de masa : si tal núcleo tiene números ( A , Z ) , los núcleos vecinos ( A , Z −1) y ( A , Z +1) tienen mayor exceso de masa y pueden desintegrarse beta en ( A , Z ) , pero no al revés. Para todos los números de masa impares A , solo hay una isobara beta-estable conocida. Para A par , hay hasta tres isobaras beta-estables diferentes conocidas experimentalmente; por ejemplo,124
50Sn
,124
52Te
, y124
54Xe
Todos son beta-estables. Se conocen unos 350 nucleidos estables a la desintegración beta . [25]
Competencia de tipos de desintegración beta
Por lo general, los nucleidos inestables son claramente "ricos en neutrones" o "ricos en protones", y los primeros experimentan desintegración beta y los segundos capturan electrones (o, más raramente, debido a los mayores requisitos de energía, desintegración de positrones). Sin embargo, en algunos casos de radionucleidos con protones y neutrones impares, puede ser energéticamente favorable que el radionucleido se desintegra en una isobara con protones y neutrones pares, ya sea mediante desintegración beta positiva o beta negativa. Un ejemplo que se cita a menudo es el isótopo único64
29Cu
(29 protones, 35 neutrones), que ilustra tres tipos de desintegración beta en competencia. El cobre-64 tiene una vida media de aproximadamente 12,7 horas. Este isótopo tiene un protón desapareado y un neutrón desapareado, por lo que tanto el protón como el neutrón pueden desintegrarse. Este nucleido en particular (aunque no todos los nucleidos en esta situación) tiene casi la misma probabilidad de desintegrarse a través de la desintegración de protones por emisión de positrones (18% ) o captura de electrones (43% ) a64
28Ni
, como ocurre a través de la desintegración de neutrones por emisión de electrones (39% ) a64
30Zinc
. [26]
Estabilidad de los nucleidos naturales
La mayoría de los nucleidos que se encuentran de forma natural en la Tierra son beta estables. Los nucleidos que no son beta estables tienen vidas medias que van desde menos de un segundo hasta períodos de tiempo significativamente mayores que la edad del universo . Un ejemplo común de un isótopo de vida larga es el nucleido de protón impar y neutrón impar.40
19K
, que sufre los tres tipos de desintegración beta (
β−
,
β+
y captura de electrones) con una vida media de1,277 × 10 9 años . [27]
Reglas de conservación para la desintegración beta
El número bariónico se conserva
dónde
- es el número de quarks constituyentes, y
- es el número de antiquarks constituyentes.
La desintegración beta solo cambia el neutrón en protón o, en el caso de la desintegración beta positiva ( captura de electrones ), el protón en neutrón, por lo que el número de quarks individuales no cambia. Lo único que cambia es el sabor bariónico, que aquí se denomina isospín .
Los quarks arriba y abajo tienen isospín total y proyecciones de isospín.
Todos los demás quarks tienen I = 0 .
En general
El número leptónico se conserva
Así, a todos los leptones se les asigna un valor de +1, a los antileptones −1 y a las partículas no leptónicas 0.
Momento angular
Para las desintegraciones permitidas, el momento angular orbital neto es cero, por lo tanto solo se consideran los números cuánticos de espín.
El electrón y el antineutrino son fermiones , objetos de espín 1/2, por lo tanto pueden acoplarse en total (paralelos) o (antiparalelos).
Para las desintegraciones prohibidas, también debe tenerse en cuenta el momento angular orbital.
Liberación de energía
El valor Q se define como la energía total liberada en una desintegración nuclear dada. En la desintegración beta, Q es por tanto también la suma de las energías cinéticas de la partícula beta emitida, el neutrino y el núcleo en retroceso. (Debido a la gran masa del núcleo en comparación con la de la partícula beta y el neutrino, la energía cinética del núcleo en retroceso puede generalmente despreciarse.) Por tanto, las partículas beta pueden emitirse con cualquier energía cinética que oscile entre 0 y Q. [1] Un valor Q típico es de alrededor de 1 MeV , pero puede oscilar entre unos pocos keV y unas pocas decenas de MeV.
Como la masa en reposo del electrón es de 511 keV, las partículas beta más energéticas son ultrarrelativistas , con velocidades muy cercanas a la de la luz . En el caso del 187 Re, la velocidad máxima de la partícula beta es de tan solo el 9,8% de la velocidad de la luz.
La siguiente tabla ofrece algunos ejemplos:
| Isótopo | Energía ( keV ) | Modo de decadencia | Comentarios |
|---|---|---|---|
| Neutrón libre | 0 782,33 | β − | |
| 00 3 H (Tritio) | 00 18,59 | β − | La segunda energía β − más baja conocida , utilizada en el experimento KATRIN . |
| 0 11 C | 0 960,4 1982,4 | β + ε + | |
| 0 14 °C | 0 156.475 | β − | |
| 0 20 F | 5390.86 | β − | |
| 0 37 K | 5125,48 6147,48 | β + ε + | |
| 163 años | 000 2.555 | ε + | |
| 187 Re | 000 2.467 | β − | La energía β − más baja conocida , que se utiliza en los conjuntos de microcalorímetros para un experimento de renio |
| 210 Bi | 1162.2 | β − |
β−decadencia
Consideremos la ecuación genérica para la desintegración beta
- A-
Zincógnita
→A-
Z +1INCÓGNITA'
+
mi−
+
no
mi.
El valor Q para esta desintegración es
- ,
¿Dónde está la masa del núcleo delA-
Zincógnita
átomo, es la masa del electrón, y es la masa del antineutrino electrónico. En otras palabras, la energía total liberada es la energía de masa del núcleo inicial, menos la energía de masa del núcleo final, electrón y antineutrino. La masa del núcleo m N está relacionada con la masa atómica estándar m por
Es decir, la masa atómica total es la masa del núcleo, más la masa de los electrones, menos la suma de todas las energías de enlace de electrones B i para el átomo. Esta ecuación se reordena para encontrar , y se encuentra de manera similar. Sustituyendo estas masas nucleares en la ecuación del valor Q , mientras se descuida la masa casi nula del antineutrino y la diferencia en las energías de enlace de electrones, que es muy pequeña para átomos de alto Z , tenemos
Esta energía es transportada como energía cinética por el electrón y el antineutrino.
Debido a que la reacción se llevará a cabo solo cuando el valor Q sea positivo, la desintegración β puede ocurrir cuando la masa del átomoA-
Zincógnita
es mayor que la masa del átomoA-
Z +1INCÓGNITA'
. [28]
β+decadencia
Las ecuaciones para la desintegración β + son similares, con la ecuación genérica
- A-
Zincógnita
→A
Z −1INCÓGNITA'
+
mi+
+
no
mi
Sin embargo, en esta ecuación, las masas de los electrones no se cancelan, y nos quedamos con
Debido a que la reacción se llevará a cabo solo cuando el valor Q sea positivo, la desintegración β + puede ocurrir cuando la masa del átomoA-
Zincógnita
supera el deA
-Z -1INCÓGNITA'
por al menos el doble de la masa del electrón. [28]
Captura de electrones
El cálculo análogo para la captura de electrones debe tener en cuenta la energía de enlace de los electrones. Esto se debe a que el átomo quedará en un estado excitado después de capturar el electrón, y la energía de enlace del electrón más interno capturado es significativa. Utilizando la ecuación genérica para la captura de electrones
- A-
Zincógnita
+
mi−
→A
Z −1INCÓGNITA'
+
no
mi
tenemos lo cual se simplifica a donde B n es la energía de enlace del electrón capturado.
Debido a que la energía de enlace del electrón es mucho menor que la masa del electrón, los núcleos que pueden sufrir una desintegración β + siempre pueden sufrir también una captura de electrones, pero lo inverso no es cierto. [28]
Espectro de emisión beta
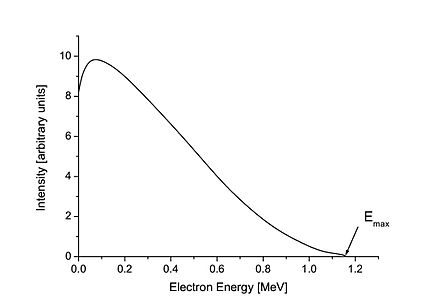
La desintegración beta puede considerarse una perturbación , tal como se describe en la mecánica cuántica, y por lo tanto puede aplicarse la regla de oro de Fermi . Esto conduce a una expresión para el espectro de energía cinética N ( T ) de las betas emitidas, como sigue: [29]
donde T es la energía cinética, C L es una función de forma que depende de la prohibición de la desintegración (es constante para las desintegraciones permitidas), F ( Z , T ) es la Función de Fermi (ver abajo) con Z la carga del núcleo del estado final, E = T + mc 2 es la energía total, es el momento, y Q es el valor Q de la desintegración. La energía cinética del neutrino emitido está dada aproximadamente por Q menos la energía cinética de la beta.
Como ejemplo, el espectro de desintegración beta de 210 Bi (originalmente llamado RaE) se muestra a la derecha.
Función de Fermi
La función de Fermi que aparece en la fórmula del espectro beta explica la atracción/repulsión de Coulomb entre la beta emitida y el núcleo del estado final. Si se aproximan las funciones de onda asociadas a simetría esférica, la función de Fermi se puede calcular analíticamente de la siguiente manera: [30]
donde p es el momento final, Γ la función Gamma , y (si α es la constante de estructura fina y r N el radio del núcleo del estado final) , (+ para electrones, − para positrones), y .
Para betas no relativistas ( Q ≪ m e c 2 ), esta expresión se puede aproximar mediante: [31]
Se pueden encontrar otras aproximaciones en la literatura. [32] [33]
Conspiración de Kurie
Un diagrama de Kurie (también conocido como diagrama de Fermi-Kurie ) es un gráfico utilizado para estudiar la desintegración beta desarrollado por Franz ND Kurie , en el que se representa gráficamente la raíz cuadrada del número de partículas beta cuyos momentos (o energía) se encuentran dentro de un cierto rango estrecho, dividido por la función de Fermi, frente a la energía de las partículas beta. [34] [35] Es una línea recta para las transiciones permitidas y algunas transiciones prohibidas, de acuerdo con la teoría de la desintegración beta de Fermi. La intersección con el eje de energía (eje x) de un diagrama de Kurie corresponde a la energía máxima impartida al electrón/positrón (el valor Q de la desintegración ). Con un diagrama de Kurie se puede encontrar el límite de la masa efectiva de un neutrino. [36]
Helicidad (polarización) de neutrinos, electrones y positrones emitidos en la desintegración beta
Después del descubrimiento de la no conservación de la paridad (ver Historia), se encontró que, en la desintegración beta, los electrones se emiten en su mayoría con helicidad negativa , es decir, se mueven, ingenuamente hablando, como tornillos levógiros introducidos en un material (tienen polarización longitudinal negativa ). [37] Por el contrario, los positrones tienen en su mayoría helicidad positiva, es decir, se mueven como tornillos diestros. Los neutrinos (emitidos en la desintegración de positrones) tienen helicidad negativa, mientras que los antineutrinos (emitidos en la desintegración de electrones) tienen helicidad positiva. [38]
Cuanto mayor sea la energía de las partículas, mayor será su polarización.
Tipos de transiciones de desintegración beta
Las desintegraciones beta se pueden clasificar según el momento angular ( valor L ) y el espín total ( valor S ) de la radiación emitida. Dado que el momento angular total debe conservarse, incluido el momento angular orbital y de espín, la desintegración beta se produce mediante una variedad de transiciones de estados cuánticos a varios estados de momento angular o espín nuclear, conocidas como transiciones de "Fermi" o "Gamow-Teller". Cuando las partículas de desintegración beta no tienen momento angular ( L = 0 ), la desintegración se denomina "permitida"; de lo contrario, está "prohibida".
Otros modos de desintegración, que son raros, se conocen como desintegración de estado ligado y desintegración beta doble.
Transiciones de Fermi
Una transición de Fermi es una desintegración beta en la que los espines del electrón (positrón) y el antineutrino (neutrino) emitidos se acoplan al espín total , lo que lleva a un cambio de momento angular entre los estados inicial y final del núcleo (suponiendo una transición permitida). En el límite no relativista, la parte nuclear del operador para una transición de Fermi está dada por con la constante de acoplamiento vectorial débil, los operadores de elevación y descenso del isospín , y que se ejecuta sobre todos los protones y neutrones en el núcleo.
Transiciones de Gamow a Teller
Una transición de Gamow-Teller es una desintegración beta en la que los espines del electrón emitido (positrón) y del antineutrino (neutrino) se acoplan al espín total , lo que lleva a un cambio de momento angular entre los estados inicial y final del núcleo (suponiendo una transición permitida). En este caso, la parte nuclear del operador está dada por con la constante de acoplamiento axial-vectorial débil y las matrices de Pauli de espín , que pueden producir un cambio de espín en el nucleón en desintegración.
Transiciones prohibidas
Cuando L > 0 , la desintegración se denomina " prohibida ". Las reglas de selección nuclear requieren que los valores altos de L estén acompañados de cambios en el espín nuclear ( J ) y la paridad ( π ). Las reglas de selección para las transiciones prohibidas L son: donde Δ π = 1 o −1 corresponde a ningún cambio de paridad o cambio de paridad, respectivamente. El caso especial de una transición entre estados análogos isobáricos, donde la estructura del estado final es muy similar a la estructura del estado inicial, se denomina "superpermitido" para la desintegración beta y se produce muy rápidamente. La siguiente tabla enumera los valores Δ J y Δ π para los primeros valores de L :
| Prohibición | ΔJ | Δπ |
|---|---|---|
| Superpermitido | 0 | No |
| Permitido | 0, 1 | No |
| Primero prohibido | 0, 1, 2 | Sí |
| Segundo prohibido | 1, 2, 3 | No |
| Tercero prohibido | 2, 3, 4 | Sí |
Modos de decaimiento raros
Estado ligado β−decadencia
Una minoría muy pequeña de desintegraciones de neutrones libres (aproximadamente cuatro por millón) son las llamadas "desintegraciones de dos cuerpos", en las que se producen el protón, el electrón y el antineutrino, pero el electrón no logra obtener la energía de 13,6 eV necesaria para escapar del protón y, por lo tanto, simplemente permanece unido a él, como un átomo de hidrógeno neutro . [39] En este tipo de desintegración beta, en esencia, toda la energía de desintegración del neutrón es transportada por el antineutrino.
En el caso de átomos completamente ionizados (núcleos desnudos), también es posible que los electrones no logren escapar del átomo y sean emitidos desde el núcleo hacia estados ligados atómicos de baja altitud (orbitales). Esto no puede ocurrir en el caso de átomos neutros con estados ligados de baja altitud que ya están ocupados por electrones.
Las desintegraciones β en estado ligado fueron predichas por Daudel , Jean y Lecoin en 1947, [40] y el fenómeno en átomos completamente ionizados fue observado por primera vez para 163 Dy 66+ en 1992 por Jung et al. del Centro de Investigación de Iones Pesados de Darmstadt . Aunque neutral163
Dy es un isótopo estable, el 163 Dy 66+ completamente ionizado sufre una desintegración β en las capas K y L con una vida media de 47 días. [41] El núcleo resultante –163
Ho – es estable solo en el estado completamente ionizado y se desintegrará mediante captura de electrones en163
Dy en estado neutro. La vida media del neutro163
Ho tiene 4750 años.
Otra posibilidad es que un átomo completamente ionizado experimente una desintegración β muy acelerada, como observaron Bosch et al. para el 187 Re, también en Darmstadt. El 187 Re neutro experimenta una desintegración β con una vida media de41,6 × 10 9 años, [42] pero para el 187 Re 75+ completamente ionizado este tiempo se acorta a solo 32,9 años. [43] A modo de comparación, la variación de las tasas de desintegración de otros procesos nucleares debido al entorno químico es inferior al 1% .
Doble desintegración beta
Algunos núcleos pueden sufrir una doble desintegración beta (desintegración ββ), en la que la carga del núcleo cambia en dos unidades. La doble desintegración beta es difícil de estudiar, ya que el proceso tiene una vida media extremadamente larga. En los núcleos en los que son posibles tanto la desintegración β como la desintegración ββ, el proceso de desintegración ββ, más raro, es prácticamente imposible de observar. Sin embargo, en los núcleos en los que la desintegración β está prohibida pero la desintegración ββ está permitida, el proceso se puede ver y se puede medir una vida media. [44] Por lo tanto, la desintegración ββ suele estudiarse solo para núcleos beta estables. Al igual que la desintegración beta simple, la desintegración beta doble no cambia A ; por lo tanto, al menos uno de los nucleidos con una A dada tiene que ser estable con respecto a la desintegración beta simple y doble.
La desintegración doble beta "ordinaria" da como resultado la emisión de dos electrones y dos antineutrinos. Si los neutrinos son partículas de Majorana (es decir, son sus propias antipartículas), se producirá una desintegración conocida como desintegración doble beta sin neutrinos . La mayoría de los físicos de neutrinos creen que nunca se ha observado una desintegración doble beta sin neutrinos. [44]
Véase también
- Emisores beta comunes
- Neutrino
- Betavoltaica
- Radiación de partículas
- Radionúclido
- Iluminación con tritio , una forma de iluminación fluorescente alimentada por desintegración beta
- Efecto pandemonio
- Espectroscopia de absorción total
Referencias
- ^ abcde Konya, J.; Nagy, NM (2012). Química nuclear y radioquímica . Elsevier . Págs. 74-75. ISBN. 978-0-12-391487-3.
- ^ Bijker, R.; Santopinto, E. (2015). "Valence and sea quarks in the nucleon". Revista de Física: Serie de conferencias . 578 (1): 012015. arXiv : 1412.5559 . Código Bibliográfico :2015JPhCS.578a2015B. doi :10.1088/1742-6596/578/1/012015. S2CID 118499855.
- ^ Cottingham, WN; Greenwood, DA (1986). Introducción a la física nuclear. Cambridge University Press . pág. 40. ISBN 978-0-521-31960-7.
- ^ Basdevant, J.-L.; Rich, J.; Spiro, M. (2005). Fundamentos de física nuclear: de la estructura nuclear a la cosmología . Springer . ISBN 978-0-387-01672-6.
- ^ L'Annunziata, Michael (2012). Manual de análisis de radiactividad (tercera edición). Elsevier Inc. pág. 3. ISBN 978-0-12-384874-1. Recuperado el 4 de octubre de 2017 .
- ^ ab Jensen, C. (2000). Controversia y consenso: desintegración beta nuclear 1911-1934. Birkhäuser Verlag . ISBN 978-3-7643-5313-1.
- ^ Chadwick, J. (1914). "Intensitätsverteilung im magnetischen Spektren der β-Strahlen von Radium B + C". Verhandlungen der Deutschen Physikalischen Gesellschaft (en alemán). 16 : 383–391.
- ^ abc Brown, LM (1978). "La idea del neutrino". Physics Today . 31 (9): 23–8. Código Bibliográfico :1978PhT....31i..23B. doi :10.1063/1.2995181.
- ^ Cowan, CL Jr.; Reines, F.; Harrison, FB; Kruse, HW; McGuire, AD (1956). "Detección del neutrino libre: una confirmación". Science . 124 (3212): 103–104. Bibcode :1956Sci...124..103C. doi :10.1126/science.124.3212.103. PMID 17796274.
- ^ "El Premio Nobel de Química 1935". www.nobelprize.org . Consultado el 25 de abril de 2018 .
- ^ ab Segré, E. (1987). "Captura de electrones K por núcleos". En Trower, PW (ed.). Descubriendo a Álvarez: Obras seleccionadas de Luis W. Álvarez . University of Chicago Press . págs. 11–12. ISBN 978-0-226-81304-2.
- ^ "El Premio Nobel de Física 1968: Luis Álvarez". The Nobel Foundation . Consultado el 7 de octubre de 2009 .
- ^ Alvarez, LW (1937). "Captura de electrones nucleares K". Physical Review . 52 (2): 134–135. Código Bibliográfico :1937PhRv...52..134A. doi :10.1103/PhysRev.52.134.
- ^ Alvarez, LW (1938). "Captura de electrones y conversión interna en galio 67". Physical Review . 53 (7): 606. Bibcode :1938PhRv...53..606A. doi :10.1103/PhysRev.53.606.
- ^ Alvarez, LW (1938). "La captura de electrones orbitales por los núcleos". Physical Review . 54 (7): 486–497. Bibcode :1938PhRv...54..486A. doi :10.1103/PhysRev.54.486.
- ^ Lee, TD; Yang, CN (1956). "Cuestión de conservación de la paridad en interacciones débiles". Physical Review . 104 (1): 254–258. Bibcode :1956PhRv..104..254L. doi : 10.1103/PhysRev.104.254 .
- ^ Wu, C.-S.; Ambler, E.; Hayward, RW; Hoppes, DD; Hudson, RP (1957). "Prueba experimental de conservación de paridad en desintegración beta". Physical Review . 105 (4): 1413–1415. Bibcode :1957PhRv..105.1413W. doi : 10.1103/PhysRev.105.1413 .
- ^ Weinstock, Maia. "Siguiendo el ejemplo de Ada Lovelace: Chien-Shiung Wu, valiente héroe de la física". scientificamerican.com .
- ^ "El Premio Nobel de Física 1957". The Nobel Foundation . Consultado el 24 de marzo de 2015 .
- ^ Ivanov, AN; Höllwieser, R.; Troitskaya, NI; Wellenzohn, M.; Berdnikov, Ya. R. (26 de junio de 2017). "Análisis teórico de precisión de la desintegración beta radiativa de neutrones al orden O (α 2 / π 2)". Revisión física D. 95 (11): 113006. arXiv : 1706.08687 . Código Bib : 2017PhRvD..95k3006I. doi : 10.1103/PhysRevD.95.113006. ISSN 2470-0010. S2CID 119103283.
- ^ Ivanov, AN; Höllwieser, R.; Troitskaya, NI; Wellenzohn, M.; Berdnikov, Ya. A. (30 de noviembre de 2018). "Propiedades de calibración de la estructura hadrónica del nucleón en la desintegración beta radiativa de neutrones hasta el orden O(α/π) en V estándar: una teoría efectiva con QED y modelo sigma lineal de interacciones fuertes de baja energía". Revista Internacional de Física Moderna A . 33 (33): 1850199. arXiv : 1805.09702 . Código Bibliográfico :2018IJMPA..3350199I. doi :10.1142/S0217751X18501993. ISSN 0217-751X. S2CID 119088802.
- ^ Loveland, WD (2005). Química nuclear moderna. Wiley . pág. 232. ISBN 978-0-471-11532-8.
- ^ ab Zuber, K. (2011). Física de neutrinos (2ª ed.). Prensa CRC . pag. 466.ISBN 978-1-4200-6471-1.
- ^ Jevremovic, T. (2009). Principios nucleares en ingeniería. Springer Science + Business Media . pág. 201. ISBN 978-0-387-85608-7.
- ^ "Gráfico interactivo de nucleidos". Centro Nacional de Datos Nucleares, Laboratorio Nacional de Brookhaven. Archivado desde el original el 10 de octubre de 2018. Consultado el 18 de septiembre de 2014 .
- ^ "Tabla WWW de isótopos radiactivos, cobre 64". Proyecto de isótopos del LBNL . Laboratorio Nacional Lawrence Berkeley. Archivado desde el original el 14 de diciembre de 2013. Consultado el 18 de septiembre de 2014 .
- ^ "Tabla WWW de isótopos radiactivos, potasio 40". Proyecto de isótopos del LBNL . Laboratorio Nacional Lawrence Berkeley. Archivado desde el original el 2013-10-09 . Consultado el 2014-09-18 .
- ^ abc Kenneth S. Krane (5 de noviembre de 1987). Introducción a la física nuclear. Wiley. ISBN 978-0-471-80553-3.
- ^ Nave, CR "Espectros de energía y momento para la desintegración beta". HyperPhysics . Consultado el 9 de marzo de 2013 .
- ^ Fermi, E. (1934). "Versuch einer Theorie der β-Strahlen. I". Zeitschrift für Physik . 88 (3–4): 161–177. Código bibliográfico : 1934ZPhy...88..161F. doi :10.1007/BF01351864. S2CID 125763380.
- ^ Mott, NF; Massey, HSW (1933). La teoría de las colisiones atómicas . Clarendon Press . LCCN 34001940.
- ^ Venkataramaiah, P.; Gopala, K.; Basavaraju, A.; Suryanarayana, SS; Sanjeeviah, H. (1985). "Una relación simple para la función de Fermi". Journal of Physics G . 11 (3): 359–364. Bibcode :1985JPhG...11..359V. doi :10.1088/0305-4616/11/3/014. S2CID 250803189.
- ^ Schenter, GK; Vogel, P. (1983). "Una aproximación simple de la función de Fermi en la desintegración beta nuclear". Ciencia nuclear e ingeniería . 83 (3): 393–396. Bibcode :1983NSE....83..393S. doi :10.13182/NSE83-A17574. OSTI 5307377.
- ^ Kurie, FND ; Richardson, JR; Paxton, HC (1936). "Las radiaciones emitidas por sustancias radiactivas producidas artificialmente. I. Los límites superiores y las formas de los espectros de rayos β de varios elementos". Physical Review . 49 (5): 368–381. Bibcode :1936PhRv...49..368K. doi :10.1103/PhysRev.49.368.
- ^ Kurie, FND (1948). "Sobre el uso de la trama de Kurie". Physical Review . 73 (10): 1207. Bibcode :1948PhRv...73.1207K. doi :10.1103/PhysRev.73.1207.
- ^ Rodejohann, W. (2012). "Desintegración beta doble sin neutrinos y física de neutrinos". Journal of Physics G: Física nuclear y de partículas . 39 (12): 124008. arXiv : 1206.2560 . Código Bibliográfico :2012JPhG...39l4008R. doi :10.1088/0954-3899/39/12/124008. S2CID 119158221.
- ^ Frauenfelder, H.; et al. (1957). "Paridad y polarización de electrones de Co60". Physical Review . 106 (2): 386–387. Bibcode :1957PhRv..106..386F. doi :10.1103/physrev.106.386.
- ^ Konopinski, EJ; Rose, ME (1966). "La teoría de la desintegración beta nuclear". En Siegbhan, K. (ed.). Espectroscopia de rayos alfa, beta y gamma . Vol. 2. North-Holland Publishing Company .
- ^ Una descripción general de la desintegración de neutrones Archivado el 19 de septiembre de 2017 en Wayback Machine J. Byrne en Quark-Mixing, CKM Unitarity (H. Abele y D. Mund, 2002), véase p. XV
- ^ Daudel, Raymond; Jean, Mauricio; Lecoin, Marcel (1947). "Sobre la posibilidad de existencia de un tipo particular de radioactividad, fenómeno de creación e". J. Física. Radio . 8 (8): 238–243. doi :10.1051/jphysrad:0194700808023800.
- ^ Jung, M.; et al. (1992). "Primera observación de la desintegración β − en estado ligado ". Physical Review Letters . 69 (15): 2164–2167. Bibcode :1992PhRvL..69.2164J. doi :10.1103/PhysRevLett.69.2164. PMID 10046415.
- ^ Smoliar, MI; Walker, RJ; Morgan, JW (1996). "Edades Re-Os de meteoritos de hierro de los grupos IIA, IIIA, IVA y IVB". Science . 271 (5252): 1099–1102. Bibcode :1996Sci...271.1099S. doi :10.1126/science.271.5252.1099. S2CID 96376008.
- ^ Bosch, F.; et al. (1996). "Observación de la desintegración beta-menos en estado ligado de 187 Re: 187 Re– 187 Os Cosmochronometry completamente ionizado". Physical Review Letters . 77 (26): 5190–5193. Bibcode :1996PhRvL..77.5190B. doi :10.1103/PhysRevLett.77.5190. PMID 10062738.
- ^ ab Bilenky, SM (2010). "Desintegración beta doble sin neutrinos". Física de partículas y núcleos . 41 (5): 690–715. arXiv : 1001.1946 . Código Bibliográfico :2010PPN....41..690B. doi :10.1134/S1063779610050035. hdl :10486/663891. S2CID 55217197.
Bibliografía
- Tomonaga, S.-I. (1997). La historia del spin . University of Chicago Press .
- Tuli, JK (2011). Tarjetas de billetera nuclear (PDF) (8.ª ed.). Laboratorio Nacional de Brookhaven . Archivado (PDF) del original el 9 de octubre de 2022.












![{\displaystyle Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}+1}X'}}\right)-m_{e}-m_{{\overline {\nu }}_{e}}\right]c^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5e1eec434e575480cf49bcab3a7f465e7ebc685)





![{\displaystyle Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}+1}X'}}\right)\right]c^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/821caea8313714b516ee3aeb19c7ae54c61a4c20)
![{\displaystyle Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-m_{e}-m_{\nu _{e}}\right]c^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b2aecfbd59ef3a2d936653889874f1850c1c75e)
![{\displaystyle Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-2m_{e}\right]c^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34016918031f38bd87c6585486db7bcb4bc0638)
![{\displaystyle Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)+m_{e}-m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-m_{\nu _{e}}\right]c^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f3a0073da219b288e4f08d1e83b74a6bcb850cc)
![{\displaystyle Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)\right]c^{2}-B_{n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/256ab0a779c0e70d9bf7858dbe54e986a938c88b)

















