Prueba matemática

Una prueba matemática es un argumento deductivo para una afirmación matemática , que muestra que las suposiciones establecidas garantizan lógicamente la conclusión. El argumento puede utilizar otras afirmaciones previamente establecidas, como teoremas ; pero cada prueba puede, en principio, construirse utilizando solo ciertas suposiciones básicas u originales conocidas como axiomas , ^{[2] [3] [4]} junto con las reglas aceptadas de inferencia . Las pruebas son ejemplos de razonamiento deductivo exhaustivo que establecen certeza lógica, que se distinguen de los argumentos empíricos o el razonamiento inductivo no exhaustivo que establecen una "expectativa razonable". Presentar muchos casos en los que la afirmación es válida no es suficiente para una prueba, que debe demostrar que la afirmación es verdadera en todos los casos posibles. Una proposición que no ha sido probada pero que se cree que es verdadera se conoce como conjetura , o hipótesis si se usa con frecuencia como suposición para un trabajo matemático posterior.

Las pruebas emplean la lógica expresada en símbolos matemáticos, junto con el lenguaje natural que generalmente admite cierta ambigüedad. En la mayor parte de la literatura matemática, las pruebas se escriben en términos de lógica informal rigurosa . Las pruebas puramente formales , escritas completamente en lenguaje simbólico sin la participación del lenguaje natural, se consideran en la teoría de la prueba . La distinción entre pruebas formales e informales ha llevado a mucho análisis de la práctica matemática actual e histórica , el cuasiempirismo en matemáticas y las llamadas matemáticas populares , tradiciones orales en la comunidad matemática dominante o en otras culturas. La filosofía de las matemáticas se ocupa del papel del lenguaje y la lógica en las pruebas, y de las matemáticas como lenguaje .

La palabra "prueba" proviene del latín probare (probar). Palabras modernas relacionadas son "probe" (probar), "probation" (probabilidad) y "probability" (probar), en español probar (oler o saborear, o a veces tocar o probar), ^[5] en italiano provare (probar) y en alemán probieren (probar). El término legal "probidad" significa autoridad o credibilidad, el poder del testimonio para probar hechos cuando lo dan personas de reputación o estatus. ^[6]

Los argumentos de plausibilidad que utilizan dispositivos heurísticos como imágenes y analogías precedieron a la prueba matemática estricta. ^[7] Es probable que la idea de demostrar una conclusión surgiera por primera vez en relación con la geometría , que se originó en problemas prácticos de medición de la tierra. ^[8] El desarrollo de la prueba matemática es principalmente el producto de las matemáticas de la antigua Grecia y uno de sus mayores logros. ^[9] Tales (624-546 a. C.) e Hipócrates de Quíos (c. 470-410 a. C.) dieron algunas de las primeras pruebas conocidas de teoremas en geometría. Eudoxo (408-355 a. C.) y Teeteto (417-369 a. C.) formularon teoremas pero no los demostraron. Aristóteles (384-322 a. C.) dijo que las definiciones deberían describir el concepto que se define en términos de otros conceptos ya conocidos.

La demostración matemática fue revolucionada por Euclides (300 a. C.), quien introdujo el método axiomático que todavía se usa hoy en día. Comienza con términos indefinidos y axiomas , proposiciones sobre los términos indefinidos que se suponen como autoevidentemente verdaderos (del griego "axios", algo digno). A partir de esta base, el método demuestra teoremas utilizando la lógica deductiva . El libro de Euclides, los Elementos , fue leído por cualquier persona que se considerara educada en Occidente hasta mediados del siglo XX. ^[10] Además de los teoremas de geometría, como el teorema de Pitágoras , los Elementos también cubren la teoría de números , incluida una prueba de que la raíz cuadrada de dos es irracional y una prueba de que hay infinitos números primos .

También se produjeron avances en las matemáticas islámicas medievales . En el siglo X d. C., el matemático iraquí Al-Hashimi trabajó con números como tales, llamados "líneas" pero no necesariamente considerados como medidas de objetos geométricos, para demostrar proposiciones algebraicas sobre la multiplicación, la división, etc., incluida la existencia de números irracionales . ^[11] Una prueba inductiva para secuencias aritméticas fue introducida en Al-Fakhri (1000) por Al-Karaji , quien la utilizó para demostrar el teorema del binomio y las propiedades del triángulo de Pascal .

La teoría de pruebas moderna trata las pruebas como estructuras de datos definidas inductivamente , sin requerir una suposición de que los axiomas sean "verdaderos" en ningún sentido. Esto permite teorías matemáticas paralelas como modelos formales de un concepto intuitivo dado, basadas en conjuntos alternativos de axiomas, por ejemplo, la teoría de conjuntos axiomáticos y la geometría no euclidiana .

En la práctica, una prueba se expresa en lenguaje natural y es un argumento riguroso destinado a convencer a la audiencia de la verdad de una afirmación. El estándar de rigor no es absoluto y ha variado a lo largo de la historia. Una prueba puede presentarse de manera diferente según la audiencia a la que se dirige. Para ser aceptada, una prueba debe cumplir con los estándares comunes de rigor; un argumento considerado vago o incompleto puede ser rechazado.

El concepto de prueba se formaliza en el campo de la lógica matemática . ^[12] Una prueba formal se escribe en un lenguaje formal en lugar de en lenguaje natural. Una prueba formal es una secuencia de fórmulas en un lenguaje formal, que comienza con una suposición y, con cada fórmula posterior, una consecuencia lógica de las anteriores. Esta definición hace que el concepto de prueba sea susceptible de estudio. De hecho, el campo de la teoría de la prueba estudia las pruebas formales y sus propiedades, siendo la más famosa y sorprendente la de que casi todos los sistemas axiomáticos pueden generar ciertas afirmaciones indecidibles no demostrables dentro del sistema.

La definición de una prueba formal pretende capturar el concepto de pruebas tal como se escriben en la práctica de las matemáticas. La solidez de esta definición equivale a la creencia de que una prueba publicada puede, en principio, convertirse en una prueba formal. Sin embargo, fuera del campo de los asistentes de prueba automatizados , esto rara vez se hace en la práctica. Una pregunta clásica en filosofía es si las pruebas matemáticas son analíticas o sintéticas . Kant , quien introdujo la distinción analítico-sintético , creía que las pruebas matemáticas son sintéticas, mientras que Quine argumentó en su obra de 1951 " Dos dogmas del empirismo " que tal distinción es insostenible. ^[13]

Las demostraciones pueden ser admiradas por su belleza matemática . El matemático Paul Erdős era conocido por describir las demostraciones que consideraba particularmente elegantes como si vinieran de "El Libro", un tomo hipotético que contiene los métodos más bellos para demostrar cada teorema. El libro Demostraciones de EL LIBRO , publicado en 2003, está dedicado a presentar 32 demostraciones que sus editores encuentran particularmente agradables.

En la prueba directa, la conclusión se establece combinando lógicamente los axiomas, las definiciones y los teoremas anteriores. ^[14] Por ejemplo, la prueba directa se puede utilizar para demostrar que la suma de dos números enteros pares es siempre par:

Consideremos dos números enteros pares x e y . Como son pares, se pueden escribir como x  = 2 a e y  = 2 b , respectivamente, para algunos números enteros a y b . Entonces la suma es x  +  y  = 2 a  + 2 b  = 2( a + b ). Por lo tanto, x + y tiene 2 como factor y, por definición, es par. Por lo tanto, la suma de dos números enteros pares cualesquiera es par.

Esta prueba utiliza la definición de números enteros pares, las propiedades enteras del cierre bajo la suma y la multiplicación, y la propiedad distributiva .

A pesar de su nombre, la inducción matemática es un método de deducción , no una forma de razonamiento inductivo . En la demostración por inducción matemática, se demuestra un único "caso base", y se demuestra una "regla de inducción" que establece que cualquier caso arbitrario implica el caso siguiente. Dado que en principio la regla de inducción se puede aplicar repetidamente (empezando por el caso base demostrado), se deduce que todos los casos (normalmente infinitos ) son demostrables. ^[15] Esto evita tener que demostrar cada caso individualmente. Una variante de la inducción matemática es la demostración por descenso infinito , que se puede utilizar, por ejemplo, para demostrar la irracionalidad de la raíz cuadrada de dos .

Una aplicación común de la prueba por inducción matemática es demostrar que una propiedad que se sabe que se cumple para un número se cumple para todos los números naturales : ^[16] Sea N = {1, 2, 3, 4, ... } el conjunto de números naturales, y sea P ( n ) un enunciado matemático que involucra al número natural n perteneciente a N tal que

• (i) P (1) es verdadera, es decir, P ( n ) es verdadera para n = 1 .
• (ii) P ( n +1) es verdadero siempre que P ( n ) sea verdadero, es decir, P ( n ) sea verdadero implica que P ( n +1) es verdadero.
• Entonces P ( n ) es verdadero para todos los números naturales n .

Por ejemplo, podemos demostrar por inducción que todos los números enteros positivos de la forma 2 n  − 1 son impares . Sea P ( n ) " 2 n  − 1 es impar":

(i) Para n = 1 , 2 n  − 1 = 2(1) − 1 = 1 , y 1 es impar, ya que deja un resto de 1 cuando se divide por 2. Por lo tanto, P (1) es verdadera.

(ii) Para cualquier n , si 2 n  − 1 es impar ( P ( n ) ), entonces (2 n  − 1) + 2 también debe ser impar, porque sumar 2 a un número impar da como resultado un número impar. Pero (2 n  − 1) + 2 = 2 n  + 1 = 2( n +1) − 1 , por lo que 2( n +1) − 1 es impar ( P ( n +1) ). Por lo tanto , P ( n ) implica P ( n +1) .

Por lo tanto, 2 n  − 1 es impar, para todos los números enteros positivos n .

A menudo se utiliza la frase más corta «prueba por inducción» en lugar de «prueba por inducción matemática». ^[17]

La prueba por contraposición infiere el enunciado "si p entonces q " estableciendo el enunciado contrapositivo lógicamente equivalente : "si no q entonces no p ".

Por ejemplo, se puede utilizar la contraposición para establecer que, dado un entero , si es par, entonces es par:${\estilo de visualización x}$${\estilo de visualización x^{2}}$${\estilo de visualización x}$

Supongamos que no es par. Entonces es impar. El producto de dos números impares es impar, por lo tanto es impar. Por lo tanto , no es par. Por lo tanto, si es par, la suposición debe ser falsa, por lo que tiene que ser par.${\estilo de visualización x}$${\estilo de visualización x}$${\displaystyle x^{2}=x\cdot x}$${\estilo de visualización x^{2}}$${\estilo de visualización x^{2}}$ ${\estilo de visualización x}$

En la prueba por contradicción, también conocida por la frase latina reductio ad absurdum (por reducción al absurdo), se demuestra que si se supone que una afirmación es verdadera, se produce una contradicción lógica , por lo que la afirmación debe ser falsa. Un ejemplo famoso es la prueba de que es un número irracional :${\displaystyle {\sqrt {2}}}$

Supongamos que fuera un número racional. Entonces podría escribirse en términos más bajos como donde a y b son números enteros distintos de cero sin factor común . Por lo tanto, . Elevando al cuadrado ambos lados se obtiene 2 b ² = a ² . Dado que la expresión de la izquierda es un múltiplo entero de 2, la expresión de la derecha es, por definición, divisible por 2. Es decir, a ² es par, lo que implica que a también debe ser par, como se ve en la proposición anterior (en #Demostración por contraposición). Así que podemos escribir a = 2 c , donde c también es un número entero. La sustitución en la ecuación original da como resultado 2 b ² = (2 c ) ² = 4 c ² . Dividiendo ambos lados por 2 se obtiene b ² = 2 c ² . Pero entonces, por el mismo argumento que antes, 2 divide a b ² , por lo que b debe ser par. Sin embargo, si a y b son ambos pares, tienen 2 como factor común. Esto contradice nuestra afirmación anterior de que a y b no tienen ningún factor común, por lo que debemos concluir que es un número irracional.${\displaystyle {\sqrt {2}}}$${\displaystyle {\sqrt {2}}={a \sobre b}}$${\displaystyle b{\sqrt {2}}=a}$${\displaystyle {\sqrt {2}}}$

Parafraseando: si uno pudiera escribir como fracción , esta fracción nunca podría escribirse en términos más bajos, ya que 2 siempre podría factorizarse a partir del numerador y el denominador.${\displaystyle {\sqrt {2}}}$

La prueba por construcción, o prueba por ejemplo, es la construcción de un ejemplo concreto con una propiedad para demostrar que algo que tiene esa propiedad existe. Joseph Liouville , por ejemplo, demostró la existencia de números trascendentales construyendo un ejemplo explícito . También se puede utilizar para construir un contraejemplo para refutar una proposición de que todos los elementos tienen una determinada propiedad.

En la prueba por agotamiento, la conclusión se establece dividiéndola en un número finito de casos y demostrando cada uno por separado. El número de casos a veces puede llegar a ser muy grande. Por ejemplo, la primera prueba del teorema de los cuatro colores fue una prueba por agotamiento con 1.936 casos. Esta prueba fue controvertida porque la mayoría de los casos se comprobaron mediante un programa informático, no a mano. ^[18]

Una inferencia de cadena cerrada muestra que una colección de declaraciones son equivalentes entre sí.

Para demostrar que las afirmaciones son equivalentes por pares, se dan pruebas para las implicaciones , , , y . ^{[19] [20]}${\displaystyle \varphi _ {1}, \ldots, \varphi _ {n}}$${\displaystyle \varphi _{1}\Flecha derecha \varphi _{2}}$${\displaystyle \varphi _{2}\Flecha derecha \varphi _{3}}$${\displaystyle \puntos}$${\displaystyle \varphi _{n-1}\Flecha derecha \varphi _{n}}$${\displaystyle \varphi _{n}\Flecha derecha \varphi _{1}}$

La equivalencia por pares de los enunciados resulta entonces de la transitividad del condicional material .

Una prueba probabilística es aquella en la que se demuestra la existencia de un ejemplo, con certeza, mediante el uso de métodos de la teoría de la probabilidad . La prueba probabilística, al igual que la prueba por construcción, es una de las muchas formas de demostrar teoremas de existencia .

En el método probabilístico, se busca un objeto que tenga una propiedad dada, comenzando con un conjunto grande de candidatos. Se asigna una cierta probabilidad a cada candidato de ser elegido y luego se demuestra que existe una probabilidad distinta de cero de que un candidato elegido tenga la propiedad deseada. Esto no especifica qué candidatos tienen la propiedad, pero la probabilidad no podría ser positiva sin al menos uno.

Una prueba probabilística no debe confundirse con un argumento de que un teorema es "probablemente" verdadero, un "argumento de plausibilidad". El trabajo en pos de la conjetura de Collatz muestra lo lejos que está la plausibilidad de una prueba genuina, como lo hace la refutación de la conjetura de Mertens . Si bien la mayoría de los matemáticos no creen que la evidencia probabilística de las propiedades de un objeto dado cuente como una prueba matemática genuina, algunos matemáticos y filósofos han argumentado que al menos algunos tipos de evidencia probabilística (como el algoritmo probabilístico de Rabin para probar la primalidad ) son tan buenos como las pruebas matemáticas genuinas. ^{[21] [22]}

Una prueba combinatoria establece la equivalencia de diferentes expresiones al mostrar que cuentan el mismo objeto de diferentes maneras. A menudo se utiliza una biyección entre dos conjuntos para mostrar que las expresiones para sus dos tamaños son iguales. Alternativamente, un argumento de doble conteo proporciona dos expresiones diferentes para el tamaño de un solo conjunto, mostrando nuevamente que las dos expresiones son iguales.

Una prueba no constructiva establece que existe un objeto matemático con una determinada propiedad, sin explicar cómo se puede encontrar dicho objeto. A menudo, esto toma la forma de una prueba por contradicción en la que se demuestra que la no existencia del objeto es imposible. Por el contrario, una prueba constructiva establece que existe un objeto particular proporcionando un método para encontrarlo. El siguiente ejemplo famoso de una prueba no constructiva muestra que existen dos números irracionales a y b tales que es un número racional . Esta prueba utiliza que es irracional (una prueba fácil se conoce desde Euclides ), pero no que es irracional (esto es cierto, pero la prueba no es elemental).$Estilo de visualización a^{b}}$${\displaystyle {\sqrt {2}}}$${\displaystyle {\sqrt {2}}^{\sqrt {2}}}$

O bien es un número racional y ya está (tomamos ), o bien es irracional, por lo que podemos escribir y . Esto da , que es un número racional de la forma${\displaystyle {\sqrt {2}}^{\sqrt {2}}}$${\displaystyle a=b={\sqrt {2}}}$${\displaystyle {\sqrt {2}}^{\sqrt {2}}}$${\displaystyle a={\sqrt {2}}^{\sqrt {2}}}$${\displaystyle b={\sqrt {2}}}$${\displaystyle \left({\sqrt {2}}^{\sqrt {2}}\right)^{\sqrt {2}}={\sqrt {2}}^{2}=2}$${\estilo de visualización a^{b}.}$

La expresión "prueba estadística" puede usarse de manera técnica o coloquial en áreas de las matemáticas puras , como la criptografía , las series caóticas y la teoría probabilística de números o la teoría analítica de números . ^{[23] [24] [25]} Se usa con menos frecuencia para referirse a una prueba matemática en la rama de las matemáticas conocida como estadística matemática . Consulte también la sección "Prueba estadística usando datos" a continuación.

Hasta el siglo XX se suponía que cualquier prueba podía, en principio, ser comprobada por un matemático competente para confirmar su validez. ^[7] Sin embargo, ahora se utilizan ordenadores tanto para demostrar teoremas como para llevar a cabo cálculos que son demasiado largos para que cualquier humano o equipo de humanos los pueda comprobar; la primera prueba del teorema de los cuatro colores es un ejemplo de prueba asistida por ordenador. A algunos matemáticos les preocupa que la posibilidad de un error en un programa informático o un error de tiempo de ejecución en sus cálculos ponga en tela de juicio la validez de dichas pruebas asistidas por ordenador. En la práctica, las posibilidades de que un error invalide una prueba asistida por ordenador se pueden reducir incorporando redundancia y autocomprobaciones en los cálculos y desarrollando múltiples enfoques y programas independientes. Los errores tampoco se pueden descartar por completo en caso de verificación de una prueba por parte de humanos, especialmente si la prueba contiene lenguaje natural y requiere un profundo conocimiento matemático para descubrir los posibles supuestos y falacias ocultos implicados.

Una afirmación que no es demostrable ni refutable a partir de un conjunto de axiomas se llama indecidible (a partir de esos axiomas). Un ejemplo es el postulado de las paralelas , que no es demostrable ni refutable a partir de los axiomas restantes de la geometría euclidiana .

Los matemáticos han demostrado que hay muchas afirmaciones que no son ni demostrables ni refutables en la teoría de conjuntos de Zermelo-Fraenkel con el axioma de elección (ZFC), el sistema estándar de la teoría de conjuntos en matemáticas (asumiendo que ZFC es consistente); ver Lista de afirmaciones indecidibles en ZFC .

El (primer) teorema de incompletitud de Gödel muestra que muchos sistemas de axiomas de interés matemático tendrán enunciados indecidibles.

Si bien los primeros matemáticos como Eudoxo de Cnido no utilizaron pruebas, desde Euclides hasta los desarrollos matemáticos fundamentales de finales del siglo XIX y XX, las pruebas fueron una parte esencial de las matemáticas. ^[26] Con el aumento de la potencia informática en la década de 1960, se empezó a realizar un trabajo significativo para investigar objetos matemáticos más allá del marco de prueba-teorema, ^[27] en matemáticas experimentales . Los primeros pioneros de estos métodos pretendían que el trabajo en última instancia se resolviera en un marco clásico de prueba-teorema, por ejemplo, el desarrollo temprano de la geometría fractal , ^[28] que en última instancia se resolvió de esa manera.

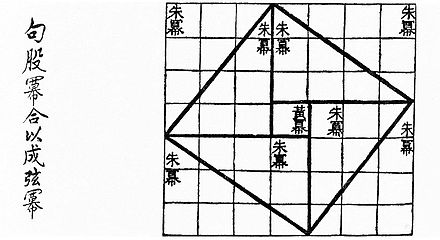
Aunque no se trata de una prueba formal, a la demostración visual de un teorema matemático a veces se la denomina " prueba sin palabras ". La imagen de la izquierda que aparece a continuación es un ejemplo de una prueba visual histórica del teorema de Pitágoras en el caso del triángulo (3,4,5) .

• 
  Prueba visual del triángulo (3,4,5) como en el Zhoubi Suanjing 500-200 a. C.
• 
  Prueba visual animada del teorema de Pitágoras por reordenamiento.
• 
  Una segunda prueba animada del teorema de Pitágoras.

Algunas pruebas visuales ilusorias, como el rompecabezas del cuadrado faltante , pueden construirse de manera tal que parezcan probar un supuesto hecho matemático, pero sólo lo hacen ignorando pequeños errores (por ejemplo, líneas supuestamente rectas que en realidad se doblan ligeramente) que son imperceptibles hasta que se examina de cerca toda la imagen, con longitudes y ángulos medidos o calculados con precisión.

Una demostración elemental es una demostración que solo utiliza técnicas básicas. Más específicamente, el término se utiliza en teoría de números para referirse a demostraciones que no hacen uso del análisis complejo . Durante algún tiempo se pensó que ciertos teoremas, como el teorema de los números primos , solo podían demostrarse utilizando matemáticas "superiores". Sin embargo, con el tiempo, muchos de estos resultados han sido refutados utilizando solo técnicas elementales.

En los Estados Unidos, en las clases de geometría elemental, se suele utilizar una forma particular de organizar una prueba utilizando dos columnas paralelas como ejercicio matemático . ^[29] La prueba se escribe como una serie de líneas en dos columnas. En cada línea, la columna de la izquierda contiene una proposición, mientras que la columna de la derecha contiene una breve explicación de cómo la proposición correspondiente en la columna de la izquierda es un axioma, una hipótesis o puede derivarse lógicamente de proposiciones anteriores. La columna de la izquierda suele tener como título "Afirmaciones" y la de la derecha "Razones". ^[30]

La expresión "prueba matemática" es utilizada por la gente común para referirse al uso de métodos matemáticos o a la argumentación con objetos matemáticos , como números, para demostrar algo sobre la vida cotidiana, o cuando los datos utilizados en una argumentación son numéricos. A veces también se utiliza para referirse a una "prueba estadística" (abajo), especialmente cuando se utiliza para argumentar a partir de datos.

La "prueba estadística" a partir de datos se refiere a la aplicación de la estadística, el análisis de datos o el análisis bayesiano para inferir proposiciones sobre la probabilidad de los datos. Si bien se utiliza una prueba matemática para establecer teoremas en estadística, por lo general no se trata de una prueba matemática, ya que las suposiciones de las que se derivan las afirmaciones de probabilidad requieren evidencia empírica externa a las matemáticas para verificarse. En física, además de los métodos estadísticos, la "prueba estadística" puede referirse a los métodos matemáticos especializados de la física aplicados para analizar datos en un experimento de física de partículas o un estudio observacional en cosmología física . La "prueba estadística" también puede referirse a datos sin procesar o un diagrama convincente que involucra datos, como diagramas de dispersión , cuando los datos o el diagrama son adecuadamente convincentes sin un análisis adicional.

Las pruebas que utilizan la lógica inductiva , si bien se consideran de naturaleza matemática, buscan establecer proposiciones con un grado de certeza, que actúa de manera similar a la probabilidad , y puede ser menor que la certeza total . La lógica inductiva no debe confundirse con la inducción matemática .

El análisis bayesiano utiliza el teorema de Bayes para actualizar la evaluación de las probabilidades de las hipótesis de una persona cuando se adquiere nueva evidencia o información.

El psicologismo considera las pruebas matemáticas como objetos psicológicos o mentales. Los filósofos matemáticos, como Leibniz , Frege y Carnap, han criticado de diversas maneras esta visión e intentaron desarrollar una semántica para lo que consideraban el lenguaje del pensamiento , mediante la cual los estándares de prueba matemática podrían aplicarse a la ciencia empírica .

Los filósofos matemáticos como Spinoza han intentado formular argumentos filosóficos de manera axiomática, de modo que los estándares de prueba matemáticos pudieran aplicarse a la argumentación en filosofía general. Otros filósofos matemáticos han intentado utilizar estándares de prueba matemática y de razonamiento, sin empirismo, para llegar a afirmaciones fuera de las matemáticas, pero que tengan la certeza de proposiciones deducidas en una prueba matemática, como el argumento del cogito de Descartes .

A veces, la abreviatura "QED" se escribe para indicar el final de una prueba. Esta abreviatura significa "quod erat demonstrandum" , que en latín significa "lo que se iba a demostrar" . Una alternativa más común es utilizar un cuadrado o un rectángulo, como □ o ∎, conocido como " lápida " o "halmos" por su epónimo Paul Halmos . A menudo, "lo que se iba a demostrar" se enuncia verbalmente al escribir "QED", "□" o "∎" durante una presentación oral. Unicode proporciona explícitamente el carácter de "fin de la prueba", U+220E (∎) (220E(hex) = 8718(dec)) .

• Pólya, G. (1954), Matemáticas y razonamiento plausible , Princeton University Press, hdl : 2027/mdp.39015008206248 , ISBN 9780691080055.
• Fallis, Don (2002), "¿Qué quieren los matemáticos? Pruebas probabilísticas y objetivos epistémicos de los matemáticos", Logique et Analyse , 45 : 373–88.
• Franklin, J. ; Daoud, A. (2011), Demostración en matemáticas: una introducción, Kew Books, ISBN 978-0-646-54509-7.
• Gold, Bonnie ; Simons, Rogers A. (2008). Demostración y otros dilemas: matemáticas y filosofía . MAA.
• Solow, D. (2004), Cómo leer y hacer demostraciones: una introducción a los procesos de pensamiento matemático , Wiley , ISBN 978-0-471-68058-1.
• Velleman, D. (2006), Cómo demostrarlo: un enfoque estructurado , Cambridge University Press, ISBN 978-0-521-67599-4.
• Hammack, Richard (2018), Libro de pruebas, Richard Hammack, ISBN 978-0-9894721-3-5.

Wikiquote tiene citas relacionadas con Prueba matemática .

Busque prueba en Wikcionario, el diccionario libre.

• Medios relacionados con Prueba matemática en Wikimedia Commons
• Demostraciones en matemáticas: simples, encantadoras y falaces
• Una lección sobre pruebas, en un curso de Wikiversidad