Potencial de acción

Un potencial de acción se produce cuando el potencial de membrana de una célula específica aumenta y disminuye rápidamente. [1] Esta despolarización hace que las ubicaciones adyacentes se despolaricen de manera similar. Los potenciales de acción se producen en varios tipos de células excitables , que incluyen células animales como las neuronas y las células musculares , así como algunas células vegetales . Ciertas células endocrinas , como las células beta pancreáticas y ciertas células de la glándula pituitaria anterior , también son células excitables. [2]
En las neuronas, los potenciales de acción desempeñan un papel central en la comunicación entre células al proporcionar (o, en lo que respecta a la conducción saltatoria , ayudar) la propagación de señales a lo largo del axón de la neurona hacia los botones sinápticos situados en los extremos de un axón; estas señales pueden luego conectarse con otras neuronas en las sinapsis, o con células motoras o glándulas. En otros tipos de células, su función principal es activar procesos intracelulares. En las células musculares, por ejemplo, un potencial de acción es el primer paso en la cadena de eventos que conducen a la contracción. En las células beta del páncreas , provocan la liberación de insulina . [a] Los potenciales de acción en las neuronas también se conocen como " impulsos nerviosos " o " picos ", y la secuencia temporal de potenciales de acción generados por una neurona se llama su " tren de picos ". A menudo se dice que una neurona que emite un potencial de acción, o impulso nervioso, "se dispara".
Los potenciales de acción son generados por tipos especiales de canales iónicos dependientes del voltaje incrustados en la membrana plasmática de una célula . [b] Estos canales se cierran cuando el potencial de membrana está cerca del potencial de reposo (negativo) de la célula, pero comienzan a abrirse rápidamente si el potencial de membrana aumenta hasta un voltaje umbral definido con precisión, despolarizando el potencial transmembrana. [b] Cuando los canales se abren, permiten un flujo entrante de iones de sodio , lo que cambia el gradiente electroquímico, que a su vez produce un aumento adicional en el potencial de membrana hacia cero. Esto luego hace que se abran más canales, produciendo una mayor corriente eléctrica a través de la membrana celular y así sucesivamente. El proceso avanza de manera explosiva hasta que todos los canales iónicos disponibles están abiertos, lo que resulta en un gran aumento en el potencial de membrana. La rápida afluencia de iones de sodio hace que la polaridad de la membrana plasmática se invierta y los canales iónicos luego se inactivan rápidamente. A medida que los canales de sodio se cierran, los iones de sodio ya no pueden ingresar a la neurona y luego son transportados activamente fuera de la membrana plasmática. Luego se activan los canales de potasio y se genera una corriente de salida de iones de potasio, que devuelve el gradiente electroquímico al estado de reposo. Después de que se produce un potencial de acción, se produce un desplazamiento negativo transitorio, denominado poshiperpolarización .
En las células animales, hay dos tipos principales de potenciales de acción. Un tipo es generado por canales de sodio dependientes de voltaje , el otro por canales de calcio dependientes de voltaje . Los potenciales de acción basados en sodio suelen durar menos de un milisegundo, pero los potenciales de acción basados en calcio pueden durar 100 milisegundos o más. [ cita requerida ] En algunos tipos de neuronas, los picos lentos de calcio proporcionan la fuerza impulsora para una ráfaga prolongada de picos de sodio emitidos rápidamente. En las células del músculo cardíaco , por otro lado, un pico rápido inicial de sodio proporciona un "cebador" para provocar la aparición rápida de un pico de calcio, que luego produce la contracción muscular. [3]
Descripción general

Casi todas las membranas celulares de animales, plantas y hongos mantienen una diferencia de voltaje entre el exterior y el interior de la célula, llamada potencial de membrana . Un voltaje típico a través de una membrana celular animal es de -70 mV. Esto significa que el interior de la célula tiene un voltaje negativo en relación con el exterior. En la mayoría de los tipos de células, el potencial de membrana suele permanecer bastante constante. Sin embargo, algunos tipos de células son eléctricamente activas en el sentido de que sus voltajes fluctúan con el tiempo. En algunos tipos de células eléctricamente activas, incluidas las neuronas y las células musculares, las fluctuaciones de voltaje con frecuencia toman la forma de un pico ascendente rápido (positivo) seguido de una caída rápida. Estos ciclos ascendentes y descendentes se conocen como potenciales de acción . En algunos tipos de neuronas, todo el ciclo ascendente y descendente tiene lugar en unas pocas milésimas de segundo. En las células musculares, un potencial de acción típico dura aproximadamente una quinta parte de un segundo. En las células vegetales , un potencial de acción puede durar tres segundos o más. [4]
Las propiedades eléctricas de una célula están determinadas por la estructura de su membrana. Una membrana celular consiste en una bicapa lipídica de moléculas en la que se encuentran incrustadas moléculas de proteínas más grandes. La bicapa lipídica es muy resistente al movimiento de iones cargados eléctricamente, por lo que funciona como aislante. Las proteínas grandes incrustadas en la membrana, por el contrario, proporcionan canales a través de los cuales los iones pueden atravesar la membrana. Los potenciales de acción son impulsados por proteínas de canal cuya configuración cambia entre estados cerrados y abiertos en función de la diferencia de voltaje entre el interior y el exterior de la célula. Estas proteínas sensibles al voltaje se conocen como canales iónicos dependientes del voltaje . [ cita requerida ]
Proceso en una neurona típica
Todas las células de los tejidos corporales animales están polarizadas eléctricamente ; en otras palabras, mantienen una diferencia de voltaje a través de la membrana plasmática de la célula , conocida como potencial de membrana . Esta polarización eléctrica es el resultado de una interacción compleja entre las estructuras proteínicas incrustadas en la membrana llamadas bombas de iones y canales iónicos . En las neuronas, los tipos de canales iónicos en la membrana suelen variar en diferentes partes de la célula, lo que da a las dendritas , al axón y al cuerpo celular diferentes propiedades eléctricas. Como resultado, algunas partes de la membrana de una neurona pueden ser excitables (capaces de generar potenciales de acción), mientras que otras no. Estudios recientes han demostrado que la parte más excitable de una neurona es la parte después del montículo axonal (el punto donde el axón sale del cuerpo celular), que se llama segmento inicial axonal , pero el axón y el cuerpo celular también son excitables en la mayoría de los casos. [5]
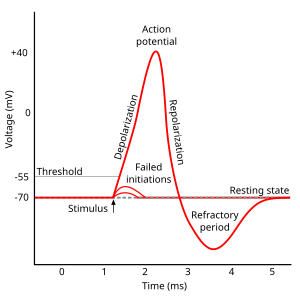
Cada zona excitable de la membrana tiene dos niveles importantes de potencial de membrana: el potencial de reposo , que es el valor que el potencial de membrana mantiene mientras nada perturbe la célula, y un valor más alto llamado potencial umbral . En el cono axónico de una neurona típica, el potencial de reposo es de alrededor de -70 milivoltios (mV) y el potencial umbral es de alrededor de -55 mV. Las entradas sinápticas a una neurona hacen que la membrana se despolarice o hiperpolarice ; es decir, hacen que el potencial de membrana suba o baje. Los potenciales de acción se activan cuando se acumula suficiente despolarización para llevar el potencial de membrana hasta el umbral. Cuando se activa un potencial de acción, el potencial de membrana se dispara abruptamente hacia arriba y luego se dispara hacia abajo de manera igualmente abrupta, a menudo terminando por debajo del nivel de reposo, donde permanece durante un período de tiempo. La forma del potencial de acción es estereotipada; esto significa que el ascenso y la caída generalmente tienen aproximadamente la misma amplitud y curso temporal para todos los potenciales de acción en una célula dada. (Las excepciones se analizan más adelante en el artículo). En la mayoría de las neuronas, todo el proceso se lleva a cabo en aproximadamente una milésima de segundo. Muchos tipos de neuronas emiten potenciales de acción de forma constante a un ritmo de hasta 10-100 por segundo. Sin embargo, algunos tipos son mucho más silenciosos y pueden pasar minutos o más tiempo sin emitir ningún potencial de acción.
Base biofísica
This section needs additional citations for verification. (February 2014) |
Los potenciales de acción son el resultado de la presencia en la membrana de una célula de tipos especiales de canales iónicos dependientes de voltaje . [6] Un canal iónico dependiente de voltaje es una proteína transmembrana que tiene tres propiedades clave:
- Es capaz de asumir más de una conformación.
- Al menos una de las conformaciones crea un canal a través de la membrana que es permeable a tipos específicos de iones.
- La transición entre conformaciones está influenciada por el potencial de membrana.
Por lo tanto, un canal iónico dependiente del voltaje tiende a estar abierto para algunos valores del potencial de membrana y cerrado para otros. Sin embargo, en la mayoría de los casos, la relación entre el potencial de membrana y el estado del canal es probabilística e implica un retraso temporal. Los canales iónicos cambian de conformaciones en momentos impredecibles: el potencial de membrana determina la velocidad de las transiciones y la probabilidad por unidad de tiempo de cada tipo de transición.

Los canales iónicos dependientes de voltaje son capaces de producir potenciales de acción porque pueden dar lugar a bucles de retroalimentación positiva : el potencial de membrana controla el estado de los canales iónicos, pero el estado de los canales iónicos controla el potencial de membrana. Por lo tanto, en algunas situaciones, un aumento del potencial de membrana puede provocar que los canales iónicos se abran, lo que provoca un aumento adicional del potencial de membrana. Se produce un potencial de acción cuando este ciclo de retroalimentación positiva ( ciclo de Hodgkin ) avanza de forma explosiva. La trayectoria temporal y de amplitud del potencial de acción están determinadas por las propiedades biofísicas de los canales iónicos dependientes de voltaje que lo producen. Existen varios tipos de canales capaces de producir la retroalimentación positiva necesaria para generar un potencial de acción. Los canales de sodio dependientes de voltaje son responsables de los potenciales de acción rápidos que intervienen en la conducción nerviosa. Los potenciales de acción más lentos en las células musculares y algunos tipos de neuronas son generados por canales de calcio dependientes de voltaje. Cada uno de estos tipos se presenta en múltiples variantes, con diferente sensibilidad al voltaje y diferente dinámica temporal.
El tipo de canales iónicos dependientes de voltaje que se ha estudiado con mayor intensidad comprende los canales de sodio que participan en la conducción nerviosa rápida. A veces se los conoce como canales de sodio de Hodgkin-Huxley porque fueron caracterizados por primera vez por Alan Hodgkin y Andrew Huxley en sus estudios ganadores del Premio Nobel sobre la biofísica del potencial de acción, pero se los puede denominar de manera más conveniente como canales de Na V. (La "V" significa "voltaje"). Un canal de Na V tiene tres estados posibles, conocidos como desactivado , activado e inactivado . El canal es permeable solo a los iones de sodio cuando está en el estado activado . Cuando el potencial de membrana es bajo, el canal pasa la mayor parte del tiempo en el estado desactivado (cerrado). Si el potencial de membrana se eleva por encima de un cierto nivel, el canal muestra una mayor probabilidad de transición al estado activado (abierto). Cuanto mayor sea el potencial de membrana, mayor será la probabilidad de activación. Una vez que un canal se ha activado, eventualmente pasará al estado inactivado (cerrado). El canal tiende a permanecer inactivo durante algún tiempo, pero si el potencial de membrana vuelve a bajar, acabará volviendo al estado desactivado . Durante un potencial de acción, la mayoría de los canales de este tipo pasan por un ciclo desactivado → activado → inactivado → desactivado . Sin embargo, este es solo el comportamiento medio de la población: en principio, un canal individual puede realizar cualquier transición en cualquier momento. Sin embargo, la probabilidad de que un canal pase del estado inactivado directamente al estado activado es muy baja: un canal en el estado inactivado es refractario hasta que haya vuelto al estado desactivado .
El resultado de todo esto es que la cinética de los canales de Na V está gobernada por una matriz de transición cuyas tasas dependen del voltaje de una manera complicada. Dado que estos canales desempeñan un papel importante en la determinación del voltaje, la dinámica global del sistema puede ser bastante difícil de calcular. Hodgkin y Huxley abordaron el problema desarrollando un conjunto de ecuaciones diferenciales para los parámetros que gobiernan los estados de los canales iónicos, conocidas como ecuaciones de Hodgkin-Huxley . Estas ecuaciones han sido ampliamente modificadas por investigaciones posteriores, pero forman el punto de partida para la mayoría de los estudios teóricos de la biofísica del potencial de acción.
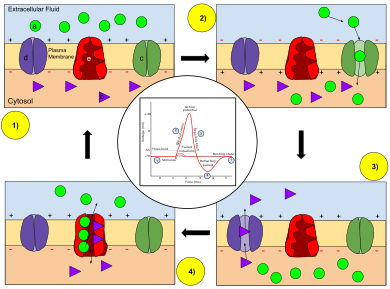
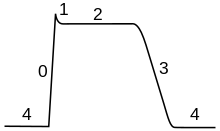
Clave: a) Ion sodio (Na + ). b) Ion potasio (K +
). c) Canal de sodio. d) Canal de potasio. e) Bomba de sodio-potasio. En las etapas de un potencial de acción, la permeabilidad de la membrana de la neurona cambia. En el estado de reposo (1), los iones sodio y potasio tienen una capacidad limitada para atravesar la membrana, y la neurona tiene una carga neta negativa en su interior. Una vez que se desencadena el potencial de acción, la despolarización (2) de la neurona activa los canales de sodio, lo que permite que los iones de sodio pasen a través de la membrana celular hacia el interior de la célula, lo que da como resultado una carga neta positiva en la neurona en relación con el líquido extracelular. Después de que se alcanza el pico del potencial de acción, la neurona comienza la repolarización (3), donde los canales de sodio se cierran y los canales de potasio se abren, lo que permite que los iones de potasio atraviesen la membrana hacia el líquido extracelular, lo que hace que el potencial de membrana vuelva a un valor negativo. Finalmente, hay un período refractario (4), durante el cual los canales iónicos dependientes del voltaje se inactivan mientras los iones Na + y K + vuelven a sus distribuciones de estado de reposo a través de la membrana (1), y la neurona está lista para repetir el proceso para el siguiente potencial de acción.
A medida que aumenta el potencial de membrana, los canales de iones de sodio se abren, lo que permite la entrada de iones de sodio en la célula. A esto le sigue la apertura de los canales de iones de potasio que permiten la salida de iones de potasio de la célula. El flujo entrante de iones de sodio aumenta la concentración de cationes cargados positivamente en la célula y causa despolarización, donde el potencial de la célula es mayor que el potencial de reposo de la célula . Los canales de sodio se cierran en el pico del potencial de acción, mientras que el potasio continúa saliendo de la célula. El eflujo de iones de potasio disminuye el potencial de membrana o hiperpolariza la célula. Para pequeños aumentos de voltaje desde el reposo, la corriente de potasio excede la corriente de sodio y el voltaje regresa a su valor de reposo normal, típicamente −70 mV. [7] [8] [9] Sin embargo, si el voltaje aumenta más allá de un umbral crítico, típicamente 15 mV más alto que el valor de reposo, la corriente de sodio domina. Esto da como resultado una condición descontrolada por la cual la retroalimentación positiva de la corriente de sodio activa aún más canales de sodio. Por lo tanto, la célula se activa , produciendo un potencial de acción. [7] [10] [11] [nota 1] La frecuencia con la que una neurona provoca potenciales de acción a menudo se denomina tasa de activación o tasa de activación neuronal .
Las corrientes producidas por la apertura de canales dependientes de voltaje en el curso de un potencial de acción son típicamente significativamente mayores que la corriente estimulante inicial. Por lo tanto, la amplitud, duración y forma del potencial de acción están determinadas en gran medida por las propiedades de la membrana excitable y no por la amplitud o duración del estímulo. Esta propiedad de todo o nada del potencial de acción lo distingue de los potenciales graduados como los potenciales de receptor , los potenciales electrotónicos , las oscilaciones del potencial de membrana subumbral y los potenciales sinápticos , que escalan con la magnitud del estímulo. Existe una variedad de tipos de potenciales de acción en muchos tipos de células y compartimentos celulares según lo determinado por los tipos de canales dependientes de voltaje, canales de fuga , distribuciones de canales, concentraciones iónicas, capacitancia de membrana, temperatura y otros factores.
Los principales iones que intervienen en un potencial de acción son los cationes sodio y potasio; los iones sodio entran en la célula y los iones potasio salen, restableciendo el equilibrio. Son relativamente pocos los iones que deben cruzar la membrana para que el voltaje de la misma cambie drásticamente. Por tanto, los iones intercambiados durante un potencial de acción producen un cambio insignificante en las concentraciones iónicas internas y externas. Los pocos iones que cruzan son bombeados de nuevo hacia fuera por la acción continua de la bomba sodio-potasio , que, junto con otros transportadores de iones , mantiene la relación normal de concentraciones iónicas a través de la membrana. Los cationes calcio y los aniones cloruro intervienen en algunos tipos de potenciales de acción, como el potencial de acción cardíaco y el potencial de acción en el alga unicelular Acetabularia , respectivamente.
Aunque los potenciales de acción se generan localmente en parches de membrana excitable, las corrientes resultantes pueden desencadenar potenciales de acción en tramos vecinos de membrana, precipitando una propagación similar al efecto dominó. A diferencia de la propagación pasiva de potenciales eléctricos ( potencial electrotónico ), los potenciales de acción se generan de nuevo a lo largo de tramos excitables de membrana y se propagan sin decaimiento. [12] Las secciones mielinizadas de los axones no son excitables y no producen potenciales de acción y la señal se propaga pasivamente como potencial electrotónico . Los parches no mielinizados espaciados regularmente, llamados nodos de Ranvier , generan potenciales de acción para potenciar la señal. Conocida como conducción saltatoria , este tipo de propagación de señal proporciona un equilibrio favorable de velocidad de señal y diámetro del axón. La despolarización de las terminales axónicas , en general, desencadena la liberación de neurotransmisor en la hendidura sináptica . Además, se han registrado potenciales de acción retropropagados en las dendritas de las neuronas piramidales , que son omnipresentes en el neocórtex. [c] Se cree que estos tienen un papel en la plasticidad dependiente del tiempo de los picos .
En el modelo de capacitancia de membrana de Hodgkin-Huxley , la velocidad de transmisión de un potencial de acción no estaba definida y se suponía que las áreas adyacentes se despolarizaban debido a la interferencia de iones liberados con canales vecinos. Las mediciones de difusión de iones y radios han demostrado desde entonces que esto no es posible. [ cita requerida ] Además, las mediciones contradictorias de los cambios de entropía y el tiempo cuestionaron el modelo de capacitancia como actuando solo. [ cita requerida ] Alternativamente, la hipótesis de adsorción de Gilbert Ling postula que el potencial de membrana y el potencial de acción de una célula viva se deben a la adsorción de iones móviles en los sitios de adsorción de las células. [13]
Maduración de las propiedades eléctricas del potencial de acción.
La capacidad de una neurona para generar y propagar un potencial de acción cambia durante el desarrollo . La cantidad de cambios en el potencial de membrana de una neurona como resultado de un impulso de corriente es una función de la resistencia de entrada de la membrana . A medida que una célula crece, se agregan más canales a la membrana, lo que provoca una disminución en la resistencia de entrada. Una neurona madura también experimenta cambios más cortos en el potencial de membrana en respuesta a las corrientes sinápticas. Las neuronas de un núcleo geniculado lateral de hurón tienen una constante de tiempo más larga y una desviación de voltaje mayor en P0 que en P30. [14] Una consecuencia de la disminución de la duración del potencial de acción es que la fidelidad de la señal se puede preservar en respuesta a la estimulación de alta frecuencia. Las neuronas inmaduras son más propensas a la depresión sináptica que a la potenciación después de la estimulación de alta frecuencia. [14]
En el desarrollo temprano de muchos organismos, el potencial de acción en realidad es transportado inicialmente por la corriente de calcio en lugar de la corriente de sodio . La cinética de apertura y cierre de los canales de calcio durante el desarrollo es más lenta que la de los canales de sodio dependientes del voltaje que transportarán el potencial de acción en las neuronas maduras. Los tiempos de apertura más largos de los canales de calcio pueden conducir a potenciales de acción que son considerablemente más lentos que los de las neuronas maduras. [14] Las neuronas de Xenopus inicialmente tienen potenciales de acción que toman 60-90 ms. Durante el desarrollo, este tiempo disminuye a 1 ms. Hay dos razones para esta disminución drástica. Primero, la corriente entrante se transporta principalmente por canales de sodio. [15] Segundo, el rectificador retardado , una corriente del canal de potasio , aumenta a 3,5 veces su fuerza inicial. [14]
Para que se produzca la transición de un potencial de acción dependiente del calcio a un potencial de acción dependiente del sodio, se deben añadir nuevos canales a la membrana. Si las neuronas de Xenopus se cultivan en un entorno con inhibidores de la síntesis de ARN o de la síntesis de proteínas , se impide esa transición. [16] Incluso la actividad eléctrica de la propia célula puede desempeñar un papel en la expresión del canal. Si se bloquean los potenciales de acción en los miocitos de Xenopus , se impide o retrasa el aumento típico de la densidad de corriente de sodio y potasio. [17]
Esta maduración de las propiedades eléctricas se observa en todas las especies. En Xenopus, las corrientes de sodio y potasio aumentan drásticamente después de que una neurona atraviesa su fase final de mitosis . La densidad de corriente de sodio de las neuronas corticales de la rata aumenta un 600 % en las primeras dos semanas posnatales. [14]
Neurotransmisión
Anatomía de una neurona
Varios tipos de células soportan un potencial de acción, como las células vegetales, las células musculares y las células especializadas del corazón (en las que se produce el potencial de acción cardíaco ). Sin embargo, la principal célula excitable es la neurona , que también tiene el mecanismo más simple para el potencial de acción. [ cita requerida ]
Las neuronas son células eléctricamente excitables compuestas, en general, por una o más dendritas, un único soma , un único axón y una o más terminales axónicas . Las dendritas son proyecciones celulares cuya función principal es recibir señales sinápticas. Sus protuberancias, conocidas como espinas dendríticas , están diseñadas para captar los neurotransmisores liberados por la neurona presináptica. Tienen una alta concentración de canales iónicos controlados por ligando . Estas espinas tienen un cuello delgado que conecta una protuberancia bulbosa a la dendrita. Esto asegura que los cambios que ocurren dentro de la espina tengan menos probabilidades de afectar a las espinas vecinas. La espina dendrítica puede, con raras excepciones (ver LTP ), actuar como una unidad independiente. Las dendritas se extienden desde el soma, que alberga el núcleo , y muchos de los orgánulos eucariotas "normales" . A diferencia de las espinas, la superficie del soma está poblada por canales iónicos activados por voltaje. Estos canales ayudan a transmitir las señales generadas por las dendritas. Emergiendo del soma está el cono axónico . Esta región se caracteriza por tener una concentración muy alta de canales de sodio activados por voltaje. En general, se considera que es la zona de iniciación de picos para potenciales de acción, [18] es decir, la zona de activación . Múltiples señales generadas en las espinas y transmitidas por el soma convergen aquí. Inmediatamente después del cono axónico está el axón. Esta es una protuberancia tubular delgada que se aleja del soma. El axón está aislado por una vaina de mielina . La mielina está compuesta de células de Schwann (en el sistema nervioso periférico) u oligodendrocitos (en el sistema nervioso central), ambos tipos de células gliales . Aunque las células gliales no están involucradas en la transmisión de señales eléctricas, se comunican y brindan un importante soporte bioquímico a las neuronas. [19] Para ser más específicos, la mielina envuelve varias veces el segmento axonal, formando una gruesa capa de grasa que impide que los iones entren o escapen del axón. Este aislamiento evita una importante disminución de la señal y garantiza una mayor velocidad de la misma. Sin embargo, este aislamiento tiene la restricción de que no puede haber canales en la superficie del axón. Por lo tanto, existen parches de membrana espaciados regularmente, que no tienen aislamiento. Estos nodos de Ranvier pueden considerarse como "mini montículos axónicos", ya que su propósito es potenciar la señal para evitar una disminución significativa de la señal. En el extremo más alejado, el axón pierde su aislamiento y comienza a ramificarse en varias terminales axónicas.Estas terminales presinápticas, o botones sinápticos, son un área especializada dentro del axón de la célula presináptica que contiene neurotransmisores encerrados en pequeñas esferas rodeadas de membrana llamadas vesículas sinápticas . [ cita requerida ]
Iniciación
Antes de considerar la propagación de potenciales de acción a lo largo de los axones y su terminación en los botones sinápticos, es útil considerar los métodos por los cuales los potenciales de acción pueden iniciarse en el cono axónico . El requisito básico es que el voltaje de la membrana en el cono se eleve por encima del umbral de activación. [7] [8] [20] [21] Hay varias formas en las que puede ocurrir esta despolarización.

Dinámica
Los potenciales de acción se inician más comúnmente por potenciales postsinápticos excitatorios de una neurona presináptica. [22] Normalmente, las moléculas de neurotransmisores son liberadas por la neurona presináptica . Estos neurotransmisores luego se unen a los receptores en la célula postsináptica. Esta unión abre varios tipos de canales iónicos . Esta apertura tiene el efecto adicional de cambiar la permeabilidad local de la membrana celular y, por lo tanto, el potencial de membrana. Si la unión aumenta el voltaje (despolariza la membrana), la sinapsis es excitatoria. Sin embargo, si la unión disminuye el voltaje (hiperpolariza la membrana), es inhibidora. Ya sea que el voltaje aumente o disminuya, el cambio se propaga pasivamente a las regiones cercanas de la membrana (como se describe en la ecuación del cable y sus refinamientos). Normalmente, el estímulo de voltaje decae exponencialmente con la distancia desde la sinapsis y con el tiempo desde la unión del neurotransmisor. Una fracción de un voltaje excitatorio puede alcanzar el cono axónico y puede (en casos raros) despolarizar la membrana lo suficiente como para provocar un nuevo potencial de acción. Lo más habitual es que los potenciales excitatorios de varias sinapsis trabajen juntos casi al mismo tiempo para provocar un nuevo potencial de acción. Sin embargo, sus esfuerzos conjuntos pueden verse frustrados por los potenciales postsinápticos inhibidores que actúan en contra . [ cita requerida ]
La neurotransmisión también puede ocurrir a través de sinapsis eléctricas . [23] Debido a la conexión directa entre células excitables en forma de uniones en hendidura , un potencial de acción puede transmitirse directamente de una célula a la siguiente en cualquier dirección. El flujo libre de iones entre células permite una transmisión rápida no mediada por sustancias químicas. Los canales rectificadores garantizan que los potenciales de acción se muevan solo en una dirección a través de una sinapsis eléctrica. [ cita requerida ] Las sinapsis eléctricas se encuentran en todos los sistemas nerviosos, incluido el cerebro humano, aunque son una minoría clara. [24]
Principio de “todo o nada”
A menudo se piensa que la amplitud de un potencial de acción es independiente de la cantidad de corriente que lo produjo. En otras palabras, corrientes más grandes no crean potenciales de acción más grandes. Por lo tanto, se dice que los potenciales de acción son señales de todo o nada , ya que o ocurren completamente o no ocurren en absoluto. [d] [e] [f] Esto contrasta con los potenciales de receptor , cuyas amplitudes dependen de la intensidad de un estímulo. [25] En ambos casos, la frecuencia de los potenciales de acción está correlacionada con la intensidad de un estímulo.
A pesar de que la visión clásica del potencial de acción como una señal estereotipada y uniforme ha dominado el campo de la neurociencia durante muchas décadas, evidencia más reciente sugiere que los potenciales de acción son eventos más complejos, de hecho, capaces de transmitir información no solo a través de su amplitud, sino también de su duración y fase, a veces incluso hasta distancias que originalmente no se creían posibles. [26] [27] [28] [29]
Neuronas sensoriales
En las neuronas sensoriales , una señal externa como la presión, la temperatura, la luz o el sonido se acopla con la apertura y el cierre de los canales iónicos , que a su vez alteran las permeabilidades iónicas de la membrana y su voltaje. [30] Estos cambios de voltaje pueden ser nuevamente excitatorios (despolarizantes) o inhibidores (hiperpolarizantes) y, en algunas neuronas sensoriales, sus efectos combinados pueden despolarizar el cono axónico lo suficiente como para provocar potenciales de acción. Algunos ejemplos en humanos incluyen la neurona receptora olfativa y el corpúsculo de Meissner , que son fundamentales para el sentido del olfato y el tacto , respectivamente. Sin embargo, no todas las neuronas sensoriales convierten sus señales externas en potenciales de acción; algunas ni siquiera tienen un axón. [31] En cambio, pueden convertir la señal en la liberación de un neurotransmisor , o en potenciales graduados continuos , cualquiera de los cuales puede estimular a la(s) neurona(s) subsiguientes a disparar un potencial de acción. A modo de ejemplo, en el oído humano , las células ciliadas convierten el sonido entrante en la apertura y el cierre de canales iónicos controlados mecánicamente , lo que puede provocar la liberación de moléculas de neurotransmisores . De manera similar, en la retina humana , las células fotorreceptoras iniciales y la siguiente capa de células (que comprende las células bipolares y las células horizontales ) no producen potenciales de acción; solo algunas células amacrinas y la tercera capa, las células ganglionares , producen potenciales de acción, que luego viajan por el nervio óptico . [ cita requerida ]
Potenciales de marcapasos
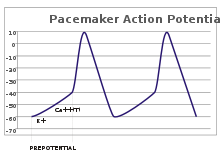
En las neuronas sensoriales, los potenciales de acción son el resultado de un estímulo externo. Sin embargo, algunas células excitables no necesitan dicho estímulo para activarse: despolarizan espontáneamente su cono axónico y activan potenciales de acción a un ritmo regular, como un reloj interno. [32] Los rastros de voltaje de dichas células se conocen como potenciales de marcapasos . [33] Las células marcapasos cardíacas del nódulo sinoatrial en el corazón son un buen ejemplo. [g] Aunque dichos potenciales de marcapasos tienen un ritmo natural , este puede ser ajustado por estímulos externos; por ejemplo, la frecuencia cardíaca puede ser alterada por fármacos, así como por señales de los nervios simpático y parasimpático . [34] Los estímulos externos no causan la activación repetitiva de la célula, sino que simplemente alteran su ritmo. [33] En algunos casos, la regulación de la frecuencia puede ser más compleja, lo que lleva a patrones de potenciales de acción, como el estallido . [ cita requerida ]
Fases
El curso del potencial de acción se puede dividir en cinco partes: la fase ascendente, la fase pico, la fase descendente, la fase de subimpulso y el período refractario. Durante la fase ascendente, el potencial de membrana se despolariza (se vuelve más positivo). El punto en el que se detiene la despolarización se denomina fase pico. En esta etapa, el potencial de membrana alcanza un máximo. Posteriormente, hay una fase descendente. Durante esta etapa, el potencial de membrana se vuelve más negativo, volviendo hacia el potencial de reposo. La fase de subimpulso, o poshiperpolarización , es el período durante el cual el potencial de membrana se carga temporalmente más negativamente que cuando está en reposo (hiperpolarizado). Finalmente, el tiempo durante el cual un potencial de acción posterior es imposible o difícil de disparar se denomina período refractario , que puede superponerse con las otras fases. [35]
El curso del potencial de acción está determinado por dos efectos acoplados. [36] Primero, los canales iónicos sensibles al voltaje se abren y cierran en respuesta a cambios en el voltaje de membrana V m . Esto cambia la permeabilidad de la membrana a esos iones. [37] Segundo, según la ecuación de Goldman , este cambio en la permeabilidad cambia el potencial de equilibrio E m , y, por lo tanto, el voltaje de membrana V m . [h] Por lo tanto, el potencial de membrana afecta la permeabilidad, que luego afecta aún más al potencial de membrana. Esto establece la posibilidad de retroalimentación positiva , que es una parte clave de la fase ascendente del potencial de acción. [7] [10] Un factor que complica es que un solo canal iónico puede tener múltiples "puertas" internas que responden a cambios en V m de maneras opuestas, o a diferentes velocidades. [38] [i] Por ejemplo, aunque aumentar V m abre la mayoría de las puertas en el canal de sodio sensible al voltaje, también cierra la "puerta de inactivación" del canal, aunque más lentamente. [39] Por lo tanto, cuando V m aumenta repentinamente, los canales de sodio se abren inicialmente, pero luego se cierran debido a la inactivación más lenta.
Los voltajes y corrientes del potencial de acción en todas sus fases fueron modelados con precisión por Alan Lloyd Hodgkin y Andrew Huxley en 1952, [i] por lo que recibieron el Premio Nobel de Fisiología o Medicina en 1963. [lower-Greek 2] Sin embargo, su modelo considera solo dos tipos de canales iónicos sensibles al voltaje y hace varias suposiciones sobre ellos, por ejemplo, que sus puertas internas se abren y cierran independientemente una de la otra. En realidad, hay muchos tipos de canales iónicos, [40] y no siempre se abren y cierran de forma independiente. [j]
Fase de estimulación y ascenso
Un potencial de acción típico comienza en el cono axónico [41] con una despolarización suficientemente fuerte, por ejemplo, un estímulo que aumenta V m . Esta despolarización a menudo es causada por la inyección de cationes de sodio adicionales en la célula; estos cationes pueden provenir de una amplia variedad de fuentes, como sinapsis químicas , neuronas sensoriales o potenciales de marcapasos . [ cita requerida ]
Para una neurona en reposo, hay una alta concentración de iones de sodio y cloruro en el líquido extracelular en comparación con el líquido intracelular , mientras que hay una alta concentración de iones de potasio en el líquido intracelular en comparación con el líquido extracelular. La diferencia de concentraciones, que hace que los iones se muevan de una concentración alta a una baja , y los efectos electrostáticos (atracción de cargas opuestas) son responsables del movimiento de iones dentro y fuera de la neurona. El interior de una neurona tiene una carga negativa, en relación con el exterior de la célula, a partir del movimiento de K + fuera de la célula. La membrana de la neurona es más permeable al K + que a otros iones, lo que permite que este ion se mueva selectivamente fuera de la célula, a favor de su gradiente de concentración. Este gradiente de concentración junto con los canales de fuga de potasio presentes en la membrana de la neurona provoca un eflujo de iones de potasio haciendo que el potencial de reposo cercano a E K ≈ –75 mV. [42] Dado que los iones Na + están en concentraciones más altas fuera de la célula, las diferencias de concentración y voltaje los impulsan hacia la célula cuando se abren los canales de Na + . La despolarización abre los canales de sodio y potasio en la membrana, lo que permite que los iones fluyan dentro y fuera del axón, respectivamente. Si la despolarización es pequeña (por ejemplo, aumentando V m de −70 mV a −60 mV), la corriente de potasio saliente abruma la corriente de sodio entrante y la membrana se repolariza de nuevo a su potencial de reposo normal alrededor de −70 mV. [7] [8] [9] Sin embargo, si la despolarización es lo suficientemente grande, la corriente de sodio entrante aumenta más que la corriente de potasio saliente y resulta una condición descontrolada ( retroalimentación positiva ): cuanto más corriente entrante hay, más aumenta V m , lo que a su vez aumenta aún más la corriente entrante. [7] [10] Una despolarización suficientemente fuerte (aumento de V m ) hace que los canales de sodio sensibles al voltaje se abran; La creciente permeabilidad al sodio hace que V m se acerque al voltaje de equilibrio del sodio E Na ≈ +55 mV. El aumento del voltaje a su vez hace que se abran aún más canales de sodio, lo que empuja a V m aún más hacia E Na . Esta retroalimentación positiva continúa hasta que los canales de sodio están completamente abiertos y V m está cerca de E Na . [7] [8] [20][21] El aumento brusco de Vm y la permeabilidad del sodio corresponden a la fase ascendente del potencial de acción. [ 7] [8] [20] [21]
El voltaje umbral crítico para esta condición de descontrol suele ser de alrededor de −45 mV, pero depende de la actividad reciente del axón. Una célula que acaba de disparar un potencial de acción no puede disparar otro inmediatamente, ya que los canales de Na + no se han recuperado del estado inactivo. El período durante el cual no se puede disparar un nuevo potencial de acción se denomina período refractario absoluto . [43] [44] [45] En tiempos más largos, después de que algunos pero no todos los canales iónicos se hayan recuperado, el axón puede ser estimulado para producir otro potencial de acción, pero con un umbral más alto, lo que requiere una despolarización mucho más fuerte, por ejemplo, a −30 mV. El período durante el cual los potenciales de acción son inusualmente difíciles de evocar se denomina período refractario relativo . [43] [44] [45]
Fase pico
La retroalimentación positiva de la fase ascendente se ralentiza y se detiene cuando los canales de iones de sodio se abren al máximo. En el pico del potencial de acción, la permeabilidad al sodio se maximiza y el voltaje de membrana V m es casi igual al voltaje de equilibrio del sodio E Na . Sin embargo, el mismo voltaje elevado que abrió los canales de sodio inicialmente también los cierra lentamente, cerrando sus poros; los canales de sodio se inactivan . [39] Esto reduce la permeabilidad de la membrana al sodio en relación con el potasio, lo que hace que el voltaje de la membrana vuelva al valor de reposo. Al mismo tiempo, el voltaje elevado abre los canales de potasio sensibles al voltaje; el aumento de la permeabilidad al potasio de la membrana lleva V m hacia E K . [39] Combinados, estos cambios en la permeabilidad al sodio y al potasio hacen que V m caiga rápidamente, repolarizando la membrana y produciendo la "fase descendente" del potencial de acción. [43] [46] [21] [47]
Poshiperpolarización
El voltaje despolarizado abre canales de potasio dependientes de voltaje adicionales, y algunos de estos no se cierran de inmediato cuando la membrana regresa a su voltaje de reposo normal. Además, se abren más canales de potasio en respuesta a la afluencia de iones de calcio durante el potencial de acción. La concentración intracelular de iones de potasio es transitoriamente inusualmente baja, lo que hace que el voltaje de membrana V m esté aún más cerca del voltaje de equilibrio de potasio E K . El potencial de membrana cae por debajo del potencial de membrana en reposo. Por lo tanto, hay una subpolarización o hiperpolarización , denominada poshiperpolarización , que persiste hasta que la permeabilidad al potasio de la membrana regresa a su valor habitual, restaurando el potencial de membrana al estado de reposo. [48] [46]
Periodo refractario
Cada potencial de acción va seguido de un período refractario , que puede dividirse en un período refractario absoluto , durante el cual es imposible evocar otro potencial de acción, y luego un período refractario relativo , durante el cual se requiere un estímulo más fuerte de lo habitual. [43] [44] [45] Estos dos períodos refractarios son causados por cambios en el estado de las moléculas de los canales de sodio y potasio. Al cerrarse después de un potencial de acción, los canales de sodio entran en un estado "inactivado" , en el que no se puede hacer que se abran independientemente del potencial de membrana; esto da lugar al período refractario absoluto. Incluso después de que una cantidad suficiente de canales de sodio hayan vuelto a su estado de reposo, ocurre con frecuencia que una fracción de los canales de potasio permanece abierta, lo que dificulta la despolarización del potencial de membrana y, por lo tanto, da lugar al período refractario relativo. Debido a que la densidad y los subtipos de canales de potasio pueden diferir en gran medida entre diferentes tipos de neuronas, la duración del período refractario relativo es muy variable. [ cita requerida ]
El período refractario absoluto es en gran medida responsable de la propagación unidireccional de los potenciales de acción a lo largo de los axones. [49] En cualquier momento dado, el parche del axón detrás de la parte que dispara activamente es refractario, pero el parche de adelante, que no se ha activado recientemente, es capaz de ser estimulado por la despolarización del potencial de acción.
Propagación
El potencial de acción generado en el cono axónico se propaga como una onda a lo largo del axón. [50] Las corrientes que fluyen hacia el interior en un punto del axón durante un potencial de acción se propagan a lo largo del axón y despolarizan las secciones adyacentes de su membrana. Si es lo suficientemente fuerte, esta despolarización provoca un potencial de acción similar en las áreas de membrana vecinas. Este mecanismo básico fue demostrado por Alan Lloyd Hodgkin en 1937. Después de aplastar o enfriar segmentos nerviosos y bloquear así los potenciales de acción, demostró que un potencial de acción que llega a un lado del bloqueo puede provocar otro potencial de acción en el otro, siempre que el segmento bloqueado sea lo suficientemente corto. [k]
Una vez que se ha producido un potencial de acción en una zona de la membrana, esta necesita tiempo para recuperarse antes de poder activarse de nuevo. A nivel molecular, este período refractario absoluto corresponde al tiempo necesario para que los canales de sodio activados por voltaje se recuperen de la inactivación, es decir, vuelvan a su estado cerrado. [44] Existen muchos tipos de canales de potasio activados por voltaje en las neuronas. Algunos de ellos se inactivan rápidamente (corrientes de tipo A) y otros se inactivan lentamente o no se inactivan en absoluto; esta variabilidad garantiza que siempre habrá una fuente de corriente disponible para la repolarización, incluso si algunos de los canales de potasio se inactivan debido a una despolarización previa. Por otro lado, todos los canales de sodio activados por voltaje neuronales se inactivan en varios milisegundos durante una despolarización fuerte, lo que hace imposible la despolarización posterior hasta que una fracción sustancial de los canales de sodio hayan vuelto a su estado cerrado. Aunque limita la frecuencia de activación, [51] el período refractario absoluto garantiza que el potencial de acción se mueva en una sola dirección a lo largo de un axón. [49] Las corrientes que fluyen debido a un potencial de acción se propagan en ambas direcciones a lo largo del axón. [52] Sin embargo, solo la parte no activada del axón puede responder con un potencial de acción; la parte que acaba de activarse no responde hasta que el potencial de acción está fuera de rango de forma segura y no puede volver a estimular esa parte. En la conducción ortodrómica habitual , el potencial de acción se propaga desde el montículo axónico hacia los botones sinápticos (los extremos axónicos); la propagación en la dirección opuesta, conocida como conducción antidrómica , es muy rara. [53] Sin embargo, si se estimula un axón de laboratorio en su parte media, ambas mitades del axón están "frescas", es decir, no activadas; entonces se generarán dos potenciales de acción, uno que viaja hacia el montículo axónico y el otro que viaja hacia los botones sinápticos.
Mielina y conducción saltatoria

Para permitir una transducción rápida y eficiente de señales eléctricas en el sistema nervioso, ciertos axones neuronales están cubiertos con vainas de mielina . La mielina es una membrana multilaminar que envuelve al axón en segmentos separados por intervalos conocidos como nódulos de Ranvier . Es producida por células especializadas: células de Schwann exclusivamente en el sistema nervioso periférico , y oligodendrocitos exclusivamente en el sistema nervioso central . La vaina de mielina reduce la capacitancia de la membrana y aumenta la resistencia de la membrana en los intervalos entre los nodos, lo que permite un movimiento rápido y saltatorio de los potenciales de acción de un nodo a otro. [l] [m] [n] La mielinización se encuentra principalmente en vertebrados , pero se ha descubierto un sistema análogo en algunos invertebrados, como algunas especies de camarones . [o] No todas las neuronas de los vertebrados están mielinizadas; por ejemplo, los axones de las neuronas que componen el sistema nervioso autónomo no están, en general, mielinizados.
La mielina impide que los iones entren o salgan del axón a lo largo de los segmentos mielinizados. Como regla general, la mielinización aumenta la velocidad de conducción de los potenciales de acción y los hace más eficientes energéticamente. Ya sea saltatorio o no, la velocidad media de conducción de un potencial de acción varía de 1 metro por segundo (m/s) a más de 100 m/s y, en general, aumenta con el diámetro axonal. [p]
Los potenciales de acción no pueden propagarse a través de la membrana en segmentos mielinizados del axón. Sin embargo, la corriente es transportada por el citoplasma, lo que es suficiente para despolarizar el primer o segundo nodo de Ranvier posterior . En cambio, la corriente iónica de un potencial de acción en un nodo de Ranvier provoca otro potencial de acción en el siguiente nodo; este aparente "salto" del potencial de acción de un nodo a otro se conoce como conducción saltatoria . Aunque el mecanismo de conducción saltatoria fue sugerido en 1925 por Ralph Lillie, [q] la primera evidencia experimental de la conducción saltatoria provino de Ichiji Tasaki [r] y Taiji Takeuchi [s] [54] y de Andrew Huxley y Robert Stämpfli. [t] Por el contrario, en los axones no mielinizados, el potencial de acción provoca otro en la membrana inmediatamente adyacente y se mueve continuamente por el axón como una onda.

La mielina tiene dos ventajas importantes: velocidad de conducción rápida y eficiencia energética. Para axones mayores que un diámetro mínimo (aproximadamente 1 micrómetro ), la mielinización aumenta la velocidad de conducción de un potencial de acción, típicamente diez veces. [v] Por el contrario, para una velocidad de conducción dada, las fibras mielinizadas son más pequeñas que sus contrapartes no mielinizadas. Por ejemplo, los potenciales de acción se mueven aproximadamente a la misma velocidad (25 m/s) en un axón de rana mielinizado y un axón gigante de calamar no mielinizado , pero el axón de rana tiene un diámetro aproximadamente 30 veces menor y un área de sección transversal 1000 veces menor. Además, dado que las corrientes iónicas están confinadas a los nódulos de Ranvier, muchos menos iones "se filtran" a través de la membrana, lo que ahorra energía metabólica. Este ahorro es una ventaja selectiva significativa , ya que el sistema nervioso humano utiliza aproximadamente el 20% de la energía metabólica del cuerpo. [v]
La longitud de los segmentos mielinizados de los axones es importante para el éxito de la conducción saltatoria. Deben ser lo más largos posible para maximizar la velocidad de conducción, pero no tan largos como para que la señal que llega sea demasiado débil para provocar un potencial de acción en el siguiente nodo de Ranvier. En la naturaleza, los segmentos mielinizados son generalmente lo suficientemente largos para que la señal propagada pasivamente viaje por al menos dos nodos mientras retiene suficiente amplitud para disparar un potencial de acción en el segundo o tercer nodo. Por lo tanto, el factor de seguridad de la conducción saltatoria es alto, lo que permite que la transmisión evite los nodos en caso de lesión. Sin embargo, los potenciales de acción pueden terminar prematuramente en ciertos lugares donde el factor de seguridad es bajo, incluso en neuronas amielínicas; un ejemplo común es el punto de ramificación de un axón, donde se divide en dos axones. [56]
Algunas enfermedades degradan la mielina y perjudican la conducción saltatoria, reduciendo la velocidad de conducción de los potenciales de acción. [w] La más conocida de ellas es la esclerosis múltiple , en la que la degradación de la mielina perjudica el movimiento coordinado. [57]
Teoría del cable

El flujo de corrientes dentro de un axón puede describirse cuantitativamente mediante la teoría del cable [58] y sus elaboraciones, como el modelo compartimental. [59] La teoría del cable fue desarrollada en 1855 por Lord Kelvin para modelar el cable telegráfico transatlántico [x] y Hodgkin y Rushton demostraron que era relevante para las neuronas en 1946. [y] En la teoría del cable simple, la neurona se trata como un cable de transmisión eléctricamente pasivo, perfectamente cilíndrico, que puede describirse mediante una ecuación diferencial parcial [58].
donde V ( x , t ) es el voltaje a través de la membrana en un tiempo t y una posición x a lo largo de la longitud de la neurona, y donde λ y τ son las escalas de longitud y tiempo características en las que esos voltajes decaen en respuesta a un estímulo. Con referencia al diagrama del circuito de la derecha, estas escalas se pueden determinar a partir de las resistencias y capacitancias por unidad de longitud. [60]
Estas escalas de tiempo y longitud se pueden utilizar para comprender la dependencia de la velocidad de conducción del diámetro de la neurona en fibras amielínicas. Por ejemplo, la escala de tiempo τ aumenta tanto con la resistencia de membrana r m como con la capacitancia c m . A medida que aumenta la capacitancia, se debe transferir más carga para producir un voltaje transmembrana dado (por la ecuación Q = CV ); a medida que aumenta la resistencia, se transfiere menos carga por unidad de tiempo, lo que hace que el equilibrio sea más lento. De manera similar, si la resistencia interna por unidad de longitud r i es menor en un axón que en otro (por ejemplo, porque el radio del primero es mayor), la longitud de decaimiento espacial λ se hace más larga y la velocidad de conducción de un potencial de acción debería aumentar. Si la resistencia transmembrana r m aumenta, eso reduce la corriente de "fuga" promedio a través de la membrana, lo que también hace que λ se haga más larga, lo que aumenta la velocidad de conducción.
Terminación
Sinapsis químicas
En general, los potenciales de acción que llegan a los botones sinápticos hacen que se libere un neurotransmisor en la hendidura sináptica. [z] Los neurotransmisores son moléculas pequeñas que pueden abrir canales iónicos en la célula postsináptica; la mayoría de los axones tienen el mismo neurotransmisor en todos sus extremos. La llegada del potencial de acción abre canales de calcio sensibles al voltaje en la membrana presináptica; la entrada de calcio hace que las vesículas llenas de neurotransmisor migren a la superficie de la célula y liberen su contenido en la hendidura sináptica . [aa] Este complejo proceso es inhibido por las neurotoxinas tetanospasmina y toxina botulínica , que son responsables del tétanos y el botulismo , respectivamente. [ab]
Sinapsis eléctricas
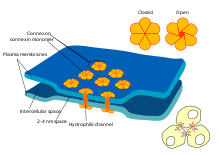
Algunas sinapsis prescinden del "intermediario" del neurotransmisor y conectan las células presinápticas y postsinápticas entre sí. [ac] Cuando un potencial de acción alcanza una de estas sinapsis, las corrientes iónicas que fluyen hacia la célula presináptica pueden cruzar la barrera de las dos membranas celulares y entrar en la célula postsináptica a través de poros conocidos como conexones . [ad] Por lo tanto, las corrientes iónicas del potencial de acción presináptico pueden estimular directamente la célula postsináptica. Las sinapsis eléctricas permiten una transmisión más rápida porque no requieren la difusión lenta de neurotransmisores a través de la hendidura sináptica. Por lo tanto, las sinapsis eléctricas se utilizan siempre que la respuesta rápida y la coordinación del tiempo son cruciales, como en los reflejos de escape , la retina de los vertebrados y el corazón .
Uniones neuromusculares
Un caso especial de sinapsis química es la unión neuromuscular , en la que el axón de una neurona motora termina en una fibra muscular . [ae] En tales casos, el neurotransmisor liberado es la acetilcolina , que se une al receptor de acetilcolina, una proteína de membrana integral en la membrana (el sarcolema ) de la fibra muscular. [af] Sin embargo, la acetilcolina no permanece unida, sino que se disocia y es hidrolizada por la enzima acetilcolinesterasa , ubicada en la sinapsis. Esta enzima reduce rápidamente el estímulo al músculo, lo que permite regular delicadamente el grado y el momento de la contracción muscular. Algunos venenos inactivan la acetilcolinesterasa para evitar este control, como los agentes nerviosos sarín y tabún , [ag] y los insecticidas diazinón y malatión . [ah]
Otros tipos de células
Potenciales de acción cardiaca
El potencial de acción cardíaco se diferencia del potencial de acción neuronal por tener una meseta extendida, en la que la membrana se mantiene a un alto voltaje durante unos cientos de milisegundos antes de ser repolarizada por la corriente de potasio como de costumbre. [ai] Esta meseta se debe a la acción de los canales de calcio más lentos que se abren y mantienen el voltaje de la membrana cerca de su potencial de equilibrio incluso después de que los canales de sodio se hayan inactivado.
El potencial de acción cardiaco desempeña un papel importante en la coordinación de la contracción del corazón. [ai] Las células cardiacas del nódulo sinoatrial proporcionan el potencial de marcapasos que sincroniza el corazón. Los potenciales de acción de esas células se propagan hacia y a través del nódulo auriculoventricular (nódulo AV), que normalmente es la única vía de conducción entre las aurículas y los ventrículos . Los potenciales de acción del nódulo AV viajan a través del haz de His y de allí a las fibras de Purkinje . [nota 2] Por el contrario, las anomalías en el potencial de acción cardiaco, ya sea debido a una mutación congénita o una lesión, pueden conducir a patologías humanas, especialmente arritmias . [ai] Varios fármacos antiarrítmicos actúan sobre el potencial de acción cardiaco, como la quinidina , la lidocaína , los betabloqueantes y el verapamilo . [aj]
Potenciales de acción muscular
El potencial de acción en una célula muscular esquelética normal es similar al potencial de acción en las neuronas. [61] Los potenciales de acción resultan de la despolarización de la membrana celular (el sarcolema ), que abre canales de sodio sensibles al voltaje; estos se inactivan y la membrana se repolariza a través de la corriente de salida de iones de potasio. El potencial de reposo antes del potencial de acción es típicamente -90 mV, algo más negativo que las neuronas típicas. El potencial de acción muscular dura aproximadamente 2-4 ms, el período refractario absoluto es aproximadamente 1-3 ms, y la velocidad de conducción a lo largo del músculo es aproximadamente 5 m/s. El potencial de acción libera iones de calcio que liberan la tropomiosina y permiten que el músculo se contraiga. Los potenciales de acción muscular son provocados por la llegada de un potencial de acción neuronal presináptico a la unión neuromuscular , que es un objetivo común para las neurotoxinas . [ag]
Potenciales de acción de las plantas
Las células vegetales y fúngicas [ak] también son eléctricamente excitables. La diferencia fundamental con los potenciales de acción animales es que la despolarización en las células vegetales no se logra mediante la captación de iones de sodio positivos, sino mediante la liberación de iones de cloruro negativos. [al] [am] [an] En 1906, JC Bose publicó las primeras mediciones de potenciales de acción en plantas, que habían sido descubiertos previamente por Burdon-Sanderson y Darwin. [62] Un aumento de los iones de calcio citoplasmáticos puede ser la causa de la liberación de aniones en la célula. Esto hace que el calcio sea un precursor de los movimientos de iones, como la entrada de iones de cloruro negativos y la salida de iones de potasio positivos, como se ve en las hojas de cebada. [63]
La entrada inicial de iones de calcio también supone una pequeña despolarización celular, lo que hace que los canales iónicos dependientes del voltaje se abran y permitan que los iones de cloruro propaguen la despolarización completa.
Algunas plantas (por ejemplo, Dionaea muscipula ) utilizan canales regulados por sodio para controlar los movimientos de las plantas y "contar" los eventos de estimulación para determinar si se alcanza un umbral de movimiento. Dionaea muscipula , también conocida como Venus atrapamoscas, se encuentra en humedales subtropicales en Carolina del Norte y Carolina del Sur. [64] Cuando los nutrientes del suelo son pobres, la Venus atrapamoscas depende de una dieta de insectos y animales. [65] A pesar de las investigaciones sobre la planta, falta una comprensión detrás de la base molecular de las Venus atrapamoscas y de las plantas carnívoras en general. [66]
Sin embargo, se han realizado muchas investigaciones sobre los potenciales de acción y cómo afectan el movimiento y el mecanismo de relojería dentro de la Venus atrapamoscas. Para empezar, el potencial de membrana en reposo de la Venus atrapamoscas (−120 mV) es menor que el de las células animales (normalmente de −90 mV a −40 mV). [66] [67] El menor potencial de reposo hace que sea más fácil activar un potencial de acción. Por tanto, cuando un insecto aterriza en la trampa de la planta, activa un mecanorreceptor con forma de pelo. [66] Este receptor activa entonces un potencial de acción que dura alrededor de 1,5 ms. [68] Esto provoca un aumento de iones de calcio positivos en la célula, despolarizándola ligeramente. Sin embargo, la Venus atrapamoscas no se cierra después de una activación. En cambio, requiere la activación de dos o más pelos. [65] [66] Si solo se activa un pelo, ignora la activación como un falso positivo. Además, el segundo pelo debe activarse dentro de un intervalo de tiempo determinado (0,75–40 s) para que se registre con la primera activación. [66] Por lo tanto, comienza una acumulación de calcio y luego disminuye lentamente después del primer desencadenante. Cuando el segundo potencial de acción se dispara dentro del intervalo de tiempo, alcanza el umbral de calcio para despolarizar la célula, cerrando la trampa sobre la presa en una fracción de segundo. [66]
Junto con la posterior liberación de iones de potasio positivos, el potencial de acción en las plantas implica una pérdida osmótica de sal (KCl). Mientras que el potencial de acción animal es osmóticamente neutro porque cantidades iguales de sodio entrante y potasio saliente se cancelan entre sí osmóticamente. La interacción de las relaciones eléctricas y osmóticas en las células vegetales [ao] parece haber surgido de una función osmótica de excitabilidad eléctrica en un ancestro unicelular común de plantas y animales en condiciones de salinidad cambiantes. Además, la función actual de transmisión rápida de señales se considera un logro más reciente de las células metazoarias en un entorno osmótico más estable. [69] Es probable que la función de señalización familiar de los potenciales de acción en algunas plantas vasculares (por ejemplo, Mimosa pudica ) surgiera independientemente de la de las células excitables de los metazoos.
A diferencia de la fase ascendente y la fase máxima, la fase descendente y la post-hiperpolarización parecen depender principalmente de cationes que no son calcio. Para iniciar la repolarización, la célula requiere el movimiento de potasio fuera de la célula a través del transporte pasivo en la membrana. Esto difiere de las neuronas porque el movimiento de potasio no domina la disminución del potencial de membrana. Para repolarizarse completamente, una célula vegetal requiere energía en forma de ATP para ayudar en la liberación de hidrógeno de la célula, utilizando un transportador llamado ATPasa de protones . [70] [66]
Distribución taxonómica y ventajas evolutivas
Los potenciales de acción se encuentran en todos los organismos multicelulares , incluidas las plantas , los invertebrados como los insectos y los vertebrados como los reptiles y los mamíferos . [ap] Las esponjas parecen ser el principal filo de eucariotas multicelulares que no transmite potenciales de acción, aunque algunos estudios han sugerido que estos organismos también tienen una forma de señalización eléctrica. [aq] El potencial de reposo, así como el tamaño y la duración del potencial de acción, no han variado mucho con la evolución, aunque la velocidad de conducción varía drásticamente con el diámetro axonal y la mielinización.
| Animal | Tipo de célula | Potencial de reposo (mV) | Aumento de AP (mV) | Duración del AP (ms) | Velocidad de conducción (m/s) |
|---|---|---|---|---|---|
| Calamar ( Loligo ) | Axón gigante | -60 | 120 | 0,75 | 35 |
| Lombriz de tierra ( Lumbricus ) | Fibra gigante mediana | -70 | 100 | 1.0 | 30 |
| Cucaracha ( Periplaneta ) | Fibra gigante | -70 | 80–104 | 0,4 | 10 |
| Rana ( Rana ) | Axón del nervio ciático | −60 a −80 | 110–130 | 1.0 | 7–30 |
| Gato ( Felis ) | Neurona motora espinal | −55 a −80 | 80–110 | 1–1,5 | 30–120 |
Dada su conservación a lo largo de la evolución, el potencial de acción parece conferir ventajas evolutivas. Una de las funciones de los potenciales de acción es la señalización rápida y de largo alcance dentro del organismo; la velocidad de conducción puede superar los 110 m/s, que es un tercio de la velocidad del sonido . A modo de comparación, una molécula de hormona transportada en el torrente sanguíneo se mueve a unos 8 m/s en las grandes arterias. Parte de esta función es la estrecha coordinación de eventos mecánicos, como la contracción del corazón. Una segunda función es el cómputo asociado a su generación. Al ser una señal de todo o nada que no decae con la distancia de transmisión, el potencial de acción tiene ventajas similares a la electrónica digital . La integración de varias señales dendríticas en el cono axónico y su umbralización para formar un tren complejo de potenciales de acción es otra forma de cómputo, que se ha explotado biológicamente para formar generadores de patrones centrales e imitados en redes neuronales artificiales .
Se cree que el ancestro común procariota/eucariota, que vivió hace quizás cuatro mil millones de años, tenía canales dependientes del voltaje. Es probable que, en algún momento posterior, esta funcionalidad se haya utilizado para proporcionar un mecanismo de comunicación. Incluso las bacterias unicelulares modernas pueden utilizar potenciales de acción para comunicarse con otras bacterias en la misma biopelícula . [72]
Métodos experimentales

El estudio de los potenciales de acción ha requerido el desarrollo de nuevos métodos experimentales. El trabajo inicial, anterior a 1955, fue realizado principalmente por Alan Lloyd Hodgkin y Andrew Fielding Huxley , quienes, junto con John Carew Eccles , recibieron el Premio Nobel de Fisiología o Medicina en 1963 por su contribución a la descripción de la base iónica de la conducción nerviosa. Se centró en tres objetivos: aislar las señales de neuronas individuales o axones, desarrollar una electrónica rápida y sensible y reducir el tamaño de los electrodos lo suficiente como para que se pudiera registrar el voltaje dentro de una sola célula.
El primer problema se resolvió estudiando los axones gigantes encontrados en las neuronas del calamar ( Loligo forbesii y Doryteuthis pealeii , en ese momento clasificados como Loligo pealeii ). [ar] Estos axones tienen un diámetro tan grande (aproximadamente 1 mm, o 100 veces más grande que una neurona típica) que pueden verse a simple vista, lo que hace que sean fáciles de extraer y manipular. [i] [as] Sin embargo, no son representativos de todas las células excitables, y se han estudiado numerosos otros sistemas con potenciales de acción.
El segundo problema se abordó con el desarrollo crucial de la pinza de voltaje , [at] que permitió a los experimentadores estudiar las corrientes iónicas subyacentes a un potencial de acción de forma aislada, y eliminó una fuente clave de ruido electrónico , la corriente I C asociada con la capacitancia C de la membrana. [74] Dado que la corriente es igual a C multiplicada por la tasa de cambio del voltaje transmembrana V m , la solución fue diseñar un circuito que mantuviera V m fijo (tasa de cambio cero) independientemente de las corrientes que fluyeran a través de la membrana. Por lo tanto, la corriente necesaria para mantener V m en un valor fijo es un reflejo directo de la corriente que fluye a través de la membrana. Otros avances electrónicos incluyeron el uso de jaulas de Faraday y electrónica con alta impedancia de entrada , de modo que la medición en sí no afectara al voltaje que se estaba midiendo. [75]
El tercer problema, el de obtener electrodos lo suficientemente pequeños para registrar voltajes dentro de un solo axón sin perturbarlo, se resolvió en 1949 con la invención del electrodo de micropipeta de vidrio, [au] que fue rápidamente adoptado por otros investigadores. [av] [aw] Los refinamientos de este método pueden producir puntas de electrodos tan finas como 100 Å (10 nm ), lo que también confiere una alta impedancia de entrada. [76] Los potenciales de acción también pueden registrarse con pequeños electrodos de metal colocados justo al lado de una neurona, con neurochips que contienen EOSFET , u ópticamente con colorantes que son sensibles al Ca 2+ o al voltaje. [ax]

Mientras que los electrodos de micropipeta de vidrio miden la suma de las corrientes que pasan a través de muchos canales iónicos, el estudio de las propiedades eléctricas de un solo canal iónico se hizo posible en la década de 1970 con el desarrollo del patch clamp por Erwin Neher y Bert Sakmann . Por este descubrimiento, fueron galardonados con el Premio Nobel de Fisiología o Medicina en 1991. [lower-Greek 3] El patch-clamping verificó que los canales iónicos tienen estados discretos de conductancia, como abierto, cerrado e inactivado.
En los últimos años se han desarrollado tecnologías de obtención de imágenes ópticas para medir los potenciales de acción, ya sea mediante registros simultáneos en múltiples sitios o con una resolución ultraespacial. Utilizando colorantes sensibles al voltaje , se han registrado ópticamente los potenciales de acción a partir de una pequeña porción de la membrana de los cardiomiocitos . [ay]
Neurotoxinas

Varias neurotoxinas , tanto naturales como sintéticas, funcionan bloqueando el potencial de acción. La tetrodotoxina del pez globo y la saxitoxina del Gonyaulax (el género de dinoflagelados responsable de las " mareas rojas ") bloquean los potenciales de acción inhibiendo el canal de sodio sensible al voltaje; [az] de manera similar, la dendrotoxina de la serpiente mamba negra inhibe el canal de potasio sensible al voltaje. Estos inhibidores de los canales iónicos cumplen una importante función de investigación, ya que permiten a los científicos "apagar" canales específicos a voluntad, aislando así las contribuciones de los otros canales; también pueden ser útiles para purificar canales iónicos mediante cromatografía de afinidad o para analizar su concentración. Sin embargo, estos inhibidores también son neurotoxinas efectivas y se ha considerado su uso como armas químicas . Las neurotoxinas dirigidas a los canales iónicos de los insectos han sido insecticidas eficaces ; un ejemplo es la permetrina sintética , que prolonga la activación de los canales de sodio involucrados en los potenciales de acción. Los canales iónicos de los insectos son suficientemente diferentes a los de sus homólogos humanos como para que haya pocos efectos secundarios en los humanos.
Historia

El papel de la electricidad en los sistemas nerviosos de los animales fue observado por primera vez en ranas disecadas por Luigi Galvani , quien la estudió entre 1791 y 1797. [ba] Los resultados de Galvani inspiraron a Alessandro Volta a desarrollar la pila voltaica —la batería eléctrica más antigua conocida— con la que estudió la electricidad animal (como las anguilas eléctricas ) y las respuestas fisiológicas a los voltajes de corriente continua aplicados . [bb]
En el siglo XIX, los científicos estudiaron la propagación de señales eléctricas en nervios completos (es decir, haces de neuronas ) y demostraron que el tejido nervioso estaba formado por células , en lugar de una red interconectada de tubos (un retículo ). [77] Carlo Matteucci siguió los estudios de Galvani y demostró que los nervios y músculos lesionados en las ranas podían producir corriente continua . El trabajo de Matteucci inspiró al fisiólogo alemán, Emil du Bois-Reymond , quien descubrió en 1843 que estimular estas preparaciones de músculos y nervios producía una notable disminución en sus corrientes de reposo, lo que lo convirtió en el primer investigador en identificar la naturaleza eléctrica del potencial de acción. [78] La velocidad de conducción de los potenciales de acción fue medida en 1850 por el amigo de du Bois-Reymond, Hermann von Helmholtz . [79] El progreso en electrofisiología se estancó a partir de entonces debido a las limitaciones de la teoría química y la práctica experimental. Para establecer que el tejido nervioso está formado por células discretas, el médico español Santiago Ramón y Cajal y sus estudiantes utilizaron una tinción desarrollada por Camillo Golgi para revelar las innumerables formas de las neuronas, que reprodujeron minuciosamente. Por sus descubrimientos, Golgi y Ramón y Cajal recibieron el Premio Nobel de Fisiología de 1906. [lower-Greek 4] Su trabajo resolvió una controversia de larga data en la neuroanatomía del siglo XIX; el propio Golgi había defendido el modelo de red del sistema nervioso.
El siglo XX fue testigo de importantes avances en electrofisiología. En 1902 y nuevamente en 1912, Julius Bernstein formuló la hipótesis de que el potencial de acción resultaba de un cambio en la permeabilidad de la membrana axonal a los iones. [bc] [80] La hipótesis de Bernstein fue confirmada por Ken Cole y Howard Curtis, quienes demostraron que la conductancia de la membrana aumenta durante un potencial de acción. [bd] En 1907, Louis Lapicque sugirió que el potencial de acción se generaba cuando se cruzaba un umbral, [be] lo que más tarde se demostraría como un producto de los sistemas dinámicos de conductancias iónicas. En 1949, Alan Hodgkin y Bernard Katz refinaron la hipótesis de Bernstein al considerar que la membrana axonal podría tener diferentes permeabilidades a diferentes iones; en particular, demostraron el papel crucial de la permeabilidad del sodio para el potencial de acción. [bf] Hicieron el primer registro real de los cambios eléctricos a través de la membrana neuronal que median el potencial de acción. [lower-Greek 5] Esta línea de investigación culminó en los cinco artículos de 1952 de Hodgkin, Katz y Andrew Huxley , en los que aplicaron la técnica de fijación de voltaje para determinar la dependencia de las permeabilidades de la membrana axonal a los iones de sodio y potasio en el voltaje y el tiempo, a partir de lo cual pudieron reconstruir el potencial de acción cuantitativamente. [i] Hodgkin y Huxley correlacionaron las propiedades de su modelo matemático con canales iónicos discretos que podrían existir en varios estados diferentes, incluidos "abierto", "cerrado" e "inactivado". Sus hipótesis fueron confirmadas a mediados de la década de 1970 y 1980 por Erwin Neher y Bert Sakmann , quienes desarrollaron la técnica de fijación de parche para examinar los estados de conductancia de canales iónicos individuales. [bg] En el siglo XXI, los investigadores están empezando a comprender la base estructural de estos estados de conductancia y de la selectividad de los canales para sus especies de iones, [bh] a través de las estructuras cristalinas de resolución atómica , [bi] mediciones de distancia de fluorescencia [bj] y estudios de microscopía crioelectrónica . [bk]
Julius Bernstein también fue el primero en introducir la ecuación de Nernst para el potencial de reposo a través de la membrana; esta fue generalizada por David E. Goldman a la ecuación de Goldman homónima en 1943. [h] La bomba de sodio-potasio fue identificada en 1957 [bl] [lower-Greek 6] y sus propiedades se dilucidaron gradualmente, [bm] [bn] [bo] culminando en la determinación de su estructura de resolución atómica por cristalografía de rayos X. [bp] Las estructuras cristalinas de bombas iónicas relacionadas también se han resuelto, lo que proporciona una visión más amplia de cómo funcionan estas máquinas moleculares . [bq]
Modelos cuantitativos

Los modelos matemáticos y computacionales son esenciales para comprender el potencial de acción y ofrecen predicciones que pueden probarse con datos experimentales, lo que proporciona una prueba rigurosa de una teoría. El más importante y preciso de los primeros modelos neuronales es el modelo de Hodgkin-Huxley , que describe el potencial de acción mediante un conjunto acoplado de cuatro ecuaciones diferenciales ordinarias (EDO). [i] Aunque el modelo de Hodgkin-Huxley puede ser una simplificación con pocas limitaciones [81] en comparación con la membrana nerviosa realista tal como existe en la naturaleza, su complejidad ha inspirado varios modelos aún más simplificados, [82] [br] como el modelo de Morris-Lecar [bs] y el modelo de FitzHugh-Nagumo [bt] , ambos de los cuales tienen solo dos EDO acopladas. Las propiedades de los modelos de Hodgkin-Huxley y FitzHugh-Nagumo y sus parientes, como el modelo de Bonhoeffer-Van der Pol, [bu] han sido bien estudiadas en matemáticas, [83] [bv] computación [84] y electrónica. [bw] Sin embargo, los modelos simples de potencial generador y potencial de acción no logran reproducir con precisión la tasa de picos neuronales y la forma de los picos cerca del umbral, específicamente para los mecanorreceptores como el corpúsculo de Pacini . [85] La investigación más moderna se ha centrado en sistemas más grandes e integrados; al unir modelos de potencial de acción con modelos de otras partes del sistema nervioso (como dendritas y sinapsis), los investigadores pueden estudiar la computación neuronal [86] y los reflejos simples , como los reflejos de escape y otros controlados por generadores de patrones centrales . [87] [bx]
Véase también
Notas
- ^ En general, aunque esta descripción simple de la iniciación del potencial de acción es precisa, no explica fenómenos como el bloqueo de la excitación (la capacidad de evitar que las neuronas generen potenciales de acción estimulándolas con grandes pasos de corriente) y la capacidad de generar potenciales de acción hiperpolarizando brevemente la membrana. Sin embargo, al analizar la dinámica de un sistema de canales de sodio y potasio en un parche de membrana utilizando modelos computacionales , estos fenómenos se explican fácilmente. [griego inferior 1]
- ^ Estas fibras de Purkinje son fibras musculares y no están relacionadas con las células de Purkinje , que son neuronas que se encuentran en el cerebelo .
Referencias
Notas al pie
- ^ Hodgkin AL, Huxley AF (agosto de 1952). "Una descripción cuantitativa de la corriente de membrana y su aplicación a la conducción y excitación en el nervio". The Journal of Physiology . 117 (4): 500–44. doi :10.1113/jphysiol.1952.sp004764. PMC 1392413 . PMID 12991237.
- ^ Williams JA (febrero de 1981). "Correlaciones eléctricas de la secreción en células endocrinas y exocrinas". Fed Proc . 40 (2): 128–34. PMID 6257554.
- ^ "Contracción del músculo cardíaco" . Consultado el 28 de mayo de 2021 .
- ^ Pickard B (junio de 1973). "Potenciales de acción en plantas superiores" (PDF) . The Botanical Review . 39 (2): 188. Bibcode :1973BotRv..39..172P. doi :10.1007/BF02859299. S2CID 5026557.
- ^ Leterrier C (febrero de 2018). "El segmento inicial del axón: un punto de vista actualizado". The Journal of Neuroscience . 38 (9): 2135–2145. doi :10.1523/JNEUROSCI.1922-17.2018. PMC 6596274 . PMID 29378864.
- ^ Purves D, Augustine GJ, Fitzpatrick D, et al., eds. (2001). "Canales iónicos dependientes del voltaje". Neurociencia (2.ª ed.). Sunderland, MA: Sinauer Associates. Archivado desde el original el 5 de junio de 2018 . Consultado el 29 de agosto de 2017 .
- ^ abcdefgh Bullock, Orkand y Grinnell 1977, págs. 150-151.
- ^ abcde Junge 1981, págs. 89–90.
- ^ ab Schmidt-Nielsen 1997, pág. 484.
- ^ abc Purves et al. 2008, págs. 48 y 49; Bullock, Orkand y Grinnell 1977, pág. 141; Schmidt-Nielsen 1997, pág. 483; Junge 1981, pág. 89.
- ^ Stevens 1966, pág. 127.
- ^ Schmidt-Nielsen , pág. 484.
- ^ Tamagawa H, Funatani M, Ikeda K (enero de 2016). "La teoría de adsorción de Ling como mecanismo de generación de potencial de membrana observado tanto en sistemas vivos como no vivos". Membranas . 6 (1): 11. doi : 10.3390/membranes6010011 . PMC 4812417 . PMID 26821050.
- ^ abcde Sanes DH, Reh TA (1 de enero de 2012). Desarrollo del sistema nervioso (tercera edición). Elsevier Academic Press. pp. 211–214. ISBN 9780080923208.OCLC 762720374 .
- ^ Partridge D (1991). Canales de calcio: sus propiedades, funciones, regulación y relevancia clínica . CRC Press. págs. 138-142. ISBN. 9780849388071.
- ^ Black I (1984). Biología celular y molecular del desarrollo neuronal | Ira Black | Springer. Springer. pág. 103. ISBN 978-1-4613-2717-2Archivado desde el original el 17 de julio de 2017.
- ^ Pedersen R (1998). Temas actuales en biología del desarrollo, volumen 39. Elsevier Academic Press. ISBN 9780080584621.
- ^ Bullock, Orkand y Grinnell 1977, pág. 11.
- ^ Silverthorn 2010, pág. 253.
- ^ abc Purves et al. 2008, págs. 49 y 50; Bullock, Orkand y Grinnell 1977, págs. 140-141; Schmidt-Nielsen 1997, págs. 480–481.
- ^ abcd Schmidt-Nielsen 1997, págs.
- ^ Bullock, Orkand y Grinnell 1977, págs. 177-240; Schmidt-Nielsen 1997, págs. 490–499; Stevens 1966, pág. 47–68.
- ^ Bullock, Orkand y Grinnell 1977, págs. 178-180; Schmidt-Nielsen 1997, págs. 490–491.
- ^ Purves y otros. 2001.
- ^ Purves et al. 2008, págs. 26-28.
- ^ "La mielinización aumenta la extensión espacial de la modulación analógica de la transmisión sináptica: un estudio de modelado". Fronteras en neurociencia celular .
- ^ Zbili, M.; Debanne, D. (2019). "Pasado y futuro de la modulación analógico-digital de la transmisión sináptica". Frontiers in Cellular Neuroscience . 13 : 160. doi : 10.3389/fncel.2019.00160 . PMC 6492051 . PMID 31105529.
- ^ Clark, Beverley; Häusser, Michael (8 de agosto de 2006). "Codificación neuronal: señalización analógica en axones". Current Biology . 16 (15): R585–R588. doi : 10.1016/j.cub.2006.07.007 . PMID 16890514. S2CID 8295969.
- ^ Liu, Wenke; Liu, Qing; Crozier, Robert A.; Davis, Robin L. (2021). "Transmisión analógica de la estructura fina del potencial de acción en los axones del ganglio espiral". Revista de neurofisiología . 126 (3): 888–905. doi :10.1152/jn.00237.2021. PMC 8461829 . PMID 34346782.
- ^ Schmidt-Nielsen 1997, págs. 535–580; Bullock, Orkand y Grinnell 1977, págs. 49–56, 76–93, 247–255; Stevens 1966, págs. 69–79.
- ^ Bullock, Orkand y Grinnell 1977, págs.53; Bullock, Orkand y Grinnell 1977, págs. 122-124.
- ^ Junge 1981, págs. 115-132.
- ^ ab Bullock, Orkand y Grinnell 1977, págs.
- ^ Bullock, Orkand y Grinnell 1977, págs. 444–445.
- ^ Purves y otros. 2008, pág. 38.
- ^ Stevens 1966, págs. 127-128.
- ^ Purves et al. 2008, págs. 61–65.
- ^ Purves y col. 2008, págs. 64 a 74; Bullock, Orkand y Grinnell 1977, págs. 149-150; Junge 1981, págs. 84–85; Stevens 1966, págs. 152-158.
- ^ abc Purves et al. 2008, pág. 47; Purves et al. 2008, pág. 65; Bullock, Orkand y Grinnell 1977, págs. 147-148; Stevens 1966, pág. 128.
- ^ Goldin, AL en Waxman 2007, Canales neuronales y receptores , págs. 43–58.
- ^ Stevens 1966, pág. 49.
- ^ Purves y col. 2008, pág. 34; Bullock, Orkand y Grinnell 1977, pág. 134; Schmidt-Nielsen 1997, págs. 478–480.
- ^ abcd Purves y otros, 2008, pág. 49.
- ^ abcd Stevens 1966, págs. 19-20.
- ^ a b C Bullock, Orkand y Grinnell 1977, pág. 151; Junge 1981, págs. 4-5.
- ^ ab Bullock, Orkand y Grinnell 1977, pág. 152.
- ^ Bullock, Orkand y Grinnell 1977, págs. 147-149; Stevens 1966, págs. 126-127.
- ^ Purves y otros. 2008, pág. 37.
- ^ ab Purves et al. 2008, pág. 56.
- ^ Bullock, Orkand y Grinnell 1977, págs. 160-164.
- ^ Stevens 1966, págs. 21-23.
- ^ Bullock, Orkand y Grinnell 1977, págs. 161-164.
- ^ Bullock, Orkand y Grinnell 1977, pág. 509.
- ^ Tasaki, I en Field 1959, págs. 75-121
- ^ Schmidt-Nielsen 1997, Figura 12.13.
- ^ Bullock, Orkand y Grinnell 1977, pág. 163.
- ^ Waxman, SG en Waxman 2007, La esclerosis múltiple como enfermedad neurodegenerativa , págs. 333–346.
- ^ ab Rall, W en Koch & Segev 1989, Cable Theory for Dendritic Neurons , págs. 9–62.
- ^ Segev I, Fleshman JW, Burke RE (1989). "Modelos compartimentados de neuronas complejas". En Koch C , Segev I (eds.). Métodos de modelado neuronal: de sinapsis a redes . Cambridge, Massachusetts: The MIT Press. págs. 63–96. ISBN 978-0-262-11133-1. LCCN 88008279. OCLC 18384545.
- ^ Purves et al. 2008, págs. 52-53.
- ^ Ganong 1991, págs. 59-60.
- ^ Tandon, Prakash N (1 de julio de 2019). "Jagdish Chandra Bose y la neurobiología vegetal: Parte I" (PDF) . Revista india de historia de la ciencia . 54 (2). doi : 10.16943/ijhs/2019/v54i2/49660 . ISSN 0019-5235.
- ^ Felle HH, Zimmermann MR (junio de 2007). "Señalización sistémica en la cebada a través de potenciales de acción". Planta . 226 (1): 203–14. Código Bibliográfico :2007Plant.226..203F. doi :10.1007/s00425-006-0458-y. PMID 17226028. S2CID 5059716.
- ^ Luken JO (diciembre de 2005). "Hábitats de Dionaea muscipula (Venus' Fly Trap), Droseraceae, asociado con Carolina Bays". Southeastern Naturalist . 4 (4): 573–584. doi :10.1656/1528-7092(2005)004[0573:HODMVF]2.0.CO;2. ISSN 1528-7092. S2CID 9246114.
- ^ ab Böhm J, Scherzer S, Krol E, Kreuzer I, von Meyer K, Lorey C, et al. (febrero de 2016). "La Venus atrapamoscas Dionaea muscipula cuenta los potenciales de acción inducidos por la presa para inducir la absorción de sodio". Current Biology . 26 (3): 286–95. Bibcode :2016CBio...26..286B. doi :10.1016/j.cub.2015.11.057. PMC 4751343 . PMID 26804557.
- ^ abcdefg Hedrich R, Neher E (marzo de 2018). "Venus atrapamoscas: cómo funciona una planta carnívora excitable". Tendencias en la ciencia de las plantas . 23 (3): 220–234. Bibcode :2018TPS....23..220H. doi :10.1016/j.tplants.2017.12.004. PMID 29336976.
- ^ Purves D, Augustine GJ, Fitzpatrick D, et al., editores. Neurociencia. 2.ª edición. Sunderland (MA): Sinauer Associates; 2001. Potenciales eléctricos a través de las membranas de las células nerviosas. Disponible en: [1]
- ^ Volkov AG, Adesina T, Jovanov E (mayo de 2007). "Cierre de la venus atrapamoscas mediante estimulación eléctrica de las células motoras". Plant Signaling & Behavior . 2 (3): 139–45. Bibcode :2007PlSiB...2..139V. doi :10.4161/psb.2.3.4217. PMC 2634039 . PMID 19516982.
- ^ Gradmann, D; Mummert, H en Spanswick, Lucas & Dainty 1980, Potenciales de acción de las plantas , págs. 333–344.
- ^ Opritov, VA, et al. "Acoplamiento directo de la generación de potencial de acción en células de una planta superior (Cucurbita Pepo) con el funcionamiento de una bomba electrogénica". Revista rusa de fisiología vegetal , vol. 49, núm. 1, 2002, págs. 142-147.
- ^ Bullock y Horridge 1965.
- ^ Kristan WB (octubre de 2016). "Evolución temprana de las neuronas". Current Biology . 26 (20): R949–R954. Bibcode :2016CBio...26.R949K. doi : 10.1016/j.cub.2016.05.030 . PMID 27780067.
- ^ Hellier JL (2014). El cerebro, el sistema nervioso y sus enfermedades. ABC-Clio. p. 532. ISBN 9781610693387.
- ^ Junge 1981, págs. 63–82.
- ^ Kettenmann y Grantyn 1992.
- ^ Snell, FM en Lavallée, Schanne & Hébert 1969, Algunas propiedades eléctricas de microelectrodos de pipeta de punta fina .
- ^ Brasero 1961; McHenry y guarnición 1969; Worden, Swazey y Adelman 1975.
- ^ Finkelstein GW (2013). Emil du Bois-Reymond: neurociencia, yo y sociedad en la Alemania del siglo XIX . Cambridge, Massachusetts. ISBN 9781461950325.OCLC 864592470 .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Olesko, Kathryn M. y Frederic L. Holmes. "Experimento, cuantificación y descubrimiento: las primeras investigaciones fisiológicas de Helmholtz, 1843-50". En Hermann von Helmholtz y los fundamentos de la ciencia del siglo XIX , ed. David Cahan, 50-108. Berkeley; Los Ángeles; Londres: Universidad de California, 1994.
- ^ Bernstein 1912.
- ^ Baranauskas G, Martina M (enero de 2006). "Las corrientes de sodio se activan sin un retraso de tipo Hodgkin y Huxley en neuronas centrales de mamíferos". The Journal of Neuroscience . 26 (2): 671–84. doi :10.1523/jneurosci.2283-05.2006. PMC 6674426 . PMID 16407565.
- ^ Hoppensteadt 1986.
- ^ Sato, S; Fukai, H; Nomura, T; Doi, S en Reeke et al. 2005, Bifurcation Analysis of the Hodgkin-Huxley Equations , págs. 459–478.
* FitzHugh, R en Schwann 1969, Mathematical models of axcitation and propagation in nerve , págs. 12–16.
* Guckenheimer & Holmes 1986, págs. 12–16 - ^ Nelson, ME; Rinzel, J en Bower & Beeman 1995, El modelo de Hodgkin-Huxley , págs. 29-49.
* Rinzel, J y Ermentrout, GB; en Koch y Segev 1989, Análisis de la excitabilidad y oscilaciones neuronales , págs. 135-169. - ^ Biswas A, Manivannan M, Srinivasan MA (2015). "Umbral de sensibilidad vibrotáctil: modelo de mecanotransducción estocástica no lineal del corpúsculo de Pacini". IEEE Transactions on Haptics . 8 (1): 102–13. doi :10.1109/TOH.2014.2369422. PMID 25398183. S2CID 15326972.
- ^ McCulloch 1988, págs. 19–39, 46–66, 72–141; Anderson y Rosenfeld 1988, págs. 15–41.
- ^ Getting, PA en Koch & Segev 1989, Reconstrucción de pequeñas redes neuronales , págs. 171–194.
Artículos de revistas
- ^ MacDonald PE, Rorsman P (febrero de 2006). "Oscilaciones, acoplamiento intercelular y secreción de insulina en células beta pancreáticas". PLOS Biology . 4 (2): e49. doi : 10.1371/journal.pbio.0040049 . PMC 1363709 . PMID 16464129.

- ^ ab Barnett MW, Larkman PM (junio de 2007). "El potencial de acción". Neurología práctica . 7 (3): 192–7. PMID 17515599. Archivado desde el original el 8 de julio de 2011.
- ^ Golding NL, Kath WL, Spruston N (diciembre de 2001). "Dicotomía de la retropropagación del potencial de acción en las dendritas de las neuronas piramidales CA1". Journal of Neurophysiology . 86 (6): 2998–3010. doi :10.1152/jn.2001.86.6.2998. PMID 11731556. S2CID 2915815.
- ^ Sasaki, T., Matsuki, N., Ikegaya, Y. 2011 Modulación del potencial de acción durante la conducción axonal Science 331 (6017), págs.
- ^ Aur D, Connolly CI, Jog MS (noviembre de 2005). "Computing spike directivity with tetrodes" (Computación de la directividad de picos con tetrodos). Journal of Neuroscience Methods . 149 (1): 57–63. doi :10.1016/j.jneumeth.2005.05.006. PMID 15978667. S2CID 34131910.
- ^ Aur D., Jog, MS., 2010 Neuroelectrodinámica: comprensión del lenguaje cerebral, IOS Press, 2010. doi :10.3233/978-1-60750-473-3-i
- ^ Noble D (noviembre de 1960). «Acción cardíaca y potenciales de marcapasos basados en las ecuaciones de Hodgkin-Huxley». Nature . 188 (4749): 495–7. Bibcode :1960Natur.188..495N. doi :10.1038/188495b0. PMID 13729365. S2CID 4147174.
- ^ ab Goldman DE (septiembre de 1943). "Potencial, impedancia y rectificación en membranas". Revista de fisiología general . 27 (1): 37–60. doi :10.1085/jgp.27.1.37. PMC 2142582 . PMID 19873371.
- ^ abcde Hodgkin AL , Huxley AF, Katz B (abril de 1952). "Medición de las relaciones corriente-voltaje en la membrana del axón gigante de Loligo". The Journal of Physiology . 116 (4): 424–48. doi :10.1113/jphysiol.1952.sp004716. PMC 1392219. PMID 14946712 .
* Hodgkin AL , Huxley AF (abril de 1952). "Corrientes transportadas por iones de sodio y potasio a través de la membrana del axón gigante de Loligo". The Journal of Physiology . 116 (4): 449–72. doi :10.1113/jphysiol.1952.sp004717. PMC 1392213. PMID 14946713 .
* Hodgkin AL , Huxley AF (abril de 1952). "Los componentes de la conductancia de la membrana en el axón gigante de Loligo". The Journal of Physiology . 116 (4): 473–96. doi :10.1113/jphysiol.1952.sp004718. PMC 1392209. PMID 14946714 .
* Hodgkin AL , Huxley AF (abril de 1952). "El efecto dual del potencial de membrana en la conductancia de sodio en el axón gigante de Loligo". The Journal of Physiology . 116 (4): 497–506. doi :10.1113/jphysiol.1952.sp004719. PMC 1392212. PMID 14946715 .
* Hodgkin AL , Huxley AF (agosto de 1952). "Una descripción cuantitativa de la corriente de membrana y su aplicación a la conducción y excitación en el nervio". The Journal of Physiology . 117 (4): 500–44. doi :10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237 . - ^ Naundorf B, Wolf F, Volgushev M (abril de 2006). «Características únicas de la iniciación del potencial de acción en neuronas corticales» (PDF) . Nature . 440 (7087): 1060–3. Bibcode :2006Natur.440.1060N. doi :10.1038/nature04610. PMID 16625198. S2CID 1328840. Archivado desde el original (PDF) el 20 de diciembre de 2018 . Consultado el 24 de septiembre de 2019 .
- ^ Hodgkin AL (julio de 1937). "Evidencia de transmisión eléctrica en nervios: Parte I". The Journal of Physiology . 90 (2): 183–210. doi :10.1113/jphysiol.1937.sp003507. PMC 1395060 . PMID 16994885.
* Hodgkin AL (julio de 1937). "Evidencia de transmisión eléctrica en los nervios: Parte II". The Journal of Physiology . 90 (2): 211–32. doi :10.1113/jphysiol.1937.sp003508. PMC 1395062 . PMID 16994886. - ^ Zalc B (2006). "La adquisición de mielina: una historia de éxito". Señalización purinérgica en interacciones neurona-glía . Simposios de la Fundación Novartis. Vol. 276. págs. 15-21, discusión 21-5, 54-7, 275-81. doi :10.1002/9780470032244.ch3. ISBN 978-0-470-03224-4. Número de identificación personal 16805421.
{{cite book}}:|journal=ignorado ( ayuda ) - ^ Poliak S, Peles E (diciembre de 2003). "La diferenciación local de los axones mielinizados en los nodos de Ranvier". Nature Reviews. Neuroscience . 4 (12): 968–80. doi :10.1038/nrn1253. PMID 14682359. S2CID 14720760.
- ^ Simons M, Trotter J (octubre de 2007). "Resumiendo: la biología celular de la mielinización". Current Opinion in Neurobiology . 17 (5): 533–40. doi :10.1016/j.conb.2007.08.003. PMID 17923405. S2CID 45470194.
- ^ Xu K, Terakawa S (agosto de 1999). "Los nódulos de fenestración y el amplio espacio submielínico forman la base de la conducción de impulsos inusualmente rápida de los axones mielinizados del camarón". The Journal of Experimental Biology . 202 (Pt 15): 1979–89. doi :10.1242/jeb.202.15.1979. PMID 10395528.
- ^ ab Hursh JB (1939). "Velocidad de conducción y diámetro de las fibras nerviosas". American Journal of Physiology . 127 : 131–39. doi :10.1152/ajplegacy.1939.127.1.131.
- ^ Lillie RS (marzo de 1925). "Factores que afectan la transmisión y la recuperación en el modelo pasivo del nervio de hierro". The Journal of General Physiology . 7 (4): 473–507. doi :10.1085/jgp.7.4.473. PMC 2140733 . PMID 19872151. Véase también Keynes y Aidley 1991, pág. 78.
- ^ Tasaki I (1939). "Transmisión electrosaltatoria del impulso nervioso y efecto de la narcosis sobre la fibra nerviosa". Am. J. Physiol . 127 : 211–27. doi :10.1152/ajplegacy.1939.127.2.211.
- ^ Tasaki I, Takeuchi T (1941). "Der am Ranvierschen Knoten entstehende Aktionsstrom und seine Bedeutung für die Erregungsleitung". Pflügers Archiv für die gesamte Physiologie . 244 (6): 696–711. doi :10.1007/BF01755414. S2CID 8628858.
* Tasaki I, Takeuchi T (1942). "Weitere Studien über den Aktionsstrom der markhaltigen Nervenfaser und über die elektrosaltatorische Übertragung des nerviosanimpulses". Pflügers Archiv für die gesamte Physiologie . 245 (5): 764–82. doi :10.1007/BF01755237. S2CID 44315437. - ^ Huxley AF , Stämpfli R (mayo de 1949). "Evidencia de conducción saltatoria en fibras nerviosas mielinizadas periféricas". The Journal of Physiology . 108 (3): 315–39. doi :10.1113/jphysiol.1949.sp004335. PMC 1392492. PMID 16991863 .
* Huxley AF , Stampfli R (febrero de 1951). "Determinación directa del potencial de reposo de la membrana y del potencial de acción en fibras nerviosas mielinizadas individuales". The Journal of Physiology . 112 (3–4): 476–95. doi :10.1113/jphysiol.1951.sp004545. PMC 1393015. PMID 14825228. - ^ Rushton WA (septiembre de 1951). "Una teoría de los efectos del tamaño de la fibra en el nervio medular". The Journal of Physiology . 115 (1): 101–22. doi :10.1113/jphysiol.1951.sp004655. PMC 1392008 . PMID 14889433.
- ^ ab Hartline DK, Colman DR (enero de 2007). "Conducción rápida y evolución de axones gigantes y fibras mielinizadas". Current Biology . 17 (1): R29-35. Bibcode :2007CBio...17R..29H. doi : 10.1016/j.cub.2006.11.042 . PMID 17208176. S2CID 10033356.
- ^ Miller RH, Mi S (noviembre de 2007). "Disección de la desmielinización". Nature Neuroscience . 10 (11): 1351–4. doi :10.1038/nn1995. PMID 17965654. S2CID 12441377.
- ^ Kelvin WT (1855). "Sobre la teoría del telégrafo eléctrico". Actas de la Royal Society . 7 : 382–99. doi :10.1098/rspl.1854.0093. S2CID 178547827.
- ^ Hodgkin AL , Rushton WA (diciembre de 1946). "Las constantes eléctricas de una fibra nerviosa de crustáceos". Actas de la Royal Society of Medicine . 134 (873): 444–79. Bibcode :1946RSPSB.133..444H. doi : 10.1098/rspb.1946.0024 . PMID 20281590.
- ^ Süudhof TC (2008). "Liberación de neurotransmisores". Farmacología de la liberación de neurotransmisores . Manual de farmacología experimental. Vol. 184. págs. 1–21. doi :10.1007/978-3-540-74805-2_1. ISBN 978-3-540-74804-5. Número de identificación personal 18064409.
- ^ Rusakov DA (agosto de 2006). "Mecanismos dependientes de Ca2+ del control presináptico en las sinapsis centrales". The Neuroscientist . 12 (4): 317–26. doi :10.1177/1073858405284672. PMC 2684670 . PMID 16840708.
- ^ Humeau Y, Doussau F, Grant NJ, Poulain B (mayo de 2000). "Cómo las neurotoxinas botulínicas y tetánicas bloquean la liberación de neurotransmisores". Biochimie . 82 (5): 427–46. doi :10.1016/S0300-9084(00)00216-9. PMID 10865130.
- ^ Zoidl G, Dermietzel R (noviembre de 2002). "En busca de la sinapsis eléctrica: una mirada al futuro". Cell and Tissue Research . 310 (2): 137–42. doi :10.1007/s00441-002-0632-x. PMID 12397368. S2CID 22414506.
- ^ Brink PR, Cronin K, Ramanan SV (agosto de 1996). "Uniones estrechas en células excitables". Revista de bioenergética y biomembranas . 28 (4): 351–8. doi :10.1007/BF02110111. PMID 8844332. S2CID 46371790.
- ^ Hirsch NP (julio de 2007). "Unión neuromuscular en la salud y la enfermedad". British Journal of Anaesthesia . 99 (1): 132–8. doi : 10.1093/bja/aem144 . PMID 17573397.
- ^ Hughes BW, Kusner LL, Kaminski HJ (abril de 2006). "Arquitectura molecular de la unión neuromuscular". Muscle & Nerve . 33 (4): 445–61. doi :10.1002/mus.20440. PMID 16228970. S2CID 1888352.
- ^ ab Newmark J (enero de 2007). "Agentes nerviosos". The Neurologist . 13 (1): 20–32. doi :10.1097/01.nrl.0000252923.04894.53. PMID 17215724. S2CID 211234081.
- ^ Costa LG (abril de 2006). "Cuestiones actuales en toxicología de organofosforados". Clinica Chimica Acta; Revista internacional de química clínica . 366 (1–2): 1–13. doi :10.1016/j.cca.2005.10.008. PMID 16337171.
- ^ abc Kléber AG, Rudy Y (abril de 2004). "Mecanismos básicos de propagación del impulso cardíaco y arritmias asociadas". Physiological Reviews . 84 (2): 431–88. doi :10.1152/physrev.00025.2003. PMID 15044680. S2CID 21823003.
- ^ Tamargo J, Caballero R, Delpón E (enero de 2004). "Enfoques farmacológicos en el tratamiento de la fibrilación auricular". Current Medicinal Chemistry . 11 (1): 13–28. doi :10.2174/0929867043456241. PMID 14754423.
- ^ Slayman CL, Long WS, Gradmann D (abril de 1976). ""Potenciales de acción" en Neurospora crassa, un hongo micelial". Biochimica et Biophysica Acta (BBA) - Biomembranes . 426 (4): 732–44. doi :10.1016/0005-2736(76)90138-3. PMID 130926.
- ^ Mummert H, Gradmann D (diciembre de 1991). "Potenciales de acción en Acetabularia: medición y simulación de flujos dependientes del voltaje". The Journal of Membrane Biology . 124 (3): 265–73. doi :10.1007/BF01994359. PMID 1664861. S2CID 22063907.
- ^ Gradmann D (2001). "Modelos para oscilaciones en plantas". Aust. J. Plant Physiol . 28 (7): 577–590. doi :10.1071/pp01017.
- ^ Beilby MJ (2007). Potencial de acción en carófitas . Revista internacional de citología. Vol. 257. págs. 43–82. doi :10.1016/S0074-7696(07)57002-6. ISBN 978-0-12-373701-4. Número de identificación personal 17280895.
- ^ Gradmann D, Hoffstadt J (noviembre de 1998). "Electroacoplamiento de transportadores de iones en plantas: interacción con concentraciones internas de iones". The Journal of Membrane Biology . 166 (1): 51–9. doi :10.1007/s002329900446. PMID 9784585. S2CID 24190001.
- ^ Fromm J, Lautner S (marzo de 2007). "Señales eléctricas y su significado fisiológico en plantas". Plant, Cell & Environment . 30 (3): 249–257. doi : 10.1111/j.1365-3040.2006.01614.x . PMID 17263772.
- ^ Leys SP, Mackie GO, Meech RW (mayo de 1999). "Conducción de impulsos en una esponja". The Journal of Experimental Biology . 202 (Pt 9) (9): 1139–50. doi :10.1242/jeb.202.9.1139. PMID 10101111.
- ^ Keynes RD (1989). "El papel de los axones gigantes en los estudios del impulso nervioso". BioEssays . 10 (2–3): 90–3. doi :10.1002/bies.950100213. PMID 2541698.
- ^ Meunier C, Segev I (noviembre de 2002). "Jugando al abogado del diablo: ¿es útil el modelo de Hodgkin-Huxley?". Tendencias en neurociencias . 25 (11): 558–63. doi :10.1016/S0166-2236(02)02278-6. PMID 12392930. S2CID 1355280.
- ^ Cole KS (1949). "Características eléctricas dinámicas de la membrana del axón del calamar". Arch. Sci. Physiol . 3 : 253–8.
- ^ Ling G, Gerard RW (diciembre de 1949). "El potencial de membrana normal de las fibras del sartorio de la rana". Journal of Cellular and Comparative Physiology . 34 (3): 383–96. doi :10.1002/jcp.1030340304. PMID 15410483.
- ^ Nastuk WL, Hodgkin A (1950). "La actividad eléctrica de fibras musculares individuales". Revista de fisiología celular y comparada . 35 : 39–73. doi :10.1002/jcp.1030350105.
- ^ Brock LG, Coombs JS, Eccles JC (agosto de 1952). "El registro de potenciales de neuronas motoras con un electrodo intracelular". The Journal of Physiology . 117 (4): 431–60. doi :10.1113/jphysiol.1952.sp004759. PMC 1392415 . PMID 12991232.
- ^ Ross WN, Salzberg BM, Cohen LB, Davila HV (diciembre de 1974). "Un gran cambio en la absorción del colorante durante el potencial de acción". Biophysical Journal . 14 (12): 983–6. Bibcode :1974BpJ....14..983R. doi :10.1016/S0006-3495(74)85963-1. PMC 1334592 . PMID 4429774.
* Grynkiewicz G, Poenie M, Tsien RY (marzo de 1985). "Una nueva generación de indicadores de Ca2+ con propiedades de fluorescencia muy mejoradas". The Journal of Biological Chemistry . 260 (6): 3440–50. doi : 10.1016/S0021-9258(19)83641-4 . PMID 3838314. - ^ Bu G, Adams H, Berbari EJ, Rubart M (marzo de 2009). "Repolarización del potencial de acción uniforme dentro del sarcolema de cardiomiocitos ventriculares in situ". Revista biofísica . 96 (6): 2532–46. Bibcode :2009BpJ....96.2532B. doi :10.1016/j.bpj.2008.12.3896. PMC 2907679 . PMID 19289075.
- ^ Milligan JV, Edwards C (julio de 1965). "Algunos factores que afectan el curso temporal de la recuperación de la capacidad de contractura después de una contractura de potasio en el músculo estriado de la rana". The Journal of General Physiology . 48 (6): 975–83. doi :10.1085/jgp.48.6.975. PMC 2195447 . PMID 5855511.
* Ritchie JM, Rogart RB (1977). "La unión de la saxitoxina y la tetrodotoxina al tejido excitable". Reseñas de fisiología, bioquímica y farmacología, volumen 79. Vol. 79. págs. 1–50. doi :10.1007/BFb0037088. ISBN . 0-387-08326-X.PMID 335473 .
* Keynes RD, Ritchie JM (agosto de 1984). "Sobre la unión de la saxitoxina marcada al axón gigante del calamar". Actas de la Royal Society de Londres. Serie B, Ciencias Biológicas . 222 (1227): 147–53. Bibcode :1984RSPSB.222..147K. doi :10.1098/rspb.1984.0055. PMID 6148754. S2CID 11465181. - ^ Piccolino M (octubre de 1997). "Luigi Galvani y la electricidad animal: dos siglos después de la fundación de la electrofisiología". Tendencias en neurociencias . 20 (10): 443–8. doi :10.1016/S0166-2236(97)01101-6. PMID 9347609. S2CID 23394494.
- ^ Piccolino M (abril de 2000). "El bicentenario de la batería voltaica (1800-2000): el órgano eléctrico artificial". Tendencias en neurociencias . 23 (4): 147–51. doi :10.1016/S0166-2236(99)01544-1. PMID 10717671. S2CID 393323.
- ^ Bernstein J (1902). "Untersuchungen zur Thermodynamik der bioelektrischen Ströme". Pflügers Archiv für die gesamte Physiologie . 92 (10–12): 521–562. doi :10.1007/BF01790181. S2CID 33229139.
- ^ Cole KS , Curtis HJ (mayo de 1939). "Impedancia eléctrica del axón gigante del calamar durante la actividad". The Journal of General Physiology . 22 (5): 649–70. doi :10.1085/jgp.22.5.649. PMC 2142006 . PMID 19873125.
- ^ Lapicque L (1907). "Investigaciones cuantitativas sobre la excitación eléctrica de los nervios tratados como una polarización". J. Physiol. Patol. Gen. 9 : 620–635.
- ^ Hodgkin AL , Katz B (marzo de 1949). "El efecto de los iones de sodio en la actividad eléctrica del axón gigante del calamar". The Journal of Physiology . 108 (1): 37–77. doi :10.1113/jphysiol.1949.sp004310. PMC 1392331. PMID 18128147 .
- ^ Neher E , Sakmann B (abril de 1976). "Corrientes de un solo canal registradas a partir de la membrana de fibras musculares de rana desnervadas". Nature . 260 (5554): 799–802. Bibcode :1976Natur.260..799N. doi :10.1038/260799a0. PMID 1083489. S2CID 4204985.
* Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ (agosto de 1981). "Técnicas de fijación de parche mejoradas para el registro de corriente de alta resolución de células y parches de membrana sin células". Pflügers Archiv . 391 (2): 85–100. doi :10.1007/BF00656997. PMID 6270629. S2CID 12014433.
* Neher E , Sakmann B (marzo de 1992). "La técnica de fijación de parches". Scientific American . 266 (3): 44–51. Bibcode :1992SciAm.266c..44N. doi :10.1038/scientificamerican0392-44. PMID 1374932. - ^ Yellen G (septiembre de 2002). "Los canales de potasio dependientes del voltaje y sus parientes". Nature . 419 (6902): 35–42. Bibcode :2002Natur.419...35Y. doi :10.1038/nature00978. PMID 12214225. S2CID 4420877.
- ^ Doyle DA, Morais Cabral J, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, et al. (abril de 1998). "La estructura del canal de potasio: base molecular de la conducción y selectividad del K+". Science . 280 (5360): 69–77. Bibcode :1998Sci...280...69D. doi :10.1126/science.280.5360.69. PMID 9525859.
* Zhou Y, Morais-Cabral JH, Kaufman A, MacKinnon R (noviembre de 2001). "Química de la coordinación e hidratación iónica revelada por un complejo Fab de canal de K+ con una resolución de 2,0 A". Nature . 414 (6859): 43–8. Bibcode :2001Natur.414...43Z. doi :10.1038/35102009. PMID 11689936. S2CID 205022645.
* Jiang Y, Lee A, Chen J, Ruta V, Cadene M, Chait BT, MacKinnon R (mayo de 2003). "Estructura de rayos X de un canal de K+ dependiente del voltaje". Nature . 423 (6935): 33–41. Bibcode :2003Natur.423...33J. doi :10.1038/nature01580. PMID 12721618. S2CID 4347957. - ^ Cha A, Snyder GE, Selvin PR, Bezanilla F (diciembre de 1999). "Movimiento a escala atómica de la región de detección de voltaje en un canal de potasio medido mediante espectroscopia". Nature . 402 (6763): 809–13. Bibcode :1999Natur.402..809C. doi : 10.1038/45552 . PMID 10617201. S2CID 4353978.
* Glauner KS, Mannuzzu LM, Gandhi CS, Isacoff EY (diciembre de 1999). "Mapeo espectroscópico del movimiento del sensor de voltaje en el canal de potasio de Shaker". Nature . 402 (6763): 813–7. Bibcode :1999Natur.402..813G. doi :10.1038/45561. PMID 10617202. S2CID 4417476.
* Bezanilla F (abril de 2000). "El sensor de voltaje en canales iónicos dependientes del voltaje". Physiological Reviews . 80 (2): 555–92. doi :10.1152/physrev.2000.80.2.555. PMID 10747201. S2CID 18629998. - ^ Catterall WA (febrero de 2001). "Una vista en 3D de los canales de sodio". Nature . 409 (6823): 988–9, 991. Bibcode :2001Natur.409..988C. doi : 10.1038/35059188 . PMID 11234048. S2CID 4371677.
* Sato C, Ueno Y, Asai K, Takahashi K, Sato M, Engel A, Fujiyoshi Y (febrero de 2001). "El canal de sodio sensible al voltaje es una molécula con forma de campana con varias cavidades". Nature . 409 (6823): 1047–51. Bibcode :2001Natur.409.1047S. doi :10.1038/35059098. PMID 11234014. S2CID 4430165. - ^ Skou JC (febrero de 1957). "La influencia de algunos cationes en una adenosina trifosfatasa de nervios periféricos". Biochimica et Biophysica Acta . 23 (2): 394–401. doi :10.1016/0006-3002(57)90343-8. PMID 13412736. S2CID 32516710.
- ^ Hodgkin AL , Keynes RD (abril de 1955). "Transporte activo de cationes en axones gigantes de Sepia y Loligo". The Journal of Physiology . 128 (1): 28–60. doi :10.1113/jphysiol.1955.sp005290. PMC 1365754. PMID 14368574 .
- ^ Caldwell PC, Hodgkin AL, Keynes RD, Shaw TL (julio de 1960). "Los efectos de la inyección de compuestos de fosfato 'ricos en energía' en el transporte activo de iones en los axones gigantes de Loligo". The Journal of Physiology . 152 (3): 561–90. doi :10.1113/jphysiol.1960.sp006509. PMC 1363339 . PMID 13806926.
- ^ Caldwell PC, Keynes RD (junio de 1957). "La utilización de la energía de enlace de fosfato para la extrusión de sodio de axones gigantes". The Journal of Physiology . 137 (1): 12–3P. doi :10.1113/jphysiol.1957.sp005830. PMID 13439598. S2CID 222188054.
- ^ Morth JP, Pedersen BP, Toustrup-Jensen MS, Sørensen TL, Petersen J, Andersen JP, et al. (Diciembre de 2007). "Estructura cristalina de la bomba de sodio-potasio". Naturaleza . 450 (7172): 1043–9. Código Bib : 2007Natur.450.1043M. doi : 10.1038/naturaleza06419. PMID 18075585. S2CID 4344526.
- ^ Lee AG, East JM (junio de 2001). "Lo que la estructura de una bomba de calcio nos dice sobre su mecanismo". The Biochemical Journal . 356 (Pt 3): 665–83. doi :10.1042/0264-6021:3560665. PMC 1221895 . PMID 11389676.
- ^ * Fitzhugh R (mayo de 1960). "Umbrales y mesetas en las ecuaciones del nervio de Hodgkin-Huxley". The Journal of General Physiology . 43 (5): 867–96. doi :10.1085/jgp.43.5.867. PMC 2195039 . PMID 13823315.
* Kepler TB, Abbott LF, Marder E (1992). "Reducción de modelos neuronales basados en conductancia". Cibernética biológica . 66 (5): 381–7. doi :10.1007/BF00197717. PMID 1562643. S2CID 6789007. - ^ Morris C, Lecar H (julio de 1981). "Oscilaciones de voltaje en la fibra muscular gigante del percebe". Biophysical Journal . 35 (1): 193–213. Bibcode :1981BpJ....35..193M. doi :10.1016/S0006-3495(81)84782-0. PMC 1327511 . PMID 7260316.
- ^ Fitzhugh R (julio de 1961). "Impulsos y estados fisiológicos en modelos teóricos de la membrana nerviosa". Revista biofísica . 1 (6): 445–66. Bibcode :1961BpJ.....1..445F. doi :10.1016/S0006-3495(61)86902-6. PMC 1366333 . PMID 19431309.
* Nagumo J, Arimoto S, Yoshizawa S (1962). "Una línea de transmisión de pulsos activa que simula el axón nervioso". Actas del IRE . 50 (10): 2061–2070. doi :10.1109/JRPROC.1962.288235. S2CID 51648050. - ^ Bonhoeffer KF (septiembre de 1948). "Activación del hierro pasivo como modelo para la excitación del nervio". The Journal of General Physiology . 32 (1): 69–91. doi :10.1085/jgp.32.1.69. PMC 2213747 . PMID 18885679.
* Bonhoeffer KF (1953). "Modelle der Nervenerregung". Naturwissenschaften . 40 (11): 301–311. Código Bib : 1953NW..... 40.. 301B. doi :10.1007/BF00632438. S2CID 19149460.
* Van der Pol B (1926). "Sobre las oscilaciones de relajación". Philosophical Magazine . 2 : 977–992.
* Van der Pol B , Van der Mark J (1928). "El latido del corazón considerado como una oscilación de relajación y un modelo eléctrico del corazón". Philosophical Magazine . 6 : 763–775. doi :10.1080/14786441108564652.
* Van der Pol B , van der Mark J (1929). "El latido del corazón considerado como una oscilación de relajación y un modelo eléctrico del corazón". Arch. Neerl. Physiol . 14 : 418–443. - ^ Evans JW (1972). "Ecuaciones de axones nerviosos. I. Aproximaciones lineales". Indiana Univ. Math. J . 21 (9): 877–885. doi : 10.1512/iumj.1972.21.21071 .
* Evans JW, Feroe J (1977). "Teoría de la estabilidad local del impulso nervioso". Math. Biosci . 37 : 23–50. doi :10.1016/0025-5564(77)90076-1. - ^ Keener JP (1983). "Circuitos analógicos para las ecuaciones de Van der Pol y FitzHugh-Nagumo". IEEE Transactions on Systems, Man, and Cybernetics . 13 (5): 1010–1014. doi :10.1109/TSMC.1983.6313098. S2CID 20077648.
- ^ Hooper SL (marzo de 2000). "Generadores de patrones centrales". Current Biology . 10 (5): R176–R179. Bibcode :2000CBio...10.R176H. CiteSeerX 10.1.1.133.3378 . doi :10.1016/S0960-9822(00)00367-5. PMID 10713861. S2CID 11388348.
Libros
- Anderson JA, Rosenfeld E, eds. (1988). Neurocomputación: fundamentos de la investigación . Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-01097-9. OCLC 15860311 .
- Bernstein J (1912). Elektrobiologie, die Lehre von den elektrischen Vorgängen im Organismus auf moderner Grundlage dargestellt [ Biología eléctrica, el estudio de los procesos eléctricos en el organismo representados de forma moderna ]. Braunschweig: Vieweg und Sohn. LCCN 12027986. OCLC 11358569.
- Bower JM, Beeman D (1995). El libro de GENESIS: exploración de modelos neuronales realistas con el sistema de simulación neuronal general . Santa Clara, California: TELOS. ISBN 978-0-387-94019-9. Código LCCN 94017624. Código OCLC 30518469.
- Brazier MA (1961). Una historia de la actividad eléctrica del cerebro . Londres: Pitman. LCCN 62001407. OCLC 556863.
- Bullock TH , Horridge GA (1965). Estructura y función de los sistemas nerviosos de los invertebrados . Una serie de libros de biología. San Francisco: WH Freeman. LCCN 65007965. OCLC 558128.
- Bullock TH , Orkand R, Grinnell A (1977). Introducción a los sistemas nerviosos . Una serie de libros de biología. San Francisco: WH Freeman. ISBN 978-0-7167-0030-2. OCLC 2048177 .
- Field J, ed. (1959). Manual de fisiología: una presentación crítica y completa de los conocimientos y conceptos fisiológicos: Sección 1: Neurofisiología . Vol. 1. Washington, DC: Sociedad Estadounidense de Fisiología. LCCN 60004587. OCLC 830755894.
- Ganong, WF (1991). Revista de fisiología médica (15.ª edición). Norwalk, Connecticut: Appleton and Lange. ISBN 978-0-8385-8418-7. ISSN 0892-1253. LCCN 87642343. OCLC 23761261.
{{cite book}}:|journal=ignorado ( ayuda ) - Guckenheimer J, Holmes P, eds. (1986). Oscilaciones no lineales, sistemas dinámicos y bifurcaciones de campos vectoriales . Applied Mathematical Sciences. Vol. 42 (2.ª ed.). Nueva York: Springer Verlag. ISBN. 978-0-387-90819-9.OCLC 751129941 .
- Hoppensteadt FC (1986). Introducción a las matemáticas de las neuronas . Estudios de Cambridge sobre biología matemática. Vol. 6. Cambridge: Cambridge University Press. ISBN 978-0-521-31574-6. OCLC 12052275 .
- Junge D (1981). Excitación nerviosa y muscular (2.ª ed.). Sunderland, Mass.: Sinauer Associates. ISBN 978-0-87893-410-2. Código LCCN: 80018158. Código OCLC : 6486925.
- Kettenmann H, Grantyn R, eds. (1992). Métodos electrofisiológicos prácticos: una guía para estudios in vitro en neurobiología de vertebrados . Nueva York: Wiley. ISBN 978-0-471-56200-9. Código LCCN 92000179. Código OCLC 25204689.
- Keynes RD , Aidley DJ (1991). Nervio y músculo (2.ª ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-41042-7. LCCN 90015167. OCLC 25204483.
- Koch C , Segev I, eds. (1989). Métodos de modelado neuronal: de sinapsis a redes . Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-11133-1. LCCN 88008279. OCLC 18384545.
- Lavallée M, Schanne OF, Hébert NC, eds. (1969). Microelectrodos de vidrio . Nueva York: Wiley. ISBN 978-0-471-51885-3. LCCN 68009252. OCLC 686.
- McCulloch WS (1988). Encarnaciones de la mente . Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-63114-3. LCCN 88002987. OCLC 237280.
- McHenry LC, Garrison FH (1969). Historia de la neurología de Garrison . Springfield, Ill.: Charles C. Thomas. OCLC 429733931.
- Silverthorn DU (2010). Fisiología humana: un enfoque integrado (5.ª ed.). San Francisco: Pearson. ISBN 978-0-321-55980-7. OCLC 268788623 .
- Spanswick RM, Lucas WJ, Dainty J, eds. (1980). Transporte de membranas vegetales: cuestiones conceptuales actuales . Desarrollos en biología vegetal. Vol. 4. Ámsterdam: Elsevier Biomedical Press. ISBN 978-0-444-80192-0. Código LCCN 79025719. Código OCLC 5799924.
- Purves D, Augustine GJ, Fitzpatrick D, Hall WC, Lamantia AS, McNamara JO, Williams SM (2001). "Liberación de transmisores de vesículas sinápticas". Neurociencia (2.ª ed.). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-742-4. Código LCCN 00059496. Código OCLC 806472664.
- Purves D, Augustine GJ, Fitzpatrick D, Hall WC, Lamantia AS, McNamara JO, White LE (2008). Neurociencia (4.ª ed.). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-697-7. OCLC 144771764 .
- Reeke GN, Poznanski RR, Sporns O, Rosenberg JR, Lindsay KA, eds. (2005). Modelado en las neurociencias: de los sistemas biológicos a la robótica neuromimética . Boca Raton, Fla.: Taylor & Francis. ISBN 978-0-415-32868-5. OCLC 489024131 .
- Schmidt-Nielsen K (1997). Fisiología animal: adaptación y medio ambiente (5.ª ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-57098-5. Código LCCN 96039295. Código OCLC 35744403.
- Schwann HP, ed. (1969). Ingeniería biológica . Serie electrónica interuniversitaria. Vol. 9. Nueva York: McGraw-Hill. ISBN 978-0-07-055734-5. LCCN 68027513. OCLC 51993.
- Stevens CF (1966). Neurofisiología: una introducción . Nueva York: John Wiley and Sons. ISBN 9780471824367. LCCN 66015872. OCLC 1175605.
- Waxman SG, ed. (2007). Neurología molecular . Burlington, Mass.: Elsevier Academic Press. ISBN 978-0-12-369509-3. OCLC 154760295 .
- Worden FG, Swazey JP, Adelman G, eds. (1975). Las neurociencias: caminos de descubrimiento. Cambridge, Massachusetts: The MIT Press. ISBN 978-0-262-23072-8. OCLC 1500233 .
Páginas web
- ^ Fitzhugh R, Izhikevich E (2006). "Modelo FitzHugh-Nagumo". Scholarpedia . 1 (9): 1349. Código Bibliográfico :2006SchpJ...1.1349I. doi : 10.4249/scholarpedia.1349 .
- ^ "El Premio Nobel de Fisiología o Medicina 1963" (Nota de prensa). Real Academia Sueca de Ciencias. 1963. Archivado desde el original el 16 de julio de 2007. Consultado el 21 de febrero de 2010 .
- ^ "El Premio Nobel de Fisiología o Medicina 1991" (Nota de prensa). Real Academia Sueca de Ciencias. 1991. Archivado desde el original el 24 de marzo de 2010. Consultado el 21 de febrero de 2010 .
- ^ "El Premio Nobel de Fisiología o Medicina 1906" (Nota de prensa). Real Academia Sueca de Ciencias. 1906. Archivado desde el original el 4 de diciembre de 2008. Consultado el 21 de febrero de 2010 .
- ^ Warlow C (junio de 2007). "La reciente evolución de un canal iónico simbiótico en la familia de las leguminosas alteró la conductancia iónica y mejoró la funcionalidad en la señalización del calcio". Practical Neurology . 7 (3). BMJ Publishing Group: 192–197. Archivado desde el original el 14 de marzo de 2012 . Consultado el 23 de marzo de 2013 .
- ^ "El Premio Nobel de Química 1997" (Nota de prensa). Real Academia Sueca de Ciencias. 1997. Archivado desde el original el 23 de octubre de 2009. Consultado el 21 de febrero de 2010 .
Lectura adicional
- Aidley DJ, Stanfield PR (1996). Canales iónicos: moléculas en acción . Cambridge: Cambridge University Press. ISBN 978-0-521-49882-1.
- Bear MF, Connors BW, Paradiso MA (2001). Neurociencia: exploración del cerebro . Baltimore: Lippincott. ISBN 0-7817-3944-6.
- Clay JR (mayo de 2005). "Revisión de la excitabilidad axonal". Progreso en biofísica y biología molecular . 88 (1): 59–90. doi : 10.1016/j.pbiomolbio.2003.12.004 . PMID 15561301.
- Deutsch S, Micheli-Tzanakou E (1987). Sistemas Neuroeléctricos . Nueva York: Prensa de la Universidad de Nueva York. ISBN 0-8147-1782-9.
- Hille B (2001). Canales iónicos de membranas excitables (3.ª ed.). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-321-1.
- Johnston D, Wu SM (1995). Fundamentos de la neurofisiología celular . Cambridge, Massachusetts: Bradford Book, The MIT Press. ISBN 0-262-10053-3.
- Kandel ER , Schwartz JH, Jessell TM (2000). Principios de la ciencia neuronal (4ª ed.). Nueva York: McGraw-Hill. ISBN 0-8385-7701-6.
- Miller C (1987). "Cómo funcionan las proteínas de los canales iónicos". En Kaczmarek LK, Levitan IB (eds.). Neuromodulación: el control bioquímico de la excitabilidad neuronal . Nueva York: Oxford University Press. págs. 39–63. ISBN 978-0-19-504097-5.
- Nelson DL, Cox MM (2008). Principios de bioquímica de Lehninger (5.ª ed.). Nueva York: WH Freeman. ISBN 978-0-7167-7108-1.
Enlaces externos
- Flujo iónico en potenciales de acción en Blackwell Publishing
- Propagación del potencial de acción en axones mielinizados y no mielinizados en Blackwell Publishing
- Generación de AP en células cardíacas y generación de AP en células neuronales
- Potencial de membrana en reposo de Life: The Science of Biology , por WK Purves, D Sadava, GH Orians y HC Heller, 8.ª edición, Nueva York: WH Freeman, ISBN 978-0-7167-7671-0 .
- Movimiento iónico y voltaje de Goldman para concentraciones iónicas arbitrarias en la Universidad de Arizona
- Una caricatura que ilustra el potencial de acción.
- Propagación del potencial de acción
- Producción del potencial de acción: simulaciones de fijación de tensión y corriente [ enlace muerto permanente ]
- Software de código abierto para simular potenciales de acción neuronales y cardíacos en SourceForge.net
- Introducción al potencial de acción, Neurociencia en línea (libro de texto electrónico sobre neurociencia de la Facultad de Medicina de la Universidad de Texas en Houston)
- Khan Academy: Electrotónica y potencial de acción Archivado el 2 de julio de 2014 en Wayback Machine





