Ecuación de Nernst

En electroquímica , la ecuación de Nernst es una relación termodinámica química que permite calcular el potencial de reducción de una reacción ( reacción de semicelda o de celda completa ) a partir del potencial de electrodo estándar , la temperatura absoluta , el número de electrones involucrados en la reacción redox y las actividades (a menudo aproximadas por concentraciones) de las especies químicas que experimentan reducción y oxidación respectivamente. Debe su nombre a Walther Nernst , un químico físico alemán que formuló la ecuación. ^{[1] [2]}

Cuando un oxidante ( Ox ) acepta un número z de electrones ( e ⁻ ) para ser convertidos en su forma reducida ( Red ), la semireacción se expresa como:  

${\displaystyle {\ce {Buey + ze- -> Rojo}}}$

El cociente de reacción ( Q _r ), también llamado a menudo producto de actividad iónica ( IAP ), es la relación entre las actividades químicas ( a ) de la forma reducida (el reductor , a _Red ) y la forma oxidada (el oxidante , a _Ox ). La actividad química de una especie disuelta corresponde a su verdadera concentración termodinámica teniendo en cuenta las interacciones eléctricas entre todos los iones presentes en solución a concentraciones elevadas. Para una especie disuelta dada, su actividad química (a) es el producto de su coeficiente de actividad (γ) por su concentración molar (mol/L de solución), o molal (mol/kg de agua), (C): a = γ C. Entonces, si la concentración ( C , también denotada aquí abajo con corchetes [ ]) de todas las especies disueltas de interés es suficientemente baja y sus coeficientes de actividad son cercanos a la unidad, sus actividades químicas pueden aproximarse por sus concentraciones como se hace comúnmente al simplificar o idealizar una reacción con fines didácticos:

${\displaystyle Q_{r}={\frac {a_{\text{Rojo}}}{a_{\text{Buey}}}}={\frac {[\operatorname {Rojo} ]}{[\operatorname {Buey} ]}}}$

En el equilibrio químico , la relación Q _r de la actividad del producto de reacción ( a _Red ) por la actividad del reactivo ( a _Ox ) es igual a la constante de equilibrio K de la semireacción:

${\displaystyle K={\frac {a_{\text{Rojo}}}{a_{\text{Buey}}}}}$

La termodinámica estándar también dice que la energía libre de Gibbs real Δ G está relacionada con el cambio de energía libre en el estado estándar Δ G^o
por la relación: donde Q _r es el cociente de reacción y R es la constante universal de los gases ideales . El potencial de celda E asociado con la reacción electroquímica se define como la disminución de la energía libre de Gibbs por culombio de carga transferida, lo que conduce a la relación La constante F (la constante de Faraday ) es un factor de conversión de unidades F = N _A q , donde N _A es la constante de Avogadro y q es la carga fundamental del electrón . Esto conduce inmediatamente a la ecuación de Nernst, que para una semicelda electroquímica es Para una reacción electroquímica completa (celda llena), la ecuación se puede escribir como$${\displaystyle \Delta G=\Delta G^{\ominus }+RT\ln Q_{r}}$$$${\displaystyle \Delta G=-zFE.}$$$${\displaystyle E_{\text{rojo}}=E_{\text{rojo}}^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}=E_{\text{rojo}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {a_{\text{Rojo}}}{a_{\text{Buey}}}}.}$$$${\displaystyle E_{\text{celda}}=E_{\text{celda}}^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}}$$

dónde:

• E _rojo es el potencial de reducción de semiceldaa la temperatura de interés,
• mi^o
  _rojoes el potencial de reducción de semicelda estándar ,
• E _cell es el potencial de celda ( fuerza electromotriz ) a la temperatura de interés,
• mi^o
  _célulaes el potencial de celda estándar ,
• R es la constante universal del gas ideal : R =8,314 462 618 153 24  JK ⁻¹ mol ⁻¹ ,
• T es la temperatura en kelvin ,
• z es el número de electrones transferidos en la reacción o semirreacción de la celda ,
• F es la constante de Faraday, la magnitud de la carga (en culombios ) por mol de electrones: F =96 485 .332 123 310 0184  C mol ⁻¹ ,
• Q _r es el cociente de reacción de la reacción celular, y,
• a es la actividad química de la especie relevante, donde a _Rojo es la actividad de la forma reducida y a _Ox es la actividad de la forma oxidada.

A temperatura ambiente (25 °C), el voltaje térmico es de aproximadamente 25,693 mV. La ecuación de Nernst se expresa con frecuencia en términos de logaritmos de base 10 ( es decir , logaritmos comunes ) en lugar de logaritmos naturales , en cuyo caso se escribe:${\displaystyle V_{T}={\frac {RT}{F}}}$

$${\displaystyle E=E^{\ominus }-{\frac {V_{T}}{z}}\ln {\frac {a_{\text{Red}}}{a_{\text{Ox}}}}=E^{\ominus }-{\frac {\lambda V_{T}}{z}}\log _{10}{\frac {a_{\text{Red}}}{a_{\text{Ox}}}}.}$$

donde λ = ln(10) ≈ 2,3026 y λV _T ≈ 0,05916 Voltios.

De manera similar a las constantes de equilibrio, las actividades siempre se miden con respecto al estado estándar (1 mol/L para solutos, 1 atm para gases y T = 298,15 K, es decir , 25 °C o 77 °F). La actividad química de una especie i , a _i , está relacionada con la concentración medida C _i a través de la relación a _i = γ _i C _i , donde γ _i es el coeficiente de actividad de la especie i . Debido a que los coeficientes de actividad tienden a la unidad en concentraciones bajas, o son desconocidos o difíciles de determinar en concentraciones medias y altas, las actividades en la ecuación de Nernst se reemplazan con frecuencia por concentraciones simples y luego, se utilizan potenciales de reducción estándar formales . ${\displaystyle E_{\text{red}}^{\ominus '}}$

Teniendo en cuenta los coeficientes de actividad ( ) la ecuación de Nernst se convierte en: ${\displaystyle \gamma }$

$${\displaystyle E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln \left({\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}{\frac {C_{\text{Red}}}{C_{\text{Ox}}}}\right)}$$

$${\displaystyle E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\left(\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}+\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}\right)}$$

$${\displaystyle E_{\text{red}}=\underbrace {\left(E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}\right)} _{E_{\text{red}}^{\ominus '}}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}}$$

Donde el primer término que incluye los coeficientes de actividad ( ) se denota y se llama potencial de reducción estándar formal, de modo que puede expresarse directamente como una función de y las concentraciones en la forma más simple de la ecuación de Nernst:${\displaystyle \gamma }$${\displaystyle E_{\text{red}}^{\ominus '}}$${\displaystyle E_{\text{red}}}$${\displaystyle E_{\text{red}}^{\ominus '}}$

$${\displaystyle E_{\text{red}}=E_{\text{red}}^{\ominus '}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}}$$

Cuando se desea utilizar concentraciones simples en lugar de actividades, pero los coeficientes de actividad están lejos de la unidad y ya no se pueden descuidar y son desconocidos o demasiado difíciles de determinar, puede ser conveniente introducir la noción del "llamado" potencial de reducción formal estándar ( ) que está relacionado con el potencial de reducción estándar de la siguiente manera: ^[3] De modo que la ecuación de Nernst para la reacción de semicelda se puede escribir formalmente de manera correcta en términos de concentraciones como: y lo mismo para la expresión de celda completa.${\displaystyle E_{\text{red}}^{\ominus '}}$$${\displaystyle E_{\text{red}}^{\ominus '}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}}$$$${\displaystyle E_{\text{red}}=E_{\text{red}}^{\ominus '}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}}$$

Según Wenzel (2020), ^[4] un potencial de reducción formal es el potencial de reducción que se aplica a una semirreacción bajo un conjunto de condiciones específicas como, por ejemplo, el pH , la fuerza iónica o la concentración de agentes complejantes .${\displaystyle E_{\text{red}}^{\ominus '}}$

El potencial de reducción formal es a menudo una forma más conveniente, pero condicional, del potencial de reducción estándar, teniendo en cuenta los coeficientes de actividad y las condiciones específicas características del medio de reacción. Por lo tanto, su valor es un valor condicional, es decir , que depende de las condiciones experimentales y debido a que la fuerza iónica afecta a los coeficientes de actividad, variará de un medio a otro. ^[3] Se pueden encontrar varias definiciones del potencial de reducción formal en la literatura, dependiendo del objetivo perseguido y de las restricciones experimentales impuestas por el sistema estudiado. La definición general de se refiere a su valor determinado cuando . Un caso más particular es cuando también se determina a pH 7, como por ejemplo para reacciones redox importantes en bioquímica o sistemas biológicos. ${\displaystyle E_{\text{red}}^{\ominus '}}$${\displaystyle E_{\text{red}}^{\ominus '}}$${\displaystyle E_{\text{red}}^{\ominus '}}$${\displaystyle {\frac {C_{\text{red}}}{C_{\text{ox}}}}=1}$${\displaystyle E_{\text{red}}^{\ominus '}}$

El potencial de reducción estándar formal se puede definir como el potencial de reducción medido de la semireacción en una relación de concentración unitaria de las especies oxidadas y reducidas ( es decir , cuando${\displaystyle E_{\text{red}}^{\ominus '}}$${\displaystyle E_{\text{red}}}$C _rojo/_{buey de} co⁠ = 1) en determinadas condiciones. ^[5]

En efecto:

como , cuando , ${\displaystyle E_{\text{red}}=E_{\text{red}}^{\ominus }}$${\displaystyle {\frac {a_{\text{red}}}{a_{\text{ox}}}}=1}$

${\displaystyle E_{\text{red}}=E_{\text{red}}^{\ominus '}}$, cuando ,${\displaystyle {\frac {C_{\text{red}}}{C_{\text{ox}}}}=1}$

porque , y que el término está incluido en . ${\displaystyle \ln {1}=0}$${\displaystyle {\frac {\gamma _{\text{red}}}{\gamma _{\text{ox}}}}}$${\displaystyle E_{\text{red}}^{\ominus '}}$

El potencial de reducción formal permite trabajar de manera más sencilla con concentraciones molares (mol/L, M) o molares (mol/kg H ₂ O , m) en lugar de actividades . Debido a que las concentraciones molares y molares alguna vez se denominaron concentraciones formales , podría explicar el origen del adjetivo formal en la expresión potencial formal . ^{[ cita requerida ]}

El potencial formal es entonces el potencial reversible de un electrodo en equilibrio inmerso en una solución donde los reactivos y productos están en concentración unitaria. ^[6] Si cualquier pequeño cambio incremental de potencial causa un cambio en la dirección de la reacción, es decir , de reducción a oxidación o viceversa , el sistema está cerca del equilibrio, es reversible y está en su potencial formal. Cuando el potencial formal se mide en condiciones estándar ( es decir , la actividad de cada especie disuelta es 1 mol/L, T = 298,15 K = 25 °C = 77 °F, P _gas = 1 bar) se convierte de facto en un potencial estándar. ^[7]
Según Brown y Swift (1949):

"Un potencial formal se define como el potencial de una semicelda, medido contra el electrodo de hidrógeno estándar , cuando la concentración total de cada estado de oxidación es un formal ". ^[8]

En este caso, al igual que para los potenciales de reducción estándar, las concentraciones de especies disueltas permanecen iguales a un molar (M) o un molal (m), y por lo tanto se dice que son un formal (F). Así, expresando la concentración C en molaridad M (1 mol/L):

${\displaystyle {\frac {C_{\text{red}}}{C_{\text{ox}}}}={\frac {1\,\mathrm {M} _{\text{red}}}{1\,\mathrm {M} _{\text{ox}}}}=1}$

El término concentración formal (F) es ahora en gran medida ignorado en la literatura actual y puede asimilarse comúnmente a concentración molar (M) o molalidad (m) en el caso de cálculos termodinámicos. ^[9]

El potencial formal también se encuentra a medio camino entre los dos picos en un voltamograma cíclico , donde en este punto la concentración de Ox (la especie oxidada) y Red (la especie reducida) en la superficie del electrodo son iguales.

Los coeficientes de actividad y están incluidos en el potencial formal y, dado que dependen de condiciones experimentales como la temperatura, la fuerza iónica y el pH , no pueden considerarse un potencial estándar inmutable, sino que deben determinarse sistemáticamente para cada conjunto específico de condiciones experimentales. ^[7]${\displaystyle \gamma _{red}}$${\displaystyle \gamma _{ox}}$${\displaystyle E_{\text{red}}^{\ominus '}}$${\displaystyle E_{\text{red}}^{\ominus '}}$

Los potenciales de reducción formales se utilizan para simplificar los cálculos de un sistema considerado en determinadas condiciones y la interpretación de las mediciones. Las condiciones experimentales en las que se determinan y su relación con los potenciales de reducción estándar deben describirse claramente para evitar confundirlos con los potenciales de reducción estándar.

Los potenciales de reducción estándar formales ( ) también se utilizan comúnmente en bioquímica y biología celular para referirse a los potenciales de reducción estándar medidos a pH 7, un valor más cercano al pH de la mayoría de los fluidos fisiológicos e intracelulares que el pH del estado estándar de 0. La ventaja es definir una escala redox más apropiada que corresponde mejor a las condiciones reales que el estado estándar. Los potenciales de reducción estándar formales ( ) permiten estimar más fácilmente si una reacción redox que se supone que ocurre en un proceso metabólico o para alimentar la actividad microbiana bajo ciertas condiciones es factible o no. ${\displaystyle E_{\text{red}}^{\ominus '}}$${\displaystyle E_{\text{red}}^{\ominus '}}$

Si bien los potenciales de reducción estándar siempre se refieren al electrodo de hidrógeno estándar (SHE), con [ H ⁺ ] = 1 M correspondiente a un pH de 0, y fijado arbitrariamente a cero por convención, ya no es el caso a un pH de 7. Entonces, el potencial de reducción de un electrodo de hidrógeno que opera a pH 7 es -0,413 V con respecto al electrodo de hidrógeno estándar (SHE). ^[10] ${\displaystyle E_{\text{red H+}}^{\ominus }}$${\displaystyle E_{\text{red}}}$

El pH de una solución está relacionado con la ecuación de Nernst, que se representa comúnmente mediante un diagrama de Pourbaix ( gráfico de pH ) . Denota explícitamente expresado frente al electrodo de hidrógeno estándar (SHE). Para una ecuación de media celda , convencionalmente escrita como una reacción de reducción ( es decir , electrones aceptados por un oxidante en el lado izquierdo):${\displaystyle E_{h}}$ ${\displaystyle E_{h}}$${\displaystyle E_{h}}$${\displaystyle E_{\text{red}}}$

${\displaystyle a\,A+b\,B+h\,{\ce {H+}}+z\,e^{-}\quad {\ce {<=>}}\quad c\,C+d\,D}$

El potencial de reducción estándar de semicelda se da por${\displaystyle E_{\text{red}}^{\ominus }}$

${\displaystyle E_{\text{red}}^{\ominus }({\text{volt}})=-{\frac {\Delta G^{\ominus }}{zF}}}$

donde es el cambio de energía libre de Gibbs estándar , z es el número de electrones involucrados y F es la constante de Faraday . La ecuación de Nernst relaciona el pH y la temperatura de la siguiente manera:${\displaystyle \Delta G^{\ominus }}$${\displaystyle E_{h}}$

${\displaystyle E_{h}=E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {0.05916}{z}}\log \left({\frac {\{C\}^{c}\{D\}^{d}}{\{A\}^{a}\{B\}^{b}}}\right)-{\frac {0.05916\,h}{z}}{\text{pH}}}$  ^{[ cita requerida ]}

donde las llaves indican actividades y los exponentes se muestran de la manera convencional. Esta ecuación es la ecuación de una línea recta para en función del pH con una pendiente de voltios (el pH no tiene unidades). ${\displaystyle E_{\text{red}}}$${\displaystyle -0.05916\,\left({\frac {h}{z}}\right)}$

Esta ecuación predice valores de pH más bajos a valores de pH más altos. Esto se observa para la reducción de O ₂ en H ₂ O u OH ⁻ y para la reducción de H ⁺ en H ₂ . Luego, a menudo se indica que se refiere al electrodo de hidrógeno estándar (SHE) cuyo = 0 por convención en condiciones estándar (T = 298,15 K = 25 °C = 77 F, _gas P = 1 atm (1,013 bar), concentraciones = 1 M y, por lo tanto, pH = 0). ${\displaystyle E_{\text{red}}}$${\displaystyle E_{\text{red}}}$${\displaystyle E_{h}}$${\displaystyle E_{\text{red}}}$

El factor principal que afecta a los potenciales de reducción formal en los procesos bioquímicos o biológicos es, en la mayoría de los casos, el pH. Para determinar valores aproximados de potenciales de reducción formal, despreciando en una primera aproximación los cambios en los coeficientes de actividad debidos a la fuerza iónica, se debe aplicar la ecuación de Nernst teniendo cuidado de expresar primero la relación como una función del pH. El segundo factor a considerar son los valores de las concentraciones tomadas en cuenta en la ecuación de Nernst. Para definir un potencial de reducción formal para una reacción bioquímica, el valor del pH, los valores de las concentraciones y las hipótesis realizadas sobre los coeficientes de actividad deben indicarse siempre explícitamente. Al utilizar o comparar varios potenciales de reducción formal, también deben ser coherentes internamente.

Pueden surgir problemas al mezclar diferentes fuentes de datos utilizando diferentes convenciones o aproximaciones ( es decir , con diferentes hipótesis subyacentes). Cuando se trabaja en la frontera entre procesos inorgánicos y biológicos (por ejemplo, al comparar procesos abióticos y bióticos en geoquímica cuando la actividad microbiana también podría estar en funcionamiento en el sistema), se debe tener cuidado de no mezclar directamente inadvertidamente los potenciales de reducción estándar versus SHE (pH = 0) con los potenciales de reducción formales (pH = 7). Las definiciones deben expresarse claramente y controlarse cuidadosamente, especialmente si las fuentes de datos son diferentes y surgen de diferentes campos (por ejemplo, seleccionar y mezclar datos de libros de texto clásicos de electroquímica y microbiología sin prestar atención a las diferentes convenciones en las que se basan).

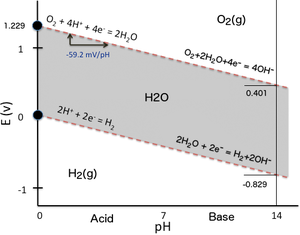
Para ilustrar la dependencia del potencial de reducción con el pH, se pueden considerar simplemente los dos equilibrios de oxido-reducción que determinan el dominio de estabilidad del agua en un diagrama de Pourbaix (gráfico E _h –pH) . Cuando el agua se somete a electrólisis aplicando una diferencia suficiente de potencial eléctrico entre dos electrodos sumergidos en agua, se produce hidrógeno en el cátodo (reducción de protones del agua) mientras que se forma oxígeno en el ánodo (oxidación de átomos de oxígeno del agua). Lo mismo puede ocurrir si un reductor más fuerte que el hidrógeno (por ejemplo, Na metálico) o un oxidante más fuerte que el oxígeno (por ejemplo, F ₂ ) entra en contacto con el agua y reacciona con ella. En el gráfico E _h –pH que se muestra aquí al lado (la versión más simple posible de un diagrama de Pourbaix), el dominio de estabilidad del agua (superficie gris) está delimitado en términos de potencial redox por dos líneas discontinuas rojas inclinadas:

• Línea de estabilidad inferior con evolución de gas hidrógeno debido a la reducción de protones a E _h muy baja :

2 H ⁺ + 2 e ⁻ ⇌ H ₂ (cátodo: reducción)

• Línea de mayor estabilidad con evolución de gas oxígeno debido a la oxidación del oxígeno del agua a E _h muy alta :

2 H ₂ O ⇌ O ₂ + 4 H ⁺ + 4 e ⁻ (ánodo: oxidación)

Al resolver la ecuación de Nernst para cada reacción de reducción correspondiente (es necesario revertir la reacción de oxidación del agua produciendo oxígeno), ambas ecuaciones tienen una forma similar porque el número de protones y el número de electrones involucrados en una reacción son los mismos y su relación es uno (2 H ⁺ /2 e ⁻ para H ₂ y 4 H ⁺ /4 e ⁻ con O ₂ respectivamente), por lo que se simplifica al resolver la ecuación de Nernst expresada como una función del pH.     

El resultado se puede expresar numéricamente de la siguiente manera:

${\displaystyle E_{\text{red}}=E_{\text{red}}^{\ominus }-0.05916\ pH}$

Nótese que las pendientes de las dos líneas superior e inferior del dominio de estabilidad del agua son las mismas (-59,16 mV/unidad de pH), por lo que son paralelas en un diagrama de Pourbaix . Como las pendientes son negativas, a un pH alto, la evolución tanto del hidrógeno como del oxígeno requiere un potencial de reducción mucho menor que a un pH bajo.

Para la reducción de H ⁺ a H2 _la relación mencionada anteriormente se convierte en:

${\displaystyle E_{\text{red}}=-0.05916\ pH}$
porque por convención = 0 V para el electrodo de hidrógeno estándar (SHE: pH = 0). Por lo tanto, a pH = 7, = -0,414 V para la reducción de protones.${\displaystyle E_{\text{red}}^{\ominus }}$
${\displaystyle E_{\text{red}}}$

Para la reducción de O ₂ en 2 H ₂ O la relación mencionada anteriormente se convierte en:

${\displaystyle E_{\text{red}}=1.229-0.05916\ pH}$
porque = +1,229 V respecto al electrodo de hidrógeno estándar (SHE: pH = 0). Por lo tanto, a pH = 7, = +0,815 V para la reducción del oxígeno.${\displaystyle E_{\text{red}}^{\ominus }}$
${\displaystyle E_{\text{red}}}$

El desfase de -414 mV es el mismo para ambas reacciones de reducción porque comparten la misma relación lineal en función del pH y las pendientes de sus líneas son las mismas. Esto se puede verificar directamente en un diagrama de Pourbaix. Para otras reacciones de reducción, el valor del potencial de reducción formal a un pH de 7, comúnmente referido para reacciones bioquímicas, también depende de la pendiente de la línea correspondiente en un diagrama de Pourbaix, es decir, de la relación h ⁄ z del número de H ⁺ al número de e ⁻ involucrados en la reacción de reducción, y por lo tanto de la estequiometría de la semirreacción. La determinación del potencial de reducción formal a pH = 7 para una semirreacción bioquímica dada requiere, por lo tanto, calcularlo con la ecuación de Nernst correspondiente en función del pH. No se puede simplemente aplicar un desfase de -414 mV al valor de E _h (SHE) cuando la relación h ⁄ z difiere de 1.${\displaystyle E_{\text{red}}}$  

Además de las importantes reacciones redox en bioquímica y microbiología , la ecuación de Nernst también se utiliza en fisiología para calcular el potencial eléctrico de una membrana celular con respecto a un tipo de ion . Puede vincularse a la constante de disociación ácida .

La ecuación de Nernst tiene una aplicación fisiológica cuando se utiliza para calcular el potencial de un ion de carga z a través de una membrana. Este potencial se determina utilizando la concentración del ion tanto dentro como fuera de la célula:

$${\displaystyle E={\frac {RT}{zF}}\ln {\frac {[{\text{ion outside cell}}]}{[{\text{ion inside cell}}]}}=2.3026{\frac {RT}{zF}}\log _{10}{\frac {[{\text{ion outside cell}}]}{[{\text{ion inside cell}}]}}.}$$

Cuando la membrana está en equilibrio termodinámico (es decir, no hay flujo neto de iones), y si la célula es permeable a un solo ion, entonces el potencial de membrana debe ser igual al potencial de Nernst para ese ion.

Cuando la membrana es permeable a más de un ion, como es inevitablemente el caso, el potencial de reposo se puede determinar a partir de la ecuación de Goldman, que es una solución de la ecuación de entrada de GHK bajo las restricciones de que la densidad de corriente total impulsada por la fuerza electroquímica es cero:

$${\displaystyle E_{\mathrm {m} }={\frac {RT}{F}}\ln {\left({\frac {\displaystyle \sum _{i}^{N}P_{\mathrm {M} _{i}^{+}}\left[\mathrm {M} _{i}^{+}\right]_{\mathrm {out} }+\displaystyle \sum _{j}^{M}P_{\mathrm {A} _{j}^{-}}\left[\mathrm {A} _{j}^{-}\right]_{\mathrm {in} }}{\displaystyle \sum _{i}^{N}P_{\mathrm {M} _{i}^{+}}\left[\mathrm {M} _{i}^{+}\right]_{\mathrm {in} }+\displaystyle \sum _{j}^{M}P_{\mathrm {A} _{j}^{-}}\left[\mathrm {A} _{j}^{-}\right]_{\mathrm {out} }}}\right)},}$$

dónde

• E _m es el potencial de membrana (en voltios , equivalente a julios por culombio ),
• _{El ion} P es la permeabilidad para ese ion (en metros por segundo),
• [ion] _out es la concentración extracelular de ese ion (en moles por metro cúbico, para que coincida con las otras unidades del SI , aunque las unidades estrictamente no importan, ya que los términos de concentración de iones se convierten en una relación adimensional),
• [ion] _en es la concentración intracelular de ese ion (en moles por metro cúbico),
• R es la constante del gas ideal (julios por kelvin por mol),
• T es la temperatura en kelvin ,
• F es la constante de Faraday (culombios por mol).

El potencial a través de la membrana celular que se opone exactamente a la difusión neta de un ion particular a través de la membrana se llama potencial de Nernst para ese ion. Como se vio anteriormente, la magnitud del potencial de Nernst está determinada por la relación de las concentraciones de ese ion específico en los dos lados de la membrana. Cuanto mayor sea esta relación, mayor será la tendencia del ion a difundirse en una dirección y, por lo tanto, mayor será el potencial de Nernst necesario para evitar la difusión. Existe una expresión similar que incluye r (el valor absoluto de la relación de transporte). Esto tiene en cuenta los transportadores con intercambios desiguales. Véase: bomba de sodio-potasio donde la relación de transporte sería 2/3, por lo que r es igual a 1,5 en la fórmula siguiente. La razón por la que insertamos un factor r = 1,5 aquí es que la densidad de corriente por fuerza electroquímica J _e.c. (Na ⁺ ) + J _e.c. (K ⁺ ) ya no es cero, sino J _e.c. (Na ⁺ ) + 1,5J _e.c. (K ⁺ ) = 0 (ya que para ambos iones el flujo por fuerza electroquímica se compensa con el de la bomba, es decir, J _e.c. = −J _bomba ), lo que altera las restricciones para aplicar la ecuación GHK. Las otras variables son las mismas que las anteriores. El siguiente ejemplo incluye dos iones: potasio (K ⁺ ) y sodio (Na ⁺ ). Se supone que el cloruro está en equilibrio.$${\displaystyle E_{m}={\frac {RT}{F}}\ln {\left({\frac {rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {out} }}{rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {in} }}}\right)}.}$$

Cuando se tiene en cuenta el cloruro (Cl ^{− ),}

$${\displaystyle E_{m}={\frac {RT}{F}}\ln {\left({\frac {rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Cl} ^{-}}\left[\mathrm {Cl} ^{-}\right]_{\mathrm {in} }}{rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Cl} ^{-}}\left[\mathrm {Cl} ^{-}\right]_{\mathrm {out} }}}\right)}.}$$

Para simplificar, consideraremos una solución de moléculas redox-activas que experimentan una reacción reversible de un electrón.

Buey + e ⁻ ⇌ Rojo

y que tienen un potencial estándar de cero, y en el que las actividades están bien representadas por las concentraciones (es decir, coeficiente de actividad unitario). El potencial químico μ _c de esta solución es la diferencia entre las barreras de energía para tomar electrones y para dar electrones al electrodo de trabajo que está fijando el potencial electroquímico de la solución . La relación de moléculas oxidadas a reducidas, ⁠[Buey]/[Rojo]⁠ , es equivalente a la probabilidad de oxidarse (ceder electrones) sobre la probabilidad de reducirse (tomar electrones), lo que podemos escribir en términos del factor de Boltzmann para estos procesos:$${\displaystyle {\begin{aligned}{\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}&={\frac {\exp \left(-[{\text{barrier for gaining an electron}}]/kT\right)}{\exp \left(-[{\text{barrier for losing an electron}}]/kT\right)}}\\[6px]&=\exp \left({\frac {\mu _{\mathrm {c} }}{kT}}\right).\end{aligned}}}$$

Tomando el logaritmo natural de ambos lados se obtiene$${\displaystyle \mu _{\mathrm {c} }=kT\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.}$$

Si μ _c ≠ 0 en ⁠[Buey]/[Rojo]⁠  = 1, necesitamos agregar esta constante adicional:$${\displaystyle \mu _{\mathrm {c} }=\mu _{\mathrm {c} }^{\ominus }+kT\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.}$$

Dividiendo la ecuación por e para convertir de potenciales químicos a potenciales de electrodo, y recordando quea/mi⁠ = ⁠R/F⁠ , ^[11] obtenemos la ecuación de Nernst para el proceso de un electrón Ox + e ⁻ ⇌ Red :

$${\displaystyle {\begin{aligned}E&=E^{\ominus }-{\frac {kT}{e}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{F}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.\end{aligned}}}$$

Las cantidades aquí se dan por molécula, no por mol , y por lo tanto se utilizan la constante de Boltzmann k y la carga del electrón e en lugar de la constante de los gases R y la constante de Faraday F. Para convertir a las cantidades molares que se dan en la mayoría de los libros de texto de química, simplemente es necesario multiplicar por la constante de Avogadro : R = kN _A y F = eN _A. La entropía de una molécula se define como

$${\displaystyle S\ {\stackrel {\mathrm {def} }{=}}\ k\ln \Omega ,}$$

donde Ω es el número de estados disponibles para la molécula. El número de estados debe variar linealmente con el volumen V del sistema (aquí se considera un sistema idealizado para una mejor comprensión, de modo que las actividades se postulan muy cerca de las concentraciones reales. La prueba estadística fundamental de la linealidad mencionada va más allá del alcance de esta sección, pero para ver que esto es cierto es más simple considerar el proceso isotérmico habitual para un gas ideal donde el cambio de entropía Δ S = nR ln( ⁠Versión ₂/V ₁) se produce. De la definición de entropía y de la condición de temperatura y cantidad de gas constantes n se deduce que el cambio en el número de estados debe ser proporcional al cambio relativo en el volumen .Versión ₂/V ₁⁠ . En este sentido, no hay diferencia en las propiedades estadísticas de los átomos de gas ideal en comparación con las especies disueltas de una solución con coeficientes de actividad iguales a uno: las partículas "flotan" libremente llenando el volumen proporcionado), que es inversamente proporcional a la concentración c , por lo que también podemos escribir la entropía como$${\displaystyle S=k\ln \ (\mathrm {constant} \times V)=-k\ln \ (\mathrm {constant} \times c).}$$

El cambio de entropía de un estado 1 a otro estado 2 es, por tanto, tal que la entropía del estado 2 es$${\displaystyle \Delta S=S_{2}-S_{1}=-k\ln {\frac {c_{2}}{c_{1}}},}$$$${\displaystyle S_{2}=S_{1}-k\ln {\frac {c_{2}}{c_{1}}}.}$$

Si el estado 1 está en condiciones estándar, en las que c ₁ es la unidad (por ejemplo, 1 atm o 1 M), simplemente cancelará las unidades de c ₂ . Por lo tanto, podemos escribir la entropía de una molécula arbitraria A como donde es la entropía en condiciones estándar y [A] denota la concentración de A. El cambio en la entropía para una reacción$${\displaystyle S(\mathrm {A} )=S^{\ominus }(\mathrm {A} )-k\ln[\mathrm {A} ],}$$${\displaystyle S^{\ominus }}$

entonces viene dado por$${\displaystyle \Delta S_{\mathrm {rxn} }={\big (}yS(\mathrm {Y} )+zS(\mathrm {Z} ){\big )}-{\big (}aS(\mathrm {A} )+bS(\mathrm {B} ){\big )}=\Delta S_{\mathrm {rxn} }^{\ominus }-k\ln {\frac {[\mathrm {Y} ]^{y}[\mathrm {Z} ]^{z}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}}.}$$

Definimos la relación en el último término como el cociente de reacción : donde el numerador es un producto de las actividades de los productos de reacción , a j , cada una elevada a la potencia de un coeficiente estequiométrico , ν j , y el denominador es un producto similar de las actividades de los reactivos. Todas las actividades se refieren a un tiempo t . En determinadas circunstancias (véase equilibrio químico ) cada término de actividad, como a$${\displaystyle Q_{r}={\frac {\displaystyle \prod _{j}a_{j}^{\nu _{j}}}{\displaystyle \prod _{i}a_{i}^{\nu _{i}}}}\approx {\frac {[\mathrm {Z} ]^{z}[\mathrm {Y} ]^{y}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}},}$$yo j
jpuede reemplazarse por un término de concentración, [A]. En una celda electroquímica, el potencial de celda E es el potencial químico disponible a partir de reacciones redox ( E = ⁠microsegundos​/mi⁠ ). E está relacionada con elcambio de energía libre de Gibbs Δ G solo por una constante: Δ G = − zFE , donde n es el número de electrones transferidos y F es la constante de Faraday . Hay un signo negativo porque una reacción espontánea tiene una energía libre de Gibbs negativa Δ G y un potencial positivo E . La energía libre de Gibbs está relacionada con la entropía por G = H − TS , donde H es la entalpía y T es la temperatura del sistema. Usando estas relaciones, ahora podemos escribir el cambio en la energía libre de Gibbs y el potencial de celda,$${\displaystyle \Delta G=\Delta H-T\Delta S=\Delta G^{\ominus }+kT\ln Q_{r},}$$$${\displaystyle E=E^{\ominus }-{\frac {kT}{ze}}\ln Q_{r}.}$$

Esta es la forma más general de la ecuación de Nernst.

Para la reacción redox Ox + z e ⁻ → Red , y tenemos:$${\displaystyle Q_{r}={\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}},}$$$${\displaystyle {\begin{aligned}E&=E^{\ominus }-{\frac {kT}{ze}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{zF}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}.\end{aligned}}}$$

El potencial de celda a temperatura y presión estándar (STP) a menudo se reemplaza por el potencial formal , que incluye los coeficientes de actividad de las especies disueltas en condiciones experimentales dadas (T, P, fuerza iónica , pH y agentes complejantes) y es el potencial que realmente se mide en una celda electroquímica.${\displaystyle E^{\ominus }}$${\displaystyle E^{\ominus '}}$

La energía libre de Gibbs estándar está relacionada con la constante de equilibrio K de la siguiente manera: ^[12]${\displaystyle \Delta G^{\ominus }}$

${\displaystyle \Delta G^{\ominus }=-RT\ln {K}}$

Al mismo tiempo, también es igual al producto de la carga total ( zF ) transferida durante la reacción y el potencial de celda ( ):${\displaystyle \Delta G^{\ominus }}$${\displaystyle E_{cell}^{\ominus }}$

${\displaystyle \Delta G^{\ominus }=-zFE_{cell}^{\ominus }}$

El signo es negativo, porque el sistema considerado realiza el trabajo y por tanto libera energía.

Entonces,

${\displaystyle -zFE_{cell}^{\ominus }=-RT\ln {K}}$

Y por lo tanto:

${\displaystyle E_{cell}^{\ominus }={\frac {RT}{zF}}\ln {K}}$

Partiendo de la ecuación de Nernst, también se puede demostrar la misma relación en sentido inverso.

En el equilibrio químico , o equilibrio termodinámico , el potencial electroquímico ( E ) = 0 y por lo tanto el cociente de reacción ₍ Qr ) alcanza el valor especial conocido como constante de equilibrio ₍ Keq ) :

Q _r = K _eq

Por lo tanto,

$${\displaystyle {\begin{aligned}0&=E^{\ominus }-{\frac {RT}{zF}}\ln K\\{\frac {RT}{zF}}\ln K&=E^{\ominus }\\\ln K&={\frac {zFE^{\ominus }}{RT}}\end{aligned}}}$$

O en estado estándar ,

$${\displaystyle \log _{10}K={\frac {zE^{\ominus }}{\lambda V_{T}}}={\frac {zE^{\ominus }}{0.05916{\text{ V}}}}\quad {\text{at }}T=298.15~{\text{K}}}$$

De esta manera hemos relacionado el potencial de electrodo estándar y la constante de equilibrio de una reacción redox.

En soluciones diluidas, la ecuación de Nernst se puede expresar directamente en términos de concentraciones (ya que los coeficientes de actividad son cercanos a la unidad). Pero a concentraciones más altas, se deben utilizar las actividades reales de los iones. Esto complica el uso de la ecuación de Nernst, ya que la estimación de actividades no ideales de iones generalmente requiere mediciones experimentales. La ecuación de Nernst también solo se aplica cuando no hay flujo de corriente neta a través del electrodo. La actividad de los iones en la superficie del electrodo cambia cuando hay flujo de corriente , y hay términos adicionales de sobrepotencial y pérdida resistiva que contribuyen al potencial medido.

En concentraciones muy bajas de los iones determinantes del potencial, el potencial predicho por la ecuación de Nernst se acerca a ±∞ . Esto no tiene sentido físico porque, en tales condiciones, la densidad de corriente de intercambio se vuelve muy baja y puede que no haya ningún equilibrio termodinámico necesario para que se cumpla la ecuación de Nernst. En tal caso, el electrodo se denomina no equilibrado. Otros efectos tienden a tomar el control del comportamiento electroquímico del sistema, como la participación del electrón solvatado en la transferencia de electricidad y los equilibrios de electrodos, como analizaron Alexander Frumkin y B. Damaskin, ^[13] Sergio Trasatti, etc.

La expresión de la dependencia del tiempo fue establecida por Karaoglanoff. ^{[14] [15] [16] [17]}

La ecuación de Nernst ha estado involucrada en la controversia científica sobre la fusión fría . Fleischmann y Pons, afirmando que la fusión fría podría existir, calcularon que un cátodo de paladio inmerso en una celda de electrólisis de agua pesada podría alcanzar hasta 10 ²⁷ atmósferas de presión dentro de la red cristalina del metal del cátodo, suficiente presión para causar la fusión nuclear espontánea . En realidad, solo se lograron entre 10.000 y 20.000 atmósferas. El físico estadounidense John R. Huizenga afirmó que su cálculo original se vio afectado por una interpretación errónea de la ecuación de Nernst. ^[18] Citó un artículo sobre aleaciones de Pd–Zr. ^[19]

La ecuación de Nernst permite calcular la extensión de la reacción entre dos sistemas redox y puede utilizarse, por ejemplo, para evaluar si una reacción particular llegará a su fin o no. En el equilibrio químico , las fuerzas electromotrices (fem) de las dos semiceldas son iguales. Esto permite calcular la constante de equilibrio K de la reacción y, por lo tanto, la extensión de la reacción.

• Celda de concentración
• Dependencia del potencial de reducción del pH
• Potencial de electrodo
• Celda galvánica
• Ecuación de Goldman
• Potencial de membrana
• Ecuación de Nernst-Planck
• Diagrama de Pourbaix
• Potencial de reducción
• Electrón solvatado
• Potencial de electrodo estándar
• Potencial de electrodo estándar (página de datos)
• Potenciales de reducción aparentes estándar en bioquímica a pH 7 (página de datos)

• Simulador de ecuaciones de Nernst/Goldman
• Calculadora de ecuaciones de Nernst
• Subprograma Java interactivo de Nernst/Goldman
• Paquete de enseñanza y aprendizaje DoITPoMS: “La ecuación de Nernst y los diagramas de Pourbaix”
• "20.5: Energía de Gibbs y reacciones redox". Chemistry LibreTexts . 2014-11-18 . Consultado el 2021-12-06 .