Diagrama de Pourbaix

En electroquímica , y más generalmente en química de soluciones, un diagrama de Pourbaix , también conocido como diagrama de potencial/pH , diagrama E _H –pH o diagrama pE/pH , es un gráfico de posibles fases termodinámicamente estables ( es decir , en equilibrio químico ) de un sistema electroquímico acuoso. Los límites (50 %/50 %) entre las especies químicas predominantes (iones acuosos en solución o fases sólidas) se representan mediante líneas. Como tal, un diagrama de Pourbaix se puede leer de manera muy similar a un diagrama de fases estándar con un conjunto diferente de ejes. De manera similar a los diagramas de fases, no permiten la velocidad de reacción ni los efectos cinéticos. Además del potencial y el pH, las concentraciones de equilibrio también dependen, por ejemplo, de la temperatura, la presión y la concentración. Los diagramas de Pourbaix se dan comúnmente a temperatura ambiente, presión atmosférica y concentraciones molares de 10 ⁻⁶ y cambiar cualquiera de estos parámetros producirá un diagrama diferente.

Los diagramas llevan el nombre de Marcel Pourbaix (1904-1998), el químico belga nacido en Rusia que los inventó.

Los diagramas de Pourbaix también se conocen como diagramas E _H -pH debido al etiquetado de los dos ejes.

El eje vertical está etiquetado como E _H para el potencial de voltaje con respecto al electrodo de hidrógeno estándar (SHE), calculado mediante la ecuación de Nernst . La "H" representa el hidrógeno, aunque se pueden utilizar otros estándares y son solo para temperatura ambiente.

Para una reacción redox reversible descrita por el siguiente equilibrio químico :

a A + b B ⇌ c C + d D

Con la constante de equilibrio correspondiente K :

${\displaystyle K={\frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}$

La ecuación de Nernst es:

${\displaystyle E_{\text{H}}=E^{0}-{\frac {RT}{zF}}\ln {K},}$

${\displaystyle E_{\text{H}}=E^{0}-{\frac {RT}{zF}}\ln {\frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}$

A veces se formula como:

${\displaystyle E_{\text{H}}=E^{0}-{\frac {V_{T}\lambda }{z}}\log {\frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}$

o, más simplemente expresado directamente numéricamente como:

${\displaystyle E_{\text{H}}=E^{0}-{\frac {0,05916}{z}}\log {\frac {[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}},}$

dónde:

• ${\displaystyle V_{T}=RT/F\aproximadamente 0,02569}$ Volt es el voltaje térmico o la "pendiente de Nernst" a temperatura estándar

• λ  = ln(10) ≈ 2,30, por lo que  voltio.${\displaystyle V_{T}\lambda \aproximadamente 0,05916}$

El eje horizontal está etiquetado como pH para la función −log de la actividad del ion H ⁺ .

${\displaystyle {\text{pH}}=-\log _{10}(a_{{\ce {H+}}})=\log _{10}\left({\frac {1}{a_{{\ce {H+}}}}}\right).}$

Las líneas del diagrama de Pourbaix muestran las condiciones de equilibrio, es decir, donde las actividades son iguales, para las especies de cada lado de esa línea. En cambio, se dirá que en cada lado de la línea predomina una forma de la especie. ^[3]

Para trazar la posición de las líneas con la ecuación de Nernst, se debe definir la actividad de las especies químicas en equilibrio. Por lo general, la actividad de una especie se aproxima a la concentración (para especies solubles) o a la presión parcial (para gases). Se deben utilizar los mismos valores para todas las especies presentes en el sistema. ^[3]

Para las especies solubles, las líneas a menudo se dibujan para concentraciones de 1 M o 10 ⁻⁶  M. A veces se dibujan líneas adicionales para otras concentraciones.

Si el diagrama implica el equilibrio entre una especie disuelta y un gas, la presión generalmente se establece en P ⁰ = 1 atm =101 325  Pa , la presión mínima requerida para la evolución del gas a partir de una solución acuosa en condiciones estándar. ^[3]

Además, los cambios en la temperatura y la concentración de iones solvatados en solución desplazarán las líneas de equilibrio de acuerdo con la ecuación de Nernst.

Los diagramas tampoco tienen en cuenta los efectos cinéticos, lo que significa que las especies mostradas como inestables podrían no reaccionar en un grado significativo en la práctica.

Un diagrama de Pourbaix simplificado indica regiones de "inmunidad", "corrosión" y "pasividad", en lugar de las especies estables. Por lo tanto, proporcionan una guía sobre la estabilidad de un metal en particular en un entorno específico. La inmunidad significa que el metal no es atacado, mientras que la corrosión muestra que se producirá un ataque general. La pasivación se produce cuando el metal forma una capa estable de un óxido u otra sal en su superficie; el mejor ejemplo es la estabilidad relativa del aluminio debido a la capa de alúmina que se forma en su superficie cuando se expone al aire.

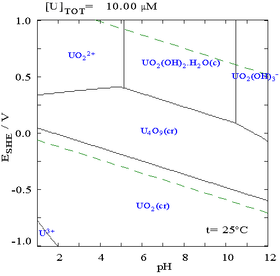
Si bien estos diagramas se pueden dibujar para cualquier sistema químico, es importante tener en cuenta que la adición de un agente de unión de metales ( ligando ) a menudo modificará el diagrama. Por ejemplo, el carbonato ( CO2−3) tiene un gran efecto sobre el diagrama del uranio (ver diagramas a la derecha). La presencia de trazas de ciertas especies, como los iones de cloruro, también puede afectar en gran medida la estabilidad de ciertas especies al destruir las capas pasivantes.

Si bien los diagramas de Pourbaix son útiles para la estimación del potencial de corrosión del metal, tienen, sin embargo, algunas limitaciones importantes: ^{[4] : 111}

1. Siempre se supone que existe equilibrio, aunque en la práctica puede diferir.
2. El diagrama no proporciona información sobre las tasas de corrosión reales.
3. No se aplica a aleaciones. ^[a]
4. No se indica si la pasivación (en forma de óxidos o hidróxidos) es protectora o no. Es posible la difusión de iones de oxígeno a través de capas delgadas de óxido.
5. Excluye la corrosión por iones cloruro ( Cl ⁻ , Cl ³⁺ etc.). ^[b]
6. Generalmente se aplica solo a temperaturas de 25 °C (77 °F), que es la que se asume por defecto. Existen diagramas de Pourbaix para temperaturas más altas.

El pH de una solución está relacionado con la ecuación de Nernst, que se representa comúnmente mediante un diagrama de Pourbaix ( gráfico de pH ) . Denota explícitamente expresado frente al electrodo de hidrógeno estándar (SHE). Para una ecuación de media celda , convencionalmente escrita como una reacción de reducción ( es decir , electrones aceptados por un oxidante en el lado izquierdo):$Estilo de visualización Eh$$Estilo de visualización Eh$$Estilo de visualización Eh$${\displaystyle E_{\text{rojo}}}$

${\displaystyle a\,A+b\,B+h\,{\ce {H+}}+z\,e^{-}\quad {\ce {<=>}}\quad c\,C+d\,D}$

La constante de equilibrio K de esta reacción de reducción es:

${\displaystyle K={\frac {\{C\}^{c}\{D\}^{d}}{\{A\}^{a}\{B\}^{b}\{{\ce {H+}}\}^{h}}}={\frac {(\gamma _{c})^{c}[C\right]^{c}\ (\gamma _{d})^{d}[D\right]^{d}}{(\gamma _{a})^{a}[A\right]^{a}\ (\gamma _{b})^{b}[B\right]^{b}\ (\gamma _{h+})^{h}[{\ce {H+}}\right]^{h}}}={\frac {(\gamma _{c})^{c}(\gamma _{d})^{d}}{(\gamma _{a})^{a}(\gamma _{b})^{b}(\gamma _{h})^{h}}}{\text{×}}{\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}\left[{\ce {H+}}\right]^{h}}}}$

donde las llaves { } indican actividades ( a ), las llaves rectangulares [ ] denotan concentraciones molares o molares ( C ), representan los coeficientes de actividad y los coeficientes estequiométricos se muestran como exponentes. ${\estilo de visualización \gamma}$

Las actividades corresponden a concentraciones termodinámicas y tienen en cuenta las interacciones electrostáticas entre los iones presentes en la solución. Cuando las concentraciones no son demasiado altas, la actividad ( ) puede relacionarse con la concentración medible ( ) mediante una relación lineal con el coeficiente de actividad ( ): $Estilo de visualización ai$$Estilo de visualización C_{i}$${\displaystyle \gamma _{i}}$

${\displaystyle a_{i}=\gamma _{i}\,C_{i}}$

El potencial de reducción estándar de semicelda se da por${\displaystyle E_{\text{red}}^{\ominus }}$

${\displaystyle E_{\text{red}}^{\ominus }({\text{volt}})=-{\frac {\Delta G^{\ominus }}{zF}}}$

donde es el cambio de energía libre de Gibbs estándar , z es el número de electrones involucrados y F es la constante de Faraday . La ecuación de Nernst relaciona el pH y la temperatura de la siguiente manera:${\displaystyle \Delta G^{\ominus }}$${\displaystyle E_{h}}$

${\displaystyle E_{h}=E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\log \left({\frac {\{C\}^{c}\{D\}^{d}}{\{A\}^{a}\{B\}^{b}}}\right)-{\frac {RT\,h}{zF}}{\text{pH}}}$

A continuación, se utiliza la pendiente de Nernst (o voltaje térmico ) , que tiene un valor de 0,02569... V en STP . Cuando se utilizan logaritmos de base 10, V _T λ = 0,05916... V en STP donde λ = ln[10] = 2,3026. ${\displaystyle V_{T}=RT/F}$

${\displaystyle E_{h}=E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {0.05916}{z}}\log \left({\frac {\{C\}^{c}\{D\}^{d}}{\{A\}^{a}\{B\}^{b}}}\right)-{\frac {0.05916\,h}{z}}{\text{pH}}}$

Esta ecuación es la ecuación de una línea recta en función del pH con una pendiente de voltios (el pH no tiene unidades). ${\displaystyle E_{\text{red}}}$${\displaystyle -0.05916\,\left({\frac {h}{z}}\right)}$

Esta ecuación predice valores de pH más bajos a valores de pH más altos. Esto se observa para la reducción de O ₂ en H ₂ O u OH ⁻ y para la reducción de H ⁺ en H ₂ . Luego, a menudo se indica que se refiere al electrodo de hidrógeno estándar (SHE) cuyo = 0 por convención en condiciones estándar (T = 298,15 K = 25 °C = 77 F, _gas P = 1 atm (1,013 bar), concentraciones = 1 M y, por lo tanto, pH = 0).${\displaystyle E_{\text{red}}}$${\displaystyle E_{\text{red}}}$${\displaystyle E_{h}}$${\displaystyle E_{\text{red}}}$

Cuando las actividades ( ) pueden considerarse iguales a las concentraciones molares , o a las concentraciones molares , ( ) en concentraciones suficientemente diluidas cuando los coeficientes de actividad ( ) tienden a uno, el término que reagrupa todos los coeficientes de actividad es igual a uno, y la ecuación de Nernst puede escribirse simplemente con las concentraciones ( ) denotadas aquí con corchetes [ ]:${\displaystyle a_{i}}$${\displaystyle C_{i}}$${\displaystyle \gamma _{i}}$${\displaystyle C_{i}}$

${\displaystyle E_{h}=E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {0.05916}{z}}\log \left({\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}}}\right)-{\frac {0.05916\,h}{z}}{\text{pH}}}$

Hay tres tipos de límites de línea en un diagrama de Pourbaix: vertical, horizontal e inclinado. ^{[5] [6]}

Cuando no se intercambian electrones ( z = 0), el equilibrio entre A , B , C y D depende únicamente de [H ⁺ ] y no se ve afectado por el potencial del electrodo. En este caso, la reacción es una reacción clásica ácido-base que implica únicamente la protonación /desprotonación de especies disueltas. La línea límite será una línea vertical en un valor particular de pH. La ecuación de reacción puede escribirse:

${\displaystyle a\,A+b\,B+h\,{\ce {H+}}\quad {\ce {<=>}}\quad c\,C+d\,D}$

y el balance de energía se escribe como , donde K es la constante de equilibrio : ${\displaystyle \Delta G^{\circ }=-RT\ln K}$

${\displaystyle K={\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}\left[{\ce {H+}}\right]^{h}}}}$

De este modo:

${\displaystyle \Delta G^{\circ }=-RT\ln \left({\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}\left[{\ce {H+}}\right]^{h}}}\right)}$

o, en logaritmos de base 10,

${\displaystyle \Delta G^{\circ }=-RT\lambda \,\left(\log \left({\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}}}\right)+h\,{\ce {pH}}\right)}$

que puede resolverse para el valor particular del pH.

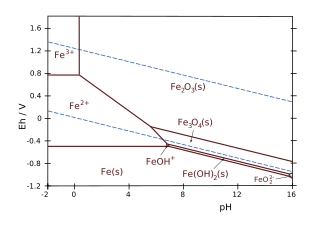
Por ejemplo ^[5] considere el sistema de hierro y agua, y la línea de equilibrio entre el ion férrico Fe ³⁺ y el ion hematita Fe ₂ O ₃ . La ecuación de reacción es:

${\displaystyle {\ce {2 Fe^{3+}(aq) + 3 H_2 O (l) <=> Fe_2 O_3 (s) + 6 H^+ (aq)}}}$

que tiene . ^[5] El pH de la línea vertical en el diagrama de Pourbaix se puede calcular entonces:${\displaystyle \Delta G^{\circ }=-8242.5\,\mathrm {J/mol} }$

${\displaystyle {\ce {pH}}=-{\frac {1}{6}}\left({\frac {\Delta G^{\circ }}{RT\lambda }}+\log \left({\frac {{\ce {[Fe2O3]}}}{{\ce {[Fe^{3+}]^2[H2O]^3}}}}\right)\right)}$

Como las actividades (o concentraciones) de las fases sólidas y del agua son iguales a la unidad:
[Fe ₂ O ₃ ] = [H ₂ O] = 1, el pH sólo depende de la concentración de Fe disuelto.³⁺
:

${\displaystyle {\ce {pH}}=-{\frac {1}{6}}\left({\frac {\Delta G^{\circ }}{RT\lambda }}+\log \left({\frac {1}{[{\ce {Fe^{3+}}}]^{2}}}\right)\right)}$

En condiciones normales, para [Fe ³⁺ ] = 10 ⁻⁶ , esto produce un pH = 1,76.

Cuando los iones H ⁺ y OH− ^no intervienen en la reacción, la línea límite es horizontal e independiente del pH.
La ecuación de reacción queda así escrita:

${\displaystyle a\,A+b\,B+z\,e^{-}\quad {\ce {<=>}}\quad c\,C+d\,D\qquad (z>0{\text{, but without}}\ {\ce {H+}})}$

Como, la energía libre de Gibbs estándar :${\displaystyle \Delta G^{\circ }=-RT\ln K}$

${\displaystyle \Delta G^{\circ }=-RT\ln \left({\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}}}\right)}$

Utilizando la definición del potencial del electrodo ∆G = -zFE , donde F es la constante de Faraday , esto puede reescribirse como una ecuación de Nernst:

${\displaystyle E_{h}={E^{\circ }}-{\frac {V_{T}}{z}}\ln \left({\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}}}\right)}$

o, utilizando logaritmos de base 10:

${\displaystyle E_{h}={E^{\circ }}-{\frac {V_{T}\lambda }{z}}\log \left({\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}}}\right)}$

Para el equilibrio Fe²⁺
/ Fe³⁺
, tomado como ejemplo aquí, considerando la línea límite entre Fe ²⁺ y Fe ³⁺ , la ecuación de semirreacción es:

${\displaystyle {\ce {Fe^3+ (aq) + e^- <=> Fe^2+ (aq)}}}$

Dado que los iones H ⁺ no están involucrados en esta reacción redox , es independiente del pH. E ^o = 0,771 V con solo un electrón involucrado en la reacción redox. ^[7] El potencial E _h es una función de la temperatura a través del voltaje térmico y depende directamente de la relación de las concentraciones de Fe${\displaystyle V_{T}}$²⁺
y Fe³⁺
iones:

${\displaystyle E_{h}={E^{\circ }}-V_{T}\lambda \log \left({\frac {{\ce {[Fe^{2+}]}}}{{\ce {[Fe^{3+}]}}}}\right)}$

Para ambas especies iónicas en la misma concentración (por ejemplo, ) en condiciones normales, log 1 = 0, por lo que, , y el límite será una línea horizontal en E _h = 0,771 voltios. El potencial variará con la temperatura.${\displaystyle 10^{-6}\mathrm {M} }$${\displaystyle E_{h}=E^{\circ }=0.771\,\mathrm {V} }$

En este caso, intervienen tanto electrones como iones H ^{+ y el potencial del electrodo es función del pH. La ecuación de reacción puede escribirse:}

${\displaystyle a\,A+b\,B+h\,{\ce {H+}}+z\,e^{-}\quad {\ce {<=>}}\quad c\,C+d\,D}$

Utilizando las expresiones para la energía libre en términos de potenciales, el balance de energía viene dado por una ecuación de Nernst:

${\displaystyle E_{h}={E^{\circ }}-{\frac {V_{T}\lambda }{z}}\left(\log \left({\frac {\left[C\right]^{c}\left[D\right]^{d}}{\left[A\right]^{a}\left[B\right]^{b}}}\right)+h\,{\ce {pH}}\right)}$

Para el ejemplo del hierro y el agua, considerando la línea límite entre el ion ferroso Fe ²⁺ y la hematita Fe ₂ O ₃ , la ecuación de reacción es:

${\displaystyle {\ce {Fe2O3(s) + 6 H+(aq) + 2 e^- <=> 2 Fe^{2+}(aq) + 3 H2O(l)}}}$

con . ^[5]${\displaystyle E^{\circ }=0.728\mathrm {V} }$

La ecuación de la línea límite, expresada en logaritmos de base 10, es:

${\displaystyle E_{h}={E^{\circ }}-{\frac {V_{T}\lambda }{2}}\left(\log \left({\frac {{\ce {[Fe^{2+}]^2[H2O]^3}}}{{\ce {[Fe2O3]}}}}\right)+6\ {\ce {pH}}\right)}$

Como, las actividades, o las concentraciones, de las fases sólidas y del agua siempre se toman iguales a la unidad por convención en la definición de la constante de equilibrio K : [Fe ₂ O ₃ ] = [H ₂ O] = 1.

La ecuación de Nernst queda así limitada a las especies disueltas Fe²⁺
y H ⁺ se escribe como:  

${\displaystyle E_{h}={E^{\circ }}-{\frac {V_{T}\lambda }{2}}\left(\log \ {\ce {[Fe^{2+}]^2}}+6\ {\ce {pH}}\right)}$

Para [Fe ²⁺ ] = 10 ⁻⁶ M, esto da:

${\displaystyle E_{h}={1.0826}-{0.1775}\ {pH}\quad ({\text{in volts}})}$

Nótese la pendiente negativa (-0,1775) de esta línea en un diagrama E _h –pH.

En muchos casos, las posibles condiciones de un sistema están limitadas por la región de estabilidad del agua. En el diagrama de Pourbaix para el uranio que se presenta aquí arriba, los límites de estabilidad del agua están marcados por las dos líneas discontinuas verdes, y la región de estabilidad del agua se encuentra entre estas dos líneas. También se representa aquí junto a las dos líneas discontinuas rojas en el diagrama de Pourbaix simplificado restringido únicamente a la región de estabilidad del agua.

En condiciones altamente reductoras ( E _H baja ), el agua se reduce a hidrógeno de acuerdo con: ^[3]

${\displaystyle {\ce {2 H+ + 2e^- -> H2(g)}}}$(a pH bajo)

y,

${\displaystyle {\ce {2 H2O + 2e^- -> H2(g) + 2 OH^-}}}$(a pH alto)

Utilizando la ecuación de Nernst, fijando E ⁰ = 0 V como se define por convención para el electrodo de hidrógeno estándar (SHE, que sirve como referencia en la serie de potenciales de reducción) y la fugacidad del gas hidrógeno (que corresponde a la actividad química de un gas) en 1, la ecuación para la línea de estabilidad inferior del agua en el diagrama de Pourbaix a temperatura y presión estándar es:

${\displaystyle E_{{\ce {H}}}=-V_{T}\lambda \,{\ce {pH}}}$

${\displaystyle E_{{\ce {H}}}=-0.05916\,{\ce {pH}}}$

Por debajo de esta línea, el agua se reduce a hidrógeno y, normalmente, no será posible pasar más allá de esta línea mientras todavía haya agua presente en el sistema para reducir.

En consecuencia, en condiciones altamente oxidantes (alto E _H ) el agua se oxida a gas oxígeno de acuerdo con: ^[3]

${\displaystyle {\ce {2 H2O -> 4 H+ + O2(g) + 4e^-}}}$    (a pH bajo)

y,

${\displaystyle {\ce {4 OH^- -> O2(g) + 2 H_2O + 4e^-}}}$(a pH alto)

Utilizando la ecuación de Nernst como se indica arriba, pero con E ⁰ = −ΔG ⁰ _{H 2 O} /2 F = 1,229 V para la oxidación del agua, se obtiene un límite superior de estabilidad del agua en función del valor del pH:

${\displaystyle E_{{\ce {H}}}=E^{0}-V_{T}\lambda \,{\ce {pH}}}$

${\displaystyle E_{{\ce {H}}}=1.229V-0.05916\,{\ce {pH}}}$

A temperatura y presión estándar. Por encima de esta línea, el agua se oxida para formar gas oxígeno y, por lo general, no será posible pasar más allá de esta línea mientras todavía haya agua presente en el sistema para oxidar.

Las dos líneas de estabilidad superior e inferior tienen la misma pendiente negativa (unidad −59 mV/pH), son paralelas en un diagrama de Pourbaix y el potencial de reducción disminuye con el pH.

Los diagramas de Pourbaix tienen muchas aplicaciones en diferentes campos relacionados con problemas de corrosión, geoquímica y ciencias ambientales . El uso correcto del diagrama de Pourbaix ayudará a arrojar luz no solo sobre la naturaleza de las especies presentes en la solución acuosa o en las fases sólidas , sino que también puede ayudar a comprender el mecanismo de reacción . ^[8]

Los diagramas de Pourbaix se utilizan ampliamente para describir el comportamiento de las especies químicas en la hidrosfera . En este contexto, se suele utilizar el potencial de reducción pe en lugar de E _H. ^[3] La principal ventaja es trabajar directamente con una escala logarítmica . pe es un número adimensional y se puede relacionar fácilmente con E _H mediante la ecuación:

${\displaystyle pe={\frac {E_{H}}{V_{T}\lambda }}={\frac {E_{H}}{0.05916}}=16.903\,{\text{×}}\,E_{H}}$

Donde, es el voltaje térmico , con R , la constante del gas (${\displaystyle V_{T}={\frac {RT}{F}}}$8,314 J⋅K ⁻¹ ⋅mol ⁻¹ ), T , la temperatura absoluta en Kelvin (298,15 K = 25 °C = 77 °F), y F , la constante de Faraday (96 485 culombios/mol de e ⁻ ). Lambda, λ = ln(10) ≈ 2,3026.  

Además,

${\displaystyle pe=-\log[e^{-}]}$, una expresión con una forma similar a la del pH.

Los valores de pe en química ambiental varían de −12 a +25, ya que a potenciales bajos o altos el agua se reducirá u oxidará respectivamente. En aplicaciones ambientales, la concentración de especies disueltas se establece generalmente en un valor entre 10 ⁻²  M y 10 ⁻⁵  M para la determinación de las líneas de equilibrio.

• 
  Fe – _H2O
• 
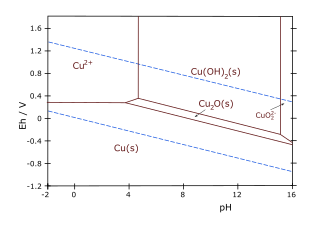
  Cu – _H2O
• 
  Au – _H2O
• 
  Al – _H2O
• 
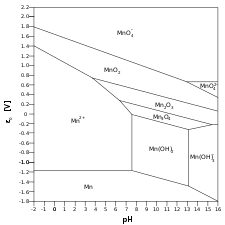
  Mn – _H2O
• 
  Zn ^– _H2O – _CO32–
• 
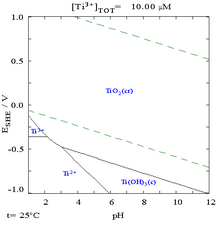
  Ti – _H2O

• Ecuación de Nernst
• Dependencia del potencial de reducción del pH
• Diagrama de Ellingham
• Diagrama de Latimer
• Diagrama de escarcha
• Diagrama de partición iónica
• El complot de Bjerrum

Wikimedia Commons alberga una categoría multimedia sobre Diagramas de Pourbaix .

• Marcel Pourbaix — Médicos de la corrosión
• Paquete de enseñanza y aprendizaje DoITPoMS: “La ecuación de Nernst y los diagramas de Pourbaix”

• ChemEQL Software gratuito para el cálculo de equilibrios químicos de Eawag .
• Software de banco de datos termodinámicos comerciales FactSage, también disponible en una aplicación web gratuita.
• El banco de trabajo del geoquímico Software de modelado geoquímico comercial de Aqueous Solutions LLC.
• GWB Community Edition Descarga gratuita del popular paquete de software de modelado geoquímico.
• HYDRA/MEDUSA Software gratuito para la creación de diagramas de equilibrio químico del Departamento de Química del KTH .
• Software de cálculo termoquímico comercial HSC Chemistry de Outotec Oy .
• PhreePlot Programa gratuito para realizar gráficos geoquímicos utilizando el código USGS PHREEQC.
• Thermo-Calc Windows Software comercial para cálculos termodinámicos de Thermo-Calc Software.
• Proyecto de materiales Sitio web público que puede generar diagramas de Pourbaix a partir de una gran base de datos de propiedades de materiales calculadas, alojada en NERSC .