Rombo

Rombo
Un rombo en dos orientaciones diferentes
Tipo	cuadrilátero , trapezoide , paralelogramo , cometa
Aristas y vértices	4
Símbolo de Schläfli	{ } + { } { 2α }
Diagramas de Coxeter-Dynkin
Grupo de simetría	Diédrico (D 2 ), [2], (*22), orden 4
Área	${\displaystyle K={\frac {p\cdot q}{2}}}$(la mitad del producto de las diagonales)
Propiedades	convexo , isotoxal
Polígono dual	rectángulo

En geometría euclidiana plana , un rombo ( pl.: rombos o rombos ) es un cuadrilátero cuyos cuatro lados tienen la misma longitud. Otro nombre es cuadrilátero equilátero , ya que equilátero significa que todos sus lados tienen la misma longitud. El rombo a menudo se llama " diamante ", por el palo de diamantes en las cartas de juego que se asemeja a la proyección de un diamante octaédrico , o un rombo , aunque el primero a veces se refiere específicamente a un rombo con un ángulo de 60° (al que algunos autores llaman calisson por el francés sweet ^[1] —ver también Polyiamond ), y el segundo a veces se refiere específicamente a un rombo con un ángulo de 45°.

Todo rombo es simple (no se interseca consigo mismo) y es un caso especial de paralelogramo y cometa . Un rombo con ángulos rectos es un cuadrado . ^[2]

La palabra "rombo" proviene del griego antiguo : ῥόμβος , romanizado :  rhómbos , que significa algo que gira, ^[3] que deriva del verbo ῥέμβω , romanizado: rhémbō , que significa "dar vueltas y vueltas". ^[4] La palabra fue utilizada tanto por Euclides como por Arquímedes , quienes usaron el término "rombo sólido" para un bicono , dos conos circulares rectos que comparten una base común. ^[5]

La superficie que hoy llamamos rombo es una sección transversal del bicono en un plano que pasa por los vértices de los dos conos.

Un cuadrilátero simple (no autointersecante ) es un rombo si y solo si es cualquiera de los siguientes: ^{[6] [7]}

• un paralelogramo en el que una diagonal biseca un ángulo interior
• un paralelogramo en el que al menos dos lados consecutivos tienen la misma longitud
• un paralelogramo en el que las diagonales son perpendiculares (un paralelogramo ortodiagonal )
• un cuadrilátero con cuatro lados de igual longitud (por definición)
• un cuadrilátero en el que las diagonales son perpendiculares y se bisecan entre sí
• un cuadrilátero en el que cada diagonal biseca dos ángulos interiores opuestos
• un cuadrilátero ABCD que posee un punto P en su plano tal que los cuatro triángulos ABP , BCP , CDP y DAP son todos congruentes ^[8]
• un cuadrilátero ABCD en el que los círculos inscritos en los triángulos ABC , BCD , CDA y DAB tienen un punto común ^[9]

Todo rombo tiene dos diagonales que unen pares de vértices opuestos y dos pares de lados paralelos. Utilizando triángulos congruentes , se puede demostrar que el rombo es simétrico en cada una de estas diagonales. De ello se deduce que cualquier rombo tiene las siguientes propiedades:

• Los ángulos opuestos de un rombo tienen la misma medida.
• Las dos diagonales de un rombo son perpendiculares ; es decir, un rombo es un cuadrilátero ortodiagonal .
• Sus diagonales bisecan ángulos opuestos.

La primera propiedad implica que todo rombo es un paralelogramo . Por lo tanto, un rombo tiene todas las propiedades de un paralelogramo : por ejemplo, los lados opuestos son paralelos; los ángulos adyacentes son suplementarios ; las dos diagonales se bisecan entre sí; cualquier línea que pase por el punto medio biseca el área; y la suma de los cuadrados de los lados es igual a la suma de los cuadrados de las diagonales (la ley del paralelogramo ). Por lo tanto, denotando el lado común como a y las diagonales como p y q , en cada rombo

${\displaystyle \displaystyle 4a^{2}=p^{2}+q^{2}.}$

No todo paralelogramo es un rombo, aunque cualquier paralelogramo con diagonales perpendiculares (la segunda propiedad) es un rombo. En general, cualquier cuadrilátero con diagonales perpendiculares, una de las cuales es un eje de simetría, es una cometa . Todo rombo es una cometa, y cualquier cuadrilátero que sea a la vez cometa y paralelogramo es un rombo.

Un rombo es un cuadrilátero tangencial . ^[10] Es decir, tiene un círculo inscrito que es tangente a sus cuatro lados.

La longitud de las diagonales p = AC y q = BD se puede expresar en términos del lado a del rombo y un ángulo del vértice α como

${\displaystyle p=a{\sqrt {2+2\cos {\alpha }}}}$

y

${\displaystyle q=a{\sqrt {2-2\cos {\alpha }}}.}$

Estas fórmulas son una consecuencia directa de la ley de los cosenos .

El radio interno (el radio de un círculo inscrito en el rombo), denotado por r , se puede expresar en términos de las diagonales p y q como ^[10]

${\displaystyle r={\frac {p\cdot q}{2{\sqrt {p^{2}+q^{2}}}}},}$

o en términos de la longitud del lado a y cualquier ángulo de vértice α o β como

${\displaystyle r={\frac {a\sin \alpha }{2}}={\frac {a\sin \beta }{2}}.}$

Como en todos los paralelogramos , el área K de un rombo es el producto de su base por su altura ( h ). La base es simplemente cualquier lado de longitud a :

${\displaystyle K=a\cdot h.}$

El área también se puede expresar como la base al cuadrado por el seno de cualquier ángulo:

${\displaystyle K=a^{2}\cdot \sin \alpha =a^{2}\cdot \sin \beta ,}$

o en términos de la altura y un ángulo de vértice :

${\displaystyle K={\frac {h^{2}}{\sin \alpha }},}$

o como la mitad del producto de las diagonales p , q :

${\displaystyle K={\frac {p\cdot q}{2}},}$

o como el semiperímetro por el radio del círculo inscrito en el rombo (inradio):

${\displaystyle K=2a\cdot r.}$

Otra forma, en común con los paralelogramos, es considerar dos lados adyacentes como vectores, formando un bivector , por lo que el área es la magnitud del bivector (la magnitud del producto vectorial de los dos vectores), que es el determinante de las coordenadas cartesianas de los dos vectores: K = x ₁ y ₂ – x ₂ y ₁ . ^[11]

El polígono dual de un rombo es un rectángulo : ^[12]

• Un rombo tiene todos los lados iguales, mientras que un rectángulo tiene todos los ángulos iguales.
• Un rombo tiene ángulos opuestos iguales, mientras que un rectángulo tiene lados opuestos iguales.
• Un rombo tiene un círculo inscrito, mientras que un rectángulo tiene un círculo circunscrito .
• Un rombo tiene un eje de simetría a través de cada par de ángulos de vértice opuestos, mientras que un rectángulo tiene un eje de simetría a través de cada par de lados opuestos.
• Las diagonales de un rombo se intersecan en ángulos iguales, mientras que las diagonales de un rectángulo tienen la misma longitud.
• La figura formada al unir los puntos medios de los lados de un rombo es un rectángulo , y viceversa.

Los lados de un rombo centrado en el origen, con diagonales cada una cayendo sobre un eje, consisten en todos los puntos ( x, y ) que satisfacen

${\displaystyle \left|{\frac {x}{a}}\right|\!+\left|{\frac {y}{b}}\right|\!=1.}$

Los vértices están en y Este es un caso especial de la superelipse , con exponente 1.${\displaystyle (\pm a,0)}$${\displaystyle (0,\pm b).}$

• Uno de los cinco tipos de redes 2D es la red rómbica, también llamada red rectangular centrada .
• Los rombos pueden teselar el plano 2D de borde a borde y periódicamente de tres maneras diferentes, incluyendo, para el rombo de 60°, el teselado en rombo .

Como teselados cuadrados topológicos		Como mosaico de rombos de 30 a 60 grados

• Los análogos tridimensionales de un rombo incluyen la bipirámide y el bicono como superficie de revolución .

Los poliedros convexos con rombos incluyen el conjunto infinito de zonohedros rómbicos , que pueden verse como envolventes proyectivas de hipercubos .

• Un romboedro (también llamado hexaedro rómbico) es una figura tridimensional como un cuboide (también llamado paralelepípedo rectangular), excepto que sus 3 pares de caras paralelas son hasta 3 tipos de rombos en lugar de rectángulos.
• El dodecaedro rómbico es un poliedro convexo con 12 rombos congruentes como caras .
• El triacontaedro rómbico es un poliedro convexo que tiene como caras 30 rombos áureos (rombos cuyas diagonales están en proporción áurea ).
• El gran triacontaedro rómbico es un poliedro isoédrico e isotoxal no convexo con 30 caras rómbicas que se intersecan.
• El hexecontaedro rómbico es una estelación del triacontaedro rómbico. Es no convexo y tiene 60 caras rómbicas áureas con simetría icosaédrica .
• El eneacontaedro rómbico es un poliedro compuesto por 90 caras rómbicas, con tres, cinco o seis rombos que se unen en cada vértice. Tiene 60 rombos anchos y 30 delgados.
• El icosaedro rómbico es un poliedro compuesto por 20 caras rómbicas, de las cuales tres, cuatro o cinco se encuentran en cada vértice. Tiene 10 caras en el eje polar y 10 caras siguiendo el ecuador.

Ejemplo de poliedros con todas las caras rómbicas

Isoédrica		Rombos dorados isoédricos		2-isoédrico	3-isoédrico
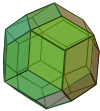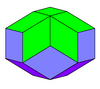Trapezoedro trigonal	Dodecaedro rómbico	Triacontaedro rómbico	Icosaedro rómbico	Eneacontaedro rómbico	Romboedro

• El camino de Merkel
• Rombo de Michaelis , en anatomía humana
• Romboide , ya sea un paralelepípedo o un paralelogramo que no es ni un rombo ni un rectángulo
• Antena rómbica
• Ajedrez rómbico
• Bandera del Departamento de Norte de Santander de Colombia, que contiene cuatro estrellas en forma de rombo
• Superelipse (incluye un rombo con esquinas redondeadas)

Busque rombo en Wikcionario, el diccionario libre.

Wikimedia Commons tiene medios relacionados con Rombo .

• Paralelogramo y Rombo - Curso animado (Construcción, Circunferencia, Área)
• Definición de rombo, Referencia abierta de matemáticas con subprograma interactivo.
• Área del rombo, Math Open Reference: muestra tres formas diferentes de calcular el área de un rombo, con una aplicación interactiva