Condensador
.jpg/440px-Capacitors_(7189597135).jpg) | |
| Tipo | Componente electrónico |
|---|---|
| Principio de funcionamiento | Capacidad |
| Inventado | Ewald Georg von Kleist (1745) Pieter van Musschenbroek (1746) |
| Símbolo electrónico | |
 | |
En ingeniería eléctrica , un condensador es un dispositivo que almacena energía eléctrica mediante la acumulación de cargas eléctricas en dos superficies muy próximas entre sí y aisladas entre sí. El condensador se conocía originalmente como condensador , [1] un término que todavía se encuentra en algunos nombres compuestos, como el de micrófono de condensador . Es un componente electrónico pasivo con dos terminales .
La utilidad de un capacitor depende de su capacitancia . Si bien existe cierta capacitancia entre dos conductores eléctricos próximos en un circuito , un capacitor es un componente diseñado específicamente para agregar capacitancia a alguna parte del circuito.
La forma física y la construcción de los condensadores prácticos varían ampliamente y muchos tipos de condensadores son de uso común. La mayoría de los condensadores contienen al menos dos conductores eléctricos , a menudo en forma de placas o superficies metálicas separadas por un medio dieléctrico . Un conductor puede ser una lámina, una película delgada, una perla sinterizada de metal o un electrolito . El dieléctrico no conductor actúa para aumentar la capacidad de carga del condensador. Los materiales que se utilizan comúnmente como dieléctricos incluyen vidrio , cerámica , película de plástico , papel , mica , aire y capas de óxido . Cuando se aplica una diferencia de potencial eléctrico (un voltaje ) a través de los terminales de un condensador, por ejemplo cuando un condensador está conectado a una batería, se desarrolla un campo eléctrico a través del dieléctrico, lo que hace que una carga positiva neta se acumule en una placa y una carga negativa neta en la otra placa. En realidad, no fluye corriente a través de un dieléctrico perfecto . Sin embargo, hay un flujo de carga a través del circuito fuente. Si la condición se mantiene durante el tiempo suficiente, la corriente a través del circuito fuente cesa. Si se aplica un voltaje que varía en el tiempo a través de los cables del capacitor, la fuente experimenta una corriente continua debido a los ciclos de carga y descarga del capacitor.
Los condensadores se utilizan ampliamente como parte de circuitos eléctricos en muchos dispositivos eléctricos comunes. A diferencia de una resistencia , un condensador ideal no disipa energía, aunque los condensadores de la vida real sí disipan una pequeña cantidad (consulte Comportamiento no ideal).
Las primeras formas de condensadores se crearon en la década de 1740, cuando los experimentadores europeos descubrieron que la carga eléctrica podía almacenarse en frascos de vidrio llenos de agua que llegaron a conocerse como frascos de Leyden . Hoy en día, los condensadores se utilizan ampliamente en circuitos electrónicos para bloquear la corriente continua mientras permiten el paso de la corriente alterna . En las redes de filtros analógicos , suavizan la salida de las fuentes de alimentación . En los circuitos resonantes , sintonizan radios a frecuencias particulares . En los sistemas de transmisión de energía eléctrica , estabilizan el voltaje y el flujo de energía. [2] La propiedad de almacenamiento de energía en los condensadores se explotó como memoria dinámica en las primeras computadoras digitales, [3] y todavía se encuentra en la DRAM moderna .
Historia
Los condensadores naturales existen desde tiempos prehistóricos. El ejemplo más común de capacitancia natural son las cargas estáticas acumuladas entre las nubes del cielo y la superficie de la Tierra, donde el aire entre ellas actúa como dieléctrico. Esto da lugar a rayos cuando se supera la tensión de ruptura del aire. [4]

En octubre de 1745, Ewald Georg von Kleist de Pomerania , Alemania, descubrió que se podía almacenar carga conectando un generador electrostático de alto voltaje mediante un cable a un volumen de agua en un frasco de vidrio portátil. [5] La mano de von Kleist y el agua actuaron como conductores y el frasco como dieléctrico (aunque los detalles del mecanismo se identificaron incorrectamente en ese momento). Von Kleist descubrió que tocar el cable producía una chispa poderosa, mucho más dolorosa que la obtenida de una máquina electrostática. Al año siguiente, el físico holandés Pieter van Musschenbroek inventó un condensador similar, que recibió el nombre de frasco de Leyden , en honor a la Universidad de Leiden donde trabajaba. [6] También quedó impresionado por la potencia de la descarga que recibió y escribió: "No aceptaría una segunda descarga por el reino de Francia". [7]
Daniel Gralath fue el primero en combinar varias botellas en paralelo para aumentar la capacidad de almacenamiento de carga. [8] Benjamin Franklin investigó la botella de Leyden y llegó a la conclusión de que la carga se almacenaba en el vidrio, no en el agua como otros habían supuesto. También adoptó el término "batería", [9] [10] (que denota el aumento de potencia con una fila de unidades similares como en una batería de cañones ), posteriormente aplicado a grupos de celdas electroquímicas . [11] En 1747, las botellas de Leyden se fabricaron recubriendo el interior y el exterior de las botellas con una lámina de metal, dejando un espacio en la boca para evitar la formación de arcos eléctricos entre las láminas. [12] La primera unidad de capacitancia fue la botella , equivalente a unos 1,11 nanofaradios . [13]
Hasta aproximadamente 1900, se utilizaron exclusivamente frascos de Leyden o dispositivos más potentes que empleaban placas de vidrio planas alternadas con conductores de papel de aluminio, cuando la invención de la radio creó una demanda de condensadores estándar y el movimiento constante hacia frecuencias más altas requirió condensadores con menor inductancia . Se empezaron a utilizar métodos de construcción más compactos, como una lámina dieléctrica flexible (como papel engrasado) intercalada entre láminas de papel de aluminio, enrollada o doblada en un paquete pequeño.

Los primeros condensadores se conocían como condensadores , un término que todavía se utiliza ocasionalmente en la actualidad, particularmente en aplicaciones de alta potencia, como los sistemas automotrices. El término condensador fue utilizado por Alessandro Volta en 1780 para referirse a un dispositivo, similar a su electróforo , que desarrolló para medir la electricidad, y traducido en 1782 como condensador , [14] donde el nombre se refería a la capacidad del dispositivo para almacenar una mayor densidad de carga eléctrica de la que era posible con un conductor aislado. [15] [1] El término quedó en desuso debido al significado ambiguo de condensador de vapor , y condensador se convirtió en el término recomendado en el Reino Unido a partir de 1926, [16] mientras que el cambio se produjo considerablemente más tarde en los Estados Unidos.
Desde el comienzo del estudio de la electricidad , se han utilizado materiales no conductores como el vidrio , la porcelana , el papel y la mica como aislantes . Décadas más tarde, estos materiales también resultaron adecuados para su uso como dieléctrico de los primeros condensadores. Los condensadores de papel, fabricados intercalando una tira de papel impregnado entre tiras de metal y enrollando el resultado hasta formar un cilindro, se utilizaron habitualmente a finales del siglo XIX; su fabricación comenzó en 1876, [17] y se utilizaron desde principios del siglo XX como condensadores de desacoplamiento en telefonía .
La porcelana se utilizó en los primeros condensadores cerámicos . En los primeros años de los aparatos de transmisión inalámbrica de Marconi , se utilizaban condensadores de porcelana para aplicaciones de alto voltaje y alta frecuencia en los transmisores . En el lado del receptor, se utilizaban condensadores de mica más pequeños para circuitos resonantes . Los condensadores de mica fueron inventados en 1909 por William Dubilier. Antes de la Segunda Guerra Mundial, la mica era el dieléctrico más común para los condensadores en los Estados Unidos. [17]
Charles Pollak (nacido Karol Pollak ), el inventor de los primeros condensadores electrolíticos , descubrió que la capa de óxido de un ánodo de aluminio permanecía estable en un electrolito neutro o alcalino , incluso cuando se cortaba la energía. En 1896 se le concedió la patente estadounidense n.º 672.913 por un "condensador líquido eléctrico con electrodos de aluminio". Los condensadores de tantalio con electrolito sólido fueron inventados por Bell Laboratories a principios de la década de 1950 como un condensador de soporte de bajo voltaje miniaturizado y más confiable para complementar su recién inventado transistor .
Con el desarrollo de materiales plásticos por parte de los químicos orgánicos durante la Segunda Guerra Mundial , la industria de los condensadores comenzó a reemplazar el papel por películas de polímero más delgadas. Uno de los primeros avances en condensadores de película se describió en la patente británica 587.953 en 1944. [17]
Los condensadores eléctricos de doble capa (ahora supercondensadores ) se inventaron en 1957 cuando H. Becker desarrolló un "condensador electrolítico de bajo voltaje con electrodos de carbono porosos". [17] [18] [19] Él creía que la energía se almacenaba como carga en los poros de carbono utilizados en su condensador, así como en los poros de las láminas grabadas de los condensadores electrolíticos. Como en ese momento no conocía el mecanismo de doble capa, escribió en la patente: "No se sabe exactamente qué está sucediendo en el componente si se usa para almacenar energía, pero conduce a una capacidad extremadamente alta".
El condensador MOS fue adoptado más tarde ampliamente como condensador de almacenamiento en chips de memoria y como el componente básico del dispositivo acoplado por carga (CCD) en la tecnología de sensores de imagen . [20] En 1966, el Dr. Robert Dennard inventó la arquitectura DRAM moderna, combinando un solo transistor MOS por condensador. [21] [22]
Teoría del funcionamiento
Descripción general


Un condensador consta de dos conductores separados por una región no conductora. [23] La región no conductora puede ser un vacío o un material aislante eléctrico conocido como dieléctrico . Ejemplos de medios dieléctricos son el vidrio, el aire, el papel, el plástico, la cerámica e incluso una región de agotamiento de semiconductores químicamente idéntica a los conductores. Según la ley de Coulomb, una carga en un conductor ejercerá una fuerza sobre los portadores de carga dentro del otro conductor, atrayendo cargas de polaridad opuesta y repeliendo cargas de polaridad similar, por lo que se inducirá una carga de polaridad opuesta en la superficie del otro conductor. De este modo, los conductores mantienen cargas iguales y opuestas en sus superficies enfrentadas, [24] y el dieléctrico desarrolla un campo eléctrico.
Un capacitor ideal se caracteriza por una capacitancia constante C , en faradios en el sistema SI de unidades, definida como la relación entre la carga positiva o negativa Q en cada conductor y el voltaje V entre ellos: [23] Una capacitancia de un faradio (F) significa que un culombio de carga en cada conductor provoca un voltaje de un voltio a través del dispositivo. [25] Debido a que los conductores (o placas) están juntos, las cargas opuestas en los conductores se atraen entre sí debido a sus campos eléctricos, lo que permite que el capacitor almacene más carga para un voltaje dado que cuando los conductores están separados, lo que produce una capacitancia mayor.
En los dispositivos prácticos, la acumulación de carga a veces afecta mecánicamente al capacitor, lo que hace que su capacitancia varíe. En este caso, la capacitancia se define en términos de cambios incrementales:
Analogía hidráulica

En la analogía hidráulica , el voltaje es análogo a la presión del agua y la corriente eléctrica a través de un cable es análoga al flujo de agua a través de una tubería. Un capacitor es como un diafragma elástico dentro de la tubería. Aunque el agua no puede pasar a través del diafragma, se mueve a medida que este se estira o se desenrolla.
- La capacitancia es análoga a la elasticidad del diafragma . De la misma manera que la relación entre la diferencia de carga y el voltaje sería mayor para un valor de capacitancia mayor ( ), la relación entre el desplazamiento del agua y la presión sería mayor para un diafragma que se flexiona más fácilmente.
- En un circuito de CA, un condensador se comporta como un diafragma en una tubería, permitiendo que la carga se mueva en ambos lados del dieléctrico mientras que ningún electrón pasa a través de él. En los circuitos de CC, un condensador es análogo a un acumulador hidráulico , que almacena la energía hasta que se libera la presión. De manera similar, se pueden utilizar para suavizar el flujo de electricidad en circuitos de CC rectificados de la misma manera que un acumulador amortigua las sobretensiones de una bomba hidráulica.
- Tanto los condensadores cargados como los diafragmas estirados almacenan energía potencial . Cuanto más cargado esté un condensador, mayor será el voltaje entre las placas ( ). Asimismo, cuanto mayor sea el volumen de agua desplazada, mayor será la energía potencial elástica.
- La corriente eléctrica afecta la diferencia de carga a través de un capacitor de la misma manera que el flujo de agua afecta la diferencia de volumen a través de un diafragma.
- Así como los capacitores experimentan una ruptura dieléctrica cuando se los somete a altos voltajes, los diafragmas explotan bajo presiones extremas.
- Así como los capacitores bloquean la CC mientras pasan la CA, los diafragmas no desplazan agua a menos que haya un cambio en la presión.
Equivalencia de circuitos en el límite de tiempo corto y en el límite de tiempo largo
En un circuito, un condensador puede comportarse de forma diferente en distintos instantes de tiempo. Sin embargo, normalmente es fácil pensar en el límite de tiempo corto y el límite de tiempo largo:
- En el límite de tiempo largo, después de que la corriente de carga/descarga ha saturado el capacitor, no entrará (ni saldrá) corriente de ninguno de los lados del capacitor; por lo tanto, la equivalencia de largo tiempo del capacitor es un circuito abierto.
- En el límite de tiempo corto, si el capacitor comienza con un cierto voltaje V, dado que la caída de voltaje en el capacitor es conocida en este instante, podemos reemplazarlo con una fuente de voltaje ideal de voltaje V. Específicamente, si V = 0 (el capacitor no está cargado), la equivalencia de tiempo corto de un capacitor es un cortocircuito.
Condensador de placas paralelas


El modelo más simple de un capacitor consiste en dos placas conductoras delgadas paralelas, cada una con un área de , separadas por un espacio uniforme de espesor lleno de un dieléctrico de permitividad . Se supone que el espacio es mucho más pequeño que las dimensiones de las placas. Este modelo se aplica bien a muchos capacitores prácticos que están construidos con láminas de metal separadas por una capa delgada de dieléctrico aislante, ya que los fabricantes intentan mantener el dieléctrico muy uniforme en espesor para evitar puntos delgados que pueden causar fallas en el capacitor.
Como la separación entre las placas es uniforme en toda su superficie, el campo eléctrico entre ellas es constante y se dirige perpendicularmente a la superficie de la placa, excepto en una zona cercana a los bordes de las placas, donde el campo disminuye porque las líneas de campo eléctrico "sobresalen" de los lados del condensador. Esta zona de "campo de borde" tiene aproximadamente el mismo ancho que la separación entre las placas, y, suponiendo que es pequeña en comparación con las dimensiones de las placas, es lo suficientemente pequeña como para ignorarla. Por lo tanto, si se coloca una carga de en una placa y en la otra (la situación de las placas cargadas de forma desigual se analiza a continuación), la carga de cada placa se distribuirá de forma uniforme en una capa de carga superficial de densidad de carga constante culombios por metro cuadrado, en la superficie interior de cada placa. Según la ley de Gauss, la magnitud del campo eléctrico entre las placas es . El voltaje (diferencia) entre las placas se define como la integral de línea del campo eléctrico sobre una línea (en la dirección z) de una placa a otra. La capacitancia se define como . Sustituyendo lo anterior en esta ecuación
Por lo tanto, en un capacitor la capacitancia más alta se logra con un material dieléctrico de alta permitividad , un área de placa grande y una pequeña separación entre las placas.
Como el área de las placas aumenta con el cuadrado de las dimensiones lineales y la separación aumenta linealmente, la capacitancia escala con la dimensión lineal de un capacitor ( ), o como la raíz cúbica del volumen.
Un condensador de placas paralelas solo puede almacenar una cantidad finita de energía antes de que se produzca la ruptura dieléctrica . El material dieléctrico del condensador tiene una rigidez dieléctrica U d que establece la tensión de ruptura del condensador en V = V bd = U d d . Por lo tanto, la energía máxima que puede almacenar el condensador es
La energía máxima es una función del volumen dieléctrico, la permitividad y la rigidez dieléctrica . Cambiar el área de la placa y la separación entre las placas mientras se mantiene el mismo volumen no provoca ningún cambio en la cantidad máxima de energía que el capacitor puede almacenar, siempre que la distancia entre las placas siga siendo mucho menor que la longitud y el ancho de las placas. Además, estas ecuaciones suponen que el campo eléctrico está completamente concentrado en el dieléctrico entre las placas. En realidad, hay campos marginales fuera del dieléctrico, por ejemplo, entre los lados de las placas del capacitor, que aumentan la capacitancia efectiva del capacitor. Esto a veces se llama capacitancia parásita . Para algunas geometrías de capacitores simples, este término de capacitancia adicional se puede calcular analíticamente. [26] Se vuelve despreciablemente pequeño cuando las relaciones entre el ancho de la placa y la separación y la longitud y la separación son grandes.
Para placas cargadas de manera desigual:
- Si una placa está cargada con mientras que la otra está cargada con , y si ambas placas están separadas de otros materiales en el entorno, entonces la superficie interna de la primera placa tendrá , y la superficie interna de la segunda placa tendrá carga. [ cita requerida ] Por lo tanto, el voltaje entre las placas es . Tenga en cuenta que la superficie externa de ambas placas tendrá , pero esas cargas no afectan el voltaje entre las placas.
- Si una placa está cargada con mientras que la otra está cargada con , y si la segunda placa está conectada a tierra, entonces la superficie interna de la primera placa tendrá , y la superficie interna de la segunda placa tendrá . Por lo tanto, el voltaje entre las placas es . Tenga en cuenta que la superficie externa de ambas placas tendrá carga cero.
Condensador intercalado

Para el número de placas en un capacitor, la capacitancia total sería donde es la capacitancia para una sola placa y es el número de placas intercaladas.
Como se muestra en la figura de la derecha, las placas intercaladas se pueden ver como placas paralelas conectadas entre sí. Cada par de placas adyacentes actúa como un capacitor separado; el número de pares es siempre uno menos que el número de placas, de ahí el multiplicador.
Energía almacenada en un condensador
Para aumentar la carga y el voltaje en un capacitor, una fuente de energía externa debe realizar trabajo para mover la carga de la placa negativa a la positiva contra la fuerza opuesta del campo eléctrico. [27] [28] Si el voltaje en el capacitor es , el trabajo requerido para mover un pequeño incremento de carga de la placa negativa a la positiva es . La energía se almacena en el campo eléctrico aumentado entre las placas. La energía total almacenada en un capacitor (expresada en julios ) es igual al trabajo total realizado para establecer el campo eléctrico desde un estado sin carga. [29] [28] [27] donde es la carga almacenada en el capacitor, es el voltaje a través del capacitor y es la capacitancia. Esta energía potencial permanecerá en el capacitor hasta que se elimine la carga. Si se permite que la carga regrese de la placa positiva a la negativa, por ejemplo conectando un circuito con resistencia entre las placas, la carga que se mueve bajo la influencia del campo eléctrico realizará trabajo en el circuito externo.
Si el espacio entre las placas del capacitor es constante, como en el modelo de placas paralelas anterior, el campo eléctrico entre las placas será uniforme (sin tener en cuenta los campos marginales) y tendrá un valor constante . En este caso, la energía almacenada se puede calcular a partir de la intensidad del campo eléctrico. La última fórmula anterior es igual a la densidad de energía por unidad de volumen en el campo eléctrico multiplicada por el volumen del campo entre las placas, lo que confirma que la energía en el capacitor se almacena en su campo eléctrico.
Relación corriente-voltaje

La corriente I ( t ) a través de cualquier componente en un circuito eléctrico se define como la velocidad de flujo de una carga Q ( t ) que pasa a través de él. Las cargas reales – electrones – no pueden pasar a través del dieléctrico de un condensador ideal . [nota 1] Más bien, un electrón se acumula en la placa negativa por cada uno que sale de la placa positiva, lo que resulta en un agotamiento de electrones y la consiguiente carga positiva en un electrodo que es igual y opuesta a la carga negativa acumulada en el otro. Por lo tanto, la carga en los electrodos es igual a la integral de la corriente, así como proporcional al voltaje, como se discutió anteriormente. Al igual que con cualquier antiderivada , se agrega una constante de integración para representar el voltaje inicial V ( t 0 ). Esta es la forma integral de la ecuación del condensador: [30]
Tomando la derivada de esto y multiplicándola por C se obtiene la forma derivada: [31] para C independiente del tiempo, voltaje y carga eléctrica.
El dual del capacitor es el inductor , que almacena energía en un campo magnético en lugar de en un campo eléctrico. Su relación corriente-voltaje se obtiene intercambiando corriente y voltaje en las ecuaciones del capacitor y reemplazando C por la inductancia L.
Circuitos de corriente continua

Un circuito en serie que contiene sólo una resistencia , un condensador, un interruptor y una fuente de CC constante de voltaje V 0 se conoce como circuito de carga . [32] Si el condensador está inicialmente descargado mientras el interruptor está abierto, y el interruptor está cerrado en t = 0 , se deduce de la ley de voltaje de Kirchhoff que
Tomando la derivada y multiplicando por C , se obtiene una ecuación diferencial de primer orden :
En t = 0 , el voltaje a través del capacitor es cero y el voltaje a través del resistor es V 0 . La corriente inicial es entonces I (0) = V 0 / R . Con esta suposición, al resolver la ecuación diferencial se obtiene donde τ 0 = RC es la constante de tiempo del sistema. A medida que el capacitor alcanza el equilibrio con el voltaje de la fuente, los voltajes a través del resistor y la corriente a través de todo el circuito decaen exponencialmente . En el caso de un capacitor que se descarga , el voltaje inicial del capacitor ( V Ci ) reemplaza a V 0 . Las ecuaciones se convierten en
Circuitos de corriente alterna
La impedancia , la suma vectorial de la reactancia y la resistencia , describe la diferencia de fase y la relación de amplitudes entre la tensión que varía sinusoidalmente y la corriente que varía sinusoidalmente a una frecuencia dada. El análisis de Fourier permite construir cualquier señal a partir de un espectro de frecuencias, de donde se puede encontrar la reacción del circuito a las distintas frecuencias. La reactancia y la impedancia de un condensador son respectivamente donde j es la unidad imaginaria y ω es la frecuencia angular de la señal sinusoidal. La fase − j indica que la tensión de CA V = ZI se retrasa 90° con respecto a la corriente de CA: la fase de corriente positiva corresponde a un aumento de la tensión a medida que se carga el condensador; la corriente cero corresponde a una tensión constante instantánea, etc.
La impedancia disminuye con el aumento de la capacitancia y la frecuencia. [33] Esto implica que una señal de mayor frecuencia o un capacitor más grande da como resultado una amplitud de voltaje más baja por amplitud de corriente: un "cortocircuito" de CA o un acoplamiento de CA. Por el contrario, para frecuencias muy bajas, la reactancia es alta, por lo que un capacitor es casi un circuito abierto en el análisis de CA: esas frecuencias han sido "filtradas".
Los capacitores se diferencian de las resistencias e inductores en que la impedancia es inversamente proporcional a la característica definitoria, es decir, la capacitancia .
Un condensador conectado a una fuente de tensión alterna tiene una corriente de desplazamiento que fluye a través de él. En el caso de que la fuente de tensión sea V 0 cos(ωt), la corriente de desplazamiento se puede expresar como:
En sen( ωt ) = −1 , el capacitor tiene una corriente máxima (o pico) por la cual I 0 = ωCV 0 . La relación entre el voltaje pico y la corriente pico se debe a la reactancia capacitiva (denotada X C ).
X C se acerca a cero cuando ω se acerca al infinito. Si X C se acerca a 0, el capacitor se parece a un cable corto que deja pasar corriente con fuerza a altas frecuencias. X C se acerca al infinito cuando ω se acerca a cero. Si X C se acerca al infinito, el capacitor se parece a un circuito abierto que deja pasar mal las frecuencias bajas.
La corriente del condensador se puede expresar en forma de cosenos para comparar mejor con el voltaje de la fuente:
En esta situación, la corriente está desfasada con respecto al voltaje en +π/2 radianes o +90 grados, es decir, la corriente adelanta al voltaje en 90°.
Análisis de circuitos de Laplace (dominio s)
Al utilizar la transformada de Laplace en el análisis de circuitos, la impedancia de un capacitor ideal sin carga inicial se representa en el dominio s por: donde
- C es la capacitancia, y
- s es la frecuencia compleja.
Análisis de circuitos
- Para condensadores en paralelo


- Los capacitores en una configuración en paralelo tienen aplicado el mismo voltaje. Sus capacidades se suman. La carga se reparte entre ellos según su tamaño. Si se utiliza el diagrama esquemático para visualizar las placas paralelas, resulta evidente que cada capacitor contribuye al área de superficie total.
- Para condensadores en serie

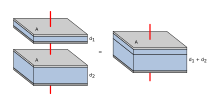
- Conectados en serie, el diagrama esquemático revela que la distancia de separación, no el área de la placa, es lo que suma. Cada condensador almacena una acumulación de carga instantánea igual a la de todos los demás condensadores de la serie. La diferencia de voltaje total de un extremo a otro se reparte entre cada condensador según la inversa de su capacitancia. La serie completa actúa como un condensador más pequeño que cualquiera de sus componentes.
- Los condensadores se combinan en serie para lograr un voltaje de trabajo más alto, por ejemplo, para suavizar una fuente de alimentación de alto voltaje. Los valores nominales de voltaje, que se basan en la separación de las placas, se suman si la capacitancia y las corrientes de fuga de cada condensador son idénticas. En una aplicación de este tipo, en ocasiones, las cadenas en serie se conectan en paralelo, formando una matriz. El objetivo es maximizar el almacenamiento de energía de la red sin sobrecargar ningún condensador. Para el almacenamiento de alta energía con condensadores en serie, se deben aplicar algunas consideraciones de seguridad para garantizar que la falla de un condensador y la fuga de corriente no apliquen demasiado voltaje a los otros condensadores en serie.
- La conexión en serie también se utiliza a veces para adaptar condensadores electrolíticos polarizados para uso en CA bipolar.
- Distribución de tensión en redes paralelo-serie.
- Para modelar la distribución de voltajes de un solo capacitor cargado conectado en paralelo a una cadena de capacitores en serie :
- Nota: Esto solo es correcto si todos los valores de capacitancia son iguales.
- La potencia transferida en esta disposición es:
Comportamiento no ideal
En la práctica, los condensadores se desvían de la ecuación ideal del condensador en varios aspectos. Algunos de ellos, como la corriente de fuga y los efectos parásitos, son lineales o pueden analizarse como casi lineales y pueden explicarse añadiendo componentes virtuales para formar un circuito equivalente. A continuación, se pueden aplicar los métodos habituales de análisis de redes . [34] En otros casos, como con la tensión de ruptura, el efecto no es lineal y no se puede utilizar el análisis de red ordinario (normal, por ejemplo, lineal), el efecto debe considerarse por separado. Puede existir otro grupo de artefactos, incluida la dependencia de la temperatura, que puede ser lineal pero invalida la suposición en el análisis de que la capacitancia es una constante. Finalmente, los efectos parásitos combinados, como la inductancia inherente, la resistencia o las pérdidas dieléctricas, pueden exhibir un comportamiento no uniforme a frecuencias de operación variables.
Tensión de ruptura
Por encima de una determinada intensidad de campo eléctrico, conocida como rigidez dieléctrica E ds , el dieléctrico de un condensador se vuelve conductor. La tensión a la que esto ocurre se denomina tensión de ruptura del dispositivo y se obtiene mediante el producto de la rigidez dieléctrica por la separación entre los conductores, [35]
La energía máxima que se puede almacenar de forma segura en un condensador está limitada por la tensión de ruptura. Si se supera esta tensión, se puede producir un cortocircuito entre las placas, lo que a menudo puede causar daños permanentes al dieléctrico, a las placas o a ambos. Debido a la escala de la capacitancia y la tensión de ruptura con el espesor del dieléctrico, todos los condensadores fabricados con un dieléctrico en particular tienen una densidad de energía máxima aproximadamente igual , en la medida en que el dieléctrico domina su volumen. [36]
En el caso de los condensadores dieléctricos de aire, la intensidad del campo de ruptura es del orden de 2–5 MV/m (o kV/mm); en el caso de la mica , la ruptura es de 100–300 MV/m; en el caso del aceite, de 15–25 MV/m; puede ser mucho menor cuando se utilizan otros materiales para el dieléctrico. [37] El dieléctrico se utiliza en capas muy delgadas, por lo que la tensión de ruptura absoluta de los condensadores es limitada. Las clasificaciones típicas de los condensadores utilizados para aplicaciones electrónicas generales varían de unos pocos voltios a 1 kV. A medida que aumenta la tensión, el dieléctrico debe ser más grueso, lo que hace que los condensadores de alto voltaje sean más grandes por capacitancia que los clasificados para tensiones más bajas.
La tensión de ruptura se ve afectada críticamente por factores como la geometría de las partes conductoras del condensador; los bordes o puntas afiladas aumentan la intensidad del campo eléctrico en ese punto y pueden provocar una ruptura local. Una vez que esto comienza a suceder, la ruptura recorre rápidamente el dieléctrico hasta llegar a la placa opuesta, dejando carbono atrás y provocando un cortocircuito (o una resistencia relativamente baja). Los resultados pueden ser explosivos, ya que el cortocircuito en el condensador extrae corriente de los circuitos circundantes y disipa la energía. [38] Sin embargo, en condensadores con dieléctricos particulares [39] [40] y electrodos metálicos delgados, no se forman cortocircuitos después de la ruptura. Sucede porque un metal se derrite o se evapora en las proximidades de la ruptura, aislándolo del resto del condensador. [41] [42]
La vía habitual de ruptura es que la intensidad del campo se haga lo suficientemente grande como para extraer electrones del dieléctrico de sus átomos, lo que provoca la conducción. También pueden darse otros escenarios, como impurezas en el dieléctrico y, si el dieléctrico es de naturaleza cristalina, las imperfecciones en la estructura cristalina pueden provocar una ruptura por avalancha, como ocurre en los dispositivos semiconductores. La tensión de ruptura también se ve afectada por la presión, la humedad y la temperatura. [43]
Circuito equivalente
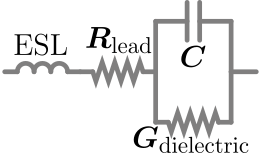
Un condensador ideal solo almacena y libera energía eléctrica, sin disipación. En la práctica, los condensadores tienen imperfecciones en sus materiales que dan lugar a los siguientes componentes parásitos: [44]
- , la inductancia en serie equivalente , debida a los conductores. Esto suele ser significativo solo a frecuencias relativamente altas.
- Dos resistencias que añaden un componente de valor real a la impedancia total, lo que desperdicia energía:
- , una pequeña resistencia en serie en los cables . Se vuelve más relevante a medida que aumenta la frecuencia.
- , una pequeña conductancia (o recíprocamente, una gran resistencia) en paralelo con la capacitancia, para tener en cuenta el material dieléctrico imperfecto. Esto provoca una pequeña corriente de fuga a través del dieléctrico (ver § Fuga) [45] que descarga lentamente el capacitor con el tiempo. Esta conductancia domina la resistencia total a frecuencias muy bajas. Su valor varía mucho según el material y la calidad del capacitor. [ cita requerida ]
Modelo simplificado de la serie RLC


A medida que aumenta la frecuencia, la impedancia capacitiva (una reactancia negativa) se reduce, por lo que la conductancia del dieléctrico se vuelve menos importante y los componentes en serie se vuelven más significativos. Por lo tanto, un modelo en serie RLC simplificado válido para un amplio rango de frecuencias simplemente trata al capacitor como si estuviera en serie con una inductancia en serie equivalente y una resistencia en serie equivalente dependiente de la frecuencia , que varía poco con la frecuencia. A diferencia del modelo anterior, este modelo no es válido en CC y frecuencias muy bajas donde es relevante.
La reactancia inductiva aumenta con la frecuencia. Como su signo es positivo, contrarresta la capacitancia.
En la frecuencia natural del circuito RLC , la inductancia cancela perfectamente la capacitancia, por lo que la reactancia total es cero. Dado que la impedancia total en es solo el valor real de , la disipación de potencia promedio alcanza su máximo de VRMS2/ESR , donde V RMS es el voltaje cuadrático medio (RMS) a través del capacitor.
En frecuencias aún más altas, predomina la impedancia inductiva, por lo que el condensador se comporta, de forma indeseable, como un inductor. La ingeniería de alta frecuencia implica tener en cuenta la inductancia de todas las conexiones y componentes.
Factor Q
Para un modelo simplificado de un capacitor como un capacitor ideal en serie con una resistencia en serie equivalente , el factor de calidad del capacitor (o Q ) es la relación entre la magnitud de su reactancia capacitiva y su resistencia a una frecuencia dada :
El factor Q es una medida de su eficiencia: cuanto mayor sea el factor Q del capacitor, más se acercará al comportamiento de un capacitor ideal. El factor de disipación es su recíproco.
Corriente de ondulación
La corriente de ondulación es el componente de CA de una fuente aplicada (a menudo una fuente de alimentación de modo conmutado ) cuya frecuencia puede ser constante o variable. La corriente de ondulación hace que se genere calor dentro del condensador debido a las pérdidas dieléctricas causadas por la intensidad de campo cambiante junto con el flujo de corriente a través de las líneas de suministro ligeramente resistivas o el electrolito en el condensador. La resistencia en serie equivalente (ESR) es la cantidad de resistencia en serie interna que se agregaría a un condensador perfecto para modelar esto.
Algunos tipos de condensadores , principalmente los condensadores electrolíticos de tantalio y aluminio , así como algunos condensadores de película, tienen un valor nominal específico para la corriente de ondulación máxima.
- Los condensadores electrolíticos de tantalio con electrolito de dióxido de manganeso sólido están limitados por la corriente de ondulación y, por lo general, tienen los valores de ESR más altos de la familia de condensadores. Si se exceden sus límites de ondulación, pueden producirse cortocircuitos y quemaduras en las piezas.
- Los condensadores electrolíticos de aluminio, el tipo más común de condensadores electrolíticos, sufren una reducción de su expectativa de vida con corrientes de ondulación más altas. Si la corriente de ondulación excede el valor nominal del condensador, tiende a producirse una falla explosiva.
- Los capacitores cerámicos generalmente no tienen limitación de corriente de ondulación [ cita requerida ] y tienen algunos de los índices ESR más bajos.
- Los condensadores de película tienen valores ESR muy bajos, pero exceder la corriente de ondulación nominal puede causar fallas por degradación.
Inestabilidad de la capacitancia
La capacitancia de ciertos capacitores disminuye a medida que el componente envejece. En los capacitores cerámicos , esto es causado por la degradación del dieléctrico. El tipo de dieléctrico, la temperatura ambiente de operación y almacenamiento son los factores de envejecimiento más significativos, mientras que el voltaje de operación generalmente tiene un efecto menor, es decir, el diseño habitual del capacitor es minimizar el coeficiente de voltaje. El proceso de envejecimiento puede revertirse calentando el componente por encima del punto de Curie . El envejecimiento es más rápido cerca del comienzo de la vida útil del componente, y el dispositivo se estabiliza con el tiempo. [46] Los capacitores electrolíticos envejecen a medida que el electrolito se evapora [ ancla rota ] . A diferencia de los capacitores cerámicos, esto ocurre hacia el final de la vida útil del componente.
La dependencia de la temperatura de la capacitancia se expresa generalmente en partes por millón (ppm) por °C. Por lo general, se puede tomar como una función ampliamente lineal, pero puede ser notablemente no lineal en los extremos de temperatura. El coeficiente de temperatura puede ser positivo o negativo, dependiendo principalmente del material dieléctrico. Algunos, designados C0G/NP0, pero llamados NPO , tienen un coeficiente algo negativo a una temperatura, positivo a otra y cero en el medio. Dichos componentes pueden especificarse para circuitos críticos para la temperatura. [47]
Los condensadores, especialmente los condensadores cerámicos, y los diseños más antiguos, como los condensadores de papel, pueden absorber las ondas sonoras, lo que produce un efecto microfónico . La vibración mueve las placas, lo que hace que varíe la capacitancia, lo que a su vez induce una corriente alterna. Algunos dieléctricos también generan piezoelectricidad . La interferencia resultante es especialmente problemática en aplicaciones de audio, ya que puede provocar retroalimentación o una grabación no deseada. En el efecto microfónico inverso, el campo eléctrico variable entre las placas del condensador ejerce una fuerza física que las mueve como un altavoz. Esto puede generar un sonido audible, pero drena energía y tensiona el dieléctrico y el electrolito, si lo hay.
Inversión de corriente y voltaje
La inversión de corriente se produce cuando la corriente cambia de dirección. La inversión de tensión es el cambio de polaridad en un circuito. La inversión se describe generalmente como el porcentaje de la tensión nominal máxima que invierte la polaridad. En los circuitos de CC, esto suele ser inferior al 100 %, a menudo en el rango de 0 a 90 %, mientras que los circuitos de CA experimentan una inversión del 100 %.
En los circuitos de CC y los circuitos pulsados, la inversión de la corriente y la tensión se ve afectada por la amortiguación del sistema. La inversión de la tensión se encuentra en los circuitos RLC que están subamortiguados . La corriente y la tensión invierten su dirección, formando un oscilador armónico entre la inductancia y la capacitancia. La corriente y la tensión tienden a oscilar y pueden invertir su dirección varias veces, siendo cada pico más bajo que el anterior, hasta que el sistema alcanza un equilibrio. Esto se suele denominar " ringing" . En comparación, los sistemas críticamente amortiguados o sobreamortiguados normalmente no experimentan una inversión de la tensión. La inversión también se encuentra en los circuitos de CA, donde la corriente pico es igual en cada dirección.
Para lograr una vida útil máxima, los capacitores generalmente deben poder soportar la cantidad máxima de inversión de voltaje que puede experimentar un sistema. Un circuito de CA experimenta una inversión de voltaje del 100 %, mientras que los circuitos de CC subamortiguados experimentan menos del 100 %. La inversión crea campos eléctricos excesivos en el dieléctrico, provoca un calentamiento excesivo tanto del dieléctrico como de los conductores y puede acortar drásticamente la expectativa de vida del capacitor. Los índices de inversión a menudo afectan las consideraciones de diseño para el capacitor, desde la elección de los materiales dieléctricos y los índices de voltaje hasta los tipos de conexiones internas utilizadas. [48]
Absorción dieléctrica
Los condensadores fabricados con cualquier tipo de material dieléctrico muestran cierto nivel de " absorción dieléctrica " o "remojo". Al descargar un condensador y desconectarlo, después de un corto tiempo puede desarrollar un voltaje debido a la histéresis en el dieléctrico. Este efecto es objetable en aplicaciones como circuitos de muestreo y retención de precisión o circuitos de temporización. El nivel de absorción depende de muchos factores, desde consideraciones de diseño hasta el tiempo de carga, ya que la absorción es un proceso dependiente del tiempo. Sin embargo, el factor principal es el tipo de material dieléctrico. Los condensadores como el electrolítico de tantalio o la película de polisulfona exhiben una absorción relativamente alta, mientras que el poliestireno o el teflón permiten niveles muy pequeños de absorción. [49] En algunos condensadores donde existen voltajes y energías peligrosas, como en tubos de flash , televisores , hornos microondas y desfibriladores , la absorción dieléctrica puede recargar el condensador a voltajes peligrosos después de que se haya cortocircuitado o descargado. Cualquier condensador que contenga más de 10 julios de energía se considera generalmente peligroso, mientras que 50 julios o más son potencialmente letales. Un condensador puede recuperar entre el 0,01 y el 20 % de su carga original en un período de varios minutos, lo que permite que un condensador aparentemente seguro se vuelva sorprendentemente peligroso. [50] [51] [52] [53] [54]
Fuga
Ningún material es un aislante perfecto, por lo que todos los dieléctricos permiten que se filtre un pequeño nivel de corriente, que se puede medir con un megóhmetro . [55] La fuga es equivalente a una resistencia en paralelo con el condensador. La exposición constante a factores como el calor, la tensión mecánica o la humedad puede provocar que el dieléctrico se deteriore y produzca una fuga excesiva, un problema que se observa a menudo en los circuitos de tubos de vacío más antiguos, en particular cuando se utilizaban condensadores de papel y láminas engrasados. En muchos circuitos de tubos de vacío, se utilizan condensadores de acoplamiento entre etapas para conducir una señal variable desde la placa de un tubo hasta el circuito de rejilla de la siguiente etapa. Un condensador con fugas puede provocar que el voltaje del circuito de rejilla se eleve desde su ajuste de polarización normal, lo que provoca una corriente excesiva o una distorsión de la señal en el tubo aguas abajo. En los amplificadores de potencia, esto puede provocar que las placas brillen en rojo o que las resistencias limitadoras de corriente se sobrecalienten o incluso fallen. Se aplican consideraciones similares a los amplificadores de estado sólido (transistores) fabricados con componentes, pero, debido a la menor producción de calor y al uso de modernas barreras dieléctricas de poliéster, este problema que alguna vez fue común se ha vuelto relativamente raro.
Fallo electrolítico por desuso
Los condensadores electrolíticos de aluminio se acondicionan cuando se fabrican aplicando un voltaje suficiente para iniciar el estado químico interno adecuado. Este estado se mantiene mediante el uso regular del equipo. Si un sistema que utiliza condensadores electrolíticos no se utiliza durante un largo período de tiempo, puede perder su acondicionamiento . A veces fallan y se produce un cortocircuito la próxima vez que se ponen en funcionamiento.
Esperanza de vida
Todos los condensadores tienen una vida útil variable, según su construcción, las condiciones de funcionamiento y las condiciones ambientales. Los condensadores cerámicos de estado sólido suelen tener una vida útil muy larga en condiciones de uso normal, que dependen poco de factores como la vibración o la temperatura ambiente, pero factores como la humedad, el estrés mecánico y la fatiga desempeñan un papel fundamental en su fallo. Los modos de fallo pueden diferir. Algunos condensadores pueden experimentar una pérdida gradual de capacidad, un aumento de las fugas o un aumento de la resistencia en serie equivalente (ESR), mientras que otros pueden fallar de forma repentina o incluso catastrófica . Por ejemplo, los condensadores de película metálica son más propensos a sufrir daños por el estrés y la humedad, pero se autocurarán cuando se produzca una avería en el dieléctrico. La formación de una descarga luminiscente en el punto de fallo evita la formación de arcos eléctricos vaporizando la película metálica en ese punto, neutralizando cualquier cortocircuito con una pérdida mínima de capacidad. Cuando se acumulan suficientes poros en la película, se produce un fallo total en un condensador de película metálica, que generalmente ocurre de forma repentina y sin previo aviso.
Los condensadores electrolíticos suelen tener una vida útil más corta. Los condensadores electrolíticos se ven muy poco afectados por la vibración o la humedad, pero factores como la temperatura ambiente y la temperatura de funcionamiento juegan un papel importante en su fallo, que se produce gradualmente como un aumento de la ESR (hasta un 300 %) y una disminución de hasta un 20 % de la capacitancia. Los condensadores contienen electrolitos que finalmente se difundirán a través de los sellos y se evaporarán. Un aumento de la temperatura también aumenta la presión interna y aumenta la velocidad de reacción de los productos químicos. Por lo tanto, la vida útil de un condensador electrolítico generalmente se define mediante una modificación de la ecuación de Arrhenius , que se utiliza para determinar las velocidades de reacción química:
Los fabricantes suelen utilizar esta ecuación para calcular la vida útil prevista, en horas, de los condensadores electrolíticos cuando se utilizan a la temperatura de funcionamiento prevista, que se ve afectada tanto por la temperatura ambiente, la ESR como por la corriente de rizado. Sin embargo, estas condiciones ideales pueden no darse en todos los casos de uso. La regla general para predecir la vida útil en diferentes condiciones de uso se determina mediante:
Esto dice que la vida del capacitor disminuye a la mitad por cada 10 grados Celsius que aumenta la temperatura, [56] donde:
- es la vida útil nominal en condiciones nominales, por ejemplo, 2000 horas
- es la temperatura operativa máxima/mínima nominal
- es la temperatura operativa media
- es la vida útil esperada en determinadas condiciones
Tipos de condensadores
Los condensadores prácticos se comercializan en muchas formas diferentes. El tipo de dieléctrico interno, la estructura de las placas y el encapsulado del dispositivo afectan en gran medida las características del condensador y sus aplicaciones.
Los valores disponibles varían desde muy bajos (rango de picofaradios; si bien en principio son posibles valores arbitrariamente bajos, la capacitancia parásita en cualquier circuito es el factor limitante) hasta supercondensadores de aproximadamente 5 kF .
Los condensadores electrolíticos de más de 1 microfaradio se utilizan generalmente debido a su pequeño tamaño y bajo coste en comparación con otros tipos, a menos que su relativamente baja estabilidad, vida útil y naturaleza polarizada los hagan inadecuados. Los supercondensadores de muy alta capacidad utilizan un material de electrodo poroso a base de carbono.
Materiales dieléctricos

La mayoría de los condensadores tienen un espaciador dieléctrico, que aumenta su capacidad en comparación con el aire o el vacío. Para maximizar la carga que puede contener un condensador, el material dieléctrico debe tener la permitividad más alta posible y, al mismo tiempo, la tensión de ruptura más alta posible. El dieléctrico también debe tener la menor pérdida con la frecuencia posible.
Sin embargo, existen condensadores de bajo valor con un alto vacío entre sus placas para permitir un funcionamiento con voltajes extremadamente altos y pérdidas bajas. Los condensadores variables con sus placas abiertas a la atmósfera se usaban comúnmente en circuitos de sintonización de radio. Los diseños posteriores utilizan un dieléctrico de lámina de polímero entre las placas móviles y estacionarias, sin espacio de aire significativo entre las placas.
Hay varios dieléctricos sólidos disponibles, incluidos papel , plástico , vidrio , mica y cerámica . [17]
El papel se utilizaba mucho en los condensadores más antiguos y ofrecía un rendimiento de voltaje relativamente alto. Sin embargo, el papel absorbe la humedad y ha sido reemplazado en gran medida por condensadores de película plástica .
La mayoría de las películas de plástico que se utilizan actualmente ofrecen una mejor estabilidad y un mejor rendimiento frente al envejecimiento que los dieléctricos más antiguos, como el papel aceitado, lo que las hace útiles en circuitos temporizadores, aunque pueden estar limitadas a temperaturas y frecuencias de funcionamiento relativamente bajas , debido a las limitaciones de la película de plástico que se utiliza. Los condensadores de película de plástico de gran tamaño se utilizan ampliamente en circuitos de supresión, circuitos de arranque de motores y circuitos de corrección del factor de potencia .
Los condensadores cerámicos son generalmente pequeños, baratos y útiles para aplicaciones de alta frecuencia, aunque su capacidad varía mucho con el voltaje y la temperatura y envejecen mal. También pueden sufrir el efecto piezoeléctrico. Los condensadores cerámicos se clasifican en general como dieléctricos de clase 1 , que tienen una variación predecible de la capacidad con la temperatura o dieléctricos de clase 2 , que pueden funcionar a un voltaje más alto. Las cerámicas multicapa modernas suelen ser bastante pequeñas, pero algunos tipos tienen tolerancias de valor inherentemente amplias, problemas microfónicos y suelen ser físicamente frágiles.
Los condensadores de vidrio y mica son extremadamente confiables, estables y tolerantes a altas temperaturas y voltajes, pero son demasiado caros para la mayoría de las aplicaciones convencionales.
Los condensadores electrolíticos y los supercondensadores se utilizan para almacenar cantidades pequeñas y grandes de energía, respectivamente, los condensadores cerámicos se utilizan a menudo en resonadores y la capacitancia parásita ocurre en circuitos donde la estructura simple conductor-aislante-conductor se forma de manera involuntaria por la configuración del diseño del circuito.


Los condensadores electrolíticos utilizan una placa de aluminio o tantalio con una capa dieléctrica de óxido. El segundo electrodo es un electrolito líquido , conectado al circuito por otra placa de aluminio. Los condensadores electrolíticos ofrecen una capacitancia muy alta, pero sufren de tolerancias pobres, alta inestabilidad, pérdida gradual de capacitancia, especialmente cuando se someten al calor, y alta corriente de fuga. Los condensadores de mala calidad pueden perder electrolito, lo que es perjudicial para las placas de circuito impreso. La conductividad del electrolito cae a bajas temperaturas, lo que aumenta la resistencia en serie equivalente. Si bien se utilizan ampliamente para el acondicionamiento de la fuente de alimentación, sus características deficientes de alta frecuencia los hacen inadecuados para muchas aplicaciones. Los condensadores electrolíticos sufren autodegradación si no se utilizan durante un período (alrededor de un año), y cuando se aplica plena potencia pueden cortocircuitarse, dañando permanentemente el condensador y generalmente fundiendo un fusible o causando fallas en los diodos rectificadores. Por ejemplo, en equipos más antiguos, esto puede causar arcos eléctricos en los tubos rectificadores. Se pueden restaurar antes de su uso aplicando gradualmente el voltaje de funcionamiento, lo que a menudo se hace en equipos antiguos de válvulas de vacío durante un período de treinta minutos utilizando un transformador variable para suministrar energía de CA. El uso de esta técnica puede ser menos satisfactorio para algunos equipos de estado sólido, que pueden dañarse por el funcionamiento por debajo de su rango de potencia normal, lo que requiere que la fuente de alimentación se aísle primero de los circuitos consumidores. Tales soluciones pueden no ser aplicables a las fuentes de alimentación de alta frecuencia modernas, ya que estas producen un voltaje de salida completo incluso con una entrada reducida. [ cita requerida ]
Los condensadores de tantalio ofrecen mejores características de frecuencia y temperatura que los de aluminio, pero mayor absorción dieléctrica y fugas. [57]
Los condensadores de polímero (OS-CON, OC-CON, KO, AO) utilizan polímero conductor sólido (o semiconductor orgánico polimerizado) como electrolito y ofrecen una vida útil más larga y una ESR más baja a un costo mayor que los condensadores electrolíticos estándar.
Un condensador pasante es un componente que, si bien no cumple su función principal, tiene capacitancia y se utiliza para conducir señales a través de una lámina conductora.
Existen otros tipos de condensadores disponibles para aplicaciones especializadas. Los supercondensadores almacenan grandes cantidades de energía. Los supercondensadores fabricados a partir de aerogel de carbono , nanotubos de carbono o materiales de electrodos altamente porosos ofrecen una capacitancia extremadamente alta (hasta 5 kF a partir de 2010 [update]) y se pueden utilizar en algunas aplicaciones en lugar de baterías recargables . Los condensadores de corriente alterna están diseñados específicamente para funcionar en circuitos de alimentación de CA con voltaje de línea (red eléctrica). Se utilizan comúnmente en circuitos de motores eléctricos y, a menudo, están diseñados para manejar grandes corrientes, por lo que tienden a ser físicamente grandes. Por lo general, están empaquetados de manera resistente, a menudo en cajas de metal que se pueden conectar a tierra fácilmente. También están diseñados con voltajes de ruptura de corriente continua de al menos cinco veces el voltaje máximo de CA.
Condensadores dependientes del voltaje
La constante dieléctrica de una serie de dieléctricos muy útiles cambia en función del campo eléctrico aplicado, por ejemplo, los materiales ferroeléctricos , por lo que la capacitancia de estos dispositivos es más compleja. Por ejemplo, al cargar un condensador de este tipo, el aumento diferencial de voltaje con la carga está gobernado por: donde la dependencia del voltaje de la capacitancia, C ( V ) , sugiere que la capacitancia es una función de la intensidad del campo eléctrico, que en un dispositivo de placas paralelas de área grande está dada por ε = V / d . Este campo polariza el dieléctrico, cuya polarización, en el caso de un ferroeléctrico, es una función no lineal en forma de S del campo eléctrico, que, en el caso de un dispositivo de placas paralelas de área grande, se traduce en una capacitancia que es una función no lineal del voltaje. [58] [59]
Correspondiente a la capacitancia dependiente del voltaje, para cargar el capacitor al voltaje V se encuentra una relación integral: que concuerda con Q = CV sólo cuando C no depende del voltaje V .
De la misma manera, la energía almacenada en el condensador ahora está dada por
Integrador: donde se utiliza el intercambio del orden de integración .
La capacitancia no lineal de una sonda de microscopio escaneada a lo largo de una superficie ferroeléctrica se utiliza para estudiar la estructura del dominio de los materiales ferroeléctricos. [60]
Otro ejemplo de capacitancia dependiente del voltaje ocurre en dispositivos semiconductores como los diodos semiconductores , donde la dependencia del voltaje no surge de un cambio en la constante dieléctrica sino de una dependencia del voltaje del espaciamiento entre las cargas en los dos lados del capacitor. [61] Este efecto se explota intencionalmente en dispositivos similares a diodos conocidos como varicaps .
Condensadores dependientes de la frecuencia
Si se aplica un voltaje a un condensador que varía con el tiempo y que cambia con la suficiente rapidez, a cierta frecuencia la polarización del dieléctrico no puede seguir el voltaje. Como ejemplo del origen de este mecanismo, los dipolos microscópicos internos que contribuyen a la constante dieléctrica no pueden moverse instantáneamente y, por lo tanto, a medida que aumenta la frecuencia de un voltaje alterno aplicado, la respuesta del dipolo se limita y la constante dieléctrica disminuye. Una constante dieléctrica cambiante con la frecuencia se denomina dispersión dieléctrica y está regida por procesos de relajación dieléctrica , como la relajación de Debye . En condiciones transitorias, el campo de desplazamiento se puede expresar como (ver susceptibilidad eléctrica ):
indicando el retraso en la respuesta por la dependencia temporal de ε r , calculada en principio a partir de un análisis microscópico subyacente, por ejemplo, del comportamiento dipolar en el dieléctrico. Véase, por ejemplo, la función de respuesta lineal . [62] [63] La integral se extiende a lo largo de toda la historia pasada hasta el momento actual. Una transformada de Fourier en el tiempo da como resultado:
donde ε r ( ω ) es ahora una función compleja , con una parte imaginaria relacionada con la absorción de energía del campo por el medio. Véase permitividad . La capacitancia, al ser proporcional a la constante dieléctrica, también exhibe este comportamiento de frecuencia. Transformada de Fourier Ley de Gauss con esta forma para el campo de desplazamiento:
donde j es la unidad imaginaria , V ( ω ) es el componente de voltaje en la frecuencia angular ω , G ( ω ) es la parte real de la corriente, llamada conductancia , y C ( ω ) determina la parte imaginaria de la corriente y es la capacitancia . Z ( ω ) es la impedancia compleja.
Cuando un condensador de placas paralelas se llena con un dieléctrico, la medición de las propiedades dieléctricas del medio se basa en la relación: donde un primo simple denota la parte real y un primo doble la parte imaginaria, Z ( ω ) es la impedancia compleja con el dieléctrico presente, C cmplx ( ω ) es la llamada capacitancia compleja con el dieléctrico presente, y C 0 es la capacitancia sin el dieléctrico. [64] [65] (La medición "sin el dieléctrico" en principio significa medición en el espacio libre , un objetivo inalcanzable ya que incluso se predice que el vacío cuántico exhibe un comportamiento no ideal, como el dicroísmo . Para fines prácticos, cuando se tienen en cuenta los errores de medición, a menudo una medición en el vacío terrestre, o simplemente un cálculo de C 0 , es suficientemente preciso. [66] )
Utilizando este método de medición, la constante dieléctrica puede exhibir una resonancia a ciertas frecuencias correspondientes a frecuencias de respuesta características (energías de excitación) de los contribuyentes a la constante dieléctrica. Estas resonancias son la base de una serie de técnicas experimentales para detectar defectos. El método de conductancia mide la absorción como una función de la frecuencia. [67] Alternativamente, la respuesta temporal de la capacitancia se puede utilizar directamente, como en la espectroscopia transitoria de nivel profundo . [68]
Otro ejemplo de capacitancia dependiente de la frecuencia ocurre con los capacitores MOS , donde la generación lenta de portadores minoritarios significa que a altas frecuencias la capacitancia mide solo la respuesta del portador mayoritario, mientras que a bajas frecuencias responden ambos tipos de portadores. [61] [69]
En las frecuencias ópticas, la constante dieléctrica de los semiconductores presenta una estructura relacionada con la estructura de bandas del sólido. Los sofisticados métodos de medición por espectroscopia de modulación basados en la modulación de la estructura cristalina por presión u otras tensiones y la observación de los cambios relacionados en la absorción o reflexión de la luz han hecho avanzar nuestro conocimiento de estos materiales. [70]
Estilos

La disposición de las placas y el dieléctrico tiene muchas variaciones en diferentes estilos según los valores nominales deseados del capacitor. Para valores pequeños de capacitancia (microfaradios y menos), los discos cerámicos utilizan recubrimientos metálicos, con cables conductores unidos al recubrimiento. Se pueden lograr valores mayores mediante múltiples pilas de placas y discos. Los capacitores de valores mayores generalmente utilizan una lámina metálica o una capa de película metálica depositada sobre la superficie de una película dieléctrica para hacer las placas, y una película dieléctrica de papel o plástico impregnado; estas se enrollan para ahorrar espacio. Para reducir la resistencia en serie y la inductancia para placas largas, las placas y el dieléctrico se escalonan de modo que la conexión se realiza en el borde común de las placas enrolladas, no en los extremos de las tiras de lámina o película metalizada que componen las placas.
El conjunto está revestido para evitar que entre humedad en el dieléctrico; los primeros equipos de radio utilizaban un tubo de cartón sellado con cera. Los condensadores dieléctricos modernos de papel o película se sumergen en un termoplástico duro. Los condensadores grandes para uso en alta tensión pueden tener la forma de rollo comprimida para encajar en una caja metálica rectangular, con terminales atornillados y casquillos para las conexiones. El dieléctrico de los condensadores más grandes suele estar impregnado con un líquido para mejorar sus propiedades.

Los cables de conexión de los condensadores pueden estar dispuestos en muchas configuraciones, por ejemplo, axial o radialmente. "Axial" significa que los cables están en un eje común, normalmente el eje del cuerpo cilíndrico del condensador; los cables se extienden desde extremos opuestos. Los cables radiales rara vez están alineados a lo largo de los radios del círculo del cuerpo, por lo que el término es convencional. Los cables (hasta que se doblan) suelen estar en planos paralelos al del cuerpo plano del condensador y se extienden en la misma dirección; a menudo son paralelos de fábrica.
Los condensadores cerámicos discoidales pequeños y económicos existen desde la década de 1930 y su uso sigue siendo generalizado. Después de la década de 1980, se han utilizado ampliamente los encapsulados de montaje superficial para condensadores. Estos encapsulados son extremadamente pequeños y carecen de cables de conexión, lo que permite soldarlos directamente sobre la superficie de las placas de circuito impreso . Los componentes de montaje superficial evitan los efectos de alta frecuencia no deseados debido a los cables y simplifican el montaje automatizado, aunque su manipulación manual se dificulta debido a su pequeño tamaño.
Los condensadores variables controlados mecánicamente permiten ajustar el espaciado de las placas, por ejemplo, girando o deslizando un conjunto de placas móviles para alinearlas con un conjunto de placas estacionarias. Los condensadores variables de bajo coste aprietan capas alternas de aluminio y plástico con un tornillo . El control eléctrico de la capacitancia se puede lograr con varactores (o varicaps), que son diodos semiconductores con polarización inversa cuyo ancho de región de agotamiento varía con el voltaje aplicado. Se utilizan en bucles de enganche de fase , entre otras aplicaciones.
Marcas de condensadores
Códigos de marcado para piezas más grandes
La mayoría de los capacitores tienen designaciones impresas en sus cuerpos para indicar sus características eléctricas. Los capacitores más grandes, como los de tipo electrolítico, generalmente muestran la capacitancia como un valor con una unidad explícita, por ejemplo, 220 μF .
Por razones tipográficas, algunos fabricantes imprimen MF en los capacitores para indicar microfaradios (μF). [71]
Código de marcado de tres o cuatro caracteres para condensadores pequeños
Los capacitores más pequeños, como los de cerámica, suelen utilizar una notación abreviada que consta de tres dígitos y una letra opcional, donde los dígitos ( XYZ ) indican la capacitancia en picofaradios (pF), calculada como XY × 10 Z , y la letra indica la tolerancia. Las tolerancias comunes son ±5 %, ±10 % y ±20 %, que se indican como J, K y M, respectivamente.
Un capacitor también puede etiquetarse con su voltaje de trabajo, temperatura y otras características relevantes.
Ejemplo: Un capacitor etiquetado o designado como 473K 330V tiene una capacitancia de47 × 10 3 pF = 47 nF (±10%) con un voltaje de trabajo máximo de 330 V. El voltaje de trabajo de un capacitor es nominalmente el voltaje más alto que se puede aplicar a través de él sin riesgo indebido de romper la capa dieléctrica.
Código de marcado de dos caracteres para condensadores pequeños
Para las capacitancias que siguen las series de valores preferidos E3 , E6 , E12 o E24 , las antiguas normas ANSI/EIA-198-D:1991, ANSI/EIA-198-1-E:1998 y ANSI/EIA-198-1-F:2002, así como la enmienda IEC 60062:2016/AMD1:2019 a IEC 60062 definen un código de marcado especial de dos caracteres para capacitores para piezas muy pequeñas que no dejan espacio para imprimir el código de tres o cuatro caracteres mencionado anteriormente en ellas. El código consiste en una letra mayúscula que denota los dos dígitos significativos del valor seguido de un dígito que indica el multiplicador. La norma EIA también define una cantidad de letras minúsculas para especificar una cantidad de valores que no se encuentran en E24. [72]
| Código | Serie | Dígito | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Carta [nb 1] | E24 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| A | 1.0 | 0,10 pF | 1,0 pF | 10 pF | 100 pF | 1,0 nF | 10nF | 100nF | 1,0 μF | 10 μF | 100 μF |
| B | 1.1 | 0,11 pF | 1,1 pF | 11 pF | 110 pF | 1,1 nF | 11nF | 110 nF | 1,1 μF | 11 μF | 110 μF |
| do | 1.2 | 0,12 pF | 1,2 pF | 12 pF | 120 pF | 1,2 nF | 12nF | 120 nF | 1,2 μF | 12 μF | 120 μF |
| D | 1.3 | 0,13 pF | 1,3 pF | 13 pF | 130 pF | 1,3 nF | 13 nF | 130 nF | 1,3 μF | 13 μF | 130 μF |
| mi | 1.5 | 0,15 pF | 1,5 pF | 15 pF | 150 pF | 1,5 nF | 15nF | 150 nF | 1,5 μF | 15 μF | 150 μF |
| F | 1.6 | 0,16 pF | 1,6 pF | 16 pF | 160 pF | 1,6 nF | 16nF | 160nF | 1,6 μF | 16 μF | 160 μF |
| GRAMO | 1.8 | 0,18 pF | 1,8 pF | 18 pF | 180 pF | 1,8 nF | 18nF | 180 nF | 1,8 μF | 18 μF | 180 μF |
| yo | 2.0 | 0,20 pF | 2,0 pF | 20 pF | 200 pF | 2,0 nF | 20nF | 200nF | 2,0 μF | 20 μF | 200 μF |
| Yo | 2.2 | 0,22 pF | 2,2 pF | 22 pF | 220 pF | 2,2 nF | 22nF | 220 nF | 2,2 μF | 22 μF | 220 μF |
| K | 2.4 | 0,24 pF | 2,4 pF | 24 pF | 240 pF | 2,4 nF | 24nF | 240 nF | 2,4 μF | 24 μF | 240 μF |
| yo | 2.7 | 0,27 pF | 2,7 pF | 27 pF | 270 pF | 2,7 nF | 27nF | 270 nF | 2,7 μF | 27 μF | 270 μF |
| METRO | 3.0 | 0,30 pF | 3,0 pF | 30 pF | 300 pF | 3,0 nF | 30nF | 300 nF | 3,0 μF | 30 μF | 300 μF |
| norte | 3.3 | 0,33 pF | 3,3 pF | 33 pF | 330 pF | 3,3 nF | 33 nF | 330 nF | 3,3 μF | 33 μF | 330 μF |
| PAG | 3.6 | 0,36 pF | 3,6 pF | 36 pF | 360 pF | 3,6 nF | 36nF | 360 nF | 3,6 μF | 36 μF | 360 μF |
| Q | 3.9 | 0,39 pF | 3,9 pF | 39 pF | 390 pF | 3,9 nF | 39nF | 390 nF | 3,9 μF | 39 μF | 390 μF |
| R | 4.3 | 0,43 pF | 4,3 pF | 43 pF | 430 pF | 4,3 nF | 43 nF | 430 nF | 4,3 μF | 43 μF | 430 μF |
| S | 4.7 | 0,47 pF | 4,7 pF | 47 pF | 470 pF | 4,7 nF | 47nF | 470 nF | 4,7 μF | 47 μF | 470 μF |
| yo | 5.1 | 0,51 pF | 5,1 pF | 51 pF | 510 pF | 5,1 nF | 51 nF | 510 nF | 5,1 μF | 51 μF | 510 μF |
| tú | 5.6 | 0,56 pF | 5,6 pF | 56 pF | 560 pF | 5,6 nF | 56nF | 560 nF | 5,6 μF | 56 μF | 560 μF |
| V | 6.2 | 0,62 pF | 6,2 pF | 62 pF | 620 pF | 6,2 nF | 62nF | 620 nF | 6,2 μF | 62 μF | 620 μF |
| Yo | 6.8 | 0,68 pF | 6,8 pF | 68 pF | 680 pF | 6,8 nF | 68nF | 680 nF | 6,8 μF | 68 μF | 680 μF |
| incógnita | 7.5 | 0,75 pF | 7,5 pF | 75 pF | 750 pF | 7,5 nF | 75 nF | 750 nF | 7,5 μF | 75 μF | 750 μF |
| Y | 8.2 | 0,82 pF | 8,2 pF | 82 pF | 820 pF | 8,2 nF | 82nF | 820 nF | 8,2 μF | 82 μF | 820 μF |
| O | 9.1 | 0,91 pF | 9,1 pF | 91 pF | 910 pF | 9,1 nF | 91 nF | 910 nF | 9,1 μF | 91 μF | 910 μF |
| Código | Serie | Dígito | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Carta | Evaluación de impacto ambiental | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| a | 2.5 | 0,25 pF | 2,5 pF | 25 pF | 250 pF | 2,5 nF | 25nF | 250 nF | 2,5 μF | 25 μF | 250 μF |
| b? [73] | 3.0? [73] | 0,30 pF | 3,0 pF | 30 pF | 300 pF | 3,0 nF | 30nF | 300 nF | 3,0 μF | 30 μF | 300 μF |
| b? [72] /c? [73] | 3.5 | 0,35 pF | 3,5 pF | 35 pF | 350 pF | 3,5 nF | 35 nF | 350 nF | 3,5 μF | 35 μF | 350 μF |
| d | 4.0 | 0,40 pF | 4,0 pF | 40 pF | 400 pF | 4,0 nF | 40nF | 400 nF | 4,0 μF | 40 μF | 400 μF |
| mi | 4.5 | 0,45 pF | 4,5 pF | 45 pF | 450 pF | 4,5 nF | 45 nF | 450 nF | 4,5 μF | 45 μF | 450 μF |
| F | 5.0 | 0,50 pF | 5,0 pF | 50 pF | 500 pF | 5,0 nF | 50nF | 500nF | 5,0 μF | 50 μF | 500 μF |
| metro | 6.0 | 0,60 pF | 6,0 pF | 60 pF | 600 pF | 6,0 nF | 60nF | 600 nF | 6,0 μF | 60 μF | 600 μF |
| norte | 7.0 | 0,70 pF | 7,0 pF | 70 pF | 700 pF | 7,0 nF | 70nF | 700 nF | 7,0 μF | 70 μF | 700 μF |
| a | 8.0 | 0,80 pF | 8,0 pF | 80 pF | 800 pF | 8,0 nF | 80nF | 800 nF | 8,0 μF | 80 μF | 800 μF |
| gramo | 9.0 | 0,90 pF | 9,0 pF | 90 pF | 900 pF | 9,0 nF | 90nF | 900 nF | 9,0 μF | 90 μF | 900 μF |
Código RKM
El código RKM, que sigue las normas IEC 60062 y BS 1852, es una notación para indicar el valor de un condensador en un diagrama de circuito. Evita el uso de un separador decimal y lo reemplaza por el símbolo del prefijo SI para el valor particular (y la letra F para el peso 1). El código también se utiliza para el marcado de piezas. Ejemplo: 4n7 para 4,7 nF o 2F2 para 2,2 F.
Histórico
En textos anteriores a la década de 1960 y en algunos paquetes de capacitores hasta hace poco, [17] se utilizaban unidades de capacitancia obsoletas en libros electrónicos, [74] revistas y catálogos de electrónica. [75] Las antiguas unidades "mfd" y "mf" significaban microfaradio (μF); y las antiguas unidades "mmfd", "mmf", "uuf", "μμf", "pfd" significaban picofaradio (pF); pero rara vez se utilizan en la actualidad. [76] Además, "micromicrofaradio" o "micro-microfaradio" son unidades obsoletas que se encuentran en algunos textos más antiguos y que son equivalentes a picofaradio (pF). [74]
Resumen de unidades de capacitancia obsoletas: (no se muestran las variaciones en mayúsculas y minúsculas)
- μF (microfaradio) = mf, mfd
- pF (picofaradio) = mmf, mmfd, pfd, μμF
Aplicaciones

Almacenamiento de energía
Un condensador puede almacenar energía eléctrica cuando se desconecta de su circuito de carga, por lo que se puede utilizar como una batería temporal o como otros tipos de sistemas de almacenamiento de energía recargables . [77] Los condensadores se utilizan comúnmente en dispositivos electrónicos para mantener el suministro de energía mientras se cambian las baterías. (Esto evita la pérdida de información en la memoria volátil).
Un condensador puede facilitar la conversión de energía cinética de partículas cargadas en energía eléctrica y almacenarla. [78]
Existen ventajas y desventajas entre los condensadores y las baterías como dispositivos de almacenamiento. Sin resistencias externas o inductores, los condensadores generalmente pueden liberar su energía almacenada en un tiempo muy corto en comparación con las baterías. Por el contrario, las baterías pueden contener una carga mucho mayor para su tamaño. Los condensadores convencionales proporcionan menos de 360 julios por kilogramo de energía específica , mientras que una batería alcalina convencional tiene una densidad de 590 kJ/kg. Existe una solución intermedia: los supercondensadores , que pueden aceptar y entregar carga mucho más rápido que las baterías y toleran muchos más ciclos de carga y descarga que las baterías recargables. Sin embargo, son 10 veces más grandes que las baterías convencionales para una carga dada. Por otro lado, se ha demostrado que la cantidad de carga almacenada en la capa dieléctrica del condensador de película delgada puede ser igual o incluso superior a la cantidad de carga almacenada en sus placas. [79]
En los sistemas de audio de los automóviles , los condensadores grandes almacenan energía para que el amplificador la utilice cuando la necesite. Además, en el caso de un tubo de destello , se utiliza un condensador para mantener el alto voltaje .
Memoria digital
En la década de 1930, John Atanasoff aplicó el principio de almacenamiento de energía en condensadores para construir memorias digitales dinámicas para las primeras computadoras binarias que usaban tubos de electrones para la lógica. [80]
Energía pulsada y armas
La energía pulsada se utiliza en muchas aplicaciones para aumentar la intensidad de potencia (vatios) de un volumen de energía (julios) liberando ese volumen en un tiempo muy corto. Se pueden lograr pulsos en el rango de nanosegundos y potencias en los gigavatios. Los pulsos cortos a menudo requieren condensadores de alto voltaje y baja inductancia especialmente construidos que a menudo se utilizan en grandes grupos ( bancos de condensadores ) para suministrar enormes pulsos de corriente para muchas aplicaciones de energía pulsada. Estas incluyen la formación electromagnética , los generadores Marx , los láseres pulsados (especialmente los láseres TEA ), las redes de formación de pulsos , el radar , la investigación de la fusión y los aceleradores de partículas . [81]
Los bancos de condensadores de gran tamaño (depósitos) se utilizan como fuentes de energía para los detonadores de puente explosivo o detonadores de percutor en armas nucleares y otras armas especiales. Se están realizando trabajos experimentales utilizando bancos de condensadores como fuentes de energía para blindajes electromagnéticos y cañones de riel y de bobina electromagnéticos .
Acondicionamiento de potencia

Los condensadores de reserva se utilizan en fuentes de alimentación donde suavizan la salida de un rectificador de onda completa o de media onda . También se pueden utilizar en circuitos de bombeo de carga como elemento de almacenamiento de energía en la generación de voltajes más altos que el voltaje de entrada.
Los condensadores se conectan en paralelo con los circuitos de alimentación de la mayoría de los dispositivos electrónicos y sistemas más grandes (como fábricas) para desviar y ocultar las fluctuaciones de corriente de la fuente de alimentación principal y proporcionar una fuente de alimentación "limpia" para los circuitos de señal o control. Los equipos de audio, por ejemplo, utilizan varios condensadores de esta manera, para desviar el zumbido de la línea eléctrica antes de que entre en los circuitos de señal. Los condensadores actúan como una reserva local para la fuente de alimentación de CC y desvían las corrientes de CA de la fuente de alimentación. Esto se utiliza en aplicaciones de audio para automóviles, cuando un condensador de refuerzo compensa la inductancia y la resistencia de los cables de la batería de plomo-ácido del automóvil .
Corrección del factor de potencia

En la distribución de energía eléctrica, los condensadores se utilizan para la corrección del factor de potencia . Estos condensadores suelen venir en forma de tres condensadores conectados como una carga trifásica . Por lo general, los valores de estos condensadores no se dan en faradios, sino como potencia reactiva en voltamperios reactivos (var). El propósito es contrarrestar la carga inductiva de dispositivos como motores eléctricos y líneas de transmisión para hacer que la carga parezca ser principalmente resistiva. Las cargas individuales de motores o lámparas pueden tener condensadores para la corrección del factor de potencia, o se pueden instalar conjuntos más grandes de condensadores (generalmente con dispositivos de conmutación automáticos) en un centro de carga dentro de un edificio o en una gran subestación de servicios públicos .
Supresión y acoplamiento
Acoplamiento de señal

Debido a que los capacitores pasan corriente alterna pero bloquean las señales de corriente continua (cuando se cargan hasta el voltaje de corriente continua aplicado), a menudo se utilizan para separar los componentes de corriente alterna y corriente continua de una señal. Este método se conoce como acoplamiento de corriente alterna o "acoplamiento capacitivo". En este caso, se utiliza un valor grande de capacitancia, cuyo valor no necesita controlarse con precisión, pero cuya reactancia es pequeña a la frecuencia de la señal.
Desacoplamiento
Un condensador de desacoplamiento es un condensador que se utiliza para proteger una parte de un circuito del efecto de otra, por ejemplo, para suprimir el ruido o los transitorios. El ruido causado por otros elementos del circuito se deriva a través del condensador, lo que reduce el efecto que tienen sobre el resto del circuito. Se utiliza más comúnmente entre la fuente de alimentación y la tierra. Un nombre alternativo es condensador de derivación , ya que se utiliza para derivar la fuente de alimentación u otro componente de alta impedancia de un circuito.
Los condensadores de desacoplamiento no siempre tienen que ser componentes discretos. Los condensadores utilizados en estas aplicaciones pueden estar integrados en una placa de circuito impreso , entre las distintas capas. A menudo se los denomina condensadores integrados. [82] Las capas de la placa que contribuyen a las propiedades capacitivas también funcionan como planos de potencia y tierra, y tienen un dieléctrico entre ellas, lo que les permite funcionar como un condensador de placas paralelas.
Filtros de paso alto y paso bajo
Supresión de ruido, picos y amortiguadores
Cuando se abre un circuito inductivo, la corriente a través de la inductancia colapsa rápidamente, creando un gran voltaje a través del circuito abierto del interruptor o relé. Si la inductancia es lo suficientemente grande, la energía puede generar una chispa, haciendo que los puntos de contacto se oxiden, se deterioren o, a veces, se suelden entre sí, o destruyendo un interruptor de estado sólido. Un condensador amortiguador a lo largo del circuito recién abierto crea una ruta para que este impulso evite los puntos de contacto, preservando así su vida; estos se encontraban comúnmente en los sistemas de encendido de disyuntores , por ejemplo. De manera similar, en circuitos de menor escala, la chispa puede no ser suficiente para dañar el interruptor, pero aún puede irradiar interferencias de radiofrecuencia (RFI) no deseadas , que un condensador de filtro absorbe. Los condensadores amortiguadores generalmente se emplean con una resistencia de bajo valor en serie, para disipar energía y minimizar la RFI. Estas combinaciones de resistencia-condensador están disponibles en un solo paquete.
Los condensadores también se utilizan en paralelo con las unidades de interrupción de un disyuntor de alta tensión para distribuir de forma uniforme la tensión entre estas unidades. Se denominan "condensadores de nivelación".
En los diagramas esquemáticos, un condensador utilizado principalmente para el almacenamiento de carga de CC suele dibujarse verticalmente en los diagramas de circuitos con la placa inferior, más negativa, dibujada como un arco. La placa recta indica el terminal positivo del dispositivo, si está polarizado (consulte condensador electrolítico ).
Arrancadores de motor
En los motores monofásicos de jaula de ardilla , el devanado primario dentro de la carcasa del motor no es capaz de iniciar un movimiento rotatorio en el rotor, pero es capaz de sostenerlo. Para arrancar el motor, un devanado de "arranque" secundario tiene un condensador de arranque no polarizado en serie para introducir un avance en la corriente sinusoidal. Cuando el devanado secundario (de arranque) se coloca en un ángulo con respecto al devanado primario (de funcionamiento), se crea un campo eléctrico giratorio. La fuerza del campo giratorio no es constante, pero es suficiente para que el rotor empiece a girar. Cuando el rotor se acerca a la velocidad de funcionamiento, un interruptor centrífugo (o un relé sensible a la corriente en serie con el devanado principal) desconecta el condensador. El condensador de arranque suele estar montado en el lateral de la carcasa del motor. Estos se denominan motores de arranque por condensador, que tienen un par de arranque relativamente alto. Normalmente pueden tener hasta cuatro veces más par de arranque que un motor de fase dividida y se utilizan en aplicaciones como compresores, hidrolimpiadoras y cualquier dispositivo pequeño que requiera pares de arranque elevados.
Los motores de inducción accionados por condensador tienen un condensador de cambio de fase conectado permanentemente en serie con un segundo devanado. El motor es muy parecido a un motor de inducción bifásico.
Los condensadores de arranque de motores suelen ser de tipo electrolítico no polarizado, mientras que los condensadores de funcionamiento son de tipo dieléctrico convencional de película de plástico o papel.
Procesamiento de señales
La energía almacenada en un condensador se puede utilizar para representar información , ya sea en forma binaria, como en las memorias DRAM , o en forma analógica, como en los filtros de muestreo analógicos y los CCD . Los condensadores se pueden utilizar en circuitos analógicos como componentes de integradores o filtros más complejos y en la estabilización de bucles de retroalimentación negativa . Los circuitos de procesamiento de señales también utilizan condensadores para integrar una señal de corriente.
Circuitos sintonizados
Los condensadores y los inductores se utilizan juntos en circuitos sintonizados para seleccionar información en bandas de frecuencia específicas. Por ejemplo, los receptores de radio dependen de condensadores variables para sintonizar la frecuencia de la estación. Los altavoces utilizan filtros analógicos pasivos y los ecualizadores analógicos utilizan condensadores para seleccionar diferentes bandas de audio.
La frecuencia de resonancia f de un circuito sintonizado es una función de la inductancia ( L ) y la capacitancia ( C ) en serie, y está dada por: donde L está en henries y C está en faradios.
Detección
La mayoría de los capacitores están diseñados para mantener una estructura física fija. Sin embargo, varios factores pueden cambiar la estructura del capacitor y el cambio resultante en la capacitancia se puede utilizar para detectar esos factores.
- Cambio del dieléctrico
- Los efectos de variar las características del dieléctrico se pueden utilizar con fines de detección. Los condensadores con un dieléctrico expuesto y poroso se pueden utilizar para medir la humedad del aire. Los condensadores se utilizan para medir con precisión el nivel de combustible en los aviones ; a medida que el combustible cubre más de un par de placas, aumenta la capacitancia del circuito. Apretar el dieléctrico puede cambiar un condensador a unas pocas decenas de bares de presión lo suficiente como para que pueda usarse como un sensor de presión. [83] Un condensador dieléctrico de polímero seleccionado, pero por lo demás estándar, cuando se sumerge en un gas o líquido compatible, puede funcionar de manera útil como un sensor de presión de muy bajo costo hasta muchos cientos de bares.
- Cambiar la distancia entre las placas
- Los condensadores con una placa flexible se pueden utilizar para medir la tensión o la presión. Los transmisores de presión industriales utilizados para el control de procesos utilizan diafragmas de detección de presión, que forman una placa de condensador de un circuito oscilador. Los condensadores se utilizan como sensor en los micrófonos de condensador , donde una placa se mueve por la presión del aire, en relación con la posición fija de la otra placa. Algunos acelerómetros utilizan condensadores MEMS grabados en un chip para medir la magnitud y la dirección del vector de aceleración. Se utilizan para detectar cambios en la aceleración, en sensores de inclinación o para detectar la caída libre, como sensores que activan el despliegue de la bolsa de aire y en muchas otras aplicaciones. Algunos sensores de huellas dactilares utilizan condensadores. Además, un usuario puede ajustar el tono de un instrumento musical theremin moviendo su mano, ya que esto cambia la capacitancia efectiva entre la mano del usuario y la antena.
- Cambiar el área efectiva de las placas
- Los interruptores táctiles capacitivos se utilizan ahora [¿ cuándo? ] en muchos productos electrónicos de consumo.
Osciladores

Un condensador puede poseer cualidades similares a las de un resorte en un circuito oscilador. En el ejemplo de la imagen, un condensador actúa para influir en el voltaje de polarización en la base del transistor npn. Los valores de resistencia de las resistencias divisoras de voltaje y el valor de capacitancia del condensador controlan juntos la frecuencia oscilatoria.
Produciendo luz
Un condensador emisor de luz está hecho de un dieléctrico que utiliza la fosforescencia para producir luz. Si una de las placas conductoras está hecha con un material transparente, la luz es visible. Los condensadores emisores de luz se utilizan en la construcción de paneles electroluminiscentes, para aplicaciones como la retroiluminación de ordenadores portátiles. En este caso, todo el panel es un condensador utilizado con el fin de generar luz.
Peligros y seguridad
Los peligros que plantea un condensador suelen estar determinados, en primer lugar, por la cantidad de energía almacenada, que es la causa de cosas como quemaduras eléctricas o fibrilación cardíaca . Factores como el voltaje y el material del chasis son de consideración secundaria, que están más relacionados con la facilidad con la que se puede iniciar una descarga en lugar de con el daño que puede producirse. [54] En determinadas condiciones, incluida la conductividad de las superficies, las condiciones médicas preexistentes, la humedad del aire o las vías que sigue a través del cuerpo (es decir, las descargas que viajan a través del núcleo del cuerpo y, especialmente, el corazón son más peligrosas que las limitadas a las extremidades), se ha informado de que descargas de tan solo un julio causan la muerte, aunque en la mayoría de los casos es posible que ni siquiera dejen una quemadura. Las descargas de más de diez julios generalmente dañan la piel y suelen considerarse peligrosas. Cualquier condensador que pueda almacenar 50 julios o más debe considerarse potencialmente letal. [84] [54]
Los condensadores pueden retener una carga mucho tiempo después de que se quita la energía de un circuito; esta carga puede causar descargas peligrosas o incluso potencialmente fatales o dañar el equipo conectado. Por ejemplo, incluso un dispositivo aparentemente inocuo como el flash de una cámara desechable , tiene un condensador de flash fotográfico que puede contener más de 15 julios de energía y cargarse a más de 300 voltios. Esto es fácilmente capaz de producir una descarga. Los procedimientos de servicio para dispositivos electrónicos generalmente incluyen instrucciones para descargar condensadores grandes o de alto voltaje, por ejemplo, utilizando una varilla Brinkley . Los condensadores más grandes, como los que se usan en hornos microondas , unidades de HVAC y desfibriladores médicos también pueden tener resistencias de descarga incorporadas para disipar la energía almacenada a un nivel seguro en unos pocos segundos después de que se quita la energía. Los condensadores de alto voltaje se almacenan con los terminales en cortocircuito , como protección contra voltajes potencialmente peligrosos debido a la absorción dieléctrica o de voltajes transitorios que el condensador puede captar de cargas estáticas o eventos climáticos pasajeros. [54]
Algunos condensadores de papel o película de plástico viejos y grandes llenos de aceite contienen bifenilos policlorados (PCB). Se sabe que los PCB de desecho pueden filtrarse a las aguas subterráneas bajo los vertederos . Los condensadores que contienen PCB se etiquetaron como que contenían "Askarel" y varios otros nombres comerciales. Los condensadores de papel llenos de PCB se encuentran en balastos de lámparas fluorescentes muy antiguos (anteriores a 1975) y en otras aplicaciones.
Los capacitores pueden fallar catastróficamente cuando se los somete a voltajes o corrientes superiores a su capacidad nominal o, en el caso de capacitores polarizados, cuando se los aplica con polaridad inversa. Las fallas pueden crear arcos eléctricos que calientan y vaporizan el fluido dieléctrico, lo que provoca una acumulación de gas presurizado que puede provocar hinchazón, ruptura o explosión. Los capacitores más grandes pueden tener respiraderos o mecanismos similares para permitir la liberación de dichas presiones en caso de falla. Los capacitores utilizados en aplicaciones de RF o de alta corriente sostenida pueden sobrecalentarse, especialmente en el centro de los rodillos del capacitor. Los capacitores utilizados dentro de bancos de capacitores de alta energía pueden explotar violentamente cuando un cortocircuito en un capacitor provoca un vertido repentino de energía almacenada en el resto del banco hacia la unidad que falla. Los capacitores de vacío de alto voltaje pueden generar rayos X suaves incluso durante el funcionamiento normal. Una contención, una fusión y un mantenimiento preventivo adecuados pueden ayudar a minimizar estos peligros.
Los capacitores de alto voltaje pueden beneficiarse de una precarga para limitar las corrientes de entrada al encender los circuitos de corriente continua de alto voltaje (HVDC). Esto extiende la vida útil del componente y puede mitigar los peligros del alto voltaje.
- Condensadores electrolíticos hinchados. La ventilación en la parte superior permite la liberación de la acumulación de gas presurizado en caso de falla, lo que evita que explote.
- Este condensador de alta energía de un desfibrilador tiene una resistencia conectada entre los terminales por seguridad, para disipar la energía almacenada.
- Un condensador electrolítico explotado, mostrando fragmentos de papel y láminas metálicas.
Véase también
- Medidor de capacitancia
- Plaga de condensadores
- Campo de desplazamiento eléctrico
- Electroluminiscencia
- Lista de fabricantes de condensadores
Notas
- ^ La mayoría de los capacitores reales pueden tener una pequeña corriente de fuga dieléctrica que pasa a través de la capa dieléctrica resistiva entre las placas.
- ^ Para reducir el riesgo de errores de lectura, no se utilizan las letras
Iy ya que sus glifos son similares a otras letras y dígitos.O
Referencias
- ^ ab Duff, Wilmer (1916) [1908]. Un libro de texto de física (4.ª ed.). Filadelfia: P. Blakiston's Son & Co. pág. 361. Consultado el 1 de diciembre de 2016 .
- ^ Bird, John (2010). Principios y tecnología eléctrica y electrónica. Routledge. pp. 63–76. ISBN 978-0-08089056-2. Consultado el 17 de marzo de 2013 .
- ^ Floyd, Thomas (2005) [1984]. Dispositivos electrónicos (7.ª ed.). Upper Saddle River, Nueva Jersey, EE. UU.: Pearson Education . pág. 10. ISBN. 0-13-127827-4.
- ^ "Expresiones moleculares: electricidad y magnetismo - Tutoriales interactivos de Java: Rayo: un condensador natural". micro.magnet.fsu.edu .
- ^ Williams, Henry Smith. "Una historia de la ciencia, volumen II, parte VI: El descubrimiento de la botella de Leyden". Archivado desde el original el 24 de octubre de 2007. Consultado el 17 de marzo de 2013 .
- ^ Keithley, Joseph F. (1999). La historia de las mediciones eléctricas y magnéticas: desde el año 500 a. C. hasta la década de 1940. John Wiley & Sons. pág. 23. ISBN 978-0780311930. Consultado el 17 de marzo de 2013 .
- ^ Houston, Edwin J. (1905). Electricidad en la vida cotidiana. PF Collier & Son. pág. 71. Consultado el 17 de marzo de 2013 .
- ^ Benjamin, Park (1895). Una historia de la electricidad: (El auge intelectual en la electricidad) desde la Antigüedad hasta los días de Benjamin Franklin. J. Wiley & Sons . págs. 522–524.
- ^ Isaacson, Walter (2003). Benjamin Franklin: An American Life [Benjamin Franklin: una vida americana]. Simon and Schuster. pág. 136. ISBN 978-0-74326084-8. Consultado el 17 de marzo de 2013 .
- ^ Franklin, Benjamin (29 de abril de 1749). "Experimentos y observaciones sobre la electricidad: Carta IV a Peter Collinson" (PDF) . pág. 28. Consultado el 9 de agosto de 2009 .
- ^ Morse, Robert A. (septiembre de 2004). "Franklin y la electrostática: Ben Franklin como mi compañero de laboratorio" (PDF) . Wright Center for Science Education . Tufts University. pág. 23. Consultado el 10 de agosto de 2009.
Después del descubrimiento de la celda electroquímica por parte de Volta en 1800, el término se aplicó a un grupo de celdas electroquímicas
. - ^ Wolf, A; McKie, D. (1962). Una historia de la ciencia, la tecnología y la filosofía en el siglo XVIII (2.ª ed.). Londres: George Allen & Unwin. pág. 224.
- ^ "eFunda: Glosario: Unidades: Capacitancia eléctrica: Jarra". eFunda . Consultado el 17 de marzo de 2013 .
- ^ Pancaldi, G. (2003). Volta: Ciencia y cultura en la era de la Ilustración . Princeton: Princeton University Press. pp. 112–126. ISBN. 0691096856.
- ^ "Boceto de Alessandro Volta". The Popular Science Monthly . Nueva York: Bonnier Corporation: 118-119. Mayo de 1892. ISSN 0161-7370.
- ^ Asociación Británica de Normas de Ingeniería, Glosario de términos estándar británicos en ingeniería eléctrica , C. Lockwood & Son, 1926
- ^ abcdef Ho, Janet; Jow, T. Richard; Boggs, Steven (enero de 2010). "Introducción histórica a la tecnología de condensadores". Revista IEEE Electrical Insulation . 26 (1): 20–25. doi :10.1109/mei.2010.5383924. S2CID 23077215.
- ^ US 2800616, Becker, HI, "Condensador electrolítico de bajo voltaje", publicado el 23 de julio de 1957
- ^ Una breve historia de los supercondensadores OTOÑO DE 2007 Baterías y tecnología de almacenamiento de energía Archivado el 6 de enero de 2014 en Wayback Machine.
- ^ Sze, Simon Min ; Lee, Ming-Kwei (mayo de 2012). "Condensador MOS y MOSFET". Dispositivos semiconductores: física y tecnología. John Wiley & Sons . ISBN 978-0-47053794-7. Recuperado el 6 de octubre de 2019 .
- ^ "DRAM". IBM100 . IBM . 2017-08-09 . Consultado el 20 de septiembre de 2019 .
- ^ Sze, Simon M. (2002). Dispositivos semiconductores: física y tecnología (PDF) (2.ª ed.). Wiley . p. 214. ISBN 0-471-33372-7. Archivado desde el original (PDF) el 23 de enero de 2023.
- ^Ab Ulaby 1999, pág. 168.
- ^ Ulaby 1999, pág. 157.
- ^ Ulaby 1999, pág. 69.
- ^ Pillai, KPP (1970). "Campo de franjas de capacitores de placas paralelas finitas". Actas de la Institución de Ingenieros Eléctricos . 117 (6): 1201–1204. doi :10.1049/piee.1970.0232.
- ^ ab Purcell, Edward (2011). Electricidad y magnetismo, 2.ª ed. Cambridge University Press . págs. 110-111. ISBN 978-1-13950355-6.
- ^ de Serway, Raymond A.; Vuille, Chris (2014). Física universitaria, 10.ª edición. Cengage Learning. pág. 582. ISBN 978-1-30514282-4.
- ^ Hammond, P. (2013). Electromagnetismo para ingenieros: un curso introductorio. Elsevier Science. págs. 44-45. ISBN 978-1-48314978-3.
- ^ Dorf y Svoboda 2001, pág. 263.
- ^ Dorf y Svoboda 2001, pág. 260.
- ^ "Carga y descarga de condensadores". Todo sobre circuitos . Consultado el 19 de febrero de 2009 .
- ^ Percolación de corriente a través de resistencias y condensadores PLoS one 2017
- ^ "(PDF) Universalidad del escalamiento emergente en redes de percolación binaria aleatoria finita".
- ^ Ulaby 1999, pág. 170.
- ^ Pai, ST; Zhang, Qi (1995). Introducción a la tecnología de pulsos de alta potencia. Serie avanzada en ingeniería eléctrica e informática. Vol. 10. World Scientific. ISBN 978-9810217143. Consultado el 17 de marzo de 2013 .
- ^ Dyer, Stephen A. (2004). Encuesta Wiley sobre instrumentación y medición. John Wiley & Sons . pág. 397. ISBN 978-0-47122165-4. Consultado el 17 de marzo de 2013 .
- ^ Scherz, Paul (2006). Electrónica práctica para inventores (2.ª ed.). McGraw Hill Professional . pág. 100. ISBN 978-0-07177644-8. Consultado el 17 de marzo de 2013 .
- ^ Inuishi, Y.; Powers, DA (1957). "Ruptura eléctrica y conducción a través de películas de Mylar". Revista de Física Aplicada . 28 (9): 1017–1022. Código Bibliográfico :1957JAP....28.1017I. doi :10.1063/1.1722899.
- ^ Reed, CW; Cichanowski, SW (1994). "Los fundamentos del envejecimiento en capacitores de película de polímero de alto voltaje". IEEE Transactions on Dielectrics and Electrical Insulation . 1 (5): 904–922. doi :10.1109/94.326658.
- ^ Klein, N.; Gafni, H. (1966). "La máxima rigidez dieléctrica de películas delgadas de óxido de silicio". IEEE Transactions on Electron Devices . 13 (2): 281–289. Bibcode :1966ITED...13..281K. doi :10.1109/T-ED.1966.15681.
- ^ Belkin, A.; et al. (2017). "Recuperación de nanocondensadores de alúmina después de una ruptura por alto voltaje". Scientific Reports . 7 (1): 932. Bibcode :2017NatSR...7..932B. doi :10.1038/s41598-017-01007-9. PMC 5430567 . PMID 28428625.
- ^ Bird, John (2007). Teoría y tecnología de circuitos eléctricos. Routledge. pág. 501. ISBN 978-0-75068139-1. Consultado el 17 de marzo de 2013 .
- ^ Bisquert, J.; Garcia-Belmonte, G.; Fabregat-Santiago, F. (2000). "El papel de la instrumentación en el proceso de modelado de condensadores reales". IEEE Transactions on Education . 43 (4): 439–442. Bibcode :2000ITEdu..43..439F. doi :10.1109/13.883355. ISSN 1557-9638.
- ^ Ulaby 1999, pág. 169.
- ^ "El envejecimiento de los condensadores cerámicos simplificado". Johanson Dielectrics. 21 de mayo de 2012. Archivado desde el original el 26 de diciembre de 2012. Consultado el 17 de marzo de 2013 .
- ^ "Guía concisa de tipos de condensadores". EETech Media LLC . Consultado el 7 de septiembre de 2023 .
- ^ "El efecto de la inversión en la vida útil del condensador" (PDF) . Boletín de ingeniería 96-004 . Sorrento Electronics. Noviembre de 2003. Archivado desde el original (PDF) el 2014-07-14 . Consultado el 2013-03-17 .
- ^ Kaiser, Cletus J. (6 de diciembre de 2012). Manual del condensador. Springer Science & Business Media. ISBN 978-9-40118090-0.
- ^ Electrónica . McGraw-Hill 1960, pág. 90.
- ^ Consejos de seguridad para el uso de flashes y luces estroboscópicas de xenón. donklipstein.com. 2006-05-29
- ^ Prutchi, David (2012). Exploración de la física cuántica a través de proyectos prácticos. John Wiley & Sons . p. 10. ISBN 978-1-11817070-0.
- ^ Dixit, JB; Yadav, Amit (2010). Calidad de la energía eléctrica. Laxmi Publications, Ltd. pág. 63. ISBN 978-9-38038674-4.
- ^ abcd Winburn (1989). Seguridad práctica del láser, segunda edición. CRC Press . p. 189. ISBN 978-0-82478240-5.
- ^ Manual de radiotelegrafía y telefonía de Robinson por SS Robinson – Instituto Naval de los EE. UU. 1924 Pág. 170
- ^ Gupta, Anunay; Yadav, Om Prakash; DeVoto, Douglas; Major, Joshua (octubre de 2018). "Una revisión del comportamiento de degradación y modelado de capacitores" (PDF) . Laboratorio Nacional de Energías Renovables. Archivado (PDF) del original el 2020-06-05 . Consultado el 2021-07-23 .
- ^ Guinta, Steve. "Pregúntele al ingeniero de aplicaciones – 21". Analog Devices . Consultado el 17 de marzo de 2013 .
- ^ de Araujo, Carlos Paz; Ramesh, Ramamoorthy; Taylor, George W., eds. (2001). Ciencia y tecnología de los ferroeléctricos integrados: artículos seleccionados de once años de las actas del Simposio internacional sobre ferroeléctricos integrados. CRC Press . Figura 2, pág. 504. ISBN 90-5699-704-1.
- ^ Musikant, Solomon (1991). Lo que todo ingeniero debería saber sobre cerámica. CRC Press . Figura 3.9, pág. 43. ISBN 0-8247-8498-7.
- ^ Yasuo Cho (2005). Microscopio dieléctrico no lineal de barrido (en Polar Oxides ; R. Waser , U. Böttger y S. Tiedke, editores ed.). Wiley-VCH. Capítulo 16. ISBN 3-527-40532-1.
- ^ ab Sze y Ng 2006, pág. 217.
- ^ Giuliani, Gabriele; Vignale, Giovanni (2005). Teoría cuántica del líquido electrónico. Prensa de la Universidad de Cambridge . pag. 111.ISBN 0-521-82112-6.
- ^ Rammer, Jørgen (2007). Teoría cuántica de campos de estados de no equilibrio. Cambridge University Press . p. 158. ISBN 978-0-52187499-1.
- ^ Czichos, Horst; Saito, Tetsuya; Smith, Leslie (2006). Manual de Springer sobre métodos de medición de materiales. Springer. pág. 475. ISBN 3-540-20785-6.
- ^ Coffey, William; Kalmykov, Yu. P. (2006). Fractales, difusión y relajación en sistemas complejos desordenados. Parte A. Wiley. p. 17. ISBN 0-470-04607-4.
- ^ Conferencia sobre tecnología de medición e instrumentación del IEEE de 2005 (IMTC): Ottawa, Ontario, Canadá, 16-19 de mayo de 2005. IEEE. 2005. págs. 1350-1353. doi :10.1109/IMTC.2005.1604368. ISBN 978-0-78038879-6. Número de identificación del sujeto 37739028.
- ^ Schröder 2006, pág. 347.
- ^ Schröder 2006, pág. 305.
- ^ Kasap, Safa O.; Capper, Peter (2006). Manual Springer de materiales electrónicos y fotónicos. Springer. Figura 20.22, pág. 425.
- ^ PY Yu; Cardona, Manuel (2001). Fundamentos de semiconductores (3.ª ed.). Springer. §6.6 "Espectroscopia de modulación". ISBN 3-540-25470-6.
- ^ Kaplan, Daniel M.; White, Christopher G. (2003). Electrónica práctica: una introducción práctica a los circuitos analógicos y digitales. Cambridge University Press . pág. 19. ISBN 978-0-52189351-0.
- ^ ab "Anexo B: Sistema especial de codificación de dos caracteres para condensadores". NORMA ESLOVENSA SIST EN 60062:2016/A1:2019 (PDF) (vista previa). 2019-12-01. págs. 3–4. Archivado (PDF) desde el original el 2022-06-17 . Consultado el 2022-06-17 .
- ^ abc Zabkar, Franc (15 de septiembre de 2011). «Códigos de capacitancia EIA-198-D». Archivado desde el original el 17 de junio de 2022. Consultado el 18 de junio de 2022 .
- ^ ab "Fundamentos de electrónica, volumen 1b: electricidad básica, corriente alterna, NAVPERS 93400A-1b". 12 de abril de 1965 – vía Internet Archive.
- ^ "Catálogo de 1930: condensadores". Allied Radio . pág. 139. Archivado desde el original el 11 de julio de 2017 . Consultado el 11 de julio de 2017 .
- ^ "Tabla de conversión de MF - MMFD de condensadores". www.justradios.com .
- ^ Miller, Charles (2011). Guía ilustrada del Código Eléctrico Nacional. Cengage Learning. pág. 445.
- ^ Shinn, Eric; et al. (2012). "Conversión de energía nuclear con pilas de nanocondensadores de grafeno". Complejidad . 18 (3): 24–27. Código Bibliográfico :2013Cmplx..18c..24S. doi :10.1002/cplx.21427.
- ^ Bezryadin, A.; Belkin, A.; et al. (2017). "Gran eficiencia de almacenamiento de energía de la capa dieléctrica de nanocondensadores de grafeno". Nanotecnología . 28 (49): 495401. arXiv : 2011.11867 . Código Bibliográfico :2017Nanot..28W5401B. doi :10.1088/1361-6528/aa935c. PMID 29027908. S2CID 44693636.
- ^ Floyd, Thomas L. (2017). Dispositivos electrónicos. Pearson. pág. 10. ISBN 978-0-13441444-7.
- ^ Energía pulsada por Gennady A. Mesyats -- Springer 2005 Página 1--5
- ^ Alam, Mohammed; Azarian, Michael H.; Osterman, Michael; Pecht, Michael (2010). "Eficacia de los condensadores integrados en la reducción del número de condensadores de montaje superficial para aplicaciones de desacoplamiento". Circuit World . 36 (1): 22. doi :10.1108/03056121011015068.
- ^ Downie, Neil A y Mathilde Pradier, 'Método y aparato para controlar la presión de fluidos', Patente de EE. UU. 7526961 (2009)
- ^ "Algunos consejos de seguridad sobre flash y luces estroboscópicas de xenón". donklipstein.com .
Bibliografía
- Dorf, Richard C.; Svoboda, James A. (2001). Introducción a los circuitos eléctricos (5.ª ed.). Nueva York: John Wiley & Sons. ISBN 978-0-47138689-6.
- Philosophical Transactions of the Royal Society LXXII, Apéndice 8, 1782 (Volta acuña la palabra condensador )
- Ulaby, Fawwaz Tayssir (1999). Fundamentos de electromagnetismo aplicado (2.ª ed.). Upper Saddle River, Nueva Jersey, EE. UU.: Prentice Hall . ISBN 978-0-13011554-6.
- Schroder, Dieter K. (2006). Caracterización de dispositivos y materiales semiconductores (3.ª ed.). Wiley. pág. 270 y siguientes . ISBN 978-0-47173906-7.
- Sze, Simon M.; Ng, Kwok K. (2006). Física de dispositivos semiconductores (3.ª ed.). Wiley. ISBN 978-0-47006830-4.
Lectura adicional
- Capacitores basados en tantalio y niobio: ciencia, tecnología y aplicaciones ; 1.ª edición; Yuri Freeman; Springer; 120 páginas; 2018; ISBN 978-3-31967869-6 .
- Condensadores ; 1.ª edición; RP Deshpande; McGraw-Hill; 342 páginas; 2014; ISBN 978-0-07184856-5 .
- El manual del condensador ; 1.ª edición; Cletus Kaiser; Van Nostrand Reinhold; 124 páginas; 1993; ISBN 978-9-40118092-4 .
- Comprensión de los capacitores y sus usos ; 1.ª edición; William Mullin; Sams Publishing; 96 páginas; 1964. (archivo)
- Capacitores fijos y variables ; 1.ª edición; GWA Dummer y Harold Nordenberg; Maple Press; 288 páginas; 1960. (archivo)
- El condensador electrolítico ; 1.ª edición; Alexander Georgiev; Murray Hill Books; 191 páginas; 1945. (archivo)
Enlaces externos
- El primer condensador: un vaso de cerveza – SparkMuseum
- Cómo funcionan los condensadores – Howstuffworks
- Tutorial sobre condensadores











































































![{\displaystyle dW=Q\,dV=\left[\int _{0}^{V}dV'\,C(V')\right]dV\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6cbac71e27b7dd2c7c9156f89df76670526292c)



![{\displaystyle {\begin{aligned}I(\omega )&=j\omega Q(\omega )=j\omega \oint _{\Sigma }{\boldsymbol {D}}({\boldsymbol {r}},\omega )\cdot d{\boldsymbol {\Sigma }}\\&=\left[G(\omega )+j\omega C(\omega )\right]V(\omega )={\frac {V(\omega )}{Z(\omega )}}\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/654a10c670f2fa6bc1763d52f2159161362b5fcb)








