Característica de funcionamiento del receptor
Este artículo necesita citas adicionales para su verificación . ( septiembre de 2023 ) |
Una curva característica operativa del receptor , o curva ROC , es un gráfico que ilustra el rendimiento de un modelo de clasificador binario (también puede usarse para clasificación de múltiples clases) en valores de umbral variables.
La curva ROC es el gráfico de la tasa de positivos verdaderos (TPR) frente a la tasa de positivos falsos (FPR) en cada ajuste de umbral.
La curva ROC también puede considerarse como un gráfico de la potencia estadística en función del error de tipo I de la regla de decisión (cuando el rendimiento se calcula a partir de una muestra de la población, puede considerarse como un estimador de estas cantidades). La curva ROC es, por tanto, la sensibilidad en función de la tasa de falsos positivos .
Dado que se conocen las distribuciones de probabilidad tanto para los verdaderos positivos como para los falsos positivos, la curva ROC se obtiene como la función de distribución acumulativa (CDF, área bajo la distribución de probabilidad desde hasta el umbral de discriminación) de la probabilidad de detección en el eje y frente a la CDF de la probabilidad de falsos positivos en el eje x .
El análisis ROC proporciona herramientas para seleccionar modelos posiblemente óptimos y descartar los subóptimos independientemente (y antes de especificar) del contexto de costos o la distribución de clases. El análisis ROC está relacionado de manera directa y natural con el análisis de costo/beneficio de la toma de decisiones diagnósticas .
Terminología
La tasa de verdaderos positivos también se conoce como sensibilidad o probabilidad de detección . [1] La tasa de falsos positivos también se conoce como probabilidad de falsa alarma [1] y es igual a (1 − especificidad ). La ROC también se conoce como curva característica operativa relativa, porque es una comparación de dos características operativas (TPR y FPR) a medida que cambia el criterio. [2]
Historia
La curva ROC fue desarrollada por primera vez por ingenieros eléctricos e ingenieros de radar durante la Segunda Guerra Mundial para detectar objetos enemigos en los campos de batalla, a partir de 1941, lo que dio lugar a su nombre ("característica operativa del receptor"). [3]
Pronto se introdujo en la psicología para explicar la detección perceptiva de estímulos. El análisis ROC se ha utilizado en medicina , radiología , biometría , pronóstico de peligros naturales , [4] meteorología , [5] evaluación del rendimiento de modelos, [6] y otras áreas durante muchas décadas y se utiliza cada vez más en la investigación de minería de datos y aprendizaje automático .
Concepto básico
Un modelo de clasificación ( clasificador o diagnóstico [7] ) es un mapeo de instancias entre ciertas clases/grupos. Debido a que el resultado del clasificador o diagnóstico puede ser un valor real arbitrario (salida continua), el límite del clasificador entre clases debe determinarse mediante un valor umbral (por ejemplo, para determinar si una persona tiene hipertensión según una medición de la presión arterial ). O puede ser una etiqueta de clase discreta , que indica una de las clases.
Considere un problema de predicción de dos clases ( clasificación binaria ), en el que los resultados se etiquetan como positivos ( p ) o negativos ( n ). Hay cuatro resultados posibles de un clasificador binario. Si el resultado de una predicción es p y el valor real también es p , entonces se llama verdadero positivo (VP); sin embargo, si el valor real es n, entonces se dice que es un falso positivo (FP). Por el contrario, se ha producido un verdadero negativo (TN) cuando tanto el resultado de la predicción como el valor real son n , y un falso negativo (FN) es cuando el resultado de la predicción es n mientras que el valor real es p .
Para obtener un ejemplo adecuado en un problema del mundo real, considere una prueba diagnóstica que busca determinar si una persona tiene una determinada enfermedad. En este caso, un falso positivo ocurre cuando la persona da positivo en la prueba, pero en realidad no tiene la enfermedad. Por otro lado, un falso negativo ocurre cuando la persona da negativo en la prueba, lo que sugiere que está sana, cuando en realidad tiene la enfermedad.
Consideremos un experimento con P casos positivos y N casos negativos para alguna condición. Los cuatro resultados se pueden formular en una tabla de contingencia o matriz de confusión de 2×2 , de la siguiente manera:
| Condición prevista | Fuentes: [8] [9] [10] [11] [12] [13] [14] [15] | ||||
| Población total = P + N | Positivo previsto (PP) | Predicción negativa (PN) | Información , información de la casa de apuestas (BM) = TPR + TNR − 1 | Umbral de prevalencia (PT) = √ TPR × FPR - FPR/TPR-FPR | |
Estado actual | Positivo (P) [a] | Verdadero positivo (VP), acierto [b] | Falso negativo (FN), error, subestimación | Tasa de verdaderos positivos (TPR), recuperación , sensibilidad (SEN), probabilidad de detección, tasa de aciertos, potencia =TP/PAG = 1 − FNR | Tasa de falsos negativos (FNR), tasa de error tipo II [c] = Enero 2016/PAG = 1 − TPR |
| Negativo (N) [d] | Falso positivo (FP), falsa alarma, sobreestimación | Verdadero negativo (VN), rechazo correcto [e] | Tasa de falsos positivos (FPR), probabilidad de falsa alarma, error tipo I de repercusión [f] = FP/norte = 1 − TNR | Tasa de verdaderos negativos (TNR), especificidad (SPC), selectividad =Tennesse/norte = 1 − FPR | |
| Prevalencia = PAG/P + N | Valor predictivo positivo (VPP), precisión = TP/PÁGINAS = 1 − FDR | Tasa de falsas omisiones (FOR) = Enero 2016/PN = 1 − VPN | Razón de verosimilitud positiva (LR+) = Reanimación térmica/FPR | Razón de verosimilitud negativa (LR−) = FNR/TNR | |
| Precisión (ACC) = TP + TN/P + N | Tasa de falsos descubrimientos (FDR) = FP/PÁGINAS = 1 − VPP | Valor predictivo negativo (VPN) = Tennesse/PN = 1 − PARA | Marcación (MK), deltaP (Δp) = PPV + VAN − 1 | Razón de posibilidades diagnóstica (DOR) = LR+/LR− | |
| Precisión equilibrada (BA) = TPR + TNR/2 | Puntuación F 1 = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN | Índice de Fowlkes-Mallows (FM) = √ PPV × TPR | Coeficiente de correlación de Matthews (MCC) = √ TPR × TNR × PPV × NPV - √ FNR × FPR × FOR × FDR | Puntuación de amenaza (TS), índice de éxito crítico (CSI), índice de Jaccard = TP/TP + FN + FP | |
- ^ el número de casos positivos reales en los datos
- ^ Un resultado de prueba que indica correctamente la presencia de una condición o característica
- ^ Error tipo II: Un resultado de prueba que indica erróneamente que una condición o atributo particular está ausente
- ^ el número de casos negativos reales en los datos
- ^ Un resultado de prueba que indica correctamente la ausencia de una condición o característica
- ^ Error tipo I: Un resultado de prueba que indica erróneamente que está presente una condición o atributo particular
Espacio ROC


La tabla de contingencia puede derivar varias "métricas" de evaluación (ver cuadro de información). Para dibujar una curva ROC, solo se necesitan la tasa de verdaderos positivos (TPR) y la tasa de falsos positivos (FPR) (como funciones de algún parámetro clasificador). La TPR define cuántos resultados positivos correctos ocurren entre todas las muestras positivas disponibles durante la prueba. La FPR, por otro lado, define cuántos resultados positivos incorrectos ocurren entre todas las muestras negativas disponibles durante la prueba.
Un espacio ROC se define por FPR y TPR como ejes x e y , respectivamente, que representan las compensaciones relativas entre verdaderos positivos (beneficios) y falsos positivos (costos). Dado que TPR es equivalente a sensibilidad y FPR es igual a 1 − especificidad , el gráfico ROC a veces se denomina gráfico de sensibilidad vs. (1 − especificidad). Cada resultado de predicción o instancia de una matriz de confusión representa un punto en el espacio ROC.
El mejor método de predicción posible produciría un punto en la esquina superior izquierda o coordenada (0,1) del espacio ROC, lo que representa una sensibilidad del 100% (sin falsos negativos) y una especificidad del 100% (sin falsos positivos). El punto (0,1) también se denomina clasificación perfecta . Una suposición aleatoria daría un punto a lo largo de una línea diagonal (la llamada línea de no discriminación ) desde la esquina inferior izquierda hasta la esquina superior derecha (independientemente de las tasas base positivas y negativas ). [16] Un ejemplo intuitivo de suposición aleatoria es una decisión al lanzar monedas. A medida que aumenta el tamaño de la muestra, el punto ROC de un clasificador aleatorio tiende hacia la línea diagonal. En el caso de una moneda equilibrada, tenderá al punto (0,5, 0,5).
La diagonal divide el espacio ROC. Los puntos por encima de la diagonal representan buenos resultados de clasificación (mejores que los aleatorios); los puntos por debajo de la línea representan malos resultados (peores que los aleatorios). Tenga en cuenta que el resultado de un predictor consistentemente malo podría simplemente invertirse para obtener un buen predictor.
Considere cuatro resultados de predicción de 100 instancias positivas y 100 negativas:
| A | B | do | DO' | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
| ||||||||||||||||||||||||||||||||||||
| TPR = 0,63 | TPR = 0,77 | TPR = 0,24 | TPR = 0,76 | ||||||||||||||||||||||||||||||||||||
| FPR = 0,28 | Tasa de refracción efectiva (FPR) = 0,77 | FPR = 0,88 | FPR = 0,12 | ||||||||||||||||||||||||||||||||||||
| VPP = 0,69 | VPP = 0,50 | VPP = 0,21 | VPP = 0,86 | ||||||||||||||||||||||||||||||||||||
| F1 = 0,66 | F1 = 0,61 | F1 = 0,23 | F1 = 0,81 | ||||||||||||||||||||||||||||||||||||
| CAC = 0,68 | CAC = 0,50 | CAC = 0,18 | CAC = 0,82 |
En la figura se muestran los gráficos de los cuatro resultados anteriores en el espacio ROC. El resultado del método A muestra claramente el mejor poder predictivo entre A , B y C. El resultado de B se encuentra en la línea de conjetura aleatoria (la línea diagonal) y se puede ver en la tabla que la precisión de B es del 50 %. Sin embargo, cuando C se refleja en el punto central (0,5, 0,5), el método resultante C′ es incluso mejor que A. Este método reflejado simplemente invierte las predicciones de cualquier método o prueba que haya producido la tabla de contingencia C. Aunque el método C original tiene un poder predictivo negativo, simplemente invertir sus decisiones conduce a un nuevo método predictivo C′ que tiene un poder predictivo positivo. Cuando el método C predice p o n , el método C′ predeciría n o p , respectivamente. De esta manera, la prueba C′ tendría el mejor rendimiento. Cuanto más cerca esté el resultado de una tabla de contingencia de la esquina superior izquierda, mejor será la predicción, pero la distancia desde la línea de conjetura aleatoria en cualquier dirección es el mejor indicador de cuánto poder predictivo tiene un método. Si el resultado está por debajo de la línea (es decir, el método es peor que una conjetura aleatoria), todas las predicciones del método deben invertirse para utilizar su poder, moviendo así el resultado por encima de la línea de conjetura aleatoria.
Curvas en el espacio ROC
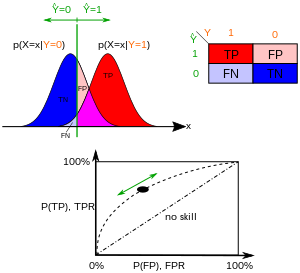
En la clasificación binaria, la predicción de clase para cada instancia se hace a menudo en base a una variable aleatoria continua , que es una "puntuación" calculada para la instancia (por ejemplo, la probabilidad estimada en regresión logística). Dado un parámetro de umbral , la instancia se clasifica como "positiva" si , y "negativa" en caso contrario. sigue una densidad de probabilidad si la instancia pertenece realmente a la clase "positiva", y si no. Por lo tanto, la tasa de verdaderos positivos viene dada por y la tasa de falsos positivos viene dada por . La curva ROC se traza paramétricamente frente a con como parámetro variable.
Por ejemplo, imaginemos que los niveles de proteínas en sangre de personas enfermas y sanas se distribuyen normalmente con medias de 2 g / dL y 1 g/dL respectivamente. Una prueba médica podría medir el nivel de una determinada proteína en una muestra de sangre y clasificar cualquier número por encima de un determinado umbral como indicador de enfermedad. El experimentador puede ajustar el umbral (línea vertical verde en la figura), lo que a su vez cambiará la tasa de falsos positivos. Aumentar el umbral daría como resultado menos falsos positivos (y más falsos negativos), lo que corresponde a un movimiento hacia la izquierda en la curva. La forma real de la curva está determinada por el grado de superposición que tengan las dos distribuciones.
Críticas

Varios estudios critican ciertas aplicaciones de la curva ROC y su área bajo la curva como medidas para evaluar clasificaciones binarias cuando no capturan la información relevante para la aplicación. [18] [17] [19] [20] [21]
La principal crítica a la curva ROC descrita en estos estudios se refiere a la incorporación de áreas con baja sensibilidad y baja especificidad (ambas inferiores a 0,5) para el cálculo del área total bajo la curva (AUC), [19] como se describe en el gráfico de la derecha.
Según los autores de estos estudios, esa porción del área bajo la curva (con baja sensibilidad y baja especificidad) se refiere a matrices de confusión donde las predicciones binarias obtienen malos resultados y, por lo tanto, no se debe incluir para la evaluación del desempeño general. Además, esa porción del AUC indica un espacio con un umbral de matriz de confusión alto o bajo, lo que rara vez es de interés para los científicos que realizan una clasificación binaria en cualquier campo. [19]
Otra crítica al ROC y su área bajo la curva es que no dicen nada sobre la precisión y el valor predictivo negativo. [17]
Un AUC ROC alto, como por ejemplo 0,9, podría corresponder a valores bajos de precisión y valor predictivo negativo, como 0,2 y 0,1 en el rango [0, 1]. Si una persona realizó una clasificación binaria, obtuvo un AUC ROC de 0,9 y decidió centrarse solo en esta métrica, podría creer de manera demasiado optimista que su prueba binaria fue excelente. Sin embargo, si esta persona observara los valores de precisión y valor predictivo negativo, podría descubrir que sus valores son bajos.
El AUC ROC resume la sensibilidad y especificidad, pero no informa sobre la precisión y el valor predictivo negativo. [17]
Otras interpretaciones
En ocasiones, el ROC se utiliza para generar una estadística resumida. Las versiones más comunes son:
- la intersección de la curva ROC con la línea a 45 grados ortogonal a la línea de no discriminación: el punto de equilibrio donde Sensibilidad = Especificidad
- la intersección de la curva ROC con la tangente a 45 grados paralela a la línea de no discriminación que está más cerca del punto libre de error (0,1) – también llamada estadística J de Youden y generalizada como Informedness [ cita requerida ]
- El área entre la curva ROC y la línea de no discriminación multiplicada por dos se llama coeficiente de Gini , especialmente en el contexto de la calificación crediticia . [22] No debe confundirse con la medida de dispersión estadística también llamada coeficiente de Gini .
- el área entre la curva ROC completa y la curva ROC triangular que incluye solo (0,0), (1,1) y un punto operativo seleccionado – Consistencia [23]
- el área bajo la curva ROC, o "AUC" ("área bajo la curva"), o A' (pronunciado "a-prime"), [24] o "c-statistic" ("estadística de concordancia"). [25]
- el índice de sensibilidad d′ (pronunciado "d-prime"), la distancia entre la media de la distribución de la actividad en el sistema en condiciones de solo ruido y su distribución en condiciones de solo señal, dividida por su desviación estándar , bajo el supuesto de que ambas distribuciones son normales con la misma desviación estándar. Bajo estos supuestos, la forma de la ROC está completamente determinada por d′ .
Sin embargo, cualquier intento de resumir la curva ROC en un solo número pierde información sobre el patrón de compensaciones del algoritmo discriminador particular.
Interpretación probabilística
El área bajo la curva (a menudo denominada simplemente AUC) es igual a la probabilidad de que un clasificador clasifique una instancia positiva elegida al azar por encima de una negativa elegida al azar (asumiendo que "positivo" se clasifica por encima de "negativo"). [26] En otras palabras, cuando se da una instancia positiva seleccionada al azar y una instancia negativa seleccionada al azar, el AUC es la probabilidad de que el clasificador pueda decir cuál es cuál.
Esto se puede ver de la siguiente manera: el área bajo la curva está dada por (los límites integrales se invierten ya que el umbral grande tiene un valor menor en el eje x )
donde es la puntuación para una instancia positiva y es la puntuación para una instancia negativa, y y son densidades de probabilidad como se definieron en la sección anterior.
Si y sigue dos distribuciones gaussianas, entonces .
Área bajo la curva
Se puede demostrar que el AUC está estrechamente relacionado con la U de Mann-Whitney [ 27] [28] , que prueba si los positivos tienen una clasificación más alta que los negativos. Para un predictor , un estimador imparcial de su AUC se puede expresar mediante la siguiente estadística de Wilcoxon-Mann-Whitney : [29]
donde denota una función indicadora que devuelve 1 si en caso contrario devuelve 0; es el conjunto de ejemplos negativos, y es el conjunto de ejemplos positivos.
En el contexto de la calificación crediticia , a menudo se utiliza una versión reescalada del AUC:
.
se denomina índice de Gini o coeficiente de Gini, [30] pero no debe confundirse con la medida de dispersión estadística que también se denomina coeficiente de Gini . es un caso especial de la D de Somers .
También es común calcular el área bajo la envoltura convexa ROC (ROC AUCH = ROCH AUC) ya que cualquier punto en el segmento de línea entre dos resultados de predicción se puede lograr usando aleatoriamente uno u otro sistema con probabilidades proporcionales a la longitud relativa del componente opuesto del segmento. [31] También es posible invertir concavidades – tal como en la figura la peor solución puede reflejarse para convertirse en una mejor solución; las concavidades se pueden reflejar en cualquier segmento de línea, pero es mucho más probable que esta forma más extrema de fusión sobreajuste los datos. [32]
La comunidad de aprendizaje automático utiliza con mayor frecuencia la estadística ROC AUC para la comparación de modelos. [33] Esta práctica ha sido cuestionada porque las estimaciones de AUC son bastante ruidosas y sufren otros problemas. [34] [35] [36] No obstante, la coherencia del AUC como medida del rendimiento de la clasificación agregada ha sido reivindicada, en términos de una distribución de tasa uniforme, [37] y el AUC se ha vinculado a una serie de otras métricas de rendimiento como la puntuación Brier . [38]
Otro problema con el AUC ROC es que reducir la curva ROC a un solo número ignora el hecho de que se trata de las compensaciones entre los diferentes sistemas o puntos de rendimiento graficados y no del rendimiento de un sistema individual, así como ignora la posibilidad de reparación de la concavidad, por lo que se recomiendan medidas alternativas relacionadas como Informedness [ cita requerida ] o DeltaP. [23] [39] Estas medidas son esencialmente equivalentes al Gini para un solo punto de predicción con DeltaP' = Informedness = 2AUC-1, mientras que DeltaP = Markedness representa el dual (es decir, predecir la predicción a partir de la clase real) y su media geométrica es el coeficiente de correlación de Matthews . [ cita requerida ]
Mientras que el AUC de ROC varía entre 0 y 1 (con un clasificador no informativo que produce 0,5), las medidas alternativas conocidas como Informalidad , [ cita requerida ] Certidumbre [23] y Coeficiente de Gini (en el caso de parametrización única o sistema único) [ cita requerida ] tienen todas la ventaja de que 0 representa el desempeño aleatorio, mientras que 1 representa el desempeño perfecto y −1 representa el caso "perverso" de plena información que siempre da la respuesta incorrecta. [40] Llevar el desempeño aleatorio a 0 permite que estas escalas alternativas se interpreten como estadísticas Kappa. Se ha demostrado que la Informalidad tiene características deseables para el aprendizaje automático frente a otras definiciones comunes de Kappa, como Cohen Kappa y Fleiss Kappa . [ cita requerida ] [41]
A veces puede ser más útil observar una región específica de la curva ROC en lugar de la curva completa. Es posible calcular el AUC parcial . [42] Por ejemplo, uno podría centrarse en la región de la curva con una baja tasa de falsos positivos, que a menudo es de gran interés para las pruebas de detección de la población. [43] Otro enfoque común para los problemas de clasificación en los que P ≪ N (común en aplicaciones de bioinformática) es utilizar una escala logarítmica para el eje x . [44]
El área ROC bajo la curva también se denomina estadística c o estadística c . [45]
Otras medidas

La característica operativa total (TOC) también caracteriza la capacidad de diagnóstico al tiempo que revela más información que la ROC. Para cada umbral, la ROC revela dos proporciones, TP/(TP + FN) y FP/(FP + TN). En otras palabras, la ROC revela y . Por otro lado, la TOC muestra la información total en la tabla de contingencia para cada umbral. [46] El método TOC revela toda la información que proporciona el método ROC, más información importante adicional que la ROC no revela, es decir, el tamaño de cada entrada en la tabla de contingencia para cada umbral. La TOC también proporciona la popular AUC de la ROC. [47]

Estas cifras son las curvas TOC y ROC que utilizan los mismos datos y umbrales. Considere el punto que corresponde a un umbral de 74. La curva TOC muestra el número de aciertos, que es 3, y, por lo tanto, el número de errores, que es 7. Además, la curva TOC muestra que el número de falsas alarmas es 4 y el número de rechazos correctos es 16. En cualquier punto dado en la curva ROC, es posible obtener valores para las razones de y . Por ejemplo, en el umbral 74, es evidente que la coordenada x es 0,2 y la coordenada y es 0,3. Sin embargo, estos dos valores son insuficientes para construir todas las entradas de la tabla de contingencia subyacente de dos por dos.
Gráfico de compensación de errores de detección
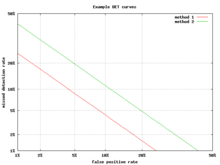
Una alternativa a la curva ROC es el gráfico de compensación de error de detección (DET), que traza la tasa de falsos negativos (detecciones fallidas) frente a la tasa de falsos positivos (falsas alarmas) en los ejes x e y transformados de forma no lineal. La función de transformación es la función cuantil de la distribución normal, es decir, la inversa de la distribución normal acumulativa. Es, de hecho, la misma transformación que zROC, a continuación, excepto que se utiliza el complemento de la tasa de aciertos, la tasa de errores o la tasa de falsos negativos. Esta alternativa dedica más área gráfica a la región de interés. La mayor parte del área ROC es de poco interés; uno se preocupa principalmente por la región ajustada al eje y y la esquina superior izquierda, que, debido a que se utiliza la tasa de errores en lugar de su complemento, la tasa de aciertos, es la esquina inferior izquierda en un gráfico DET. Además, los gráficos DET tienen la propiedad útil de linealidad y un comportamiento de umbral lineal para distribuciones normales. [48] El gráfico DET se utiliza ampliamente en la comunidad de reconocimiento automático de hablantes , donde se utilizó por primera vez el nombre DET. El análisis del rendimiento ROC en gráficos con esta deformación de los ejes fue utilizado por psicólogos en estudios de percepción a mediados del siglo XX, [ cita requerida ] donde esto fue denominado "trabajo de doble probabilidad". [49]
Puntuación Z
Si se aplica una puntuación estándar a la curva ROC, la curva se transformará en una línea recta. [50] Esta puntuación z se basa en una distribución normal con una media de cero y una desviación estándar de uno. En la teoría de la fuerza de la memoria , se debe asumir que la zROC no solo es lineal, sino que tiene una pendiente de 1,0. Las distribuciones normales de objetivos (objetos estudiados que los sujetos necesitan recordar) y señuelos (objetos no estudiados que los sujetos intentan recordar) son el factor que hace que la zROC sea lineal.
La linealidad de la curva zROC depende de las desviaciones estándar de las distribuciones de fuerza del objetivo y del señuelo. Si las desviaciones estándar son iguales, la pendiente será 1,0. Si la desviación estándar de la distribución de fuerza del objetivo es mayor que la desviación estándar de la distribución de fuerza del señuelo, entonces la pendiente será menor que 1,0. En la mayoría de los estudios, se ha encontrado que las pendientes de la curva zROC caen constantemente por debajo de 1, generalmente entre 0,5 y 0,9. [51] Muchos experimentos arrojaron una pendiente zROC de 0,8. Una pendiente de 0,8 implica que la variabilidad de la distribución de fuerza del objetivo es un 25 % mayor que la variabilidad de la distribución de fuerza del señuelo. [52]
Otra variable utilizada es d' (d prima) (discutida anteriormente en "Otras medidas"), que puede expresarse fácilmente en términos de valores z. Aunque d ' es un parámetro de uso común, debe reconocerse que solo es relevante cuando se adhiere estrictamente a los supuestos muy sólidos de la teoría de la fuerza que se hicieron anteriormente. [53]
La puntuación z de una curva ROC es siempre lineal, como se supone, excepto en situaciones especiales. El modelo de familiaridad-recuerdo de Yonelinas es una explicación bidimensional de la memoria de reconocimiento. En lugar de que el sujeto simplemente responda sí o no a una entrada específica, el sujeto le da a la entrada una sensación de familiaridad, que funciona como la curva ROC original. Lo que cambia, sin embargo, es un parámetro para el Recuerdo (R). Se supone que el recuerdo es todo o nada, y triunfa sobre la familiaridad. Si no hubiera un componente de recuerdo, zROC tendría una pendiente prevista de 1. Sin embargo, al agregar el componente de recuerdo, la curva zROC será cóncava hacia arriba, con una pendiente reducida. Esta diferencia en forma y pendiente resulta de un elemento adicional de variabilidad debido a que se recuerdan algunos elementos. Los pacientes con amnesia anterógrada son incapaces de recordar, por lo que su curva zROC de Yonelinas tendría una pendiente cercana a 1,0. [54]
Historia
La curva ROC se utilizó por primera vez durante la Segunda Guerra Mundial para el análisis de señales de radar antes de emplearse en la teoría de detección de señales . [55] Después del ataque a Pearl Harbor en 1941, el ejército de los Estados Unidos comenzó una nueva investigación para aumentar la predicción de aviones japoneses detectados correctamente a partir de sus señales de radar. Para estos fines, midieron la capacidad de un operador de receptor de radar para hacer estas importantes distinciones, lo que se denominó la característica operativa del receptor. [56]
En la década de 1950, las curvas ROC se emplearon en psicofísica para evaluar la detección humana (y ocasionalmente de animales no humanos) de señales débiles. [55] En medicina , el análisis ROC se ha utilizado ampliamente en la evaluación de pruebas de diagnóstico . [57] [58] Las curvas ROC también se utilizan ampliamente en epidemiología e investigación médica y se mencionan con frecuencia junto con la medicina basada en la evidencia . En radiología , el análisis ROC es una técnica común para evaluar nuevas técnicas de radiología. [59] En las ciencias sociales, el análisis ROC a menudo se denomina índice de precisión ROC, una técnica común para juzgar la precisión de los modelos de probabilidad predeterminados. Las curvas ROC se utilizan ampliamente en medicina de laboratorio para evaluar la precisión diagnóstica de una prueba, para elegir el punto de corte óptimo de una prueba y para comparar la precisión diagnóstica de varias pruebas.
Las curvas ROC también resultaron útiles para la evaluación de técnicas de aprendizaje automático . La primera aplicación de las curvas ROC en el aprendizaje automático fue realizada por Spackman, quien demostró el valor de las curvas ROC para comparar y evaluar diferentes algoritmos de clasificación . [60]
Las curvas ROC también se utilizan en la verificación de pronósticos en meteorología. [61]
Radar en detalle
Como se mencionó, las curvas ROC son fundamentales para el funcionamiento y la teoría del radar . Las señales recibidas en una estación receptora, tal como se reflejan en un objetivo, suelen tener una energía muy baja en comparación con el nivel de ruido . La relación señal/ruido es una métrica importante para determinar si se detectará un objetivo. Esta relación señal/ruido está directamente relacionada con las características operativas del receptor de todo el sistema de radar, que se utilizan para cuantificar la capacidad de un sistema de radar.
Consideremos el desarrollo de un sistema de radar. Se puede proporcionar una especificación de las capacidades del sistema en términos de probabilidad de detección, , con una cierta tolerancia para las falsas alarmas, . Se puede calcular una aproximación simplificada de la relación señal/ruido requerida en la estación receptora resolviendo [62]
para la relación señal/ruido . Aquí, no se expresa en decibeles , como es habitual en muchas aplicaciones de radar. La conversión a decibeles se realiza mediante . A partir de esta figura, se pueden resolver las entradas comunes en la ecuación de alcance del radar (con factores de ruido) para estimar la potencia radiada efectiva requerida .
Curvas ROC más allá de la clasificación binaria
La extensión de las curvas ROC para problemas de clasificación con más de dos clases es engorrosa. Dos enfoques comunes para cuando hay múltiples clases son (1) promediar todos los valores de AUC por pares [63] y (2) calcular el volumen bajo la superficie (VUS). [64] [65] Para promediar todas las clases por pares, se calcula el AUC para cada par de clases, utilizando solo los ejemplos de esas dos clases como si no hubiera otras clases, y luego se promedian estos valores de AUC sobre todos los pares posibles. Cuando hay c clases, habrá c ( c − 1) / 2 pares de clases posibles.
El enfoque del volumen bajo la superficie implica trazar una hipersuperficie en lugar de una curva y luego medir el hipervolumen debajo de esa hipersuperficie. Cada posible regla de decisión que se podría usar para un clasificador para c clases se puede describir en términos de sus tasas positivas verdaderas (TPR 1 , . . . , TPR c ) . Es este conjunto de tasas lo que define un punto, y el conjunto de todas las posibles reglas de decisión produce una nube de puntos que define la hipersuperficie. Con esta definición, la VUS es la probabilidad de que el clasificador pueda etiquetar correctamente todos los c ejemplos cuando se le da un conjunto que tiene un ejemplo seleccionado aleatoriamente de cada clase. La implementación de un clasificador que sabe que su conjunto de entrada consta de un ejemplo de cada clase podría calcular primero una puntuación de bondad de ajuste para cada uno de los c 2 posibles emparejamientos de un ejemplo con una clase, y luego emplear el algoritmo húngaro para maximizar la suma de las c puntuaciones seleccionadas sobre todas las c ! formas posibles de asignar exactamente un ejemplo a cada clase.
Dado el éxito de las curvas ROC para la evaluación de modelos de clasificación, también se ha investigado la extensión de las curvas ROC para otras tareas supervisadas. Las propuestas notables para problemas de regresión son las llamadas curvas características de error de regresión (REC) [66] y las curvas de regresión ROC (RROC). [67] En estas últimas, las curvas RROC se vuelven extremadamente similares a las curvas ROC para clasificación, con las nociones de asimetría, dominancia y envoltura convexa. Además, el área bajo las curvas RROC es proporcional a la varianza del error del modelo de regresión.
Véase también
- Puntuación de Brier
- Coeficiente de determinación
- Tasa constante de falsas alarmas
- Compensación por error de detección
- Teoría de la detección
- Puntuación de F1
- Falsa alarma
- Pruebas de hipótesis para comprobar la exactitud
- Precisión y recuperación
- ROCCET
- Sensibilidad y especificidad
- Característica operativa total
Referencias
- ^ ab "Análisis del rendimiento del detector mediante curvas ROC: ejemplo de MATLAB y Simulink". www.mathworks.com . Consultado el 11 de agosto de 2016 .
- ^ Swets, John A.; Teoría de detección de señales y análisis ROC en psicología y diagnóstico: artículos recopilados, Lawrence Erlbaum Associates, Mahwah, NJ, 1996
- ^ Junge, MR; Dettori, JR (3 de mayo de 2024). "ROC Solid: curvas ROC como base para mejores pruebas diagnósticas". Revista Global Spine . 8 (4): 424–429. doi :10.1177/2192568218778294. PMC 6022965 . PMID 29977728.
- ^ Peres, DJ; Cancelliere, A. (8 de diciembre de 2014). "Derivación y evaluación de umbrales de activación de deslizamientos de tierra mediante un enfoque de Monte Carlo". Hydrol. Earth Syst. Sci . 18 (12): 4913–4931. Bibcode :2014HESS...18.4913P. doi : 10.5194/hess-18-4913-2014 . ISSN 1607-7938.
- ^ Murphy, Allan H. (1 de marzo de 1996). "El caso Finley: un acontecimiento clave en la historia de la verificación de pronósticos". Tiempo y pronóstico . 11 (1): 3–20. Bibcode :1996WtFor..11....3M. doi : 10.1175/1520-0434(1996)011<0003:tfaase>2.0.co;2 . ISSN 0882-8156.
- ^ Peres, DJ; Iuppa, C.; Cavallaro, L.; Cancelliere, A.; Foti, E. (1 de octubre de 2015). "Extensión significativa del registro de altura de ola mediante redes neuronales y reanálisis de datos de viento". Ocean Modelling . 94 : 128–140. Bibcode :2015OcMod..94..128P. doi :10.1016/j.ocemod.2015.08.002.
- ^ Sushkova, Olga; Morozov, Alexei; Gabova, Alexandra; Karabanov, Alexei; Illarioshkin, Sergey (2021). "Un método estadístico para el análisis exploratorio de datos basado en diagramas de área bajo curva 2D y 3D: investigación de la enfermedad de Parkinson". Sensores . 21 (14): 4700. Bibcode :2021Senso..21.4700S. doi : 10.3390/s21144700 . PMC 8309570 . PMID 34300440.
- ^ Fawcett, Tom (2006). "Introducción al análisis ROC" (PDF) . Pattern Recognition Letters . 27 (8): 861–874. doi :10.1016/j.patrec.2005.10.010. S2CID 2027090.
- ^ Provost, Foster; Tom Fawcett (1 de agosto de 2013). "Ciencia de datos para empresas: lo que necesita saber sobre minería de datos y pensamiento analítico de datos". O'Reilly Media, Inc.
- ^ Powers, David MW (2011). "Evaluación: desde precisión, recuperación y medida F hasta ROC, información, marcación y correlación". Revista de tecnologías de aprendizaje automático . 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Enciclopedia del aprendizaje automático . Springer. doi :10.1007/978-0-387-30164-8. ISBN. 978-0-387-30164-8.
- ^ Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (26 de enero de 2015). "Grupo de trabajo conjunto WWRP/WGNE sobre investigación de verificación de pronósticos". Colaboración para la investigación meteorológica y climática australiana . Organización Meteorológica Mundial . Consultado el 17 de julio de 2019 .
- ^ Chicco D, Jurman G (enero de 2020). "Las ventajas del coeficiente de correlación de Matthews (MCC) sobre la puntuación F1 y la precisión en la evaluación de la clasificación binaria". BMC Genomics . 21 (1): 6-1–6-13. doi : 10.1186/s12864-019-6413-7 . PMC 6941312 . PMID 31898477.
- ^ Chicco D, Toetsch N, Jurman G (febrero de 2021). "El coeficiente de correlación de Matthews (MCC) es más confiable que la precisión equilibrada, la información de la casa de apuestas y la marcación en la evaluación de la matriz de confusión de dos clases". Minería de datos biológicos . 14 (13): 13. doi : 10.1186/s13040-021-00244-z . PMC 7863449 . PMID 33541410.
- ^ Tharwat A. (agosto de 2018). "Métodos de evaluación de la clasificación". Computación e informática aplicada . 17 : 168–192. doi : 10.1016/j.aci.2018.08.003 .
- ^ "clasificación - AUC-ROC de un clasificador aleatorio". Data Science Stack Exchange . Consultado el 30 de noviembre de 2020 .
- ^ abcd Chicco, Davide; Jurman, Giuseppe (17 de febrero de 2023). "El coeficiente de correlación de Matthews (MCC) debería reemplazar al AUC de ROC como métrica estándar para evaluar la clasificación binaria". Minería de datos biológicos . 16 (1). Springer Science and Business Media LLC: 4. doi : 10.1186/s13040-023-00322-4 . hdl : 10281/430042 . ISSN 1756-0381. PMC 9938573 . PMID 36800973.
- ^ Muschelli, John (23 de diciembre de 2019). "ROC y AUC con un predictor binario: una métrica potencialmente engañosa". Revista de clasificación . 37 (3). Springer Science and Business Media LLC: 696–708. doi :10.1007/s00357-019-09345-1. ISSN 0176-4268. PMC 7695228 . PMID 33250548.
- ^ abc Lobo, Jorge M.; Jiménez-Valverde, Alberto; Real, Raimundo (2008). "AUC: una medida engañosa del desempeño de los modelos predictivos de distribución". Ecología global y biogeografía . 17 (2). Wiley: 145–151. Bibcode :2008GloEB..17..145L. doi :10.1111/j.1466-8238.2007.00358.x. ISSN 1466-822X.
- ^ Halligan, Steve; Altman, Douglas G.; Mallett, Susan (20 de enero de 2015). "Desventajas de utilizar el área bajo la curva característica operativa del receptor para evaluar las pruebas de imagen: una discusión y propuesta para un enfoque alternativo". Radiología europea . 25 (4). Springer Science and Business Media LLC: 932–939. doi : 10.1007/s00330-014-3487-0 . ISSN 0938-7994. PMC 4356897 . PMID 25599932.
- ^ Berrar, D.; Flach, P. (21 de marzo de 2011). "Advertencias y trampas del análisis ROC en la investigación clínica de microarrays (y cómo evitarlas)". Briefings in Bioinformatics . 13 (1). Oxford University Press (OUP): 83–97. doi : 10.1093/bib/bbr008 . ISSN 1467-5463. PMID 21422066.
- ^ Řezáč, M., Řezáč, F. (2011). "Cómo medir la calidad de los modelos de calificación crediticia". Revista Checa de Economía y Finanzas (Finance a úvěr) . 61 (5). Universidad Carolina de Praga, Facultad de Ciencias Sociales: 486–507.
- ^ abc Powers, David MW (2012). "ROC-ConCert: medición de consistencia y certeza basada en ROC" (PDF) . Congreso de primavera sobre ingeniería y tecnología (SCET) . Vol. 2. IEEE. págs. 238–241.[ enlace muerto ]
- ^ Fogarty, James; Baker, Ryan S.; Hudson, Scott E. (2005). "Estudios de casos sobre el uso del análisis de curvas ROC para estimaciones basadas en sensores en la interacción hombre-ordenador". Serie de actas de conferencias internacionales de la ACM, Actas de la Interfaz Gráfica 2005. Waterloo, ON: Sociedad Canadiense de Comunicaciones Hombre-Ordenador.
- ^ Hastie, Trevor ; Tibshirani, Robert ; Friedman, Jerome H. (2009). Los elementos del aprendizaje estadístico: minería de datos, inferencia y predicción (2.ª ed.).
- ^ Fawcett, Tom (2006); Una introducción al análisis ROC , Pattern Recognition Letters, 27, 861–874.
- ^ Hanley, James A.; McNeil, Barbara J. (1982). "El significado y el uso del área bajo una curva ROC (Receiver Operating Characteristic)". Radiología . 143 (1): 29–36. doi :10.1148/radiology.143.1.7063747. PMID 7063747. S2CID 10511727.
- ^ Mason, Simon J.; Graham, Nicholas E. (2002). "Áreas bajo las curvas de características operativas relativas (ROC) y niveles operativos relativos (ROL): significación estadística e interpretación" (PDF) . Quarterly Journal of the Royal Meteorological Society . 128 (584): 2145–2166. Bibcode :2002QJRMS.128.2145M. CiteSeerX 10.1.1.458.8392 . doi :10.1256/003590002320603584. S2CID 121841664. Archivado desde el original (PDF) el 20 de noviembre de 2008.
- ^ Calders, dibujo animado; Jaroszewicz, Szymon (2007). "Optimización eficiente de AUC para la clasificación". En Kok, Joost N.; Koronacki, Jacek; López de Mantarás, Ramón; Matwin, Stan; Mladenič, Dunja; Skowron, Andrzej (eds.). Descubrimiento de conocimientos en bases de datos: PKDD 2007 . Apuntes de conferencias sobre informática. vol. 4702. Berlín, Heidelberg: Springer. págs. 42–53. doi : 10.1007/978-3-540-74976-9_8 . ISBN 978-3-540-74976-9.
- ^ Hand, David J.; y Till, Robert J. (2001); Una generalización simple del área bajo la curva ROC para problemas de clasificación de clases múltiples , Machine Learning, 45, 171–186.
- ^ Provost, F.; Fawcett, T. (2001). "Clasificación robusta para entornos imprecisos". Aprendizaje automático . 42 (3): 203–231. arXiv : cs/0009007 . doi :10.1023/a:1007601015854. S2CID 5415722.
- ^ Flach, PA; Wu, S. (2005). "Reparación de concavidades en curvas ROC". (PDF) . 19.ª Conferencia conjunta internacional sobre inteligencia artificial (IJCAI'05) . págs. 702–707.
- ^ Hanley, James A.; McNeil, Barbara J. (1983-09-01). "Un método para comparar las áreas bajo las curvas de características operativas del receptor derivadas de los mismos casos". Radiología . 148 (3): 839–843. doi : 10.1148/radiology.148.3.6878708 . PMID 6878708.
- ^ Hanczar, Blaise; Hua, Jianping; Sima, Chao; Weinstein, John; Bittner, Michael; Dougherty, Edward R (2010). "Precisión de muestras pequeñas de estimaciones relacionadas con ROC". Bioinformática . 26 (6): 822–830. doi : 10.1093/bioinformatics/btq037 . PMID 20130029.
- ^ Lobo, Jorge M.; Jiménez-Valverde, Alberto; Real, Raimundo (2008). "AUC: una medida engañosa del desempeño de los modelos predictivos de distribución". Ecología global y biogeografía . 17 (2): 145–151. Bibcode :2008GloEB..17..145L. doi :10.1111/j.1466-8238.2007.00358.x. S2CID 15206363.
- ^ Hand, David J (2009). "Medición del rendimiento del clasificador: una alternativa coherente al área bajo la curva ROC". Aprendizaje automático . 77 : 103–123. doi : 10.1007/s10994-009-5119-5 . hdl : 10044/1/18420 .
- ^ Flach, PA; Hernandez-Orallo, J.; Ferri, C. (2011). "Una interpretación coherente del AUC como medida del rendimiento de la clasificación agregada". (PDF) . Actas de la 28.ª Conferencia Internacional sobre Aprendizaje Automático (ICML-11) . págs. 657–664.
- ^ Hernandez-Orallo, J.; Flach, PA; Ferri, C. (2012). "Una visión unificada de las métricas de rendimiento: traducir la elección del umbral en pérdida de clasificación esperada" (PDF) . Journal of Machine Learning Research . 13 : 2813–2869.
- ^ Powers, David MW (2012). "El problema del área bajo la curva". Conferencia internacional sobre ciencia y tecnología de la información .
- ^ Powers, David MW (2003). "Recall and Precision versus the Bookmaker" (PDF) . Actas de la Conferencia Internacional sobre Ciencia Cognitiva (ICSC-2003), Sydney (Australia), 2003, págs. 529–534 .
- ^ Powers, David MW (2012). "El problema con Kappa" (PDF) . Conferencia del Capítulo Europeo de la Asociación de Lingüística Computacional (EACL2012) Taller conjunto ROBUS-UNSUP . Archivado desde el original (PDF) el 2016-05-18 . Consultado el 2012-07-20 .
- ^ McClish, Donna Katzman (1 de agosto de 1989). "Análisis de una parte de la curva ROC". Toma de decisiones médicas . 9 (3): 190–195. doi :10.1177/0272989X8900900307. PMID 2668680. S2CID 24442201.
- ^ Dodd, Lori E.; Pepe, Margaret S. (2003). "Estimación y regresión parcial del AUC". Biometrics . 59 (3): 614–623. doi : 10.1111/1541-0420.00071 . PMID 14601762. S2CID 23054670.
- ^ Karplus, Kevin (2011); Mejor que el azar: la importancia de los modelos nulos, Universidad de California, Santa Cruz, en Actas del primer taller internacional sobre reconocimiento de patrones en proteómica, biología estructural y bioinformática (PR PS BB 2011)
- ^ "Estadística C: definición, ejemplos, ponderación y significancia". Cómo hacer estadísticas . 28 de agosto de 2016.
- ^ Pontius, Robert Gilmore; Parmentier, Benoit (2014). "Recomendaciones para el uso de la característica operativa relativa (ROC)". Ecología del paisaje . 29 (3): 367–382. Código Bibliográfico :2014LaEco..29..367P. doi :10.1007/s10980-013-9984-8. S2CID 15924380.
- ^ Pontius, Robert Gilmore; Si, Kangping (2014). "La característica operativa total para medir la capacidad de diagnóstico para múltiples umbrales". Revista Internacional de Ciencias de la Información Geográfica . 28 (3): 570–583. Bibcode :2014IJGIS..28..570P. doi :10.1080/13658816.2013.862623. S2CID 29204880.
- ^ Navratil, J.; Klusacek, D. (1 de abril de 2007). "Sobre los DET lineales". Conferencia internacional IEEE de 2007 sobre acústica, habla y procesamiento de señales - ICASSP '07 . Vol. 4. págs. IV–229–IV–232. doi :10.1109/ICASSP.2007.367205. ISBN 978-1-4244-0727-9. Número de identificación del sujeto 18173315.
- ^ Dev P. Chakraborty (14 de diciembre de 2017). "double+probability+paper"&pg=PT214 Métodos de rendimiento del observador para diagnóstico por imágenes: fundamentos, modelado y aplicaciones con ejemplos basados en R. CRC Press. pág. 214. ISBN 9781351230711. Recuperado el 11 de julio de 2019 .
- ^ MacMillan, Neil A.; Creelman, C. Douglas (2005). Teoría de detección: guía del usuario (2.ª edición). Mahwah, Nueva Jersey: Lawrence Erlbaum Associates. ISBN 978-1-4106-1114-7.
- ^ Glanzer, Murray; Kisok, Kim; Hilford, Andy; Adams, John K. (1999). "Pendiente de la característica operativa del receptor en la memoria de reconocimiento". Revista de psicología experimental: aprendizaje, memoria y cognición . 25 (2): 500–513. doi :10.1037/0278-7393.25.2.500.
- ^ Ratcliff, Roger; McCoon, Gail; Tindall, Michael (1994). "Generalidad empírica de los datos de las funciones ROC de la memoria de reconocimiento y sus implicaciones para los GMM". Revista de psicología experimental: aprendizaje, memoria y cognición . 20 (4): 763–785. CiteSeerX 10.1.1.410.2114 . doi :10.1037/0278-7393.20.4.763. PMID 8064246.
- ^ Zhang, Jun; Mueller, Shane T. (2005). "Una nota sobre el análisis ROC y la estimación no paramétrica de la sensibilidad". Psychometrika . 70 : 203–212. CiteSeerX 10.1.1.162.1515 . doi :10.1007/s11336-003-1119-8. S2CID 122355230.
- ^ Yonelinas, Andrew P.; Kroll, Neal EA; Dobbins, Ian G.; Lazzara, Michele; Knight, Robert T. (1998). "Déficits de recuerdo y familiaridad en la amnesia: convergencia de datos de recordar-conocer, disociación de procesos y características operativas del receptor". Neuropsicología . 12 (3): 323–339. doi :10.1037/0894-4105.12.3.323. PMID 9673991.
- ^ ab Green, David M.; Swets, John A. (1966). Teoría de detección de señales y psicofísica . Nueva York, NY: John Wiley and Sons Inc. ISBN 978-0-471-32420-1.
- ^ "Uso de la curva ROC (Receiver Operating Characteristic) para analizar un modelo de clasificación: una nota final de interés histórico" (PDF) . Departamento de Matemáticas, Universidad de Utah . Archivado (PDF) desde el original el 22 de agosto de 2020 . Consultado el 25 de mayo de 2017 .
- ^ Zweig, Mark H.; Campbell, Gregory (1993). "Gráficos de curvas ROC (Receiver-Operating Characteristic, ROC): una herramienta de evaluación fundamental en medicina clínica" (PDF) . Química clínica . 39 (8): 561–577. doi : 10.1093/clinchem/39.4.561 . PMID 8472349.
- ^ Pepe, Margaret S. (2003). La evaluación estadística de pruebas médicas para clasificación y predicción . Nueva York, NY: Oxford. ISBN 978-0-19-856582-6.
- ^ Obuchowski, Nancy A. (2003). "Curvas características operativas del receptor y su uso en radiología". Radiología . 229 (1): 3–8. doi :10.1148/radiol.2291010898. PMID 14519861.
- ^ Spackman, Kent A. (1989). "Teoría de detección de señales: herramientas valiosas para evaluar el aprendizaje inductivo". Actas del Sexto Taller Internacional sobre Aprendizaje Automático . San Mateo, CA: Morgan Kaufmann . págs. 160–163.
- ^ Kharin, Viatcheslav (2003). "Sobre la puntuación ROC de los pronósticos de probabilidad". Journal of Climate . 16 (24): 4145–4150. Bibcode :2003JCli...16.4145K. doi : 10.1175/1520-0442(2003)016<4145:OTRSOP>2.0.CO;2 .
- ^ "Fundamentos del radar", Técnicas de procesamiento de señales digitales y aplicaciones en el procesamiento de imágenes de radar , Hoboken, NJ, EE. UU.: John Wiley & Sons, Inc., págs. 93-115, 29 de enero de 2008, doi : 10.1002/9780470377765.ch4, ISBN 9780470377765, consultado el 20 de mayo de 2023
- ^ Till, DJ; Hand, RJ (2001). "Una generalización simple del área bajo la curva ROC para problemas de clasificación de clases múltiples". Aprendizaje automático . 45 (2): 171–186. doi : 10.1023/A:1010920819831 .
- ^ Mossman, D. (1999). "Recopilación de resultados de tres vías". Toma de decisiones médicas . 19 (1): 78–89. doi :10.1177/0272989x9901900110. PMID 9917023. S2CID 24623127.
- ^ Ferri, C.; Hernandez-Orallo, J.; Salido, MA (2003). "Volumen bajo la superficie ROC para problemas multiclase". Aprendizaje automático: ECML 2003. págs. 108–120.
- ^ Bi, J.; Bennett, KP (2003). "Curvas características de error de regresión" (PDF) . Vigésima Conferencia Internacional sobre Aprendizaje Automático (ICML-2003). Washington, DC .
- ^ Hernandez-Orallo, J. (2013). "Curvas ROC para regresión". Reconocimiento de patrones . 46 (12): 3395–3411. Bibcode :2013PatRe..46.3395H. doi :10.1016/j.patcog.2013.06.014. hdl : 10251/40252 . S2CID 15651724.
Enlaces externos
- Calculadora ROC fácil
- Demostración animada de ROC
- Demostración de ROC
- Otra demostración de ROC
- Explicación en video de ROC
- Introducción a la característica operativa total: utilidad en la evaluación del modelo de cambio de la tierra
- Cómo ejecutar el paquete TOC en R
- Paquete TOC R en Github
- Libro de trabajo de Excel para generar curvas TOC
Lectura adicional
- Balakrishnan, Narayanaswamy (1991); Manual de distribución logística , Marcel Dekker, Inc., ISBN 978-0-8247-8587-1
- Brown, Christopher D.; Davis, Herbert T. (2006). "Curvas características operativas del receptor y medidas de decisión relacionadas: un tutorial". Quimiometría y sistemas de laboratorio inteligentes . 80 : 24–38. doi :10.1016/j.chemolab.2005.05.004.
- Rotello, Caren M.; Heit, Evan; Dubé, Chad (2014). "Cuando más datos nos llevan por el camino equivocado: las réplicas con la medida dependiente equivocada perpetúan conclusiones erróneas" (PDF) . Psychonomic Bulletin & Review . 22 (4): 944–954. doi : 10.3758/s13423-014-0759-2 . PMID 25384892. S2CID 6046065.
- Fawcett, Tom (2004). "Gráficos ROC: notas y consideraciones prácticas para investigadores" (PDF) . Pattern Recognition Letters . 27 (8): 882–891. CiteSeerX 10.1.1.145.4649 . doi :10.1016/j.patrec.2005.10.012.
- Gonen, Mithat (2007); Análisis de las curvas características operativas del receptor mediante SAS , SAS Press, ISBN 978-1-59994-298-8
- Green, William H., (2003) Análisis econométrico , quinta edición, Prentice Hall , ISBN 0-13-066189-9
- Heagerty, Patrick J.; Lumley, Thomas; Pepe, Margaret S. (2000). "Curvas ROC dependientes del tiempo para datos de supervivencia censurados y un marcador de diagnóstico". Biometrics . 56 (2): 337–344. doi :10.1111/j.0006-341x.2000.00337.x. PMID 10877287. S2CID 8822160.
- Hosmer, David W.; y Lemeshow, Stanley (2000); Applied Logistic Regression , 2.ª ed., Nueva York, NY: Wiley , ISBN 0-471-35632-8
- Lasko, Thomas A.; Bhagwat, Jui G.; Zou, Kelly H.; Ohno-Machado, Lucila (2005). "El uso de curvas características operativas del receptor en informática biomédica". Revista de informática biomédica . 38 (5): 404–415. CiteSeerX 10.1.1.97.9674 . doi :10.1016/j.jbi.2005.02.008. PMID 16198999.
- Mas, Jean-François; Filho, Britaldo Soares; Poncio, Jr, Robert Gilmore; Gutiérrez, Michelle Farfán; Rodrigues, Hermann (2013). "Un conjunto de herramientas para el análisis ROC de modelos espaciales". Revista internacional de información geográfica de ISPRS . 2 (3): 869–887. Código Bib : 2013IJGI....2..869M. doi : 10.3390/ijgi2030869 .
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Pontius, Jr, Robert Gilmore; Parmentier, Benoit (2014). "Recomendaciones para el uso de la característica operativa relativa (ROC)". Ecología del paisaje . 29 (3): 367–382. Código Bibliográfico :2014LaEco..29..367P. doi :10.1007/s10980-013-9984-8. S2CID 15924380.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Pontius, Jr, Robert Gilmore; Pacheco, Pablo (2004). "Calibración y validación de un modelo de perturbación forestal en los Ghats occidentales, India, 1920-1990". GeoJournal . 61 (4): 325–334. Bibcode :2004GeoJo..61..325G. doi :10.1007/s10708-004-5049-5. S2CID 155073463.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Pontius, Jr, Robert Gilmore; Batchu, Kiran (2003). "Uso de la característica operativa relativa para cuantificar la certeza en la predicción de la ubicación del cambio de la cobertura terrestre en la India". Transactions in GIS . 7 (4): 467–484. Bibcode :2003TrGIS...7..467P. doi :10.1111/1467-9671.00159. S2CID 14452746.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Pontius, Jr, Robert Gilmore; Schneider, Laura (2001). "Validación del modelo de cambio de uso de la tierra mediante un método ROC para la cuenca hidrográfica de Ipswich, Massachusetts, EE. UU." Agricultura, ecosistemas y medio ambiente . 85 (1–3): 239–248. doi :10.1016/S0167-8809(01)00187-6.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Stephan, Carsten; Wesseling, Sebastian; Schink, Tania; Jung, Klaus (2003). "Comparación de ocho programas informáticos para el análisis de las características operativas del receptor". Química clínica . 49 (3): 433–439. doi : 10.1373/49.3.433 . PMID 12600955.
- Swets, John A.; Dawes, Robyn M.; y Monahan, John (2000); Mejores decisiones a través de la ciencia , Scientific American , octubre, págs. 82–87
- Zou, Kelly H.; O'Malley, A. James; Mauri, Laura (2007). "Análisis de la característica receptor-operatoria para evaluar pruebas diagnósticas y modelos predictivos". Circulation . 115 (5): 654–7. doi : 10.1161/circulationaha.105.594929 . PMID 17283280.
- Zhou, Xiao-Hua; Obuchowski, Nancy A .; McClish, Donna K. (2002). Métodos estadísticos en medicina diagnóstica . Nueva York, NY: Wiley & Sons. ISBN 978-0-471-34772-9.
- Chicco D.; Jurman G. (2023). "El coeficiente de correlación de Matthews (MCC) debería reemplazar el AUC ROC como métrica estándar para evaluar la clasificación binaria". Minería de datos biológicos . 16 (1): 4. doi : 10.1186/s13040-023-00322-4 . PMC 9938573 . PMID 36800973.














![{\displaystyle {\begin{aligned}A&=\int _{x=0}^{1}{\mbox{TPR}}({\mbox{FPR}}^{-1}(x))\,dx\\[5pt]&=\int _{\infty }^{-\infty }{\mbox{TPR}}(T){\mbox{FPR}}'(T)\,dT\\[5pt]&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }I(T'\geq T)f_{1}(T')f_{0}(T)\,dT'\,dT=P(X_{1}\geq X_{0})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdb0372c3b4aa60b02b19360ef1fbf8ddd8d221e)






![{\displaystyle {\text{AUC}}(f)={\frac {\sum _{t_{0}\in {\mathcal {D}}^{0}}\sum _{t_{1}\in {\mathcal {D}}^{1}}{\textbf {1}}[f(t_{0})<f(t_{1})]}{|{\mathcal {D}}^{0} |\cdot |{\mathcal {D}}^{1}|}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ad12d9aef8c040aea59bc20304b821fc9b99232)
![{\textstyle {\textbf {1}}[f(t_{0})<f(t_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03407a2c3018d99fb12703e2327bfbf84b9ce426)













