Solución tampón

Ácidos y bases
Número de aceptor Ácido Reacción ácido-base Homeostasis ácido-base Fuerza del ácido Función de acidez Anfoterismo Base Soluciones tampón Constante de disociación Número de donante Química del equilibrio Extracción Función de acidez de Hammett pH Afinidad de protones Autoionización del agua Valoración Catálisis ácida de Lewis Pareja de Lewis frustrada Ácido de Lewis quiral Modelo ECW
Tipos de ácidos
Brønsted–Lowry Ametralladora Mineral Orgánico Óxido Fuerte Superácidos Débil Sólido
Tipos de base
Brønsted–Lowry Ametralladora Orgánico Óxido Fuerte Superbases No nucleofílico Débil
en a mi

Una solución tampón es una solución en la que el pH no cambia significativamente al diluirse o si se añade un ácido o una base a temperatura constante. ^[1] Su pH cambia muy poco cuando se le añade una pequeña cantidad de ácido o base fuerte . Las soluciones tampón se utilizan como un medio para mantener el pH a un valor casi constante en una amplia variedad de aplicaciones químicas. En la naturaleza, hay muchos sistemas vivos que utilizan el tampón para regular el pH. Por ejemplo, el sistema tampón de bicarbonato se utiliza para regular el pH de la sangre , y el bicarbonato también actúa como tampón en el océano .

Las soluciones tampón resisten el cambio de pH debido a un equilibrio químico entre el ácido débil HA y su base conjugada A ⁻ :

Cuando se añade un ácido fuerte a una mezcla en equilibrio del ácido débil y su base conjugada, se añaden iones hidrógeno (H ^{+ ) y el equilibrio se desplaza hacia la izquierda, de acuerdo con} el principio de Le Chatelier . Debido a esto, la concentración de iones hidrógeno aumenta en una cantidad menor que la esperada para la cantidad de ácido fuerte añadido. De manera similar, si se añade un álcali fuerte a la mezcla, la concentración de iones hidrógeno disminuye en una cantidad menor que la esperada para la cantidad de álcali añadido. En la Figura 1, el efecto se ilustra mediante la titulación simulada de un ácido débil con p K _a  = 4,7. La concentración relativa del ácido no disociado se muestra en azul y la de su base conjugada en rojo. El pH cambia relativamente lento en la región tampón, pH = p K _a  ± 1, centrado en pH = 4,7, donde [HA] = [A ⁻ ]. La concentración de iones hidrógeno disminuye en una cantidad menor que la esperada porque la mayor parte del ion hidróxido añadido se consume en la reacción.

y sólo se consume un poco en la reacción de neutralización (que es la reacción que da como resultado un aumento del pH)

Una vez que el ácido está desprotonado en más del 95% , el pH aumenta rápidamente porque la mayor parte del álcali añadido se consume en la reacción de neutralización.

La capacidad tampón es una medida cuantitativa de la resistencia al cambio de pH de una solución que contiene un agente tampón con respecto a un cambio de concentración de ácido o álcali. Puede definirse de la siguiente manera: ^{[2] [3]} donde es una cantidad infinitesimal de base añadida, o donde es una cantidad infinitesimal de ácido añadido. El pH se define como −log ₁₀ [H ⁺ ], y d (pH) es un cambio infinitesimal en el pH. $${\displaystyle \beta ={\frac {dC_{b}}{d(\mathrm {pH} )}},}$$${\displaystyle dC_{b}}$$${\displaystyle \beta =-{\frac {dC_{a}}{d(\mathrm {pH} )}},}$$${\displaystyle dC_{a}}$

Con cualquiera de las definiciones, la capacidad tampón para un ácido débil HA con constante de disociación K _a se puede expresar como ^{[4] [5] [3]} donde [H ⁺ ] es la concentración de iones de hidrógeno y es la concentración total de ácido añadido. K _w es la constante de equilibrio para la autoionización del agua , igual a 1,0 × 10 ⁻¹⁴ . Nótese que en solución H ⁺ existe como el ion hidronio H ₃ O ^{+ , y} la acuación adicional del ion hidronio tiene un efecto insignificante en el equilibrio de disociación, excepto a una concentración de ácido muy alta. $${\displaystyle \beta =2.303\left([{\ce {H+}}]+{\frac {T_{{\ce {HA}}}K_{a}[{\ce {H+}}]}{(K_{a}+[{\ce {H+}}])^{2}}}+{\frac {K_{\text{w}}}{[{\ce {H+}}]}}\right),}$$${\displaystyle T_{\text{HA}}}$

Esta ecuación muestra que hay tres regiones con mayor capacidad de amortiguación (ver figura 2).

• En la región central de la curva (coloreada en verde en el gráfico), el segundo término es dominante y la capacidad tampón aumenta hasta un máximo local a pH =  pK _a . La altura de este pico depende del valor de pK _a . La capacidad tampón es insignificante cuando la concentración [HA] del agente tampón es muy pequeña y aumenta con el aumento de la concentración del agente tampón. ^[3] Algunos autores muestran solo esta región en gráficos de capacidad tampón. ^[2]$${\displaystyle \beta \approx 2.303{\frac {T_{{\ce {HA}}}K_{a}[{\ce {H+}}]}{(K_{a}+[{\ce {H+}}])^{2}}}.}$$
  La capacidad tampón cae al 33% del valor máximo a pH = p K _a ± 1, al 10% a pH = p K _a ± 1,5 y al 1% a pH = p K _a ± 2. Por esta razón, el rango más útil es aproximadamente p K _a  ± 1. Al elegir un tampón para usar a un pH específico, debe tener _{un valor de p} K a lo más cercano posible a ese pH. ^[2]
• En el caso de soluciones muy ácidas, con un pH inferior a aproximadamente 2 (coloreado en rojo en el gráfico), predomina el primer término de la ecuación y la capacidad tampón aumenta exponencialmente con la disminución del pH: esto se debe a que el segundo y el tercer término se vuelven insignificantes a un pH muy bajo. Este término es independiente de la presencia o ausencia de un agente tampón.$${\displaystyle \beta \approx 10^{-\mathrm {pH} }.}$$
• En el caso de soluciones fuertemente alcalinas, con un pH superior a 12 (coloreado en azul en el gráfico), predomina el tercer término de la ecuación y la capacidad tampón aumenta exponencialmente con el aumento del pH: esto se debe a que el primer y el segundo término se vuelven insignificantes a un pH muy alto. Este término también es independiente de la presencia o ausencia de un agente tampón.$${\displaystyle \beta \approx 10^{\mathrm {pH} -\mathrm {p} K_{\text{w}}}.}$$

El pH de una solución que contiene un agente tampón solo puede variar dentro de un rango estrecho, independientemente de lo que pueda estar presente en la solución. En los sistemas biológicos, esta es una condición esencial para que las enzimas funcionen correctamente. Por ejemplo, en la sangre humana una mezcla de ácido carbónico (H
₂CO
₃) y bicarbonato (HCO⁻
₃) está presente en la fracción plasmática ; esto constituye el principal mecanismo para mantener el pH de la sangre entre 7,35 y 7,45. Fuera de este estrecho rango (7,40 ± 0,05 unidades de pH), se desarrollan rápidamente estados metabólicos de acidosis y alcalosis , que finalmente conducen a la muerte si no se restablece rápidamente la capacidad tampón correcta.

Si el valor de pH de una solución aumenta o disminuye demasiado, la eficacia de una enzima disminuye en un proceso, conocido como desnaturalización , que suele ser irreversible. ^[6] La mayoría de las muestras biológicas que se utilizan en investigación se mantienen en una solución tampón, a menudo solución salina tamponada con fosfato (PBS) a pH 7,4.

En la industria, los agentes tampón se utilizan en procesos de fermentación y para establecer las condiciones correctas para los colorantes utilizados en la coloración de tejidos. También se utilizan en análisis químicos ^[5] y en la calibración de medidores de pH .

Agente tampón	pK a​	Rango de pH útil
Ácido cítrico	3,13, 4,76, 6,40	2.1–7.4
Ácido acético	4.8	3.8–5.8
KH2PO4​​​	7.2	6.2–8.2
CHE	9.3	8.3–10.3
Borato	9.24	8.25–10.25

En el caso de los tampones en regiones ácidas, el pH se puede ajustar a un valor deseado añadiendo un ácido fuerte, como ácido clorhídrico, al agente tampón en particular. En el caso de los tampones alcalinos, se puede añadir una base fuerte, como hidróxido de sodio . Como alternativa, se puede preparar una mezcla tampón a partir de una mezcla de un ácido y su base conjugada. Por ejemplo, se puede preparar un tampón de acetato a partir de una mezcla de ácido acético y acetato de sodio . De forma similar, se puede preparar un tampón alcalino a partir de una mezcla de la base y su ácido conjugado.

Combinando sustancias con valores de p K _a que difieren en solo dos o menos y ajustando el pH, se puede obtener una amplia gama de soluciones tampón. El ácido cítrico es un componente útil de una mezcla tampón porque tiene tres valores de p K _a separados por menos de dos. El rango de soluciones tampón se puede ampliar añadiendo otros agentes tampón. Las siguientes mezclas ( soluciones tampón de McIlvaine ) tienen un rango de pH tampón de 3 a 8. ^[7]

0,2 M de Na2HPO4 ( ml )	Ácido cítrico 0,1 M (ml)	pH
20,55	79,45	3.0
38,55	61,45	4.0
51,50	48,50	5.0
63,15	36,85	6.0
82.35	17,65	7.0
97,25	2,75	8.0

Se puede preparar una mezcla que contenga ácido cítrico , fosfato monopotásico , ácido bórico y ácido dietilbarbitúrico para cubrir el rango de pH de 2,6 a 12. ^[8]

Otros buffers universales son el buffer Carmody ^[9] y el buffer Britton-Robinson , desarrollado en 1931.

Para conocer el alcance efectivo, consulte Capacidad de tampón, más arriba. Consulte también los tampones de Good para conocer los principios de diseño históricos y las propiedades favorables de estas sustancias tampón en aplicaciones bioquímicas.

Nombre común (nombre químico)	Estructura	pK a , 25 ° C	Efecto temporal , ⁠dpH/el T⁠ (K −1 ) [10]	Peso molecular
TAPS , (ácido [tris(hidroximetil)metilamino]propanosulfónico)		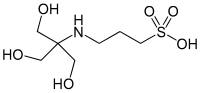8.43	-0,018	243.3
Bicina , ácido (2-(bis(2-hidroxietil)amino)acético)		8.35	-0,018	163.2
Tris , (tris(hidroximetil)aminometano o 2-amino-2-(hidroximetil)propano-1,3-diol)		8.07 [a]	-0,028	121.14
Tricina , (N-[tris(hidroximetil)metil]glicina)		8.05	-0,021	179.2
TAPSO , (ácido 3-[N-tris(hidroximetil)metilamino]-2-hidroxipropanosulfónico)		7.635		259.3
HEPES , (ácido 4-(2-hidroxietil)-1-piperazinetanosulfónico)		7.48	-0,014	238.3
TES , (ácido 2-[[1,3-dihidroxi-2-(hidroximetil)propan-2-il]amino]etanosulfónico)		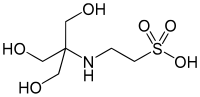7.40	-0,020	229,20
MOPS , (ácido 3-(N-morfolino)propanosulfónico)		7.20	-0,015	209.3
PIPES , (ácido piperazina-N,N′-bis(2-etanosulfónico))		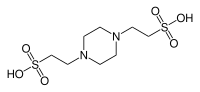6,76	-0,008	302.4
Cacodilato (ácido dimetilarsénico )		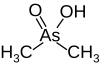6.27		138.0
MES , (ácido 2-(N-morfolino)etanosulfónico)		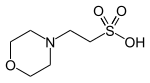6.15	-0,011	195.2

Primero escribe la expresión de equilibrio

Esto demuestra que cuando el ácido se disocia, se producen cantidades iguales de iones de hidrógeno y aniones. Las concentraciones de equilibrio de estos tres componentes se pueden calcular en una tabla ICE (ICE significa "inicial, cambio, equilibrio").

Tabla ICE para un ácido monoprótico

	[JA]	[Un − ]	[H + ]
I	C 0	0	y
do	- x	incógnita	incógnita
mi	C 0 − x	incógnita	x + y

La primera fila, etiquetada como I , enumera las condiciones iniciales: la concentración de ácido es C ₀ , inicialmente no disociado, por lo que las concentraciones de A ⁻ y H ⁺ serían cero; y es la concentración inicial del ácido fuerte añadido , como el ácido clorhídrico. Si se añade un álcali fuerte, como el hidróxido de sodio, entonces y tendrá un signo negativo porque el álcali elimina los iones de hidrógeno de la solución. La segunda fila, etiquetada como C por "cambio", especifica los cambios que ocurren cuando el ácido se disocia. La concentración de ácido disminuye en una cantidad − x , y las concentraciones de A ⁻ y H ⁺ aumentan en una cantidad + x . Esto se desprende de la expresión de equilibrio. La tercera fila, etiquetada como E por "equilibrio", suma las dos primeras filas y muestra las concentraciones en equilibrio.

Para encontrar x , utilice la fórmula para la constante de equilibrio en términos de concentraciones:$${\displaystyle K_{\text{a}}={\frac {[{\ce {H+}}][{\ce {A-}}]}{[{\ce {HA}}]}}.}$$

Sustituya las concentraciones con los valores que se encuentran en la última fila de la tabla ICE:$${\displaystyle K_{\text{a}}={\frac {x(x+y)}{C_{0}-x}}.}$$

Simplificar a$${\displaystyle x^{2}+(K_{\text{a}}+y)x-K_{\text{a}}C_{0}=0.}$$

Con valores específicos para C ₀ , K _a e y , esta ecuación se puede resolver para x . Suponiendo que pH = −log ₁₀ [H ⁺ ], el pH se puede calcular como pH = −log ₁₀ ( x  +  y ).

Los ácidos polipróticos son ácidos que pueden perder más de un protón. La constante de disociación del primer protón se puede denotar como K _a1 y las constantes de disociación de los protones sucesivos como K _a2 , etc. El ácido cítrico es un ejemplo de ácido poliprótico H ₃ A, ya que puede perder tres protones.

Constantes de disociación escalonada

Equilibrio	Ácido cítrico
H3A ⇌ H2A − + H +​	pKa1 = 3,13​
H2A − ⇌HA2− + H +​​	pKa2 = 4,76​
HA2− ⇌ A3− + H +	pKa3 = 6,40​

Cuando la diferencia entre valores sucesivos de p K _a es menor que aproximadamente 3, existe una superposición entre el rango de pH de existencia de las especies en equilibrio. Cuanto menor sea la diferencia, mayor será la superposición. En el caso del ácido cítrico, la superposición es extensa y las soluciones de ácido cítrico se tamponan en todo el rango de pH de 2,5 a 7,5.

El cálculo del pH con un ácido poliprótico requiere la realización de un cálculo de especiación . En el caso del ácido cítrico, esto implica la solución de las dos ecuaciones de balance de masa:

$${\displaystyle {\begin{aligned}C_{{\ce {A}}}&=[{\ce {A^3-}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3},\\C_{{\ce {H}}}&=[{\ce {H+}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+2\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+3\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3}-K_{\text{w}}[{\ce {H+}}]^{-1}.\end{aligned}}}$$

C _A es la concentración analítica del ácido, C _H es la concentración analítica de iones de hidrógeno añadidos, β _q son las constantes de asociación acumuladas . K _w es la constante de autoionización del agua . Hay dos ecuaciones simultáneas no lineales en dos cantidades desconocidas [A ³⁻ ] y [H ⁺ ]. Hay muchos programas informáticos disponibles para realizar este cálculo. El diagrama de especiación del ácido cítrico se produjo con el programa HySS. ^[11]

NB La numeración de las constantes acumulativas y generales es inversa a la numeración de las constantes de disociación escalonadas.

Relación entre los valores de la constante de asociación acumulativa (β) y los valores de la constante de disociación escalonada (K) para un ácido tribásico.

Equilibrio	Relación
A 3− + H + ⇌ AH 2+	Logaritmo β 1 = pk a3
A 3− + 2H + ⇌ AH 2 +	Logaritmo β 2 = pk a2 + pk a3
A 3− + 3H + ⇌ AH 3	Logaritmo β 3 = pk a1 + pk a2 + pk a3

Las constantes de asociación acumulativa se utilizan en programas informáticos de propósito general, como el utilizado para obtener el diagrama de especiación anterior.

• Ecuación de Henderson-Hasselbalch
• Los buenos buffers
• Efecto del ion común
• Tampón de iones metálicos
• Tampón redox mineral

"Amortiguadores biológicos". Dispositivos REACH.