Grupo alterno

Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . Por favor, ayude a mejorar este artículo introduciendo citas más precisas. ( Enero de 2008 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Estructura algebraica → Teoría de grupos Teoría de grupos
Nociones básicas Subgrupo Subgrupo normal Acción grupal Grupo de cocientes Producto (semi) directo Suma directa Producto gratuito Producto de corona Homomorfismos de grupo núcleo imagen simple finito infinito continuo multiplicativo aditivo cíclico abeliano diedro nilpotente soluble Glosario de teoría de grupos Lista de temas de teoría de grupos
Grupos finitos Grupo cíclico Z n Grupo simétrico S n Grupo alterno A n Grupo diedro D n Quaternion group Q Cauchy's theorem Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Classification of finite simple groups cyclic alternating Lie type sporadic
Discrete groups Lattices Integers (${\displaystyle \mathbb {Z} }$) Free group Modular groups PSL(2, ${\displaystyle \mathbb {Z} }$) SL(2, ${\displaystyle \mathbb {Z} }$) Arithmetic group Lattice Hyperbolic group
Topological and Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Linear algebraic group Reductive group Abelian variety Elliptic curve
v t e

En matemáticas , un grupo alterno es el grupo de permutaciones pares de un conjunto finito . El grupo alterno de un conjunto de n elementos se denomina grupo alterno de grado n o grupo alterno de n letras y se denota por A _n o Alt( n ).

Para n > 1 , el grupo A _n es el subgrupo conmutador del grupo simétrico S _n con índice 2 y tiene por tanto n ! /2 elementos. Es el núcleo del homomorfismo de grupo característico sgn : S _n → {1, −1} explicado en grupo simétrico .

El grupo A _n es abeliano si y sólo si n ≤ 3 y simple si y sólo si n = 3 o n ≥ 5. A _{5 es el} grupo simple no abeliano más pequeño , de orden 60, y por tanto el grupo no resoluble más pequeño .

El grupo A ₄ tiene como subgrupo normal propio el cuatrigrupo de Klein V , es decir la identidad y las dobles transposiciones { (), (12)(34), (13)(24), (14)(23) } , es decir el núcleo de la sobreyección de A ₄ sobre A ₃ ≅ Z ₃ . Tenemos la sucesión exacta V → A ₄ → A ₃ = Z ₃ . En la teoría de Galois , esta función, o más bien la función correspondiente S ₄ → S ₃ , corresponde a asociar la cúbica resolvente de Lagrange a una cuártica, lo que permite resolver el polinomio cuártico por radicales, como lo estableció Lodovico Ferrari .

Al igual que en el grupo simétrico , dos elementos cualesquiera de A _n que sean conjugados por un elemento de A _n deben tener la misma forma de ciclo . Sin embargo, lo inverso no es necesariamente cierto. Si la forma de ciclo consiste únicamente en ciclos de longitud impar sin dos ciclos de la misma longitud, donde los ciclos de longitud uno están incluidos en el tipo de ciclo, entonces hay exactamente dos clases de conjugación para esta forma de ciclo (Scott 1987, §11.1, p299).

Ejemplos:

• Las dos permutaciones (123) y (132) no son conjugadas en A ₃ , aunque tienen la misma forma de ciclo, y por lo tanto son conjugadas en S ₃ .
• La permutación (123)(45678) no es conjugada a su inversa (132)(48765) en A ₈ , aunque las dos permutaciones tienen la misma forma de ciclo, por lo que son conjugadas en S ₈ .

Ver grupo simétrico .

Como los grupos simétricos finitos son los grupos de todas las permutaciones de un conjunto con elementos finitos, y los grupos alternados son grupos de permutaciones pares, los grupos alternados son subgrupos de los grupos simétricos finitos.

Para n ≥ 3, A _n se genera mediante 3-ciclos, ya que los 3-ciclos se pueden obtener combinando pares de transposiciones. Este conjunto generador se utiliza a menudo para demostrar que A _n es simple para n ≥ 5 .

Para n > 3 , excepto para n = 6 , el grupo de automorfismos de A _n es el grupo simétrico S _n , con grupo de automorfismo interno A _n y grupo de automorfismo externo Z ₂ ; el automorfismo externo proviene de la conjugación por una permutación impar.

Para n = 1 y 2, el grupo de automorfismos es trivial. Para n = 3 , el grupo de automorfismos es Z ₂ , con un grupo de automorfismos interno y externo triviales Z ₂ .

El grupo de automorfismo externo de A ₆ es el cuatrigrupo de Klein V = Z ₂ × Z ₂ , y está relacionado con el automorfismo externo de S ₆ . El automorfismo externo adicional en A ₆ intercambia los 3-ciclos (como (123)) con elementos de forma 3 ² (como  (123)(456) ).

Existen algunos isomorfismos excepcionales entre algunos de los pequeños grupos alternantes y los pequeños grupos de tipo Lie , en particular los grupos lineales especiales proyectivos . Estos son:

• A ₄ es isomorfo a PSL ₂ (3) ^[1] y al grupo de simetría de simetría tetraédrica quiral .
• A ₅ es isomorfo a PSL ₂ (4), PSL ₂ (5) y al grupo de simetría de simetría icosaédrica quiral . (Véase ^[1] para un isomorfismo indirecto de PSL ₂ (F ₅ ) → A ₅ usando una clasificación de grupos simples de orden 60, y aquí para una prueba directa).
• A ₆ es isomorfo a PSL ₂ (9) y PSp ₄ (2)'.
• A ₈ es isomorfo a PSL ₄ (2).

Más obviamente, A ₃ es isomorfo al grupo cíclico Z ₃ , y A ₀ , A ₁ y A ₂ son isomorfos al grupo trivial (que también es SL ₁ ( q ) = PSL ₁ ( q ) para cualquier q ).

Gráficas de ciclos

A 3 = Z 3 (orden 3)	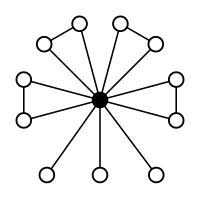A 4 (orden 12)	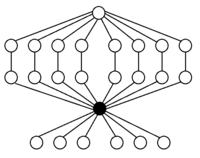A 4 × Z 2 (orden 24)
S 3 = Dih 3 (orden 6)	S 4 (orden 24)	A 4 en S 4 a la izquierda

A ₅ es el grupo de isometrías de un dodecaedro en el 3-espacio, por lo que existe una representación A ₅ → SO ₃ ( R ) .

En esta imagen, los vértices de los poliedros representan los elementos del grupo, y el centro de la esfera representa el elemento identidad. Cada vértice representa una rotación sobre el eje que apunta desde el centro hasta ese vértice, en un ángulo igual a la distancia desde el origen, en radianes. Los vértices del mismo poliedro están en la misma clase de conjugación. Como la ecuación de clase de conjugación para A ₅ es 1 + 12 + 12 + 15 + 20 = 60 , obtenemos cuatro poliedros distintos (no triviales).

Los vértices de cada poliedro están en correspondencia biyectiva con los elementos de su clase de conjugación, con excepción de la clase de conjugación de los (2,2)-ciclos, que está representada por un icosidodecaedro en la superficie exterior, con sus vértices antípodas identificados entre sí. La razón de esta redundancia es que las rotaciones correspondientes son de π radianes, y por lo tanto pueden representarse por un vector de longitud π en cualquiera de las dos direcciones. Así, la clase de los (2,2)-ciclos contiene 15 elementos, mientras que el icosidodecaedro tiene 30 vértices.

Las dos clases de conjugación de doce 5-ciclos en A ₅ están representadas por dos icosaedros, de radios 2 π /5 y 4 π /5, respectivamente. El automorfismo externo no trivial en Out(A ₅ ) ≃ Z ₂ intercambia estas dos clases y los icosaedros correspondientes.

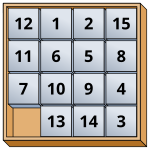
Se puede demostrar que el rompecabezas 15 , un famoso ejemplo de rompecabezas deslizante , se puede representar mediante el grupo alterno A ₁₅ , ^[2] porque las combinaciones del rompecabezas 15 se pueden generar mediante 3-ciclos . De hecho, cualquier rompecabezas deslizante 2 k − 1 con piezas cuadradas de igual tamaño se puede representar mediante A _{2 k −1} .

A ₄ es el grupo más pequeño que demuestra que el inverso del teorema de Lagrange no es cierto en general: dado un grupo finito G y un divisor d de | G |, no existe necesariamente un subgrupo de G con orden d : el grupo G = A ₄ ​​, de orden 12, no tiene ningún subgrupo de orden 6. Un subgrupo de tres elementos (generado por una rotación cíclica de tres objetos) con cualquier elemento no trivial distinto genera todo el grupo.

Para todo n > 4 , A _n no tiene subgrupos normales no triviales (es decir, propios) . Por lo tanto, A _n es un grupo simple para todo n > 4 . A ₅ es el grupo no resoluble más pequeño .

La homología de grupo de los grupos alternantes exhibe estabilización, como en la teoría de homotopía estable : para n suficientemente grande , es constante. Sin embargo, existen algunas homologías excepcionales de baja dimensión. Nótese que la homología del grupo simétrico exhibe una estabilización similar, pero sin las excepciones de baja dimensión (elementos de homología adicionales).

El primer grupo de homología coincide con la abelianización , y (ya que A _n es perfecto , salvo las excepciones citadas) es así:

H ₁ (A _n , Z) = Z ₁ para n = 0, 1, 2;

H1 (A3 _{, Z} ) = A^desde
₃= _A3 = _Z3 ;

H1 (A4 _{, Z} ) = A^desde
₄= _Z3 ;

H ₁ (A _n , Z) = Z ₁ para n ≥ 5.

Esto se ve fácilmente de manera directa, como sigue. A _n se genera por 3-ciclos – por lo que las únicas funciones de abelianización no triviales son A _n → Z ₃ , ya que los elementos de orden 3 deben corresponder a elementos de orden 3 – y para n ≥ 5 todos los 3-ciclos son conjugados, por lo que deben corresponder al mismo elemento en la abelianización, ya que la conjugación es trivial en los grupos abelianos. Por lo tanto, un 3-ciclo como (123) debe corresponder al mismo elemento que su inverso (321), pero por lo tanto debe corresponder a la identidad, ya que debe tener entonces un orden que divida a 2 y 3, por lo que la abelianización es trivial.

Para n < 3 , A _n es trivial y, por lo tanto, tiene abelianización trivial. Para A ₃ y A ₄ se puede calcular la abelianización directamente, notando que los 3-ciclos forman dos clases de conjugación (en lugar de ser todos conjugados) y hay funciones no triviales A ₃ ↠ Z ₃ (de hecho, un isomorfismo) y A ₄ ↠ Z ₃ .

Los multiplicadores de Schur de los grupos alternantes A _n (en el caso en que n sea al menos 5) son los grupos cíclicos de orden 2, excepto en el caso en que n sea 6 o 7, en cuyo caso también hay una triple cobertura. En estos casos, entonces, el multiplicador de Schur es (el grupo cíclico) de orden 6. ^[3] Estos se calcularon por primera vez en (Schur 1911).

H ₂ (A _n , Z) = Z ₁ para n = 1, 2, 3;

H ₂ (A _n , Z) = Z ₂ para n = 4, 5;

H ₂ (A _n , Z) = Z ₆ para n = 6, 7;

H ₂ (A _n , Z) = Z ₂ para n ≥ 8.

• Weisstein, Eric W. "Grupo alterno". MathWorld .
• Weisstein, Eric W. "Gráfico de grupo alterno". MathWorld .