E8 (matemáticas)
El uso de enlaces externos en este artículo puede no seguir las políticas o pautas de Wikipedia . ( Mayo de 2024 ) |
| Algebraic structure → Group theory Group theory |
|---|
 |
| Lie groups and Lie algebras |
|---|
 |
En matemáticas , E 8 es cualquiera de varios grupos de Lie simples excepcionales estrechamente relacionados , grupos algebraicos lineales o álgebras de Lie de dimensión 248; la misma notación se utiliza para la red de raíces correspondiente , que tiene rango 8. La designación E 8 proviene de la clasificación de Cartan-Killing de las álgebras de Lie simples complejas , que se dividen en cuatro series infinitas etiquetadas A n , B n , C n , D n , y cinco casos excepcionales etiquetados G 2 , F 4 , E 6 , E 7 y E 8 . El álgebra E 8 es el más grande y complicado de estos casos excepcionales.
Descripción básica
El grupo de Lie E 8 tiene dimensión 248. Su rango , que es la dimensión de su toro máximo , es ocho.
Por lo tanto, los vectores del sistema de raíces están en el espacio euclidiano de ocho dimensiones : se describen explícitamente más adelante en este artículo. El grupo de Weyl de E 8 , que es el grupo de simetrías del toro máximo que se inducen por conjugaciones en todo el grupo, tiene orden 2 14 3 5 5 2 7 = 696 729 600 .
El grupo compacto E 8 es único entre los grupos de Lie compactos simples en que su representación no trivial de menor dimensión es la representación adjunta (de dimensión 248) que actúa sobre el álgebra de Lie E 8 misma; también es el único que tiene las siguientes cuatro propiedades: centro trivial, compacto, simplemente conexo y simplemente enlazado (todas las raíces tienen la misma longitud).
Existe un álgebra de Lie E k para cada entero k ≥ 3. El mayor valor de k para el cual E k es de dimensión finita es k = 8, es decir, E k es de dimensión infinita para cualquier k > 8.
Formas reales y complejas
Existe un álgebra de Lie compleja única de tipo E 8 , correspondiente a un grupo complejo de dimensión compleja 248. El grupo de Lie complejo E 8 de dimensión compleja 248 puede considerarse como un grupo de Lie real simple de dimensión real 496. Este es simplemente conexo, tiene un subgrupo compacto máximo en la forma compacta (ver más abajo) de E 8 , y tiene un grupo de automorfismo externo de orden 2 generado por conjugación compleja.
Además del grupo de Lie complejo de tipo E 8 , existen tres formas reales del álgebra de Lie, tres formas reales del grupo con centro trivial (dos de las cuales tienen recubrimientos dobles no algebraicos, lo que da lugar a dos formas reales más), todas de dimensión real 248, como sigue:
- La forma compacta (que suele ser la que se busca si no se da otra información), que es simplemente conexa y tiene un grupo de automorfismos externos trivial.
- La forma dividida, EVIII (o E 8(8) ), que tiene un subgrupo compacto máximo Spin(16)/( Z /2 Z ), un grupo fundamental de orden 2 (lo que implica que tiene una doble cubierta , que es un grupo real de Lie simplemente conexo pero no es algebraico, ver más abajo) y tiene un grupo de automorfismo externo trivial.
- EIX (o E 8(−24) ), que tiene un subgrupo compacto máximo E 7 ×SU(2)/(−1,−1), un grupo fundamental de orden 2 (lo que nuevamente implica una doble cobertura, lo cual no es algebraico) y tiene un grupo de automorfismo externo trivial.
Para obtener una lista completa de formas reales de álgebras de Lie simples, consulte la lista de grupos de Lie simples .
mi8como un grupo algebraico
Mediante una base de Chevalley para el álgebra de Lie, se puede definir E 8 como un grupo algebraico lineal sobre los números enteros y, en consecuencia, sobre cualquier anillo conmutativo y en particular sobre cualquier cuerpo: esto define la llamada forma dividida (a veces también conocida como "desenrollada") de E 8 . Sobre un cuerpo algebraicamente cerrado, esta es la única forma; sin embargo, sobre otros cuerpos, a menudo hay muchas otras formas, o "giros" de E 8 , que se clasifican en el marco general de la cohomología de Galois (sobre un cuerpo perfecto k ) por el conjunto H 1 ( k ,Aut(E 8 )), que, debido a que el diagrama de Dynkin de E 8 (ver más abajo) no tiene automorfismos, coincide con H 1 ( k ,E 8 ). [1]
Sobre R , las componentes reales conexas de la identidad de estas formas algebraicamente retorcidas de E 8 coinciden con los tres grupos de Lie reales mencionados anteriormente, pero con una sutileza respecto del grupo fundamental: todas las formas de E 8 están simplemente conexas en el sentido de la geometría algebraica, lo que significa que no admiten recubrimientos algebraicos no triviales; las formas de grupos de Lie reales no compactos y simplemente conexos de E 8 no son, por lo tanto, algebraicas y no admiten representaciones fieles de dimensión finita.
Sobre campos finitos, el teorema de Lang-Steinberg implica que H 1 ( k ,E 8 )=0, lo que significa que E 8 no tiene formas retorcidas: ver más abajo.
Los caracteres de las representaciones de dimensión finita de las álgebras de Lie reales y complejas y de los grupos de Lie están dados por la fórmula de caracteres de Weyl . Las dimensiones de las representaciones irreducibles más pequeñas son (secuencia A121732 en la OEIS ):
- 1, 248, 3875, 27000, 30380, 147250, 779247, 1763125, 2450240, 4096000, 4881384, 6696000, 26411008, 70680000, 76271625, 43000, 146325270, 203205000, 281545875, 301694976, 344452500, 820260000, 1094951000, 2172667860, 2275896000, 2642777280, 2903770000, 3929713760, 4076399250, 4825673125, 6899079264, 8634368000 (dos veces), 12692520960...
La representación de 248 dimensiones es la representación adjunta . Hay dos representaciones irreducibles no isomórficas de dimensión 8634368000 (no es única; sin embargo, el siguiente entero con esta propiedad es 175898504162692612600853299200000 (secuencia A181746 en la OEIS )). Las representaciones fundamentales son aquellas con dimensiones 3875, 6696000, 6899079264, 146325270, 2450240, 30380, 248 y 147250 (correspondientes a los ocho nodos en el diagrama de Dynkin en el orden elegido para la matriz de Cartan a continuación, es decir, los nodos se leen primero en la cadena de siete nodos, y el último nodo se conecta al tercero).
Los coeficientes de las fórmulas de caracteres para representaciones irreducibles de dimensión infinita de E 8 dependen de algunas matrices cuadradas grandes que consisten en polinomios, los polinomios de Lusztig–Vogan , un análogo de los polinomios de Kazhdan–Lusztig introducidos para grupos reductivos en general por George Lusztig y David Kazhdan (1983). Los valores en 1 de los polinomios de Lusztig–Vogan dan los coeficientes de las matrices que relacionan las representaciones estándar (cuyos caracteres son fáciles de describir) con las representaciones irreducibles.
Estas matrices fueron calculadas después de cuatro años de colaboración por un grupo de 18 matemáticos y científicos informáticos , dirigido por Jeffrey Adams , con gran parte de la programación realizada por Fokko du Cloux . El caso más difícil (para grupos excepcionales) es la forma real dividida de E 8 (ver arriba), donde la matriz más grande tiene un tamaño de 453060×453060. Los polinomios de Lusztig-Vogan para todos los demás grupos simples excepcionales se conocen desde hace algún tiempo; el cálculo para la forma dividida de E 8 es mucho más largo que cualquier otro caso. El anuncio del resultado en marzo de 2007 recibió una atención extraordinaria de los medios (ver los enlaces externos), para sorpresa de los matemáticos que trabajaban en él.
Las representaciones de los grupos E 8 sobre cuerpos finitos están dadas por la teoría de Deligne-Lusztig .
Construcciones
Se puede construir la (forma compacta del) grupo E 8 como el grupo de automorfismos del álgebra de Lie e 8 correspondiente . Esta álgebra tiene una subálgebra de 120 dimensiones , por lo que (16) generada por J ij, así como 128 nuevos generadores Q a que se transforman como un espinor de Weyl–Majorana de espín (16). Estas afirmaciones determinan los conmutadores
así como
mientras que los conmutadores restantes (¡no anticonmutadores!) entre los generadores de espinores se definen como
Es posible entonces comprobar que se cumple la identidad de Jacobi .
Geometría
La forma real compacta de E 8 es el grupo de isometría del espacio simétrico compacto excepcional de Riemann EVIII de 128 dimensiones (en la clasificación de Cartan ). Se le conoce informalmente como el " plano proyectivo octooctoniónico " porque se puede construir usando un álgebra que es el producto tensorial de los octoniones consigo mismos, y también se le conoce como plano proyectivo de Rosenfeld , aunque no obedece a los axiomas habituales de un plano proyectivo. Esto se puede ver sistemáticamente usando una construcción conocida como el cuadrado mágico , debido a Hans Freudenthal y Jacques Tits (Landsberg & Manivel 2001).
mi8sistema de raíces















- tu = (1, φ , 0, −1, φ , 0,0,0)
- v = ( φ , 0, 1, φ , 0, −1,0,0)
- w = (0, 1, φ , 0, −1, φ , 0,0)
- 4 puntos en el origen
- 2 icosaedros
- 2 dodecaedros
- 4 icosaedros
- 1 icosidodecaedro
- 2 dodecaedros
- 2 icosaedros
- 1 icosidodecaedro
Un sistema de raíces de rango r es una configuración finita particular de vectores, llamados raíces , que abarcan un espacio euclidiano de dimensión r y satisfacen ciertas propiedades geométricas. En particular, el sistema de raíces debe ser invariante bajo reflexión a través del hiperplano perpendicular a cualquier raíz.
El sistema de raíces E 8 es un sistema de raíces de rango 8 que contiene 240 vectores de raíz que abarcan R 8 . Es irreducible en el sentido de que no se puede construir a partir de sistemas de raíces de rango menor. Todos los vectores de raíz en E 8 tienen la misma longitud. Es conveniente para varios propósitos normalizarlos para que tengan una longitud √ 2 . Estos 240 vectores son los vértices de un politopo semirregular descubierto por Thorold Gosset en 1900, a veces conocido como el politopo 4 21 .
Construcción
En el llamado sistema de coordenadas pares , E 8 se da como el conjunto de todos los vectores en R 8 con longitud al cuadrado igual a 2 tales que las coordenadas son todos números enteros o todos semienteros y la suma de las coordenadas es par.
Explícitamente, hay 112 raíces con entradas enteras obtenidas de
tomando una combinación arbitraria de signos y una permutación arbitraria de coordenadas, y 128 raíces con entradas de medio entero obtenidas de
tomando un número par de signos menos (o, equivalentemente, exigiendo que la suma de las ocho coordenadas sea par). Hay 240 raíces en total.
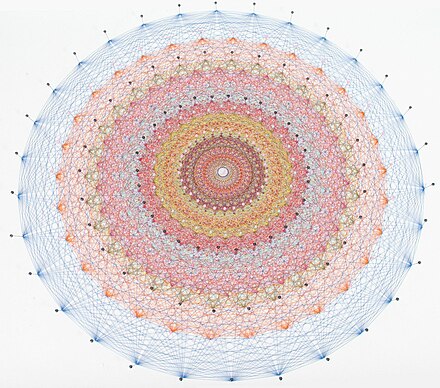
Las 112 raíces con entradas enteras forman un sistema de raíces D 8. El sistema de raíces E 8 también contiene una copia de A 8 (que tiene 72 raíces), así como E 6 y E 7 (de hecho, los dos últimos suelen definirse como subconjuntos de E 8 ).
En el sistema de coordenadas impar , E 8 se obtiene tomando las raíces en el sistema de coordenadas par y cambiando el signo de cualquiera de las coordenadas. Las raíces con entradas enteras son las mismas, mientras que aquellas con entradas semienteras tienen un número impar de signos negativos en lugar de un número par.
Diagrama de Dynkin
El diagrama de Dynkin para E 8 está dado por .
.
Este diagrama ofrece un resumen visual conciso de la estructura de la raíz. Cada nodo de este diagrama representa una raíz simple. Una línea que une dos raíces simples indica que están en un ángulo de 120° entre sí. Dos raíces simples que no están unidas por una línea son ortogonales .
Matriz de Cartan
La matriz de Cartan de un sistema de raíces de rango r es una matriz r × r cuyas entradas se derivan de las raíces simples. En concreto, las entradas de la matriz de Cartan están dadas por
donde ( , ) es el producto interno euclidiano y α i son las raíces simples. Las entradas son independientes de la elección de raíces simples (hasta el ordenamiento).
La matriz de Cartan para E 8 está dada por
El determinante de esta matriz es igual a 1.
Raíces simples

Un conjunto de raíces simples para un sistema de raíces Φ es un conjunto de raíces que forman una base para el espacio euclidiano abarcado por Φ con la propiedad especial de que cada raíz tiene componentes con respecto a esta base que son todos no negativos o todos no positivos.
Dada la matriz E 8 de Cartan (arriba) y un ordenamiento de nodos del diagrama de Dynkin de:
Una elección de raíces simples está dada por las filas de la siguiente matriz:
Con esta numeración de nodos en el diagrama de Dynkin, la raíz más alta del sistema de raíces tiene etiquetas de Coxeter (2, 3, 4, 5, 6, 4, 2, 3). Usando esta representación de las raíces simples, la raíz más baja viene dada por
La única raíz simple que se puede agregar a la raíz más baja para obtener otra raíz es la correspondiente al nodo 1 en esta etiqueta del diagrama de Dynkin, como se espera del diagrama de Dynkin afín para . El diagrama de Hasse a la derecha enumera las 120 raíces de altura positiva en relación con cualquier elección particular de raíces simples consistentes con esta numeración de nodos.
Obsérvese que el diagrama de Hasse no representa el álgebra de Lie completa, ni siquiera el sistema de raíces completo. Las 120 raíces de altura negativa relativas al mismo conjunto de raíces simples se pueden representar adecuadamente mediante una segunda copia del diagrama de Hasse con las flechas invertidas; pero es menos sencillo conectar estos dos diagramas mediante una base para el subálgebra de Cartan de ocho dimensiones. En la notación de la exposición de los generadores de Chevalley y las relaciones de Serre : En la medida en que una flecha representa el corchete de Lie por el generador asociado con una raíz simple, cada raíz en la capa de altura -1 del diagrama de Hasse invertido debe corresponder a algunos y solo puede tener una flecha hacia arriba, conectada a un nodo en la capa de altura 0 que representa el elemento del subálgebra de Cartan dado por . Pero las flechas hacia arriba de la capa de altura 0 deben representar entonces , donde es (la transpuesta de) la matriz de Cartan. Se podrían dibujar múltiples flechas hacia arriba desde cada una asociada con todo para lo cual es distinto de cero; pero esto no captura las entradas numéricas en la matriz de Cartan ni refleja el hecho de que cada una solo tiene un corchete de Lie distinto de cero con un grado de libertad en el subálgebra de Cartan (simplemente no el mismo grado de libertad que ).
Más fundamentalmente, esta organización implica que el lapso de los generadores designados como "la" subálgebra de Cartan es de alguna manera inherentemente especial, cuando en la mayoría de las aplicaciones, cualquier conjunto de ocho de los 248 generadores del álgebra de Lie (¡de los cuales hay muchos!) que conmuten mutuamente —o cualesquiera ocho derivaciones de Lie linealmente independientes y que conmuten mutuamente en cualquier variedad con estructura E 8— habrían servido igual de bien. Una vez que se ha seleccionado una subálgebra de Cartan (o se ha definido a priori , como en el caso de una red), una base de "generadores de Cartan" (los entre los generadores de Chevalley) y un sistema de raíces son una forma útil de describir la estructura relativa a esta subálgebra . Pero el mapa del sistema de raíces no es el territorio del álgebra de Lie (¡y mucho menos del grupo!). Dado un conjunto de generadores de Chevalley, la mayoría de los grados de libertad en un álgebra de Lie y sus escasos corchetes de Lie se pueden representar esquemáticamente como círculos y flechas, pero esto simplemente no funciona en la subálgebra de Cartan elegida. Tales son los peligros de las representaciones visuales esquemáticas de las estructuras matemáticas.
Grupo Weyl
El grupo Weyl de E 8 es del orden 696729600 y puede describirse como O+
8(2): tiene la forma 2. G .2 (es decir, una extensión del radical por el grupo cíclico de orden 2 de una extensión del grupo cíclico de orden 2 por un grupo G ) donde G es el único grupo simple de orden 174182400 (que puede describirse como PSΩ 8 + (2)). [3]
mi8enrejado de raíces
El tramo integral del sistema de raíces E 8 forma una red en R 8 llamada naturalmente red de raíces E 8. Esta red es bastante notable porque es la única red uniforme y unimodular (no trivial) con un rango menor a 16.
Subálgebras simples de E8

El álgebra de Lie E 8 contiene como subálgebras todas las álgebras de Lie excepcionales , así como muchas otras álgebras de Lie importantes en matemáticas y física. La altura del álgebra de Lie en el diagrama corresponde aproximadamente al rango del álgebra. Una línea desde un álgebra hacia abajo hasta un álgebra inferior indica que el álgebra inferior es una subálgebra del álgebra superior.
Grupos Chevalley de tipo E8
Chevalley (1955) demostró que los puntos del grupo algebraico (dividido) E 8 (ver arriba) sobre un cuerpo finito con q elementos forman un grupo de Chevalley finito , escrito generalmente E 8 ( q ), que es simple para cualquier q , [4] [5] y constituye una de las familias infinitas abordadas por la clasificación de grupos simples finitos . Su número de elementos está dado por la fórmula (secuencia A008868 en la OEIS ):
El primer término de esta secuencia, el orden de E 8 (2), es decir, 337 804 753 143 634 806 261 388 190 614 085 595 079 991 692 242 467 651 576 160 959 909 068 800 000 ≈3,38 × 10 74 , ya es mayor que el tamaño del grupo Monstruo . Este grupo E 8 (2) es el último descrito (pero sin su tabla de caracteres) en el ATLAS de Grupos Finitos . [6]
El multiplicador de Schur de E 8 ( q ) es trivial, y su grupo de automorfismos externos es el de los automorfismos de campo (es decir, cíclico de orden f si q = p f , donde p es primo).
Lusztig (1979) describió las representaciones unipotentes de grupos finitos de tipo E 8 .
Subgrupos, subálgebras y extensiones
Los grupos excepcionales más pequeños E 7 y E 6 se encuentran dentro de E 8 . En el grupo compacto, tanto E 6 ×SU(3)/( Z / 3 Z ) como E 7 ×SU(2)/(+1,−1) son subgrupos máximos de E 8 .

La representación adjunta de 248 dimensiones de E 8 puede considerarse en términos de su representación restringida al primero de estos subgrupos. Se transforma bajo E 6 ×SU(3) como una suma de representaciones de productos tensoriales , que pueden etiquetarse como un par de dimensiones como (78,1) + (1,8) + ( 27 ,3) + (27, 3 . (Dado que el subgrupo maximal es en realidad el cociente de este producto de grupo por un grupo finito, estas notaciones pueden tomarse estrictamente como indicativas de las representaciones infinitesimales (álgebra de Lie).) Dado que la representación adjunta puede describirse por las raíces junto con los generadores en el subálgebra de Cartan , podemos elegir un sistema de raíces E 6 particular dentro de E 8 y descomponer la representación de suma relativa a este E 6 . En esta descripción,
- (78,1), una copia de , consta de las 72 raíces con (− 1 ⁄ 2 ,− 1 ⁄ 2 ,− 1 ⁄ 2 ), (0,0,0), o ( 1 ⁄ 2 , 1 ⁄ 2 , 1 ⁄ 2 ) en las últimas tres dimensiones, junto con cinco generadores de Cartan correspondientes a las primeras cinco dimensiones y un generador de Cartan correspondiente a una suma igualmente ponderada de los últimos tres generadores de Cartan del sistema E 8 ;
- (1,8), una copia de , consta de las seis raíces con permutaciones de (0,1,−1) en las últimas tres dimensiones, junto con dos generadores de Cartan correspondientes a las dos combinaciones sin trazas de los últimos tres generadores de Cartan del sistema E 8 ;
- ( 27 ,3) consta de todas las raíces con permutaciones de (-1,0,0), (− 1 ⁄ 2 , 1 ⁄ 2 , 1 ⁄ 2 ), o (0,1,1) en las últimas tres dimensiones; y
- (27, 3 ) consta de todas las raíces con permutaciones de (1,0,0), ( 1 ⁄ 2 ,− 1 ⁄ 2 ,− 1 ⁄ 2 ), o (0,-1,-1) en las últimas tres dimensiones.
La representación adjunta de 248 dimensiones de E 8 , cuando se restringe de manera similar al segundo subgrupo máximo, se transforma bajo E 7 ×SU(2) como: (133,1) + (1,3) + (56,2). Podemos ver nuevamente la descomposición al observar las raíces junto con los generadores en el subálgebra de Cartan. En esta descripción,
- (133,1), una copia de , consta de las 126 raíces con (−1,−1), (− 1 ⁄ 2 ,− 1 ⁄ 2 ), (0,0), ( 1 ⁄ 2 , 1 ⁄ 2 ), o (1,1) en las dos últimas dimensiones, junto con seis generadores de Cartan correspondientes a las primeras seis dimensiones y un generador de Cartan correspondiente a una suma igualmente ponderada de los dos últimos generadores de Cartan del sistema E 8 ;
- (1,3), una copia de , consta de las dos raíces (0,0,0,0,0,0,1,−1), (0,0,0,0,0,0,−1,1), junto con un generador de Cartan correspondiente a la combinación sin trazas de los dos últimos generadores de Cartan del sistema E 8 ; y
- (56,2) consta de todas las raíces con permutaciones de (0,-1), ( 1 ⁄ 2 ,− 1 ⁄ 2 ), o (1,0) en las dos últimas dimensiones.
La conexión entre estas dos descripciones está dada por las construcciones de álgebra de Lie excepcional graduada de J. Tits y BN Allison . Cualquier representación de 27 dimensiones de E 6 puede ser equipada con una operación de producto de Jordan no asociativa (pero estrictamente asociativa de potencia ) para formar un álgebra de Albert (un caso excepcional importante en las construcciones algebraicas). La construcción de Kantor–Koecher–Tits aplicada a esta álgebra de Albert recupera la 78-dimensional como el álgebra de estructura reducida del álgebra de Albert. Esto , junto con las representaciones 27 y 27 y el operador de grado (el elemento del subálgebra de Cartan con peso -1 en el 27, +1 en el 27 y 0 en el 78), forma un álgebra de Lie de 3 grados. Una exposición completa de esta construcción se puede encontrar en textos estándar sobre álgebras de Jordan como Jacobson 1968 o McCrimmon 2004.
Comenzando esta construcción de álgebra de Lie de 3 grados con cualquier representación particular de 27 dimensiones, incrustada dentro de , de cualquier subgrupo E 6 particular de E 8 produce la subálgebra correspondiente . El particular en la descomposición E 7 ×SU(2) dada anteriormente corresponde a elegir el 27 que consiste en todas las raíces con (1,0,0), ( 1 ⁄ 2 ,- 1 ⁄ 2 ,- 1 ⁄ 2 ), o (0,-1,-1) en las últimas tres dimensiones (en orden), con el operador de grado que tiene peso (-1, 1 ⁄ 2 , 1 ⁄ 2 ) en estas dimensiones; o equivalentemente a elegir el " 27 " que consiste en todas las raíces con (-1,0,0), (− 1 ⁄ 2 , 1 ⁄ 2 , 1 ⁄ 2 ), o (0,1,1) en las últimas tres dimensiones (en orden), con el operador de grado teniendo peso (1,- 1 ⁄ 2 ,- 1 ⁄ 2 ) en estas dimensiones. Nótese que no hay nada especial en esta elección de dimensiones — el dentro del cual está incrustado el sistema de raíces no es el conjunto de ocho ejes independientes pero no ortogonales correspondientes a las raíces simples, y tres dimensiones cualesquiera servirán — y también hay construcciones que utilizan otras agrupaciones equivalentes de raíces. Lo que importa es que el núcleo del corchete de Lie con el generador elegido como el "operador de grado" sea una subálgebra (más una central asociada con el operador de grado mismo y el generador restante de la subálgebra de Cartan), no , , , etc.
(En el caso del álgebra de Lie simple, el signo del grado de la representación 27 versus 27 es una cuestión de convención, como lo es la escala de la calificación. Sin embargo, elegir -1 como el grado de la representación "vectorial" de 27 dimensiones es consistente con una extensión del álgebra de 3 grados a grados positivos más altos a través del álgebra exterior sobre la representación "covectorial" de 27. La representación "vectorial" se encuentra entonces, no en esta álgebra exterior de grado no negativo, sino en el álgebra graduada de derivaciones sobre el álgebra exterior; la de 78 dimensiones es el subálgebra de grado 0 (un subálgebra de las derivaciones internas por "formas 1 con valores vectoriales") de esta álgebra graduada de derivaciones. Para obtener detalles sobre cómo funciona esta estructura asimétrica a partir de un álgebra general de 3 grados, consulte las referencias en el corchete de Frölicher–Nijenhuis . La relevancia de esta observación para E 8 es simplemente que E 7 y ( Los E 8 son sus propios conjuntos de estructuras, que se distinguen como grupos/álgebras de Lie simples excepcionales, y que cualquier reconstrucción particular de ellos utilizando representaciones de sus subgrupos/subálgebras tendrá extensiones más allá del caso motivador. Las diferentes convenciones de signo, escala y relación conjugada en la literatura se deben no sólo a imprecisiones sino también a las direcciones en las que los autores buscan extender sus construcciones).
El distinguido en la descomposición E 7 ×SU(2) anterior se da entonces por el subálgebra de que conmuta con el operador de grado (que se encuentra en el subálgebra de Cartan de este ). De las cuatro raíces restantes en el , dos son de grado 1 ⁄ 2 y dos son de grado - 1 ⁄ 2 . En la convención donde el 27 de E 6 usado para construir el tiene grado -1 y el 27 tiene grado +1, los otros dos 27 tienen grado + 1 ⁄ 2 y los otros dos 27 tienen grado - 1 ⁄ 2 , como es evidente al permutar los valores de las últimas tres raíces en la descripción anterior. Agrupando estos 4×(1+27)=112 generadores para formar los subespacios grado + 1 ⁄ 2 y - 1 ⁄ 2 de (en relación con la elección original del operador grado dentro de ), a cada subespacio se le puede dar una operación de producto no asociativa (ni siquiera asociativa de potencia) bastante particular, lo que da como resultado dos copias del álgebra estructurable de 56 dimensiones de Brown. La construcción del álgebra de Lie de 5 grados de Allison basada en esta álgebra estructurable recupera el original . (La 5-graduación de Allison difiere de la anterior por un factor -2). Agrupar estos generadores de manera diferente, en función de sus pesos relativos al generador de Cartan del ortogonal a , da dos subespacios de 56 dimensiones que llevan cada uno la representación irreducible no trivial de dimensión más baja de E 7 . Cualquiera de estos puede combinarse con el generador de Cartan para formar un álgebra de Heisenberg de 57 dimensiones , y al unirlo se produce el álgebra de Lie (no simple) E 7 1/2 descrita por Landsberg y Manivel.
Desde la perspectiva en la que el subespacio de grado -1 de 27 dimensiones de (en relación con una elección de operador de grado) desempeña el papel de representación "vectorial" de E 6 y el 27 con raíces opuestas desempeña el papel de representación "covectorial", es natural buscar representaciones de "espinores" en los subespacios de grado + 1 ⁄ 2 y - 1 ⁄ 2 , o en alguna otra combinación de las representaciones ( 27 ,3) y (27, 3 ) de E 6 ×SU(3), e intentar relacionarlas con espinores geométricos en el sentido del álgebra de Clifford tal como se emplea en la teoría cuántica de campos . Las variaciones de esta idea son comunes en la literatura de física. Véase Distler y Garibaldi 2009 para una discusión de los obstáculos matemáticos para construir una teoría de calibre quiral basada en E 8 . La estructura relativa a su subálgebra, junto con la escala convencional de los elementos de la subálgebra de Cartan, invita a extensiones por analogía geométrica, pero no implica necesariamente una relación con la geometría de baja dimensión o la física de baja energía. Lo mismo puede decirse de las conexiones con las álgebras de Jordan y Heisenberg, cuyos orígenes históricos están entrelazados con el desarrollo de la mecánica cuántica. No todas las representaciones visuales que evocan una pipa de tabaco contendrán tabaco.
Los grupos cuasi-simples finitos que pueden incrustarse en (la forma compacta de) E8 fueron descubiertos por Griess y Ryba (1999).
El grupo de Dempwolff es un subgrupo de (la forma compacta de) E 8 . Está contenido en el grupo esporádico de Thompson , que actúa sobre el espacio vectorial subyacente del grupo de Lie E 8 pero no conserva el corchete de Lie. El grupo de Thompson fija una red y sí conserva el corchete de Lie de esta red módulo 3, lo que da una incrustación del grupo de Thompson en E 8 ( F 3 ).
A la derecha se muestran las incrustaciones de los subgrupos máximos de E 8 hasta la dimensión 248.
Aplicaciones
El grupo de Lie E 8 tiene aplicaciones en física teórica y especialmente en teoría de cuerdas y supergravedad . E 8 × E 8 es el grupo de calibración de uno de los dos tipos de cuerda heterótica y es uno de los dos grupos de calibración libres de anomalías que se pueden acoplar a la supergravedad N = 1 en diez dimensiones. E 8 es el grupo de dualidad U de la supergravedad en un ocho-toro (en su forma dividida).
Una forma de incorporar el modelo estándar de física de partículas a la teoría de cuerdas heterótica es la ruptura de simetría de E 8 a su subálgebra máxima SU(3)×E 6 .
En 1982, Michael Freedman utilizó la red E 8 para construir un ejemplo de una variedad topológica de 4 elementos , la variedad E 8 , que no tiene una estructura suave .
La incompleta "Teoría excepcionalmente simple del todo " de Antony Garrett Lisi intenta describir todas las interacciones fundamentales conocidas en física como parte del álgebra de Lie E 8. [7] [8]
R. Coldea, DA Tennant y EM Wheeler et al. (2010) informaron sobre un experimento en el que los espines electrónicos de un cristal de cobalto - niobio exhibieron, bajo ciertas condiciones, dos de los ocho picos relacionados con E8 que fueron predichos por Zamolodchikov (1989). [9] [10]
Historia
Wilhelm Killing (1888a, 1888b, 1889, 1890) descubrió el álgebra de Lie compleja E 8 durante su clasificación de álgebras de Lie simples y compactas, aunque no demostró su existencia, que fue demostrada por primera vez por Élie Cartan . Cartan determinó que un álgebra de Lie compleja simple de tipo E 8 admite tres formas reales. Cada una de ellas da lugar a un grupo de Lie simple de dimensión 248, exactamente uno de los cuales (como para cualquier álgebra de Lie compleja simple) es compacto . Chevalley (1955) introdujo grupos algebraicos y álgebras de Lie de tipo E 8 sobre otros cuerpos : por ejemplo, en el caso de cuerpos finitos conducen a una familia infinita de grupos finitos simples de tipo Lie. E 8 sigue siendo un área de investigación básica activa por parte de Atlas of Lie Groups and Representations , que tiene como objetivo determinar las representaciones unitarias de todos los grupos de Lie. [11]
Véase también
Notas al pie
- ^ Платонов, Владимир П.; Рапинчук, Андрей С. (1991), Алгебраические группы и теория чисел , Наука, ISBN 5-02-014191-7(Traducción al inglés: Platonov, Vladimir P.; Rapinchuk, Andrei S. (1994), Grupos algebraicos y teoría de números , Academic Press, ISBN 0-12-558180-7), §2.2.4
- ^ "Las 600 celdas (Parte 1)". 16 de diciembre de 2017.
- ^ Conway, John Horton ; Curtis, Robert Turner; Norton, Simon Phillips ; Parker, Richard A ; Wilson, Robert Arnott (1985), Atlas de grupos finitos : subgrupos máximos y caracteres ordinarios para grupos simples , Oxford University Press, pág. 85, ISBN 0-19-853199-0
- ^ Carter, Roger W. (1989), Grupos simples de tipo Lie , Wiley Classics Library, John Wiley & Sons, ISBN 0-471-50683-4
- ^ Wilson, Robert A. (2009), Los grupos finitos simples , Textos de posgrado en matemáticas , vol. 251, Springer-Verlag , ISBN 978-1-84800-987-5
- ^ Conway y otros, op. cit. , pág. 235.
- ^ AG Lisi ; JO Weatherall (2010). "Una teoría geométrica del todo". Scientific American . 303 (6): 54–61. Código Bibliográfico :2010SciAm.303f..54L. doi :10.1038/scientificamerican1210-54. PMID 21141358.
- ^ Greg Boustead (17 de noviembre de 2008). "El enfoque excepcional de Garrett Lisi para todo". Revista SEED . Archivado desde el original el 2 de febrero de 2009.
{{cite news}}: CS1 maint: unfit URL (link) - ^ Shiga, David (7 de enero de 2010). «La estructura matemática más hermosa aparece en el laboratorio por primera vez». New Scientist . Consultado el 1 de febrero de 2023 .
- ^¿ Un imán unidimensional detectó un álgebra de Lie de 248 dimensiones?, Avisos de la Sociedad Matemática Americana , septiembre de 2011.
- ^ "Matemáticas AIM: Representaciones de E8". aimath.org .
Referencias
- Adams, J. Frank (1996), Conferencias sobre grupos de Lie excepcionales, Chicago Lectures in Mathematics, University of Chicago Press , ISBN 978-0-226-00526-3, Sr. 1428422
- Baez, John C. (2002), "Los octoniones", Boletín de la American Mathematical Society , Nueva serie, 39 (2): 145–205, arXiv : math/0105155 , doi :10.1090/S0273-0979-01-00934-X, MR 1886087, S2CID 586512
- Chevalley, Claude (1955), "Sur sures groupes simples", The Tohoku Mathematical Journal , segunda serie, 7 (1–2): 14–66, doi : 10.2748/tmj/1178245104 , ISSN 0040-8735, MR 0073602
- Coldea, R.; Tennant, DA; Wheeler, EM; Wawrzynska, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P.; Kiefer, K. (2010), "Criticidad cuántica en una cadena de Ising: evidencia experimental de simetría E 8 emergente ", Science , 327 (5962): 177–180, arXiv : 1103.3694 , Bibcode :2010Sci...327..177C, doi :10.1126/science.1180085, PMID 20056884, S2CID 206522808
- Garibaldi, Skip (2016), "E 8 , el grupo más excepcional", Boletín de la Sociedad Matemática Americana , 53 (4): 643–671, arXiv : 1605.01721 , doi :10.1090/bull/1540, S2CID 15810796
- Griess, Robert L.; Ryba, AJE (1999), "¡Los grupos finitos simples que se incrustan proyectivamente en un grupo de Lie excepcional están clasificados!", Boletín de la American Mathematical Society , Nueva serie, 36 (1): 75–93, doi : 10.1090/S0273-0979-99-00771-5 , MR 1653177
- Matar, Wilhelm (1888a), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen , 31 (2): 252–290, doi :10.1007/BF01211904, S2CID 120501356
- Matar, Wilhelm (1888b), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen , 33 (1): 1–48, doi :10.1007/BF01444109, S2CID 124198118
- Killing, Wilhelm (1889), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen , 34 (1): 57–122, doi :10.1007/BF01446792, S2CID 179177899, archivado desde el original el 21 de febrero de 2015 , recuperado en 2013 -09-12
- Matar, Wilhelm (1890), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen , 36 (2): 161–189, doi :10.1007/BF01207837, S2CID 179178061
- Landsberg, Joseph M.; Manivel, Laurent (2001), "La geometría proyectiva del cuadrado mágico de Freudenthal", Journal of Algebra , 239 (2): 477–512, arXiv : math/9908039 , doi :10.1006/jabr.2000.8697, MR 1832903, S2CID 16320642
- Lusztig, George (1979), "Representaciones unipotentes de un grupo Chevalley finito de tipo E8", The Quarterly Journal of Mathematics , Segunda serie, 30 (3): 315–338, doi :10.1093/qmath/30.3.301, ISSN 0033-5606, MR 0545068
- Lusztig, George ; Vogan, David (1983), "Singularidades de cierres de órbitas K en variedades bandera", Inventiones Mathematicae , 71 (2), Springer-Verlag : 365–379, Bibcode :1983InMat..71..365L, doi :10.1007/BF01389103, S2CID 120917588
- Zamolodchikov, AB (1989), "Integrales de movimiento y matriz S del modelo de Ising (escalado) T=T c con campo magnético", International Journal of Modern Physics A , 4 (16): 4235–4248, Bibcode :1989IJMPA...4.4235Z, doi :10.1142/S0217751X8900176X, MR 1017357
Enlaces externos
Cálculo del polinomio de Lusztig-Vogan
- Atlas de grupos de Lie
- Polinomios de Kazhdan-Lusztig-Vogan para E8
- Narrativa del proyecto para calcular polinomios de Kazhdan-Lusztig para E8
- Instituto Americano de Matemáticas (marzo de 2007), Mapa de Matemáticos E8
- El n-Category Café, una publicación del blog de la Universidad de Texas escrita por John Baez en E 8 .
Otros enlaces
- Representación gráfica del sistema radicular E8.
- La lista de dimensiones de las representaciones irreducibles de la forma compleja de E 8 es la secuencia A121732 en la OEIS .


![{\displaystyle \left[J_{ij},J_{k\ell}\right]=\delta _{jk}J_{i\ell}-\delta _{j\ell}J_{ik}-\delta _{ik}J_{j\ell}+\delta _{i\ell}J_{jk}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bec09a9b82bdba74164819ce65265a0a00b09979)
![{\displaystyle \left[J_{ij},Q_{a}\right]={\frac {1}{4}}\left(\gamma _{i}\gamma _{j}-\gamma _{j}\gamma _{i}\right)_{ab}Q_{b},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95c26842f45b69aa8321bb2824eb3cae60a765fe)
![{\displaystyle \left[Q_{a},Q_{b}\right]=\gamma _{ac}^{[i}\gamma _{cb}^{j]}J_{ij}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d9a1b2b940688a05ba4c1fe3c678cf45c498ec)



![{\displaystyle \left[{\begin{array}{rr}2&-1&0&0&0&0&0&0\\-1&2&-1&0&0&0&0&0\\0&-1&2&-1&0&0&0&0\\0&0&-1&2&-1&0&0&0\\0&0&-1&2&-1&0&-1\\0&0&0&0&-1&2&-1&0\\0&0&0&0&-1&2&-1&0\\0&0&0&0&0&-1&2&0\\0&0&0&0&-1&0&0&2\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/744a9f7c0ba8232d9458e553177042d90ff6ebd5)
![{\displaystyle \left[{\begin{array}{rr}1&-1&0&0&0&0&0&0\\0&1&-1&0&0&0&0&0\\0&0&1&-1&0&0&0&0\\0&0&0&1&-1&0&0&0\\0&0&0&0&1&-1&0&0\\0&0&0&0&0&1&-1&0&0\\0&0&0&0&0&1&1&0\\-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&0&0&0&0&0&1&-1&0\\\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ced7ddba33a94a3b3e33d95c8b34d1dd94200e01)
![{\displaystyle \left[{\begin{array}{rr}-1&0&0&0&0&0&0&1\\\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe60dcef180bbd3b7a5ae0d5cfa9c94a7fc3a3f5)



![{\displaystyle h_{i}=[e_{i},f_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dab22318667163fed6ffa024e12c7511763d312)
![{\ Displaystyle [e_ {i}, h_ {j}] = -a_ {ji} e_ {i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70c091066e333cb11e80abc1881690737b2179b9)


![{\displaystyle [e_{i},h_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/418b426256d20d8a6ea4c47bd1623b53cb7c9845)












