Rotación óptica

La rotación óptica , también conocida como rotación de polarización o birrefringencia circular , es la rotación de la orientación del plano de polarización sobre el eje óptico de la luz polarizada linealmente a medida que viaja a través de ciertos materiales. La birrefringencia circular y el dicroísmo circular son las manifestaciones de la actividad óptica . La actividad óptica ocurre solo en materiales quirales , aquellos que carecen de simetría especular microscópica. A diferencia de otras fuentes de birrefringencia que alteran el estado de polarización de un haz, la actividad óptica se puede observar en fluidos . Esto puede incluir gases o soluciones de moléculas quirales como azúcares, moléculas con estructura secundaria helicoidal como algunas proteínas y también cristales líquidos quirales . También se puede observar en sólidos quirales como ciertos cristales con una rotación entre planos cristalinos adyacentes (como el cuarzo ) o metamateriales .

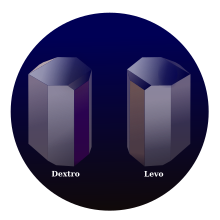
Al observar la fuente de luz, la rotación del plano de polarización puede ser hacia la derecha ( dextrógiro o dextrógiro — d -rotativo, representado por (+), en el sentido de las agujas del reloj), o hacia la izquierda ( levógiro o levógiro — l -rotativo, representado por (−), en el sentido contrario a las agujas del reloj) dependiendo de qué estereoisómero sea dominante. Por ejemplo, la sacarosa y el alcanfor son d -rotativos mientras que el colesterol es l -rotativo. Para una sustancia dada, el ángulo por el cual se rota la polarización de la luz de una longitud de onda específica es proporcional a la longitud del camino a través del material y (para una solución) proporcional a su concentración.

La actividad óptica se mide utilizando una fuente polarizada y un polarímetro . Se trata de una herramienta que se utiliza especialmente en la industria azucarera para medir la concentración de azúcar del jarabe y, en general, en química para medir la concentración o la relación enantiomérica de las moléculas quirales en solución. La modulación de la actividad óptica de un cristal líquido, observada entre dos polarizadores de láminas , es el principio de funcionamiento de las pantallas de cristal líquido (que se utilizan en la mayoría de los televisores y monitores de ordenador modernos).

La dextrorrotación y la levorrotación (también escritas levorrotación ) ^{[1] [2]} en química y física son la rotación óptica de la luz polarizada en un plano . Desde el punto de vista del observador, la dextrorrotación se refiere a la rotación en el sentido de las agujas del reloj o hacia la derecha, y la levorrotación se refiere a la rotación en el sentido contrario a las agujas del reloj o hacia la izquierda. ^{[3] [4]}

Un compuesto químico que causa dextrorrotación es dextrógiro o dextrógiro , mientras que un compuesto que causa levógiro es levógiro o levógiro . ^[5] Los compuestos con estas propiedades consisten en moléculas quirales y se dice que tienen actividad óptica. Si una molécula quiral es dextrógira, su enantiómero (imagen especular geométrica) será levógiro, y viceversa. Los enantiómeros rotan la luz polarizada en el plano la misma cantidad de grados, pero en direcciones opuestas.

Un compuesto puede etiquetarse como dextrógiro utilizando el prefijo "(+)-" o " d -". Del mismo modo, un compuesto levógiro puede etiquetarse utilizando el prefijo "(−)-" o " l -". Los prefijos " d -" y " l -" en minúscula están obsoletos y son distintos de los prefijos " D -" y " L -" en MAYÚSCULAS . Los prefijos " D -" y " L -" se utilizan para especificar el enantiómero de compuestos orgánicos quirales en bioquímica y se basan en la configuración absoluta del compuesto en relación con el (+)- gliceraldehído , que es la forma D por definición. El prefijo utilizado para indicar la configuración absoluta no está directamente relacionado con el prefijo (+) o (−) utilizado para indicar la rotación óptica en la misma molécula. Por ejemplo, nueve de los diecinueve L - aminoácidos presentes de forma natural en las proteínas son, a pesar del prefijo L- , en realidad dextrógiros (a una longitud de onda de 589 nm), y la D - fructosa a veces se denomina "levulosa" porque es levógira.

Los prefijos D y L describen la molécula como un todo, al igual que los prefijos (+) y (−) para la rotación óptica. Por el contrario, los prefijos ( R ) y ( S ) de las reglas de prioridad de Cahn–Ingold–Prelog caracterizan la configuración absoluta de cada estereocentro quiral específico con la molécula, en lugar de una propiedad de la molécula como un todo. Una molécula que tiene exactamente un estereocentro quiral (generalmente un átomo de carbono asimétrico ) puede etiquetarse como ( R ) o ( S ), pero una molécula que tiene múltiples estereocentros necesita más de una etiqueta. Por ejemplo, el aminoácido esencial L -treonina contiene dos estereocentros quirales y se escribe (2 S ,3 S )-treonina. No existe una relación estricta entre las designaciones R/S, D / L y (+)/(−), aunque existen algunas correlaciones. Por ejemplo, de los aminoácidos naturales, todos son L , y la mayoría son ( S ). En algunas moléculas, el enantiómero ( R ) es el enantiómero dextrógiro (+) y en otros casos es el enantiómero levógiro (−). La relación debe determinarse caso por caso con mediciones experimentales o modelos informáticos detallados. ^[6]

La rotación de la orientación de la luz polarizada linealmente fue observada por primera vez en 1811 en cuarzo por el físico francés François Arago . ^[7] En 1820, el astrónomo inglés Sir John FW Herschel descubrió que diferentes cristales de cuarzo individuales, cuyas estructuras cristalinas son imágenes especulares entre sí (ver ilustración), rotan la polarización lineal en cantidades iguales pero en direcciones opuestas. ^[8] Jean Baptiste Biot también observó la rotación del eje de polarización en ciertos líquidos ^[9] y vapores de sustancias orgánicas como la trementina . ^[10] En 1822, Augustin-Jean Fresnel descubrió que la rotación óptica podía explicarse como una especie de birrefringencia : mientras que los casos previamente conocidos de birrefringencia se debían a las diferentes velocidades de la luz polarizada en dos planos perpendiculares, la rotación óptica se debía a las diferentes velocidades de la luz polarizada circularmente de derecha e izquierda. ^{[11] Desde entonces se han utilizado} polarímetros simples para medir las concentraciones de azúcares simples, como la glucosa , en solución. De hecho, un nombre para la D -glucosa (el isómero biológico) es dextrosa , en referencia al hecho de que hace que la luz polarizada linealmente rote hacia la derecha o el lado dextrógiro. De manera similar, la levulosa, más comúnmente conocida como fructosa , hace que el plano de polarización rote hacia la izquierda. La fructosa es incluso más fuertemente levógira de lo que la glucosa es dextrógira. El jarabe de azúcar invertido , formado comercialmente por la hidrólisis del jarabe de sacarosa a una mezcla de los azúcares simples componentes, fructosa y glucosa, recibe su nombre del hecho de que la conversión hace que la dirección de rotación se "invierta" de derecha a izquierda.

En 1849, Louis Pasteur resolvió un problema relativo a la naturaleza del ácido tartárico . ^[12] Una solución de este compuesto derivado de seres vivos (en concreto, de las heces del vino ) hace rotar el plano de polarización de la luz que pasa a través de ella, pero el ácido tartárico derivado por síntesis química no tiene ese efecto, aunque sus reacciones son idénticas y su composición elemental es la misma. Pasteur se dio cuenta de que los cristales vienen en dos formas asimétricas que son imágenes especulares una de la otra. Al clasificar los cristales a mano se obtuvieron dos formas del compuesto: las soluciones de una forma hacen rotar la luz polarizada en el sentido de las agujas del reloj, mientras que la otra forma hace rotar la luz en el sentido contrario a las agujas del reloj. Una mezcla igual de las dos no tiene efecto polarizador sobre la luz. Pasteur dedujo que la molécula en cuestión es asimétrica y podría existir en dos formas diferentes que se parecen entre sí como lo harían los guantes para la mano izquierda y la derecha, y que la forma orgánica del compuesto consiste puramente en un tipo.

En 1874, Jacobus Henricus van 't Hoff ^[13] y Joseph Achille Le Bel ^[14] propusieron de forma independiente que este fenómeno de actividad óptica en compuestos de carbono podría explicarse suponiendo que los 4 enlaces químicos saturados entre los átomos de carbono y sus vecinos están dirigidos hacia las esquinas de un tetraedro regular. Si los 4 vecinos son todos diferentes, entonces hay dos posibles ordenaciones de los vecinos alrededor del tetraedro, que serán imágenes especulares entre sí. Esto condujo a una mejor comprensión de la naturaleza tridimensional de las moléculas.

En 1945, Charles William Bunn ^[15] predijo la actividad óptica de las estructuras aquirales, si la dirección de propagación de la onda y la estructura aquiral forman una disposición experimental que es diferente de su imagen especular. Esta actividad óptica debida a la quiralidad extrínseca se observó en los años 1960 en cristales líquidos. ^{[16] [17]}

En 1950, Sergey Vavilov ^[18] predijo una actividad óptica que depende de la intensidad de la luz y el efecto de la actividad óptica no lineal se observó en 1979 en cristales de yodato de litio . ^[19]

La actividad óptica se observa normalmente en la luz transmitida. Sin embargo, en 1988, MP Silverman descubrió que la rotación de polarización también puede ocurrir en la luz reflejada desde sustancias quirales. ^[20] Poco después, se observó que los medios quirales también pueden reflejar ondas polarizadas circularmente dextrógiras y levógiras con diferentes eficiencias. ^[21] Estos fenómenos de birrefringencia circular especular y dicroísmo circular especular se conocen conjuntamente como actividad óptica especular. La actividad óptica especular es muy débil en los materiales naturales.

En 1898, Jagadish Chandra Bose describió la capacidad de las estructuras artificiales retorcidas para rotar la polarización de las microondas . ^[22] Desde principios del siglo XXI, el desarrollo de materiales artificiales ha llevado a la predicción ^[23] y realización ^{[24] [25]} de metamateriales quirales con actividad óptica que excede la de los medios naturales en órdenes de magnitud en la parte óptica del espectro. Se ha observado que la quiralidad extrínseca asociada con la iluminación oblicua de metasuperficies que carecen de simetría rotacional doble conduce a una gran actividad óptica lineal en transmisión ^[26] y reflexión, ^[27] así como a una actividad óptica no lineal que excede la del yodato de litio en 30 millones de veces. ^[28]

La actividad óptica se produce debido a las moléculas disueltas en un fluido o debido al propio fluido sólo si las moléculas son uno de dos (o más) estereoisómeros ; esto se conoce como enantiómero . La estructura de una molécula de este tipo es tal que no es idéntica a su imagen especular (que sería la de un estereoisómero diferente, o el "enantiómero opuesto"). En matemáticas, esta propiedad también se conoce como quiralidad . Por ejemplo, una varilla de metal no es quiral, ya que su apariencia en un espejo no se distingue de sí misma. Sin embargo, un tornillo o la base de una bombilla (o cualquier tipo de hélice ) sí lo es ; una rosca de tornillo derecha ordinaria, vista en un espejo, aparecería como un tornillo zurdo (muy poco común) que no podría enroscarse en una tuerca ordinaria (diestra). Un humano visto en un espejo tendría su corazón en el lado derecho, clara evidencia de quiralidad, mientras que el reflejo en el espejo de una muñeca podría ser perfectamente indistinguible de la muñeca misma.

Para que se manifieste actividad óptica, un fluido debe contener solo un estereoisómero o la preponderancia de uno. Si hay dos enantiómeros presentes en proporciones iguales, sus efectos se cancelan y no se observa actividad óptica; esto se denomina mezcla racémica . Pero cuando hay un exceso enantiomérico , más de un enantiómero que del otro, la cancelación es incompleta y se observa actividad óptica. Muchas moléculas naturales están presentes como un solo enantiómero (como muchos azúcares). Las moléculas quirales producidas dentro de los campos de la química orgánica o la química inorgánica son racémicas a menos que se emplee un reactivo quiral en la misma reacción.

En el nivel fundamental, la rotación de polarización en un medio ópticamente activo es causada por la birrefringencia circular, y puede entenderse mejor de esa manera. Mientras que la birrefringencia lineal en un cristal implica una pequeña diferencia en la velocidad de fase de la luz de dos polarizaciones lineales diferentes, la birrefringencia circular implica una pequeña diferencia en las velocidades entre polarizaciones circulares dextrógiras e levógiras . ^[11] Piense en un enantiómero en una solución como una gran cantidad de pequeñas hélices (o tornillos), todas dextrógiras, pero en orientaciones aleatorias. La birrefringencia de este tipo es posible incluso en un fluido porque la lateralidad de las hélices no depende de su orientación: incluso cuando se invierte la dirección de una hélice, todavía parece dextrógiras. Y la luz polarizada circularmente en sí misma es quiral: a medida que la onda avanza en una dirección, los campos eléctricos (y magnéticos) que la componen giran en el sentido de las agujas del reloj (o en sentido contrario para la polarización circular opuesta), trazando un patrón de tornillo dextrógiratorio (o levógiratorio) en el espacio. Además del índice de refracción en masa , que reduce sustancialmente la velocidad de fase de la luz en cualquier material dieléctrico (transparente) en comparación con la velocidad de la luz (en el vacío), existe una interacción adicional entre la quiralidad de la onda y la quiralidad de las moléculas. Cuando sus quiralidades son las mismas, habrá un pequeño efecto adicional en la velocidad de la onda, pero la polarización circular opuesta experimentará un pequeño efecto opuesto, ya que su quiralidad es opuesta a la de las moléculas.

Sin embargo, a diferencia de la birrefringencia lineal, la rotación óptica natural (en ausencia de un campo magnético) no se puede explicar en términos de un tensor de permitividad material local (es decir, una respuesta de carga que solo depende del vector de campo eléctrico local), ya que las consideraciones de simetría lo prohíben. En cambio, la birrefringencia circular solo aparece cuando se considera la no localidad de la respuesta del material, un fenómeno conocido como dispersión espacial . ^[29] La no localidad significa que los campos eléctricos en una ubicación del material impulsan corrientes en otra ubicación del material. La luz viaja a una velocidad finita, y aunque es mucho más rápida que los electrones, hay una diferencia si la respuesta de carga quiere viajar naturalmente junto con el frente de onda electromagnético o en sentido opuesto. La dispersión espacial significa que la luz que viaja en diferentes direcciones (diferentes vectores de onda) ve un tensor de permitividad ligeramente diferente. La rotación óptica natural requiere un material especial, pero también depende del hecho de que el vector de onda de la luz es distinto de cero, y un vector de onda distinto de cero pasa por alto las restricciones de simetría en la respuesta local (vector de onda cero). Sin embargo, todavía existe simetría inversa, por lo que la dirección de la rotación óptica natural debe "invertirse" cuando se invierte la dirección de la luz, en contraste con la rotación magnética de Faraday . Todos los fenómenos ópticos tienen cierta influencia de no localidad/vector de onda, pero generalmente es insignificante; la rotación óptica natural, de manera bastante única, la requiere absolutamente. ^[29]

La velocidad de fase de la luz en un medio se expresa comúnmente utilizando el índice de refracción n , definido como la velocidad de la luz (en el espacio libre) dividida por su velocidad en el medio. La diferencia en los índices de refracción entre las dos polarizaciones circulares cuantifica la fuerza de la birrefringencia circular (rotación de polarización).

${\displaystyle \Delta n=n_{RHC}-n_{LHC}\,}$.

Si bien es pequeño en materiales naturales, se han reportado ejemplos de birrefringencia circular gigante que resulta en un índice de refracción negativo para una polarización circular para metamateriales quirales. ^{[30] [31]}${\displaystyle \Delta n}$

La rotación familiar del eje de polarización lineal se basa en la comprensión de que una onda polarizada linealmente también puede describirse como la superposición (adición) de una onda polarizada circularmente izquierda y derecha en igual proporción. La diferencia de fase entre estas dos ondas depende de la orientación de la polarización lineal, que llamaremos , y sus campos eléctricos tienen una diferencia de fase relativa de la cual luego se suma para producir la polarización lineal:${\displaystyle \theta_{0}}$${\displaystyle 2\theta _{0}}$

${\displaystyle \mathbf {E} _{\theta _{0}}={\frac {\sqrt {2}}{2}}(e^{-i\theta _{0}}\mathbf {E} _{RHC}+e^{i\theta _{0}}\mathbf {E} _{LHC})\,\,,}$

donde es el campo eléctrico de la onda neta, mientras que y son las dos funciones base polarizadas circularmente (que tienen una diferencia de fase cero). Suponiendo que la propagación se produce en la dirección +z , podríamos escribir y en términos de sus componentes x e y de la siguiente manera:${\displaystyle \mathbf {E} _ {\theta _ {0}}}$${\displaystyle \mathbf {E} _ {RHC}}$${\displaystyle \mathbf {E} _ {LHC}}$${\displaystyle \mathbf {E} _ {RHC}}$${\displaystyle \mathbf {E} _ {LHC}}$

${\displaystyle \mathbf {E} _{RHC}={\frac {\sqrt {2}}{2}}({\hat {x}}+i{\hat {y}})}$

${\displaystyle \mathbf {E} _{LHC}={\frac {\sqrt {2}}{2}}({\hat {x}}-i{\hat {y}})}$

donde y son vectores unitarios, e i es la unidad imaginaria , que en este caso representa el desfase de 90 grados entre los componentes x e y en los que hemos descompuesto cada polarización circular. Como es habitual cuando se trabaja con notación fasorial , se entiende que dichas cantidades se deben multiplicar por y luego el campo eléctrico real en cualquier instante se da por la parte real de ese producto.${\displaystyle {\hat {x}}}$${\displaystyle {\hat {y}}}$${\displaystyle e^{-i\omega t}}$

Sustituyendo estas expresiones por y en la ecuación por obtenemos:${\displaystyle \mathbf {E} _ {RHC}}$${\displaystyle \mathbf {E} _ {LHC}}$${\displaystyle \mathbf {E} _ {\theta _ {0}}}$

${\displaystyle \mathbf {E} _{\theta _{0}}={\frac {\sqrt {2}}{2}}(e^{-i\theta _{0}}\mathbf {E} _{RHC}+e^{i\theta _{0}}\mathbf {E} _{LHC})\,\,}$

${\displaystyle ={\frac {1}{2}}({\hat {x}}(e^{-i\theta _{0}}+e^{i\theta _{0}})+{\hat {y}}i(e^{-i\theta _{0}}-e^{i\theta _{0}}))\,\,}$

${\displaystyle ={\hat {x}}\cos(\theta _{0})+{\hat {y}}\sin(\theta _{0})}$

La última ecuación muestra que el vector resultante tiene los componentes x e y en fase y orientados exactamente en la dirección, como habíamos previsto, lo que justifica la representación de cualquier estado polarizado linealmente en ángulo como la superposición de componentes polarizados circularmente derecho e izquierdo con una diferencia de fase relativa de . Ahora supongamos la transmisión a través de un material ópticamente activo que induce una diferencia de fase adicional entre las ondas polarizadas circularmente derecha e izquierda de . Llamemos al resultado de pasar la onda original linealmente polarizada en ángulo a través de este medio. Esto aplicará factores de fase adicionales de y a los componentes polarizados circularmente derecho e izquierdo de :${\displaystyle \theta_{0}}$${\estilo de visualización \theta}$${\estilo de visualización 2\theta}$${\displaystyle 2\Delta \theta}$${\displaystyle \mathbf {E} _ {fuera}}$${\estilo de visualización \theta}$${\displaystyle -\Delta \theta}$${\displaystyle \Delta \theta}$${\displaystyle \mathbf {E} _ {\theta _ {0}}}$

${\displaystyle \mathbf {E} _{out}={\frac {\sqrt {2}}{2}}(e^{-i\Delta \theta }e^{-i\theta _{0}} \mathbf {E} _{RHC}+e^{i\Delta \theta }e^{i\theta _{0}}\mathbf {E} {LHC})\,\,.}$

Utilizando matemáticas similares a las anteriores encontramos:

${\displaystyle \mathbf {E} _{out}={\hat {x}}\cos(\theta _{0}+\Delta \theta )+{\hat {y}}\sin(\theta _{ 0}+\Delta \theta )}$

describiendo así una onda polarizada linealmente en un ángulo , por lo tanto rotada en relación con la onda entrante:${\displaystyle \theta _{0}+\Delta \theta }$${\displaystyle \Delta \theta}$${\displaystyle \mathbf {E} _ {\theta _ {0}}}$

Hemos definido anteriormente la diferencia en los índices de refracción para ondas polarizadas circularmente derecha e izquierda de . Considerando la propagación a través de una longitud L en dicho material, habrá una diferencia de fase adicional inducida entre ellos de (como usamos anteriormente) dada por:${\displaystyle \Delta n}$${\displaystyle 2\Delta \theta}$

${\displaystyle 2\Delta \theta ={\frac {\Delta nL2\pi }{\lambda }}}$,

donde es la longitud de onda de la luz (en el vacío). Esto provocará una rotación del eje lineal de polarización como hemos demostrado.${\estilo de visualización \lambda}$${\displaystyle \Delta \theta}$

En general, el índice de refracción depende de la longitud de onda (véase dispersión ) y el índice de refracción diferencial también dependerá de la longitud de onda. La variación resultante en la rotación con la longitud de onda de la luz se denomina dispersión rotatoria óptica (ORD). Los espectros de ORD y los espectros de dicroísmo circular están relacionados a través de las relaciones de Kramers-Kronig . El conocimiento completo de un espectro permite el cálculo del otro.${\displaystyle \Delta n}$

Así, encontramos que el grado de rotación depende del color de la luz (la línea D amarilla del sodio cerca de la longitud de onda de 589 nm se usa comúnmente para mediciones) y es directamente proporcional a la longitud del camino a través de la sustancia y a la cantidad de birrefringencia circular del material que, para una solución, puede calcularse a partir de la rotación específica de la sustancia y su concentración en la solución.${\estilo de visualización L}$${\displaystyle \Delta n}$

Aunque normalmente se piensa que la actividad óptica es una propiedad de los fluidos, particularmente de las soluciones acuosas , también se ha observado en cristales como el cuarzo (SiO ₂ ). Aunque el cuarzo tiene una birrefringencia lineal sustancial, ese efecto se cancela cuando la propagación es a lo largo del eje óptico . En ese caso, se observa la rotación del plano de polarización debido a la rotación relativa entre los planos cristalinos, lo que hace que el cristal sea formalmente quiral como lo hemos definido anteriormente. La rotación de los planos cristalinos puede ser dextrógira o levógira, produciendo nuevamente actividades ópticas opuestas. Por otro lado, las formas amorfas de sílice como el cuarzo fundido , como una mezcla racémica de moléculas quirales, no tienen actividad óptica neta ya que una u otra estructura cristalina no domina la estructura molecular interna de la sustancia.

En el caso de una sustancia pura en solución, si el color y la longitud del recorrido son fijos y se conoce la rotación específica , la rotación observada se puede utilizar para calcular la concentración. Este uso hace que el polarímetro sea una herramienta de gran importancia para quienes comercializan o utilizan jarabes de azúcar a granel.

La rotación del plano de polarización de la luz también puede ocurrir a través del efecto Faraday , que implica un campo magnético estático . Sin embargo, este es un fenómeno distinto que no se clasifica como "actividad óptica". La actividad óptica es recíproca, es decir, es la misma para direcciones opuestas de propagación de ondas a través de un medio ópticamente activo, por ejemplo, la rotación de polarización en el sentido de las agujas del reloj desde el punto de vista de un observador. En el caso de medios isotrópicos ópticamente activos, la rotación es la misma para cualquier dirección de propagación de ondas. Por el contrario, el efecto Faraday no es recíproco, es decir, las direcciones opuestas de propagación de ondas a través de un medio Faraday darán como resultado una rotación de polarización en el sentido de las agujas del reloj y en el sentido contrario a las agujas del reloj desde el punto de vista de un observador. La rotación de Faraday depende de la dirección de propagación relativa a la del campo magnético aplicado. Todos los compuestos pueden exhibir rotación de polarización en presencia de un campo magnético aplicado, siempre que (un componente de) el campo magnético esté orientado en la dirección de propagación de la luz. El efecto Faraday es uno de los primeros descubrimientos de la relación entre la luz y los efectos electromagnéticos.

• Eugene Hecht, Óptica , 3.ª ed., Addison-Wesley, 1998, ISBN 0-201-30425-2 
• Akhlesh Lakhtakia , Beltrami Fields in Chiral Media, World Scientific, Singapur, 1994
• Un tutorial paso a paso sobre rotación óptica
• Morrison, Robert T. y Boyd, Robert N., Química orgánica (6.ª ed.), Prentice-Hall Inc. (1992).