Espacio vectorial

En matemáticas y física , un espacio vectorial (también llamado espacio lineal ) es un conjunto cuyos elementos, a menudo llamados vectores , pueden sumarse y multiplicarse ("escalarse") por números llamados escalares . Las operaciones de suma vectorial y multiplicación escalar deben satisfacer ciertos requisitos, llamados axiomas vectoriales . Los espacios vectoriales reales y los espacios vectoriales complejos son tipos de espacios vectoriales basados ​​en diferentes tipos de escalares: números reales y números complejos . Los escalares también pueden ser, de forma más general, elementos de cualquier cuerpo .

Los espacios vectoriales generalizan los vectores euclidianos , que permiten modelar magnitudes físicas , como fuerzas y velocidades , que no solo tienen una magnitud , sino también una dirección . El concepto de espacios vectoriales es fundamental para el álgebra lineal , junto con el concepto de matrices , que permite realizar cálculos en espacios vectoriales. Esto proporciona una forma concisa y sintética de manipular y estudiar sistemas de ecuaciones lineales .

Los espacios vectoriales se caracterizan por su dimensión , que, a grandes rasgos, especifica el número de direcciones independientes en el espacio. Esto significa que, para dos espacios vectoriales sobre un cuerpo dado y con la misma dimensión, las propiedades que dependen solo de la estructura del espacio vectorial son exactamente las mismas (técnicamente, los espacios vectoriales son isomorfos ). Un espacio vectorial es de dimensión finita si su dimensión es un número natural . De lo contrario, es de dimensión infinita , y su dimensión es un cardinal infinito . Los espacios vectoriales de dimensión finita se dan de forma natural en geometría y áreas relacionadas. Los espacios vectoriales de dimensión infinita se dan en muchas áreas de las matemáticas. Por ejemplo, los anillos polinómicos son espacios vectoriales de dimensión infinita numerables , y muchos espacios funcionales tienen la cardinalidad del continuo como dimensión.

Muchos espacios vectoriales que se consideran en matemáticas también están dotados de otras estructuras . Es el caso de las álgebras , que incluyen extensiones de cuerpo , anillos polinómicos, álgebras asociativas y álgebras de Lie . También es el caso de los espacios vectoriales topológicos , que incluyen espacios de funciones, espacios de producto interno , espacios normados , espacios de Hilbert y espacios de Banach .

En este artículo, los vectores se representan en negrita para distinguirlos de los escalares. ^{[nb 1] [1]}

Un espacio vectorial sobre un cuerpo F es un conjunto  no vacío V junto con una operación binaria y una función binaria que satisfacen los ocho axiomas que se enumeran a continuación. En este contexto, los elementos de V se denominan comúnmente vectores y los elementos de  F se denominan escalares . ^[2]

• La operación binaria, llamada suma vectorial o simplemente adición, asigna a cualesquiera dos vectores  v y w en V un tercer vector en V que comúnmente se escribe como v + w , y se llama suma de estos dos vectores.

• La función binaria, llamada multiplicación escalar , asigna a cualquier escalar  a en F y a cualquier vector  v en V otro vector en V , que se denota  como v . ^{[nb 2]}

Para tener un espacio vectorial, se deben satisfacer los ocho axiomas siguientes para cada u , v y w en V , y a y b en F. ^[3]

Cuando el campo escalar son los números reales , el espacio vectorial se denomina espacio vectorial real , y cuando el campo escalar son los números complejos , el espacio vectorial se denomina espacio vectorial complejo . ^[4] Estos dos casos son los más comunes, pero también se consideran comúnmente espacios vectoriales con escalares en un campo arbitrario F. Un espacio vectorial de este tipo se denomina espacio vectorial F o espacio vectorial sobre F. ^[5 ]

Se puede dar una definición equivalente de un espacio vectorial, que es mucho más concisa pero menos elemental: los primeros cuatro axiomas (relacionados con la adición de vectores) dicen que un espacio vectorial es un grupo abeliano bajo adición, y los cuatro axiomas restantes (relacionados con la multiplicación escalar) dicen que esta operación define un homomorfismo de anillo del cuerpo F en el anillo de endomorfismo de este grupo. ^[6]

La resta de dos vectores se puede definir como$${\displaystyle \mathbf {v} -\mathbf {w} =\mathbf {v} +(-\mathbf {w} ).}$$

Las consecuencias directas de los axiomas incluyen que, para cada y uno tiene${\displaystyle s\in F}$${\displaystyle \mathbf {v} \in V,}$

• ${\displaystyle 0\mathbf {v} =\mathbf {0} ,}$
• ${\displaystyle s\mathbf {0} =\mathbf {0} ,}$
• ${\displaystyle (-1)\mathbf {v} =-\mathbf {v} ,}$
• ${\displaystyle s\mathbf {v} =\mathbf {0} }$implica o${\displaystyle s=0}$${\displaystyle \mathbf {v} =\mathbf {0} .}$

De manera aún más concisa, un espacio vectorial es un módulo sobre un campo . ^[7]

Combinación lineal

Dado un conjunto G de elementos de un F -espacio vectorial V , una combinación lineal de elementos de G es un elemento de V de la forma donde y Los escalares se denominan coeficientes de la combinación lineal. ^[8]$${\displaystyle a_{1}\mathbf {g} _{1}+a_{2}\mathbf {g} _{2}+\cdots +a_{k}\mathbf {g} _{k},}$$${\displaystyle a_{1},\ldots ,a_{k}\in F}$${\displaystyle \mathbf {g} _{1},\ldots ,\mathbf {g} _{k}\in G.}$${\displaystyle a_{1},\ldots ,a_{k}}$

Independencia lineal

Se dice que los elementos de un subconjunto G de un espacio vectorial F V son linealmente independientes si ningún elemento de G puede escribirse como una combinación lineal de los otros elementos de G. De manera equivalente, son linealmente independientes si dos combinaciones lineales de elementos de G definen el mismo elemento de V si y solo si tienen los mismos coeficientes. También de manera equivalente, son linealmente independientes si una combinación lineal da como resultado el vector cero si y solo si todos sus coeficientes son cero. ^[9]

Subespacio lineal

Un subespacio lineal o subespacio vectorial W de un espacio vectorial V es un subconjunto no vacío de V que está cerrado bajo la adición vectorial y la multiplicación escalar; es decir, la suma de dos elementos de W y el producto de un elemento de W por un escalar pertenecen a W . ^[10] Esto implica que cada combinación lineal de elementos de W pertenece a W . Un subespacio lineal es un espacio vectorial para la adición inducida y la multiplicación escalar; esto significa que la propiedad de clausura implica que se satisfacen los axiomas de un espacio vectorial. ^[11]
La propiedad de clausura también implica que cada intersección de subespacios lineales es un subespacio lineal. ^[11]

Tramo lineal

Dado un subconjunto G de un espacio vectorial V , el espacio lineal abarcado o simplemente el espacio de G es el subespacio lineal más pequeño de V que contiene a G , en el sentido de que es la intersección de todos los subespacios lineales que contienen a G . El espacio de G es también el conjunto de todas las combinaciones lineales de elementos de G .
Si W es el espacio de G , se dice que G abarca o genera a W , y que G es un conjunto abarcado o un conjunto generador de W . ^[12]

Base y dimensión

Un subconjunto de un espacio vectorial es una base si sus elementos son linealmente independientes y abarcan el espacio vectorial. ^[13] Todo espacio vectorial tiene al menos una base, o muchas en general (véase Base (álgebra lineal) § Prueba de que todo espacio vectorial tiene una base ). ^[14] Además, todas las bases de un espacio vectorial tienen la misma cardinalidad , que se denomina dimensión del espacio vectorial (véase Teorema de la dimensión para espacios vectoriales ). ^[15] Esta es una propiedad fundamental de los espacios vectoriales, que se detalla en el resto de la sección.

Las bases son una herramienta fundamental para el estudio de los espacios vectoriales, especialmente cuando la dimensión es finita. En el caso de dimensión infinita, la existencia de bases infinitas, a menudo llamadas bases de Hamel , depende del axioma de elección . De ello se deduce que, en general, ninguna base puede describirse explícitamente. ^[16] Por ejemplo, los números reales forman un espacio vectorial de dimensión infinita sobre los números racionales , para los que no se conoce ninguna base específica.

Considérese una base de un espacio vectorial V de dimensión n sobre un cuerpo F . La definición de una base implica que cada uno puede escribirse con en F , y que esta descomposición es única. Los escalares se denominan coordenadas de v en la base. También se dice que son los coeficientes de la descomposición de v en la base. También se dice que la n - tupla de las coordenadas es el vector de coordenadas de v en la base, ya que el conjunto de las n - tuplas de elementos de F es un espacio vectorial para la adición por componentes y la multiplicación escalar, cuya dimensión es n .${\displaystyle (\mathbf {b} _{1},\mathbf {b} _{2},\ldots ,\mathbf {b} _{n})}$${\displaystyle \mathbf {v} \in V}$$${\displaystyle \mathbf {v} =a_{1}\mathbf {b} _{1}+\cdots +a_{n}\mathbf {b} _{n},}$$${\displaystyle a_{1},\dots ,a_{n}}$${\displaystyle a_{1},\ldots ,a_{n}}$${\displaystyle F^{n}}$

La correspondencia biunívoca entre vectores y sus vectores de coordenadas hace que la suma de vectores se convierta en suma de vectores y la multiplicación escalar en multiplicación escalar. Por lo tanto, se trata de un isomorfismo del espacio vectorial , que permite traducir los razonamientos y cálculos sobre vectores en razonamientos y cálculos sobre sus coordenadas. ^[17]

Los espacios vectoriales se derivan de la geometría afín , a través de la introducción de coordenadas en el plano o espacio tridimensional. Alrededor de 1636, los matemáticos franceses René Descartes y Pierre de Fermat fundaron la geometría analítica al identificar soluciones a una ecuación de dos variables con puntos en una curva plana . ^[18] Para lograr soluciones geométricas sin utilizar coordenadas, Bolzano introdujo, en 1804, ciertas operaciones sobre puntos, líneas y planos, que son predecesoras de los vectores. ^[19] Möbius (1827) introdujo la noción de coordenadas baricéntricas . ^[20] Bellavitis (1833) introdujo una relación de equivalencia en segmentos de línea dirigidos que comparten la misma longitud y dirección a la que llamó equipolencia . ^[21] Un vector euclidiano es entonces una clase de equivalencia de esa relación. ^[22]

Los vectores fueron reconsiderados con la presentación de los números complejos por Argand y Hamilton y el inicio de los cuaterniones por este último. ^[23] Son elementos en R ² y R ⁴ ; su tratamiento mediante combinaciones lineales se remonta a Laguerre en 1867, quien también definió sistemas de ecuaciones lineales .

En 1857, Cayley introdujo la notación matricial que permite la armonización y simplificación de los mapas lineales . Casi al mismo tiempo, Grassmann estudió el cálculo baricéntrico iniciado por Möbius. Previó conjuntos de objetos abstractos dotados de operaciones. ^[24] En su trabajo, están presentes los conceptos de independencia lineal y dimensión , así como los productos escalares . El trabajo de Grassmann de 1844 también excede el marco de los espacios vectoriales, ya que su consideración de la multiplicación lo llevó a lo que hoy se llama álgebras . El matemático italiano Peano fue el primero en dar la definición moderna de espacios vectoriales y mapas lineales en 1888, ^[25] aunque los llamó "sistemas lineales". ^[26] La axiomatización de Peano permitió espacios vectoriales con dimensión infinita, pero Peano no desarrolló más esa teoría. En 1897, Salvatore Pincherle adoptó los axiomas de Peano e hizo incursiones iniciales en la teoría de espacios vectoriales de dimensión infinita. ^[27]

Un desarrollo importante de los espacios vectoriales se debe a la construcción de los espacios funcionales por parte de Henri Lebesgue , que luego fue formalizada por Banach y Hilbert , alrededor de 1920. ^[28] En ese momento, el álgebra y el nuevo campo del análisis funcional comenzaron a interactuar, en particular con conceptos clave como los espacios de funciones p -integrables y los espacios de Hilbert . ^[29]

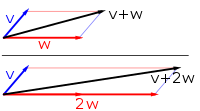
El primer ejemplo de un espacio vectorial consiste en flechas en un plano fijo , comenzando en un punto fijo. Esto se utiliza en física para describir fuerzas o velocidades . ^[30] Dadas dos flechas cualesquiera, v y w , el paralelogramo abarcado por estas dos flechas contiene una flecha diagonal que comienza también en el origen. Esta nueva flecha se llama suma de las dos flechas y se denota v + w . En el caso especial de dos flechas en la misma línea, su suma es la flecha en esta línea cuya longitud es la suma o la diferencia de las longitudes, dependiendo de si las flechas tienen la misma dirección. Otra operación que se puede hacer con flechas es el escalado: dado cualquier número real positivo a , la flecha que tiene la misma dirección que v , pero se dilata o se encoge multiplicando su longitud por a , se llama multiplicación de v por a . Se denota a v . Cuando a es negativo, a v se define como la flecha que apunta en la dirección opuesta. ^[31]

A continuación se muestran algunos ejemplos: si a = 2 , el vector resultante a w tiene la misma dirección que w , pero se estira hasta el doble de la longitud de w (la segunda imagen). De manera equivalente, 2 w es la suma w + w . Además, (−1) v = − v tiene la dirección opuesta y la misma longitud que v (el vector azul que apunta hacia abajo en la segunda imagen).

Un segundo ejemplo clave de un espacio vectorial lo proporcionan los pares de números reales x e y . El orden de los componentes x e y es significativo, por lo que a este par también se lo denomina par ordenado . Este par se escribe como ( x , y ) . La suma de dos pares de este tipo y la multiplicación de un par por un número se define de la siguiente manera: ^[32]$${\displaystyle {\begin{aligned}(x_{1},y_{1})+(x_{2},y_{2})&=(x_{1}+x_{2},y_{1}+y_{2}),\\a(x,y)&=(ax,ay).\end{aligned}}}$$

El primer ejemplo anterior se reduce a este ejemplo si una flecha está representada por un par de coordenadas cartesianas de su punto final.

El ejemplo más simple de un espacio vectorial sobre un cuerpo F es el propio cuerpo F con su adición vista como adición vectorial y su multiplicación vista como multiplicación escalar. De manera más general, todas las n -tuplas (secuencias de longitud n ) de elementos a _i de F forman un espacio vectorial que usualmente se denota F ⁿ y se llama espacio de coordenadas . ^[33] El caso n = 1 es el ejemplo más simple mencionado anteriormente, en el que el cuerpo F también se considera como un espacio vectorial sobre sí mismo. El caso F = R y n = 2 (por lo tanto R ² ) se reduce al ejemplo anterior.$${\displaystyle (a_{1},a_{2},\dots ,a_{n})}$$

El conjunto de números complejos C , números que pueden escribirse en la forma x + iy para los números reales x e y donde i es la unidad imaginaria , forman un espacio vectorial sobre los reales con la adición y multiplicación usuales: ( x + iy ) + ( a + ib ) = ( x + a ) + i ( y + b ) y c ⋅ ( x + iy ) = ( c ⋅ x ) + i ( c ⋅ y ) para los números reales x , y , a , b y c . Los diversos axiomas de un espacio vectorial se deducen del hecho de que las mismas reglas se cumplen para la aritmética de números complejos. El ejemplo de los números complejos es esencialmente el mismo (es decir, es isomorfo ) que el espacio vectorial de pares ordenados de números reales mencionado anteriormente: si pensamos en el número complejo x + i y como representante del par ordenado ( x , y ) en el plano complejo , entonces vemos que las reglas para la suma y la multiplicación escalar corresponden exactamente a las del ejemplo anterior.

De manera más general, las extensiones de campo proporcionan otra clase de ejemplos de espacios vectoriales, particularmente en álgebra y teoría de números algebraicos : un campo F que contiene un campo más pequeño E es un E -espacio vectorial, por las operaciones de multiplicación y adición dadas de F. [ ^34] Por ejemplo, los números complejos son un espacio vectorial sobre R , y la extensión de campo es un espacio vectorial sobre Q.${\displaystyle \mathbf {Q} (i{\sqrt {5}})}$

Las funciones de cualquier conjunto fijo Ω a un cuerpo F también forman espacios vectoriales, al realizar la adición y la multiplicación escalar punto por punto. Es decir, la suma de dos funciones f y g es la función dada por y de manera similar para la multiplicación. Tales espacios de funciones ocurren en muchas situaciones geométricas, cuando Ω es la línea real o un intervalo , u otros subconjuntos de R . Muchas nociones en topología y análisis, como continuidad , integrabilidad o diferenciabilidad se comportan bien con respecto a la linealidad: sumas y múltiplos escalares de funciones que poseen tal propiedad aún tienen esa propiedad. ^[35] Por lo tanto, el conjunto de tales funciones son espacios vectoriales, cuyo estudio pertenece al análisis funcional .${\displaystyle (f+g)}$$${\displaystyle (f+g)(w)=f(w)+g(w),}$$

Los sistemas de ecuaciones lineales homogéneas están estrechamente ligados a los espacios vectoriales. ^[36] Por ejemplo, las soluciones de están dadas por ternas con y arbitrarias Forman un espacio vectorial: las sumas y los múltiplos escalares de dichas ternas aún satisfacen las mismas razones de las tres variables; por lo tanto, también son soluciones. Las matrices se pueden utilizar para condensar múltiples ecuaciones lineales como las anteriores en una ecuación vectorial, es decir$${\displaystyle {\begin{alignedat}{9}&&a\,&&+\,3b\,&\,+&\,&c&\,=0\\4&&a\,&&+\,2b\,&\,+&\,2&c&\,=0\\\end{alignedat}}}$$${\displaystyle a,}$ ${\displaystyle b=a/2,}$${\displaystyle c=-5a/2.}$

$${\displaystyle A\mathbf {x} =\mathbf {0} ,}$$

donde es la matriz que contiene los coeficientes de las ecuaciones dadas, es el vector que denota el producto matricial y es el vector cero. De manera similar, las soluciones de ecuaciones diferenciales lineales homogéneas forman espacios vectoriales. Por ejemplo,${\displaystyle A={\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}}$${\displaystyle \mathbf {x} }$${\displaystyle (a,b,c),}$ ${\displaystyle A\mathbf {x} }$${\displaystyle \mathbf {0} =(0,0)}$

$${\displaystyle f^{\prime \prime }(x)+2f^{\prime }(x)+f(x)=0}$$

produce donde y son constantes arbitrarias, y es la función exponencial natural .${\displaystyle f(x)=ae^{-x}+bxe^{-x},}$${\displaystyle a}$${\displaystyle b}$${\displaystyle e^{x}}$

La relación de dos espacios vectoriales se puede expresar mediante una función lineal o una transformación lineal . Son funciones que reflejan la estructura del espacio vectorial, es decir, conservan las sumas y la multiplicación escalar: para todos y en todos en ^[37]$${\displaystyle {\begin{aligned}f(\mathbf {v} +\mathbf {w} )&=f(\mathbf {v} )+f(\mathbf {w} ),\\f(a\cdot \mathbf {v} )&=a\cdot f(\mathbf {v} )\end{aligned}}}$$${\displaystyle \mathbf {v} }$${\displaystyle \mathbf {w} }$${\displaystyle V,}$${\displaystyle a}$${\displaystyle F.}$

Un isomorfismo es una función lineal f  : V → W tal que existe una función inversa g  : W → V , que es una función tal que las dos composiciones posibles f ∘ g  : W → W y g ∘ f  : V → V son funciones identidad . De manera equivalente, f es tanto uno a uno ( inyectiva ) como sobreyectiva ( sobreyectiva ). ^[38] Si existe un isomorfismo entre V y W , se dice que los dos espacios son isomorfos ; entonces son esencialmente idénticos como espacios vectoriales, ya que todas las identidades que se cumplen en V son, a través de f , transportadas a otras similares en W , y viceversa a través de g .

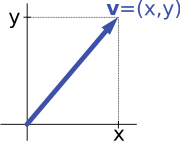
Por ejemplo, las flechas en el plano y los pares ordenados de espacios vectoriales de números en la introducción anterior (ver § Ejemplos) son isomorfos: una flecha plana v que parte del origen de algún sistema de coordenadas (fijo) se puede expresar como un par ordenado considerando los componentes x e y de la flecha, como se muestra en la imagen de la derecha. Por el contrario, dado un par ( x , y ) , la flecha que va por x hacia la derecha (o hacia la izquierda, si x es negativo), y y hacia arriba (hacia abajo, si y es negativo) hace retroceder la flecha v . ^[39]

Las aplicaciones lineales V → W entre dos espacios vectoriales forman un espacio vectorial Hom _F ( V , W ) , también denotado L( V , W ) , o 𝓛( V , W ) . ^[40] El espacio de aplicaciones lineales de V a F se llama espacio vectorial dual , denotado V ^∗ . ^[41] A través de la función natural inyectiva V → V ^∗∗ , cualquier espacio vectorial puede ser incorporado a su bidual ; la función es un isomorfismo si y solo si el espacio es de dimensión finita. ^[42]

Una vez que se elige una base de V , las aplicaciones lineales f  : V → W se determinan completamente especificando las imágenes de los vectores base, porque cualquier elemento de V se expresa únicamente como una combinación lineal de ellos. ^[43] Si dim V = dim W , una correspondencia biunívoca entre bases fijas de V y W da lugar a una aplicación lineal que asigna cualquier elemento base de V al elemento base correspondiente de W . Es un isomorfismo, por su propia definición. ^[44] Por lo tanto, dos espacios vectoriales sobre un cuerpo dado son isomorfos si sus dimensiones concuerdan y viceversa. Otra forma de expresar esto es que cualquier espacio vectorial sobre un cuerpo dado se clasifica completamente ( hasta el isomorfismo) por su dimensión, un solo número. En particular, cualquier espacio vectorial F n -dimensional V es isomorfo a F ⁿ . Sin embargo, no existe un isomorfismo "canónico" o preferido; un isomorfismo φ  : F ⁿ → V es equivalente a la elección de una base de V , al mapear la base estándar de F ⁿ a V , a través de φ .

Las matrices son un concepto útil para codificar aplicaciones lineales. ^[45] Se escriben como una matriz rectangular de escalares como en la imagen de la derecha. Cualquier matriz de m por n da lugar a una aplicación lineal de F ⁿ a F ^m , mediante la siguiente fórmula donde denota suma , o mediante la multiplicación matricial de la matriz con el vector de coordenadas :${\displaystyle A}$$${\displaystyle \mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})\mapsto \left(\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\ldots ,\sum _{j=1}^{n}a_{mj}x_{j}\right),}$$${\textstyle \sum }$${\displaystyle A}$${\displaystyle \mathbf {x} }$

$${\displaystyle \mathbf {x} \mapsto A\mathbf {x} .}$$

Además, después de elegir las bases de V y W , cualquier mapa lineal f  : V → W está representado de forma única por una matriz a través de esta asignación. ^[46]

El determinante det ( A ) de una matriz cuadrada A es un escalar que indica si la función asociada es un isomorfismo o no: para serlo es suficiente y necesario que el determinante sea distinto de cero. ^[47] La ​​transformación lineal de R ⁿ correspondiente a una matriz real n -por- n preserva la orientación si y sólo si su determinante es positivo.

Los endomorfismos , aplicaciones lineales f  : V → V , son particularmente importantes ya que en este caso los vectores v pueden compararse con su imagen bajo f , f ( v ) . Cualquier vector distinto de cero v que satisfaga λ v = f ( v ) , donde λ es un escalar, se llama vector propio de f con valor propio λ . ^[48] De manera equivalente, v es un elemento del núcleo de la diferencia f − λ · Id (donde Id es la aplicación identidad V → V ) . Si V es de dimensión finita, esto puede reformularse utilizando determinantes: f que tiene valor propio λ es equivalente a Al deletrear la definición del determinante, se puede ver que la expresión del lado izquierdo es una función polinómica en λ , llamada polinomio característico de f . ^[49] Si el campo F es lo suficientemente grande para contener un cero de este polinomio (lo que ocurre automáticamente para F algebraicamente cerrado , como F = C ), cualquier función lineal tiene al menos un vector propio. El espacio vectorial V puede o no poseer una base propia , una base que consiste en vectores propios. Este fenómeno está regido por la forma canónica de Jordan de la función. ^[50] El conjunto de todos los vectores propios correspondientes a un valor propio particular de f forma un espacio vectorial conocido como el espacio propio correspondiente al valor propio (y f ) en cuestión.$${\displaystyle \det(f-\lambda \cdot \operatorname {Id} )=0.}$$

Además de los ejemplos concretos anteriores, hay una serie de construcciones algebraicas lineales estándar que producen espacios vectoriales relacionados con los dados.

Un subconjunto no vacío de un espacio vectorial que está cerrado bajo la adición y la multiplicación escalar (y por lo tanto contiene el -vector de ) se denomina subespacio lineal de , o simplemente subespacio de , cuando el espacio ambiente es inequívocamente un espacio vectorial. ^{[51] [nb 4]} Los subespacios de son espacios vectoriales (sobre el mismo cuerpo) por derecho propio. La intersección de todos los subespacios que contienen un conjunto dado de vectores se denomina su amplitud , y es el subespacio más pequeño de que contiene el conjunto . Expresado en términos de elementos, la amplitud es el subespacio que consiste en todas las combinaciones lineales de elementos de . ^[52]${\displaystyle W}$${\displaystyle V}$${\displaystyle \mathbf {0} }$${\displaystyle V}$${\displaystyle V}$${\displaystyle V}$${\displaystyle V}$${\displaystyle S}$${\displaystyle V}$${\displaystyle S}$${\displaystyle S}$

Los subespacios lineales de dimensión 1 y 2 se denominan línea (también línea vectorial ) y plano respectivamente. Si W es un espacio vectorial n -dimensional, cualquier subespacio de dimensión 1 menos, es decir, de dimensión 1, se denomina hiperplano . ^[53]${\displaystyle n-1}$

La contraparte de los subespacios son los espacios vectoriales cocientes . ^[54] Dado cualquier subespacio , el espacio cociente (" módulo ") se define de la siguiente manera: como un conjunto, consiste en donde es un vector arbitrario en . La suma de dos de tales elementos y es , y la multiplicación escalar está dada por . El punto clave en esta definición es que si y solo si la diferencia de y se encuentra en . ^{[nb 5]} De esta manera, el espacio cociente "olvida" información que está contenida en el subespacio .${\displaystyle W\subseteq V}$${\displaystyle V/W}$${\displaystyle V}$ ${\displaystyle W}$$${\displaystyle \mathbf {v} +W=\{\mathbf {v} +\mathbf {w} :\mathbf {w} \in W\},}$$${\displaystyle \mathbf {v} }$${\displaystyle V}$${\displaystyle \mathbf {v} _{1}+W}$${\displaystyle \mathbf {v} _{2}+W}$${\displaystyle \left(\mathbf {v} _{1}+\mathbf {v} _{2}\right)+W}$${\displaystyle a\cdot (\mathbf {v} +W)=(a\cdot \mathbf {v} )+W}$${\displaystyle \mathbf {v} _{1}+W=\mathbf {v} _{2}+W}$ ${\displaystyle \mathbf {v} _{1}}$${\displaystyle \mathbf {v} _{2}}$${\displaystyle W}$${\displaystyle W}$

El núcleo de un mapa lineal consta de vectores que se asignan a en . ^[55] El núcleo y la imagen son subespacios de y , respectivamente. ^[56]${\displaystyle \ker(f)}$${\displaystyle f:V\to W}$${\displaystyle \mathbf {v} }$${\displaystyle \mathbf {0} }$${\displaystyle W}$ ${\displaystyle \operatorname {im} (f)=\{f(\mathbf {v} ):\mathbf {v} \in V\}}$${\displaystyle V}$${\displaystyle W}$

Un ejemplo importante es el núcleo de una función lineal para alguna matriz fija . El núcleo de esta función es el subespacio de vectores tales que , que es precisamente el conjunto de soluciones del sistema de ecuaciones lineales homogéneas perteneciente a . Este concepto también se extiende a ecuaciones diferenciales lineales donde los coeficientes son funciones en también. En la función correspondiente, las derivadas de la función aparecen linealmente (en oposición a , por ejemplo). Dado que la diferenciación es un procedimiento lineal (es decir, y para una constante ), esta asignación es lineal, llamada operador diferencial lineal . En particular, las soluciones de la ecuación diferencial forman un espacio vectorial (sobre R o C ). ^[57]${\displaystyle \mathbf {x} \mapsto A\mathbf {x} }$${\displaystyle A}$${\displaystyle \mathbf {x} }$${\displaystyle A\mathbf {x} =\mathbf {0} }$${\displaystyle A}$$${\displaystyle a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0,}$$${\displaystyle a_{i}}$${\displaystyle x,}$$${\displaystyle f\mapsto D(f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}},}$$${\displaystyle f}$${\displaystyle f^{\prime \prime }(x)^{2}}$${\displaystyle (f+g)^{\prime }=f^{\prime }+g^{\prime }}$${\displaystyle (c\cdot f)^{\prime }=c\cdot f^{\prime }}$${\displaystyle c}$${\displaystyle D(f)=0}$

La existencia de núcleos e imágenes es parte de la afirmación de que la categoría de espacios vectoriales (sobre un cuerpo fijo ) es una categoría abeliana , es decir, un corpus de objetos matemáticos y mapas que preservan la estructura entre ellos (una categoría ) que se comporta de manera muy similar a la categoría de grupos abelianos . ^[58] Debido a esto, muchas afirmaciones como el primer teorema de isomorfismo (también llamado teorema de rango-nulidad en términos relacionados con matrices) y el segundo y tercer teorema de isomorfismo se pueden formular y demostrar de una manera muy similar a las afirmaciones correspondientes para los grupos .${\displaystyle F}$$${\displaystyle V/\ker(f)\;\equiv \;\operatorname {im} (f)}$$

El producto directo de espacios vectoriales y la suma directa de espacios vectoriales son dos formas de combinar una familia indexada de espacios vectoriales en un nuevo espacio vectorial.

El producto directo de una familia de espacios vectoriales consiste en el conjunto de todas las tuplas , que especifican para cada índice en algún conjunto de índices un elemento de . ^[59] La adición y la multiplicación escalar se realizan componente por componente. Una variante de esta construcción es la suma directa (también llamada coproducto y denotada como ), donde solo se permiten tuplas con un número finito de vectores distintos de cero. Si el conjunto de índices es finito, las dos construcciones coinciden, pero en general son diferentes.${\displaystyle \textstyle {\prod _{i\in I}V_{i}}}$${\displaystyle V_{i}}$${\displaystyle \left(\mathbf {v} _{i}\right)_{i\in I}}$${\displaystyle i}$ ${\displaystyle I}$${\displaystyle \mathbf {v} _{i}}$${\displaystyle V_{i}}$ ${\textstyle \bigoplus _{i\in I}V_{i}}$${\textstyle \coprod _{i\in I}V_{i}}$${\displaystyle I}$

El producto tensorial o simplemente de dos espacios vectoriales es una de las nociones centrales del álgebra multilineal que trata de extender nociones como las aplicaciones lineales a varias variables. Una aplicación del producto cartesiano se llama bilineal si es lineal en ambas variables y Es decir, para fija la aplicación es lineal en el sentido anterior y lo mismo para fija${\displaystyle V\otimes _{F}W,}$${\displaystyle V\otimes W,}$${\displaystyle V}$${\displaystyle W}$${\displaystyle g:V\times W\to X}$ ${\displaystyle V\times W}$${\displaystyle g}$${\displaystyle \mathbf {v} }$${\displaystyle \mathbf {w} .}$${\displaystyle \mathbf {w} }$${\displaystyle \mathbf {v} \mapsto g(\mathbf {v} ,\mathbf {w} )}$${\displaystyle \mathbf {v} .}$

El producto tensorial es un espacio vectorial particular que es un receptor universal de aplicaciones bilineales como sigue. Se define como el espacio vectorial que consiste en sumas finitas (formales) de símbolos llamados tensores sujetos a las reglas ^[60] Estas reglas aseguran que la aplicación desde el a que asigna una tupla a es bilineal. La universalidad establece que dado cualquier espacio vectorial y cualquier aplicación bilineal existe una aplicación única mostrada en el diagrama con una flecha punteada, cuya composición con es igual a ^[61] Esto se llama la propiedad universal del producto tensorial, una instancia del método—muy usado en álgebra abstracta avanzada—para definir objetos indirectamente especificando aplicaciones desde o hacia este objeto.${\displaystyle g,}$$${\displaystyle \mathbf {v} _{1}\otimes \mathbf {w} _{1}+\mathbf {v} _{2}\otimes \mathbf {w} _{2}+\cdots +\mathbf {v} _{n}\otimes \mathbf {w} _{n},}$$$${\displaystyle {\begin{alignedat}{6}a\cdot (\mathbf {v} \otimes \mathbf {w} )~&=~(a\cdot \mathbf {v} )\otimes \mathbf {w} ~=~\mathbf {v} \otimes (a\cdot \mathbf {w} ),&&~~{\text{ where }}a{\text{ is a scalar}}\\(\mathbf {v} _{1}+\mathbf {v} _{2})\otimes \mathbf {w} ~&=~\mathbf {v} _{1}\otimes \mathbf {w} +\mathbf {v} _{2}\otimes \mathbf {w} &&\\\mathbf {v} \otimes (\mathbf {w} _{1}+\mathbf {w} _{2})~&=~\mathbf {v} \otimes \mathbf {w} _{1}+\mathbf {v} \otimes \mathbf {w} _{2}.&&\\\end{alignedat}}}$$${\displaystyle f}$${\displaystyle V\times W}$${\displaystyle V\otimes W}$ ${\displaystyle (\mathbf {v} ,\mathbf {w} )}$${\displaystyle \mathbf {v} \otimes \mathbf {w} }$${\displaystyle X}$${\displaystyle g:V\times W\to X,}$${\displaystyle u,}$${\displaystyle f}$${\displaystyle g:}$ ${\displaystyle u(\mathbf {v} \otimes \mathbf {w} )=g(\mathbf {v} ,\mathbf {w} ).}$

Desde el punto de vista del álgebra lineal, los espacios vectoriales se entienden completamente en la medida en que cualquier espacio vectorial sobre un cuerpo dado se caracteriza, salvo isomorfismo, por su dimensión. Sin embargo, los espacios vectoriales per se no ofrecen un marco para tratar la cuestión —crucial para el análisis— de si una secuencia de funciones converge a otra función. Asimismo, el álgebra lineal no está adaptada para tratar series infinitas , ya que la operación de adición sólo permite sumar un número finito de términos. Por lo tanto, las necesidades del análisis funcional requieren considerar estructuras adicionales. ^[62]

A un espacio vectorial se le puede dar un orden parcial bajo el cual se pueden comparar algunos vectores. ^[63] Por ejemplo, el espacio real de dimensión 1 puede ordenarse comparando sus vectores por componentes. Los espacios vectoriales ordenados , por ejemplo los espacios de Riesz , son fundamentales para la integración de Lebesgue , que se basa en la capacidad de expresar una función como una diferencia de dos funciones positivas donde denota la parte positiva de y la parte negativa. ^[64]${\displaystyle \,\leq ,\,}$${\displaystyle n}$${\displaystyle \mathbf {R} ^{n}}$$${\displaystyle f=f^{+}-f^{-}.}$$${\displaystyle f^{+}}$${\displaystyle f}$${\displaystyle f^{-}}$

La "medición" de vectores se realiza especificando una norma , un dato que mide las longitudes de los vectores, o mediante un producto interno , que mide los ángulos entre vectores. Las normas y los productos internos se denotan como y respectivamente. El dato de un producto interno implica que las longitudes de los vectores también se pueden definir, definiendo la norma asociada. Los espacios vectoriales dotados de tales datos se conocen como espacios vectoriales normados y espacios de producto interno , respectivamente. ^[65]${\displaystyle |\mathbf {v} |}$${\displaystyle \langle \mathbf {v} ,\mathbf {w} \rangle ,}$${\textstyle |\mathbf {v} |:={\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}.}$

El espacio de coordenadas puede estar equipado con el producto escalar estándar : En esto refleja la noción común del ángulo entre dos vectores y por la ley de los cosenos : Debido a esto, dos vectores que satisfacen se llaman ortogonales . Una variante importante del producto escalar estándar se utiliza en el espacio de Minkowski : dotado con el producto de Lorentz ^[66] En contraste con el producto escalar estándar, no es definido positivo : también toma valores negativos, por ejemplo, para La selección de la cuarta coordenada , correspondiente al tiempo , en oposición a tres dimensiones espaciales, lo hace útil para el tratamiento matemático de la relatividad especial . Nótese que en otras convenciones el tiempo a menudo se escribe como el primer componente, o "cero", de modo que el producto de Lorentz se escribe${\displaystyle F^{n}}$$${\displaystyle \langle \mathbf {x} ,\mathbf {y} \rangle =\mathbf {x} \cdot \mathbf {y} =x_{1}y_{1}+\cdots +x_{n}y_{n}.}$$${\displaystyle \mathbf {R} ^{2},}$${\displaystyle \mathbf {x} }$${\displaystyle \mathbf {y} ,}$$${\displaystyle \mathbf {x} \cdot \mathbf {y} =\cos \left(\angle (\mathbf {x} ,\mathbf {y} )\right)\cdot |\mathbf {x} |\cdot |\mathbf {y} |.}$$${\displaystyle \langle \mathbf {x} ,\mathbf {y} \rangle =0}$${\displaystyle \mathbf {R} ^{4}}$$${\displaystyle \langle \mathbf {x} |\mathbf {y} \rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}.}$$${\displaystyle \langle \mathbf {x} |\mathbf {x} \rangle }$${\displaystyle \mathbf {x} =(0,0,0,1).}$$${\displaystyle \langle \mathbf {x} |\mathbf {y} \rangle =-x_{0}y_{0}+x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}.}$$

Las cuestiones de convergencia se tratan considerando espacios vectoriales que tienen una topología compatible , una estructura que permite hablar de elementos que están cerca unos de otros . ^[67] Compatible aquí significa que la suma y la multiplicación escalar tienen que ser mapas continuos . Aproximadamente, si y en , y en varían en una cantidad acotada, entonces también lo hacen y ^{[nb 6]} Para que tenga sentido especificar la cantidad que cambia un escalar, el cuerpo también tiene que tener una topología en este contexto; una elección común son los números reales o los números complejos.${\displaystyle V}$${\displaystyle \mathbf {x} }$${\displaystyle \mathbf {y} }$${\displaystyle V}$${\displaystyle a}$${\displaystyle F}$${\displaystyle \mathbf {x} +\mathbf {y} }$${\displaystyle a\mathbf {x} .}$${\displaystyle F}$

En tales espacios vectoriales topológicos se pueden considerar series de vectores. La suma infinita denota el límite de las sumas parciales finitas correspondientes de la secuencia de elementos de Por ejemplo, podrían ser funciones (reales o complejas) pertenecientes a algún espacio de funciones , en cuyo caso la serie es una serie de funciones . El modo de convergencia de la serie depende de la topología impuesta al espacio de funciones. En tales casos, la convergencia puntual y la convergencia uniforme son dos ejemplos destacados. ^[68]$${\displaystyle \sum _{i=1}^{\infty }f_{i}~=~\lim _{n\to \infty }f_{1}+\cdots +f_{n}}$$${\displaystyle f_{1},f_{2},\ldots }$${\displaystyle V.}$${\displaystyle f_{i}}$ ${\displaystyle V,}$

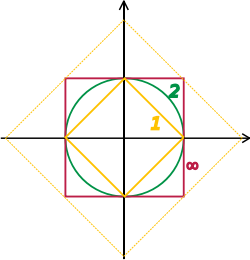
Una forma de asegurar la existencia de límites de ciertas series infinitas es restringir la atención a espacios donde cualquier secuencia de Cauchy tiene un límite; un espacio vectorial de este tipo se llama completo . En términos generales, un espacio vectorial es completo siempre que contenga todos los límites necesarios. Por ejemplo, el espacio vectorial de polinomios en el intervalo unitario equipado con la topología de convergencia uniforme no es completo porque cualquier función continua en puede aproximarse uniformemente mediante una secuencia de polinomios, por el teorema de aproximación de Weierstrass . ^[69] En contraste, el espacio de todas las funciones continuas en con la misma topología es completo. ^[70] Una norma da lugar a una topología al definir que una secuencia de vectores converge a si y solo si los espacios de Banach y Hilbert son espacios vectoriales topológicos completos cuyas topologías están dadas, respectivamente, por una norma y un producto interno. Su estudio, una pieza clave del análisis funcional, se centra en los espacios vectoriales de dimensión infinita, ya que todas las normas sobre espacios vectoriales topológicos de dimensión finita dan lugar a la misma noción de convergencia. ^[71] La imagen de la derecha muestra la equivalencia de la norma y la norma en . A medida que las "bolas" unitarias se encierran entre sí, una secuencia converge a cero en una norma si y solo si lo hace también en la otra norma. Sin embargo, en el caso de dimensión infinita, generalmente habrá topologías no equivalentes, lo que hace que el estudio de los espacios vectoriales topológicos sea más rico que el de los espacios vectoriales sin datos adicionales.${\displaystyle [0,1],}$${\displaystyle [0,1]}$${\displaystyle [0,1]}$${\displaystyle \mathbf {v} _{n}}$${\displaystyle \mathbf {v} }$$${\displaystyle \lim _{n\to \infty }|\mathbf {v} _{n}-\mathbf {v} |=0.}$$${\displaystyle 1}$${\displaystyle \infty }$${\displaystyle \mathbf {R} ^{2}:}$

Desde un punto de vista conceptual, todas las nociones relacionadas con los espacios vectoriales topológicos deben coincidir con la topología. Por ejemplo, en lugar de considerar todos los mapas lineales (también llamados funcionales ), se requiere que los mapas entre espacios vectoriales topológicos sean continuos. ^[72] En particular, el espacio dual (topológico) consta de funcionales continuos (o a ). El teorema fundamental de Hahn-Banach se ocupa de separar subespacios de espacios vectoriales topológicos apropiados por funcionales continuos. ^[73]${\displaystyle V\to W,}$${\displaystyle V^{*}}$${\displaystyle V\to \mathbf {R} }$${\displaystyle \mathbf {C} }$

Los espacios de Banach , introducidos por Stefan Banach , son espacios vectoriales normados completos. ^[74]

Un primer ejemplo es el espacio vectorial${\displaystyle \ell ^{p}}$ constituido por infinitos vectores con entradas reales cuya -norma está dada por ${\displaystyle \mathbf {x} =\left(x_{1},x_{2},\ldots ,x_{n},\ldots \right)}$${\displaystyle p}$ ${\displaystyle (1\leq p\leq \infty )}$$${\displaystyle \|\mathbf {x} \|_{\infty }:=\sup _{i}|x_{i}|\qquad {\text{ for }}p=\infty ,{\text{ and }}}$$$${\displaystyle \|\mathbf {x} \|_{p}:=\left(\sum _{i}|x_{i}|^{p}\right)^{\frac {1}{p}}\qquad {\text{ for }}p<\infty .}$$

Las topologías en el espacio de dimensión infinita son inequivalentes para diferentes Por ejemplo, la secuencia de vectores en la que los primeros componentes son y los siguientes son converge al vector cero para pero no para pero ${\displaystyle \ell ^{p}}$${\displaystyle p.}$${\displaystyle \mathbf {x} _{n}=\left(2^{-n},2^{-n},\ldots ,2^{-n},0,0,\ldots \right),}$${\displaystyle 2^{n}}$${\displaystyle 2^{-n}}$${\displaystyle 0,}$${\displaystyle p=\infty ,}$${\displaystyle p=1:}$$${\displaystyle \|\mathbf {x} _{n}\|_{\infty }=\sup(2^{-n},0)=2^{-n}\to 0,}$$$${\displaystyle \|\mathbf {x} _{n}\|_{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1.}$$

De manera más general que las secuencias de números reales, las funciones están dotadas de una norma que reemplaza la suma anterior por la integral de Lebesgue.${\displaystyle f:\Omega \to \mathbb {R} }$ $${\displaystyle \|f\|_{p}:=\left(\int _{\Omega }|f(x)|^{p}\,{d\mu (x)}\right)^{\frac {1}{p}}.}$$

El espacio de funciones integrables en un dominio dado (por ejemplo un intervalo) que satisfacen y están dotadas de esta norma se denominan espacios de Lebesgue , denotados ^{[nb 7]}${\displaystyle \Omega }$${\displaystyle \|f\|_{p}<\infty ,}$${\displaystyle L^{\;\!p}(\Omega ).}$

Estos espacios son completos. ^[75] (Si se utiliza la integral de Riemann en su lugar, el espacio no es completo, lo que puede verse como una justificación de la teoría de integración de Lebesgue. ^{[nb 8]} ) Concretamente, esto significa que para cualquier secuencia de funciones integrables de Lebesgue que satisfagan la condición existe una función que pertenece al espacio vectorial tal que${\displaystyle f_{1},f_{2},\ldots ,f_{n},\ldots }$${\displaystyle \|f_{n}\|_{p}<\infty ,}$$${\displaystyle \lim _{k,\ n\to \infty }\int _{\Omega }\left|f_{k}(x)-f_{n}(x)\right|^{p}\,{d\mu (x)}=0}$$${\displaystyle f(x)}$${\displaystyle L^{\;\!p}(\Omega )}$$${\displaystyle \lim _{k\to \infty }\int _{\Omega }\left|f(x)-f_{k}(x)\right|^{p}\,{d\mu (x)}=0.}$$

La imposición de condiciones de acotación no sólo a la función, sino también a sus derivadas conduce a espacios de Sobolev . ^[76]

Los espacios de producto interno completos se conocen como espacios de Hilbert , en honor a David Hilbert . ^[77] El espacio de Hilbert con producto interno dado por donde denota el conjugado complejo de ^{[78] [nb 9]} es un caso clave.${\displaystyle L^{2}(\Omega ),}$$${\displaystyle \langle f\ ,\ g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\,dx,}$$${\displaystyle {\overline {g(x)}}}$${\displaystyle g(x),}$

Por definición, en un espacio de Hilbert, cualquier secuencia de Cauchy converge a un límite. A la inversa, encontrar una secuencia de funciones con propiedades deseables que se aproximen a una función límite dada es igualmente crucial. Un análisis temprano, bajo la apariencia de la aproximación de Taylor , estableció una aproximación de funciones diferenciables por polinomios. ^[79] Por el teorema de Stone-Weierstrass , cada función continua en puede aproximarse tan cerca como se desee por un polinomio. ^[80] Una técnica de aproximación similar por funciones trigonométricas se llama comúnmente expansión de Fourier , y se aplica mucho en ingeniería. De manera más general, y más conceptual, el teorema produce una descripción simple de qué "funciones básicas", o, en espacios de Hilbert abstractos, qué vectores básicos son suficientes para generar un espacio de Hilbert en el sentido de que el cierre de su espacio (es decir, combinaciones lineales finitas y límites de aquellas) es todo el espacio. Tal conjunto de funciones se llama base de su cardinalidad se conoce como la dimensión del espacio de Hilbert . ^{[nb 10]} El teorema no sólo muestra funciones base adecuadas como suficientes para fines de aproximación, sino que, junto con el proceso de Gram-Schmidt , permite construir una base de vectores ortogonales . ^{[81] Dichas bases ortogonales son la generalización del espacio de Hilbert de los ejes de coordenadas en} el espacio euclidiano de dimensión finita .${\displaystyle f_{n}}$ ${\displaystyle f}$${\displaystyle [a,b]}$${\displaystyle H,}$${\displaystyle H,}$

Las soluciones de varias ecuaciones diferenciales pueden interpretarse en términos de espacios de Hilbert. Por ejemplo, una gran cantidad de campos en física e ingeniería conducen a tales ecuaciones, y con frecuencia se utilizan soluciones con propiedades físicas particulares como funciones base, a menudo ortogonales. ^[82] Como ejemplo de la física, la ecuación de Schrödinger dependiente del tiempo en mecánica cuántica describe el cambio de propiedades físicas en el tiempo por medio de una ecuación diferencial parcial , cuyas soluciones se denominan funciones de onda . ^[83] Los valores definidos para propiedades físicas como la energía o el momento corresponden a valores propios de un determinado operador diferencial (lineal) y las funciones de onda asociadas se denominan estados propios . El teorema espectral descompone un operador compacto lineal que actúa sobre funciones en términos de estas funciones propias y sus valores propios. ^[84]

Los espacios vectoriales generales no poseen una multiplicación entre vectores. Un espacio vectorial equipado con un operador bilineal adicional que define la multiplicación de dos vectores es un álgebra sobre un cuerpo (o F -álgebra si se especifica el cuerpo F ). ^[85]

Por ejemplo, el conjunto de todos los polinomios forma un álgebra conocida como anillo polinomial : al utilizar que la suma de dos polinomios es un polinomio, forman un espacio vectorial; forman un álgebra ya que el producto de dos polinomios es nuevamente un polinomio. Los anillos de polinomios (en varias variables) y sus cocientes forman la base de la geometría algebraica , porque son anillos de funciones de objetos geométricos algebraicos . ^[86]${\displaystyle p(t)}$

Otro ejemplo crucial son las álgebras de Lie , que no son ni conmutativas ni asociativas, pero el hecho de no serlo está limitado por las restricciones ( denota el producto de y ):${\displaystyle [x,y]}$${\displaystyle x}$${\displaystyle y}$

• ${\displaystyle [x,y]=-[y,x]}$( anticonmutatividad ), y
• ${\displaystyle [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0}$( Identidad de Jacobi ). ^[87]

Los ejemplos incluyen el espacio vectorial de matrices -por- , con el conmutador de dos matrices, y dotado del producto vectorial .${\displaystyle n}$${\displaystyle n}$${\displaystyle [x,y]=xy-yx,}$${\displaystyle \mathbf {R} ^{3},}$

El álgebra tensorial es una forma formal de sumar productos a cualquier espacio vectorial para obtener un álgebra. ^[88] Como espacio vectorial, está abarcado por símbolos, llamados tensores simples donde el grado varía. La multiplicación se da concatenando dichos símbolos, imponiendo la ley distributiva bajo la adición y requiriendo que la multiplicación escalar conmute con el producto tensorial ⊗, de forma muy similar al producto tensorial de dos espacios vectoriales introducido en la sección anterior sobre productos tensoriales. En general, no hay relaciones entre y Forzar dos de estos elementos para que sean iguales conduce al álgebra simétrica , mientras que forzar produce el álgebra exterior . ^[89]${\displaystyle \operatorname {T} (V)}$${\displaystyle V}$$${\displaystyle \mathbf {v} _{1}\otimes \mathbf {v} _{2}\otimes \cdots \otimes \mathbf {v} _{n},}$$ ${\displaystyle n}$${\displaystyle \mathbf {v} _{1}\otimes \mathbf {v} _{2}}$${\displaystyle \mathbf {v} _{2}\otimes \mathbf {v} _{1}.}$${\displaystyle \mathbf {v} _{1}\otimes \mathbf {v} _{2}=-\mathbf {v} _{2}\otimes \mathbf {v} _{1}}$

Un fibrado vectorial es una familia de espacios vectoriales parametrizados de forma continua por un espacio topológico X . ^[90] Más precisamente, un fibrado vectorial sobre X es un espacio topológico E equipado con una función continua tal que para cada x en X , la fibra π ⁻¹ ( x ) es un espacio vectorial. El caso dim V = 1 se denomina fibrado lineal . Para cualquier espacio vectorial V , la proyección X × V → X convierte el producto X × V en un fibrado vectorial "trivial" . Se requiere que los fibrados vectoriales sobre X sean localmente un producto de X y algún espacio vectorial (fijo) V : para cada x en X , existe una vecindad U de x tal que la restricción de π a π ⁻¹ ( U ) es isomorfa ^{[nb 11]} al fibrado trivial U × V → U . A pesar de su carácter localmente trivial, los fibrados vectoriales pueden (dependiendo de la forma del espacio subyacente X ) estar "retorcidos" en el espacio grande (es decir, el fibrado no necesita ser (globalmente isomorfo al) fibrado trivial X × V ). Por ejemplo, la banda de Möbius puede verse como un fibrado lineal sobre el círculo S ¹ ( identificando intervalos abiertos con la línea real ). Sin embargo, es diferente del cilindro S ¹ × R , porque este último es orientable mientras que el primero no lo es. ^[91]$${\displaystyle \pi :E\to X}$$

Las propiedades de ciertos fibrados vectoriales proporcionan información sobre el espacio topológico subyacente. Por ejemplo, el fibrado tangente consiste en la colección de espacios tangentes parametrizados por los puntos de una variedad diferenciable. El fibrado tangente del círculo S ¹ es globalmente isomorfo a S ¹ × R , ya que hay un campo vectorial global distinto de cero en S ¹ . ^{[nb 12]} En contraste, por el teorema de la bola peluda , no hay ningún campo vectorial (tangente) en la 2-esfera S ² que sea en todas partes distinto de cero. ^[92] La teoría K estudia las clases de isomorfismo de todos los fibrados vectoriales sobre algún espacio topológico. ^{[93] Además de profundizar en la comprensión topológica y geométrica, tiene consecuencias puramente algebraicas, como la clasificación de} las álgebras de división real de dimensión finita : R , C , los cuaterniones H y los octoniones O .

El fibrado cotangente de una variedad diferenciable está constituido, en cada punto de la variedad, por el dual del espacio tangente, el espacio cotangente . Las secciones de ese fibrado se conocen como uniformas diferenciales .

Los módulos son a los anillos lo que los espacios vectoriales son a los cuerpos: los mismos axiomas, aplicados a un anillo R en lugar de a un cuerpo F , producen módulos. ^[94] La teoría de módulos, comparada con la de espacios vectoriales, se complica por la presencia de elementos de anillo que no tienen inversos multiplicativos . Por ejemplo, los módulos no necesitan tener bases, como lo muestra el módulo Z (es decir, grupo abeliano ) Z /2 Z ; aquellos módulos que sí las tienen (incluyendo todos los espacios vectoriales) se conocen como módulos libres . Sin embargo, un espacio vectorial puede definirse de forma compacta como un módulo sobre un anillo que es un cuerpo , y los elementos se denominan vectores. Algunos autores utilizan el término espacio vectorial para referirse a los módulos sobre un anillo de división . ^[95] La interpretación algebrogeométrica de los anillos conmutativos a través de su espectro permite el desarrollo de conceptos como módulos localmente libres , la contraparte algebraica de los fibrados vectoriales.

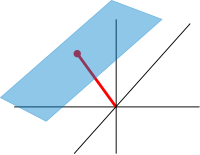
Aproximadamente, los espacios afines son espacios vectoriales cuyos orígenes no están especificados. ^[96] Más precisamente, un espacio afín es un conjunto con una acción de espacio vectorial transitiva libre . En particular, un espacio vectorial es un espacio afín sobre sí mismo, por la función Si W es un espacio vectorial, entonces un subespacio afín es un subconjunto de W obtenido al trasladar un subespacio lineal V por un vector fijo x ∈ W ; este espacio se denota por x + V (es una clase lateral de V en W ) y consiste en todos los vectores de la forma x + v para v ∈ V . Un ejemplo importante es el espacio de soluciones de un sistema de ecuaciones lineales no homogéneas que generalizan el caso homogéneo discutido en la sección anterior sobre ecuaciones lineales, que se puede encontrar al establecer en esta ecuación. ^[97] El espacio de soluciones es el subespacio afín x + V donde x es una solución particular de la ecuación, y V es el espacio de soluciones de la ecuación homogénea (el espacio nulo de A ).$${\displaystyle V\times V\to W,\;(\mathbf {v} ,\mathbf {a} )\mapsto \mathbf {a} +\mathbf {v} .}$$$${\displaystyle A\mathbf {v} =\mathbf {b} }$$${\displaystyle \mathbf {b} =\mathbf {0} }$

El conjunto de subespacios unidimensionales de un espacio vectorial fijo de dimensión finita V se conoce como espacio proyectivo ; puede usarse para formalizar la idea de líneas paralelas que se intersecan en el infinito. ^[98] Los grassmannianos y las variedades de banderas generalizan esto parametrizando subespacios lineales de dimensión fija k y banderas de subespacios, respectivamente.

El Wikilibro Álgebra lineal tiene una página sobre el tema: Espacios vectoriales reales

El Wikilibro Álgebra lineal tiene una página sobre el tema: Espacios vectoriales

• "Espacio vectorial", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]