Gráfico de la función integral del seno hiperbólico Shi(z) en el plano complejo desde -2-2i hasta 2+2i con colores creados con la función ComplexPlot3D de Mathematica 13.1
Función especial definida por una integral
Si( x ) (azul) y Ci( x ) (verde) representados en el mismo gráfico. Seno integral en el plano complejo, trazado con una variante de coloración del dominio . Coseno integral en el plano complejo. Nótese la rama cortada a lo largo del eje real negativo. En matemáticas , las integrales trigonométricas son una familia de integrales no elementales que involucran funciones trigonométricas .
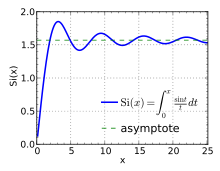
Integral de seno Gráfico de Si( x ) para 0 ≤ x ≤ 8 π . Gráfico de la función integral del coseno Ci( z ) en el plano complejo desde −2 − 2 i hasta 2 + 2 i con colores creados con la función ComplexPlot3D de Mathematica 13.1 Las diferentes definiciones de integral senoidal son Si ( incógnita ) = ∫ 0 incógnita pecado a a d a {\displaystyle \operatorname {Si} (x)=\int _{0}^{x}{\frac {\sin t}{t}}\,dt} si ( incógnita ) = − ∫ incógnita ∞ pecado a a d a . {\displaystyle \operatorname {si} (x)=-\int _{x}^{\infty }{\frac {\sin t}{t}}\,dt~.}
Nótese que el integrando es la función sinc y también la función esférica de Bessel cero . Como sinc es una función entera par ( holomórfica sobre todo el plano complejo), Si es entera, impar y la integral en su definición puede tomarse a lo largo de cualquier camino que conecte los puntos finales. pecado ( a ) a {\displaystyle {\frac {\sin(t)}{t}}}
Por definición, Si( x ) es la antiderivada de sen x / x cuyo valor es cero en x = 0si( x ) es la antiderivada cuyo valor es cero en x = ∞integral de Dirichlet , Si ( incógnita ) − si ( incógnita ) = ∫ 0 ∞ pecado a a d a = π 2 o Si ( incógnita ) = π 2 + si ( incógnita ) . {\displaystyle \operatorname {Si} (x)-\operatorname {si} (x)=\int _{0}^{\infty }{\frac {\sin t}{t}}\,dt={\frac {\pi }{2}}\quad {\text{ o }}\quad \operatorname {Si} (x)={\frac {\pi }{2}}+\operatorname {si} (x)~.}
En el procesamiento de señales , las oscilaciones de la integral sinusoidal provocan sobreimpulsos y artefactos de zumbido cuando se utiliza el filtro sinc , y zumbido en el dominio de frecuencia si se utiliza un filtro sinc truncado como filtro de paso bajo .
Relacionado con esto está el fenómeno de Gibbs : si la integral seno se considera como la convolución de la función sinc con la función escalón de Heaviside , esto corresponde a truncar la serie de Fourier , que es la causa del fenómeno de Gibbs.
Integral del coseno Gráfica de Ci( x ) para 0 < x ≤ 8 π . Las diferentes definiciones de la integral del coseno son
donde γ ≈ 0,57721566 ... es la constante de Euler-Mascheroni . Algunos textos utilizan ci en lugar de Ci . Cin ( incógnita ) = ∫ 0 incógnita 1 − porque a a d a , {\displaystyle \operatorname {Cin} (x)=\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt~,} Ci ( incógnita ) = − ∫ incógnita ∞ porque a a d a = gamma + En incógnita − ∫ 0 incógnita 1 − porque a a d a para | Argento ( incógnita ) | < π , {\displaystyle \operatorname {Ci} (x)=-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt=\gamma +\ln x-\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt\qquad ~{\text{ para }}~\left|\operatorname {Arg} (x)\right|<\pi ~,}
Ci( x ) es la antiderivada de cos x / x (que se anula cuando ). Las dos definiciones están relacionadas por incógnita → ∞ {\displaystyle x\to \infty} Ci ( incógnita ) = gamma + En incógnita − Cin ( incógnita ) . {\displaystyle \operatorname {Ci} (x)=\gamma +\ln x-\operatorname {Cin} (x)~.}
Cin es una función par y entera . Por esa razón, algunos textos tratan a Cin como la función primaria y derivan Ci en términos de Cin .
Integral de seno hiperbólico La integral del seno hiperbólico se define como Shi ( x ) = ∫ 0 x sinh ( t ) t d t . {\displaystyle \operatorname {Shi} (x)=\int _{0}^{x}{\frac {\sinh(t)}{t}}\,dt.}
Está relacionada con la integral del seno ordinario por Si ( i x ) = i Shi ( x ) . {\displaystyle \operatorname {Si} (ix)=i\operatorname {Shi} (x).}
Integral del coseno hiperbólico La integral del coseno hiperbólico es
Gráfico de la función integral del coseno hiperbólico Chi(z) en el plano complejo desde -2-2i hasta 2+2i con colores creados con la función ComplexPlot3D de Mathematica 13.1 Chi ( x ) = γ + ln x + ∫ 0 x cosh t − 1 t d t for | Arg ( x ) | < π , {\displaystyle \operatorname {Chi} (x)=\gamma +\ln x+\int _{0}^{x}{\frac {\cosh t-1}{t}}\,dt\qquad ~{\text{ for }}~\left|\operatorname {Arg} (x)\right|<\pi ~,} constante de Euler-Mascheroni ? γ {\displaystyle \gamma }
Tiene la expansión de la serie. Chi ( x ) = γ + ln ( x ) + x 2 4 + x 4 96 + x 6 4320 + x 8 322560 + x 10 36288000 + O ( x 12 ) . {\displaystyle \operatorname {Chi} (x)=\gamma +\ln(x)+{\frac {x^{2}}{4}}+{\frac {x^{4}}{96}}+{\frac {x^{6}}{4320}}+{\frac {x^{8}}{322560}}+{\frac {x^{10}}{36288000}}+O(x^{12}).}
Funciones auxiliares Las integrales trigonométricas pueden entenderse en términos de las llamadas " funciones auxiliares ".
Utilizando estas funciones, las integrales trigonométricas pueden reexpresarse como (cf. Abramowitz & Stegun, p. 232) f ( x ) ≡ ∫ 0 ∞ sin ( t ) t + x d t = ∫ 0 ∞ e − x t t 2 + 1 d t = Ci ( x ) sin ( x ) + [ π 2 − Si ( x ) ] cos ( x ) , g ( x ) ≡ ∫ 0 ∞ cos ( t ) t + x d t = ∫ 0 ∞ t e − x t t 2 + 1 d t = − Ci ( x ) cos ( x ) + [ π 2 − Si ( x ) ] sin ( x ) . {\displaystyle {\begin{array}{rcl}f(x)&\equiv &\int _{0}^{\infty }{\frac {\sin(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {e^{-xt}}{t^{2}+1}}\,dt&=&\operatorname {Ci} (x)\sin(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)~,\\g(x)&\equiv &\int _{0}^{\infty }{\frac {\cos(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}\,dt&=&-\operatorname {Ci} (x)\cos(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)~.\end{array}}} π 2 − Si ( x ) = − si ( x ) = f ( x ) cos ( x ) + g ( x ) sin ( x ) , and Ci ( x ) = f ( x ) sin ( x ) − g ( x ) cos ( x ) . {\displaystyle {\begin{array}{rcl}{\frac {\pi }{2}}-\operatorname {Si} (x)=-\operatorname {si} (x)&=&f(x)\cos(x)+g(x)\sin(x)~,\qquad {\text{ and }}\\\operatorname {Ci} (x)&=&f(x)\sin(x)-g(x)\cos(x)~.\\\end{array}}}
La espiral de Nielsen. La espiral formada por la gráfica paramétrica de si, ci se conoce como espiral de Nielsen. x ( t ) = a × ci ( t ) {\displaystyle x(t)=a\times \operatorname {ci} (t)} y ( t ) = a × si ( t ) {\displaystyle y(t)=a\times \operatorname {si} (t)}
La espiral está estrechamente relacionada con las integrales de Fresnel y la espiral de Euler . La espiral de Nielsen tiene aplicaciones en el procesamiento de visión, la construcción de carreteras y vías y otras áreas. [1]
Expansión Se pueden utilizar varias expansiones para la evaluación de integrales trigonométricas, dependiendo del rango del argumento.
Si ( x ) ∼ π 2 − cos x x ( 1 − 2 ! x 2 + 4 ! x 4 − 6 ! x 6 ⋯ ) − sin x x ( 1 x − 3 ! x 3 + 5 ! x 5 − 7 ! x 7 ⋯ ) {\displaystyle \operatorname {Si} (x)\sim {\frac {\pi }{2}}-{\frac {\cos x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\sin x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)} Ci ( x ) ∼ sin x x ( 1 − 2 ! x 2 + 4 ! x 4 − 6 ! x 6 ⋯ ) − cos x x ( 1 x − 3 ! x 3 + 5 ! x 5 − 7 ! x 7 ⋯ ) . {\displaystyle \operatorname {Ci} (x)\sim {\frac {\sin x}{x}}\left(1-{\frac {2!}{x^{2}}}+{\frac {4!}{x^{4}}}-{\frac {6!}{x^{6}}}\cdots \right)-{\frac {\cos x}{x}}\left({\frac {1}{x}}-{\frac {3!}{x^{3}}}+{\frac {5!}{x^{5}}}-{\frac {7!}{x^{7}}}\cdots \right)~.}
Estas series son asintóticas y divergentes, aunque pueden utilizarse para estimaciones e incluso para evaluaciones precisas en ℜ( x ) ≫ 1 .
Serie convergente Si ( x ) = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ( 2 n + 1 ) ! = x − x 3 3 ! ⋅ 3 + x 5 5 ! ⋅ 5 − x 7 7 ! ⋅ 7 ± ⋯ {\displaystyle \operatorname {Si} (x)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)(2n+1)!}}=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}\pm \cdots } Ci ( x ) = γ + ln x + ∑ n = 1 ∞ ( − 1 ) n x 2 n 2 n ( 2 n ) ! = γ + ln x − x 2 2 ! ⋅ 2 + x 4 4 ! ⋅ 4 ∓ ⋯ {\displaystyle \operatorname {Ci} (x)=\gamma +\ln x+\sum _{n=1}^{\infty }{\frac {(-1)^{n}x^{2n}}{2n(2n)!}}=\gamma +\ln x-{\frac {x^{2}}{2!\cdot 2}}+{\frac {x^{4}}{4!\cdot 4}}\mp \cdots }
Estas series son convergentes en cualquier complejo x , aunque para | x , la serie convergerá lentamente al principio, requiriendo muchos términos para lograr una alta precisión.
Derivación de la expansión de series De la expansión en serie de Maclaurin del seno: sin x = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + x 9 9 ! − x 11 11 ! + ⋯ {\displaystyle \sin \,x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{9}}{9!}}-{\frac {x^{11}}{11!}}+\cdots }
sin x x = 1 − x 2 3 ! + x 4 5 ! − x 6 7 ! + x 8 9 ! − x 10 11 ! + ⋯ {\displaystyle {\frac {\sin \,x}{x}}=1-{\frac {x^{2}}{3!}}+{\frac {x^{4}}{5!}}-{\frac {x^{6}}{7!}}+{\frac {x^{8}}{9!}}-{\frac {x^{10}}{11!}}+\cdots }
∴ ∫ sin x x d x = x − x 3 3 ! ⋅ 3 + x 5 5 ! ⋅ 5 − x 7 7 ! ⋅ 7 + x 9 9 ! ⋅ 9 − x 11 11 ! ⋅ 11 + ⋯ {\displaystyle \therefore \int {\frac {\sin \,x}{x}}dx=x-{\frac {x^{3}}{3!\cdot 3}}+{\frac {x^{5}}{5!\cdot 5}}-{\frac {x^{7}}{7!\cdot 7}}+{\frac {x^{9}}{9!\cdot 9}}-{\frac {x^{11}}{11!\cdot 11}}+\cdots }
Relación con la integral exponencial del argumento imaginario La función
se llama integral exponencial y está estrechamente relacionada con Si y Ci . E 1 ( z ) = ∫ 1 ∞ exp ( − z t ) t d t for ℜ ( z ) ≥ 0 {\displaystyle \operatorname {E} _{1}(z)=\int _{1}^{\infty }{\frac {\exp(-zt)}{t}}\,dt\qquad ~{\text{ for }}~\Re (z)\geq 0} E 1 ( i x ) = i ( − π 2 + Si ( x ) ) − Ci ( x ) = i si ( x ) − ci ( x ) for x > 0 . {\displaystyle \operatorname {E} _{1}(ix)=i\left(-{\frac {\pi }{2}}+\operatorname {Si} (x)\right)-\operatorname {Ci} (x)=i\operatorname {si} (x)-\operatorname {ci} (x)\qquad ~{\text{ for }}~x>0~.}
Como cada función respectiva es analítica excepto el corte en valores negativos del argumento, el área de validez de la relación debe extenderse a (Fuera de este rango, aparecen en la expresión términos adicionales que son factores enteros de π
Los casos de argumento imaginario de la función integro-exponencial generalizada son
los que son la parte real de ∫ 1 ∞ cos ( a x ) ln x x d x = − π 2 24 + γ ( γ 2 + ln a ) + ln 2 a 2 + ∑ n ≥ 1 ( − a 2 ) n ( 2 n ) ! ( 2 n ) 2 , {\displaystyle \int _{1}^{\infty }\cos(ax){\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}+\sum _{n\geq 1}{\frac {(-a^{2})^{n}}{(2n)!(2n)^{2}}}~,} ∫ 1 ∞ e i a x ln x x d x = − π 2 24 + γ ( γ 2 + ln a ) + ln 2 a 2 − π 2 i ( γ + ln a ) + ∑ n ≥ 1 ( i a ) n n ! n 2 . {\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}-{\frac {\pi }{2}}i\left(\gamma +\ln a\right)+\sum _{n\geq 1}{\frac {(ia)^{n}}{n!n^{2}}}~.}
Similarmente ∫ 1 ∞ e i a x ln x x 2 d x = 1 + i a [ − π 2 24 + γ ( γ 2 + ln a − 1 ) + ln 2 a 2 − ln a + 1 ] + π a 2 ( γ + ln a − 1 ) + ∑ n ≥ 1 ( i a ) n + 1 ( n + 1 ) ! n 2 . {\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}\,dx=1+ia\left[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1\right]+{\frac {\pi a}{2}}{\Bigl (}\gamma +\ln a-1{\Bigr )}+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.}
Evaluación eficiente Las aproximaciones de Padé de la serie convergente de Taylor proporcionan una manera eficiente de evaluar las funciones para argumentos pequeños. Las siguientes fórmulas, dadas por Rowe et al. (2015), [2] tienen una precisión mejor que 10 −16 para 0 ≤ x ≤ 4 , Si ( x ) ≈ x ⋅ ( 1 − 4.54393409816329991 ⋅ 10 − 2 ⋅ x 2 + 1.15457225751016682 ⋅ 10 − 3 ⋅ x 4 − 1.41018536821330254 ⋅ 10 − 5 ⋅ x 6 + 9.43280809438713025 ⋅ 10 − 8 ⋅ x 8 − 3.53201978997168357 ⋅ 10 − 10 ⋅ x 10 + 7.08240282274875911 ⋅ 10 − 13 ⋅ x 12 − 6.05338212010422477 ⋅ 10 − 16 ⋅ x 14 1 + 1.01162145739225565 ⋅ 10 − 2 ⋅ x 2 + 4.99175116169755106 ⋅ 10 − 5 ⋅ x 4 + 1.55654986308745614 ⋅ 10 − 7 ⋅ x 6 + 3.28067571055789734 ⋅ 10 − 10 ⋅ x 8 + 4.5049097575386581 ⋅ 10 − 13 ⋅ x 10 + 3.21107051193712168 ⋅ 10 − 16 ⋅ x 12 ) Ci ( x ) ≈ γ + ln ( x ) + x 2 ⋅ ( − 0.25 + 7.51851524438898291 ⋅ 10 − 3 ⋅ x 2 − 1.27528342240267686 ⋅ 10 − 4 ⋅ x 4 + 1.05297363846239184 ⋅ 10 − 6 ⋅ x 6 − 4.68889508144848019 ⋅ 10 − 9 ⋅ x 8 + 1.06480802891189243 ⋅ 10 − 11 ⋅ x 10 − 9.93728488857585407 ⋅ 10 − 15 ⋅ x 12 1 + 1.1592605689110735 ⋅ 10 − 2 ⋅ x 2 + 6.72126800814254432 ⋅ 10 − 5 ⋅ x 4 + 2.55533277086129636 ⋅ 10 − 7 ⋅ x 6 + 6.97071295760958946 ⋅ 10 − 10 ⋅ x 8 + 1.38536352772778619 ⋅ 10 − 12 ⋅ x 10 + 1.89106054713059759 ⋅ 10 − 15 ⋅ x 12 + 1.39759616731376855 ⋅ 10 − 18 ⋅ x 14 ) {\displaystyle {\begin{array}{rcl}\operatorname {Si} (x)&\approx &x\cdot \left({\frac {\begin{array}{l}1-4.54393409816329991\cdot 10^{-2}\cdot x^{2}+1.15457225751016682\cdot 10^{-3}\cdot x^{4}-1.41018536821330254\cdot 10^{-5}\cdot x^{6}\\~~~+9.43280809438713025\cdot 10^{-8}\cdot x^{8}-3.53201978997168357\cdot 10^{-10}\cdot x^{10}+7.08240282274875911\cdot 10^{-13}\cdot x^{12}\\~~~-6.05338212010422477\cdot 10^{-16}\cdot x^{14}\end{array}}{\begin{array}{l}1+1.01162145739225565\cdot 10^{-2}\cdot x^{2}+4.99175116169755106\cdot 10^{-5}\cdot x^{4}+1.55654986308745614\cdot 10^{-7}\cdot x^{6}\\~~~+3.28067571055789734\cdot 10^{-10}\cdot x^{8}+4.5049097575386581\cdot 10^{-13}\cdot x^{10}+3.21107051193712168\cdot 10^{-16}\cdot x^{12}\end{array}}}\right)\\&~&\\\operatorname {Ci} (x)&\approx &\gamma +\ln(x)+\\&&x^{2}\cdot \left({\frac {\begin{array}{l}-0.25+7.51851524438898291\cdot 10^{-3}\cdot x^{2}-1.27528342240267686\cdot 10^{-4}\cdot x^{4}+1.05297363846239184\cdot 10^{-6}\cdot x^{6}\\~~~-4.68889508144848019\cdot 10^{-9}\cdot x^{8}+1.06480802891189243\cdot 10^{-11}\cdot x^{10}-9.93728488857585407\cdot 10^{-15}\cdot x^{12}\\\end{array}}{\begin{array}{l}1+1.1592605689110735\cdot 10^{-2}\cdot x^{2}+6.72126800814254432\cdot 10^{-5}\cdot x^{4}+2.55533277086129636\cdot 10^{-7}\cdot x^{6}\\~~~+6.97071295760958946\cdot 10^{-10}\cdot x^{8}+1.38536352772778619\cdot 10^{-12}\cdot x^{10}+1.89106054713059759\cdot 10^{-15}\cdot x^{12}\\~~~+1.39759616731376855\cdot 10^{-18}\cdot x^{14}\\\end{array}}}\right)\end{array}}}
Las integrales pueden evaluarse indirectamente a través de funciones auxiliares y , que se definen mediante f ( x ) {\displaystyle f(x)} g ( x ) {\displaystyle g(x)}
Si ( x ) = π 2 − f ( x ) cos ( x ) − g ( x ) sin ( x ) {\displaystyle \operatorname {Si} (x)={\frac {\pi }{2}}-f(x)\cos(x)-g(x)\sin(x)} Ci ( x ) = f ( x ) sin ( x ) − g ( x ) cos ( x ) {\displaystyle \operatorname {Ci} (x)=f(x)\sin(x)-g(x)\cos(x)} o equivalentemente f ( x ) ≡ [ π 2 − Si ( x ) ] cos ( x ) + Ci ( x ) sin ( x ) {\displaystyle f(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)+\operatorname {Ci} (x)\sin(x)} g ( x ) ≡ [ π 2 − Si ( x ) ] sin ( x ) − Ci ( x ) cos ( x ) {\displaystyle g(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)-\operatorname {Ci} (x)\cos(x)}
funciones racionales de Padé que se dan a continuación se aproximan y tienen un error menor que 10 −16 : [2] x ≥ 4 {\displaystyle x\geq 4} f ( x ) {\displaystyle f(x)} g ( x ) {\displaystyle g(x)}
f ( x ) ≈ 1 x ⋅ ( 1 + 7.44437068161936700618 ⋅ 10 2 ⋅ x − 2 + 1.96396372895146869801 ⋅ 10 5 ⋅ x − 4 + 2.37750310125431834034 ⋅ 10 7 ⋅ x − 6 + 1.43073403821274636888 ⋅ 10 9 ⋅ x − 8 + 4.33736238870432522765 ⋅ 10 10 ⋅ x − 10 + 6.40533830574022022911 ⋅ 10 11 ⋅ x − 12 + 4.20968180571076940208 ⋅ 10 12 ⋅ x − 14 + 1.00795182980368574617 ⋅ 10 13 ⋅ x − 16 + 4.94816688199951963482 ⋅ 10 12 ⋅ x − 18 − 4.94701168645415959931 ⋅ 10 11 ⋅ x − 20 1 + 7.46437068161927678031 ⋅ 10 2 ⋅ x − 2 + 1.97865247031583951450 ⋅ 10 5 ⋅ x − 4 + 2.41535670165126845144 ⋅ 10 7 ⋅ x − 6 + 1.47478952192985464958 ⋅ 10 9 ⋅ x − 8 + 4.58595115847765779830 ⋅ 10 10 ⋅ x − 10 + 7.08501308149515401563 ⋅ 10 11 ⋅ x − 12 + 5.06084464593475076774 ⋅ 10 12 ⋅ x − 14 + 1.43468549171581016479 ⋅ 10 13 ⋅ x − 16 + 1.11535493509914254097 ⋅ 10 13 ⋅ x − 18 ) g ( x ) ≈ 1 x 2 ⋅ ( 1 + 8.1359520115168615 ⋅ 10 2 ⋅ x − 2 + 2.35239181626478200 ⋅ 10 5 ⋅ x − 4 + 3.12557570795778731 ⋅ 10 7 ⋅ x − 6 + 2.06297595146763354 ⋅ 10 9 ⋅ x − 8 + 6.83052205423625007 ⋅ 10 10 ⋅ x − 10 + 1.09049528450362786 ⋅ 10 12 ⋅ x − 12 + 7.57664583257834349 ⋅ 10 12 ⋅ x − 14 + 1.81004487464664575 ⋅ 10 13 ⋅ x − 16 + 6.43291613143049485 ⋅ 10 12 ⋅ x − 18 − 1.36517137670871689 ⋅ 10 12 ⋅ x − 20 1 + 8.19595201151451564 ⋅ 10 2 ⋅ x − 2 + 2.40036752835578777 ⋅ 10 5 ⋅ x − 4 + 3.26026661647090822 ⋅ 10 7 ⋅ x − 6 + 2.23355543278099360 ⋅ 10 9 ⋅ x − 8 + 7.87465017341829930 ⋅ 10 10 ⋅ x − 10 + 1.39866710696414565 ⋅ 10 12 ⋅ x − 12 + 1.17164723371736605 ⋅ 10 13 ⋅ x − 14 + 4.01839087307656620 ⋅ 10 13 ⋅ x − 16 + 3.99653257887490811 ⋅ 10 13 ⋅ x − 18 ) {\displaystyle {\begin{array}{rcl}f(x)&\approx &{\dfrac {1}{x}}\cdot \left({\frac {\begin{array}{l}1+7.44437068161936700618\cdot 10^{2}\cdot x^{-2}+1.96396372895146869801\cdot 10^{5}\cdot x^{-4}+2.37750310125431834034\cdot 10^{7}\cdot x^{-6}\\~~~+1.43073403821274636888\cdot 10^{9}\cdot x^{-8}+4.33736238870432522765\cdot 10^{10}\cdot x^{-10}+6.40533830574022022911\cdot 10^{11}\cdot x^{-12}\\~~~+4.20968180571076940208\cdot 10^{12}\cdot x^{-14}+1.00795182980368574617\cdot 10^{13}\cdot x^{-16}+4.94816688199951963482\cdot 10^{12}\cdot x^{-18}\\~~~-4.94701168645415959931\cdot 10^{11}\cdot x^{-20}\end{array}}{\begin{array}{l}1+7.46437068161927678031\cdot 10^{2}\cdot x^{-2}+1.97865247031583951450\cdot 10^{5}\cdot x^{-4}+2.41535670165126845144\cdot 10^{7}\cdot x^{-6}\\~~~+1.47478952192985464958\cdot 10^{9}\cdot x^{-8}+4.58595115847765779830\cdot 10^{10}\cdot x^{-10}+7.08501308149515401563\cdot 10^{11}\cdot x^{-12}\\~~~+5.06084464593475076774\cdot 10^{12}\cdot x^{-14}+1.43468549171581016479\cdot 10^{13}\cdot x^{-16}+1.11535493509914254097\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\&&\\g(x)&\approx &{\dfrac {1}{x^{2}}}\cdot \left({\frac {\begin{array}{l}1+8.1359520115168615\cdot 10^{2}\cdot x^{-2}+2.35239181626478200\cdot 10^{5}\cdot x^{-4}+3.12557570795778731\cdot 10^{7}\cdot x^{-6}\\~~~+2.06297595146763354\cdot 10^{9}\cdot x^{-8}+6.83052205423625007\cdot 10^{10}\cdot x^{-10}+1.09049528450362786\cdot 10^{12}\cdot x^{-12}\\~~~+7.57664583257834349\cdot 10^{12}\cdot x^{-14}+1.81004487464664575\cdot 10^{13}\cdot x^{-16}+6.43291613143049485\cdot 10^{12}\cdot x^{-18}\\~~~-1.36517137670871689\cdot 10^{12}\cdot x^{-20}\end{array}}{\begin{array}{l}1+8.19595201151451564\cdot 10^{2}\cdot x^{-2}+2.40036752835578777\cdot 10^{5}\cdot x^{-4}+3.26026661647090822\cdot 10^{7}\cdot x^{-6}\\~~~+2.23355543278099360\cdot 10^{9}\cdot x^{-8}+7.87465017341829930\cdot 10^{10}\cdot x^{-10}+1.39866710696414565\cdot 10^{12}\cdot x^{-12}\\~~~+1.17164723371736605\cdot 10^{13}\cdot x^{-14}+4.01839087307656620\cdot 10^{13}\cdot x^{-16}+3.99653257887490811\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\\end{array}}}
Véase también
Referencias ^ Gray (1993). Geometría diferencial moderna de curvas y superficies . Boca Raton. pág. 119. {{cite book }}: CS1 maint: location missing publisher (link )^ ab Rowe, B.; et al. (2015). "GALSIM: El kit de herramientas modular para simulación de imágenes de galaxias". Astronomía y computación . 10 : 121. arXiv : 1407.7676 . Bibcode :2015A&C....10..121R. doi :10.1016/j.ascom.2015.02.002. S2CID 62709903.
Lectura adicional Mathar, RJ (2009). "Evaluación numérica de la integral oscilatoria sobre exp( i π x )· x 1/ x entre 1 y ∞". Apéndice B. arXiv : 0912.3844 [math.CA]. Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Sección 6.8.2 – Integrales de seno y coseno". Recetas numéricas: el arte de la computación científica (3.ª ed.). Nueva York: Cambridge University Press. ISBN 978-0-521-88068-8 Sloughter, Dan. "Demostración de la serie de Taylor de la integral seno-lineal" (PDF) . Ecuaciones diferenciales a ecuaciones diferenciales . Temme, NM (2010), "Integrales exponenciales, logarítmicas, seno y coseno", en Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), Manual del NIST de funciones matemáticas ISBN 978-0-521-19225-5 Sr. 2723248
Enlaces externos 



















![{\displaystyle {\begin{array}{rcl}f(x)&\equiv &\int _{0}^{\infty }{\frac {\sin(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {e^{-xt}}{t^{2}+1}}\,dt&=&\operatorname {Ci} (x)\sin(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\cos(x)~,\\g(x)&\equiv &\int _{0}^{\infty }{\frac {\cos(t)}{t+x}}\,dt&=&\int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}\,dt&=&-\nombre del operador {Ci} (x)\cos(x)+\left[{\frac {\pi }{2}}-\nombre del operador {Si} (x)\right]\sin(x)~.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b43b57fdff2c9f86d9685bbf1d8a0eb7b30c11)














![{\displaystyle \int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}\,dx=1+ia\left[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1\right]+{\frac {\pi a}{2}}{\Bigl (}\gamma +\ln a-1{\Bigr )}+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61671b32bbb8068361dfa5d582a6d6f3230a43cf)





![{\displaystyle f(x)\equiv \left[{\frac {\pi }{2}}-\operadornombre {Si} (x)\right]\cos(x)+\operadornombre {Ci} (x)\sin(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a843910ab6cb92c362e68ac401c28c1e7cda148)
![{\displaystyle g(x)\equiv \left[{\frac {\pi }{2}}-\operadornombre {Si} (x)\right]\sin(x)-\operadornombre {Ci} (x)\cos(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f74128afc0519376e13432f0e9f5b0bf6627de7)

