Nucleosíntesis estelar

En astrofísica , la nucleosíntesis estelar es la creación de elementos químicos mediante reacciones de fusión nuclear dentro de las estrellas . La nucleosíntesis estelar ha ocurrido desde la creación original del hidrógeno , helio y litio durante el Big Bang . Como teoría predictiva , produce estimaciones precisas de las abundancias observadas de los elementos. Explica por qué las abundancias observadas de elementos cambian con el tiempo y por qué algunos elementos y sus isótopos son mucho más abundantes que otros. La teoría fue propuesta inicialmente por Fred Hoyle en 1946, ^[1] quien luego la refinó en 1954. ^[2] Se hicieron avances adicionales, especialmente en la nucleosíntesis por captura de neutrones de los elementos más pesados ​​​​que el hierro , por Margaret y Geoffrey Burbidge , William Alfred Fowler y Fred Hoyle en su famoso artículo B ² FH de 1957 , ^[3] que se convirtió en uno de los artículos más citados en la historia de la astrofísica.

Las estrellas evolucionan debido a cambios en su composición (la abundancia de sus elementos constituyentes) a lo largo de su vida, primero quemando hidrógeno ( estrella de secuencia principal ), luego helio ( estrella de rama horizontal ) y quemando progresivamente elementos superiores . Sin embargo, esto por sí solo no altera significativamente las abundancias de elementos en el universo ya que los elementos están contenidos dentro de la estrella. Más adelante en su vida, una estrella de baja masa expulsará lentamente su atmósfera a través del viento estelar , formando una nebulosa planetaria , mientras que una estrella de mayor masa expulsará masa a través de un evento catastrófico repentino llamado supernova . El término nucleosíntesis de supernova se utiliza para describir la creación de elementos durante la explosión de una estrella masiva o enana blanca .

La secuencia avanzada de combustión de combustibles es impulsada por el colapso gravitacional y su calentamiento asociado, lo que resulta en la combustión posterior de carbono , oxígeno y silicio . Sin embargo, la mayor parte de la nucleosíntesis en el rango de masa A = 28-56 (desde el silicio hasta el níquel) es causada en realidad por las capas superiores de la estrella que colapsan sobre el núcleo , creando una onda de choque compresiva que rebota hacia afuera. El frente de choque eleva brevemente las temperaturas en aproximadamente un 50%, lo que causa una combustión furiosa durante aproximadamente un segundo. Esta combustión final en estrellas masivas, llamada nucleosíntesis explosiva o nucleosíntesis de supernova , es la época final de la nucleosíntesis estelar.

Un estímulo para el desarrollo de la teoría de la nucleosíntesis fue el descubrimiento de variaciones en las abundancias de los elementos que se encuentran en el universo . La necesidad de una descripción física ya estaba inspirada por las abundancias relativas de los elementos químicos en el sistema solar. Esas abundancias, cuando se representan en un gráfico como una función del número atómico del elemento, tienen una forma dentada dentada que varía en factores de decenas de millones (véase la historia de la teoría de la nucleosíntesis ). ^[4] Esto sugirió un proceso natural que no es aleatorio. Un segundo estímulo para comprender los procesos de nucleosíntesis estelar ocurrió durante el siglo XX, cuando se comprendió que la energía liberada de las reacciones de fusión nuclear explicaba la longevidad del Sol como fuente de calor y luz. ^[5]

En 1920, Arthur Eddington , basándose en las mediciones precisas de masas atómicas de FW Aston y una sugerencia preliminar de Jean Perrin , propuso que las estrellas obtenían su energía de la fusión nuclear de hidrógeno para formar helio y planteó la posibilidad de que los elementos más pesados ​​se produzcan en las estrellas. ^{[6] [7] [8]} Este fue un paso preliminar hacia la idea de la nucleosíntesis estelar. En 1928, George Gamow derivó lo que ahora se llama el factor de Gamow , una fórmula mecánico-cuántica que produce la probabilidad de que dos núcleos contiguos superen la barrera electrostática de Coulomb entre ellos y se acerquen lo suficiente como para experimentar una reacción nuclear debido a la fuerza nuclear fuerte que es efectiva solo a distancias muy cortas. ^{[9] : 410} En la década siguiente, el factor de Gamow fue utilizado por Atkinson y Houtermans y más tarde por Edward Teller y el propio Gamow para derivar la velocidad a la que se producirían las reacciones nucleares a las altas temperaturas que se cree que existen en el interior de las estrellas.

En 1939, en una conferencia Nobel titulada "Producción de energía en las estrellas", Hans Bethe analizó las diferentes posibilidades de reacciones por las que el hidrógeno se fusiona en helio. ^[10] Definió dos procesos que creía que eran las fuentes de energía en las estrellas. El primero, la reacción en cadena protón-protón , es la fuente de energía dominante en estrellas con masas de hasta aproximadamente la masa del Sol. El segundo proceso, el ciclo carbono-nitrógeno-oxígeno , que también fue considerado por Carl Friedrich von Weizsäcker en 1938, es más importante en estrellas de secuencia principal más masivas. ^{[11] : 167} Estos trabajos se ocupaban de la generación de energía capaz de mantener calientes a las estrellas. Una descripción física clara de la cadena protón-protón y del ciclo CNO aparece en un libro de texto de 1968. ^{[12] : 365} Sin embargo, los dos artículos de Bethe no abordaron la creación de núcleos más pesados. Esta teoría fue iniciada por Fred Hoyle en 1946 con su argumento de que una colección de núcleos muy calientes se ensamblaría termodinámicamente en hierro . ^[1] Hoyle continuó en 1954 con un artículo que describe cómo las etapas avanzadas de fusión dentro de estrellas masivas sintetizarían los elementos desde el carbono hasta el hierro en masa. ^{[2] [13]}

La teoría de Hoyle se extendió a otros procesos, comenzando con la publicación del artículo de revisión de 1957 "Síntesis de los elementos en las estrellas" por Burbidge , Burbidge , Fowler y Hoyle , más comúnmente conocido como el artículo B ² FH . ^[3] Este artículo de revisión recopiló y refinó la investigación anterior en una imagen profusamente citada que prometía explicar las abundancias relativas observadas de los elementos; pero no amplió en sí mismo la imagen de Hoyle de 1954 para el origen de los núcleos primarios tanto como muchos suponían, excepto en la comprensión de la nucleosíntesis de aquellos elementos más pesados ​​​​que el hierro por captura de neutrones. Alastair GW Cameron y Donald D. Clayton hicieron mejoras significativas . En 1957, Cameron presentó su propio enfoque independiente para la nucleosíntesis, ^[14] informado por el ejemplo de Hoyle, e introdujo las computadoras en los cálculos dependientes del tiempo de la evolución de los sistemas nucleares. Clayton calculó los primeros modelos dependientes del tiempo del proceso s en 1961 ^[15] y del proceso r en 1965, ^[16] así como de la quema de silicio en los abundantes núcleos de partículas alfa y elementos del grupo del hierro en 1968, ^{[17] [18]} y descubrió cronologías radiogénicas ^[19] para determinar la edad de los elementos.

Las reacciones más importantes en la nucleosíntesis estelar:

• Fusión de hidrógeno :
  • Fusión de deuterio
  • La cadena protón-protón
  • El ciclo del carbono-nitrógeno-oxígeno
• Fusión de helio :
  • El proceso triple alfa
  • El proceso alfa
• Fusión de elementos más pesados:
  • Quema de litio : un proceso que se encuentra más comúnmente en las enanas marrones
  • Proceso de quema de carbono
  • Proceso de quema de neón
  • Proceso de quema de oxígeno
  • Proceso de quema de silicio
• Producción de elementos más pesados ​​que el hierro :
  • Captura de neutrones :
    • El proceso r
    • El proceso s
  • Captura de protones :
    • El proceso rp
    • El proceso p
  • Fotodesintegración

La fusión de hidrógeno (fusión nuclear de cuatro protones para formar un núcleo de helio-4 ^[20] ) es el proceso dominante que genera energía en los núcleos de las estrellas de la secuencia principal . También se denomina "quema de hidrógeno", que no debe confundirse con la combustión química del hidrógeno en una atmósfera oxidante . Hay dos procesos predominantes por los que se produce la fusión estelar de hidrógeno: la cadena protón-protón y el ciclo carbono-nitrógeno-oxígeno (CNO). El noventa por ciento de todas las estrellas, con la excepción de las enanas blancas , fusionan hidrógeno mediante estos dos procesos. ^{[21] : 245}

En los núcleos de estrellas de la secuencia principal de menor masa, como el Sol , el proceso de producción de energía dominante es la reacción en cadena protón-protón . Esto crea un núcleo de helio-4 a través de una secuencia de reacciones que comienzan con la fusión de dos protones para formar un núcleo de deuterio (un protón más un neutrón) junto con un positrón y un neutrino expulsados. ^[22] En cada ciclo de fusión completo, la reacción en cadena protón-protón libera alrededor de 26,2 MeV. ^[22] El ciclo de reacción en cadena protón-protón es relativamente insensible a la temperatura; un aumento del 10% de la temperatura aumentaría la producción de energía por este método en un 46%, por lo tanto, este proceso de fusión de hidrógeno puede ocurrir en hasta un tercio del radio de la estrella y ocupar la mitad de la masa de la estrella. Para estrellas por encima del 35% de la masa del Sol, ^[23] el flujo de energía hacia la superficie es suficientemente bajo y la transferencia de energía desde la región del núcleo permanece por transferencia de calor radiativo , en lugar de por transferencia de calor convectivo . ^[24] Como resultado, hay poca mezcla de hidrógeno fresco en el núcleo o de productos de fusión hacia el exterior.

En las estrellas de mayor masa, el proceso de producción de energía dominante es el ciclo CNO , que es un ciclo catalítico que utiliza núcleos de carbono, nitrógeno y oxígeno como intermediarios y al final produce un núcleo de helio como con la cadena protón-protón. ^[22] Durante un ciclo CNO completo, se liberan 25,0 MeV de energía. La diferencia en la producción de energía de este ciclo, en comparación con la reacción en cadena protón-protón, se explica por la energía perdida a través de la emisión de neutrinos . ^[22] El ciclo CNO es muy sensible a la temperatura, un aumento del 10% de la temperatura produciría un aumento del 350% en la producción de energía. Aproximadamente el 90% de la generación de energía del ciclo CNO ocurre dentro del 15% interior de la masa de la estrella, por lo tanto, está fuertemente concentrada en el núcleo. ^[25] Esto da como resultado un flujo de energía hacia afuera tan intenso que la transferencia de energía convectiva se vuelve más importante que la transferencia radiativa . Como resultado, la región del núcleo se convierte en una zona de convección , que agita la región de fusión de hidrógeno y la mantiene bien mezclada con la región circundante rica en protones. ^[26] Esta convección del núcleo ocurre en estrellas donde el ciclo CNO contribuye con más del 20% de la energía total. A medida que la estrella envejece y la temperatura del núcleo aumenta, la región ocupada por la zona de convección se reduce lentamente del 20% de la masa hasta el 8% interior de la masa. ^[25] El Sol produce alrededor del 1% de su energía a partir del ciclo CNO. ^{[27] [a] [28] : 357  [29] [b]}

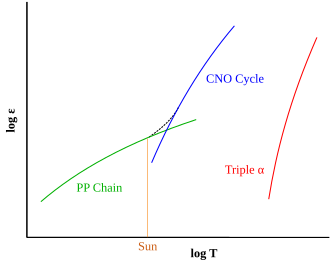
El tipo de proceso de fusión de hidrógeno que predomina en una estrella está determinado por las diferencias de dependencia de la temperatura entre las dos reacciones. La reacción en cadena protón-protón comienza a temperaturas de aproximadamente4 × 10 ⁶  K , ^[30] lo que lo convierte en el mecanismo de fusión dominante en estrellas más pequeñas. Una cadena CNO automantenida requiere una temperatura más alta de aproximadamente1,6 × 10 ⁷  K , pero a partir de entonces aumenta más rápidamente en eficiencia a medida que aumenta la temperatura, que la reacción protón-protón. ^[31] Por encima de aproximadamente1,7 × 10 ⁷  K , el ciclo CNO se convierte en la fuente dominante de energía. Esta temperatura se alcanza en los núcleos de estrellas de la secuencia principal con al menos 1,3 veces la masa del Sol . ^[32] El propio Sol tiene una temperatura central de aproximadamente1,57 × 10 ⁷  K . ^{[33] : 5} A medida que una estrella de secuencia principal envejece, la temperatura del núcleo aumentará, lo que dará como resultado una contribución cada vez mayor de su ciclo CNO. ^[25]

Las estrellas de secuencia principal acumulan helio en sus núcleos como resultado de la fusión de hidrógeno, pero el núcleo no se calienta lo suficiente como para iniciar la fusión de helio. La fusión de helio comienza cuando una estrella abandona la rama gigante roja después de acumular suficiente helio en su núcleo para encenderla. En estrellas alrededor de la masa del Sol, esto comienza en la punta de la rama gigante roja con un destello de helio de un núcleo de helio degenerado , y la estrella se mueve a la rama horizontal donde quema helio en su núcleo. Las estrellas más masivas encienden helio en su núcleo sin un destello y ejecutan un bucle azul antes de alcanzar la rama gigante asintótica . Una estrella de este tipo se aleja inicialmente de la AGB hacia colores más azules, luego vuelve a realizar un bucle a lo que se llama la trayectoria de Hayashi . Una consecuencia importante de los bucles azules es que dan lugar a las variables cefeidas clásicas , de importancia central para determinar las distancias en la Vía Láctea y a las galaxias cercanas. ^{[34] : 250} A pesar del nombre, las estrellas en un bucle azul de la rama de las gigantes rojas no suelen ser de color azul, sino gigantes amarillas, posiblemente variables cefeidas. Fusionan helio hasta que el núcleo es en gran parte carbono y oxígeno . Las estrellas más masivas se convierten en supergigantes cuando abandonan la secuencia principal y rápidamente comienzan la fusión de helio a medida que se convierten en supergigantes rojas . Después de que el helio se agote en el núcleo de una estrella, la fusión de helio continuará en una capa alrededor del núcleo de carbono y oxígeno. ^{[20] [24]}

En todos los casos, el helio se fusiona con el carbono a través del proceso triple alfa, es decir, tres núcleos de helio se transforman en carbono a través de ⁸ Be . ^{[35] : 30} Esto puede formar oxígeno, neón y elementos más pesados ​​a través del proceso alfa. De esta manera, el proceso alfa produce preferentemente elementos con números pares de protones mediante la captura de núcleos de helio. Los elementos con números impares de protones se forman mediante otras vías de fusión. ^{[36] : 398}

La densidad de velocidad de reacción entre las especies A y B , que tienen densidades numéricas n _{A , B} , viene dada por: donde k es la constante de velocidad de reacción de cada reacción binaria elemental individual que compone el proceso de fusión nuclear : aquí, σ ( v ) es la sección transversal a la velocidad relativa v , y el promedio se realiza sobre todas las velocidades.$${\displaystyle r=n_{A}\,n_{B}\,k}$$$${\displaystyle k=\langle \sigma (v)\,v\rangle }$$

Semiclásicamente, la sección transversal es proporcional a , donde es la longitud de onda de De Broglie . Por lo tanto, de manera semiclásica, la sección transversal es proporcional a .${\displaystyle \pi \,\lambda ^{2}}$${\displaystyle \lambda = h/p}$${\textstyle {\frac {m}{E}}}$

Sin embargo, dado que la reacción implica un efecto túnel cuántico , hay una amortiguación exponencial a bajas energías que depende del factor de Gamow E _G , dando una ecuación de Arrhenius : donde S ( E ) depende de los detalles de la interacción nuclear y tiene la dimensión de una energía multiplicada por una sección transversal.$${\displaystyle \sigma (E)={\frac {S(E)}{E}}e^{-{\sqrt {\frac {E_{\text{G}}}{E}}}}}$$

Luego se integran todas las energías para obtener la velocidad de reacción total, utilizando la distribución de Maxwell-Boltzmann y la relación: donde es la masa reducida .$${\displaystyle {\frac {r}{V}}=n_{A}n_{B}\int _{0}^{\infty }{\frac {S(E)}{E}}\,e^{-{\sqrt {\frac {E_{\text{G}}}{E}}}}2{\sqrt {\frac {E}{\pi (kT)^{3}}}}e^{-{\frac {E}{kT}}}\,{\sqrt {\frac {2E}{m_{\text{R}}}}}dE}$$${\displaystyle m_{\text{R}}={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}}$

Dado que esta integración tiene una amortiguación exponencial a altas energías de la forma y a bajas energías del factor de Gamow, la integral casi desaparece en todas partes excepto alrededor del pico, llamado pico de Gamow , ^{[37] : 185} en E ₀ , donde:${\displaystyle \sim e^{-{\frac {E}{kT}}}}$$${\displaystyle {\frac {\parcial }{\parcial E}}\left(-{\sqrt {\frac {E_{\text{G}}}{E}}}-{\frac {E}{kT}}\right)\,=\,0}$$

De este modo:$${\displaystyle E_{0}=\left({\frac {1}{2}}kT{\sqrt {E_{\text{G}}}}\right)^{\frac {2}{3}}}$$

El exponente puede entonces aproximarse alrededor de E ₀ como:$${\displaystyle e^{-{\frac {E}{kT}}-{\sqrt {\frac {E_{\text{G}}}{E}}}}\approx e^{-{\frac { 3E_{0}}{kT}}}\exp \left(-{\frac {(E-E_{0})^{2}}{{\frac {4}{3}}E_{0}kT} }\bien)}$$

Y la velocidad de reacción se aproxima como: ^[38]$${\displaystyle {\frac {r}{V}}\approx n_{A}\,n_{B}\,{\frac {4{\sqrt {2}}}{\sqrt {3m_{\text{R}}}}}\,{\sqrt {E_{0}}}{\frac {S(E_{0})}{kT}}e^{-{\frac {3E_{0}}{kT}}}}$$

Los valores de S ( E ₀ ) son típicamente 10 ⁻³ – 10 ³ keV · b , pero se ven atenuados por un factor enorme cuando se trata de una desintegración beta , debido a la relación entre la vida media del estado intermedio ligado (por ejemplo, diprotón ) y la vida media de la desintegración beta, como en la reacción en cadena protón-protón . Nótese que las temperaturas típicas del núcleo en las estrellas de la secuencia principal dan kT del orden de keV. ^{[39] : cap. 3}

Así, la reacción limitante en el ciclo CNO , la captura de protones por¹⁴
₇norte
, tiene S ( E ₀ ) ~ S (0) = 3,5  keV·b, mientras que la reacción limitante en la reacción en cadena protón-protón , la creación de deuterio a partir de dos protones, tiene un S ( E ₀ ) ~ S (0) = 4×10 ⁻²²  keV·b mucho menor. ^{[40] [41]} Por cierto, dado que la primera reacción tiene un factor de Gamow mucho mayor, y debido a la abundancia relativa de elementos en estrellas típicas, las dos velocidades de reacción son iguales a un valor de temperatura que está dentro de los rangos de temperatura central de las estrellas de la secuencia principal. ^[42]

• Bethe, HA (1939). "Producción de energía en las estrellas". Physical Review . 55 (1): 541–547. Bibcode :1939PhRv...55..103B. doi : 10.1103/PhysRev.55.103 . PMID  17835673.
• Bethe, HA (1939). "Producción de energía en las estrellas". Physical Review . 55 (5): 434–456. Bibcode :1939PhRv...55..434B. doi : 10.1103/PhysRev.55.434 . PMID  17835673.
• Hoyle, F. (1954). "Sobre las reacciones nucleares que ocurren en estrellas muy calientes: síntesis de elementos desde el carbono hasta el níquel". Suplemento de la revista Astrophysical Journal . 1 : 121–146. Código Bibliográfico :1954ApJS....1..121H. doi :10.1086/190005.
• Clayton, Donald D. (1968). Principios de evolución estelar y nucleosíntesis . Nueva York: McGraw-Hill .
• Ray, A. (2004). "Las estrellas como reactores termonucleares: sus combustibles y cenizas". arXiv : astro-ph/0405568 .
• G. Wallerstein ; I. Iben, Jr. ; P. Parker; AM Boesgaard ; GM Hale; AE Champagne; et al. (1997). "Síntesis de los elementos en las estrellas: cuarenta años de progreso" (PDF) . Reviews of Modern Physics . 69 (4): 995–1084. Bibcode :1997RvMP...69..995W. doi :10.1103/RevModPhys.69.995. hdl : 2152/61093 . Archivado desde el original (PDF) el 2009-03-26 . Consultado el 2006-08-04 .
• Woosley, SE ; A. Heger; TA Weaver (2002). "La evolución y explosión de estrellas masivas". Reseñas de Física Moderna . 74 (4): 1015–1071. Bibcode :2002RvMP...74.1015W. doi :10.1103/RevModPhys.74.1015. S2CID  55932331.
• Clayton, Donald D. (2003). Manual de isótopos en el cosmos. Cambridge: Cambridge University Press . ISBN 978-0-521-82381-4.
• Iliadis, Christian (2007). Física nuclear de las estrellas. Weinheim: Wiley-VCH. doi :10.1002/9783527618750. ISBN 978-3-527-40602-9.

• "Cómo brilla el sol", de John N. Bahcall (sitio del premio Nobel, consultado el 6 de enero de 2020)
• Nucleosíntesis en la Cosmicopia de la NASA