Problema de secretaria

El problema de la secretaria muestra un escenario que involucra la teoría de detención óptima ^{[1] [2]} que se estudia ampliamente en los campos de la probabilidad aplicada , la estadística y la teoría de la decisión . También se lo conoce como el problema del matrimonio , el problema de la dote del sultán , el problema del pretendiente quisquilloso , el juego del gúgol y el problema de la mejor elección . Su solución también se conoce como la regla del 37% . ^[3]

La forma básica del problema es la siguiente: imaginemos a un administrador que quiere contratar a la mejor secretaria de entre los candidatos que pueden clasificarse para un puesto. Los candidatos son entrevistados uno por uno en orden aleatorio. Se debe tomar una decisión sobre cada candidato en particular inmediatamente después de la entrevista. Una vez rechazado, no se puede volver a llamar a un candidato. Durante la entrevista, el administrador obtiene información suficiente para clasificar al candidato entre todos los candidatos entrevistados hasta el momento, pero desconoce la calidad de los candidatos que aún no ha visto. La pregunta es sobre la estrategia óptima ( regla de detención ) para maximizar la probabilidad de seleccionar al mejor candidato. Si la decisión se puede aplazar hasta el final, esto se puede resolver mediante el algoritmo simple de selección máxima de seguimiento del máximo actual (y quién lo logró) y selección del máximo general al final. La dificultad es que la decisión debe tomarse inmediatamente.${\estilo de visualización n}$

La prueba rigurosa más corta conocida hasta ahora la proporciona el algoritmo de probabilidades . Implica que la probabilidad óptima de ganar es siempre al menos (donde e es la base del logaritmo natural ), y que esto último se cumple incluso en una generalidad mucho mayor. La regla de detención óptima prescribe rechazar siempre a los primeros solicitantes que se entrevistan y luego detenerse en el primer solicitante que sea mejor que todos los solicitantes entrevistados hasta ahora (o continuar hasta el último solicitante si esto nunca ocurre). A veces, esta estrategia se llama regla de detención, porque la probabilidad de detenerse en el mejor solicitante con esta estrategia ya es de aproximadamente para valores moderados de . Una razón por la que el problema de la secretaria ha recibido tanta atención es que la política óptima para el problema (la regla de detención) es simple y selecciona al mejor candidato individual aproximadamente el 37% del tiempo, independientemente de si hay 100 o 100 millones de solicitantes.${\estilo de visualización 1/e}$${\displaystyle \sim n/e}$${\estilo de visualización 1/e}$${\estilo de visualización 1/e}$${\estilo de visualización n}$

Aunque existen muchas variantes, el problema básico puede enunciarse de la siguiente manera:

• Hay un único puesto a cubrir.
• Hay n solicitantes para el puesto y se conoce el valor de n .
• Si se consideran todos los solicitantes en conjunto, se pueden clasificar de mejor a peor sin ambigüedades.
• Los solicitantes son entrevistados secuencialmente en orden aleatorio, siendo cada orden igualmente probable.
• Inmediatamente después de la entrevista, el solicitante entrevistado es aceptado o rechazado, y la decisión es irrevocable.
• La decisión de aceptar o rechazar a un solicitante puede basarse únicamente en las clasificaciones relativas de los solicitantes entrevistados hasta el momento.
• El objetivo de la solución general es tener la mayor probabilidad de seleccionar al mejor candidato de todo el grupo. Esto es lo mismo que maximizar el resultado esperado, donde el resultado se define como uno para el mejor candidato y cero en caso contrario.

Se define como candidato a aquel que, al ser entrevistado, es mejor que todos los candidatos entrevistados anteriormente. Skip se utiliza para significar "rechazar inmediatamente después de la entrevista". Dado que el objetivo del problema es seleccionar al mejor candidato, solo se considerará la aceptación de candidatos. El "candidato" en este contexto corresponde al concepto de récord en permutación.

La política óptima para el problema es una regla de detención . Según ella, el entrevistador rechaza a los primeros r  − 1 solicitantes (sea el solicitante M el mejor solicitante entre estos r  − 1 solicitantes), y luego selecciona al primer solicitante posterior que sea mejor que el solicitante M. Se puede demostrar que la estrategia óptima se encuentra en esta clase de estrategias. ^{[ cita requerida ]} (Tenga en cuenta que nunca debemos elegir a un solicitante que no sea el mejor que hemos visto hasta ahora, ya que no puede ser el mejor solicitante en general). Para un punto de corte arbitrario r , la probabilidad de que se seleccione al mejor solicitante es

${\displaystyle {\begin{aligned}P(r)&=\sum _{i=1}^{n}P\left({\text{solicitante }}i{\text{ es seleccionado}}\cap {\text{solicitante }}i{\text{ es el mejor}}\right)\\&=\sum _{i=1}^{n}P\left({\text{solicitante }}i{\text{ es seleccionado}}|{\text{solicitante }}i{\text{ es el mejor}}\right)\cdot P\left({\text{solicitante }}i{\text{ es el mejor}}\right)\\&=\left[\sum _{i=1}^{r-1}0+\sum _{i=r}^{n}P\left(\left.{\begin{array}{l}{\text{el mejor del primero }}i-1{\text{ solicitantes}}\\{\text{está en el primer }}r-1{\text{ solicitantes}}\end{array}}\right|{\text{solicitante }}i{\text{ es el mejor}}\right)\right]\cdot {\frac {1}{n}}\\&=\left[\sum _{i=r}^{n}{\frac {r-1}{i-1}}\right]\cdot {\frac {1}{n}}\\&={\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}.\end{aligned}}}$

La suma no está definida para r = 1, pero en este caso la única política factible es seleccionar al primer solicitante, y por lo tanto P (1) = 1/ n . Esta suma se obtiene notando que si el solicitante i es el mejor solicitante, entonces se selecciona si y solo si el mejor solicitante entre los primeros i  − 1 solicitantes está entre los primeros r  − 1 solicitantes que fueron rechazados. Dejando que n tienda a infinito, escribiendo como el límite de (r−1) / n , usando t para (i−1) / n y dt para 1/ n , la suma se puede aproximar por la integral${\estilo de visualización x}$

${\displaystyle P(x)=x\int _{x}^{1}{\frac {1}{t}}\,dt=-x\ln(x)\;.}$

Tomando la derivada de P ( x ) con respecto a , fijándola en 0 y despejando x , encontramos que el x óptimo es igual a 1/ e . Por lo tanto, el punto de corte óptimo tiende a n / e a medida que n aumenta, y se selecciona al mejor candidato con probabilidad 1/ e .${\estilo de visualización x}$

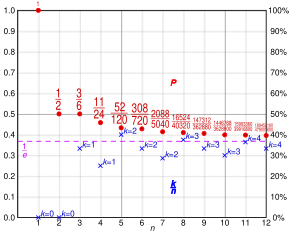
Para valores pequeños de n , el r óptimo también se puede obtener mediante métodos de programación dinámica estándar . Los umbrales óptimos r y la probabilidad de seleccionar la mejor alternativa P para varios valores de n se muestran en la siguiente tabla. ^{[nota 1]}

${\estilo de visualización n}$	1	2	3	4	5	6	7	8	9	10
${\estilo de visualización r}$	1	1	2	2	3	3	3	4	4	4
${\estilo de visualización P}$	1.000	0,500	0,500	0,458	0,433	0,428	0,414	0,410	0,406	0,399

La probabilidad de seleccionar al mejor candidato en el problema clásico de la secretaria converge hacia .${\displaystyle 1/e\aproximadamente 0,368}$

Este problema y varias modificaciones pueden resolverse (incluida la prueba de optimalidad) de manera sencilla mediante el algoritmo de probabilidades , que también tiene otras aplicaciones. Las modificaciones para el problema de la secretaria que pueden resolverse mediante este algoritmo incluyen disponibilidades aleatorias de solicitantes, hipótesis más generales para que los solicitantes sean de interés para el tomador de decisiones, entrevistas grupales para los solicitantes, así como ciertos modelos para un número aleatorio de solicitantes. ^{[ cita requerida ]}

La solución del problema de la secretaria sólo tiene sentido si se justifica suponer que los solicitantes no tienen conocimiento de la estrategia de decisión empleada, porque de lo contrario los solicitantes anticipados no tienen ninguna posibilidad y es posible que no se presenten.

Un inconveniente importante para las aplicaciones de la solución del problema clásico de la secretaria es que el número de solicitantes debe conocerse de antemano, lo que rara vez ocurre. Una forma de superar este problema es suponer que el número de solicitantes es una variable aleatoria con una distribución conocida de (Presman y Sonin, 1972). Sin embargo, para este modelo, la solución óptima es en general mucho más difícil. Además, la probabilidad óptima de éxito ya no está alrededor de 1/ e sino que normalmente es menor. Esto se puede entender en el contexto de tener un "precio" que pagar por no saber el número de solicitantes. Sin embargo, en este modelo el precio es alto. Dependiendo de la elección de la distribución de , la probabilidad óptima de ganar puede acercarse a cero. La búsqueda de formas de hacer frente a este nuevo problema condujo a un nuevo modelo que produjo la llamada ley 1/e de la mejor elección.${\estilo de visualización n}$${\estilo de visualización N}$${\displaystyle P(N=k)_{k=1,2,\cpuntos}}$${\estilo de visualización N}$

La esencia del modelo se basa en la idea de que la vida es secuencial y que los problemas del mundo real se plantean en tiempo real. Además, es más fácil estimar los momentos en los que determinados acontecimientos (llegadas de solicitantes) deberían producirse con mayor frecuencia (si es que lo hacen) que estimar la distribución del número de acontecimientos concretos que se producirán. Esta idea dio lugar al siguiente enfoque, el denominado enfoque unificado (1984):

El modelo se define de la siguiente manera: un solicitante debe ser seleccionado en un intervalo de tiempo determinado de un número desconocido de solicitantes clasificables. El objetivo es maximizar la probabilidad de seleccionar solo al mejor bajo la hipótesis de que todos los órdenes de llegada de diferentes rangos son igualmente probables. Supongamos que todos los solicitantes tienen la misma densidad de tiempo de llegada, pero independientes entre sí, en y sea la función de distribución de tiempo de llegada correspondiente, es decir${\estilo de visualización [0,T]}$${\estilo de visualización N}$${\estilo de visualización f}$${\estilo de visualización [0,T]}$${\estilo de visualización F}$

${\displaystyle F(t)=\int _{0}^{t}f(s)ds}$, .${\displaystyle \,0\leq t\leq T}$

Sea tal que Consideremos la estrategia de esperar y observar a todos los postulantes hasta el momento y luego seleccionar, si es posible, al primer candidato después del tiempo que sea mejor que todos los anteriores. Entonces esta estrategia, llamada 1/e-strategy , tiene las siguientes propiedades:${\estilo de visualización \tau}$${\displaystyle F(\tau )=1/e.}$${\estilo de visualización \tau}$${\estilo de visualización \tau}$

La estrategia 1/e

(i) produce para todos una probabilidad de éxito de al menos 1/e,${\estilo de visualización N}$

(ii) es una estrategia minimax-óptima para el selector que no sabe ,${\estilo de visualización N}$

(iii) selecciona, si hay al menos un solicitante, ninguno con una probabilidad exactamente de 1/e.

La ley 1/e, demostrada en 1984 por F. Thomas Bruss , fue una sorpresa. La razón fue que antes se había considerado que un valor de aproximadamente 1/e estaba fuera de alcance en un modelo para valores desconocidos , mientras que ahora se lograba ese valor 1/e como límite inferior para la probabilidad de éxito, y esto en un modelo con hipótesis posiblemente mucho más débiles (véase, por ejemplo, Math. Reviews 85:m).${\estilo de visualización N}$

Sin embargo, existen muchas otras estrategias que logran (i) y (ii) y, además, funcionan estrictamente mejor que la estrategia 1/e simultáneamente para todos los >2. Un ejemplo simple es la estrategia que selecciona (si es posible) al primer candidato relativamente mejor después del tiempo, siempre que al menos un solicitante haya llegado antes de este tiempo, y de lo contrario selecciona (si es posible) al segundo candidato relativamente mejor después del tiempo . ^[4]${\estilo de visualización N}$${\estilo de visualización \tau}$${\estilo de visualización \tau}$

La ley 1/e se confunde a veces con la solución del problema clásico de la secretaria descrito anteriormente debido al papel similar del número 1/e. Sin embargo, en la ley 1/e, este papel es más general. El resultado también es más sólido, ya que se cumple para un número desconocido de solicitantes y dado que el modelo basado en una distribución de tiempo de llegada F es más manejable para las solicitudes.

En el artículo "¿Quién resolvió el problema de la secretaria?" ( Ferguson , 1989) ^[1] , se afirma que el problema de la secretaria apareció impreso por primera vez en la columna Mathematical Games de Martin Gardner de febrero de 1960 en Scientific American :

Pídele a alguien que tome tantas tiras de papel como quiera y que escriba en cada una de ellas un número positivo diferente. Los números pueden variar desde pequeñas fracciones de 1 hasta un número del tamaño de un googol (1 seguido de cien ceros) o incluso mayor. Estas tiras se dan vuelta y se barajan sobre una mesa. Una a una, las vas dando vuelta. El objetivo es dejar de dar vueltas cuando llegues al número que crees que es el mayor de la serie. No puedes volver atrás y coger una tira girada anteriormente. Si das vuelta todas las tiras, entonces, por supuesto, debes coger la última que hayas dado vuelta. ^[5]

Ferguson señaló que el juego de la secretaria seguía sin resolverse, como un juego de suma cero con dos jugadores antagónicos. ^[1] En este juego:

• Alicia, la jugadora informada, escribe en secreto números distintos en las cartas.${\estilo de visualización n}$
• Bob, el jugador que se detiene, observa los valores reales y puede dejar de girar las cartas cuando quiera, ganando si la última carta girada tiene el número máximo general.
• Bob quiere adivinar el número máximo con la mayor probabilidad posible, mientras que el objetivo de Alice es mantener esta probabilidad lo más baja posible.

Las diferencias con el problema básico de la secretaria son dos:

• Alice no tiene por qué escribir los números de manera uniforme y aleatoria. Puede escribirlos de acuerdo con cualquier distribución de probabilidad conjunta para engañar a Bob.
• Bob observa los valores reales escritos en las tarjetas, que puede utilizar en sus procedimientos de decisión.

Alice primero escribe n números, que luego se mezclan. Por lo tanto, su orden no importa, lo que significa que los números de Alice deben ser una secuencia de variables aleatorias intercambiables . La estrategia de Alice es simplemente elegir la secuencia de variables aleatorias intercambiables más complicada.${\displaystyle X_{1},X_{2},...,X_{n}}$

La estrategia de Bob se puede formalizar como una regla de detención para la secuencia .${\estilo de visualización \tau}$${\displaystyle X_{1},X_{2},...,X_{n}}$

Decimos que una regla de detención para Bob es una estrategia de detención por rango relativo si depende solo de los rangos relativos de , y no de sus valores numéricos. En otras palabras, es como si alguien interviniera secretamente después de que Alicia escogiera sus números y cambiara cada número en a su rango relativo (rompiendo los empates aleatoriamente). Por ejemplo, se cambia a o con igual probabilidad. Esto hace que sea como si Alicia jugara una permutación aleatoria intercambiable en . Ahora, dado que la única permutación aleatoria intercambiable en es solo la distribución uniforme sobre todas las permutaciones en , la estrategia de detención por rango relativo óptima es la regla de detención óptima para el problema de la secretaria, dada anteriormente, con una probabilidad de ganar. El objetivo de Alicia es asegurarse de que Bob no pueda hacerlo mejor que la estrategia de detención por rango relativo.${\estilo de visualización \tau}$${\displaystyle X_{1},X_{2},...,X_{n}}$${\displaystyle X_{1},X_{2},...,X_{n}}$${\displaystyle 0.2,0.3,0.3,0.1}$${\estilo de visualización 2,3,4,1}$${\estilo de visualización 2,4,3,1}$${\displaystyle \{1,2,...,n\}}$${\displaystyle \{1,2,...,n\}}$${\displaystyle \{1,2,...,n\}}$$${\displaystyle Pr(X_{\tau}=\max _{i\en 1:n}X_{i})=\max _{r\en 1:n}{\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}}$$

Según las reglas del juego, la secuencia de Alice debe ser intercambiable, pero para tener éxito en el juego, Alice no debería elegirla como independiente. Si Alice toma muestras de los números de forma independiente de alguna distribución fija, esto le permitiría a Bob tener un mejor desempeño. Para ver esto intuitivamente, imaginemos que , y Alice debe elegir ambos números de la distribución normal , de forma independiente. Entonces, si Bob da vuelta un número y ve , entonces puede dar vuelta con bastante confianza el segundo número, y si Bob da vuelta un número y ve , entonces puede elegir con bastante confianza el primer número. Alice puede tener un mejor desempeño si elige que estén correlacionados positivamente.${\estilo de visualización n=2}$${\estilo de visualización N(0,1)}$${\estilo de visualización -3}$${\estilo de visualización +3}$$Estilo de visualización X_{1}, X_{2}}$

Así pues, la declaración totalmente formal es la siguiente:

¿Existe una secuencia intercambiable de variables aleatorias tal que para cualquier regla de detención , ?${\displaystyle X_{1},...,X_{n}}$${\estilo de visualización \tau}$$${\displaystyle Pr(X_{\tau}=\max _{i\en 1:n}X_{i})\leq \max _{r\en 1:n}{\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}}$$

Para , si Bob juega la estrategia óptima de paradas de rango relativo, entonces Bob tiene una probabilidad de ganar de 1/2. Sorprendentemente, Alice no tiene una estrategia minimax , que está estrechamente relacionada con una paradoja de T. Cover ^[6] y la paradoja de las dos envolventes . Concretamente, Bob puede jugar esta estrategia: muestrear un número aleatorio . Si , entonces elegir , de lo contrario elegir . Ahora, Bob puede ganar con una probabilidad estrictamente mayor que 1/2. Supongamos que los números de Alice son diferentes, entonces, condicional a , Bob gana con una probabilidad de 1/2, pero condicional a , Bob gana con una probabilidad de 1. ${\estilo de visualización n=2}$${\estilo de visualización Y}$$Estilo de visualización X_{1}>Y}$$Estilo de visualización X_{1}$$Estilo de visualización X_{2}$${\displaystyle Y\no \en [\min(X_{1},X_{2}),\max(X_{1},X_{2})]}$${\displaystyle Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]}$

Tenga en cuenta que el número aleatorio puede extraerse de cualquier distribución aleatoria, siempre que tenga una probabilidad distinta de cero.${\estilo de visualización Y}$${\displaystyle Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]}$

Sin embargo, para cualquier , Alice puede construir una secuencia intercambiable tal que la probabilidad de ganar de Bob sea como máximo . ^[1]${\displaystyle \epsilon >0}$$Estilo de visualización X_{1}, X_{2}}$${\displaystyle 1/2+\épsilon}$

Pero para , la respuesta es sí: Alice puede elegir números aleatorios (que son variables aleatorias dependientes) de tal manera que Bob no puede jugar mejor que usando la estrategia de detención clásica basada en los rangos relativos. ^[7]${\estilo de visualización n>2}$

El resto del artículo vuelve a abordar el problema de la secretaria para un número conocido de solicitantes.

Stein, Seale y Rapoport (2003) derivaron las probabilidades de éxito esperadas para varias heurísticas psicológicamente plausibles que podrían emplearse en el problema de la secretaria. Las heurísticas que examinaron fueron:

• Regla de corte (CR): no se acepta a ninguno de los primeros y solicitantes; a partir de entonces, se selecciona al primer candidato encontrado (es decir, un solicitante con rango relativo 1). Esta regla tiene como caso especial la política óptima para el problema clásico de la secretaria para el cual y  =  r .
• Regla de recuento de candidatos (CCR): seleccione el candidato encontrado número y . Tenga en cuenta que esta regla no necesariamente omite ningún candidato; solo tiene en cuenta cuántos candidatos se han observado, no qué tan profundo se encuentra el responsable de la toma de decisiones en la secuencia de candidatos.
• Regla de no candidatos sucesivos (SNCR): seleccione el primer candidato encontrado después de observar y no candidatos (es decir, solicitantes con rango relativo > 1).

Cada heurística tiene un único parámetro y . La figura (que se muestra a la derecha) muestra las probabilidades de éxito esperadas para cada heurística en función de y para problemas con n  = 80.

Encontrar al mejor candidato puede parecer un objetivo bastante estricto. Es de suponer que el entrevistador preferiría contratar a un candidato de mayor valor que a uno de menor valor, y no solo preocuparse por conseguir al mejor. Es decir, el entrevistador obtendrá algún valor al seleccionar a un candidato que no sea necesariamente el mejor, y el valor obtenido aumenta con el valor del candidato seleccionado.

Para modelar este problema, supongamos que los solicitantes tienen valores "verdaderos" que son variables aleatorias X extraídas iid de una distribución uniforme en [0, 1]. De manera similar al problema clásico descrito anteriormente, el entrevistador solo observa si cada solicitante es el mejor hasta el momento (un candidato), debe aceptar o rechazar a cada uno en el acto y debe aceptar al último si lo alcanza. (Para ser claros, el entrevistador no conoce el rango relativo real de cada solicitante. Solo conoce si el solicitante tiene un rango relativo de 1). Sin embargo, en esta versión, el pago está dado por el valor verdadero del solicitante seleccionado. Por ejemplo, si selecciona a un solicitante cuyo valor verdadero es 0,8, entonces ganará 0,8. El objetivo del entrevistador es maximizar el valor esperado del solicitante seleccionado.${\estilo de visualización n}$

Dado que los valores del solicitante son iid extraídos de una distribución uniforme en [0, 1], el valor esperado del t -ésimo solicitante dado que está dado por${\displaystyle x_{t}=\max \left\{x_{1},x_{2},\ldots ,x_{t}\right\}}$

${\displaystyle E_{t}=E\left(X_{t}|I_{t}=1\right)={\frac {t}{t+1}}.}$

Al igual que en el problema clásico, la política óptima viene dada por un umbral, que para este problema denotaremos por , en el que el entrevistador debería comenzar a aceptar candidatos. Bearden demostró que c es o . ^[8] (De hecho, lo que esté más cerca de ). Esto se deduce del hecho de que, dado un problema con solicitantes, el pago esperado para un umbral arbitrario es${\displaystyle c}$${\displaystyle \lfloor {\sqrt {n}}\rfloor }$${\displaystyle \lceil {\sqrt {n}}\rceil }$${\displaystyle {\sqrt {n}}}$${\displaystyle n}$${\displaystyle 1\leq c\leq n}$

${\displaystyle V_{n}(c)=\sum _{t=c}^{n-1}\left[\prod _{s=c}^{t-1}\left({\frac {s-1}{s}}\right)\right]\left({\frac {1}{t+1}}\right)+\left[\prod _{s=c}^{n-1}\left({\frac {s-1}{s}}\right)\right]{\frac {1}{2}}={\frac {2cn-{c}^{2}+c-n}{2cn}}.}$

Derivando con respecto a c , se obtiene${\displaystyle V_{n}(c)}$

${\displaystyle {\frac {\partial V}{\partial c}}={\frac {-{c}^{\,2}+n}{2{c}^{\,2}n}}.}$

Dado que para todos los valores permisibles de , encontramos que se maximiza en . Dado que V es convexo en , el umbral óptimo de valor entero debe ser o . Por lo tanto, para la mayoría de los valores de el entrevistador comenzará a aceptar solicitantes antes en la versión de pago cardinal que en la versión clásica donde el objetivo es seleccionar al mejor solicitante. Tenga en cuenta que este no es un resultado asintótico: se cumple para todos los . Curiosamente, si cada una de las secretarias tiene un valor fijo y distinto de a , entonces se maximiza en , con las mismas afirmaciones de convexidad que antes. ^[9] Para otras distribuciones conocidas, el juego óptimo se puede calcular mediante programación dinámica.${\displaystyle \partial ^{\,2}V/\partial c^{\,2}<0}$${\displaystyle c}$${\displaystyle V}$${\displaystyle c={\sqrt {n}}}$${\displaystyle c}$${\displaystyle \lfloor {\sqrt {n}}\rfloor }$${\displaystyle \lceil {\sqrt {n}}\rceil }$${\displaystyle n}$${\displaystyle n}$${\displaystyle n}$${\displaystyle 1}$${\displaystyle n}$${\displaystyle V}$${\displaystyle c={\sqrt {n}}-1}$

Una forma más general de este problema introducida por Palley y Kremer (2014) ^[10] supone que, a medida que llega cada nuevo solicitante, el entrevistador observa su clasificación en relación con todos los solicitantes que se han observado previamente. Este modelo es coherente con la noción de que un entrevistador aprende a medida que continúa el proceso de búsqueda mediante la acumulación de un conjunto de puntos de datos pasados ​​que puede utilizar para evaluar a los nuevos candidatos a medida que llegan. Un beneficio de este llamado modelo de información parcial es que las decisiones y los resultados logrados dada la información de clasificación relativa se pueden comparar directamente con las decisiones y los resultados óptimos correspondientes si el entrevistador hubiera recibido información completa sobre el valor de cada solicitante. Este problema de información completa, en el que los solicitantes se extraen independientemente de una distribución conocida y el entrevistador busca maximizar el valor esperado del solicitante seleccionado, fue resuelto originalmente por Moser (1956), ^[11] Sakaguchi (1961), ^[12] y Karlin (1962).

Existen varias variantes del problema de la secretaria que también tienen soluciones simples y elegantes.

Una variante reemplaza el deseo de elegir al mejor por el deseo de elegir al segundo mejor. ^{[13] [14] [15]} Robert J. Vanderbei llama a esto el problema del "postdoctorado" argumentando que el "mejor" irá a Harvard. Para este problema, la probabilidad de éxito para un número par de solicitantes es exactamente . Esta probabilidad tiende a 1/4 a medida que n tiende a infinito, lo que ilustra el hecho de que es más fácil elegir al mejor que al segundo mejor.${\displaystyle {\frac {0.25n^{2}}{n(n-1)}}}$

Consideremos el problema de seleccionar las k mejores secretarias entre n candidatas, utilizando k intentos.

En general, el método de decisión óptima comienza observando a los candidatos sin elegir a ninguno de ellos, y luego elige a todos los candidatos que sean mejores que los primeros candidatos hasta que nos quedemos sin candidatos o selecciones. Si se mantiene constante mientras , entonces la probabilidad de éxito converge a . ^[16] Según Vanderbei 1980, si , entonces la probabilidad de éxito es .${\displaystyle r=\left\lfloor {\frac {n}{ke^{1/k}}}\right\rfloor }$${\displaystyle r}$${\displaystyle k}$${\displaystyle n\to \infty }$${\displaystyle {\frac {1}{ek}}}$${\displaystyle k=n/2}$${\displaystyle {\frac {1}{n/2+1}}}$

En esta variante, al jugador se le permiten elegir entre varias opciones y gana si alguna de ellas es la mejor. Una estrategia óptima para este problema pertenece a la clase de estrategias definidas por un conjunto de números umbral , donde . ${\displaystyle r}$${\displaystyle (a_{1},a_{2},...,a_{r})}$${\displaystyle a_{1}>a_{2}>\cdots >a_{r}}$

En concreto, imagina que tienes cartas de aceptación etiquetadas de a . Tendrías a funcionarios encargados de la solicitud, cada uno de ellos con una carta en la mano. Entrevistarías a los candidatos y los clasificarías en un cuadro que todos los funcionarios encargados de la solicitud pueden ver. Ahora, el funcionario enviaría su carta de aceptación al primer candidato que sea mejor que todos los candidatos a . (Las cartas de aceptación no enviadas se entregan por defecto a los últimos solicitantes, lo mismo que en el problema estándar de la secretaria). ^[17]${\displaystyle r}$${\displaystyle 1}$${\displaystyle r}$${\displaystyle r}$${\displaystyle i}$${\displaystyle 1}$${\displaystyle a_{i}}$

En el límite, cada , para algún número racional . ^[18]${\displaystyle n\rightarrow \infty }$${\displaystyle a_{i}\sim ne^{-k_{i}}}$${\displaystyle k_{i}}$

Cuando , la probabilidad de ganar converge a . De manera más general, para números enteros positivos , la probabilidad de ganar converge a , donde . ^[18]${\displaystyle r=2}$${\displaystyle e^{-1}+e^{-{\frac {3}{2}}},(n\rightarrow \infty )}$${\displaystyle r}$${\displaystyle p_{1}+p_{2}+\cdots +p_{r}}$${\displaystyle p_{i}=\lim _{n\rightarrow \infty }{\frac {a_{i}}{n}}}$

^[17] calculado hasta , con .${\displaystyle r=4}$${\displaystyle e^{-1}+e^{-{\frac {3}{2}}}+e^{-{\frac {47}{24}}}+e^{-{\frac {2761}{1152}}}}$

Matsui & Ano 2016 dieron un algoritmo general. Por ejemplo, .${\displaystyle p_{5}=e^{-{\frac {4162637}{1474560}}}}$

Los psicólogos experimentales y los economistas han estudiado el comportamiento de decisión de personas reales en situaciones de problemas de secretariado. ^[19] En gran parte, este trabajo ha demostrado que las personas tienden a dejar de buscar demasiado pronto. Esto puede explicarse, al menos en parte, por el costo de evaluar a los candidatos. En situaciones del mundo real, esto podría sugerir que las personas no buscan lo suficiente cuando se enfrentan a problemas en los que las alternativas de decisión se encuentran secuencialmente. Por ejemplo, al tratar de decidir en qué estación de servicio a lo largo de una carretera parar a cargar combustible, las personas podrían no buscar lo suficiente antes de detenerse. Si es así, entonces tenderían a pagar más por la gasolina que si hubieran buscado más tiempo. Lo mismo puede ser cierto cuando las personas buscan boletos de avión en línea. La investigación experimental sobre problemas como el problema de la secretaria a veces se conoce como investigación de operaciones conductuales .

Si bien existe un cuerpo sustancial de investigación en neurociencia sobre la integración de información, o la representación de creencias, en tareas de toma de decisiones perceptivas que utilizan sujetos animales ^{[20] [21] y humanos, [22]} se sabe relativamente poco sobre cómo se llega a la decisión de dejar de recopilar información.

Los investigadores han estudiado las bases neuronales de la solución del problema de la secretaria en voluntarios sanos utilizando resonancia magnética funcional . ^[23] Se utilizó un proceso de decisión de Markov (MDP) para cuantificar el valor de continuar la búsqueda frente a comprometerse con la opción actual. Las decisiones de tomar o rechazar una opción involucraron las cortezas prefrontales parietal y dorsolateral , así como el estriado ventral , la ínsula anterior y la corteza cingulada anterior . Por lo tanto, las regiones cerebrales previamente implicadas en la integración de la evidencia y la representación de la recompensa codifican los cruces de umbral que desencadenan las decisiones de comprometerse con una elección.

El problema de la secretaria fue aparentemente introducido en 1949 por Merrill M. Flood , quien lo llamó el problema de la prometida en una conferencia que dio ese año. Se refirió a él varias veces durante la década de 1950, por ejemplo, en una conferencia en Purdue el 9 de mayo de 1958, y finalmente se hizo ampliamente conocido en el folclore aunque nada se publicó en ese momento. En 1958 envió una carta a Leonard Gillman , con copias a una docena de amigos, incluidos Samuel Karlin y J. Robbins, esbozando una prueba de la estrategia óptima, con un apéndice de R. Palermo, quien demostró que todas las estrategias están dominadas por una estrategia de la forma "rechazar el primer p incondicionalmente, luego aceptar el siguiente candidato que sea mejor". ^[24]

La primera publicación fue aparentemente de Martin Gardner en Scientific American, febrero de 1960. Había oído hablar de él de John H. Fox Jr. y L. Gerald Marnie, quienes habían ideado independientemente un problema equivalente en 1958; lo llamaron el "juego del googol". Fox y Marnie no sabían la solución óptima; Gardner pidió consejo a Leo Moser , quien (junto con JR Pounder) proporcionó un análisis correcto para su publicación en la revista. Poco después, varios matemáticos escribieron a Gardner para contarle sobre el problema equivalente que habían escuchado a través de la vid, todo lo cual probablemente se puede rastrear hasta el trabajo original de Flood. ^[25]

La ley 1/ e de mejor elección se debe a F. Thomas Bruss . ^[26]

Ferguson tiene una extensa bibliografía y señala que un problema similar (pero diferente) había sido considerado por Arthur Cayley en 1875 e incluso por Johannes Kepler mucho antes, quien pasó dos años investigando a 11 candidatos para el matrimonio durante 1611-1613 después de la muerte de su primera esposa. ^[27]

El problema de la secretaria se puede generalizar al caso en el que existen múltiples empleos diferentes. Nuevamente, hay postulantes que llegan en orden aleatorio. Cuando llega un candidato, revela un conjunto de números no negativos. Cada valor especifica su calificación para uno de los empleos. El administrador no solo tiene que decidir si acepta o no al candidato, sino que, en caso afirmativo, también tiene que asignarlo permanentemente a uno de los empleos. El objetivo es encontrar una asignación donde la suma de calificaciones sea lo más grande posible. Este problema es idéntico a encontrar una coincidencia de peso máximo en un grafo bipartito ponderado por aristas donde los nodos de un lado llegan en línea en orden aleatorio. Por lo tanto, es un caso especial del problema de coincidencia bipartita en línea .${\displaystyle n}$${\displaystyle n}$

Mediante una generalización del algoritmo clásico para el problema de la secretaria, es posible obtener una asignación donde la suma esperada de calificaciones es solo un factor menor que una asignación óptima (fuera de línea). ^[28]${\displaystyle e}$

• Problema de asignación
• Algoritmo de probabilidades
• Parada óptima
• El problema de Robbins
• Teoría de la búsqueda
• Problema de matrimonio estable

• Bearden, JN (2006). "Un nuevo problema de secretaria con selección basada en rango y pagos cardinales". Journal of Mathematical Psychology . 50 : 58–9. doi :10.1016/j.jmp.2005.11.003.
• Bearden, JN; Murphy, RO; Rapoport, A. (2005). "Una extensión multiatributo del problema de la secretaria: teoría y experimentos". Revista de psicología matemática . 49 (5): 410–425. CiteSeerX  10.1.1.497.6468 . doi :10.1016/j.jmp.2005.08.002. S2CID  9186039.
• Bearden, J. Neil; Rapoport, Amnon; Murphy, Ryan O. (septiembre de 2006). "Observación y selección secuencial con resultados dependientes del rango: un estudio experimental". Management Science . 52 (9): 1437–1449. doi :10.1287/mnsc.1060.0535.
• Bruss, F. Thomas (junio de 2000). "Suma las probabilidades a uno y deténte". Anales de probabilidad . 28 (3): 1384–1391. doi : 10.1214/aop/1019160340 .
• Bruss, F. Thomas (octubre de 2003). "Una nota sobre los límites para el teorema de probabilidades de parada óptima". Anales de probabilidad . 31 (4): 1859–1961. doi : 10.1214/aop/1068646368 .
• Bruss, F. Thomas (agosto de 1984). "Un enfoque unificado para una clase de problemas de mejor elección con un número desconocido de opciones". Anales de probabilidad . 12 (3): 882–889. doi : 10.1214/aop/1176993237 .
• Flood, Merrill R. (1958). "Demostración de la estrategia óptima". Carta a Martin Gardner. Documentos de Martin Gardner, serie 1, caja 5, carpeta 19: Archivos de la Universidad de Stanford.{{cite press release}}: CS1 maint: location (link)
• Freeman, PR (1983). "El problema de la secretaria y sus extensiones: una revisión". Revista Internacional de Estadística / Revue Internationale de Statistique . 51 (2): 189–206. doi :10.2307/1402748. JSTOR  1402748.
• Gardner, Martin (1966). "3". Nuevas diversiones matemáticas de Scientific American . Simon and Schuster.[reimprime su columna original publicada en febrero de 1960 con comentarios adicionales]
• Girdhar, Yogesh; Dudek, Gregory (2009). "Muestreo óptimo de datos en línea o cómo contratar a las mejores secretarias". Conferencia canadiense de 2009 sobre visión artificial y robótica . pp. 292–298. CiteSeerX  10.1.1.161.41 . doi :10.1109/CRV.2009.30. ISBN. 978-1-4244-4211-9.S2CID2742443  .​
• Gilbert, J; Mosteller, F (1966). "Reconocimiento del máximo de una secuencia". Revista de la Asociación Estadounidense de Estadística . 61 (313): 35–73. doi :10.2307/2283044. JSTOR  2283044.
• Gnedin, A. (1994). "Una solución al juego de Googol". Anales de probabilidad . 22 (3): 1588–1595. doi : 10.1214/aop/1176988613 .
• Gnedin, A. (2021). "El problema de la mejor elección con llegadas aleatorias: cómo superar la estrategia 1/e". Procesos estocásticos y sus aplicaciones . 145 : 226–240. doi :10.1016/j.spa.2021.12.008. S2CID  245449000.
• Hill, TP "Saber cuándo parar". American Scientist , vol. 97, 126-133 (2009). (Para la traducción al francés, véase el artículo de portada en la edición de julio de Pour la Science (2009))
• Ketelaar, Timothy; Todd, Peter M. (2001). "Enmarcando nuestros pensamientos: la racionalidad ecológica como respuesta de la psicología evolutiva al problema del marco". Desafíos conceptuales en psicología evolutiva . Estudios en sistemas cognitivos. Vol. 27. págs. 179–211. doi :10.1007/978-94-010-0618-7_7. ISBN 978-94-010-3890-4.
• Matsui, T; Ano, K (2016). "Límites inferiores para el problema de probabilidades de Bruss con múltiples paradas". Matemáticas de la investigación de operaciones . 41 (2): 700–714. arXiv : 1204.5537 . doi :10.1287/moor.2015.0748. S2CID  31778896.
• Miller, Geoffrey F. (2001). La mente de apareamiento: cómo la elección sexual moldeó la evolución de la naturaleza humana . Anchor Books. ISBN 978-0-385-49517-2.
• Sardelis, Dimitris A.; Valahas, Theodoros M. (marzo de 1999). "Toma de decisiones: una regla de oro". The American Mathematical Monthly . 106 (3): 215. doi :10.2307/2589677. JSTOR  2589677.
• Seale, DA; Rapoport, A. (1997). "Toma de decisiones secuencial con rangos relativos: una investigación experimental del 'problema de la secretaria'"". Comportamiento organizacional y procesos de decisión humana . 69 (3): 221–236. doi :10.1006/obhd.1997.2683.
• Stein, WE; Seale, DA; Rapoport, A. (2003). "Análisis de soluciones heurísticas al problema de la mejor elección". Revista Europea de Investigación Operativa . 151 : 140–152. doi :10.1016/S0377-2217(02)00601-X.
• Vanderbei, RJ (noviembre de 1980). "La elección óptima de un subconjunto de una población". Matemáticas de la investigación de operaciones . 5 (4): 481–486. doi :10.1287/moor.5.4.481.
• Vanderbei, Robert J. (2012). La variante postdoctoral del problema de la secretaria (PDF) (Informe). CiteSeerX  10.1.1.366.1718 .

• Secuencia OEIS A054404 (Número de hijas que se deben esperar antes de elegir en el problema de la dote del sultán con n hijas)
• Weisstein, Eric W. "El problema de la dote del sultán". MathWorld .
• Neil Bearden. «Búsqueda óptima (problemas con las secretarias)». Archivado desde el original el 4 de enero de 2017.
• Libro de aplicaciones y frenado óptimo de Thomas S. Ferguson