Teoría de la renovación

La teoría de renovación es la rama de la teoría de la probabilidad que generaliza el proceso de Poisson para tiempos de espera arbitrarios. En lugar de tiempos de espera distribuidos exponencialmente , un proceso de renovación puede tener tiempos de espera independientes e idénticamente distribuidos (IID) que tengan una media finita. Un proceso de renovación-recompensa tiene además una secuencia aleatoria de recompensas incurridas en cada tiempo de espera, que son IID pero no necesitan ser independientes de los tiempos de espera.

Un proceso de renovación tiene propiedades asintóticas análogas a la ley fuerte de los grandes números y al teorema del límite central . La función de renovación (número esperado de llegadas) y la función de recompensa (valor esperado de la recompensa) son de importancia clave en la teoría de renovación. La función de renovación satisface una ecuación integral recursiva, la ecuación de renovación. La ecuación de renovación clave proporciona el valor límite de la convolución de con una función no negativa adecuada. La superposición de procesos de renovación se puede estudiar como un caso especial de procesos de renovación de Markov .${\estilo de visualización m(t)}$${\estilo de visualización g(t)}$${\displaystyle m'(t)}$

Las aplicaciones incluyen el cálculo de la mejor estrategia para reemplazar la maquinaria desgastada en una fábrica y la comparación de los beneficios a largo plazo de diferentes pólizas de seguro. La paradoja de la inspección se relaciona con el hecho de que la observación de un intervalo de renovación en el tiempo t da como resultado un intervalo con un valor promedio mayor que el de un intervalo de renovación promedio.

El proceso de renovación es una generalización del proceso de Poisson . En esencia, el proceso de Poisson es un proceso de Markov de tiempo continuo sobre los números enteros positivos (que normalmente empiezan en cero) que tiene tiempos de espera distribuidos exponencialmente independientes en cada número entero antes de avanzar al siguiente número entero, . En un proceso de renovación, los tiempos de espera no necesitan tener una distribución exponencial; más bien, los tiempos de espera pueden tener cualquier distribución sobre los números positivos, siempre que los tiempos de espera sean independientes y estén distribuidos de forma idéntica ( IID ) y tengan una media finita.${\estilo de visualización i}$${\estilo de visualización i+1}$

Sea una secuencia de variables aleatorias independientes positivas distribuidas de forma idéntica con un valor esperado finito${\displaystyle (S_{i})_{i\geq 1}}$

${\displaystyle 0<\operatorname {E} [S_{i}]<\infty .}$

Nos referimos a la variable aleatoria como el " -ésimo tiempo de retención".$Estilo de visualización S_{i}}$${\estilo de visualización i}$

Definir para cada n > 0 :

${\displaystyle J_{n}=\sum _{i=1}^{n}S_{i},}$

Cada uno de ellos se denomina " tiempo de salto -ésimo" y los intervalos se denominan "intervalos de renovación".$Estilo de visualización J_{n}$${\estilo de visualización n}$${\displaystyle [J_{n},J_{n+1}]}$

Entonces viene dado por variable aleatoria${\displaystyle (X_{t})_{t\geq 0}}$

${\displaystyle X_{t}=\sum _{n=1}^{\infty }\operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}=\sup \left\{\,n:J_{n}\leq t\,\right\}}$

¿Dónde está la función indicadora?${\displaystyle \operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}}$

${\displaystyle \operatorname {\mathbb {I} } _{\{J_{n}\leq t\}}={\begin{cases}1,&{\text{si }}J_{n}\leq t\\0,&{\text{en caso contrario}}\end{cases}}}$

${\displaystyle (X_{t})_{t\geq 0}}$representa el número de saltos que han ocurrido en el tiempo t , y se llama proceso de renovación.

Si se consideran los eventos que ocurren en momentos aleatorios, se puede optar por pensar en los tiempos de espera como el tiempo aleatorio transcurrido entre dos eventos consecutivos. Por ejemplo, si el proceso de renovación está modelando la cantidad de averías de diferentes máquinas, entonces el tiempo de espera representa el tiempo que transcurre entre la avería de una máquina y la de otra.${\displaystyle \{S_{i}:i\geq 1\}}$

El proceso de Poisson es el único proceso de renovación con la propiedad de Markov , ^[1] ya que la distribución exponencial es la única variable aleatoria continua con la propiedad de no tener memoria.

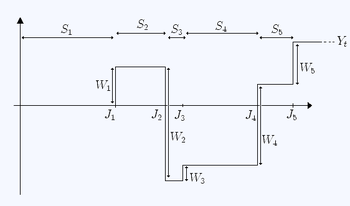
Sea una secuencia de variables aleatorias IID ( recompensas ) que satisfacen${\displaystyle W_{1},W_{2},\ldots }$

${\displaystyle \operatorname {E} |W_{i}|<\infty .\,}$

Entonces la variable aleatoria

${\displaystyle Y_{t}=\sum _{i=1}^{X_{t}}W_{i}}$

se denomina proceso de renovación-recompensa . Nótese que, a diferencia de , cada uno puede tomar valores negativos y positivos.$Estilo de visualización S_{i}}$$Estilo de visualización W_{i}}$

La variable aleatoria depende de dos secuencias: los tiempos de retención y las recompensas . Estas dos secuencias no necesitan ser independientes. En particular, pueden ser una función de .${\displaystyle Y_{t}}$${\displaystyle S_{1},S_{2},\ldots}$${\displaystyle W_{1},W_{2},\ldots }$$Estilo de visualización W_{i}}$$Estilo de visualización S_{i}}$

En el contexto de la interpretación anterior de los tiempos de espera como el tiempo entre fallos sucesivos de una máquina, las "recompensas" (que en este caso resultan ser negativas) pueden verse como los sucesivos costos de reparación incurridos como resultado de los fallos sucesivos.${\displaystyle W_{1},W_{2},\ldots }$

Una analogía alternativa es que tenemos un ganso mágico que pone huevos a intervalos (tiempos de espera) distribuidos como . A veces pone huevos de oro de peso aleatorio y, a veces, pone huevos tóxicos (también de peso aleatorio) que requieren una eliminación responsable (y costosa). Las "recompensas" son las pérdidas/ganancias financieras sucesivas (aleatorias) resultantes de los huevos sucesivos ( i = 1, 2, 3, ...) y registra la "recompensa" financiera total en el momento t .$Estilo de visualización S_{i}}$$Estilo de visualización W_{i}}$${\displaystyle Y_{t}}$

Definimos la función de renovación como el valor esperado del número de saltos observados hasta un momento determinado :${\estilo de visualización t}$

${\displaystyle m(t)=\nombre del operador {E} [X_{t}].\,}$

La función de renovación satisface

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}m(t)={\frac {1}{\operatorname {E} [S_{1}]}}.}$

Prueba

La ley fuerte de los grandes números para los procesos de renovación implica ${\displaystyle \lim _{t\to \infty }{\frac {X_{t}}{t}}={\frac {1}{\operatorname {E} [S_{1}]}}.}$ Para demostrar el teorema de renovación elemental, basta demostrar que es uniformemente integrable.${\displaystyle \left\{{\frac {X_{t}}{t}};t\geq 0\right\}}$ Para ello, considere un proceso de renovación truncado donde los tiempos de retención están definidos por donde es un punto tal que existe para todos los procesos de renovación no deterministas. Este nuevo proceso de renovación es un límite superior en y sus renovaciones solo pueden ocurrir en la red . Además, el número de renovaciones en cada momento es geométrico con el parámetro . Entonces tenemos${\displaystyle {\overline {S_{n}}}=a\nombre del operador {\mathbb {I} } \{S_{n}>a\}}$${\estilo de visualización a}$${\displaystyle 0<F(a)=p<1}$${\displaystyle {\overline {X}}_{t}}$$Estilo de visualización X_{t}}$${\displaystyle \{na;n\in \mathbb {N} \}}$${\estilo de visualización p}$ ${\displaystyle {\begin{aligned}{\overline {X_{t}}}&\leq \sum _{i=1}^{[at]}\operatorname {Geométrico} (p)\\\operatorname {E} \left[\,{\overline {X_{t}}}^{2}\,\right]&\leq C_{1}t+C_{2}t^{2}\\P\left({\frac {X_{t}}{t}}>x\right)&\leq {\frac {\operatorname {E} \left[X_{t}^{2}\right]}{t^{2}x^{2}}}\leq {\frac {\operatorname {E} \left[{\overline {X_{t}}}^{2}\right]}{t^{2}x^{2}}}\leq {\frac {C}{x^{2}}}.\end{aligned}}}$

Definimos la función de recompensa :

${\displaystyle g(t)=\nombre del operador {E} [Y_{t}].\,}$

La función de recompensa satisface

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}g(t)={\frac {\operatorname {E} [W_{1}]}{\operatorname {E} [S_{1}]}}.}$

La función de renovación satisface

${\displaystyle m(t)=F_{S}(t)+\int _{0}^{t}m(ts)f_{S}(s)\,ds}$

donde es la función de distribución acumulativa de y es la función de densidad de probabilidad correspondiente.$Estilo de visualización F_{S}$$Estilo de visualización S_{1}$$estilo de visualización f_{S}}$

Prueba [2]

Podemos iterar la expectativa sobre el primer tiempo de retención: ${\displaystyle m(t)=\nombredeloperador {E} [X_{t}]=\nombredeloperador {E} [\nombredeloperador {E} (X_{t}\mid S_{1})].\,}$ De la definición del proceso de renovación, tenemos: ${\displaystyle \operatorname {E} (X_{t}\mid S_{1}=s)=\operatorname {\mathbb {I} } _{\{t\geq s\}}\left(1+\operatorname {E} [X_{t-s}]\right).\,}$ Entonces ${\displaystyle {\begin{aligned}m(t)&=\operatorname {E} [X_{t}]\\[12pt]&=\operatorname {E} [\operatorname {E} (X_{t}\mid S_{1})]\\[12pt]&=\int _{0}^{\infty }\operatorname {E} (X_{t}\mid S_{1}=s)f_{S}(s)\,ds\\[12pt]&=\int _{0}^{\infty }\operatorname {\mathbb {I} } _{\{t\geq s\}}\left(1+\operatorname {E} [X_{t-s}]\right)f_{S}(s)\,ds\\[12pt]&=\int _{0}^{t}\left(1+m(t-s)\right)f_{S}(s)\,ds\\[12pt]&=F_{S}(t)+\int _{0}^{t}m(t-s)f_{S}(s)\,ds,\end{aligned}}}$ según sea necesario.

Sea X un proceso de renovación con función de renovación y media entre renovaciones . Sea una función que satisface:${\displaystyle m(t)}$${\displaystyle \mu }$${\displaystyle g:[0,\infty )\rightarrow [0,\infty )}$

• ${\displaystyle \int _{0}^{\infty }g(t)\,dt<\infty }$
• g es monótona y no creciente

El teorema de renovación clave establece que, como : ^[3]${\displaystyle t\rightarrow \infty }$

${\displaystyle \int _{0}^{t}g(t-x)m'(x)\,dx\rightarrow {\frac {1}{\mu }}\int _{0}^{\infty }g(x)\,dx}$

Considerando para cualquier caso especial el teorema de renovación: ^[4]${\displaystyle g(x)=\mathbb {I} _{[0,h]}(x)}$${\displaystyle h>0}$

${\displaystyle m(t+h)-m(t)\rightarrow {\frac {h}{\mu }}}$como${\displaystyle t\rightarrow \infty }$

El resultado puede demostrarse utilizando ecuaciones integrales o mediante un argumento de acoplamiento . ^[5] Aunque es un caso especial del teorema de renovación de clave, puede usarse para deducir el teorema completo, considerando funciones escalonadas y luego secuencias crecientes de funciones escalonadas. ^[3]

Los procesos de renovación y los procesos de renovación-recompensa tienen propiedades análogas a la ley fuerte de los grandes números , que se puede derivar del mismo teorema. Si es un proceso de renovación y es un proceso de renovación-recompensa entonces:${\displaystyle (X_{t})_{t\geq 0}}$${\displaystyle (Y_{t})_{t\geq 0}}$

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}X_{t}={\frac {1}{\operatorname {E} [S_{1}]}}}$^[6]

${\displaystyle \lim _{t\to \infty }{\frac {1}{t}}Y_{t}={\frac {1}{\operatorname {E} [S_{1}]}}\operatorname {E} [W_{1}]}$

Casi seguro.

Prueba

Consideremos primero . Por definición tenemos:${\displaystyle (X_{t})_{t\geq 0}}$ ${\displaystyle J_{X_{t}}\leq t\leq J_{X_{t}+1}}$ para todos y así${\displaystyle t\geq 0}$ ${\displaystyle {\frac {J_{X_{t}}}{X_{t}}}\leq {\frac {t}{X_{t}}}\leq {\frac {J_{X_{t}+1}}{X_{t}}}}$ para todo t ≥ 0. Ahora ya que tenemos:${\displaystyle 0<\operatorname {E} [S_{i}]<\infty }$ ${\displaystyle X_{t}\to \infty }$ como casi seguro (con probabilidad 1). Por lo tanto:${\displaystyle t\to \infty }$ ${\displaystyle {\frac {J_{X_{t}}}{X_{t}}}={\frac {J_{n}}{n}}={\frac {1}{n}}\sum _{i=1}^{n}S_{i}\to \operatorname {E} [S_{1}]}$ casi con seguridad (usando la ley fuerte de los grandes números); de manera similar: ${\displaystyle {\frac {J_{X_{t}+1}}{X_{t}}}={\frac {J_{X_{t}+1}}{X_{t}+1}}{\frac {X_{t}+1}{X_{t}}}={\frac {J_{n+1}}{n+1}}{\frac {n+1}{n}}\to \operatorname {E} [S_{1}]\cdot 1}$ Casi seguro. Por lo tanto (ya que está intercalado entre los dos términos)${\displaystyle t/X_{t}}$ ${\displaystyle {\frac {1}{t}}X_{t}\to {\frac {1}{\operatorname {E} [S_{1}]}}}$ casi con toda seguridad. [3] Consideremos a continuación . Tenemos${\displaystyle (Y_{t})_{t\geq 0}}$ ${\displaystyle {\frac {1}{t}}Y_{t}={\frac {X_{t}}{t}}{\frac {1}{X_{t}}}Y_{t}\to {\frac {1}{\operatorname {E} [S_{1}]}}\cdot \operatorname {E} [W_{1}]}$ casi con seguridad (usando el primer resultado y usando la ley de grandes números en ).${\displaystyle Y_{t}}$

Los procesos de renovación tienen además una propiedad análoga al teorema del límite central : ^[6]

${\displaystyle {\frac {X_{t}-t/\mu }{\sqrt {t\sigma ^{2}/\mu ^{3}}}}\to {\mathcal {N}}(0,1)}$

Una característica curiosa de los procesos de renovación es que si esperamos un tiempo predeterminado t y luego observamos qué tan grande es el intervalo de renovación que contiene t , deberíamos esperar que sea típicamente más grande que un intervalo de renovación de tamaño promedio.

Matemáticamente, la paradoja de inspección establece que, para cualquier t > 0, el intervalo de renovación que contiene a t es estocásticamente mayor que el primer intervalo de renovación. Es decir, para todo x > 0 y para todo t > 0:

${\displaystyle \operatorname {P} (S_{X_{t}+1}>x)\geq \operatorname {P} (S_{1}>x)=1-F_{S}(x)}$

donde F _S es la función de distribución acumulada de los tiempos de espera del IID S _i . Un ejemplo claro es la paradoja del tiempo de espera del autobús : para una distribución aleatoria dada de llegadas de autobuses, el pasajero promedio en una parada de autobús observa más demoras que el operador promedio de los autobuses.

La solución de la paradoja es que nuestra distribución muestreada en el momento t está sesgada por el tamaño (véase sesgo de muestreo ), en el sentido de que la probabilidad de que se elija un intervalo es proporcional a su tamaño. Sin embargo, un intervalo de renovación de tamaño promedio no está sesgado por el tamaño.

Prueba

Observe que el último tiempo de salto antes de t es ; y que el intervalo de renovación que contiene a t es . Entonces${\displaystyle J_{X_{t}}}$${\displaystyle S_{X_{t}+1}}$ ${\displaystyle {\begin{aligned}\operatorname {P} (S_{X_{t}+1}>x)&{}=\int _{0}^{\infty }\operatorname {P} (S_{X_{t}+1}>x\mid J_{X_{t}}=s)f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }\operatorname {P} (S_{X_{t}+1}>x|S_{X_{t}+1}>t-s)f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }{\frac {\operatorname {P} (S_{X_{t}+1}>x\,,\,S_{X_{t}+1}>t-s)}{\operatorname {P} (S_{X_{t}+1}>t-s)}}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }{\frac {1-F(\max\{x,t-s\})}{1-F(t-s)}}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }\min \left\{{\frac {1-F(x)}{1-F(t-s)}},{\frac {1-F(t-s)}{1-F(t-s)}}\right\}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}=\int _{0}^{\infty }\min \left\{{\frac {1-F(x)}{1-F(t-s)}},1\right\}f_{J_{X_{t}}}(s)\,ds\\[12pt]&{}\geq \int _{0}^{\infty }(1-F(x))f_{J_{X_{t}}}(s)\,ds=1-F(x)=\operatorname {P} (S_{1}>x),\\[12pt]\end{aligned}}}$ ya que ambos son mayores o iguales que para todos los valores de s .${\displaystyle {\frac {1-F(x)}{1-F(t-s)}}}$${\displaystyle 1}$${\displaystyle 1-F(x)}$

A menos que el proceso de renovación sea un proceso de Poisson, la superposición (suma) de dos procesos de renovación independientes no es un proceso de renovación. ^[7] Sin embargo, dichos procesos pueden describirse dentro de una clase más grande de procesos llamados procesos de renovación de Markov . ^[8] Sin embargo, la función de distribución acumulativa del primer tiempo entre eventos en el proceso de superposición está dada por ^[9]

${\displaystyle R(t)=1-\sum _{k=1}^{K}{\frac {\alpha _{k}}{\sum _{l=1}^{K}\alpha _{l}}}(1-R_{k}(t))\prod _{j=1,j\neq k}^{K}\alpha _{j}\int _{t}^{\infty }(1-R_{j}(u))\,{\text{d}}u}$

donde R _k ( t ) y α _k  > 0 son la CDF de los tiempos entre eventos y la tasa de llegada del proceso k . ^[10]

Eric, el empresario, tiene n máquinas, cada una de ellas con una vida útil uniformemente distribuida entre cero y dos años. Eric puede dejar que cada máquina funcione hasta que falle, con un coste de sustitución de 2600 €; o bien puede sustituir una máquina en cualquier momento mientras aún esté en funcionamiento, con un coste de 200 €.

¿Cuál es su política de reemplazo óptima?

Solución

La vida útil de las n máquinas se puede modelar como n procesos de renovación-recompensa concurrentes e independientes, por lo que es suficiente considerar el caso n=1 . Denotemos este proceso por . Las vidas útiles sucesivas S de las máquinas de reemplazo son independientes y se distribuyen de manera idéntica, por lo que la política óptima es la misma para todas las máquinas de reemplazo en el proceso.${\displaystyle (Y_{t})_{t\geq 0}}$ Si Eric decide al comienzo de la vida de una máquina reemplazarla en el momento 0 < t < 2 pero la máquina falla antes de ese momento, entonces la vida útil S de la máquina se distribuye uniformemente en [0,  t ] y, por lo tanto, tiene una expectativa de 0,5 t . Por lo tanto, la vida útil esperada general de la máquina es: ${\displaystyle {\begin{aligned}\operatorname {E} [S]&=\operatorname {E} [S\mid {\text{fails before }}t]\cdot \operatorname {P} [{\text{fails before }}t]+\operatorname {E} [S\mid {\text{does not fail before }}t]\cdot \operatorname {P} [{\text{does not fail before }}t]\\[6pt]&=0.5t({\frac {t}{2}})+t({\frac {2-t}{2}})\end{aligned}}}$ y el costo esperado W por máquina es: ${\displaystyle {\begin{aligned}\operatorname {E} [W]&=\operatorname {E} [W\mid {\text{fails before }}t]\cdot \operatorname {P} ({\text{fails before }}t)+\operatorname {E} [W\mid {\text{does not fail before }}t]\cdot \operatorname {P} ({\text{does not fail before }}t)\\[6pt]&=2600({\frac {t}{2}})+200({\frac {2-t}{2}})=1200t+200.\end{aligned}}}$ Así pues, según la fuerte ley de los grandes números, su coste medio a largo plazo por unidad de tiempo es: ${\displaystyle {\frac {1}{t}}Y_{t}\simeq {\frac {\operatorname {E} [W]}{\operatorname {E} [S]}}={\frac {4(1200t+200)}{t^{2}+4t-2t^{2}}}}$ Luego diferenciando con respecto a t : ${\displaystyle {\frac {\partial }{\partial t}}{\frac {4(1200t+200)}{t^{2}+4t-2t^{2}}}=4{\frac {(4t-t^{2})(1200)-(4-2t)(1200t+200)}{(t^{2}+4t-2t^{2})^{2}}},}$ Esto implica que los puntos de inflexión satisfacen: ${\displaystyle {\begin{aligned}0&=(4t-t^{2})(1200)-(4-2t)(1200t+200)=4800t-1200t^{2}-4800t-800+2400t^{2}+400t\\[6pt]&=-800+400t+1200t^{2},\end{aligned}}}$ y por lo tanto ${\displaystyle 0=3t^{2}+t-2=(3t-2)(t+1).}$ Tomamos la única solución t en [0, 2]: t = 2/3. Esto es, en efecto, un mínimo (y no un máximo) ya que el coste por unidad de tiempo tiende a infinito cuando t tiende a cero, lo que significa que el coste va disminuyendo a medida que t aumenta, hasta el punto 2/3 donde empieza a aumentar.

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2010) (Learn how and when to remove this message)

• Cox, David (1970). Teoría de la renovación . Londres: Methuen & Co., pág. 142. ISBN 0-412-20570-X.
• Doob, JL (1948). "Teoría de la renovación desde el punto de vista de la teoría de la probabilidad" (PDF) . Transactions of the American Mathematical Society . 63 (3): 422–438. doi : 10.2307/1990567 . JSTOR  1990567.
• Feller, William (1971). Introducción a la teoría de la probabilidad y sus aplicaciones . Vol. 2 (segunda edición). Wiley.
• Grimmett, GR ; Stirzaker, DR (1992). Probabilidad y procesos aleatorios (segunda edición). Oxford University Press. ISBN 0198572220.
• Smith, Walter L. (1958). "Teoría de la renovación y sus ramificaciones". Revista de la Royal Statistical Society, Serie B. 20 ( 2): 243–302. JSTOR  2983891.
• Wanli Wang, Johannes HP Schulz, Weihua Deng y Eli Barkai (2018). "Teoría de la renovación con tiempos de permanencia distribuidos de cola gruesa: típicos versus raros". Phys. Rev. E . 98 (4): 042139. arXiv : 1809.05856 . Código Bibliográfico :2018PhRvE..98d2139W. doi :10.1103/PhysRevE.98.042139. S2CID  54727926.{{cite journal}}: CS1 maint: multiple names: authors list (link)