Desvanecimiento de Rayleigh

El desvanecimiento de Rayleigh es un modelo estadístico del efecto de un entorno de propagación en una señal de radio , como el que utilizan los dispositivos inalámbricos .

Los modelos de desvanecimiento de Rayleigh suponen que la magnitud de una señal que ha pasado a través de dicho medio de transmisión (también llamado canal de comunicación ) variará aleatoriamente, o se desvanecerá , de acuerdo con una distribución de Rayleigh , el componente radial de la suma de dos variables aleatorias gaussianas no correlacionadas .

El desvanecimiento de Rayleigh se considera un modelo razonable para la propagación de señales troposféricas e ionosféricas , así como para el efecto de los entornos urbanos densamente edificados en las señales de radio. ^{[1] [2]} El desvanecimiento de Rayleigh es más aplicable cuando no hay propagación dominante a lo largo de una línea de visión entre el transmisor y el receptor. Si hay una línea de visión dominante, el desvanecimiento de Rician puede ser más aplicable. El desvanecimiento de Rayleigh es un caso especial de desvanecimiento de dos ondas con potencia difusa (TWDP) .

El desvanecimiento de Rayleigh es un modelo razonable cuando hay muchos objetos en el entorno que dispersan la señal de radio antes de que llegue al receptor. El teorema del límite central sostiene que, si hay suficiente dispersión, la respuesta al impulso del canal se modelará bien como un proceso gaussiano independientemente de la distribución de los componentes individuales. Si no hay un componente dominante en la dispersión, entonces dicho proceso tendrá una media cero y una fase distribuida uniformemente entre 0 y 2π radianes . Por lo tanto, la envolvente de la respuesta del canal tendrá una distribución de Rayleigh .

Al llamar a esta variable aleatoria , tendrá una función de densidad de probabilidad : ^[1]${\estilo de visualización R}$

${\displaystyle p_{R}(r)={\frac {2r}{\Omega }}e^{-r^{2}/\Omega },\ r\geq 0}$

dónde .${\displaystyle \Omega =\operatorname {E} (R^{2})}$

A menudo, los elementos de ganancia y fase de la distorsión de un canal se representan convenientemente como un número complejo . En este caso, el desvanecimiento de Rayleigh se manifiesta mediante la suposición de que las partes reales e imaginarias de la respuesta están modeladas por procesos gaussianos de media cero independientes e idénticamente distribuidos, de modo que la amplitud de la respuesta es la suma de dos de esos procesos.

El requisito de que haya muchos dispersores presentes significa que el desvanecimiento de Rayleigh puede ser un modelo útil en centros urbanos densamente edificados donde no hay línea de visión entre el transmisor y el receptor y muchos edificios y otros objetos atenúan , reflejan , refractan y difractan la señal. El trabajo experimental en Manhattan ha encontrado desvanecimiento cercano a Rayleigh allí. ^[3] En la propagación de señales troposféricas e ionosféricas, las muchas partículas en las capas atmosféricas actúan como dispersores y este tipo de entorno también puede aproximarse al desvanecimiento de Rayleigh. Si el entorno es tal que, además de la dispersión, hay una señal fuertemente dominante vista en el receptor, generalmente causada por una línea de visión , entonces la media del proceso aleatorio ya no será cero, variando en cambio alrededor del nivel de potencia de la trayectoria dominante. Tal situación puede modelarse mejor como desvanecimiento de Rician .

Tenga en cuenta que el desvanecimiento de Rayleigh es un efecto de pequeña escala. Habrá propiedades generales del entorno, como pérdida de trayectoria y sombras , sobre las que se superpone el desvanecimiento.

La velocidad con la que se desvanezca el canal se verá afectada por la velocidad con la que se muevan el receptor y/o el transmisor. El movimiento provoca un desplazamiento Doppler en los componentes de la señal recibida. Las figuras muestran la variación de potencia durante 1 segundo de una señal constante después de pasar por un canal de desvanecimiento Rayleigh de trayectoria única con un desplazamiento Doppler máximo de 10 Hz y 100 Hz. Estos desplazamientos Doppler corresponden a velocidades de aproximadamente 6 km/h (4 mph) y 60 km/h (40 mph) respectivamente a 1800 MHz, una de las frecuencias operativas de los teléfonos móviles GSM . Esta es la forma clásica del desvanecimiento Rayleigh. Nótese en particular los "desvanecimientos profundos" donde la intensidad de la señal puede caer en un factor de varios miles, o 30–40 dB .

Dado que se basa en una distribución bien estudiada con propiedades especiales, la distribución de Rayleigh se presta al análisis, y las características clave que afectan el rendimiento de una red inalámbrica tienen expresiones analíticas .

Tenga en cuenta que los parámetros que se analizan aquí corresponden a un canal no estático. Si un canal no cambia con el tiempo, no se desvanece y, en cambio, permanece en un nivel determinado. En este caso, las instancias separadas del canal no estarán correlacionadas entre sí, debido a la suposición de que cada uno de los componentes dispersos se desvanece de forma independiente. Una vez que se introduce un movimiento relativo entre cualquiera de los transmisores, receptores y dispersores, el desvanecimiento se correlaciona y varía en el tiempo.

La tasa de cruce de nivel es una medida de la rapidez del desvanecimiento. Cuantifica la frecuencia con la que el desvanecimiento cruza un umbral, generalmente en la dirección positiva. Para el desvanecimiento de Rayleigh, la tasa de cruce de nivel es: ^[4]

${\displaystyle \mathrm {LCR} ={\sqrt {2\pi }}f_{d}\rho e^{-\rho ^{2}}}$

donde es el desplazamiento Doppler máximo y es el nivel de umbral normalizado al nivel de señal de raíz cuadrada media (RMS):$estilo de visualización f_ {d}}$${\estilo de visualización \,\!\rho }$

${\displaystyle \rho ={\frac {R_{\mathrm {umbral} }}{R_{\mathrm {rms} }}}.}$

La duración media del desvanecimiento cuantifica el tiempo que la señal permanece por debajo del umbral . En el caso del desvanecimiento Rayleigh, la duración media del desvanecimiento es: ^[4]${\estilo de visualización \,\!\rho }$

${\displaystyle \mathrm {AFD} ={\frac {e^{\rho ^{2}}-1}{\rho f_{d}{\sqrt {2\pi }}}}.}$

La tasa de cruce de nivel y la duración promedio del desvanecimiento tomados en conjunto proporcionan un medio útil para caracterizar la gravedad del desvanecimiento a lo largo del tiempo.

Para un valor de umbral normalizado particular , el producto de la duración promedio del desvanecimiento y la tasa de cruce de nivel es una constante y se expresa mediante${\estilo de visualización \rho}$

${\displaystyle \mathrm {AFD} \times \mathrm {LCR} =1-e^{-\rho ^{2}}.}$

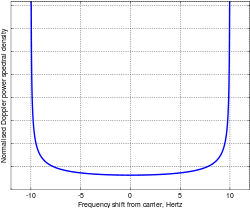
La densidad espectral de potencia Doppler de un canal que se desvanece describe cuánto ensanchamiento espectral causa. Esto muestra cómo una frecuencia pura, por ejemplo, una sinusoide pura, que es un impulso en el dominio de la frecuencia, se distribuye a través de la frecuencia cuando pasa a través del canal. Es la transformada de Fourier de la función de autocorrelación temporal. Para el desvanecimiento de Rayleigh con una antena receptora vertical con la misma sensibilidad en todas las direcciones, se ha demostrado que esto es: ^[5]

${\displaystyle S(\nu )={\frac {1}{\pi f_{d}{\sqrt {1-\left({\frac {\nu }{f_{d}}}\right)^{2}}}}},}$

donde es el desplazamiento de frecuencia con respecto a la frecuencia portadora. Esta ecuación es válida solo para valores entre ; el espectro es cero fuera de este rango. Este espectro se muestra en la figura para un desplazamiento Doppler máximo de 10 Hz. La "forma de cuenco" o "forma de bañera" es la forma clásica de este espectro Doppler.${\estilo de visualización \,\!\nu }$${\estilo de visualización \,\!\nu }$$estilo de visualización \pm f_{d}}$

Como se ha descrito anteriormente, un canal de desvanecimiento de Rayleigh puede modelarse mediante la generación de las partes real e imaginaria de un número complejo según variables gaussianas normales independientes. Sin embargo, a veces ocurre que lo que interesa son simplemente las fluctuaciones de amplitud (como en la figura que se muestra arriba). Existen dos enfoques principales para esto. En ambos casos, el objetivo es producir una señal que tenga el espectro de potencia Doppler indicado anteriormente y las propiedades de autocorrelación equivalentes.

En su libro, ^[6] Jakes popularizó un modelo para el desvanecimiento de Rayleigh basado en la suma de sinusoides . Dejemos que los dispersores se distribuyan uniformemente alrededor de un círculo en ángulos con rayos que emergen de cada dispersor. El desplazamiento Doppler en el rayo es${\displaystyle \alpha_{n}}$${\estilo de visualización k}$${\estilo de visualización n}$

${\displaystyle \,\!f_{n}=f_{d}\cos \alpha _{n}}$

y, con tales dispersores, el desvanecimiento de Rayleigh de la forma de onda a lo largo del tiempo se puede modelar como:${\estilo de visualización M}$${\displaystyle k^{\text{ésimo}}}$${\estilo de visualización t}$

${\displaystyle {\begin{aligned}R(t,k)=2{\sqrt {2}}\left[\sum _{n=1}^{M}\right.&\left(\cos \beta _{n}+j\sin \beta _{n}\right)\cos \left(2\pi f_{n}t+\theta _{n,k}\right)\\[4pt]&\left.{}+{\frac {1}{\sqrt {2}}}\left(\cos \alpha +j\sin \alpha \right)\cos(2\pi f_{d}t)\right].\end{aligned}}}$

Aquí, y son parámetros del modelo que normalmente se establecen en cero, elegidos de modo que no haya correlación cruzada entre las partes reales e imaginarias de :${\estilo de visualización \,\!\alfa }$${\displaystyle \,\!\beta _ {n}}$${\displaystyle \,\!\theta _{n,k}}$${\estilo de visualización \,\!\alfa }$${\displaystyle \,\!\beta _ {n}}$${\estilo de visualización R(t)}$

${\displaystyle \,\!\beta _ {n}={\frac {\pi n}{M+1}}}$

y se utiliza para generar múltiples formas de onda. Si se está modelando un canal de trayectoria única, de modo que solo haya una forma de onda, entonces puede ser cero. Si se está modelando un canal de trayectoria múltiple, selectivo en frecuencia, de modo que se necesitan múltiples formas de onda, Jakes sugiere que las formas de onda no correlacionadas se dan por${\displaystyle \,\!\theta _{n,k}}$${\displaystyle \,\!\theta _{n}}$

${\displaystyle \theta_{n,k}=\beta_{n}+{\frac {2\pi(k-1)}{M+1}}.}$

De hecho, se ha demostrado que las formas de onda están correlacionadas entre sí (tienen una correlación cruzada distinta de cero), excepto en circunstancias especiales. ^[7] El modelo también es determinista (no tiene ningún elemento aleatorio una vez que se eligen los parámetros). Un modelo de Jakes modificado ^[8] elige espaciamientos ligeramente diferentes para los dispersores y escala sus formas de onda utilizando secuencias de Walsh-Hadamard para garantizar una correlación cruzada cero.

${\displaystyle \alpha _{n}={\frac {\pi (n-0.5)}{2M}}{\text{ y }}\beta _{n}={\frac {\pi n}{M}},}$

El resultado es el siguiente modelo, normalmente denominado modelo Dent o modelo Jakes modificado:

${\displaystyle R(t,k)={\sqrt {\frac {2}{M}}}\sum _{n=1}^{M}A_{k}(n)\left(\cos \beta _{n}+j\sin \beta _{n}\right)\cos \left(2\pi f_{d}t\cos \alpha _{n}+\theta _{n}\right).}$

Las funciones de ponderación son la secuencia ^de Walsh-Hadamard en . Dado que tienen correlación cruzada cero por diseño, este modelo genera formas de onda no correlacionadas. Las fases se pueden inicializar aleatoriamente y no tienen efecto en las propiedades de correlación. La rápida transformada de Walsh se puede utilizar para generar muestras de manera eficiente utilizando este modelo.$Estilo de visualización A_{k}(n)}$${\estilo de visualización k}$${\estilo de visualización n}$${\displaystyle \,\!\theta _{n}}$

El modelo de Jakes también popularizó el espectro Doppler asociado con el desvanecimiento de Rayleigh y, como resultado, este espectro Doppler a menudo se denomina espectro de Jakes.

Otra forma de generar una señal con el espectro de potencia Doppler requerido es pasar una señal de ruido gaussiano blanco a través de un filtro gaussiano con una respuesta de frecuencia igual a la raíz cuadrada del espectro Doppler requerido. Aunque es más simple que los modelos anteriores y no es determinista, presenta algunas cuestiones de implementación relacionadas con la necesidad de filtros de orden superior para aproximar la función de raíz cuadrada irracional en la respuesta y muestrear la forma de onda gaussiana a una velocidad adecuada.

Según ^{[9] [10] [11],} la PSD Doppler también se puede modelar a través del filtro Butterworth como:

${\displaystyle S_{Doppler}(f)=|H_{Butterworth}|^{2}={\frac {B}{\sqrt {1-(f/f_{0})^{2k}}}}}$

donde f es una frecuencia, es la respuesta del filtro Butterworth, B es la constante de normalización, k es el orden del filtro y es la frecuencia de corte que debe seleccionarse con respecto al desplazamiento Doppler máximo.${\displaystyle H_{Butterworth}}$${\displaystyle f_{0}}$

• Desvanecimiento
• Dispersión de Rayleigh
• El desvanecimiento de Rician
• Propagación sin línea de visión
• Propagación por línea de visión
• Inalámbrico
• Distribución de Rayleigh
• Desvanecimiento de potencia difusa (TWDP) de dos ondas
• Señor Rayleigh

• Generador de señales de canal de desvanecimiento de Rayleigh utilizando el modelo Dent (Matlab)