Brecha principal

Un espacio entre primos es la diferencia entre dos números primos sucesivos . El espacio entre primos n -ésimo, denotado g n o g ( p n ), es la diferencia entre el ( n + 1) -primero y el n -ésimo número primo, es decir
Tenemos g 1 = 1, g 2 = g 3 = 2 y g 4 = 4. La secuencia ( g n ) de primos ha sido ampliamente estudiada; sin embargo, muchas preguntas y conjeturas permanecen sin respuesta.
Los primeros 60 huecos principales son:
- 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2, ... (secuencia A001223 en la OEIS ).
Por la definición de g n cada primo puede escribirse como
Observaciones simples
El primer, más pequeño y único número primo impar es el espacio de tamaño 1 entre 2, el único número primo par , y 3, el primer primo impar. Todos los demás espacios entre primos son pares. Solo hay un par de espacios consecutivos de longitud 2: los espacios g 2 y g 3 entre los primos 3, 5 y 7.
Para cualquier entero n , el factorial n ! es el producto de todos los enteros positivos hasta n inclusive . Entonces, en la secuencia
el primer término es divisible por 2, el segundo término es divisible por 3, y así sucesivamente. Por lo tanto, se trata de una secuencia de n − 1 números enteros compuestos consecutivos , y debe pertenecer a un espacio entre primos que tenga una longitud de al menos n . De ello se deduce que hay espacios entre primos que son arbitrariamente grandes, es decir, para cualquier número entero N , existe un número entero m con g m ≥ N .
Sin embargo, los huecos entre primos de n números pueden ocurrir en números mucho más pequeños que n !. Por ejemplo, el primer hueco entre primos de tamaño mayor que 14 ocurre entre los primos 523 y 541, mientras que 15! es el número mucho más grande 1307674368000.
La brecha promedio entre primos aumenta a medida que el logaritmo natural de estos primos, y por lo tanto la razón de la brecha de primos a los primos involucrados disminuye (y es asintóticamente cero). Esto es una consecuencia del teorema de los números primos . Desde un punto de vista heurístico, esperamos que la probabilidad de que la razón de la longitud de la brecha al logaritmo natural sea mayor o igual a un número positivo fijo k sea e − k ; en consecuencia, la razón puede ser arbitrariamente grande. De hecho, la razón de la brecha al número de dígitos de los enteros involucrados aumenta sin límite. Esto es una consecuencia de un resultado de Westzynthius. [2]
En la dirección opuesta, la conjetura de los primos gemelos postula que g n = 2 para infinitos números enteros n .
Resultados numéricos
Generalmente, la razón de se denomina mérito de la brecha g n . De manera informal, el mérito de una brecha g n se puede considerar como la razón del tamaño de la brecha en comparación con los tamaños promedio de brechas primarias en la vecindad de p n .
El mayor gap de primos conocido con extremos de gap de primos probables identificados tiene una longitud de 16.045.848, con primos probables de 385.713 dígitos y un mérito M = 18,067, descubierto por Andreas Höglund en marzo de 2024. [3] El mayor gap de primos conocido con primos probados identificados como extremos de gap tiene una longitud de 1.113.106 y un mérito de 25,90, con primos de 18.662 dígitos descubiertos por P. Cami, M. Jansen y JK Andersen. [4] [5]
A partir de septiembre de 2022 [update], el mayor valor de mérito conocido y el primero con mérito superior a 40, descubierto por la red Gapcoin, es 41,93878373 con el primo de 87 dígitos 293703234068022590158723766104419463425709075574811762098588798217895728858676728143227. La diferencia entre este número y el siguiente es 8350. [6] [7]
| Mérito | gn | dígitos | pn | Fecha | Descubridor |
|---|---|---|---|---|---|
| 41.938784 | 0 8350 | 00 87 | ver arriba | 2017 | Moneda Gap |
| 39.620154 | 15900 | 0 175 | 3483347771 × 409 # / 00 30 − 7016 | 2017 | Dana Jacobsen |
| 38.066960 | 18306 | 0 209 | 0 650094367 × 491#/2310 − 8936 | 2017 | Dana Jacobsen |
| 38.047893 | 35308 | 0 404 | 0 100054841 × 953#/ 0 210 − 9670 | 2020 | Seth Troisi |
| 37.824126 | 0 8382 | 00 97 | 0 512950801 × 229#/5610 − 4138 | 2018 | Dana Jacobsen |
La razón de Cramér–Shanks–Granville es el cociente de g n / (ln( p n )) 2 . [6] Si descartamos valores anómalamente altos de la razón para los primos 2, 3, 7, entonces el mayor valor conocido de esta razón es 0,9206386 para el primo 1693182318746371. Otros términos de registro se pueden encontrar en OEIS : A111943 .
Decimos que g n es un gap máximo , si g m < g n para todo m < n . A octubre de 2024 [update], el gap máximo entre primos más grande conocido tiene una longitud de 1676, hallado por Brian Kehrig. Es el 83.º gap máximo entre primos, y se produce después del primo 20733746510561442863. [11] Se pueden encontrar otros tamaños de gap (máximos) de registro en OEIS : A005250 , con los primos correspondientes p n en OEIS : A002386 , y los valores de n en OEIS : A005669 . Se conjetura que la secuencia de gaps máximos hasta el primo n tiene aproximadamente términos [12] (véase la tabla siguiente).
|
|
|
Resultados adicionales
Límites superiores
El postulado de Bertrand , demostrado en 1852, establece que siempre hay un número primo entre k y 2 k , por lo que en particular p n +1 < 2 p n , lo que significa g n < p n .
El teorema de los números primos , demostrado en 1896, dice que la longitud media del intervalo entre un primo p y el primo siguiente se aproximará asintóticamente a ln( p ), el logaritmo natural de p , para primos suficientemente grandes. La longitud real del intervalo puede ser mucho mayor o menor que esto. Sin embargo, se puede deducir del teorema de los números primos un límite superior para la longitud de los intervalos entre primos:
Para cada , hay un número tal que para todos
- .
También se puede deducir que los huecos se hacen arbitrariamente más pequeños en proporción a los primos: el cociente
Hoheisel (1930) fue el primero en demostrar [13] que existe una constante θ < 1 tal que
por lo que se demuestra que
para n suficientemente grande .
Hoheisel obtuvo el valor posible 32999/33000 para θ . Heilbronn lo mejoró a 249/250 [ 14] y Chudakov lo mejoró a θ = 3/4 + ε para cualquier ε > 0 [15] .
Una mejora importante se debe a Ingham , [16] quien demostró que para alguna constante positiva c ,
- si entonces por cualquier
Aquí, O se refiere a la notación O mayúscula , ζ denota la función zeta de Riemann y π la función de conteo de primos . Sabiendo que cualquier c > 1/6 es admisible, se obtiene que θ puede ser cualquier número mayor que 5/8.
Una consecuencia inmediata del resultado de Ingham es que siempre hay un número primo entre n 3 y ( n + 1) 3 , si n es suficientemente grande. [17] La hipótesis de Lindelöf implicaría que la fórmula de Ingham es válida para c cualquier número positivo: pero incluso esto no sería suficiente para implicar que hay un número primo entre n 2 y ( n + 1) 2 para n suficientemente grande (véase la conjetura de Legendre ). Para verificar esto, se necesitaría un resultado más fuerte como la conjetura de Cramér .
Huxley en 1972 demostró que se puede elegir θ = 7/12 = 0,58(3). [18]
Un resultado, debido a Baker, Harman y Pintz en 2001, muestra que θ puede tomarse como 0,525. [19]
En 2005, Daniel Goldston , János Pintz y Cem Yıldırım demostraron que
y 2 años después mejoró esto [20] a
En 2013, Yitang Zhang demostró que
lo que significa que hay infinitos huecos que no superan los 70 millones. [21] Un esfuerzo colaborativo del Proyecto Polymath para optimizar el límite de Zhang logró reducir el límite a 4680 el 20 de julio de 2013. [22] En noviembre de 2013, James Maynard introdujo un nuevo refinamiento de la criba GPY , lo que le permitió reducir el límite a 600 y demostrar que para cualquier m existe un intervalo acotado con un número infinito de traslaciones, cada una de las cuales contiene m números primos. [23] Utilizando las ideas de Maynard, el proyecto Polymath mejoró el límite a 246; [22] [24] asumiendo la conjetura de Elliott-Halberstam y su forma generalizada, el límite se ha reducido a 12 y 6, respectivamente. [22]
Límites inferiores
En 1931, Erik Westzynthius demostró que los gaps máximos entre primos crecen más que logarítmicamente. Es decir, [2]
En 1938, Robert Rankin demostró la existencia de una constante c > 0 tal que la desigualdad
se cumple para infinitos valores de n , mejorando los resultados de Westzynthius y Paul Erdős . Más tarde demostró que se puede tomar cualquier constante c < e γ , donde γ es la constante de Euler-Mascheroni . El valor de la constante c se mejoró en 1997 a cualquier valor menor que 2 e γ . [25]
Paul Erdős ofreció un premio de 10.000 dólares a quien demostrara o refutara que la constante c en la desigualdad anterior puede tomarse arbitrariamente grande. [26] Esto fue demostrado en 2014 por Ford–Green–Konyagin–Tao y, de forma independiente, James Maynard. [27] [28]
El resultado se mejoró aún más
para infinitos valores de n por Ford–Green–Konyagin–Maynard–Tao. [29]
Siguiendo el espíritu del premio original de Erdős, Terence Tao ofreció 10.000 dólares por una prueba de que c puede tomarse arbitrariamente grande en esta desigualdad. [30]
También se han determinado límites inferiores para cadenas de números primos. [31]
Conjeturas sobre las brechas entre números primos
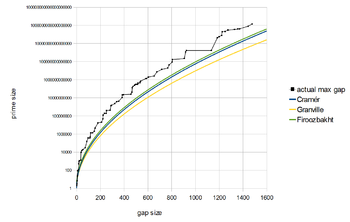
Se pueden obtener resultados aún mejores con la hipótesis de Riemann . Harald Cramér demostró [32] que la hipótesis de Riemann implica que la brecha g n satisface
utilizando la notación O grande . (De hecho, este resultado solo necesita la hipótesis más débil de Lindelöf , si se puede tolerar un exponente infinitesimalmente mayor. [33] ) Más tarde, conjeturó que las brechas son incluso más pequeñas. En términos generales, la conjetura de Cramér establece que
La conjetura de Firoozbakht establece que (donde es el n -ésimo primo) es una función estrictamente decreciente de n , es decir,
Si esta conjetura es verdadera, entonces la función satisface [34] Esto implica una forma fuerte de la conjetura de Cramér pero es inconsistente con las heurísticas de Granville y Pintz [35] [36] [37] que sugieren que infinitamente a menudo para cualquier lugar denota la constante de Euler-Mascheroni .
Mientras tanto, la conjetura de Oppermann es más débil que la de Cramér. El tamaño de la brecha esperada con la conjetura de Oppermann es del orden de
En consecuencia, según la conjetura de Oppermann existe (probablemente ) para la cual todo número natural satisface
La conjetura de Andrica , que es más débil que la de Oppermann, establece que [38]
Esto es un ligero fortalecimiento de la conjetura de Legendre de que entre números cuadrados sucesivos siempre hay un primo.
La conjetura de Polignac afirma que todo número par positivo k aparece como primo hueco una cantidad infinita de veces. El caso k = 2 es la conjetura de los primos gemelos . La conjetura aún no ha sido probada ni refutada para ningún valor específico de k , pero las mejoras en el resultado de Zhang que se analizaron anteriormente prueban que es cierta para al menos un valor (actualmente desconocido) de k ≤ 246.
Como función aritmética
La diferencia g n entre el n º y el ( n + 1) º número primo es un ejemplo de función aritmética . En este contexto, se suele denotar d n y se denomina función de diferencia de primos. [38] La función no es ni multiplicativa ni aditiva .
Véase también
Referencias
- ^ Ares, Saul; Castro, Mario (1 de febrero de 2006). "¿Estructura oculta en la aleatoriedad de la secuencia de números primos?". Physica A: Mecánica estadística y sus aplicaciones . 360 (2): 285–296. arXiv : cond-mat/0310148 . Bibcode :2006PhyA..360..285A. doi :10.1016/j.physa.2005.06.066. S2CID 16678116.
- ^ ab Westzynthius, E. (1931), "Über die Verteilung der Zahlen die zu den n ersten Primzahlen teilerfremd sind", Commentationes Physico-Mathematicae Helsingsfors (en alemán), 5 : 1–37, JFM 57.0186.02, Zbl 0003.24601.
- ^ ATH (11 de marzo de 2024). «Anuncio en Mersenneforum.org». Mersenneforum.org . Archivado desde el original el 12 de marzo de 2024.
- ^ Andersen, Jens Kruse. «Las 20 principales brechas de precios». Archivado desde el original el 27 de diciembre de 2019. Consultado el 13 de junio de 2014 .
- ^ Andersen, Jens Kruse (8 de marzo de 2013). "Un megagap con mérito 25,9". primerecords.dk . Archivado desde el original el 25 de diciembre de 2019 . Consultado el 29 de septiembre de 2022 .
- ^ abc Nicely, Thomas R. (2019). "NUEVA BRECHA PRINCIPAL DE MÁXIMO MÉRITO CONOCIDO". Faculty.lynchburg.edu . Archivado desde el original el 30 de abril de 2021. Consultado el 29 de septiembre de 2022 .
- ^ "Prime Gap Records". GitHub . 11 de junio de 2022.
- ^ "Información sobre el gap de prima de registro". ntheory.org . Archivado desde el original el 13 de octubre de 2016. Consultado el 29 de septiembre de 2022 .
- ^ Bien, Thomas R. (2019). "TABLA DE BRECHAS PRIMARIAS". Faculty.lynchburg.edu . Archivado desde el original el 27 de noviembre de 2020. Consultado el 29 de septiembre de 2022 .
- ^ "Los 20 mejores méritos generales". Lista de los mejores . Archivado desde el original el 27 de julio de 2022. Consultado el 29 de septiembre de 2022 .
- ^ Andersen, Jens Kruse. «Record prime gaps» (Brechas récord de precios) . Consultado el 10 de octubre de 2024 .
- ^ Kourbatov, A.; Wolf, M. (2020). "Sobre las primeras apariciones de huecos entre primos en una clase de residuos". Journal of Integer Sequences . 23 (Artículo 20.9.3). arXiv : 2002.02115 . MR 4167933. S2CID 211043720. Zbl 1444.11191. Archivado desde el original el 12 de abril de 2021 . Consultado el 3 de diciembre de 2020 .
- ^ Hoheisel, G. (1930). "Primzahlprobleme in der Analysis". Sitzunsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin . 33 : 3–11. JFM 56.0172.02.
- ^ Heilbronn, HA (1933). "Über den Primzahlsatz von Herrn Hoheisel". Mathematische Zeitschrift . 36 (1): 394–423. doi :10.1007/BF01188631. JFM 59.0947.01. S2CID 123216472.
- ^ Tchudakoff, NG (1936). "Sobre la diferencia entre dos números primos vecinos". Mat. Sb . 1 : 799–814. Zbl 0016.15502.
- ^ Ingham, AE (1937). "Sobre la diferencia entre primos consecutivos". Quarterly Journal of Mathematics . Oxford Series. 8 (1): 255–266. Bibcode :1937QJMat...8..255I. doi :10.1093/qmath/os-8.1.255.
- ^ Cheng, Yuan-You Fu-Rui (2010). "Estimación explícita de primos entre cubos consecutivos". Rocky Mt. J. Math . 40 : 117–153. arXiv : 0810.2113 . doi :10.1216/rmj-2010-40-1-117. S2CID 15502941. Zbl 1201.11111.
- ^ Huxley, MN (1972). "Sobre la diferencia entre primos consecutivos". Inventiones Mathematicae . 15 (2): 164–170. Bibcode :1971InMat..15..164H. doi :10.1007/BF01418933. S2CID 121217000.
- ^ Baker, RC; Harman, G.; Pintz, J. (2001). "La diferencia entre primos consecutivos, II". Actas de la London Mathematical Society . 83 (3): 532–562. CiteSeerX 10.1.1.360.3671 . doi :10.1112/plms/83.3.532. S2CID 8964027.
- ^ Goldston, Daniel A.; Pintz, János; Yıldırım, Cem Yalçin (2010). "Primes en tuplas II". Acta Matemática . 204 (1): 1–47. arXiv : 0710.2728 . doi :10.1007/s11511-010-0044-9. S2CID 7993099.
- ^ Zhang, Yitang (2014). "Bounded gaps between primes" (Brechas acotadas entre primos). Anales de Matemáticas . 179 (3): 1121–1174. doi : 10.4007/annals.2014.179.3.7 . MR 3171761.
- ^ abc «Bounded gaps between primes» (Huecos acotados entre primos). Polymath. Archivado desde el original el 28 de febrero de 2020. Consultado el 21 de julio de 2013 .
- ^ Maynard, James (2015). "Pequeñas brechas entre números primos". Anales de Matemáticas . 181 (1): 383–413. arXiv : 1311.4600 . doi :10.4007/annals.2015.181.1.7. MR 3272929. S2CID 55175056.
- ^ DHJ Polymath (2014). "Variantes de la criba de Selberg e intervalos acotados que contienen muchos primos". Investigación en las ciencias matemáticas . 1 (12). arXiv : 1407.4897 . doi : 10.1186/s40687-014-0012-7 . MR 3373710. S2CID 119699189.
- ^ Pintz, J. (1997). "Brechas muy grandes entre primos consecutivos". J. Number Theory . 63 (2): 286–301. doi : 10.1006/jnth.1997.2081 .
- ^ Erdős, Paul; Bollobás, Béla; Thomason, Andrés, eds. (1997). Combinatoria, geometría y probabilidad: un tributo a Paul Erdős. Prensa de la Universidad de Cambridge. pag. 1.ISBN 9780521584722Archivado del original el 29 de septiembre de 2022 . Consultado el 29 de septiembre de 2022 .
- ^ Ford, Kevin; Green, Ben; Konyagin, Sergei; Tao, Terence (2016). "Grandes brechas entre números primos consecutivos". Ann. of Math. 183 (3): 935–974. arXiv : 1408.4505 . doi :10.4007/annals.2016.183.3.4. MR 3488740. S2CID 16336889.
- ^ Maynard, James (2016). "Grandes brechas entre números primos". Ann. of Math. 183 (3): 915–933. arXiv : 1408.5110 . doi :10.4007/annals.2016.183.3.3. MR 3488739. S2CID 119247836.
- ^ Ford, Kevin; Green, Ben; Konyagin, Sergei; Maynard, James; Tao, Terence (2018). "Largos espacios entre primos". J. Amer. Math. Soc. 31 (1): 65–105. arXiv : 1412.5029 . doi :10.1090/jams/876. MR 3718451. S2CID 14487001.
- ^ Tao, Terence (16 de diciembre de 2014). «Largos intervalos entre números primos / Novedades». Archivado desde el original el 9 de junio de 2019. Consultado el 29 de agosto de 2019 .
- ^ Ford, Kevin; Maynard, James; Tao, Terence (13 de octubre de 2015). "Cadenas de grandes brechas entre números primos". arXiv : 1511.04468 [math.NT].
- ^ Cramér, Harald (1936). "Sobre el orden de magnitud de la diferencia entre números primos consecutivos". Acta Arithmetica . 2 : 23–46. doi : 10.4064/aa-2-1-23-46 .
- ^ Ingham, Albert E. (1937). "Sobre la diferencia entre primos consecutivos" (PDF) . Quart. J. Math . 8 (1). Oxford: 255–266. Bibcode :1937QJMat...8..255I. doi :10.1093/qmath/os-8.1.255. Archivado (PDF) desde el original el 5 de diciembre de 2022.
- ^ Sinha, Nilotpal Kanti (2010). "Sobre una nueva propiedad de los números primos que conduce a una generalización de la conjetura de Cramer". arXiv : 1010.1399 [math.NT]..
- ^ Granville, Andrew (1995). «Harald Cramér y la distribución de los números primos» (PDF) . Scandinavian Actuarial Journal . 1 : 12–28. CiteSeerX 10.1.1.129.6847 . doi :10.1080/03461238.1995.10413946. Archivado (PDF) desde el original el 23 de septiembre de 2015. Consultado el 2 de marzo de 2016 . .
- ^ Granville, Andrew (1995). "Irregularidades inesperadas en la distribución de números primos" (PDF) . Actas del Congreso Internacional de Matemáticos . Vol. 1. págs. 388–399. doi :10.1007/978-3-0348-9078-6_32. ISBN . 978-3-0348-9897-3. Archivado (PDF) del original el 7 de mayo de 2016 . Consultado el 2 de marzo de 2016 ..
- ^ Pintz, János (septiembre de 2007). "Cramér vs. Cramér: sobre el modelo probabilístico de números primos de Cramér". Functiones et Approximatio Commentarii Mathematici . 37 (2): 232–471. doi : 10.7169/facm/1229619660 .
- ^ de Guy (2004) §A8
- Guy, Richard K. (2004). Problemas no resueltos en teoría de números (3.ª ed.). Springer-Verlag . ISBN 978-0-387-20860-2.Zbl 1058.11001 .
Lectura adicional
- Soundararajan, Kannan (2007). "Pequeñas brechas entre números primos: el trabajo de Goldston-Pintz-Yıldırım". Bull. Am. Math. Soc . Nuevas series. 44 (1): 1–18. arXiv : math/0605696 . doi :10.1090/s0273-0979-06-01142-6. S2CID 119611838. Zbl 1193.11086.
- Mihăilescu, Preda (junio de 2014). "Sobre algunas conjeturas en teoría aditiva de números" (PDF) . EMS Newsletter (92): 13–16. doi :10.4171/NEWS. hdl : 2117/17085 . ISSN 1027-488X.
Enlaces externos
- Thomas R. Nicely, Algunos resultados de la investigación computacional en números primos -- Teoría de números computacionales. Este sitio web de referencia incluye una lista de todos los números primos que aparecen por primera vez.
- Weisstein, Eric W. "Función de diferencia de primos". MathWorld .
- "Función de diferencia de primos". PlanetMath .
- Armin Shams, al ampliar el teorema de Chebyshev sobre la conjetura de Bertrand, no implica una constante "arbitrariamente grande" como algunos otros resultados informados.
- Chris Caldwell , Brechas entre números primos: una introducción elemental
- Andrew Granville , Primos en intervalos de longitud acotada; visión general de los resultados obtenidos hasta el momento incluyendo el trabajo de James Maynard de noviembre de 2013.
- Birke Heeren, [1] Aquí encontrará las grandes brechas de números primos y un artículo sobre cómo calcular esas grandes brechas.




































