Pársec
Unidad de longitud utilizada en astronomía.

Pársec
Un parsec es la distancia del Sol a un objeto astronómico que tiene un ángulo de paralaje de un segundo de arco (no a escala)
información general
Sistema de unidadesunidades astronómicas
Unidad delongitud / distancia
Símboloordenador personal
Conversiones
1 pieza en...... es igual a...
   unidades métricas ( SI )   3,0857 × 10 16  m
   ~31 petámetros
      Unidades imperiales de EE.UU.   1.9174 × 10 13  millas
   unidades astronómicas   2.062 65 × 10 5  au
   3.261 56  años luz

El parsec (símbolo: pc ) es una unidad de longitud utilizada para medir las grandes distancias a objetos astronómicos fuera del Sistema Solar , aproximadamente igual a 3,26 años luz o 206.265 unidades astronómicas (UA), es decir, 30,9  billones de kilómetros (19,2 billones de millas ). [a] La unidad parsec se obtiene mediante el uso de paralaje y trigonometría , y se define como la distancia a la que 1 UA subtiende un ángulo de un segundo de arco [1] (1/3600⁠ de un grado ). La estrella más cercana, Próxima Centauri , está a unos 1,3 parsecs (4,2 años luz) del Sol : desde esa distancia, la brecha entre la Tierra y el Sol abarca un poco menos de ⁠1/3600⁠ de un grado de visión. [2] La mayoría de las estrellas visibles a simple vista están a unos pocos cientos de parsecs del Sol, las más distantes a unos pocos miles de parsecs y la galaxia de Andrómeda a más de 700.000 parsecs. [3]

La palabra pársec es un acrónimo de "paralaje de un segundo" y fue acuñada por el astrónomo británico Herbert Hall Turner en 1913 [4] para simplificar los cálculos de los astrónomos de distancias astronómicas a partir de datos de observación en bruto. En parte por esta razón, es la unidad preferida en astronomía y astrofísica , aunque el año luz sigue siendo prominente en los textos de divulgación científica y el uso común. Aunque los pársecs se utilizan para las distancias más cortas dentro de la Vía Láctea , se requieren múltiplos de pársecs para las escalas más grandes en el universo, incluidos los kilo pársecs (kpc) para los objetos más distantes dentro y alrededor de la Vía Láctea, los mega pársecs (Mpc) para las galaxias de distancia media y los giga pársecs (Gpc) para muchos cuásares y las galaxias más distantes.

En agosto de 2015, la Unión Astronómica Internacional (UAI) aprobó la Resolución B2 que, como parte de la definición de una escala de magnitud bolométrica absoluta y aparente estandarizada , mencionó una definición explícita existente del pársec como exactamente648 000/π⁠  au, o aproximadamente3.085 677 581 491 3673 × 10 16  metros (según la definición de la unidad astronómica de la UAI de 2012). Esto corresponde a la definición de ángulo pequeño del pársec que se encuentra en muchas referencias astronómicas. [5] [6]

Historia y derivación

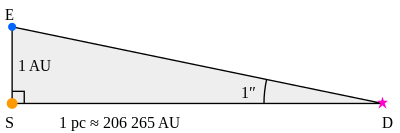
Imaginando un triángulo rectángulo alargado en el espacio, donde el cateto más corto mide una ua ( unidad astronómica , la distancia media entre la Tierra y el Sol ) y el ángulo subtendido del vértice opuesto a ese cateto mide un segundo de arco ( 1 ⁄ 3600 de un grado), el pársec se define como la longitud del cateto adyacente . El valor de un pársec se puede derivar a través de las reglas de la trigonometría . La distancia desde la Tierra a la que el radio de su órbita solar subtiende un segundo de arco.

Uno de los métodos más antiguos utilizados por los astrónomos para calcular la distancia a una estrella es registrar la diferencia de ángulo entre dos mediciones de la posición de la estrella en el cielo. La primera medición se toma desde la Tierra en un lado del Sol, y la segunda se toma aproximadamente medio año después, cuando la Tierra está en el lado opuesto del Sol. [b] La distancia entre las dos posiciones de la Tierra cuando se tomaron las dos mediciones es el doble de la distancia entre la Tierra y el Sol. La diferencia de ángulo entre las dos mediciones es el doble del ángulo de paralaje, que se forma mediante líneas desde el Sol y la Tierra hasta la estrella en el vértice distante . Luego, la distancia a la estrella podría calcularse utilizando trigonometría. [7] Las primeras mediciones directas publicadas con éxito de un objeto a distancias interestelares fueron realizadas por el astrónomo alemán Friedrich Wilhelm Bessel en 1838, quien utilizó este enfoque para calcular la distancia de 3,5 parsecs de 61 Cygni . [8]

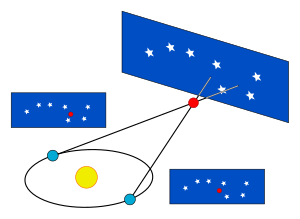
Diagramas que ilustran el cambio aparente en la posición de un objeto celeste cuando se observa desde diferentes posiciones en la órbita de la Tierra.
Movimiento de paralaje estelar a partir de paralaje anual

La paralaje de una estrella se define como la mitad de la distancia angular que una estrella parece recorrer en relación con la esfera celeste cuando la Tierra orbita alrededor del Sol. De manera equivalente, es el ángulo subtendido, desde la perspectiva de esa estrella, del semieje mayor de la órbita de la Tierra. Sustituyendo la paralaje de la estrella por el ángulo de un segundo de arco en el triángulo rectángulo imaginario, el cateto más largo del triángulo medirá la distancia desde el Sol hasta la estrella. Un pársec se puede definir como la longitud del lado del triángulo rectángulo adyacente al vértice ocupado por una estrella cuyo ángulo de paralaje es de un segundo de arco.

El uso del parsec como unidad de distancia se desprende naturalmente del método de Bessel, porque la distancia en parsecs se puede calcular simplemente como el recíproco del ángulo de paralaje en segundos de arco (es decir: si el ángulo de paralaje es 1 segundo de arco, el objeto está a 1 pc del Sol; si el ángulo de paralaje es 0,5 segundos de arco, el objeto está a 2 pc de distancia; etc.). No se requieren funciones trigonométricas en esta relación porque los ángulos muy pequeños involucrados significan que se puede aplicar la solución aproximada del triángulo delgado .

Aunque puede que ya se haya utilizado antes, el término pársec se mencionó por primera vez en una publicación astronómica en 1913. El astrónomo real Frank Watson Dyson expresó su preocupación por la necesidad de un nombre para esa unidad de distancia. Propuso el nombre astron , pero mencionó que Carl Charlier había sugerido siriómetro y Herbert Hall Turner había propuesto pársec . [4] Fue la propuesta de Turner la que se mantuvo.

Calcular el valor de un parsec

Según la definición de 2015,1 au de longitud de arco subtiende un ángulo de1″ en el centro del círculo de radio1 pc . Es decir, 1 pc = 1 au/tan(1″ ) ≈ 206,264.8 au por definición. [9] Convirtiendo de unidades de grados/minutos/segundos a radianes ,

1  ordenador personal 1  es = 180 × 60 × 60 π {\displaystyle {\frac {1{\text{ pc}}}{1{\text{ au}}}}={\frac {180\times 60\times 60}{\pi }}} , y
1  es = 149 597 870 700  metro {\displaystyle 1{\text{au}}=149\,597\,870\,700{\text{m}}} (exactamente según la definición de 2012 de la au)

Por lo tanto, (según la definición de 2015) π   pag do = 180 × 60 × 60   a tú = 180 × 60 × 60 × 149 597 870 700   metro = 96 939 420 213 600 000   metro {\displaystyle \pi ~\mathrm {pc} =180\times 60\times 60~\mathrm {au} =180\times 60\times 60\times 149\,597\,870\,700~\mathrm {m } =96\,939\,420\,213\,600\,000~\mathrm {m} }

Por lo tanto,

1   pag do = 96 939 420 213 600 000 π   metro = 30 856 775 814 913 673   metro {\displaystyle 1~\mathrm {pc} ={\frac {96\,939\,420\,213\,600\,000}{\pi }}~\mathrm {m} =30\,856\, 775\,814\,913\,673~\mathrm {m} } (al metro más cercano ).

Aproximadamente,

Diagrama de parsec.

En el diagrama anterior (no a escala), S representa al Sol y E a la Tierra en un punto de su órbita (de manera que forme un ángulo recto en S [b] ). Por lo tanto, la distancia ES es una unidad astronómica (ua). El ángulo SDE es un segundo de arco ( ⁠1/3600⁠ de un grado ) por lo que por definición D es un punto en el espacio a una distancia de un parsec del Sol. A través de la trigonometría, la distancia SD se calcula de la siguiente manera:

S D = mi S broncearse ⁡ 1 " = mi S broncearse ⁡ ( 1 60 × 60 × π 180 ) ≈ 1 a tú 1 60 × 60 × π 180 = 648 000 π a tú ≈ 206 264,81   a tú . {\displaystyle {\begin{aligned}\mathrm {SD} &={\frac {\mathrm {ES} }{\tan 1''}}\\&={\frac {\mathrm {ES} }{\tan \left({\frac {1}{60\times 60}}\times {\frac {\pi }{180}}\right)}}\\&\approx {\frac {1\,\mathrm {au} }{{\frac {1}{60\times 60}}\times {\frac {\pi }{180}}}}={\frac {648\,000}{\pi }}\,\mathrm {au} \approx 206\,264.81~\mathrm {au} .\end{aligned}}}

Porque la unidad astronómica se define como149 597 870 700  m , [10] se puede calcular lo siguiente:

Por lo tanto, 1 parsec≈206 264 .806 247 096 unidades astronómicas
≈3.085 677 581 × 10 16 metros
≈30.856 775 815  billones de kilómetros
≈19.173 511 577  billones de millas

Por lo tanto, si1  año luz ≈ 9,46 × 10 15  m,

Entonces1 pieza ≈3.261 563 777 años  luz

Un corolario establece que un parsec es también la distancia desde la cual se debe observar un disco de una au de diámetro para que tenga un diámetro angular de un segundo de arco (colocando al observador en D y un disco que abarca ES ).

Matemáticamente, para calcular la distancia, dadas las medidas angulares obtenidas de los instrumentos en segundos de arco, la fórmula sería:

Distancia estrella = Distancia Tierra-sol broncearse ⁡ θ 3600 {\displaystyle {\text{Distancia}}_{\text{estrella}}={\frac {{\text{Distancia}}_{\text{tierra-sol}}}{\tan {\frac {\theta }{3600}}}}}

donde θ es el ángulo medido en segundos de arco, la distancia Tierra-Sol es una constante (1 au o 1,5813 × 10 −5  años luz). La distancia estelar calculada estará en la misma unidad de medida que se utiliza en Distancia Tierra-Sol (por ejemplo, si Distancia Tierra-Sol =1 au , la unidad para la distancia entre estrellas está en unidades astronómicas; si la distancia Tierra-Sol = 1,5813 × 10 −5  años luz, la unidad para la distancia entre estrellas está en años luz).

La longitud del parsec utilizado en la Resolución B2 de la IAU 2015 [11] (exactamente ⁠648 000/π⁠ unidades astronómicas) corresponde exactamente a la derivada utilizando el cálculo de ángulos pequeños. Esto difiere de la definición clásica de tangente inversa en aproximadamente200 km , es decir: solo después de la undécima cifra significativa . Como la unidad astronómica fue definida por la IAU (2012) como una longitud exacta en metros, ahora el pársec corresponde a una longitud exacta en metros. Redondeado al metro más cercano, el pársec de ángulo pequeño corresponde a30 856 775 814 913 673  metros .

Uso y medición

El método de paralaje es el paso de calibración fundamental para la determinación de la distancia en astrofísica ; sin embargo, la precisión de las mediciones del ángulo de paralaje con telescopios terrestres está limitada a aproximadamente0,01″ , y por lo tanto a las estrellas no más de100 pc de distancia. [12] Esto se debe a que la atmósfera de la Tierra limita la nitidez de la imagen de una estrella. [ cita requerida ] Los telescopios espaciales no están limitados por este efecto y pueden medir con precisión las distancias a los objetos más allá del límite de las observaciones terrestres. Entre 1989 y 1993, el satélite Hipparcos , lanzado por la Agencia Espacial Europea (ESA), midió paralajes de aproximadamente100.000 estrellas con una precisión astrométrica de aproximadamente0,97  mas , y obtuvo mediciones precisas para distancias estelares de estrellas de hasta1000 pc de distancia. [13] [14]

El satélite Gaia de la ESA , que se lanzó el 19 de diciembre de 2013, tiene como objetivo medir mil millones de distancias estelares con un margen de error de 100 000 millones de veces.20 microsegundos de arco, produciendo errores del 10% en las mediciones hasta el Centro Galáctico , aproximadamenteA 8000 pc de distancia en la constelación de Sagitario . [15]

Distancias en parsecs

Distancias menores a un parsec

Las distancias expresadas en fracciones de pársec suelen referirse a objetos que se encuentran dentro de un mismo sistema estelar. Por ejemplo:

Como se observa mediante el telescopio espacial Hubble , el chorro astrofísico que surge del núcleo galáctico activo de M87 subtiende 20″ y se cree que tiene 1,5 kiloparsecs (4.892  años luz ) de largo (el chorro está algo escorzado desde la perspectiva de la Tierra).

Parsecs y kiloparsecs

Las distancias expresadas en parsecs (pc) incluyen distancias entre estrellas cercanas, como las que se encuentran en el mismo brazo espiral o cúmulo globular . Una distancia de 1000 parsecs (3262 años luz) se denota por el kiloparsec (kpc). Los astrónomos suelen utilizar kiloparsecs para expresar distancias entre partes de una galaxia o dentro de grupos de galaxias . Así, por ejemplo:

  • Próxima Centauri , la estrella conocida más cercana a la Tierra aparte del Sol, está a unos 1,3 parsecs (4,24 años luz) de distancia según la medición directa de paralaje.
  • La distancia al cúmulo abierto Pléyades es130 ± 10 piezas (420 ± 30 ly ) de nosotros según la medición de paralaje de Hipparcos .
  • El centro de la Vía Láctea está a más de 8 kiloparsecs (26.000 años luz) de la Tierra y la Vía Láctea tiene aproximadamente 34 kiloparsecs (110.000 años luz) de diámetro.
  • ESO 383-76 , una de las galaxias más grandes conocidas , tiene un diámetro de 540,9 kpc (1,8 millones de años luz).
  • La galaxia de Andrómeda ( M31 ) está a unos 780 kpc (2,5 millones de años luz) de la Tierra.

Megaparsecs y gigaparsecs

Los astrónomos suelen expresar las distancias entre galaxias vecinas y cúmulos de galaxias en megaparsecs (Mpc). Un megaparsec es un millón de parsecs, o unos 3.260.000 años luz. [16] A veces, las distancias galácticas se dan en unidades de Mpc/ h (como en "50/ h  Mpc", también escrito " 50 Mpc h −1 "). h es una constante (la " constante de Hubble adimensional ") en el rango 0,5 < h < 0,75 que refleja la incertidumbre en el valor de la constante de Hubble H para la tasa de expansión del universo: h = ⁠yo/100 (km/s)/Mpc⁠ . La constante de Hubble se vuelve relevante al convertir un corrimiento al rojo observado z en una distancia d utilizando la fórmula d ≈ ⁠do/yo× z . [17 ]

Un gigaparsec (Gpc) equivale a mil millones de pársecs, una de las unidades de longitud más grandes que se utilizan habitualmente. Un gigaparsec equivale a unos 3260 millones de años luz, o aproximadamente ⁠1/14⁠ de la distancia al horizonte del universo observable (dictada por la radiación de fondo de microondas cósmica ). Los astrónomos suelen utilizar gigaparsecs para expresar los tamaños de estructuras a gran escala, como el tamaño y la distancia a la Gran Muralla CfA2 ; las distancias entre cúmulos de galaxias; y la distancia a los cuásares .

Por ejemplo:

Unidades de volumen

Para determinar el número de estrellas en la Vía Láctea, se seleccionan volúmenes en kiloparsecs cúbicos [c] (kpc 3 ) en varias direcciones. Se cuentan todas las estrellas en estos volúmenes y se determina estadísticamente el número total de estrellas. El número de cúmulos globulares, nubes de polvo y gas interestelar se determina de manera similar. Para determinar el número de galaxias en supercúmulos , se seleccionan volúmenes en megaparsecs cúbicos [c] (Mpc 3 ). Se clasifican y se cuentan todas las galaxias en estos volúmenes. Luego se puede determinar estadísticamente el número total de galaxias. El enorme vacío de Boötes se mide en megaparsecs cúbicos. [20]

En cosmología física , se seleccionan volúmenes de gigaparsecs cúbicos [c] (Gpc 3 ) para determinar la distribución de la materia en el universo visible y para determinar el número de galaxias y cuásares. El Sol es actualmente la única estrella en su parsec cúbico, [c] (pc 3 ) pero en los cúmulos globulares la densidad estelar podría ser de100–1000 pc −3 .

El volumen de observación de los interferómetros de ondas gravitacionales (por ejemplo, LIGO , Virgo ) se expresa en términos de megaparsecs cúbicos [c] (Mpc 3 ) y es esencialmente el valor de la distancia efectiva al cubo.

Véase también

Notas

  1. ^ Un billón aquí es escala corta , es decir, 10 12 (un millón de millones, o mil millones en escala larga).
  2. ^ ab Las observaciones terrestres de la posición de una estrella deben realizarse cuando la Tierra está en el punto más alejado de su órbita de una línea entre el Sol y la estrella, para formar un ángulo recto con el Sol y una ua completa de separación visto desde la estrella.
  3. ^ abcde
    1 pieza 3≈ 2.938 × 10 49  m3​
    1 kpc3≈2.938 × 10 58  m3​
    1 megaciclo 3≈2.938 × 10 67  m3​
    1 Gpc3≈2.938 × 10 76  m3​
    1 pieza 3≈2.938 × 10 85  m3​

Referencias

  1. ^ "Escalas de distancia cósmica: la Vía Láctea" . Consultado el 24 de septiembre de 2014 .
  2. ^ Benedict, G. F.; et al. "Estabilidad astrométrica y precisión del sensor de guía fina n.º 3: el paralaje y el movimiento propio de Próxima Centauri" (PDF) . Actas del taller de calibración del HST . págs. 380–384 . Consultado el 11 de julio de 2007 .
  3. ^ "Estrellas más lejanas". StarDate . Universidad de Texas en Austin . 15 de mayo de 2021 . Consultado el 5 de septiembre de 2021 .
  4. ^ ab Dyson, F. W. (marzo de 1913). "La distribución en el espacio de las estrellas en el Catálogo Circumpolar de Carrington". Monthly Notices of the Royal Astronomical Society . 73 (5): 342. Bibcode :1913MNRAS..73..334D. doi : 10.1093/mnras/73.5.334 . [ párrafo 14, página 342 ] Tomando la unidad de distancia R* como la correspondiente a una paralaje de 1″·0 [… Nota al pie:] * Es necesario un nombre para esta unidad de distancia. El Sr. Charlier ha sugerido Siriómetro , pero si se puede pasar por alto la violencia al idioma griego, se podría adoptar la palabra Astron . El profesor Turner sugiere Parsec , que puede tomarse como una forma abreviada de "una distancia correspondiente a una paralaje de un segundo".
  5. ^ Cox, Arthur N., ed. (2000). Allen's Astrophysical Quantities (4.ª ed.). Nueva York: AIP Press / Springer. Código Bibliográfico : 2000asqu.book.....C. ISBN 978-0387987460.
  6. ^ Binney, James; Tremaine, Scott (2008). Dinámica galáctica (2.ª ed.). Princeton, NJ: Princeton University Press. Código Bibliográfico : 2008gady.book.....B. ISBN 978-0-691-13026-2.
  7. ^ Centro de investigación del archivo científico de astrofísica de altas energías (HEASARC). "Derivación de la fórmula de paralaje". Imagine the Universe! de la NASA . División de ciencia astrofísica (ASD) del Centro de vuelo espacial Goddard de la NASA . Consultado el 26 de noviembre de 2011 .
  8. ^ Bessel, FW (1838). "Bestimmung der Entfernung des 61sten Sterns des Schwans" [Determinación de la distancia de la estrella 61 del Cisne]. Astronomische Nachrichten . 16 (5): 65–96. Código bibliográfico : 1838AN.....16...65B. doi :10.1002/asna.18390160502.
  9. ^ B. Luque; FJ Ballesteros (2019). "Título: Hasta el Sol y más allá". Nature Physics . 15 (12): 1302. Bibcode :2019NatPh..15.1302L. doi : 10.1038/s41567-019-0685-3 .
  10. ^ Unión Astronómica Internacional, ed. (31 de agosto de 2012), "RESOLUCIÓN B2 sobre la redefinición de la unidad astronómica de longitud" (PDF) , RESOLUCIÓN B2 , Beijing: Unión Astronómica Internacional , La XXVIII Asamblea General de la Unión Astronómica Internacional recomienda [adoptada] que la unidad astronómica se redefina para que sea una unidad convencional de longitud exactamente igual a149 597 870 700  m , de acuerdo con el valor adoptado en la Resolución B2 de la UAI de 2009
  11. ^ Unión Astronómica Internacional, ed. (13 de agosto de 2015), "RESOLUCIÓN B2 sobre los puntos cero recomendados para las escalas de magnitud bolométrica absoluta y aparente" (PDF) , RESOLUCIÓN B2 , Honolulu: Unión Astronómica Internacional , La XXIX Asamblea General de la Unión Astronómica Internacional señala [4] que el pársec se define exactamente como (648 000/ ) au según la definición de la UA en la Resolución B2 de la UAI de 2012 π {\displaystyle \pi }
  12. ^ Pogge, Richard. "Astronomía 162". Universidad Estatal de Ohio.
  13. ^ "La misión de astrometría espacial Hipparcos" . Consultado el 28 de agosto de 2007 .
  14. ^ Turón, Catherine. "De Hiparco a Hiparco".
  15. ^ "GAIA". Agencia Espacial Europea .
  16. ^ "¿Por qué un pársec mide 3,26 años luz?". Astronomy.com . 1 de febrero de 2020 . Consultado el 20 de julio de 2021 .
  17. ^ "Estructuras de galaxias: la estructura a gran escala del universo cercano". Archivado desde el original el 5 de marzo de 2007. Consultado el 22 de mayo de 2007 .
  18. ^ Mei, S.; Blakeslee, J. P.; Côté, P.; et al. (2007). "El sondeo del cúmulo de Virgo de la ACS. XIII. Catálogo de distancias SBF y la estructura tridimensional del cúmulo de Virgo". The Astrophysical Journal . 655 (1): 144–162. arXiv : astro-ph/0702510 . Código Bibliográfico :2007ApJ...655..144M. doi :10.1086/509598. S2CID  16483538.
  19. ^ Lineweaver, Charles H.; Davis, Tamara M. (1 de marzo de 2005). «Misconceptions about the Big Bang» (Conceptos erróneos sobre el Big Bang). Scientific American . 292 (3): 36–45. Bibcode :2005SciAm.292c..36L. doi :10.1038/scientificamerican0305-36. Archivado desde el original el 10 de agosto de 2011 . Consultado el 4 de febrero de 2016 .
  20. ^ Kirshner, R. P.; Oemler, A. Jr.; Schechter, P. L.; Shectman, S. A. (1981). "Un vacío de un millón de megaparsecs cúbicos en Bootes". The Astrophysical Journal . 248 : L57. Bibcode :1981ApJ...248L..57K. doi :10.1086/183623. ISSN  0004-637X.
  • Guidry, Michael. "Escalas de distancias astronómicas". Astronomía 162: estrellas, galaxias y cosmología . Universidad de Tennessee, Knoxville. Archivado desde el original el 12 de diciembre de 2012. Consultado el 26 de marzo de 2010 .
  • Merrifield, Michael. "pc Parsec". Sesenta símbolos . Brady Haran para la Universidad de Nottingham .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Parsec&oldid=1250907416"