Momento (física)

Parte de una serie sobre
Mecánica clásica
${\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales Aplicado Celestial Continuo Dinámica Teoría de campos Cinemática Cinética Estática Mecánica estadística
Fundamentos Aceleración Momento angular Pareja Principio de D'Alembert Energía cinético potencial Fuerza Marco de referencia Marco de referencia inercial Impulso Inercia  / Momento de inercia Masa Potencia mecánica Trabajo mecánico Momento Impulso Espacio Velocidad Tiempo Esfuerzo de torsión Velocidad Trabajo virtual
Formulaciones Leyes del movimiento de Newton Mecánica analítica Mecánica lagrangiana Mecánica hamiltoniana Mecánica de Routh Ecuación de Hamilton-Jacobi Ecuación de movimiento de Appell Mecánica de Koopman-von Neumann
Temas centrales Mojadura Desplazamiento Ecuaciones de movimiento Leyes del movimiento de Euler Fuerza ficticia Fricción Oscilador armónico Marco de referencia inercial  / no inercial Mecánica del movimiento de partículas planas Movimiento  ( lineal ) Ley de gravitación universal de Newton Leyes del movimiento de Newton Velocidad relativa Cuerpo rígido dinámica Ecuaciones de Euler Movimiento armónico simple Vibración
Rotación Movimiento circular Marco de referencia giratorio Fuerza centrípeta Fuerza centrífuga reactivo Fuerza de Coriolis Péndulo Velocidad tangencial Frecuencia rotacional Aceleración angular  / desplazamiento  / frecuencia  / velocidad
Científicos Kepler Galileo Huygens Newton Horrocas Halley Maupertuis Daniel Bernoulli Juan Bernoulli Euler de Alembert Claro Lagrange Laplace Pescado Hamilton Jacobi Cauchy Rutina Liouville Apelar Gibbs Hombre de negocios de Neumann
Portal de física  Categoría
en a mi

Un momento es una expresión matemática que implica el producto de una distancia y una cantidad física como una fuerza o una carga eléctrica. Los momentos se definen generalmente con respecto a un punto de referencia fijo y se refieren a cantidades físicas ubicadas a cierta distancia del punto de referencia. Por ejemplo, el momento de fuerza, a menudo llamado torque , es el producto de una fuerza sobre un objeto y la distancia desde el punto de referencia hasta el objeto. En principio, cualquier cantidad física se puede multiplicar por una distancia para producir un momento. Las cantidades que se usan comúnmente incluyen fuerzas, masas y distribuciones de carga eléctrica ; se proporciona una lista de ejemplos más adelante.

En su forma más básica, un momento es el producto de la distancia a un punto, elevado a una potencia, y una cantidad física (como fuerza o carga eléctrica) en ese punto:

${\displaystyle \mu _{n}=r^{n}\,Q,}$

donde es la cantidad física tal como una fuerza aplicada en un punto, o una carga puntual, o una masa puntual, etc. Si la cantidad no está concentrada únicamente en un único punto, el momento es la integral de la densidad de esa cantidad en el espacio:${\displaystyle Q}$

${\displaystyle \mu _{n}=\int r^{n}\rho (r)\,dr}$

¿Dónde está la distribución de la densidad de carga, masa o cualquier cantidad que se esté considerando?${\displaystyle \rho }$

Las formas más complejas tienen en cuenta las relaciones angulares entre la distancia y la cantidad física, pero las ecuaciones anteriores capturan la característica esencial de un momento, es decir, la existencia de un término subyacente o equivalente. Esto implica que existen múltiples momentos (uno para cada valor de n ) y que el momento generalmente depende del punto de referencia desde el que se mide la distancia, aunque para ciertos momentos (técnicamente, el momento más bajo distinto de cero) esta dependencia desaparece y el momento se vuelve independiente del punto de referencia.${\displaystyle r^{n}\rho (r)}$${\displaystyle r}$

Cada valor de n corresponde a un momento diferente: el primer momento corresponde a n  = 1; el segundo momento a n  = 2, etc. El momento 0 ( n  = 0) a veces se denomina momento monopolar ; el primer momento ( n  = 1) a veces se denomina momento dipolar , y el segundo momento ( n  = 2) a veces se denomina momento cuadrupolar , especialmente en el contexto de distribuciones de carga eléctrica.

• El momento de fuerza , o torque , es un primer momento: , o, más generalmente, .${\displaystyle \mathbf {\tau } =rF}$${\displaystyle \mathbf {r} \times \mathbf {F} }$
• De manera similar, el momento angular es el primer momento del momento : . El momento en sí no es un momento.${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }$
• El momento dipolar eléctrico es también un 1er momento: para dos cargas puntuales opuestas o para una carga distribuida con densidad de carga .${\displaystyle \mathbf {p} =q\,\mathbf {d} }$${\textstyle \int \mathbf {r} \,\rho (\mathbf {r} )\,d^{3}r}$${\displaystyle \rho (\mathbf {r} )}$

Momentos de misa:

• La masa total es el momento cero de masa.
• El centro de masa es el primer momento de masa normalizado por la masa total: para una colección de masas puntuales o para un objeto con distribución de masa .${\textstyle \mathbf {R} ={\frac {1}{M}}\sum _{i}\mathbf {r} _{i}m_{i}}$${\textstyle {\frac {1}{M}}\int \mathbf {r} \rho (\mathbf {r} )\,d^{3}r}$${\displaystyle \rho (\mathbf {r} )}$
• El momento de inercia es el segundo momento de masa: para una masa puntual, para un conjunto de masas puntuales o para un objeto con distribución de masa . El centro de masa se toma a menudo (pero no siempre) como punto de referencia.${\displaystyle I=r^{2}m}$${\textstyle \sum _{i}r_{i}^{2}m_{i}}$${\textstyle \int r^{2}\rho (\mathbf {r} )\,d^{3}r}$${\displaystyle \rho (\mathbf {r} )}$

Suponiendo una función de densidad finita y localizada en una región particular, fuera de esa región un potencial 1/ r puede expresarse como una serie de armónicos esféricos :

${\displaystyle \Phi (\mathbf {r} )=\int {\frac {\rho (\mathbf {r'} )}{|\mathbf {r} -\mathbf {r'} |}}\,d^{3}r'=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left({\frac {4\pi }{2\ell +1}}\right)q_{\ell m}\,{\frac {Y_{\ell m}(\theta ,\varphi )}{r^{\ell +1}}}}$

Los coeficientes se conocen como momentos multipolares y toman la forma:${\displaystyle q_{\ell m}}$

${\displaystyle q_{\ell m}=\int (r')^{\ell }\,\rho (\mathbf {r'} )\,Y_{\ell m}^{*}(\theta ',\varphi ')\,d^{3}r'}$

donde expresado en coordenadas esféricas es una variable de integración. Se puede encontrar un tratamiento más completo en las páginas que describen la expansión multipolar o los momentos multipolares esféricos . (La convención en las ecuaciones anteriores se tomó de Jackson ^[1] ; las convenciones utilizadas en las páginas a las que se hace referencia pueden ser ligeramente diferentes).${\displaystyle \mathbf {r} '}$${\displaystyle \left(r',\varphi ',\theta '\right)}$

Cuando representa una densidad de carga eléctrica, las son, en cierto sentido, proyecciones de los momentos de carga eléctrica: es el momento monopolar; las son proyecciones del momento dipolar, las son proyecciones del momento cuadrupolar, etc.${\displaystyle \rho }$${\displaystyle q_{lm}}$${\displaystyle q_{00}}$${\displaystyle q_{1m}}$${\displaystyle q_{2m}}$

La expansión multipolar se aplica a potenciales escalares 1/ r , entre los que se incluyen el potencial eléctrico y el potencial gravitatorio . Para estos potenciales, la expresión se puede utilizar para aproximar la intensidad de un campo producido por una distribución localizada de cargas (o masa) calculando los primeros momentos. Para valores de r suficientemente grandes , se puede obtener una aproximación razonable a partir de los momentos monopolar y dipolar. Se puede lograr una mayor fidelidad calculando momentos de orden superior. Se pueden utilizar extensiones de la técnica para calcular energías de interacción y fuerzas intermoleculares.

La técnica también se puede utilizar para determinar las propiedades de una distribución desconocida . Se pueden tomar medidas relativas a los momentos multipolares y utilizarlas para inferir las propiedades de la distribución subyacente. Esta técnica se aplica a objetos pequeños como las moléculas, ^{[2] [3]} pero también se ha aplicado al propio universo, ^[4] siendo por ejemplo la técnica empleada por los experimentos WMAP y Planck para analizar la radiación de fondo cósmico de microondas .${\displaystyle \rho }$

En obras que se cree que provienen de la Antigua Grecia , el concepto de momento se alude con la palabra ῥοπή ( rhopḗ , lit. "inclinación") y compuestos como ἰσόρροπα ( isorropa , lit. "de inclinaciones iguales"). ^{[5] [6] [7]} El contexto de estas obras es la mecánica y la geometría que involucran la palanca . ^[8] En particular, en las obras existentes atribuidas a Arquímedes , el momento se señala en frases como:

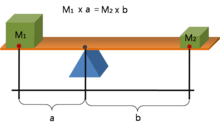
" Las magnitudes conmensurables ( σύμμετρα μεγέθεα ) [A y B] están igualmente equilibradas ( ἰσορροπέοντι ) ^[a] si sus distancias [al centro Γ, es decir, ΑΓ y ΓΒ] son ​​inversamente proporcionales ( ἀντιπεπονθότως ) a sus pesos ( βάρεσιν )." ^{[6] [9]}

Además, en textos existentes como El método de teoremas mecánicos , se utilizan momentos para inferir el centro de gravedad , el área y el volumen de figuras geométricas.

En 1269, Guillermo de Moerbeke traduce varias obras de Arquímedes y Eutócico al latín . El término ῥοπή se transcribe como ropen . ^[6]

Alrededor de 1450, Jacobus Cremonensis traduce ῥοπή en textos similares al término latino momentum ( lit. "movimiento" ^[10] ). ^{[11] [6] : 331} El mismo término se mantiene en una traducción de 1501 de Giorgio Valla , y posteriormente por Francesco Maurolico , Federico Commandino , Guidobaldo del Monte , Adriaan van Roomen , Florence Rivault , Francesco Buonamici , Marin Mersenne ^[5] y Galileo Galilei . Dicho esto, ¿por qué se eligió la palabra momentum para la traducción? Una pista, según Treccani , es que momento en la Italia medieval, el lugar donde vivieron los primeros traductores, en un sentido transferido significaba tanto un "momento de tiempo" como un "momento de peso" (una pequeña cantidad de peso que hace girar la balanza ). ^[b]

En 1554, Francesco Maurolico aclara el término latino momentum en la obra Prologi sive sermones . A continuación se ofrece una traducción del latín al inglés proporcionada por Marshall Clagett : ^[6]

"[...] pesos iguales a distancias desiguales no pesan igual, pero pesos desiguales [a estas distancias desiguales pueden] pesar igual. Porque un peso suspendido a una distancia mayor es más pesado, como es obvio en una balanza . Por lo tanto, existe un tercer tipo de potencia o tercera diferencia de magnitud, una que difiere tanto del cuerpo como del peso, y a esto lo llaman momento . ^[c] Por lo tanto, un cuerpo adquiere peso tanto de la cantidad [es decir, tamaño] como de la calidad [es decir, material], pero un peso recibe su momento de la distancia a la que está suspendido. Por lo tanto, cuando las distancias son recíprocamente proporcionales a los pesos, los momentos [de los pesos] son ​​iguales, como demostró Arquímedes en El libro de los momentos iguales . ^[d] Por lo tanto, los pesos o [más bien] los momentos como otras cantidades continuas, se unen en algún término común, es decir, en algo común a ambos como el centro de peso, o en un punto de equilibrio. Ahora bien, el centro de gravedad de cualquier peso es ese punto que, sin importar con qué frecuencia o cuando sea que se mueva, se mueve. El cuerpo está suspendido, siempre inclinado perpendicularmente hacia el centro universal.

"Además del cuerpo, el peso y el momento, existe una cuarta potencia, que puede llamarse impulso o fuerza. ^[e] Aristóteles la investiga en Sobre las cuestiones mecánicas , y es completamente diferente de [las] ​​tres [potencias o magnitudes] mencionadas. [...]"

En 1586, Simon Stevin utiliza el término holandés staltwicht ("peso estacionado") para referirse al momento en De Beghinselen Der Weeghconst .

En 1632, Galileo Galilei publica el Diálogo sobre los dos principales sistemas del mundo y utiliza el término italiano momento con muchos significados, incluido el de sus predecesores. ^[12]

En 1643, Thomas Salusbury traduce algunas de las obras de Galileo al inglés . Salusbury traduce el término latino momentum y el italiano momento al término inglés moment . ^[f]

En 1765, el término latino momentum inertiae ( en español : momento de inercia ) es utilizado por Leonhard Euler para referirse a una de las magnitudes de Christiaan Huygens en Horologium Oscillatorium . ^[13] El trabajo de Huygens de 1673 que implicaba encontrar el centro de oscilación había sido estimulado por Marin Mersenne , quien se lo sugirió en 1646. ^{[14] [15]}

En 1811, el término francés moment d'une force ( en español : momento de una fuerza ) con respecto a un punto y un plano es utilizado por Siméon Denis Poisson en Traité de mécanique . ^[16] Una traducción al inglés aparece en 1842.

En 1884, el término torque es sugerido por James Thomson en el contexto de la medición de fuerzas rotacionales de máquinas (con hélices y rotores ). ^{[17] [18]} Hoy en día, se utiliza un dinamómetro para medir el torque de las máquinas.

En 1893, Karl Pearson utiliza el término momento n-ésimo en el contexto de las mediciones científicas de ajuste de curvas . ^[19] Pearson escribió en respuesta a John Venn , quien, algunos años antes, observó un patrón peculiar que involucraba datos meteorológicos y pidió una explicación de su causa. ^[20] En la respuesta de Pearson, se utiliza esta analogía: el "centro de gravedad" mecánico es la media y la "distancia" es la desviación de la media. Esto luego evolucionó a momentos en matemáticas . La analogía entre el concepto mecánico de un momento y la función estadística que involucra la suma de las n- ésimas potencias de las desviaciones fue notada por varios antes, incluidos Laplace , Kramp , Gauss , Encke , Czuber , Quetelet y De Forest . ^[21]${\displaystyle \mu _{n}}$

• Par (o momento de fuerza ), véase también el artículo par (mecánica)
• Momento (matemáticas)
• Equilibrio mecánico , se aplica cuando un objeto está equilibrado de manera que la suma de los momentos en el sentido de las agujas del reloj alrededor de un pivote es igual a la suma de los momentos en el sentido contrario a las agujas del reloj alrededor del mismo pivote.
• Momento de inercia , análogo a la masa en las discusiones sobre el movimiento rotacional. Es una medida de la resistencia de un objeto a los cambios en su velocidad de rotación.${\displaystyle \left(I=\Sigma mr^{2}\right)}$
• Momento de momento , el análogo rotacional del momento lineal .${\displaystyle (\mathbf {L} =\mathbf {r} \times m\mathbf {v} )}$
• Momento magnético , momento dipolar que mide la fuerza y ​​la dirección de una fuente magnética.${\displaystyle \left(\mathbf {\mu } =I\mathbf {A} \right)}$
• Momento dipolar eléctrico , momento dipolar que mide la diferencia de carga y la dirección entre dos o más cargas. Por ejemplo, el momento dipolar eléctrico entre una carga de – q y q separadas por una distancia de d es${\displaystyle (\mathbf {p} =q\mathbf {d} )}$
• Momento flector , momento que produce la flexión de un elemento estructural.
• Primer momento del área , una propiedad de un objeto relacionada con su resistencia al esfuerzo cortante.
• Segundo momento del área , una propiedad de un objeto relacionada con su resistencia a la flexión y la deflexión.
• Momento polar de inercia , propiedad de un objeto relacionada con su resistencia a la torsión.
• Momentos de la imagen , propiedades estadísticas de una imagen
• Momento sísmico , magnitud utilizada para medir la magnitud de un terremoto.
• Momentos plasmáticos , descripción fluida del plasma en términos de densidad, velocidad y presión.
• Lista de momentos de inercia del área
• Lista de momentos de inercia
• Expansión multipolar
• Momentos multipolares esféricos

Busque momento en Wikcionario, el diccionario libre.

• Medios relacionados con Momento (física) en Wikimedia Commons
• [1] Una definición de diccionario de momento.