Estimación máxima a posteriori

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Estimación máxima a posteriori» – noticias  · periódicos  · libros  · académico  · JSTOR ( septiembre de 2011 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Parte de una serie sobre
Estadísticas bayesianas
Posterior = Probabilidad × Anterior ÷ Evidencia
Fondo
Inferencia bayesiana Probabilidad bayesiana Teorema de Bayes Teorema de Bernstein-von Mises Coherencia Teorema de Cox El gobierno de Cromwell Principio de verosimilitud Principio de indiferencia Principio de máxima entropía
Construcción de modelos
Conjugado anterior Regresión lineal Bayes empírico Modelo jerárquico
Aproximación posterior
Cadena de Markov Monte Carlo Aproximación de Laplace Aproximaciones de Laplace anidadas integradas Inferencia variacional Cálculo bayesiano aproximado
Estimadores
Estimador bayesiano Intervalo creíble Estimación máxima a posteriori
Aproximación de evidencia
Límite inferior de evidencia Muestreo anidado
Evaluación del modelo
Factor de Bayes ( criterio de Schwarz ) Promedio del modelo Predicción posterior
Portal de matemáticas
en a mi

En estadística bayesiana , una estimación de probabilidad a posteriori máxima ( MAP ) es una estimación de una cantidad desconocida, que es igual a la moda de la distribución posterior . La MAP se puede utilizar para obtener una estimación puntual de una cantidad no observada sobre la base de datos empíricos. Está estrechamente relacionada con el método de estimación de máxima verosimilitud (ML), pero emplea un objetivo de optimización aumentada que incorpora una distribución previa (que cuantifica la información adicional disponible a través del conocimiento previo de un evento relacionado) sobre la cantidad que se desea estimar. Por lo tanto, la estimación MAP puede verse como una regularización de la estimación de máxima verosimilitud.

Supongamos que queremos estimar un parámetro de población no observado sobre la base de observaciones . Sea , la distribución de muestreo de , de modo que sea la probabilidad de cuando el parámetro de población subyacente sea . Entonces, la función:${\estilo de visualización \theta}$${\estilo de visualización x}$${\estilo de visualización f}$${\estilo de visualización x}$${\displaystyle f(x\mid \theta )}$${\estilo de visualización x}$${\estilo de visualización \theta}$

${\displaystyle \theta \mapsto f(x\mid \theta )\!}$

se conoce como función de verosimilitud y la estimación:

${\displaystyle {\hat {\theta }}_{\mathrm {MLE} }(x)={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta ) \!}$

es la estimación de máxima verosimilitud de .${\estilo de visualización \theta}$

Supongamos ahora que existe una distribución previa sobre . Esto nos permite tratarla como una variable aleatoria como en la estadística bayesiana . Podemos calcular la distribución posterior de utilizando el teorema de Bayes :${\estilo de visualización g}$${\estilo de visualización \theta}$${\estilo de visualización \theta}$${\estilo de visualización \theta}$

${\displaystyle \theta \mapsto f(\theta \mid x)={\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\ mid \vartheta )\,g(\vartheta )\,d\vartheta }}\!}$

donde es la función de densidad de , es el dominio de .${\estilo de visualización g}$${\estilo de visualización \theta}$${\estilo de visualización \Theta}$${\estilo de visualización g}$

El método de estimación máxima a posteriori estima entonces como moda de la distribución posterior de esta variable aleatoria:${\estilo de visualización \theta}$

${\displaystyle {\begin{aligned}{\hat {\theta }}_{\mathrm {MAP} }(x)&={\underset {\theta }{\operatorname {arg\,max} }}\ f(\theta \mid x)\\&={\underset {\theta }{\operatorname {arg\,max} }}\ {\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\mid \vartheta )\,g(\vartheta )\,d\vartheta }}\\&={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta )\,g(\theta ).\end{aligned}}\!}$

El denominador de la distribución posterior (denominado verosimilitud marginal ) es siempre positivo y no depende de la optimización y, por lo tanto, no desempeña ningún papel en ella. Observe que la estimación MAP de coincide con la estimación ML cuando la distribución previa es uniforme (es decir, es una función constante ).${\displaystyle \theta }$${\displaystyle \theta }$${\displaystyle g}$${\displaystyle g}$

Cuando la función de pérdida es de la forma

${\displaystyle L(\theta ,a)={\begin{cases}0,&{\text{if }}|a-\theta |<c,\\1,&{\text{otherwise}},\\\end{cases}}}$

a medida que tiende a 0, el estimador de Bayes se aproxima al estimador MAP, siempre que la distribución de sea cuasi cóncava. ^[1] Pero, en general, un estimador MAP no es un estimador de Bayes a menos que sea discreto .${\displaystyle c}$${\displaystyle \theta }$${\displaystyle \theta }$

Las estimaciones de MAP se pueden calcular de varias maneras:

1. Analíticamente, cuando la(s) moda(s) de la distribución posterior se puede(n) dar en forma cerrada . Este es el caso cuando se utilizan valores a priori conjugados .
2. Mediante optimización numérica , como el método del gradiente conjugado o el método de Newton . Esto suele requerir derivadas primeras o segundas , que deben evaluarse analítica o numéricamente.
3. Mediante una modificación de un algoritmo de maximización de expectativas . Esto no requiere derivadas de la densidad posterior.
4. Mediante un método de Monte Carlo utilizando recocido simulado

Aunque solo se requieren condiciones leves para que la estimación MAP sea un caso límite de la estimación bayesiana (bajo la función de pérdida 0-1), ^[1] no es muy representativa de los métodos bayesianos en general. Esto se debe a que las estimaciones MAP son estimaciones puntuales, mientras que los métodos bayesianos se caracterizan por el uso de distribuciones para resumir datos y extraer inferencias: por lo tanto, los métodos bayesianos tienden a informar la media o mediana posterior en su lugar, junto con intervalos creíbles . Esto se debe a que estos estimadores son óptimos bajo la pérdida de error cuadrático y error lineal respectivamente, que son más representativos de las funciones de pérdida típicas , y para una distribución posterior continua no hay una función de pérdida que sugiera que MAP es el estimador puntual óptimo. Además, la distribución posterior a menudo puede no tener una forma analítica simple: en este caso, la distribución se puede simular utilizando técnicas de Monte Carlo de cadena de Markov , mientras que la optimización para encontrar su(s) modo(s) puede ser difícil o imposible. ^{[ cita requerida ]}

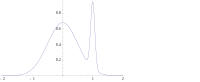
En muchos tipos de modelos, como los modelos de mezcla , la variable posterior puede ser multimodal . En tal caso, la recomendación habitual es que se elija la moda más alta: esto no siempre es factible ( la optimización global es un problema difícil), ni siquiera es posible en algunos casos (como cuando surgen problemas de identificabilidad ). Además, la moda más alta puede no ser característica de la mayoría de la variable posterior.

Por último, a diferencia de los estimadores ML, la estimación MAP no es invariante bajo la reparametrización. Pasar de una parametrización a otra implica introducir un jacobiano que afecta la ubicación del máximo. ^[2]

Como ejemplo de la diferencia entre los estimadores de Bayes mencionados anteriormente (estimadores de media y mediana) y el uso de una estimación MAP, considere el caso en el que existe la necesidad de clasificar las entradas como positivas o negativas (por ejemplo, préstamos como riesgosos o seguros). Suponga que solo hay tres hipótesis posibles sobre el método correcto de clasificación , y con posteriores 0,4, 0,3 y 0,3 respectivamente. Suponga que dada una nueva instancia, , la clasifica como positiva, mientras que las otras dos la clasifican como negativa. Usando la estimación MAP para el clasificador correcto , se clasifica como positivo, mientras que los estimadores de Bayes promediarían todas las hipótesis y la clasificarían como negativa.${\displaystyle x}$${\displaystyle h_{1}}$${\displaystyle h_{2}}$${\displaystyle h_{3}}$${\displaystyle x}$${\displaystyle h_{1}}$${\displaystyle h_{1}}$${\displaystyle x}$${\displaystyle x}$

Supongamos que se nos da una secuencia de variables aleatorias IID y una distribución a priori de está dada por . Deseamos encontrar la estimación MAP de . Tenga en cuenta que la distribución normal es su propia distribución a priori conjugada , por lo que podremos encontrar una solución de forma cerrada analíticamente.${\displaystyle (x_{1},\dots ,x_{n})}$ ${\displaystyle N(\mu ,\sigma _{v}^{2})}$ ${\displaystyle \mu }$${\displaystyle N(\mu _{0},\sigma _{m}^{2})}$${\displaystyle \mu }$

La función a maximizar viene dada entonces por ^[3]

${\displaystyle g(\mu )f(x\mid \mu )=\pi (\mu )L(\mu )={\frac {1}{{\sqrt {2\pi }}\sigma _{m}}}\exp \left(-{\frac {1}{2}}\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}\right)\prod _{j=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma _{v}}}\exp \left(-{\frac {1}{2}}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}\right),}$

lo que equivale a minimizar la siguiente función de :${\displaystyle \mu }$

${\displaystyle \sum _{j=1}^{n}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}+\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}.}$

Así, vemos que el estimador MAP para μ está dado por ^[3]

${\displaystyle {\hat {\mu }}_{\mathrm {MAP} }={\frac {\sigma _{m}^{2}\,n}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\left({\frac {1}{n}}\sum _{j=1}^{n}x_{j}\right)+{\frac {\sigma _{v}^{2}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\,\mu _{0}={\frac {\sigma _{m}^{2}\left(\sum _{j=1}^{n}x_{j}\right)+\sigma _{v}^{2}\,\mu _{0}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}.}$

que resulta ser una interpolación lineal entre la media anterior y la media de la muestra ponderada por sus respectivas covarianzas.

El caso de se llama prior no informativo y conduce a una distribución de probabilidad impropia ; en este caso${\displaystyle \sigma _{m}\to \infty }$${\displaystyle {\hat {\mu }}_{\mathrm {MAP} }\to {\hat {\mu }}_{\mathrm {MLE} }.}$

• DeGroot, M. (1970). Decisiones estadísticas óptimas . McGraw-Hill. ISBN 0-07-016242-5.
• Sorenson, Harold W. (1980). Estimación de parámetros: principios y problemas . Marcel Dekker. ISBN 0-8247-6987-2.
• Hald, Anders (2007). "Derivación de la distribución normal y el método de mínimos cuadrados de Gauss, 1809". Una historia de la inferencia estadística paramétrica desde Bernoulli hasta Fisher, 1713-1935 . Nueva York: Springer. págs. 55-61. ISBN 978-0-387-46409-1.