Armónico

Onda con frecuencia múltiplo entero de la frecuencia fundamental

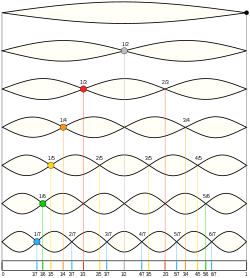
En física , acústica y telecomunicaciones , un armónico es una onda sinusoidal con una frecuencia que es un múltiplo entero positivo de la frecuencia fundamental de una señal periódica . La frecuencia fundamental también se denomina 1.er armónico ; los demás armónicos se conocen como armónicos superiores . Como todos los armónicos son periódicos en la frecuencia fundamental, la suma de armónicos también es periódica en esa frecuencia. El conjunto de armónicos forma una serie armónica .

El término se emplea en diversas disciplinas, entre ellas la música, la física, la acústica , la transmisión de energía electrónica, la tecnología de radio y otros campos. Por ejemplo, si la frecuencia fundamental es 50 Hz , una frecuencia de suministro de energía de CA común , las frecuencias de los primeros tres armónicos superiores son 100 Hz (2.º armónico), 150 Hz (3.º armónico), 200 Hz (4.º armónico) y cualquier adición de ondas con estas frecuencias es periódica a 50 Hz.

Un modo característico n ^-ésimo , para n > 1, tendrá nodos que no estén vibrando. Por ejemplo, el tercer modo característico tendrá nodos en L y L , donde L es la longitud de la cuerda. De hecho, cada modo característico n- ^ésimo , para n no múltiplo de 3, no tendrá nodos en estos puntos. Estos otros modos característicos vibrarán en las posiciones L y L . Si el ejecutante toca suavemente una de estas posiciones, estos otros modos característicos se suprimirán. Los armónicos tonales de estos otros modos característicos también se suprimirán. En consecuencia, los armónicos tonales de los modos característicos n ^-ésimos , donde n es múltiplo de 3, se harán relativamente más prominentes. ^[1] ${\frac {1}{3}}$ ${\frac {2}{3}}$ ${\frac {1}{3}}$ ${\frac {2}{3}}$

En música, los armónicos se utilizan en instrumentos de cuerda y de viento como una forma de producir sonido en el instrumento, en particular para tocar notas más altas y, con las cuerdas, obtener notas que tienen una calidad de sonido única o "color de tono". En las cuerdas, los armónicos tocados con arco tienen un tono "vidrioso", puro. En los instrumentos de cuerda, los armónicos se tocan tocando (pero sin presionar completamente la cuerda) en un punto exacto de la cuerda mientras se hace sonar la cuerda (pulsando, tocando con el arco, etc.); esto permite que el armónico suene, un tono que siempre es más alto que la frecuencia fundamental de la cuerda.

Terminología

Los armónicos pueden denominarse "sobretonos", "parciales" o "parciales superiores" y, en algunos contextos musicales, los términos "armónico", "sobretono" y "parcial" se utilizan de forma bastante intercambiable. Pero, más precisamente, el término "armónico" incluye todos los tonos de una serie armónica (incluida la frecuencia fundamental), mientras que el término "sobretono" solo incluye los tonos superiores a la fundamental.

Características

Un carácter tonal silbante y zumbante distingue todos los armónicos, tanto naturales como artificiales, de los intervalos firmemente detenidos; por lo tanto, su aplicación en conexión con estos últimos siempre debe considerarse con cuidado. ^{[ cita requerida ]}
— Richard Scholz ( c. 1888-1912 ) ^[2]

La mayoría de los instrumentos acústicos emiten tonos complejos que contienen muchos parciales individuales (tonos simples componentes u ondas sinusoidales), pero el oído humano inexperto normalmente no percibe esos parciales como fenómenos separados. Más bien, una nota musical se percibe como un sonido, siendo la calidad o timbre de ese sonido el resultado de las intensidades relativas de los parciales individuales. Muchos osciladores acústicos , como la voz humana o una cuerda de violín frotada , producen tonos complejos que son más o menos periódicos y, por lo tanto, están compuestos de parciales que casi coinciden con los múltiplos enteros de la frecuencia fundamental y, por lo tanto, se parecen a los armónicos ideales y se denominan "parciales armónicos" o simplemente "armónicos" por conveniencia (aunque no es estrictamente preciso llamar a un parcial un armónico , siendo el primero real y el segundo teórico).

Los osciladores que producen armónicos parciales se comportan de manera similar a los resonadores unidimensionales y, a menudo, son largos y delgados, como una cuerda de guitarra o una columna de aire abierta en ambos extremos (como en la flauta transversal de orquesta moderna metálica ). Los instrumentos de viento cuya columna de aire está abierta solo en un extremo, como las trompetas y los clarinetes , también producen armónicos parciales similares a los armónicos impares. Sin embargo, solo producen armónicos parciales que coinciden con los armónicos impares , al menos en teoría. En el uso práctico, ningún instrumento acústico real se comporta tan perfectamente como predicen los modelos físicos simplificados; por ejemplo, los instrumentos hechos de madera elástica no lineal , en lugar de metal, o encordados con tripa en lugar de cuerdas de latón o acero , tienden a tener armónicos parciales no del todo enteros.

Los parciales cuyas frecuencias no son múltiplos enteros de la fundamental se denominan parciales inarmónicos . Algunos instrumentos acústicos emiten una mezcla de parciales armónicos e inarmónicos pero aún producen un efecto en el oído de tener un tono fundamental definido, como pianos , cuerdas pulsadas pizzicato , vibráfonos, marimbas y ciertas campanas o carillones de sonido puro. Los cuencos cantores antiguos son conocidos por producir múltiples parciales armónicos o multifónicos . ^[3]^[4] Otros osciladores, como platillos , parches de tambor y la mayoría de los instrumentos de percusión, producen naturalmente una abundancia de parciales inarmónicos y no implican ningún tono en particular, y por lo tanto no se pueden usar melódicamente o armónicamente de la misma manera que otros instrumentos.

Basándose en Sethares (2004), ^[5] la tonalidad dinámica introduce la noción de parciales pseudoarmónicos, en los que la frecuencia de cada parcial se alinea para que coincida con el tono de una nota correspondiente en una afinación pseudo-justa, maximizando así la consonancia de ese timbre pseudoarmónico con las notas de esa afinación pseudo-justa. ^[6]^[7]^[8]^[9]

Parciales, sobretonos y armónicos

Un sobretono es cualquier parte más alta que la parte más baja de un tono compuesto. Las relaciones de fuerza y frecuencia relativas de las partes componentes determinan el timbre de un instrumento. La similitud entre los términos sobretono y parte a veces hace que se utilicen indistintamente en un contexto musical , pero se cuentan de forma diferente, lo que puede dar lugar a cierta confusión. En el caso especial de los timbres instrumentales cuyos partes componentes coinciden estrechamente con una serie armónica (como ocurre con la mayoría de los instrumentos de cuerda y viento) en lugar de ser partes inarmónicas (como ocurre con la mayoría de los instrumentos de percusión de tono alto ), también es conveniente llamar a las partes componentes "armónicos", pero no es estrictamente correcto, porque los armónicos se numeran de la misma manera incluso cuando faltan, mientras que las partes y los sobretonos solo se cuentan cuando están presentes. Este cuadro demuestra cómo se cuentan los tres tipos de nombres (parcial, sobretono y armónico) (suponiendo que los armónicos están presentes):

Frecuencia	Orden ( $n$ )	Nombre 1	Nombre 2	Nombre 3
1 × $f$ = 0 440 Hz	$n$ = 1	1er parcial	tono fundamental	1er armónico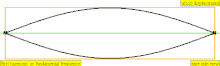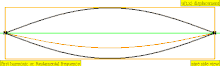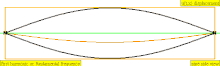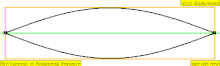
2 × $f$ = 0 880 Hz	$n$ = 2	2do parcial	1er armónico	2do armónico
3 × $f$ = 1320 Hz	$n$ = 3	3er parcial	2do armónico	3er armónico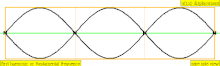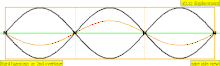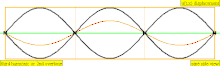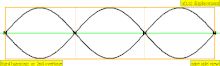
4 × $f$ = 1760 Hz	$n$ = 4	4to parcial	3er armónico	4to armónico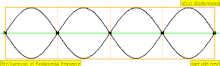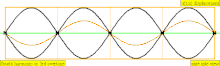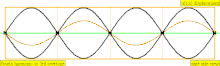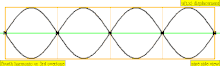

En muchos instrumentos musicales , es posible tocar los armónicos superiores sin que esté presente la nota fundamental. En un caso simple (por ejemplo, la flauta dulce ), esto tiene el efecto de hacer que la nota suba de tono una octava , pero en casos más complejos se obtienen muchas otras variaciones de tono. En algunos casos, también cambia el timbre de la nota. Esto es parte del método normal para obtener notas más altas en instrumentos de viento , donde se llama sobresoplado . La técnica extendida de tocar multifónicos también produce armónicos. En los instrumentos de cuerda, es posible producir notas de sonido muy puro, llamadas armónicos o flageolets por los intérpretes de cuerda, que tienen una calidad inquietante, además de ser de tono alto. Los armónicos se pueden usar para verificar al unísono la afinación de cuerdas que no están afinadas al unísono. Por ejemplo, tocar ligeramente el nodo que se encuentra a la mitad de la cuerda más alta de un violonchelo produce el mismo tono que tocar ligeramente el nodo 1 /3⁠ del camino hacia abajo en la segunda cuerda más alta. Para la voz humana, véase el canto de armónicos , que utiliza armónicos.

Si bien es cierto que los tonos periódicos producidos electrónicamente (por ejemplo, ondas cuadradas u otras ondas no sinusoidales) tienen "armónicos" que son múltiplos enteros de la frecuencia fundamental, no todos los instrumentos prácticos tienen esta característica. Por ejemplo, los "armónicos" más altos de las notas del piano no son armónicos verdaderos sino "sobretonos" y pueden ser muy agudos, es decir, una frecuencia más alta que la dada por una serie armónica pura . Esto es especialmente cierto para instrumentos que no sean de cuerda , metal o viento . Ejemplos de estos "otros" instrumentos son los xilófonos, tambores, campanas, carillones, etc.; no todas sus frecuencias de sobretonos forman una simple relación de números enteros con la frecuencia fundamental. (La frecuencia fundamental es el recíproco del período de tiempo más largo de la colección de vibraciones en algún fenómeno periódico único. ^[10] )

Sobre instrumentos de cuerda

Los armónicos pueden producirse individualmente [en instrumentos de cuerda] (1) variando el punto de contacto con el arco, o (2) presionando ligeramente la cuerda en los nodos, o divisiones de sus partes alícuotas ( , , , etc.). (1) En el primer caso, avanzando el arco desde el lugar habitual donde se produce la nota fundamental, hacia el puente, se puede producir toda la escala de armónicos en sucesión, en un instrumento antiguo y muy resonante. El empleo de este medio produce el efecto llamado ' sul ponticello '. (2) La producción de armónicos mediante la ligera presión del dedo sobre la cuerda al aire es más útil. Cuando se producen presionando ligeramente sobre los diversos nodos de las cuerdas al aire se denominan 'armónicos naturales'. ... Los violinistas saben bien que cuanto más larga sea la cuerda en proporción a su grosor, mayor será el número de armónicos superiores que puede producir. ${\frac {\ 1\ }{2}}$ ${\frac {\ 1\ }{3}}$ ${\frac {\ 1\ }{4}}$
— Diccionario de música y músicos de Grove (1879) ^[11]

La siguiente tabla muestra los puntos de parada en un instrumento de cuerda en los que un toque suave de una cuerda la obligará a entrar en un modo armónico cuando vibre. Los armónicos de cuerda (tonos de flauta) se describen como que tienen una "calidad plateada similar a la de una flauta" que puede ser muy eficaz como un color especial o color de tono ( timbre ) cuando se usa y se escucha en orquestación . ^[12] Es inusual encontrar armónicos naturales más altos que el quinto parcial en cualquier instrumento de cuerda, excepto el contrabajo, debido a que sus cuerdas son mucho más largas. ^[12]

Armónico	Nota de parada	Nota sonada (en relación con la cuerda al aire)	Frecuencia de audio ( Hz )	Cents por encima del fundamental (desplazado por octava)	Audio (desplazado por octava)
1	fundamental , unísono perfecto	P1	600	0.0	Jugar ^ⓘ
2	primera octava perfecta	P8	1.200	0.0	Jugar ^ⓘ
3	quinta perfecta	P8 + P5	1.800	702.0	Jugar ^ⓘ
4	octava perfecta duplicada	2·P8	2.400	0.0	Jugar ^ⓘ
5	solo tercera mayor , tercera mayor	2·P8 + M3	3.000	386.3	Jugar ^ⓘ
6	quinta perfecta	2·P8 + P5	3.600	702.0	Jugar ^ⓘ
7	séptima armónica , séptima menor septimal ('el acorde perdido')	2·P8 + m7↓	4.200	968.8	Jugar ^ⓘ
8	tercera octava perfecta	3·P8	4.800	0.0	Jugar ^ⓘ
9	Novena armónica mayor pitagórica de segunda generación	3·P8+M2	5.400	203.9	Jugar ^ⓘ
10	Sólo tercera mayor	3·P8+M3	6.000	386.3	Jugar ^ⓘ
11	Tritono indecimal menor , cuarta semiaumentada indecimal	3·P8 + a4	6.600	551.3	Jugar ^ⓘ
12	quinta perfecta	3·P8 + P5	7.200	702.0	Jugar ^ⓘ
13	Sexto neutro tridecimal	3·P8 + n6 ↓	7.800	840.5	Jugar ^ⓘ
14	séptima armónica , séptima menor septimal ('el acorde perdido')	3·P8 + m7⤈	8.400	968.8	Jugar ^ⓘ
15	Sólo séptima mayor	3·P8 + M7	9.000	1.088,3	Jugar ^ⓘ
16	cuarta octava perfecta	4·P8	9.600	0.0	Jugar ^ⓘ
17	semitono septidecimales	4·P8+m2⇟	10.200	105.0	Jugar ^ⓘ
18	Segunda mayor pitagórica	4·P8+M2	10.800	203.9	Jugar ^ⓘ
19	nanodecimal tercera menor	4·P8+m3	11.400	297,5	Jugar ^ⓘ
20	Sólo tercera mayor	4·P8 + M3	12.000	386.3	Jugar ^ⓘ

Armónicos artificiales

En ocasiones, una partitura requerirá un armónico artificial , que se produce tocando un sobretono en una cuerda que ya está parada. Como técnica de interpretación, se logra utilizando dos dedos en el diapasón, el primero para acortar la cuerda hasta la nota fundamental deseada y el segundo tocando el nodo correspondiente al armónico apropiado.

Otra información

Los armónicos pueden utilizarse en sistemas de entonación justa o considerarse como la base de los mismos . El compositor Arnold Dreyblatt es capaz de crear diferentes armónicos en la cuerda única de su contrabajo modificado modificando ligeramente su técnica única de arco a medio camino entre el golpe y el arco en las cuerdas. El compositor Lawrence Ball utiliza armónicos para generar música electrónicamente.

Véase también

Armónicos del violín

Puntos de parada armónicos naturales del violín en la cuerda A

Armónicos 110x16

Demostración de 16 armónicos mediante tonos sinusoidales electrónicos, comenzando con una frecuencia fundamental de 110 Hz, 0,5 s cada una. Nótese que cada armónico se presenta en el mismo nivel de señal que la frecuencia fundamental; los tonos de muestra suenan más fuertes a medida que aumentan de frecuencia.

¿Tiene problemas para reproducir estos archivos? Consulte la ayuda multimedia .

Referencias

^ Walker, Russell (14 de junio de 2019). "Russell Walker" . Grupo de autores . doi :10.1287/7648739e-8e59-466e-82cb-3ded22bbebf6. S2CID 241172832 . Consultado el 21 de diciembre de 2020 .
^ "Categoría:Scholz, Richard". Biblioteca musical Petrucci / Proyecto de biblioteca internacional de partituras musicales (IMSLP) (imslp.org) (subíndice del sitio y minibiografía de Scholz). Canadá . Consultado el 21 de diciembre de 2020 .
^ Galembo, Alexander; Cuddly, Lola L. (2 de diciembre de 1997). "Large grand and small upright pianos". acoustics.org (Nota de prensa). Acoustical Society of America . Archivado desde el original el 2012-02-09 . Consultado el 13 de enero de 2024. Hay muchas formas de empeorar las cosas, pero muy pocas de mejorarlas.— Resumen mínimamente técnico de la investigación sobre acústica de cuerdas presentada en una conferencia; analiza las percepciones de los oyentes sobre los parciales inarmónicos de los pianos.
^ Court, Sophie RA (abril de 1927). " Golo und Genovefa [por] Hanna Rademacher". Books Abroad (reseña de libro). 1 (2): 34–36. doi :10.2307/40043442. ISSN 0006-7431. JSTOR 40043442.
^ Sethares, WA (2004). Afinación, timbre, espectro, escala. Springer. ISBN 978-1852337971– a través de Google Books.
^ Sethares, WA ; Milne, A.; Tiedje, S.; Prechtl, A.; Plamondon, J. (2009). "Herramientas espectrales para tonalidad dinámica y transformación de audio". Computer Music Journal . 33 (2): 71–84. doi : 10.1162/comj.2009.33.2.71 . S2CID 216636537 . Consultado el 20 de septiembre de 2009 .
^ Milne, Andrew; Sethares, William ; Plamondon, James (29 de agosto de 2008). "Afinación de continuos y diseños de teclado" (PDF) . Journal of Mathematics and Music . 2 (1): 1–19. doi :10.1080/17459730701828677. S2CID 1549755. Archivado (PDF) desde el original el 2022-10-09. "URL alternativa" (PDF) . Sitio académico personal de Sethares . Universidad de Wisconsin .
^ Milne, A.; Sethares, WA ; Plamondon, J. (invierno de 2007). "Digitaciones invariantes a lo largo de un continuo de afinación". Computer Music Journal . 31 (4): 15–32. doi : 10.1162/comj.2007.31.4.15 . S2CID 27906745.
^ Milne, A.; Sethares, WA ; Plamondon, J. (2006). X System (PDF) (informe técnico). Thumtronics Inc. . Consultado el 2 de mayo de 2020 .
^ Este artículo incorpora material de dominio público de la Norma Federal 1037C. Administración de Servicios Generales . Archivado desde el original el 22 de enero de 2022.
^ George alike (21 de enero de 2011). "Juegos en línea gratuitos para niños". MyFavoritegamez.com / SciVee.tv . doi :10.4016/26742.01. Archivado desde el original el 14 de febrero de 2021 . Consultado el 21 de diciembre de 2020 .
^ ab Marrocco, W. Thomas (2001). "Kennan, Kent". Oxford Music Online . Oxford University Press. doi :10.1093/gmo/9781561592630.article.14882 . Consultado el 21 de diciembre de 2020 .

Enlaces externos

Las conferencias Feynman sobre física: Armónicos
Armónicos, parciales y sobretonos a partir de la frecuencia fundamental
Chisholm, Hugh , ed. (1911). "Armónica" . Encyclopædia Britannica (11.ª ed.). Cambridge University Press.
Armonía
Escuchar y ver armónicos en un piano

[1] Walker, Russell (14 de junio de 2019). "Russell Walker" . Grupo de autores . doi :10.1287/7648739e-8e59-466e-82cb-3ded22bbebf6. S2CID 241172832 . Consultado el 21 de diciembre de 2020 .

[2] "Categoría:Scholz, Richard". Biblioteca musical Petrucci / Proyecto de biblioteca internacional de partituras musicales (IMSLP) (imslp.org) (subíndice del sitio y minibiografía de Scholz). Canadá . Consultado el 21 de diciembre de 2020 .

[3] Galembo, Alexander; Cuddly, Lola L. (2 de diciembre de 1997). "Large grand and small upright pianos". acoustics.org (Nota de prensa). Acoustical Society of America . Archivado desde el original el 2012-02-09 . Consultado el 13 de enero de 2024. Hay muchas formas de empeorar las cosas, pero muy pocas de mejorarlas.— Resumen mínimamente técnico de la investigación sobre acústica de cuerdas presentada en una conferencia; analiza las percepciones de los oyentes sobre los parciales inarmónicos de los pianos.

[4] Court, Sophie RA (abril de 1927). " Golo und Genovefa [por] Hanna Rademacher". Books Abroad (reseña de libro). 1 (2): 34–36. doi :10.2307/40043442. ISSN 0006-7431. JSTOR 40043442.

[TTSS-5] Sethares, WA (2004). Afinación, timbre, espectro, escala. Springer. ISBN 978-1852337971– a través de Google Books.

[Spectral_Tools-6] Sethares, WA ; Milne, A.; Tiedje, S.; Prechtl, A.; Plamondon, J. (2009). "Herramientas espectrales para tonalidad dinámica y transformación de audio". Computer Music Journal . 33 (2): 71–84. doi : 10.1162/comj.2009.33.2.71 . S2CID 216636537 . Consultado el 20 de septiembre de 2009 .

[Continua-7] Milne, Andrew; Sethares, William ; Plamondon, James (29 de agosto de 2008). "Afinación de continuos y diseños de teclado" (PDF) . Journal of Mathematics and Music . 2 (1): 1–19. doi :10.1080/17459730701828677. S2CID 1549755. Archivado (PDF) desde el original el 2022-10-09. "URL alternativa" (PDF) . Sitio académico personal de Sethares . Universidad de Wisconsin .

[Fingering-8] Milne, A.; Sethares, WA ; Plamondon, J. (invierno de 2007). "Digitaciones invariantes a lo largo de un continuo de afinación". Computer Music Journal . 31 (4): 15–32. doi : 10.1162/comj.2007.31.4.15 . S2CID 27906745.

[X_System-9] Milne, A.; Sethares, WA ; Plamondon, J. (2006). X System (PDF) (informe técnico). Thumtronics Inc. . Consultado el 2 de mayo de 2020 .

[10] Este artículo incorpora material de dominio público de la Norma Federal 1037C. Administración de Servicios Generales . Archivado desde el original el 22 de enero de 2022.

[11] George alike (21 de enero de 2011). "Juegos en línea gratuitos para niños". MyFavoritegamez.com / SciVee.tv . doi :10.4016/26742.01. Archivado desde el original el 14 de febrero de 2021 . Consultado el 21 de diciembre de 2020 .

[Marroco-2001-12] Marrocco, W. Thomas (2001). "Kennan, Kent". Oxford Music Online . Oxford University Press. doi :10.1093/gmo/9781561592630.article.14882 . Consultado el 21 de diciembre de 2020 .