Cinética enzimática
Estudio de las velocidades de reacción bioquímica catalizada por una enzima.

Dihidrofolato reductasa de E. coli con sus dos sustratos dihidrofolato (derecha) y NADPH (izquierda), unidos en el sitio activo. La proteína se muestra como un diagrama de cintas , con hélices alfa en rojo, vainas beta en amarillo y bucles en azul. ( PDB : 7DFR ​)

La cinética enzimática es el estudio de las velocidades de las reacciones químicas catalizadas por enzimas . En la cinética enzimática, se mide la velocidad de reacción y se investigan los efectos de la variación de las condiciones de la reacción. Estudiar la cinética de una enzima de esta manera puede revelar el mecanismo catalítico de esta enzima, su papel en el metabolismo , cómo se controla su actividad y cómo un fármaco o un modificador ( inhibidor o activador ) podría afectar la velocidad.

Una enzima (E) es una molécula de proteína que sirve como catalizador biológico para facilitar y acelerar una reacción química en el cuerpo. Lo hace mediante la unión de otra molécula, su sustrato (S), sobre la que actúa la enzima para formar el producto deseado. El sustrato se une al sitio activo de la enzima para producir un complejo enzima-sustrato ES, y se transforma en un complejo enzima-producto EP y de allí al producto P, a través de un estado de transición ES*. La serie de pasos se conoce como el mecanismo :

E + S ⇄ ES ⇄ ES* ⇄ EP ⇄ E + P

Este ejemplo supone el caso más simple de una reacción con un sustrato y un producto. Tales casos existen: por ejemplo, una mutasa como la fosfoglucomutasa cataliza la transferencia de un grupo fosfato de una posición a otra, y la isomerasa es un término más general para una enzima que cataliza cualquier reacción de un sustrato y un producto, como la triosafosfato isomerasa . Sin embargo, tales enzimas no son muy comunes y son superadas en número por las enzimas que catalizan reacciones de dos sustratos y dos productos: estas incluyen, por ejemplo, las deshidrogenasas dependientes de NAD como la alcohol deshidrogenasa , que cataliza la oxidación del etanol por NAD + . Las reacciones con tres o cuatro sustratos o productos son menos comunes, pero existen. No es necesario que el número de productos sea igual al número de sustratos; por ejemplo, la gliceraldehído 3-fosfato deshidrogenasa tiene tres sustratos y dos productos.

Cuando las enzimas se unen a múltiples sustratos, como la dihidrofolato reductasa (que se muestra a la derecha), la cinética enzimática también puede mostrar la secuencia en la que se unen estos sustratos y la secuencia en la que se liberan los productos. Un ejemplo de enzimas que se unen a un solo sustrato y liberan múltiples productos son las proteasas , que escinden un sustrato proteico en dos productos polipeptídicos. Otras unen dos sustratos, como la ADN polimerasa que une un nucleótido al ADN . Aunque estos mecanismos suelen ser una serie compleja de pasos, normalmente hay un paso que determina la velocidad y que determina la cinética general. Este paso que determina la velocidad puede ser una reacción química o un cambio conformacional de la enzima o los sustratos, como los que intervienen en la liberación de los productos de la enzima.

El conocimiento de la estructura de la enzima es útil para interpretar los datos cinéticos. Por ejemplo, la estructura puede sugerir cómo se unen los sustratos y los productos durante la catálisis; qué cambios ocurren durante la reacción; e incluso el papel de residuos de aminoácidos particulares en el mecanismo. Algunas enzimas cambian de forma significativamente durante el mecanismo; en tales casos, es útil determinar la estructura de la enzima con y sin análogos de sustrato unidos que no experimentan la reacción enzimática.

No todos los catalizadores biológicos son enzimas proteicas: los catalizadores basados ​​en ARN , como las ribozimas y los ribosomas, son esenciales para muchas funciones celulares, como el empalme y la traducción del ARN . La principal diferencia entre las ribozimas y las enzimas es que los catalizadores de ARN están compuestos de nucleótidos, mientras que las enzimas están compuestas de aminoácidos. Las ribozimas también realizan un conjunto más limitado de reacciones, aunque sus mecanismos de reacción y cinética se pueden analizar y clasificar mediante los mismos métodos.

Principios generales

A medida que se añaden mayores cantidades de sustrato a una reacción, los sitios de unión de la enzima disponibles se llenan hasta el límite de . Más allá de este límite, la enzima se satura con sustrato y la velocidad de reacción deja de aumentar. V máximo {\displaystyle V_{\max}}

La reacción catalizada por una enzima utiliza exactamente los mismos reactivos y produce exactamente los mismos productos que la reacción no catalizada. Al igual que otros catalizadores , las enzimas no alteran la posición de equilibrio entre sustratos y productos. [1] Sin embargo, a diferencia de las reacciones químicas no catalizadas, las reacciones catalizadas por enzimas muestran una cinética de saturación. Para una concentración de enzima dada y para concentraciones de sustrato relativamente bajas, la velocidad de reacción aumenta linealmente con la concentración de sustrato; las moléculas de enzima son en gran medida libres para catalizar la reacción, y el aumento de la concentración de sustrato significa un aumento de la velocidad a la que las moléculas de enzima y sustrato se encuentran entre sí. Sin embargo, a concentraciones de sustrato relativamente altas, la velocidad de reacción se acerca asintóticamente al máximo teórico; los sitios activos de la enzima están casi todos ocupados por sustratos, lo que resulta en saturación, y la velocidad de reacción está determinada por la tasa de recambio intrínseco de la enzima. [2] La concentración de sustrato a medio camino entre estos dos casos límite se denota por K M . Por lo tanto, K M es la concentración de sustrato a la que la velocidad de reacción es la mitad de la velocidad máxima. [2]

Las dos propiedades importantes de la cinética enzimática son la facilidad con la que la enzima puede saturarse con un sustrato y la velocidad máxima que puede alcanzar. Conocer estas propiedades sugiere lo que una enzima podría hacer en la célula y puede mostrar cómo responderá a los cambios en estas condiciones.

Ensayos enzimáticos

Curva de progreso de una reacción enzimática. La pendiente en el período de velocidad inicial es la velocidad inicial de reacción v . La ecuación de Michaelis-Menten describe cómo varía esta pendiente con la concentración de sustrato.

Los ensayos enzimáticos son procedimientos de laboratorio que miden la velocidad de las reacciones enzimáticas. Dado que las enzimas no se consumen en las reacciones que catalizan, los ensayos enzimáticos suelen seguir los cambios en la concentración de sustratos o productos para medir la velocidad de reacción. Hay muchos métodos de medición. Los ensayos espectrofotométricos observan el cambio en la absorbancia de la luz entre productos y reactivos; los ensayos radiométricos implican la incorporación o liberación de radiactividad para medir la cantidad de producto formado a lo largo del tiempo. Los ensayos espectrofotométricos son los más convenientes ya que permiten medir la velocidad de la reacción de forma continua. Aunque los ensayos radiométricos requieren la extracción y el recuento de muestras (es decir, son ensayos discontinuos), suelen ser extremadamente sensibles y pueden medir niveles muy bajos de actividad enzimática. [3] Un enfoque análogo es utilizar la espectrometría de masas para controlar la incorporación o liberación de isótopos estables a medida que el sustrato se convierte en producto. Ocasionalmente, un ensayo falla y los enfoques son esenciales para resucitar un ensayo fallido.

Los ensayos enzimáticos más sensibles utilizan láseres enfocados a través de un microscopio para observar los cambios en las moléculas de enzimas individuales a medida que catalizan sus reacciones. Estas mediciones utilizan cambios en la fluorescencia de los cofactores durante el mecanismo de reacción de una enzima o de colorantes fluorescentes añadidos en sitios específicos de la proteína para informar sobre los movimientos que ocurren durante la catálisis. [4] Estos estudios proporcionan una nueva visión de la cinética y la dinámica de las enzimas individuales, en contraposición a la cinética enzimática tradicional, que observa el comportamiento promedio de poblaciones de millones de moléculas de enzimas. [5] [6]

En la imagen de arriba se muestra un ejemplo de curva de progreso para un ensayo enzimático. La enzima produce un producto a una velocidad inicial que es aproximadamente lineal durante un breve período después del inicio de la reacción. A medida que avanza la reacción y se consume el sustrato, la velocidad disminuye continuamente (siempre que el sustrato no se encuentre todavía en niveles de saturación). Para medir la velocidad inicial (y máxima), los ensayos enzimáticos se llevan a cabo normalmente mientras la reacción ha progresado solo un pequeño porcentaje hacia su finalización total. La duración del período de velocidad inicial depende de las condiciones del ensayo y puede variar desde milisegundos hasta horas. Sin embargo, el equipo para mezclar líquidos rápidamente permite realizar mediciones cinéticas rápidas a velocidades iniciales de menos de un segundo. [7] Estos ensayos muy rápidos son esenciales para medir la cinética en estado preestacionario, que se analiza a continuación.

La mayoría de los estudios de cinética enzimática se concentran en esta parte inicial, aproximadamente lineal, de las reacciones enzimáticas. Sin embargo, también es posible medir la curva de reacción completa y ajustar estos datos a una ecuación de velocidad no lineal . Esta forma de medir las reacciones enzimáticas se denomina análisis de curva de progreso. [8] Este enfoque es útil como alternativa a la cinética rápida cuando la velocidad inicial es demasiado rápida para medirla con precisión.

Las pautas para la presentación de datos enzimáticos proporcionan la información mínima necesaria para presentar de forma exhaustiva datos cinéticos y de equilibrio de investigaciones sobre actividades enzimáticas, incluidas las condiciones experimentales correspondientes. Las pautas se han desarrollado para presentar datos funcionales de enzimas con rigor y solidez.

Reacciones de un solo sustrato

Las enzimas con mecanismos de sustrato único incluyen isomerasas como la triosafosfato isomerasa o la bisfosfoglicerato mutasa , liasas intramoleculares como la adenilato ciclasa y la ribozima cabeza de martillo , una ARN liasa. [9] Sin embargo, algunas enzimas que solo tienen un sustrato único no entran en esta categoría de mecanismos. La catalasa es un ejemplo de esto, ya que la enzima reacciona con una primera molécula de sustrato de peróxido de hidrógeno , se oxida y luego se reduce por una segunda molécula de sustrato. Aunque está involucrado un solo sustrato, la existencia de un intermediario enzimático modificado significa que el mecanismo de la catalasa es en realidad un mecanismo de ping-pong, un tipo de mecanismo que se analiza en la sección Reacciones de múltiples sustratos a continuación.

Cinética de Michaelis-Menten

Como las reacciones catalizadas por enzimas son saturables, su tasa de catálisis no muestra una respuesta lineal al aumento del sustrato. Si la tasa inicial de la reacción se mide en un rango de concentraciones de sustrato (indicado como [S]), la tasa de reacción inicial ( ) aumenta a medida que [S] aumenta, como se muestra a la derecha. Sin embargo, a medida que [S] aumenta, la enzima se satura con sustrato y la tasa inicial alcanza Vmax , la tasa máxima de la enzima . en 0 estilo de visualización v_{0}}

El modelo cinético de Michaelis-Menten de una reacción de un solo sustrato se muestra a la derecha. Hay una reacción bimolecular inicial entre la enzima E y el sustrato S para formar el complejo enzima-sustrato ES. La velocidad de la reacción enzimática aumenta con el aumento de la concentración del sustrato hasta un cierto nivel llamado Vmax ; en Vmax , el aumento de la concentración del sustrato no provoca ningún aumento en la velocidad de reacción ya que no hay más enzima (E) disponible para reaccionar con el sustrato (S). Aquí, la velocidad de reacción se vuelve dependiente del complejo ES y la reacción se convierte en una reacción unimolecular con un orden de cero. Aunque el mecanismo enzimático para la reacción unimolecular puede ser bastante complejo, normalmente hay un paso enzimático que determina la velocidad y que permite modelar esta reacción como un solo paso catalítico con una constante de velocidad unimolecular aparente k cat . Si la reacción transcurre sobre uno o varios intermediarios, k cat será una función de varias constantes de velocidad elementales, mientras que en el caso más simple de una única reacción elemental (por ejemplo, sin intermediarios) será idéntica a la constante de velocidad unimolecular elemental k 2 . La constante de velocidad unimolecular aparente k cat también se denomina número de recambio y denota el número máximo de reacciones enzimáticas catalizadas por segundo. ES → a do a a mi + PAG {\displaystyle {\ce {ES ->[k_{cat}] E + P}}}

La ecuación de Michaelis-Menten [10] describe cómo la velocidad de reacción (inicial) v 0 depende de la posición del equilibrio de unión del sustrato y de la constante de velocidad k 2 .

en 0 = V máximo [ S ] K METRO + [ S ] {\displaystyle v_{0}={\frac {V_{\max }[{\ce {S}}]}{K_{M}+[{\ce {S}}]}}}     (Ecuación de Michaelis-Menten)

con las constantes

K METRO   = d mi F   a 2 + a − 1 a 1 ≈ K D V máximo   = d mi F   a do a a [ mi ] a o a {\displaystyle {\begin{aligned}K_{M}\ &{\stackrel {\mathrm {def} }{=}}\ {\frac {k_{2}+k_{-1}}{k_{1}}}\approx K_{D}\\V_{\max }\ &{\stackrel {\mathrm {def} }{=}}\ k_{cat}{\ce {[E]}}_{tot}\end{aligned}}}

Esta ecuación de Michaelis-Menten es la base de la mayoría de las cinéticas enzimáticas de sustrato único. Dos suposiciones cruciales subyacen a esta ecuación (aparte de la suposición general sobre el mecanismo que solo implica que no hay inhibición de intermediarios o productos, y no hay alostericidad o cooperatividad ). La primera suposición es la llamada suposición de estado cuasi-estacionario (o hipótesis de estado pseudo-estacionario), es decir, que la concentración de la enzima unida al sustrato (y, por lo tanto, también la enzima no unida) cambia mucho más lentamente que las del producto y el sustrato y, por lo tanto, el cambio a lo largo del tiempo del complejo puede establecerse en cero . La segunda suposición es que la concentración total de enzima no cambia con el tiempo, por lo tanto . d [ ES ] / d a = ! 0 {\displaystyle d{\ce {[ES]}}/{dt}\;{\overset {!}{=}}\;0} [ mi ] nene = [ mi ] + [ ES ] = ! constante {\displaystyle {\ce {[E]}}_{\text{tot}}={\ce {[E]}}+{\ce {[ES]}}\;{\overset {!}{= }}\;{\text{const}}}

La constante de Michaelis K M se define experimentalmente como la concentración a la que la velocidad de la reacción enzimática es la mitad de V max , lo que se puede verificar sustituyendo [S] = K M en la ecuación de Michaelis-Menten y también se puede ver gráficamente. Si el paso enzimático que determina la velocidad es lento en comparación con la disociación del sustrato ( ), la constante de Michaelis K M es aproximadamente la constante de disociación K D del complejo ES. a 2 ≪ a − 1 {\displaystyle k_{2}\ll k_{-1}}

Si es pequeño en comparación con el término y también se forma muy poco complejo ES, por lo tanto, la tasa de formación del producto es [ S ] {\displaystyle {\ce {[S]}}} K METRO Estilo de visualización K_ {M}} [ S ] / ( K METRO + [ S ] ) ≈ [ S ] / K METRO {\displaystyle [{\ce {S}}]/(K_{M}+[{\ce {S}}])\aprox [{\ce {S}}]/K_{M}} [ mi ] nene ≈ [ mi ] {\displaystyle {\ce {[E]_{\rm {tot}}\aprox [E]}}}

en 0 ≈ a do a a K METRO [ mi ] [ S ] si  [ S ] ≪ K METRO {\displaystyle v_{0}\approx {\frac {k_{cat}}{K_{M}}}{\ce {[E][S]}}\qquad \qquad {\text{si }}[{\ce {S}}]\ll K_{M}}

Por lo tanto, la tasa de formación del producto depende de la concentración de enzima, así como de la concentración de sustrato; la ecuación se asemeja a una reacción bimolecular con una constante de velocidad de pseudo-segundo orden correspondiente . Esta constante es una medida de la eficiencia catalítica . Las enzimas más eficientes alcanzan un en el rango de 10 8 – 10 10 M −1 s −1 . Estas enzimas son tan eficientes que catalizan efectivamente una reacción cada vez que encuentran una molécula de sustrato y, por lo tanto, han alcanzado un límite teórico superior para la eficiencia ( límite de difusión ); y a veces se las denomina enzimas cinéticamente perfectas . [11] Pero la mayoría de las enzimas están lejos de ser perfectas: los valores promedio de y son aproximadamente y , respectivamente. [12] a 2 / K METRO estilo de visualización k2/KM a 2 / K METRO estilo de visualización k2/KM    a 2 / K METRO {\displaystyle k_{2}/K_{\rm {M}}} a 2 estilo de visualización k_{2} 10 5 s − 1 METRO − 1 {\displaystyle 10^{5}{\rm {s}}^{-1}{\rm {M}}^{-1}} 10 s − 1 {\displaystyle 10{\rm {s}}^{-1}}

Uso directo de la ecuación de Michaelis-Menten para el análisis cinético del curso temporal

Las velocidades observadas predichas por la ecuación de Michaelis-Menten se pueden utilizar para modelar directamente la desaparición del sustrato y la producción del producto en el transcurso del tiempo mediante la incorporación de la ecuación de Michaelis-Menten en la ecuación para la cinética química de primer orden. Sin embargo, esto solo se puede lograr si se reconoce el problema asociado con el uso del número de Euler en la descripción de la cinética química de primer orden, es decir, e − k es una constante dividida que introduce un error sistemático en los cálculos y se puede reescribir como una constante única que representa el sustrato restante después de cada período de tiempo. [13]

[ S ] = [ S ] 0 ( 1 − a ) a {\displaystyle [S]=[S]_{0}(1-k)^{t}\,}
[ S ] = [ S ] 0 ( 1 − en / [ S ] 0 ) a {\displaystyle [S]=[S]_{0}(1-v/[S]_{0})^{t}\,}
[ S ] = [ S ] 0 ( 1 − ( V máximo [ S ] 0 / ( K METRO + [ S ] 0 ) / [ S ] 0 ) ) a {\displaystyle [S]=[S]_{0}(1-(V_{\max }[S]_{0}/(K_{M}+[S]_{0})/[S]_{0}))^{t}\,}

En 1983 Stuart Beal (y también independientemente Santiago Schnell y Claudio Mendoza en 1997) derivaron una solución en forma cerrada para el análisis cinético del curso temporal del mecanismo de Michaelis-Menten. [14] [15] La solución, conocida como ecuación de Schnell-Mendoza, tiene la forma:

[ S ] K METRO = Yo [ F ( a ) ] {\displaystyle {\frac {[S]}{K_{M}}}=W\left[F(t)\right]\,}

donde W[ ] es la función Lambert-W . [16] [17] y donde F(t) es

F ( a ) = [ S ] 0 K METRO exp ( [ S ] 0 K METRO − V máximo K METRO a ) {\displaystyle F(t)={\frac {[S]_{0}}{K_{M}}}\exp \!\left({\frac {[S]_{0}}{K_{M}}}-{\frac {V_{\max }}{K_{M}}}\,t\right)\,}

Esta ecuación está englobada en la ecuación siguiente, obtenida por Berberan-Santos, [18] que también es válida cuando la concentración inicial del sustrato es cercana a la de la enzima,

[ S ] K METRO = Yo [ F ( a ) ] − V máximo a do a a K METRO   Yo [ F ( a ) ] 1 + Yo [ F ( a ) ] {\displaystyle {\frac {[S]}{K_{M}}}=W\left[F(t)\right]-{\frac {V_{\max }}{k_{cat}K_{M}}}\ {\frac {W\left[F(t)\right]}{1+W\left[F(t)\right]}}\,}

donde W[ ] es nuevamente la función Lambert-W .

Gráficas lineales de la ecuación de Michaelis-Menten

Gráfico de Lineweaver-Burk o gráfico recíproco doble de datos cinéticos, que muestra la importancia de las intersecciones con los ejes y el gradiente.

La gráfica de v versus [S] anterior no es lineal; aunque inicialmente es lineal a baja [S], se inclina hasta saturarse a alta [S]. Antes de la era moderna del ajuste de curvas no lineal en computadoras, esta no linealidad podía dificultar la estimación precisa de K M y V max . Por lo tanto, varios investigadores desarrollaron linealizaciones de la ecuación de Michaelis-Menten, como el diagrama de Lineweaver-Burk , el diagrama de Eadie-Hofstee y el diagrama de Hanes-Woolf . Todas estas representaciones lineales pueden ser útiles para visualizar datos, pero ninguna debe usarse para determinar parámetros cinéticos, ya que hay software de computadora fácilmente disponible que permite una determinación más precisa mediante métodos de regresión no lineal . [19]

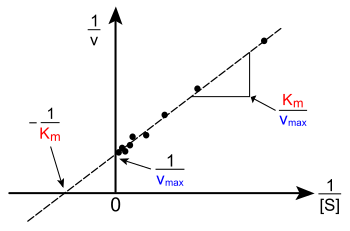
El diagrama de Lineweaver-Burk o diagrama recíproco doble es una forma común de ilustrar datos cinéticos. Esto se produce tomando el recíproco de ambos lados de la ecuación de Michaelis-Menten. Como se muestra a la derecha, esta es una forma lineal de la ecuación de Michaelis-Menten y produce una línea recta con la ecuación y = m x + c con una intersección con el eje y equivalente a 1/ V max y una intersección con el eje x del gráfico que representa −1/ K M .

1 en = K METRO V máximo [ S ] + 1 V máximo {\displaystyle {\frac {1}{v}}={\frac {K_{M}}{V_{\max }[{\mbox{S}}]}}+{\frac {1}{V_{ \max }}}}

Naturalmente, no se pueden tomar valores experimentales en -1/[S]; el valor límite inferior 1/[S] = 0 (la intersección con el eje y ) corresponde a una concentración de sustrato infinita, donde 1/v = 1/V max como se muestra a la derecha; por lo tanto, la intersección con el eje x es una extrapolación de los datos experimentales tomados en concentraciones positivas. De manera más general, el gráfico de Lineweaver-Burk sesga la importancia de las mediciones tomadas en bajas concentraciones de sustrato y, por lo tanto, puede producir estimaciones inexactas de V max y K M . [20] Un método de trazado lineal más preciso es el gráfico de Eadie-Hofstee . En este caso, v se grafica contra v /[S]. En la tercera representación lineal común, el gráfico de Hanes-Woolf , [S]/ v se grafica contra [S]. En general, la normalización de datos puede ayudar a disminuir la cantidad de trabajo experimental y puede aumentar la confiabilidad del resultado, y es adecuada tanto para el análisis gráfico como numérico. [21]

Significado práctico de las constantes cinéticas

El estudio de la cinética enzimática es importante por dos razones básicas. En primer lugar, ayuda a explicar cómo funcionan las enzimas y, en segundo lugar, ayuda a predecir cómo se comportan las enzimas en los organismos vivos. Las constantes cinéticas definidas anteriormente, K M y V max , son fundamentales para intentar comprender cómo funcionan las enzimas juntas para controlar el metabolismo .

Hacer estas predicciones no es trivial, incluso para sistemas simples. Por ejemplo, el oxaloacetato es formado por la malato deshidrogenasa dentro de la mitocondria . El oxaloacetato puede luego ser consumido por la citrato sintasa , la fosfoenolpiruvato carboxiquinasa o la aspartato aminotransferasa , alimentando el ciclo del ácido cítrico , la gluconeogénesis o la biosíntesis del ácido aspártico , respectivamente. Ser capaz de predecir cuánto oxaloacetato entra en qué vía requiere conocimiento de la concentración de oxaloacetato, así como de la concentración y cinética de cada una de estas enzimas. Este objetivo de predecir el comportamiento de las vías metabólicas alcanza su expresión más compleja en la síntesis de enormes cantidades de datos cinéticos y de expresión genética en modelos matemáticos de organismos enteros. Alternativamente, una simplificación útil del problema de modelado metabólico es ignorar la cinética enzimática subyacente y confiar solo en la información sobre la estequiometría de la red de reacción, una técnica llamada análisis de balance de flujo . [22] [23]

Cinética de Michaelis-Menten con intermedios

También se podría considerar el caso menos simple

mi + S ⇌ a − 1 a 1 ES → a 2 EI → a 3 mi + PAG {\displaystyle {\ce {{E}+S<=>[k_{1}][k_{-1}]ES->[k_{2}]EI->[k_{3}]{E}+ PAGS}}}

donde existe un complejo con la enzima y un intermediario y el intermediario se convierte en producto en un segundo paso. En este caso tenemos una ecuación muy similar [24]

en 0 = a do a a [ S ] [ mi ] 0 K METRO " + [ S ] {\displaystyle v_{0}=k_{cat}{\frac {{\ce {[S] [E]_0}}}{K_{M}^{\prime }+{\ce {[S]}} }}}

pero las constantes son diferentes

K METRO "   = d mi F   a 3 a 2 + a 3 K METRO = a 3 a 2 + a 3 ⋅ a 2 + a − 1 a 1 a do a a   = d mi F   a 3 a 2 a 2 + a 3 {\displaystyle {\begin{aligned}K_{M}^{\prime }\ &{\stackrel {\mathrm {def} }{=}}\ {\frac {k_{3}}{k_{2}+k_{3}}}K_{M}={\frac {k_{3}}{k_{2}+k_{3}}}\cdot {\frac {k_{2}+k_{-1}}{k_{1}}}\\k_{cat}\ &{\stackrel {\mathrm {def} }{=}}\ {\dfrac {k_{3}k_{2}}{k_{2}+k_{3}}}\end{aligned}}}

Vemos que para el caso límite , es decir, cuando el último paso desde es mucho más rápido que el paso anterior, obtenemos nuevamente la ecuación original. Matemáticamente tenemos entonces y . a 3 ≫ a 2 {\displaystyle k_{3}\gg k_{2}} EI ⟶ mi + PAG {\displaystyle {\ce {EI -> E + P}}} K METRO " ≈ K METRO {\displaystyle K_{M}^{\prime }\approx K_{M}} a do a a ≈ a 2 {\displaystyle k_{cat}\aproximadamente k_{2}}

Reacciones multisustrato

Las reacciones con múltiples sustratos siguen ecuaciones de velocidad complejas que describen cómo se unen los sustratos y en qué secuencia. El análisis de estas reacciones es mucho más simple si la concentración del sustrato A se mantiene constante y la del sustrato B varía. En estas condiciones, la enzima se comporta como una enzima con un solo sustrato y una gráfica de v por [S] da las constantes aparentes de K M y V max para el sustrato B. Si se realiza un conjunto de estas mediciones a diferentes concentraciones fijas de A, estos datos se pueden utilizar para determinar cuál es el mecanismo de la reacción. Para una enzima que toma dos sustratos A y B y los convierte en dos productos P y Q, hay dos tipos de mecanismo: complejo ternario y ping-pong.

Mecanismos ternarios complejos

Mecanismo complejo ternario de orden aleatorio para una reacción enzimática. La ruta de reacción se muestra como una línea y los intermediarios enzimáticos que contienen los sustratos A y B o los productos P y Q se escriben debajo de la línea.

En estas enzimas, ambos sustratos se unen a la enzima al mismo tiempo para producir un complejo ternario EAB. El orden de unión puede ser aleatorio (en un mecanismo aleatorio) o los sustratos deben unirse en una secuencia particular (en un mecanismo ordenado). Cuando un conjunto de curvas v por [S] (A fija, B variable) de una enzima con un mecanismo de complejo ternario se trazan en un diagrama de Lineweaver-Burk , el conjunto de líneas producidas se intersectarán.

Las enzimas con mecanismos de complejo ternario incluyen la glutatión S -transferasa , [25] la dihidrofolato reductasa [26] y la ADN polimerasa . [27] Los siguientes enlaces muestran animaciones cortas de los mecanismos de complejo ternario de las enzimas dihidrofolato reductasa [β] y la ADN polimerasa [γ] .

Mecanismos de ping-pong

mi → A ↓ EA ↽ − − ⇀ mi ∗ PAG → PAG ↑ mi ∗ → B ↓ mi ∗ B ↽ − − ⇀ Ecualizador → Q ↑ mi {\displaystyle {\ce {\overset {}{E->[{\ce {A \arriba \flecha abajo }}]EA<=>E^{\ast }P->[{\ce {P \arriba \flecha arriba }}]E^{\ast }->[{\ce {B \arriba \flecha abajo }}]E^{\ast }B<=>EQ->[{\ce {Q \arriba \flecha arriba }}]E}}}}
Mecanismo de ping-pong para una reacción enzimática. Los intermediarios contienen los sustratos A y B o los productos P y Q.

Como se muestra a la derecha, las enzimas con un mecanismo de ping-pong pueden existir en dos estados, E y una forma químicamente modificada de la enzima E*; esta enzima modificada se conoce como intermediario . En tales mecanismos, el sustrato A se une, cambia la enzima a E*, por ejemplo, transfiriendo un grupo químico al sitio activo, y luego se libera. Solo después de que se libera el primer sustrato, el sustrato B puede unirse y reaccionar con la enzima modificada, regenerando la forma E no modificada. Cuando un conjunto de curvas v por [S] (A fija, B variable) de una enzima con un mecanismo de ping-pong se trazan en un diagrama de Lineweaver-Burk, se producirá un conjunto de líneas paralelas. Esto se llama diagrama secundario .

Las enzimas con mecanismos de ping-pong incluyen algunas oxidorreductasas como la tiorredoxina peroxidasa , [28] transferasas como la acilneuraminato citidililtransferasa [29] y serina proteasas como la tripsina y la quimotripsina . [30] Las serina proteasas son una familia de enzimas muy común y diversa, que incluye enzimas digestivas (tripsina, quimotripsina y elastasa), varias enzimas de la cascada de coagulación sanguínea y muchas otras. En estas serina proteasas, el intermediario E* es una especie de enzima acil formada por el ataque de un residuo de serina del sitio activo sobre un enlace peptídico en un sustrato proteico. Una breve animación que muestra el mecanismo de la quimotripsina está vinculada aquí. [δ]

Catálisis reversible y la ecuación de Haldane

Los factores externos pueden limitar la capacidad de una enzima para catalizar una reacción en ambas direcciones (mientras que la naturaleza de un catalizador en sí significa que no puede catalizar solo en una dirección, según el principio de reversibilidad microscópica ). Consideremos el caso de una enzima que cataliza la reacción en ambas direcciones:

mi + S ⇌ a − 1 a 1 ES ⇌ a − 2 a 2 mi + PAG {\displaystyle {\ce {{E}+{S}<=>[k_{1}][k_{-1}]ES<=>[k_{2}][k_{-2}]{E}+{P}}}}

La velocidad inicial de la reacción en estado estacionario es v 0 = d [ P ] d t = ( k 1 k 2 [ S ] − k − 1 k − 2 [ P ] ) [ E ] 0 k − 1 + k 2 + k 1 [ S ] + k − 2 [ P ] {\displaystyle v_{0}={\frac {d\,[{\rm {P}}]}{dt}}={\frac {(k_{1}k_{2}\,[{\rm {S}}]-k_{-1}k_{-2}[{\rm {P}}])[{\rm {E}}]_{0}}{k_{-1}+k_{2}+k_{1}\,[{\rm {S}}]+k_{-2}\,[{\rm {P}}]}}}

v 0 {\displaystyle v_{0}} es positivo si la reacción continúa en dirección hacia adelante ( ) y negativo en caso contrario. S → P {\displaystyle S\rightarrow P}

El equilibrio requiere que , lo que ocurre cuando . Esto demuestra que la termodinámica fuerza una relación entre los valores de las 4 constantes de velocidad. v = 0 {\displaystyle v=0} [ P ] e q [ S ] e q = k 1 k 2 k − 1 k − 2 = K e q {\displaystyle {\frac {[{\rm {P}}]_{\rm {eq}}}{[{\rm {S}}]_{\rm {eq}}}}={\frac {k_{1}k_{2}}{k_{-1}k_{-2}}}=K_{\rm {eq}}}

Los valores de las velocidades máximas hacia delante y hacia atrás , obtenidos para , , y , , respectivamente, son y , respectivamente. Su relación no es igual a la constante de equilibrio, lo que implica que la termodinámica no restringe la relación de las velocidades máximas. Esto explica que las enzimas puedan ser "catalizadores mucho mejores" ( en términos de velocidades máximas ) en una dirección particular de la reacción. [31] [ S ] → ∞ {\displaystyle [{\rm {S}}]\rightarrow \infty } [ P ] = 0 {\displaystyle [{\rm {P}}]=0} [ S ] = 0 {\displaystyle [{\rm {S}}]=0} [ P ] → ∞ {\displaystyle [{\rm {P}}]\rightarrow \infty } V m a x f = k 2 [ E ] t o t {\displaystyle V_{\rm {max}}^{f}=k_{2}{\rm {[E]}}_{tot}} V m a x b = − k − 1 [ E ] t o t {\displaystyle V_{\rm {max}}^{b}=-k_{-1}{\rm {[E]}}_{tot}}

También se pueden derivar las dos constantes de Michaelis y . La ecuación de Haldane es la relación . K M S = ( k − 1 + k 2 ) / k 1 {\displaystyle K_{M}^{S}=(k_{-1}+k_{2})/k_{1}} K M P = ( k − 1 + k 2 ) / k − 2 {\displaystyle K_{M}^{P}=(k_{-1}+k_{2})/k_{-2}} K e q = [ P ] e q [ S ] e q = V m a x f / K M S V m a x b / K M P {\displaystyle K_{\rm {eq}}={\frac {[{\rm {P}}]_{\rm {eq}}}{[{\rm {S}}]_{\rm {eq}}}}={\frac {V_{\rm {max}}^{f}/K_{M}^{S}}{V_{\rm {max}}^{b}/K_{M}^{P}}}}

Por lo tanto, la termodinámica restringe la relación entre los valores hacia adelante y hacia atrás, no la relación de valores. V m a x / K M {\displaystyle V_{\rm {max}}/K_{M}} V m a x {\displaystyle V_{\rm {max}}}

Cinética no Michaelis-Menten

Curva de saturación de una reacción enzimática que muestra la cinética sigmoidea.

Muchos sistemas enzimáticos diferentes siguen un comportamiento distinto al de Michaelis-Menten. Algunos ejemplos selectos incluyen la cinética de enzimas autocatalíticas, enzimas cooperativas y alostéricas, enzimas interfaciales e intracelulares, enzimas procesivas, etc. Algunas enzimas producen un diagrama v por [S] sigmoide , que a menudo indica una unión cooperativa del sustrato al sitio activo. Esto significa que la unión de una molécula de sustrato afecta la unión de las moléculas de sustrato posteriores. Este comportamiento es más común en enzimas multiméricas con varios sitios activos que interactúan. [32] Aquí, el mecanismo de cooperación es similar al de la hemoglobina , donde la unión del sustrato a un sitio activo altera la afinidad de los otros sitios activos por las moléculas de sustrato. La cooperatividad positiva ocurre cuando la unión de la primera molécula de sustrato aumenta la afinidad de los otros sitios activos por el sustrato. La cooperatividad negativa ocurre cuando la unión del primer sustrato disminuye la afinidad de la enzima por otras moléculas de sustrato.

Las enzimas alostéricas incluyen la tirosil ARNt-sintetasa de mamíferos, que muestra cooperatividad negativa, [33] y la aspartato transcarbamoilasa bacteriana [34] y la fosfofructoquinasa [35] , que muestran cooperatividad positiva.

La cooperatividad es sorprendentemente común y puede ayudar a regular las respuestas de las enzimas a los cambios en las concentraciones de sus sustratos. La cooperatividad positiva hace que las enzimas sean mucho más sensibles a [S] y sus actividades pueden mostrar grandes cambios en un rango estrecho de concentración de sustrato. Por el contrario, la cooperatividad negativa hace que las enzimas sean insensibles a pequeños cambios en [S].

La ecuación de Hill [36] se utiliza a menudo para describir cuantitativamente el grado de cooperatividad en cinéticas distintas de la de Michaelis-Menten. El coeficiente de Hill n derivado mide en qué medida la unión del sustrato a un sitio activo afecta la unión del sustrato a los otros sitios activos. Un coeficiente de Hill de <1 indica cooperatividad negativa y un coeficiente de >1 indica cooperatividad positiva .

Cinética en estado preestacionario

Curva de progreso en estado preestablecido, que muestra la fase de explosión de una reacción enzimática.

En el primer momento después de que una enzima se mezcla con el sustrato, no se ha formado ningún producto y no existen intermediarios . El estudio de los siguientes milisegundos de la reacción se denomina cinética pre-estado estacionario. Por lo tanto, la cinética pre-estado estacionario se ocupa de la formación y el consumo de intermediarios enzima-sustrato (como ES o E*) hasta que se alcanzan sus concentraciones en estado estacionario .

Este enfoque se aplicó por primera vez a la reacción de hidrólisis catalizada por quimotripsina . [37] A menudo, la detección de un intermediario es una pieza vital de evidencia en las investigaciones sobre qué mecanismo sigue una enzima. Por ejemplo, en los mecanismos de ping-pong que se muestran arriba, las mediciones cinéticas rápidas pueden seguir la liberación del producto P y medir la formación del intermediario enzimático modificado E*. [38] En el caso de la quimotripsina, este intermediario se forma por un ataque al sustrato por la serina nucleófila en el sitio activo y la formación del intermediario acil-enzima.

En la figura de la derecha, la enzima produce E* rápidamente en los primeros segundos de la reacción. Luego, la velocidad disminuye a medida que se alcanza el estado estable. Esta fase de explosión rápida de la reacción mide una sola renovación de la enzima. En consecuencia, la cantidad de producto liberado en esta explosión, que se muestra como la intersección en el eje y del gráfico, también indica la cantidad de enzima funcional presente en el ensayo. [39]

Mecanismo químico

Un objetivo importante de la medición de la cinética enzimática es determinar el mecanismo químico de una reacción enzimática, es decir, la secuencia de pasos químicos que transforman el sustrato en un producto. Los métodos cinéticos analizados anteriormente mostrarán a qué velocidad se forman y se interconvierten los intermediarios , pero no pueden identificar exactamente cuáles son estos intermediarios.

Las mediciones cinéticas tomadas bajo diversas condiciones de solución o en enzimas o sustratos ligeramente modificados a menudo arrojan luz sobre este mecanismo químico, ya que revelan el paso o los intermediarios que determinan la velocidad en la reacción. Por ejemplo, la ruptura de un enlace covalente a un átomo de hidrógeno es un paso común que determina la velocidad. Cuál de las posibles transferencias de hidrógeno es determinante de la velocidad se puede mostrar midiendo los efectos cinéticos de sustituir cada hidrógeno por deuterio , su isótopo estable . La velocidad cambiará cuando se reemplace el hidrógeno crítico, debido a un efecto isotópico cinético primario , que ocurre porque los enlaces al deuterio son más difíciles de romper que los enlaces al hidrógeno. [40] También es posible medir efectos similares con otras sustituciones de isótopos, como 13 C/ 12 C y 18 O/ 16 O, pero estos efectos son más sutiles. [41]

Los isótopos también se pueden utilizar para revelar el destino de varias partes de las moléculas del sustrato en los productos finales. Por ejemplo, a veces es difícil discernir el origen de un átomo de oxígeno en el producto final, ya que puede provenir del agua o de parte del sustrato. Esto se puede determinar sustituyendo sistemáticamente el isótopo estable del oxígeno 18 O en las diversas moléculas que participan en la reacción y comprobando el isótopo en el producto. [42] El mecanismo químico también se puede dilucidar examinando la cinética y los efectos de los isótopos en diferentes condiciones de pH, [43] alterando los iones metálicos u otros cofactores unidos , [44] mediante mutagénesis dirigida al sitio de residuos de aminoácidos conservados o estudiando el comportamiento de la enzima en presencia de análogos del sustrato o sustratos. [45]

Inhibición y activación enzimática

Esquema cinético de inhibidores enzimáticos reversibles.

Los inhibidores de enzimas son moléculas que reducen o eliminan la actividad enzimática, mientras que los activadores de enzimas son moléculas que aumentan la tasa catalítica de las enzimas. Estas interacciones pueden ser reversibles (es decir, la eliminación del inhibidor restablece la actividad enzimática) o irreversibles (es decir, el inhibidor inactiva permanentemente la enzima).

Inhibidores reversibles

Tradicionalmente, los inhibidores enzimáticos reversibles se han clasificado como competitivos , no competitivos o no competitivos , según sus efectos sobre K M y V max . Estos diferentes efectos resultan de la unión del inhibidor a la enzima E, al complejo enzima-sustrato ES, o a ambos, respectivamente. La división de estas clases surge de un problema en su derivación y da como resultado la necesidad de utilizar dos constantes de unión diferentes para un evento de unión. La unión de un inhibidor y su efecto sobre la actividad enzimática son dos cosas claramente diferentes, otro problema que las ecuaciones tradicionales no reconocen. En la inhibición no competitiva, la unión del inhibidor da como resultado una inhibición del 100% de la enzima solamente, y no considera la posibilidad de nada intermedio. [46] En la inhibición no competitiva, el inhibidor se unirá a una enzima en su sitio alostérico; por lo tanto, la afinidad de unión, o inversa de K M , del sustrato con la enzima seguirá siendo la misma. Por otro lado, la V max disminuirá en relación con una enzima no inhibida. En un gráfico de Lineweaver-Burk, la presencia de un inhibidor no competitivo se ilustra mediante un cambio en la intersección con el eje y, definida como 1/V max . La intersección con el eje x, definida como −1/ K M , permanecerá igual. En la inhibición competitiva, el inhibidor se unirá a una enzima en el sitio activo, compitiendo con el sustrato. Como resultado, la K M aumentará y la V max permanecerá igual. [47] La ​​forma común del término inhibidor también oscurece la relación entre la unión del inhibidor a la enzima y su relación con cualquier otro término de unión, ya sea la ecuación de Michaelis-Menten o una curva de respuesta a la dosis asociada con la unión del receptor del ligando. Para demostrar la relación se puede realizar la siguiente reorganización:

V max 1 + [ I ] K i = V max [ I ] + K i K i {\displaystyle {\cfrac {V_{\max }}{1+{\cfrac {[I]}{K_{i}}}}}={\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{K_{i}}}}}

Añadiendo cero al final ([I]-[I])

V max [ I ] + K i [ I ] + K i − [ I ] {\displaystyle {\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{[I]+K_{i}-[I]}}}}

Dividiendo por [I]+K i

V max 1 1 − [ I ] [ I ] + K i = V max − V max [ I ] [ I ] + K i {\displaystyle {\cfrac {V_{\max }}{\cfrac {1}{1-{\cfrac {[I]}{[I]+K_{i}}}}}}=V_{\max }-V_{\max }{\cfrac {[I]}{[I]+K_{i}}}}

Esta notación demuestra que, de manera similar a la ecuación de Michaelis-Menten, donde la velocidad de reacción depende del porcentaje de la población de enzimas que interactúa con el sustrato, el efecto del inhibidor es un resultado del porcentaje de la población de enzimas que interactúa con el inhibidor. El único problema con esta ecuación en su forma actual es que supone una inhibición absoluta de la enzima con la unión del inhibidor, cuando en realidad puede haber una amplia gama de efectos, desde una inhibición del 100% de la renovación del sustrato hasta solo >0%. Para tener esto en cuenta, la ecuación se puede modificar fácilmente para permitir diferentes grados de inhibición mediante la inclusión de un término delta Vmax .

V max − Δ V max [ I ] [ I ] + K i {\displaystyle V_{\max }-\Delta V_{\max }{\cfrac {[I]}{[I]+K_{i}}}}

o

V max 1 − ( V max 1 − V max 2 ) [ I ] [ I ] + K i {\displaystyle V_{\max 1}-(V_{\max 1}-V_{\max 2}){\cfrac {[I]}{[I]+K_{i}}}}

Este término puede definir la actividad enzimática residual presente cuando el inhibidor interactúa con enzimas individuales en la población. Sin embargo, la inclusión de este término tiene el valor agregado de permitir la posibilidad de activación si el término Vmax secundario resulta ser mayor que el término inicial. Para tener en cuenta también la posibilidad de activación, la notación puede reescribirse reemplazando el inhibidor "I" con un término modificador denotado aquí como "X".

V max 1 − ( V max 1 − V max 2 ) [ X ] [ X ] + K x {\displaystyle V_{\max 1}-(V_{\max 1}-V_{\max 2}){\cfrac {[X]}{[X]+K_{x}}}}

Si bien esta terminología simplifica el tratamiento de los efectos cinéticos relacionados con la velocidad máxima de la ecuación de Michaelis-Menten, pone de relieve los posibles problemas que plantea el término utilizado para describir los efectos relacionados con la K M . La K M relacionada con la afinidad de la enzima por el sustrato debería relacionarse en la mayoría de los casos con los posibles cambios en el sitio de unión de la enzima que resultarían directamente de las interacciones de los inhibidores de la enzima. Por lo tanto, un término similar al propuesto anteriormente para modular la V max debería ser adecuado en la mayoría de las situaciones: [48]

K m 1 − ( K m 1 − K m 2 ) [ X ] [ X ] + K x {\displaystyle K_{m1}-(K_{m1}-K_{m2}){\cfrac {[X]}{[X]+K_{x}}}}

Inhibidores irreversibles

Los inhibidores de enzimas también pueden inactivar irreversiblemente las enzimas, generalmente modificando covalentemente los residuos del sitio activo. Estas reacciones, que pueden denominarse sustratos suicidas, siguen funciones de decaimiento exponencial y suelen ser saturables. Por debajo de la saturación, siguen una cinética de primer orden con respecto al inhibidor. La inhibición irreversible podría clasificarse en dos tipos distintos. El marcaje por afinidad es un tipo de inhibición irreversible en la que un grupo funcional que es altamente reactivo modifica un residuo catalíticamente crítico en la proteína de interés para provocar la inhibición. La inhibición basada en mecanismos, por otro lado, implica la unión del inhibidor seguida de alteraciones mediadas por enzimas que transforman este último en un grupo reactivo que modifica irreversiblemente la enzima.

Discurso filosófico sobre la reversibilidad e irreversibilidad de la inhibición

Habiendo analizado la inhibición reversible y la inhibición irreversible en los dos apartados anteriores, habría que señalar que el concepto de reversibilidad (o irreversibilidad) es una construcción puramente teórica que depende exclusivamente del marco temporal del ensayo, es decir, un ensayo reversible que implica la asociación y disociación de la molécula inhibidora en escalas de tiempo de minutos parecería irreversible si un ensayo evalúa el resultado en segundos y viceversa. Existe un continuo de comportamientos de inhibidores que abarcan la reversibilidad y la irreversibilidad en un marco temporal de ensayo determinado no arbitrario. Hay inhibidores que muestran un comportamiento de inicio lento y la mayoría de estos inhibidores, invariablemente, también muestran una unión estrecha a la proteína diana de interés.

Mecanismos de catálisis

La variación de energía en función de la coordenada de reacción muestra la estabilización del estado de transición por una enzima.

El modelo preferido para la interacción enzima-sustrato es el modelo de ajuste inducido. [49] Este modelo propone que la interacción inicial entre enzima y sustrato es relativamente débil, pero que estas interacciones débiles inducen rápidamente cambios conformacionales en la enzima que fortalecen la unión. Estos cambios conformacionales también acercan los residuos catalíticos en el sitio activo a los enlaces químicos en el sustrato que se alterarán en la reacción. [50] Los cambios conformacionales se pueden medir utilizando dicroísmo circular o interferometría de polarización dual . Después de que se produce la unión, uno o más mecanismos de catálisis reducen la energía del estado de transición de la reacción al proporcionar una vía química alternativa para la reacción. Los mecanismos de catálisis incluyen catálisis por tensión de enlace; por proximidad y orientación; por donantes o aceptores de protones del sitio activo; catálisis covalente y tunelización cuántica . [38] [51]

La cinética enzimática no puede demostrar qué modos de catálisis utiliza una enzima. Sin embargo, algunos datos cinéticos pueden sugerir posibilidades que se pueden examinar mediante otras técnicas. Por ejemplo, un mecanismo de ping-pong con una cinética de estado preestacionario en fase de explosión sugeriría que la catálisis covalente podría ser importante en el mecanismo de esta enzima. Alternativamente, la observación de un fuerte efecto del pH en Vmax pero no en Km podría indicar que un residuo en el sitio activo necesita estar en un estado de ionización particular para que se produzca la catálisis.

Historia

En 1902, Victor Henri propuso una teoría cuantitativa de la cinética enzimática, [52] pero en ese momento aún no se reconocía la importancia experimental de la concentración de iones de hidrógeno . Después de que Peter Lauritz Sørensen definiera la escala de pH logarítmica e introdujera el concepto de amortiguación en 1909 [53], la química alemana Leonor Michaelis y la Dra. Maud Leonora Menten (investigadora postdoctoral en el laboratorio de Michaelis en ese momento) repitieron los experimentos de Henri y confirmaron su ecuación, que ahora generalmente se conoce como cinética de Michaelis-Menten (a veces también cinética de Henri-Michaelis-Menten ). [54] Su trabajo fue desarrollado aún más por GE Briggs y JBS Haldane , quienes derivaron ecuaciones cinéticas que todavía hoy se consideran ampliamente un punto de partida en el modelado de la actividad enzimática. [55]

La principal contribución del enfoque de Henri-Michaelis-Menten fue pensar en las reacciones enzimáticas en dos etapas. En la primera, el sustrato se une reversiblemente a la enzima, formando el complejo enzima-sustrato, a veces llamado complejo de Michaelis. Luego, la enzima cataliza el paso químico en la reacción y libera el producto. La cinética de muchas enzimas se describe adecuadamente mediante el modelo simple de Michaelis-Menten, pero todas las enzimas tienen movimientos internos que no se tienen en cuenta en el modelo y pueden tener contribuciones significativas a la cinética general de la reacción. Esto se puede modelar introduciendo varias vías de Michaelis-Menten que están conectadas con tasas fluctuantes, [56] [57] [58] que es una extensión matemática del mecanismo básico de Michaelis-Menten. [59]

Software

ENZO (Enzyme Kinetics) es una herramienta de interfaz gráfica para construir modelos cinéticos de reacciones catalizadas por enzimas. ENZO genera automáticamente las ecuaciones diferenciales correspondientes a partir de un esquema de reacción enzimática estipulado. Estas ecuaciones diferenciales son procesadas por un solucionador numérico y un algoritmo de regresión que ajusta los coeficientes de las ecuaciones diferenciales a las curvas de evolución temporal observadas experimentalmente. ENZO permite la evaluación rápida de esquemas de reacción rivales y puede utilizarse para pruebas de rutina en cinética enzimática. [60]

Véase también

Notas al pie

α. ^ Enlace: Tutorial interactivo de cinética de Michaelis-Menten (se requiere Java)
β. ^ Enlace: mecanismo de la dihidrofolato reductasa (Gif)
γ. ^ Enlace: mecanismo de la ADN polimerasa (Gif)
δ. ^ Enlace: Mecanismo de la quimotripsina (se requiere Flash)

Referencias

  1. ^ Wrighton MS, Ebbing DD (1993). Química general (4.ª ed.). Boston: Houghton Mifflin. ISBN 978-0-395-63696-1.
  2. ^ ab Fromm HJ, Hargrove MS (2012) Cinética enzimática. En: Fundamentos de bioquímica. Springer, Berlín, Heidelberg
  3. ^ Danson M, Eisenthal R (2002). Ensayos enzimáticos: un enfoque práctico . Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-963820-8.
  4. ^ Xie XS, Lu HP (junio de 1999). "Enzimología de moléculas individuales". The Journal of Biological Chemistry . 274 (23): 15967–15970. doi : 10.1074/jbc.274.23.15967 . PMID  10347141.
  5. ^ Lu HP (junio de 2004). "Estudios de espectroscopia de moléculas individuales sobre la dinámica de cambios conformacionales en reacciones enzimáticas". Current Pharmaceutical Biotechnology . 5 (3): 261–269. doi :10.2174/1389201043376887. PMID  15180547.
  6. ^ Schnell JR, Dyson HJ , Wright PE (2004). "Estructura, dinámica y función catalítica de la dihidrofolato reductasa". Revisión anual de biofísica y estructura biomolecular . 33 : 119–140. doi :10.1146/annurev.biophys.33.110502.133613. PMID  15139807.
  7. ^ Gibson QH (1969). "[6] Mezcla rápida: flujo detenido". Mezcla rápida: flujo detenido . Métodos en enzimología. Vol. 16. págs. 187–228. doi :10.1016/S0076-6879(69)16009-7. ISBN 978-0-12-181873-9.
  8. ^ Duggleby RG (1995). "[3] Análisis de curvas de progreso enzimático mediante regresión no lineal". Análisis de curvas de progreso enzimático mediante regresión no lineal . Métodos en enzimología. Vol. 249. págs. 61–90. doi :10.1016/0076-6879(95)49031-0. ISBN 978-0-12-182150-0. Número de identificación personal  7791628.
  9. ^ Murray JB, Dunham CM, Scott WG (enero de 2002). "Un cambio conformacional dependiente del pH, en lugar del paso químico, parece ser el factor limitante de la velocidad en la reacción de escisión de la ribozima cabeza de martillo". Journal of Molecular Biology . 315 (2): 121–130. doi :10.1006/jmbi.2001.5145. PMID  11779233. S2CID  18102624.
  10. ^ Michaelis L. y Menten ML Kinetik der Invertinwirkung Biochem. Z. 1913; 49:333–369 traducción al inglés Consultado el 6 de abril de 2007.
  11. ^ Stroppolo ME, Falconi M, Caccuri AM, Desideri A (septiembre de 2001). "Enzimas supereficientes". Ciencias de la vida celular y molecular . 58 (10): 1451–1460. doi :10.1007/PL00000788. PMC 11337273 . PMID  11693526. S2CID  24874575. 
  12. ^ Bar-Even A, Noor E, Savir Y, Liebermeister W, Davidi D, Tawfik DS, Milo R (mayo de 2011). "La enzima moderadamente eficiente: tendencias evolutivas y fisicoquímicas que configuran los parámetros enzimáticos". Bioquímica . 50 (21): 4402–4410. doi :10.1021/bi2002289. PMID  21506553.
  13. ^ Walsh R, Martin E, Darvesh S (enero de 2010). "Un método para describir reacciones catalizadas por enzimas mediante la combinación de parámetros cinéticos enzimáticos en estado estacionario y en el transcurso del tiempo". Biochimica et Biophysica Acta (BBA) - Temas generales . 1800 (1): 1–5. doi :10.1016/j.bbagen.2009.10.007. PMID  19840832.
  14. ^ Beal SL (diciembre de 1983). "Cálculo de la solución explícita de la ecuación de Michaelis-Menten". Revista de farmacocinética y biofarmacia . 11 (6): 641–657. doi :10.1007/BF01059062. PMID  6689584. S2CID  32571415.
  15. ^ Schnell S, Mendoza C (1997). "Solución de forma cerrada para cinética enzimática dependiente del tiempo". Journal of Theoretical Biology . 187 (2): 207–212. Código Bibliográfico :1997JThBi.187..207S. doi :10.1006/jtbi.1997.0425.
  16. ^ Goudar CT, Sonnad JR, Duggleby RG (enero de 1999). "Estimación de parámetros utilizando una solución directa de la ecuación integrada de Michaelis-Menten" (PDF) . Biochimica et Biophysica Acta (BBA) - Estructura de proteínas y enzimología molecular . 1429 (2): 377–383. doi :10.1016/s0167-4838(98)00247-7. PMID  9989222. Archivado desde el original (PDF) el 9 de noviembre de 2015.
  17. ^ Goudar CT, Harris SK, McInerney MJ, Suflita JM (diciembre de 2004). "Análisis de la curva de progreso para reacciones cinéticas enzimáticas y microbianas utilizando soluciones explícitas basadas en la función W de Lambert". Journal of Microbiological Methods . 59 (3): 317–326. doi :10.1016/j.mimet.2004.06.013. PMID  15488275.
  18. ^ Berberan-Santos MN (2010). "Un tratamiento general de la cinética enzimática de Henri Michaelis Menten: solución en serie exacta y soluciones analíticas aproximadas" (PDF) . MATCH Communications in Mathematical and in Computer Chemistry . 63 : 283.
  19. ^ Jones ME (diciembre de 1992). "Análisis de estimadores de mínimos cuadrados ponderados algebraicos para parámetros enzimáticos". The Biochemical Journal . 288 (Parte 2) (Parte 2): 533–538. doi :10.1042/bj2880533. PMC 1132043 . PMID  1463456. 
  20. ^ Tseng SJ, Hsu JP (agosto de 1990). "Una comparación de los procedimientos de estimación de parámetros para el modelo de Michaelis-Menten". Journal of Theoretical Biology . 145 (4): 457–464. Bibcode :1990JThBi.145..457T. doi :10.1016/S0022-5193(05)80481-3. PMID  2246896.
  21. ^ Bravo IG, Busto F, De Arriaga D, Ferrero MA, Rodríguez-Aparicio LB, Martínez-Blanco H, Reglero A (septiembre de 2001). "Un gráfico normalizado como una herramienta novedosa y que ahorra tiempo en el análisis cinético de enzimas complejas". The Biochemical Journal . 358 (Pt 3): 573–583. doi :10.1042/bj3580573. PMC 1222113 . PMID  11577687. 
  22. ^ Almaas E, Kovács B, Vicsek T, Oltvai ZN, Barabási AL (febrero de 2004). "Organización global de los flujos metabólicos en la bacteria Escherichia coli". Naturaleza . 427 (6977): 839–843. arXiv : q-bio/0403001 . Código Bib : 2004Natur.427..839A. doi : 10.1038/naturaleza02289. PMID  14985762. S2CID  715721.
  23. ^ Reed JL, Vo TD, Schilling CH, Palsson BO (2003). "Un modelo a escala del genoma expandido de Escherichia coli K-12 (iJR904 GSM/GPR)". Genome Biology . 4 (9): R54. doi : 10.1186/gb-2003-4-9-r54 . PMC 193654 . PMID  12952533. 
  24. ^ para una derivación completa, ver aquí
  25. ^ Dirr H, Reinemer P, Huber R (marzo de 1994). "Estructuras cristalinas de rayos X de glutatión S-transferasas citosólicas. Implicaciones para la arquitectura de proteínas, reconocimiento de sustratos y función catalítica". Revista Europea de Bioquímica . 220 (3): 645–661. doi :10.1111/j.1432-1033.1994.tb18666.x. PMID  8143720.
  26. ^ Stone SR, Morrison JF (julio de 1988). "Dihidrofolato reductasa de Escherichia coli: mecanismo cinético con NADPH y acetilpiridina adenina dinucleótido fosfato reducido como sustratos". Bioquímica . 27 (15): 5493–5499. doi :10.1021/bi00415a016. PMID  3052577.
  27. ^ Fisher PA (1994). Mecanismo enzimático de las polimerasas de ADN replicativas en eucariotas superiores. Progreso en la investigación de ácidos nucleicos y biología molecular. Vol. 47. págs. 371–97. doi :10.1016/S0079-6603(08)60257-3. ISBN 978-0-12-540047-3. Número PMID  8016325.
  28. ^ Akerman SE, Müller S (agosto de 2003). "La 2-Cys peroxirredoxina PfTrx-Px1 está implicada en la defensa antioxidante del Plasmodium falciparum". Parasitología molecular y bioquímica . 130 (2): 75–81. doi :10.1016/S0166-6851(03)00161-0. PMID  12946843.
  29. ^ Bravo IG, Barrallo S, Ferrero MA, Rodríguez-Aparicio LB, Martínez-Blanco H, Reglero A (septiembre de 2001). "Propiedades cinéticas de la acilneuraminato citidililtransferasa de Pasteurella haemolytica A2". La revista bioquímica . 358 (Parte 3): 585–598. doi :10.1042/bj3580585. PMC 1222114 . PMID  11577688. 
  30. ^ Kraut J (1977). "Serina proteasas: estructura y mecanismo de catálisis". Revista Anual de Bioquímica . 46 : 331–358. doi :10.1146/annurev.bi.46.070177.001555. PMID  332063.
  31. ^ Cornish-Bowden A (2012). Fundamentos de la cinética enzimática . Wiley-Blackwell. Algunas enzimas son catalizadores mucho más eficaces para una dirección que para la otra. Como ejemplo llamativo, las velocidades limitantes de la reacción directa catalizada por la metionina adenosiltransferasa son aproximadamente 10 5 mayores que las de la dirección inversa, aunque la constante de equilibrio es cercana a la unidad (página 59).
  32. ^ Ricard J, Cornish-Bowden A (julio de 1987). "Enzimas cooperativas y alostéricas: 20 años después". Revista Europea de Bioquímica . 166 (2): 255–272. doi : 10.1111/j.1432-1033.1987.tb13510.x . PMID  3301336.
  33. ^ Ward WH, Fersht AR (julio de 1988). "La tirosil-ARNt sintetasa actúa como un dímero asimétrico en la carga del ARNt. Una justificación para la actividad en la mitad de los sitios". Bioquímica . 27 (15): 5525–5530. doi :10.1021/bi00415a021. PMID  3179266.
  34. ^ Helmstaedt K, Krappmann S, Braus GH (septiembre de 2001). "Regulación alostérica de la actividad catalítica: aspartato transcarbamoilasa de Escherichia coli frente a corismato mutasa de levadura". Microbiology and Molecular Biology Reviews . 65 (3): 404–21, tabla de contenidos. doi :10.1128/MMBR.65.3.404-421.2001. PMC 99034 . PMID  11528003. 
  35. ^ Schirmer T, Evans PR (enero de 1990). "Base estructural del comportamiento alostérico de la fosfofructoquinasa". Nature . 343 (6254): 140–145. Bibcode :1990Natur.343..140S. doi :10.1038/343140a0. PMID  2136935. S2CID  4272821.
  36. ^ Hill AV (1910). "Los posibles efectos de la agregación de las moléculas de hemoglobina en sus curvas de disociación". J. Physiol . 40 : iv–vii.
  37. ^ Hartley BS, Kilby BA (febrero de 1954). "La reacción de ésteres de p-nitrofenilo con quimotripsina e insulina". The Biochemical Journal . 56 (2): 288–297. doi :10.1042/bj0560288. PMC 1269615 . PMID  13140189. 
  38. ^ ab Fersht, Alan (1999). Estructura y mecanismo en la ciencia de las proteínas: una guía para la catálisis enzimática y el plegamiento de proteínas . San Francisco: WH Freeman. ISBN 978-0-7167-3268-6.
  39. ^ Bender ML, Begué-Cantón ML, Blakeley RL, Brubacher LJ, Feder J, Gunter CR, et al. (diciembre de 1966). "La determinación de la concentración de soluciones de enzimas hidrolíticas: alfa-quimotripsina, tripsina, papaína, elastasa, subtilisina y acetilcolinesterasa". Journal of the American Chemical Society . 88 (24): 5890–5913. doi :10.1021/ja00976a034. PMID  5980876.
  40. ^ Cleland WW (enero de 2005). "El uso de efectos isotópicos para determinar mecanismos enzimáticos". Archivos de bioquímica y biofísica . 433 (1): 2–12. doi :10.1016/j.abb.2004.08.027. PMID  15581561.
  41. ^ Northrop DB (1981). "La expresión de los efectos de los isótopos en las reacciones catalizadas por enzimas". Revista anual de bioquímica . 50 : 103–131. doi :10.1146/annurev.bi.50.070181.000535. PMID  7023356.
  42. ^ Baillie TA, Rettenmeier AW (1986). "Biotransformación de fármacos: estudios mecanísticos con isótopos estables". Revista de farmacología clínica . 26 (6): 448–451. doi :10.1002/j.1552-4604.1986.tb03556.x. PMID  3734135. S2CID  39193680.
  43. ^ Cleland WW (1982). "Uso de efectos isotópicos para dilucidar mecanismos enzimáticos". CRC Critical Reviews in Biochemistry . 13 (4): 385–428. doi :10.3109/10409238209108715. PMID  6759038.
  44. ^ Christianson DW , Cox JD (1999). "Catálisis por hidróxido activado por metal en metaloenzimas de zinc y manganeso". Revisión anual de bioquímica . 68 : 33–57. doi :10.1146/annurev.biochem.68.1.33. PMID  10872443.
  45. ^ Kraut DA, Carroll KS, Herschlag D (2003). "Desafíos en el mecanismo y la energía enzimática". Revisión anual de bioquímica . 72 : 517–571. doi :10.1146/annurev.biochem.72.121801.161617. PMID  12704087.
  46. ^ Walsh R, Martin E, Darvesh S (diciembre de 2011). "Limitaciones de las clasificaciones convencionales de inhibidores". Integrative Biology . 3 (12): 1197–1201. doi :10.1039/c1ib00053e. PMID  22038120.
  47. ^ Cleland WW (febrero de 1963). "La cinética de las reacciones catalizadas por enzimas con dos o más sustratos o productos. III. Predicción de la velocidad inicial y los patrones de inhibición por inspección". Biochimica et Biophysica Acta . 67 : 188–196. doi :10.1016/0006-3002(63)91816-x. PMID  14021669.
  48. ^ Walsh R, Martin E, Darvesh S (mayo de 2007). "Una ecuación versátil para describir la inhibición enzimática reversible y la cinética de activación: modelado de la beta-galactosidasa y la butirilcolinesterasa". Biochimica et Biophysica Acta (BBA) - Temas generales . 1770 (5): 733–746. doi :10.1016/j.bbagen.2007.01.001. PMID  17307293.
  49. ^ Koshland DE (febrero de 1958). "Aplicación de una teoría de la especificidad enzimática a la síntesis de proteínas". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 44 (2): 98–104. Bibcode :1958PNAS...44...98K. doi : 10.1073/pnas.44.2.98 . PMC 335371 . PMID  16590179. 
  50. ^ Hammes GG (julio de 2002). "Cambios conformacionales múltiples en la catálisis enzimática". Bioquímica . 41 (26): 8221–8228. doi :10.1021/bi0260839. PMID  12081470.
  51. ^ Sutcliffe MJ, Scrutton NS (julio de 2002). "Un nuevo marco conceptual para la catálisis enzimática. Tunelización de hidrógeno acoplada a la dinámica enzimática en enzimas de flavoproteínas y quinoproteínas". Revista Europea de Bioquímica . 269 (13): 3096–3102. doi :10.1046/j.1432-1033.2002.03020.x. PMID  12084049.
  52. ^ Enrique V (1902). "Teoría general de la acción de las diástasis". Compt. Desgarrar. Acad. Ciencia. París . 135 : 916–9.
  53. ^ Sørensen PL (1909). "Enzymstudien {II}. Über die Messung und Bedeutung der Wasserstoffionenkonzentration bei enzymatischen Prozessen" [Estudios enzimáticos III: Acerca de la medición y la importancia de la concentración de iones de hidrógeno en procesos enzimáticos]. Bioquímica. Z. (en alemán). 21 : 131–304.
  54. ^ Michaelis L, Menten M (1913). "Die Kinetik der Invertinwirkung" [La cinética de la acción de la invertasa]. Biochem. Z. (en alemán). 49 : 333–369.; Michaelis L, Menten ML, Johnson KA, Goody RS (octubre de 2011). "La constante original de Michaelis: traducción del artículo de Michaelis-Menten de 1913". Bioquímica . 50 (39): 8264–8269. doi :10.1021/bi201284u. PMC 3381512 . PMID  21888353. 
  55. ^ Briggs GE, Haldane JB (1925). "Una nota sobre la cinética de la acción enzimática". The Biochemical Journal . 19 (2): 338–339. doi :10.1042/bj0190338. PMC 1259181 . PMID  16743508. 
  56. ^ Flomenbom O, Velonia K, Loos D, Masuo S, Cotlet M, Engelborghs Y, et al. (febrero de 2005). "Decaimiento exponencial extendido y correlaciones en la actividad catalítica de moléculas de lipasa individuales fluctuantes". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 102 (7): 2368–2372. Bibcode :2005PNAS..102.2368F. doi : 10.1073/pnas.0409039102 . PMC 548972 . PMID  15695587. 
  57. ^ English BP, Min W, van Oijen AM, Lee KT, Luo G, Sun H, et al. (febrero de 2006). "Moléculas enzimáticas individuales en constante fluctuación: ecuación de Michaelis-Menten revisada". Nature Chemical Biology . 2 (2): 87–94. doi :10.1038/nchembio759. PMID  16415859. S2CID  2201882.
  58. ^ Lu HP, Xun L, Xie XS (diciembre de 1998). "Dinámica enzimática de moléculas individuales". Science . 282 (5395): 1877–1882. Bibcode :1998Sci...282.1877P. doi :10.1126/science.282.5395.1877. PMID  9836635.
  59. ^ Xue X, Liu F, Ou-Yang ZC (septiembre de 2006). "Ecuación de Michaelis-Menten de una sola molécula más allá del desorden cuasiestático". Physical Review E . 74 (3 Pt 1): 030902. arXiv : cond-mat/0604364 . Bibcode :2006PhRvE..74c0902X. doi :10.1103/PhysRevE.74.030902. PMID  17025584. S2CID  41674948.
  60. ^ Bevc S, Konc J, Stojan J, Hodošček M, Penca M, Praprotnik M, Janežič D (2011). "ENZO: una herramienta web para la derivación y evaluación de modelos cinéticos de reacciones catalizadas por enzimas". PLOS ONE . ​​6 (7): e22265. Bibcode :2011PLoSO...622265B. doi : 10.1371/journal.pone.0022265 . PMC 3139599 . PMID  21818304.  Servidor ENZO

Lectura adicional

Introductorio

  • Cornish-Bowden A (2012). Fundamentos de la cinética enzimática (4.ª ed.). Weinheim: Wiley-Blackwell. ISBN 978-3-527-33074-4.
  • Stevens L, Price NC (1999). Fundamentos de enzimología: la biología celular y molecular de las proteínas catalíticas . Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-850229-6.
  • Bugg T (2004). Introducción a la química de enzimas y coenzimas . Cambridge, MA: Blackwell Publishers. ISBN 978-1-4051-1452-3.
  • Segel IH (1993). Cinética enzimática: comportamiento y análisis de sistemas enzimáticos de equilibrio rápido y estado estacionario . Nueva York: Wiley. ISBN 978-0-471-30309-1.

Avanzado

  • Fersht A (1999). Estructura y mecanismo en la ciencia de las proteínas: una guía para la catálisis enzimática y el plegamiento de proteínas . San Francisco: WH Freeman. ISBN 978-0-7167-3268-6.
  • Schnell S, Maini PK (2004). "Un siglo de cinética enzimática: fiabilidad de las estimaciones de K M y v max ". Comentarios sobre biología teórica . 8 (2–3): 169–87. CiteSeerX  10.1.1.493.7178 . doi :10.1080/08948550302453.
  • Walsh C (1979). Mecanismos de reacción enzimática . San Francisco: WH Freeman. ISBN 978-0-7167-0070-8.
  • Cleland WW, Cook P (2007). Cinética y mecanismo de las enzimas . Nueva York: Garland Science. ISBN 978-0-8153-4140-6.
  • Animación de un ensayo enzimático: muestra los efectos de manipular las condiciones del ensayo
  • MACiE: una base de datos de mecanismos de reacción enzimática
  • ENZIMA — Base de datos de nomenclatura de enzimas Expasy
  • ENZO — Aplicación web para la construcción sencilla y prueba rápida de modelos cinéticos de reacciones catalizadas por enzimas.
  • ExCatDB: una base de datos de mecanismos catalíticos enzimáticos
  • BRENDA: base de datos completa de enzimas, que ofrece sustratos, inhibidores y diagramas de reacción
  • SABIO-RK — Una base de datos de cinética de reacciones
  • Grupo de investigación de Joseph Kraut, Universidad de California en San Diego: animaciones de varios mecanismos de reacción enzimática
  • Simbolismo y terminología en cinética enzimática: una explicación completa de los conceptos y la terminología en cinética enzimática
  • Introducción a la cinética enzimática: un conjunto accesible de tutoriales en línea sobre cinética enzimática
  • Tutorial animado de cinética enzimática: un tutorial animado con audio

Retrieved from "https://en.wikipedia.org/w/index.php?title=Enzyme_kinetics&oldid=1242303810"