Compresor centrífugo



Los compresores centrífugos , a veces llamados compresores de impulsor o compresores radiales , son una subclase de turbomáquinas de absorción de trabajo axisimétricas dinámicas . [1]
Logran un aumento de presión añadiendo energía al flujo continuo de fluido a través del rotor/impulsor. La ecuación de la siguiente sección muestra esta entrada de energía específica. Una parte sustancial de esta energía es cinética, que se convierte en mayor energía potencial/presión estática al reducir la velocidad del flujo a través de un difusor. El aumento de la presión estática en el impulsor puede ser aproximadamente igual al aumento en el difusor.
Componentes de un compresor centrífugo simple

Una etapa simple de un compresor centrífugo tiene cuatro componentes (enumerados en orden de flujo): entrada, impulsor/rotor, difusor y colector. [1] La Figura 1.1 muestra cada uno de los componentes de la trayectoria del flujo, con el flujo (gas de trabajo) entrando al impulsor centrífugo axialmente de izquierda a derecha. Este impulsor de turboeje (o turbohélice) gira en sentido antihorario cuando se mira hacia abajo en el compresor. El flujo pasará a través de los compresores de izquierda a derecha.
Entrada
La entrada más simple a un compresor centrífugo es típicamente una tubería simple. Dependiendo de su uso/aplicación, las entradas pueden ser muy complejas. Pueden incluir otros componentes como una válvula de mariposa de entrada, un puerto cubierto, un conducto anular (ver Figura 1.1), un conducto bifurcado, álabes guía/perfiles aerodinámicos estacionarios utilizados para flujo recto o en remolino (ver Figura 1.1), álabes guía móviles (utilizados para variar el pre-remolino de manera ajustable). Las entradas del compresor a menudo incluyen instrumentación para medir la presión y la temperatura con el fin de controlar el rendimiento del compresor.
El principio de dinámica de fluidos de Bernoulli desempeña un papel importante en la comprensión de los componentes estacionarios sin álabes, como una entrada. En situaciones de ingeniería en las que se supone un flujo adiabático , esta ecuación se puede escribir de la siguiente forma:
Ecuación-1.1
dónde:
- 0 es la entrada del compresor, estación 0
- 1 es la entrada del impulsor, estación 1
- p es la presión
- ρ es la densidad e indica que es una función de la presión.
- es la velocidad del flujo
- γ es la relación de los calores específicos del fluido
Impulsor centrífugo

El componente que identifica a una etapa de compresor centrífugo es el rotor del impulsor centrífugo. Los impulsores están diseñados en muchas configuraciones, incluidas "abierto" (álabes visibles), "cubierto o envuelto", "con divisores" (se eliminan todos los demás inductores) y "sin divisores" (todos los álabes completos). Las figuras 0.1, 1.2.1 y 1.3 muestran tres rotores de inductores abiertos completos diferentes con álabes/álabes completos alternados y álabes/álabes divisores de longitud más corta. En general, la nomenclatura matemática aceptada se refiere al borde delantero del impulsor con el subíndice 1. En consecuencia, el borde trasero del impulsor se conoce como el subíndice 2.
A medida que el gas de trabajo/flujo pasa a través del impulsor desde las estaciones 1 a 2, la energía cinética y potencial aumentan. Esto es idéntico a un compresor axial, con la excepción de que los gases pueden alcanzar niveles de energía más altos a través del radio creciente del impulsor. En muchos compresores centrífugos modernos de alta eficiencia, el gas que sale del impulsor viaja a una velocidad cercana a la del sonido.
La mayoría de los impulsores modernos de alta eficiencia utilizan "barrido inverso" en la forma de las aspas. [2] [3] [4]
Una derivación de las ecuaciones generales de Euler (dinámica de fluidos) es la ecuación de Euler para bombas y turbinas , que desempeña un papel importante para comprender el rendimiento del impulsor. Esta ecuación se puede escribir de la siguiente forma:
Ecuación 1.2 (ver las figuras 1.2.2 y 1.2.3 que ilustran los triángulos de velocidad del impulsor)
dónde:
- 1 subíndice 1 es el borde delantero del impulsor (entrada), estación 1
- 2 subíndice 2 es el borde de salida del impulsor (descarga), estación 2
- E es la energía añadida al fluido
- g es la aceleración debida a la gravedad
- u es la velocidad circunferencial del impulsor, unidades de velocidad
- w es la velocidad del flujo relativa al impulsor, unidades de velocidad
- c es la velocidad absoluta del flujo con respecto a la velocidad estacionaria, unidades
- Figura 1.2.2 - Triángulos de velocidad de entrada para impulsor de compresor centrífugo
- Figura 1.2.3 - Triángulos de velocidad de salida para impulsor de compresor centrífugo
Difusor

El siguiente componente, aguas abajo del impulsor dentro de un compresor centrífugo simple, puede ser el difusor. [5] [4] El difusor convierte la energía cinética del flujo (alta velocidad) en energía potencial aumentada (presión estática) al reducir gradualmente (difundir) la velocidad del gas. Los difusores pueden ser sin álabes, con álabes o una combinación alternada. Los difusores con álabes de alta eficiencia también están diseñados para una amplia gama de solideces, desde menos de 1 hasta más de 4. Las versiones híbridas de difusores con álabes incluyen difusores de cuña (ver Figura 1.3), de canal y de tubo. Algunos turbocompresores no tienen difusor. La nomenclatura generalmente aceptada puede referirse al borde de entrada del difusor como estación 3 y al borde de salida como estación 4.
El principio de dinámica de fluidos de Bernoulli desempeña un papel importante para comprender el rendimiento de los difusores. En situaciones de ingeniería en las que se supone que el flujo es adiabático, esta ecuación se puede escribir de la siguiente forma:
Ecuación-1.3
dónde:
- 2 es la entrada del difusor, estación 2
- 4 es la descarga del difusor, estación 4
- (ver entrada más arriba.)
Coleccionista

El colector de un compresor centrífugo puede adoptar muchas formas y tamaños. [5] [4] Cuando el difusor descarga en una gran cámara vacía de forma circunferencial (área constante), el colector puede denominarse Plenum . Cuando el difusor descarga en un dispositivo que se parece a una concha de caracol, un cuerno de toro o una trompa, es probable que el colector se denomine voluta o espiral .
Cuando el difusor descarga en una curva anular, el colector puede denominarse entrada de la cámara de combustión (como se utiliza en motores a reacción o turbinas de gas) o canal de retorno (como se utiliza en un compresor multietapa en línea). Como su nombre lo indica, el propósito de un colector es reunir el flujo del anillo de descarga del difusor y entregar este flujo aguas abajo a cualquier componente que requiera la aplicación. El colector o la tubería de descarga también pueden contener válvulas e instrumentación para controlar el compresor. En algunas aplicaciones, los colectores difundirán el flujo (convirtiendo la energía cinética en presión estática) de manera mucho menos eficiente que un difusor. [6]
El principio de dinámica de fluidos de Bernoulli desempeña un papel importante para comprender el rendimiento de los difusores. En situaciones de ingeniería en las que se supone que el flujo es adiabático, esta ecuación se puede escribir de la siguiente forma:
Ecuación-1.4
dónde:
- 4 es la entrada del difusor, estación 4
- 5 es la descarga del difusor, estación 5
- (ver entrada más arriba.)
Aportaciones históricas, los pioneros
Durante los últimos 100 años, científicos aplicados, entre ellos Stodola (1903, 1927–1945), [7] Pfleiderer (1952), [8] Hawthorne (1964), [9] Shepherd (1956), [1] Lakshminarayana (1996), [10] y Japikse (muchos textos incluyen citas), [2] [11] [ cita requerida ] [12] han educado a ingenieros jóvenes en los fundamentos de la turbomáquina. Estos conocimientos se aplican a todas las bombas, ventiladores, sopladores y compresores dinámicos, de flujo continuo y axisimétricos en configuraciones axiales, de flujo mixto y radiales/centrífugas.
Esta relación es la razón por la que los avances en turbinas y compresores axiales suelen llegar a otras turbomáquinas, incluidos los compresores centrífugos. Las figuras 2.1 y 2.2 ilustran el dominio de las turbomáquinas con etiquetas que muestran los compresores centrífugos. [13] [14] Las mejoras en los compresores centrífugos no se han logrado mediante grandes descubrimientos. Más bien, las mejoras se han logrado mediante la comprensión y la aplicación de conocimientos incrementales descubiertos por muchas personas.
Dominio aerodinámico-termodinámico

La Figura 2.1 (mostrada a la derecha ) representa el dominio aerotermo de la turbomaquinaria. El eje horizontal representa la ecuación de energía derivable de la primera ley de la termodinámica . [1] [14] El eje vertical, que puede caracterizarse por el número de Mach, representa el rango de compresibilidad (o elasticidad) del fluido. [1] [14] El eje Z, que puede caracterizarse por el número de Reynolds , representa el rango de viscosidades (o pegajosidad) del fluido. [14] Los matemáticos y físicos que establecieron las bases de este dominio aerotermo incluyen: [15] [16] Isaac Newton , Daniel Bernoulli , Leonhard Euler , Claude-Louis Navier , George Stokes , Ernst Mach , Nikolay Yegorovich Zhukovsky , Martin Kutta , Ludwig Prandtl , Theodore von Kármán , Paul Richard Heinrich Blasius y Henri Coandă .
Dominio físico-mecánico

La figura 2.2 (mostrada a la derecha) representa el dominio físico o mecánico de la turbomaquinaria. Nuevamente, el eje horizontal representa la ecuación de energía con las turbinas generando energía a la izquierda y los compresores absorbiendo energía a la derecha. [1] [14] Dentro del dominio físico, el eje vertical diferencia entre velocidades altas y bajas dependiendo de la aplicación de la turbomaquinaria. [1] [14] El eje Z diferencia entre la geometría de flujo axial y la geometría de flujo radial dentro del dominio físico de la turbomaquinaria. [1] [14] Se da a entender que la turbomaquinaria de flujo mixto se encuentra entre la axial y la radial. [1] [14] Los principales contribuyentes a los logros técnicos que impulsaron la aplicación práctica de la turbomaquinaria incluyen: [15] [16] Denis Papin , [17] Kernelien Le Demour, Daniel Gabriel Fahrenheit , John Smeaton, Dr. ACE Rateau, [18] John Barber , Alexander Sablukov , Sir Charles Algernon Parsons , Ægidius Elling , Sanford Alexander Moss , Willis Carrier , Adolf Busemann , Hermann Schlichting , Frank Whittle y Hans von Ohain .
Cronología parcial de contribuciones históricas
| <1689 | Primeras turbomáquinas | Bombas, sopladores, ventiladores |
| 1689 | Denis Papin | Origen del compresor centrífugo |
| 1754 | Leonhard Euler | Ecuación de “bomba y turbina” de Euler |
| 1791 | Juan Barbero | Primera patente de turbina de gas |
| 1899 | Tarifa ACE | Primer compresor centrífugo práctico |
| 1927 | Aurel Boleslav Stodola | "Factor de deslizamiento" formalizado |
| 1928 | Adolfo Busemann | "Factor de deslizamiento" derivado |
| 1937 | Frank Whittle y Hans von Ohain, de forma independiente | Primera turbina de gas que utiliza un compresor centrífugo |
| >1970 | Turbomáquinas modernas | 3D-CFD, turbobombas para cohetes, bombas de asistencia cardíaca, pilas de combustible turboalimentadas |
Similitudes de las turbomáquinas
Los compresores centrífugos son similares en muchos aspectos a otras turbomáquinas y se comparan y contrastan de la siguiente manera:
Similitudes con el compresor axial

Los compresores centrífugos son similares a los compresores axiales en que son compresores basados en perfiles aerodinámicos rotativos. Ambos se muestran en la fotografía adyacente de un motor con 5 etapas de compresores axiales y una etapa de un compresor centrífugo. [10] La primera parte del impulsor centrífugo se parece mucho a un compresor axial. Esta primera parte del impulsor centrífugo también se denomina inductor . Los compresores centrífugos se diferencian de los axiales en que utilizan un cambio significativo en el radio desde la entrada hasta la salida del impulsor para producir un aumento de presión mucho mayor en una sola etapa (por ejemplo, 8 [19] en la serie de motores para helicópteros Pratt & Whitney Canada PW200 ) que una etapa axial. El motor experimental alemán Heinkel HeS 011 de la década de 1940 fue el primer turborreactor de aviación en tener una etapa de compresor con un giro de flujo radial a mitad de camino entre ninguno para un axial y 90 grados para un centrífugo. Se conoce como compresor de flujo mixto/diagonal. En la serie PW600 de turbofán pequeños de Pratt & Whitney Canada se utiliza una etapa diagonal .
Ventilador centrífugo

Los compresores centrífugos también son similares a los ventiladores centrífugos del estilo que se muestra en la figura vecina, ya que ambos aumentan la energía del flujo a través del radio creciente. [1] A diferencia de los ventiladores centrífugos, los compresores funcionan a velocidades más altas para generar mayores aumentos de presión. En muchos casos, los métodos de ingeniería utilizados para diseñar un ventilador centrífugo son los mismos que los utilizados para diseñar un compresor centrífugo, por lo que pueden parecer muy similares.
A los efectos de generalización y definición, se puede decir que los compresores centrífugos suelen tener aumentos de densidad superiores al 5 por ciento. Además, suelen experimentar velocidades relativas del fluido superiores al número de Mach 0,3 [20] cuando el fluido de trabajo es aire o nitrógeno. Por el contrario, se considera que los ventiladores o sopladores suelen tener aumentos de densidad inferiores al cinco por ciento y velocidades relativas máximas del fluido inferiores a Mach 0,3.
Ventilador de jaula de ardilla
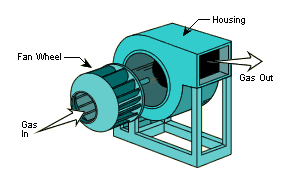
Los ventiladores de jaula de ardilla se utilizan principalmente para ventilación. El campo de flujo dentro de este tipo de ventilador tiene recirculaciones internas. En comparación, un ventilador centrífugo es uniforme en su circunferencia.
Bomba centrífuga
Los compresores centrífugos también son similares a las bombas centrífugas [1] del estilo que se muestra en las figuras adyacentes. La diferencia clave entre estos compresores y bombas es que el fluido de trabajo del compresor es un gas (compresible) y el fluido de trabajo de la bomba es un líquido (incompresible). Nuevamente, los métodos de ingeniería utilizados para diseñar una bomba centrífuga son los mismos que los utilizados para diseñar un compresor centrífugo. Sin embargo, existe una diferencia importante: la necesidad de lidiar con la cavitación en las bombas.
Turbina radial
Los compresores centrífugos también se parecen mucho a su contraparte de turbomáquina, la turbina radial , como se muestra en la figura. Mientras que un compresor transfiere energía a un flujo para aumentar su presión, una turbina funciona a la inversa, extrayendo energía de un flujo, reduciendo así su presión. [ cita requerida ] En otras palabras, la energía se ingresa a los compresores y se obtiene de las turbinas.
Turbomáquinas que utilizan compresores centrífugos
Normas
A medida que las turbomáquinas se hicieron más comunes, se crearon normas para orientar a los fabricantes y asegurarles a los usuarios finales que sus productos cumplen con los requisitos mínimos de seguridad y rendimiento. Las asociaciones formadas para codificar estas normas dependen de los fabricantes, los usuarios finales y los especialistas técnicos relacionados. A continuación, se incluye una lista parcial de estas asociaciones y sus normas:
- Sociedad Estadounidense de Ingenieros Mecánicos : BPVC , PTC. [21] [22]
- Instituto Americano del Petróleo : API STD 617 8.ª ED (E1), API STD 672 5.ª ED (2019). [23] [24]
- Sociedad Estadounidense de Ingenieros de Calefacción, Refrigeración y Aire Acondicionado : Manual de Fundamentos. [25]
- Sociedad de Ingenieros Automotrices [26]
- Instituto de Aire Comprimido y Gas [27]
- Organización Internacional de Normalización ISO 10439, ISO 10442, ISO 18740, ISO 6368, ISO 5389 [28]
Aplicaciones
A continuación se presenta una lista parcial de aplicaciones de compresores centrífugos, cada una con una breve descripción de algunas de las características generales que poseen dichos compresores. Para comenzar esta lista se enumeran dos de las aplicaciones de compresores centrífugos más conocidas: turbinas de gas y turbocompresores. [10]


- En turbinas de gas y unidades de potencia auxiliares. [29] Ref. Figuras 4.1–4.2En su forma más simple, las turbinas de gas modernas funcionan en el ciclo Brayton. (Ref. Figura 5.1) Se utilizan compresores axiales y centrífugos o ambos para proporcionar compresión. Los tipos de turbinas de gas que más a menudo incluyen compresores centrífugos incluyen motores de aeronaves pequeñas (es decir, turboejes, turbohélices y turbofán), unidades de potencia auxiliares y microturbinas. Las normas de la industria que se aplican a todos los compresores centrífugos utilizados en aplicaciones aeronáuticas son establecidas por las autoridades de certificación civiles y militares pertinentes para lograr la seguridad y durabilidad requeridas en servicio. Los impulsores centrífugos utilizados en turbinas de gas se fabrican comúnmente a partir de forjados de aleación de titanio. Sus álabes de trayectoria de flujo se fresan comúnmente en los flancos o en las puntas en fresadoras de 5 ejes. Cuando las holguras de funcionamiento deben ser lo más pequeñas posible sin que el impulsor roce su cubierta, el impulsor primero se estira con su forma desviada de alta temperatura y alta velocidad y luego se estira en su forma estática fría equivalente para su fabricación. Esto es necesario porque las deflexiones del impulsor en las condiciones de funcionamiento más severas pueden ser 100 veces mayores que la holgura requerida para funcionamiento en caliente entre el impulsor y su cubierta.
- En turbocompresores y sobrealimentadores de motores de automóviles y motores diésel . [30] Ref. Figura 1.1Los compresores centrífugos que se utilizan junto con los motores de combustión interna alternativos se conocen como turbocompresores si son accionados por los gases de escape del motor y como turbocompresores si son accionados mecánicamente por el motor. Las normas establecidas por la industria para los turbocompresores pueden haber sido establecidas por la SAE . [26] Las propiedades de los gases ideales suelen funcionar bien para el diseño, la prueba y el análisis del rendimiento del compresor centrífugo del turbocompresor.
- En los compresores de tuberías de gas natural se traslada el gas desde el lugar de producción hasta el consumidor. [31]Los compresores centrífugos para tales usos pueden ser de una o varias etapas y accionados por grandes turbinas de gas. Las normas establecidas por la industria (ANSI/API, ASME) dan como resultado carcasas gruesas para lograr un nivel requerido de seguridad. Los impulsores suelen ser, si no siempre, del estilo cubierto, lo que los hace parecer mucho a los impulsores de las bombas. Este tipo de compresor también se suele denominar estilo API . La potencia necesaria para accionar estos compresores suele ser de miles de caballos de fuerza (HP). Se necesita el uso de propiedades reales del gas para diseñar, probar y analizar adecuadamente el rendimiento de los compresores centrífugos para tuberías de gas natural.
- En refinerías de petróleo , plantas procesadoras de gas natural , petroquímicas y químicas . [31]Los compresores centrífugos para tales usos suelen ser de un solo eje, multietapa y accionados por grandes turbinas de vapor o gas. Sus carcasas se denominan de división horizontal si el rotor se baja a la mitad inferior durante el montaje o de barril si no tiene una línea de división longitudinal con el rotor deslizándose hacia adentro. Las normas establecidas por la industria (ANSI/API, ASME) para estos compresores dan como resultado carcasas gruesas para lograr un nivel requerido de seguridad. Los impulsores suelen ser del estilo cubierto, lo que los hace parecer mucho a los impulsores de bomba. Este tipo de compresor también suele denominarse estilo API . La potencia necesaria para impulsar estos compresores suele ser de miles de HP. Es necesario utilizar las propiedades reales del gas para diseñar, probar y analizar adecuadamente su rendimiento.
- Aire acondicionado , refrigeración y HVAC : Los compresores centrífugos a menudo suministran la compresión en los ciclos de enfriadores de agua . [32]Debido a la amplia variedad de ciclos de compresión de vapor ( ciclo termodinámico , termodinámica ) y la amplia variedad de fluidos de trabajo ( refrigerantes ), los compresores centrífugos se utilizan en una variedad de tamaños y configuraciones. Es necesario utilizar las propiedades reales del gas para diseñar, probar y analizar adecuadamente el rendimiento de estas máquinas. Las normas establecidas por la industria para estos compresores incluyen ASHRAE, ASME y API.
- En la industria y la fabricación para suministrar aire comprimido para todo tipo de herramientas neumáticas . [33]Los compresores centrífugos para tales usos suelen ser multietapa y accionados por motores eléctricos. A menudo se necesita refrigeración intermedia entre etapas para controlar la temperatura del aire. Los equipos de reparación de carreteras y los talleres de reparación de automóviles consideran que los compresores de tornillo se adaptan mejor a sus necesidades. Las normas establecidas por la industria para estos compresores incluyen la ASME y las regulaciones gubernamentales que enfatizan la seguridad. Las relaciones de gases ideales se utilizan a menudo para diseñar, probar y analizar adecuadamente el rendimiento de estas máquinas. La ecuación de Carrier se utiliza a menudo para tratar la humedad.
- En plantas de separación de aire para fabricar gases de producto final purificados. [33]Los compresores centrífugos para tales usos suelen ser multietapa y utilizan refrigeración intermedia para controlar la temperatura del aire. Las normas establecidas por la industria para estos compresores incluyen las normas ASME y las regulaciones gubernamentales que enfatizan la seguridad. Las relaciones de gases ideales se utilizan a menudo para diseñar, probar y analizar adecuadamente el rendimiento de estas máquinas cuando el gas de trabajo es aire o nitrógeno. Otros gases requieren propiedades de gas reales.
- En yacimientos petrolíferos, reinyección de gas natural a alta presión para mejorar la recuperación de petróleo. [31]Los compresores centrífugos para tales usos suelen ser de un solo eje, multietapa y accionados por turbinas de gas. Con presiones de descarga cercanas a los 700 bar, las carcasas son de tipo barril. Las normas establecidas por la industria (API, ASME) para estos compresores dan como resultado carcasas grandes y gruesas para maximizar la seguridad. Los impulsores suelen ser, si no siempre, de tipo cubierto, lo que los hace parecerse mucho a los impulsores de las bombas. Este tipo de compresor también suele denominarse de tipo API . Se necesita el uso de propiedades reales del gas para diseñar, probar y analizar adecuadamente su rendimiento.
Teoría del funcionamiento
En el caso en que el flujo pasa a través de una tubería recta para ingresar a un compresor centrífugo, el flujo es axial, uniforme y no tiene vorticidad, es decir, movimiento de remolino. A medida que el flujo pasa a través del impulsor centrífugo, el impulsor obliga al flujo a girar más rápido a medida que se aleja del eje de rotación. Según una forma de la ecuación de dinámica de fluidos de Euler , conocida como ecuación de bomba y turbina , la entrada de energía al fluido es proporcional a la velocidad de giro local del flujo multiplicada por la velocidad tangencial local del impulsor .
En muchos casos, el flujo que sale del impulsor centrífugo viaja cerca de la velocidad del sonido . Luego fluye a través de un compresor estacionario, lo que hace que desacelere. El compresor estacionario está canalizando con un área de flujo creciente donde se produce la transformación de energía. Si el flujo tiene que girar en dirección hacia atrás para ingresar a la siguiente parte de la máquina, por ejemplo, otro impulsor o una cámara de combustión, las pérdidas de flujo se pueden reducir dirigiendo el flujo con álabes giratorios estacionarios o tubos giratorios individuales (difusores de tubos). Como se describe en el principio de Bernoulli , la reducción de la velocidad hace que la presión aumente. [1]
Actuación


Al ilustrar el ciclo Brayton de una turbina de gas, [15] la Figura 5.1 incluye ejemplos de gráficos de volumen específico de presión y de entropía de temperatura. Estos tipos de gráficos son fundamentales para comprender el rendimiento del compresor centrífugo en un punto de funcionamiento. Los dos gráficos muestran que la presión aumenta entre la entrada del compresor (estación 1) y la salida del compresor (estación 2). Al mismo tiempo, el volumen específico disminuye mientras que la densidad aumenta. El gráfico de entropía de temperatura muestra que la temperatura aumenta con el aumento de la entropía (pérdida). Suponiendo aire seco, la ecuación de estado del gas ideal y un proceso isentrópico, hay suficiente información para definir la relación de presión y la eficiencia para este punto. El mapa del compresor es necesario para comprender el rendimiento del compresor en todo su rango de funcionamiento.
La Figura 5.2, un mapa de rendimiento de un compresor centrífugo (ya sea de prueba o estimado), muestra la relación de caudal y presión para cada una de las 4 líneas de velocidad (un total de 23 puntos de datos). También se incluyen contornos de eficiencia constante. El rendimiento del compresor centrífugo presentado en este formato proporciona suficiente información para hacer coincidir el hardware representado por el mapa con un conjunto simple de requisitos del usuario final.
En comparación con la estimación del rendimiento, que es muy rentable (y, por lo tanto, útil en el diseño), las pruebas, aunque costosas, siguen siendo el método más preciso. [12] Además, probar el rendimiento del compresor centrífugo es muy complejo. Las sociedades profesionales como ASME (es decir, PTC–10, Fluid Meters Handbook, PTC-19.x), [34] ASHRAE ( ASHRAE Handbook ) y API (ANSI/API 617–2002, 672–2007) [31] [33] han establecido estándares para métodos experimentales detallados y análisis de resultados de pruebas. A pesar de esta complejidad, se pueden presentar algunos conceptos básicos sobre el rendimiento examinando un ejemplo de mapa de rendimiento de prueba.
Mapas de rendimiento
La relación de presión y el caudal son los parámetros principales [15] [31] [33] [34] necesarios para adaptar el mapa de rendimiento de la Figura 5.2 a una aplicación de compresor simple. En este caso, se puede suponer que la temperatura de entrada es la estándar a nivel del mar. Esta suposición no es aceptable en la práctica, ya que las variaciones de temperatura de entrada causan variaciones significativas en el rendimiento del compresor. La Figura 5.2 muestra:
- Caudal másico corregido: 0,04 – 0,34 kg/s
- Relación de presión total , entrada a descarga (PR t-t = P t, descarga / P t, entrada ): 1,0 – 2,6
Como es práctica habitual, la Figura 5.2 tiene un eje horizontal marcado con un parámetro de caudal. Si bien las mediciones de caudal utilizan una variedad de unidades, todas encajan en una de las dos categorías siguientes:
Flujo másico por unidad de tiempo
Las unidades de caudal másico, como kg/s, son las más fáciles de usar en la práctica, ya que hay poco margen de confusión. Las preguntas pendientes se referirían a la entrada o salida (que podrían implicar fugas del compresor o condensación de humedad). Para el aire atmosférico, el caudal másico puede ser húmedo o seco (incluyendo o excluyendo la humedad). A menudo, la especificación del caudal másico se presentará sobre la base de un número de Mach equivalente, . [35] En estos casos, es estándar que la temperatura equivalente, la presión equivalente y el gas se especifiquen explícitamente o implícitamente en una condición estándar.
Caudal volumétrico por unidad de tiempo
En cambio, todas las especificaciones de caudal volumétrico requieren la especificación adicional de la densidad. El principio de dinámica de fluidos de Bernoulli es de gran utilidad para comprender este problema. La confusión surge por imprecisiones o por un uso incorrecto de las constantes de presión, temperatura y gas.
Como es práctica habitual, la Figura 5.2 tiene un eje vertical marcado con un parámetro de presión. Hay una variedad de unidades de medición de presión. Todas encajan en una de dos categorías:
- Una △presión, es decir, aumento desde la entrada hasta la salida (medida con un manómetro)
- Una presión de descarga
El aumento de presión también puede especificarse como una relación que no tiene unidades:
- Una relación de presión (salida/entrada)
Otras características comunes a los mapas de rendimiento son:
Líneas de velocidad constante
Los dos métodos más comunes para producir un mapa para un compresor centrífugo son a velocidad de eje constante o con un ajuste de aceleración constante. Si la velocidad se mantiene constante, los puntos de prueba se toman a lo largo de una línea de velocidad constante cambiando las posiciones de aceleración. Por el contrario, si una válvula de aceleración se mantiene constante, los puntos de prueba se establecen cambiando la velocidad y se repiten con diferentes posiciones de aceleración (práctica común de turbinas de gas). El mapa que se muestra en la Figura 5.2 ilustra el método más común; líneas de velocidad constante. En este caso, vemos puntos de datos conectados a través de líneas rectas a velocidades de 50%, 71%, 87% y 100% RPM. Las primeras tres líneas de velocidad tienen 6 puntos cada una, mientras que la línea de velocidad más alta tiene cinco.
Islas de eficiencia constante
La siguiente característica que se analizará son las curvas ovaladas que representan islas de eficiencia constante. En esta figura, vemos 11 contornos que van desde el 56 % de eficiencia (decimal 0,56) hasta el 76 % de eficiencia (decimal 0,76). La práctica estándar general es interpretar estas eficiencias como isoentrópicas en lugar de politrópicas. La inclusión de islas de eficiencia genera efectivamente una topología tridimensional para este mapa bidimensional. Si se especifica la densidad de entrada, se obtiene una capacidad adicional para calcular la potencia aerodinámica. Las líneas de potencia constante se podrían sustituir con la misma facilidad.
Punto(s) de diseño o garantía
En cuanto al funcionamiento y rendimiento de la turbina de gas, se pueden establecer una serie de puntos de garantía para el compresor centrífugo de la turbina de gas. Estos requisitos son de importancia secundaria con respecto al rendimiento global de la turbina de gas. Por este motivo, sólo es necesario resumir que, en el caso ideal, el menor consumo específico de combustible se produciría cuando la curva de eficiencia pico del compresor centrífugo coincidiera con la línea de operación requerida de la turbina de gas.
A diferencia de las turbinas de gas, la mayoría de las demás aplicaciones (incluidas las industriales) necesitan cumplir con un conjunto de requisitos de rendimiento menos estrictos. Históricamente, los compresores centrífugos aplicados a aplicaciones industriales debían lograr un rendimiento con un caudal y una presión específicos. Los compresores industriales modernos suelen ser necesarios para lograr objetivos de rendimiento específicos en una variedad de caudales y presiones, lo que supone un paso significativo hacia la sofisticación que se observa en las aplicaciones de turbinas de gas.
Si el compresor representado en la Figura 5.2 se utiliza en una aplicación sencilla, cualquier punto (presión y caudal) dentro del 76 % de eficiencia proporcionaría un rendimiento muy aceptable. Un "usuario final" estaría muy satisfecho con los requisitos de rendimiento de una relación de presión de 2,0 a 0,21 kg/s.
Aumento
Surge - es un fenómeno de bajo flujo donde el impulsor no puede agregar suficiente energía para superar la resistencia del sistema o la contrapresión. [36] En la operación de bajo caudal, la relación de presión sobre el impulsor es alta, al igual que la contrapresión del sistema. En condiciones críticas, el flujo se revertirá sobre las puntas de las palas del rotor hacia el ojo del impulsor (entrada). [37] Esta inversión de flujo de estancamiento puede pasar desapercibida ya que la fracción de flujo másico o energía es demasiado baja. Cuando es lo suficientemente grande, se produce una rápida inversión de flujo (es decir, surge). El flujo inverso que sale de la entrada del impulsor exhibe un fuerte componente rotacional, que afecta los ángulos de flujo de radio más bajo (más cerca del cubo del impulsor) en el borde delantero de las palas. El deterioro de los ángulos de flujo hace que el impulsor sea ineficiente. Puede ocurrir una inversión de flujo total. (Por lo tanto, el surge a veces se conoce como estancamiento axisimétrico). Cuando el flujo inverso se reduce a un nivel lo suficientemente bajo, el impulsor se recupera y recupera la estabilidad por un breve momento en el que la etapa puede surgir nuevamente. Estos eventos cíclicos causan grandes vibraciones, aumentan la temperatura y cambian rápidamente el empuje axial. Estos eventos pueden dañar los sellos del rotor, los cojinetes del rotor, el controlador del compresor y el funcionamiento del ciclo. La mayoría de las turbomáquinas están diseñadas para soportar fácilmente las sobrecargas ocasionales. Sin embargo, si la máquina se ve obligada a sobrecargar repetidamente durante un largo período de tiempo, o si está mal diseñada, las sobrecargas repetidas pueden provocar una falla catastrófica. De particular interés es que, si bien las turbomáquinas pueden ser muy duraderas, su sistema físico puede ser mucho menos robusto.
Línea de sobretensión

La línea de sobretensión que se muestra en la Figura 5.2 es la curva que pasa por los puntos de flujo más bajos de cada una de las cuatro líneas de velocidad. Como mapa de prueba, estos puntos serían los puntos de flujo más bajos posibles para registrar una lectura estable dentro de la instalación/plataforma de prueba. En muchas aplicaciones industriales, puede ser necesario aumentar la línea de pérdida debido a la contrapresión del sistema. Por ejemplo, a 100 % de RPM, el flujo de pérdida puede aumentar de aproximadamente 0,170 kg/s a 0,215 kg/s debido a la pendiente positiva de la curva de relación de presión.
Como se indicó anteriormente, la razón de esto es que la línea de alta velocidad de la Figura 5.2 presenta una característica de estancamiento o pendiente positiva dentro de ese rango de caudales. Cuando se coloca en un sistema diferente, es posible que esos caudales más bajos no se puedan lograr debido a la interacción con ese sistema. Se ha demostrado matemáticamente que la resistencia del sistema o la presión adversa son los factores críticos que contribuyen al aumento repentino del compresor.
Línea de flujo máximo versus estrangulador
El estrangulamiento se produce en una de dos condiciones. Normalmente, en el caso de los equipos de alta velocidad, a medida que aumenta el flujo, la velocidad del flujo puede acercarse a la velocidad del sonido en algún lugar dentro de la etapa del compresor. Esta ubicación puede ocurrir en la "garganta" de entrada del impulsor o en la "garganta" de entrada del difusor de álabes. Por el contrario, en el caso de los equipos de menor velocidad, a medida que aumentan los flujos, las pérdidas aumentan de tal manera que la relación de presión finalmente cae a 1:1. En este caso, la ocurrencia del estrangulamiento es poco probable.
Las líneas de velocidad de los compresores centrífugos de turbinas de gas suelen presentar estrangulamiento. Se trata de una situación en la que la relación de presión de una línea de velocidad cae rápidamente (verticalmente) con poco o ningún cambio en el flujo. En la mayoría de los casos, la razón de esto es que se han alcanzado velocidades cercanas a Mach 1 en algún lugar dentro del impulsor y/o difusor, lo que genera un rápido aumento de las pérdidas. Los compresores centrífugos de turbocompresor con una relación de presión más alta presentan este mismo fenómeno. El fenómeno de estrangulamiento real es una función de la compresibilidad, medida por el número de Mach local dentro de una restricción de área dentro de la etapa de presión centrífuga.
La línea de caudal máximo, que se muestra en la Figura 5.2, es la curva que pasa por los puntos de caudal más altos de cada línea de velocidad. Al inspeccionarlos, se puede observar que cada uno de estos puntos se ha tomado cerca del 56 % de eficiencia. Seleccionar una eficiencia baja (<60 %) es la práctica más común que se utiliza para terminar los mapas de rendimiento del compresor en caudales altos. Otro factor que se utiliza para establecer la línea de caudal máximo es una relación de presión cercana o igual a 1. La línea de velocidad del 50 % puede considerarse un ejemplo de esto.
La forma de las líneas de velocidad de la Figura 5.2 proporciona un buen ejemplo de por qué no es apropiado utilizar el término estrangulador en asociación con un caudal máximo de todas las líneas de velocidad de los compresores centrífugos. En resumen, la mayoría de los compresores centrífugos industriales y comerciales se seleccionan o diseñan para funcionar en o cerca de sus eficiencias más altas y evitar el funcionamiento a eficiencias bajas. Por esta razón, rara vez hay una razón para ilustrar el rendimiento de un compresor centrífugo por debajo del 60 % de eficiencia.
Muchos mapas de rendimiento de compresores multietapa industriales y comerciales exhiben esta misma característica vertical por una razón diferente relacionada con lo que se conoce como apilamiento de etapas.
Otros límites operativos
- Velocidad mínima de funcionamiento
- La velocidad mínima para un funcionamiento aceptable, por debajo de este valor el compresor puede ser controlado para que se detenga o pase a una condición "inactiva".
- Velocidad máxima permitida
- La velocidad máxima de funcionamiento del compresor. Más allá de este valor, las tensiones pueden superar los límites prescritos y las vibraciones del rotor pueden aumentar rápidamente. A velocidades superiores a este nivel, el equipo puede volverse muy peligroso y se debe controlar a velocidades más bajas.
Análisis dimensional
Para sopesar las ventajas entre los compresores centrífugos es importante comparar 8 parámetros clásicos de las turbomáquinas. En concreto, aumento de presión (p), caudal (Q), velocidad angular (N), potencia (P), densidad (ρ), diámetro (D), viscosidad (μ) y elasticidad (e). Esto crea un problema práctico a la hora de intentar determinar experimentalmente el efecto de cualquier parámetro, ya que es casi imposible cambiar uno de estos parámetros de forma independiente.
El método de procedimiento conocido como el teorema π de Buckingham puede ayudar a resolver este problema generando 5 formas adimensionales de estos parámetros. [1] [ cita requerida ] [16] Estos parámetros Pi proporcionan la base para la "similitud" y las "leyes de afinidad" en turbomáquinas. Permiten la creación de relaciones adicionales (al ser adimensionales) que se consideran valiosas en la caracterización del rendimiento.
Para el ejemplo siguiente, se sustituirá la altura por la presión y la velocidad del sonido por la elasticidad.
Teorema de Buckingham P
Las tres dimensiones independientes utilizadas en este procedimiento para turbomáquinas son:
- masa (la fuerza es una alternativa)
- longitud
- tiempo
Según el teorema, cada uno de los ocho parámetros principales se equipara a sus dimensiones independientes de la siguiente manera:
| Fluir | ej. = m3 / s | ||
| Cabeza | ej. = kg·m/s 2 | ||
| Velocidad | ej. = m/s | ||
| Fuerza | ej. = kg· m2 / s3 | ||
| Densidad | ej. = kg/ m3 | ||
| Viscosidad | ej. = kg/m·s | ||
| Diámetro | ej. = m | ||
| Velocidad del sonido | ej. = m/s |
Similitud clásica de turbomáquinas
Completar la tarea de seguir el procedimiento formal da como resultado la generación de este conjunto clásico de cinco parámetros adimensionales para turbomáquinas. [1] La similitud total se logra cuando cada uno de los 5 parámetros Pi es equivalente al comparar dos casos diferentes. Esto, por supuesto, significaría que las dos turbomáquinas que se comparan son similares, tanto geométricamente como en términos de rendimiento.
| 1 | Coeficiente de flujo | ||
| Coeficiente de carga | |||
| 3 | Coeficiente de velocidad | ||
| 4 | Coeficiente de potencia | ||
| 5 | Coeficiente de Reynolds |
Los analistas de turbomáquinas obtienen una visión enorme del rendimiento mediante la comparación de los 5 parámetros que se muestran en la tabla anterior. En particular, los parámetros de rendimiento como las eficiencias y los coeficientes de pérdida, que también son adimensionales. En la aplicación general, el coeficiente de caudal y el coeficiente de altura se consideran de importancia primaria. Generalmente, para los compresores centrífugos, el coeficiente de velocidad es de importancia secundaria, mientras que el coeficiente de Reynolds es de importancia terciaria. En cambio, como se espera para las bombas, el coeficiente de Reynolds pasa a ser de importancia secundaria y el coeficiente de velocidad de importancia terciaria. Puede resultar interesante que el coeficiente de velocidad se pueda elegir para definir el eje y de la Figura 1.1, mientras que al mismo tiempo se puede elegir el coeficiente de Reynolds para definir el eje z.
Otras combinaciones adimensionales
En la tabla siguiente se muestra otro valor del análisis dimensional. Se puede calcular cualquier cantidad de nuevos parámetros adimensionales mediante exponentes y multiplicación. Por ejemplo, una variación del primer parámetro que se muestra a continuación se utiliza popularmente en el análisis de sistemas de motores de aeronaves. El tercer parámetro es una variación dimensional simplificada del primero y el segundo. Esta tercera definición es aplicable con limitaciones estrictas. El cuarto parámetro, la velocidad específica, es muy conocido y útil porque elimina el diámetro. El quinto parámetro, el diámetro específico, es un parámetro adimensional menos discutido que Balje encontró útil. [38]
| 1 | Coeficiente de flujo másico corregido | ||
| 2 | Forma de Mach equivalente alternativa n.° 1 | ||
| 3 | Forma dimensional simplificada alternativa n.° 2 | ||
| 4 | Coeficiente de velocidad específico | ||
| 5 | Coeficiente de diámetro específico |
Puede resultar interesante que el coeficiente de velocidad específico se pueda utilizar en lugar de la velocidad para definir el eje y de la Figura 1.2, mientras que, al mismo tiempo, el coeficiente de diámetro específico se pueda utilizar en lugar del diámetro para definir el eje z.
Leyes de afinidad
Las siguientes leyes de afinidad se derivan de los cinco parámetros Π que se muestran arriba. Proporcionan una base sencilla para escalar la turbomaquinaria de una aplicación a la siguiente.
| Del coeficiente de flujo | |||
| Del coeficiente de carga | |||
| Del coeficiente de potencia |
Fundamentos aerotermodinámicos
Las siguientes ecuaciones describen un problema matemático completamente tridimensional que es muy difícil de resolver incluso con suposiciones simplificadoras. [10] [39] Hasta hace poco, las limitaciones en el poder computacional obligaban a simplificar estas ecuaciones a un problema bidimensional no viscoso con pseudopérdidas. Antes de la llegada de las computadoras, estas ecuaciones casi siempre se simplificaban a un problema unidimensional.
Resolver este problema unidimensional sigue siendo valioso hoy en día y a menudo se lo denomina análisis de línea media . Incluso con toda esta simplificación, todavía se requieren grandes libros de texto para describirlo y grandes programas informáticos para resolverlo en la práctica.
Conservación de la masa
También denominada continuidad , esta ecuación fundamental escrita en forma general es la siguiente:
Conservación del momento
También denominada ecuación de Navier-Stokes , esta ecuación fundamental se deriva de la segunda ley de Newton cuando se aplica al movimiento de fluidos . Escrita en forma compresible para un fluido newtoniano, esta ecuación se puede escribir de la siguiente manera:
Conservación de energía
La primera ley de la termodinámica es la declaración de la conservación de la energía. En condiciones específicas, el funcionamiento de un compresor centrífugo se considera un proceso reversible. Para un proceso reversible, la cantidad total de calor añadido a un sistema se puede expresar como donde es la temperatura y es la entropía . Por lo tanto, para un proceso reversible:
Dado que U, S y V son funciones termodinámicas del estado, la relación anterior también se cumple para cambios no reversibles. La ecuación anterior se conoce como la relación termodinámica fundamental .
Ecuación de estado
La ley clásica de los gases ideales se puede escribir:
La ley de los gases ideales también puede expresarse de la siguiente manera
donde es la densidad, es el índice adiabático ( relación de calores específicos ), es la energía interna por unidad de masa (la "energía interna específica"), es el calor específico a volumen constante, y es el calor específico a presión constante.
En relación con la ecuación de estado, es importante recordar que, si bien las propiedades del aire y del nitrógeno (en condiciones atmosféricas casi estándar) se pueden estimar de manera fácil y precisa mediante esta sencilla relación, existen muchas aplicaciones de compresores centrífugos en las que la relación ideal es inadecuada. Por ejemplo, los compresores centrífugos utilizados para grandes sistemas de aire acondicionado (enfriadores de agua) utilizan un refrigerante como gas de trabajo que no se puede modelar como un gas ideal. Otro ejemplo son los compresores centrífugos diseñados y construidos para la industria petrolera. La mayoría de los gases de hidrocarburos, como el metano y el etileno, se modelan mejor como una ecuación de estado de gas real en lugar de gases ideales. La entrada de Wikipedia sobre ecuaciones de estado es muy completa.
Pros y contras
- Ventajas
- Los compresores centrífugos ofrecen las ventajas de una fabricación sencilla y un coste relativamente bajo, ya que requieren menos etapas para conseguir el mismo aumento de presión.
- Los compresores centrífugos se utilizan en toda la industria porque tienen menos piezas que rozan, son relativamente eficientes energéticamente y proporcionan un flujo de aire constante mayor y no oscilante que un compresor alternativo de tamaño similar o cualquier otra bomba de desplazamiento positivo .
- Los compresores centrífugos se utilizan principalmente como turbocompresores y en pequeños motores de turbina de gas , como en una APU ( unidad de potencia auxiliar ) y como motor principal para aeronaves más pequeñas, como helicópteros . Una razón importante para esto es que con la tecnología actual, el compresor axial de flujo de aire equivalente será menos eficiente debido principalmente a una combinación de pérdidas de espacio libre variable en las puntas del rotor y del estator.
- Contras
- Su principal inconveniente es que no pueden lograr la alta relación de compresión de los compresores alternativos sin múltiples etapas. Hay pocos compresores centrífugos de una etapa capaces de alcanzar relaciones de presión superiores a 10:1, debido a consideraciones de estrés que limitan gravemente la seguridad, la durabilidad y la expectativa de vida del compresor.
- Los compresores centrífugos son poco prácticos, en comparación con los compresores axiales, para su uso en grandes turbinas de gas y motores turborreactores que propulsan aviones de gran tamaño, debido al peso y al estrés resultantes, y al área frontal que presenta el gran diámetro del difusor radial.
Mecánica estructural, compromiso de fabricación y diseño.
Lo ideal es que los impulsores de los compresores centrífugos tengan álabes aerodinámicos delgados y resistentes, cada uno de ellos montado sobre un rotor ligero. Este material sería fácil de mecanizar o fundir y económico. Además, no generaría ruido de funcionamiento y tendría una larga vida útil en cualquier entorno. [ Aclaración necesaria ]
Desde el comienzo mismo del proceso de diseño aerotermodinámico, las consideraciones y optimizaciones aerodinámicas [29,30] son fundamentales para lograr un diseño exitoso. Durante el diseño, se debe tener en cuenta el material y el método de fabricación del impulsor centrífugo, ya sea plástico para un soplador de aspiradora, aleación de aluminio para un turbocompresor, aleación de acero para un compresor de aire o aleación de titanio para una turbina de gas. Es una combinación de la forma del impulsor del compresor centrífugo, su entorno operativo, su material y su método de fabricación lo que determina la integridad estructural del impulsor. [40] [41]
Véase también
- Momento angular
- Compresor axial
- Fuerza centrífuga
- Fuerza centrípeta
- Efecto Coanda
- Dinámica de fluidos computacional
- Compresibilidad
- Mapa del compresor
- Fuerza de Coriolis
- Ecuación de Darcy-Weisbach
- Entalpía
- Entropía
- Ecuaciones de Euler (dinámica de fluidos)
- Método de elementos finitos
- Dinámica de fluidos
- Leyes de los gases
- Gustavo de Laval
- Ley de los gases ideales
- Cinemática
- Número de Mach
- Flujo multifásico
- Ecuaciones de Navier-Stokes
- Gas real
- Ecuaciones de Navier-Stokes promediadas por Reynolds
- Teorema de transporte de Reynolds
- Número de Reynolds
- Número de Rossby
- Pérdidas tridimensionales y correlación en turbomáquinas
- Turbulencia
- Viscosidad
- Instituto von Karman de Dinámica de Fluidos
Referencias
- ^ abcdefghijklmn Shepherd, Dennis G. (1956). Principios de turbomáquinas (6.ª ed.). Nueva York: Macmillan . LCCN 56002849. OCLC 5899719.
- ^ ab Japikse, David (1996). Diseño y rendimiento de compresores centrífugos . Conceptos ETI. ISBN 978-0-933283-03-9.
- ^ Whitfield, A.; Baines, NC (1990). Diseño de turbomáquinas radiales . Longman Scientific and Technical. ISBN 978-0-470-21667-5.
- ^ abc Aungier, Ronald H. (2000). Compresores centrífugos: una estrategia para el diseño y análisis aerodinámicos . ASME Press. ISBN 978-0-7918-0093-5.
- ^ abJapikse , David; Baines, Carolina del Norte (1998). Tecnología de diseño de difusores . Conceptos ETI. ISBN 978-0-933283-01-5.
- ^ Heinrich, Martin ; Schwarze, Rüdiger (enero de 2016). "Optimización del algoritmo genético de la forma de voluta de un compresor centrífugo". Revista internacional de maquinaria rotatoria . 2016 : 1–13. doi : 10.1155/2016/4849025 .
- ^ Aurel Stodola (1945). Turbinas de vapor y de gas . Nueva York: P. Smith. OL 18625767M.
- ^ Pfleiderer, C. (1952). Turbomáquinas . Nueva York: Springer-Verlag.
- ^ WR Hawthorne (1964). Aerodinámica de turbinas y compresores . Princeton, Nueva Jersey: Princeton University Press. LCCN 58-5029.
- ^ abcd Lakshminarayana, B. (1996). Dinámica de fluidos y transferencia de calor de turbomáquinas . Nueva York: John Wiley & Sons Inc. ISBN 978-0-471-85546-0.
- ^ Japikse, David; Baines, Nicholas C. (1997). Introducción a la turbomáquina . Oxford: Oxford University Press. ISBN 978-0-933283-10-7.
- ^ ab Japikse, David (diciembre de 1986). Técnicas experimentales avanzadas en turbomáquinas . Conceptos ETI. ISBN 978-0-933283-01-5.
- ^ Peng, WW (2007). Fundamentos de turbomáquinas . Nueva York: John Wiley & Sons Inc. ISBN 978-0-470-12422-2.
- ^ abcdefgh Wislicenus, George Friedrich (1965). Mecánica de fluidos de turbomáquinas en dos volúmenes . Nueva York: Dover. ISBN 978-0-486-61345-1.
- ^ abcd Wood, Bernard D. (1969). Aplicaciones de la termodinámica . Reading, Massachusetts: Addison-Wesley Publishing Company. LCCN 75-79598.
- ^ abc Streeter, Victor L. (1971). Mecánica de fluidos, quinta edición . Nueva York: McGraw Hill Book Company. ISBN 978-0-07-062191-6.
- ^ Engeda, Abraham (1999). "Del Palacio de Cristal a la sala de bombas". Ingeniería mecánica . ASME. Archivado desde el original el 15 de enero de 2009.
- ^ Elliott Company. «Pasado, presente, futuro, 1910-2010» (PDF) . Elliott . Consultado el 1 de mayo de 2011 .
- ^ =El desarrollo de motores aeronáuticos a reacción y de turbina, 4.ª edición, Bill Gunston 2006, ISBN 0 7509 4477 3 , pág. 217
- ^ API (julio de 2002). Norma 673-2002 Ventiladores centrífugos para servicios de la industria petrolera, química y del gas. Nueva York: API.[ enlace muerto permanente ]
- ^ Sociedad Estadounidense de Ingenieros Mecánicos. "ASME BPVC". www.asme.org . ASME . Consultado el 13 de diciembre de 2021 .
- ^ Sociedad Estadounidense de Ingenieros Mecánicos. "ASME PTC". www.asme.org . ASME . Consultado el 13 de diciembre de 2021 .
- ^ Instituto Americano del Petróleo. "API STD 617 8.ª ED (E1)". www.api.org . Instituto Americano del Petróleo . Consultado el 13 de diciembre de 2021 .
- ^ Instituto Americano del Petróleo. "API STD 672 5.ª ED (2019)". www.api.org . Instituto Americano del Petróleo . Consultado el 13 de diciembre de 2021 .
- ^ "Descripción del Manual ASHRAE 2021: Fundamentos". www.ashrae.org . Consultado el 20 de febrero de 2022 .
- ^ ab "Normas SAE". SAE/normas/potencia y propulsión/motores . SAE International . Consultado el 23 de abril de 2011 .
- ^ Instituto de Aire y Gas Comprimido. "CAGI". www.cagi.org . Instituto de Aire y Gas Comprimido . Consultado el 13 de diciembre de 2021 .
{{cite web}}: Verificar|url=valor ( ayuda ) - ^ ISO. «ISO - Búsqueda». Organización Internacional de Normalización . Consultado el 13 de diciembre de 2021 .
- ^ Saravanamuttoo, HIH; Rogers, GFC; Cohen, H. (2001). Teoría de la turbina de gas . Prentice-Hall. ISBN 978-0-13-015847-5.
- ^ Baines, Nicholas C. (2005). Fundamentos de la turboalimentación . Conceptos ETI. ISBN 978-0-933283-14-5.
- ^ abcde API (julio de 2002). Std 617-2002 Compresores axiales y centrífugos y compresores expansores para servicios de la industria petrolera, química y del gas . Nueva York: API.
- ^ ASHRAE, Sociedad Estadounidense de Ingenieros de Calefacción, Refrigeración y Aire Acondicionado. "Estándares y pautas". ASHRAE . Consultado el 23 de abril de 2011 .
{{cite web}}: CS1 maint: multiple names: authors list (link) - ^ abcd API (octubre de 2007). Estándar 672-2007 Compresores de aire centrífugos con engranajes integrados y empaquetados para servicios de la industria petrolera, química y del gas . Nueva York: API.
- ^ ab ASME PTC 10-1997 Código de prueba de compresores y extractores. Nueva York: ASME. 1997. ISBN 978-0-7918-2450-4.
- ^ Compresores centrífugos: una guía básica, Boyce 2003, ISBN 0 87814 801 9 , Figura 2-11 Mapa de rendimiento típico de un compresor centrífugo
- ^ Pampreen, Ronald C. (1993). Sobretensión y pérdida de potencia del compresor . Conceptos ETI. ISBN 978-0-933283-05-3.
- ^ Semlitsch, Bernhard; Mihăescu, Mihai (mayo de 2016). "Fenómenos de flujo que provocan picos de presión en un compresor centrífugo". Energía . 103 : 572–587. doi :10.1016/j.energy.2016.03.032.
- ^ Balje, OE (1961). Turbomáquinas: una guía para el diseño, la selección y la teoría . Nueva York: John Wiley & Sons. ISBN 978-0-471-06036-9.
- ^ Cumpsty, NA (2004). Aerodinámica del compresor . Krieger Publishing. ISBN 978-1-57524-247-7.
- ^ Xu, C. y RS Amano, El desarrollo de un impulsor de compresor centrífugo, Revista internacional de métodos computacionales en ciencias de la ingeniería y mecánica, volumen 10, número 4, 2009, páginas 290-301.
- ^ Xu, C., Experiencia de diseño y consideraciones para el desarrollo de compresores centrífugos., J. of Aerospace Eng. 2007
Enlaces externos
- Laboratorio de turbinas de gas del MIT
- (1948), Primera turbina de gas marina en servicio. Revista de la Sociedad Estadounidense de Ingenieros Navales, 60: 66–86. doi :10.1111/j.1559-3584.1948.tb02754.x
- Una historia de los coches de turbina de Chrysler
- Para encontrar códigos API, estándares y publicaciones
- Para encontrar códigos, normas y publicaciones ASME
- Para encontrar códigos, normas y publicaciones ASHRAE
- Centro de Investigación Glenn de la NASA Archivado el 30 de junio de 2009 en Wayback Machine.
- Hidrodinámica de bombas, por Christopher Earls Brennen
- Sitio web de Ctrend para calcular la altura del compresor centrífugo en línea



































































