Esferas celestiales
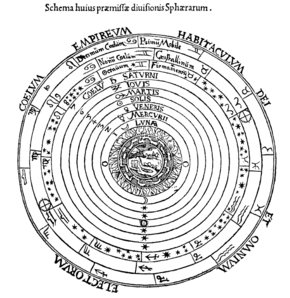
Elementos de algunos modelos cosmológicos

Esferas celestes geocéntricas; Cosmographia de Peter Apian (Amberes, 1539)

Las esferas celestes , u orbes celestes , fueron las entidades fundamentales de los modelos cosmológicos desarrollados por Platón , Eudoxo , Aristóteles , Ptolomeo , Copérnico y otros. En estos modelos celestes, los movimientos aparentes de las estrellas fijas y los planetas se explican tratándolos como incrustados en esferas giratorias hechas de un quinto elemento etéreo y transparente ( quintaesencia ), como gemas engastadas en orbes. Dado que se creía que las estrellas fijas no cambiaban sus posiciones relativas entre sí, se argumentó que debían estar en la superficie de una única esfera estelar. [1]

En el pensamiento moderno, las órbitas de los planetas se consideran como las trayectorias de esos planetas a través del espacio mayoritariamente vacío. Sin embargo, los pensadores antiguos y medievales consideraban que los orbes celestes eran esferas gruesas de materia enrarecida anidadas una dentro de otra, cada una en completo contacto con la esfera superior y la esfera inferior. [2] Cuando los eruditos aplicaron los epiciclos de Ptolomeo , supusieron que cada esfera planetaria era exactamente lo suficientemente gruesa como para acomodarlos. [2] Al combinar este modelo de esfera anidada con observaciones astronómicas, los eruditos calcularon lo que se convirtieron en valores generalmente aceptados en ese momento para las distancias al Sol: aproximadamente 4 millones de millas (6,4 millones de kilómetros), a los otros planetas y al borde del universo: aproximadamente 73 millones de millas (117 millones de kilómetros). [3] Las distancias del modelo de esfera anidada al Sol y los planetas difieren significativamente de las mediciones modernas de las distancias, [4] y ahora se sabe que el tamaño del universo es inconcebiblemente grande y está en continua expansión . [5]

Albert Van Helden ha sugerido que desde aproximadamente 1250 hasta el siglo XVII, prácticamente todos los europeos cultos estaban familiarizados con el modelo ptolemaico de "esferas anidadas y las dimensiones cósmicas derivadas de él". [6] Incluso después de la adopción del modelo heliocéntrico del universo de Copérnico, se introdujeron nuevas versiones del modelo de esfera celeste, con las esferas planetarias siguiendo esta secuencia a partir del Sol central: Mercurio, Venus, Tierra-Luna, Marte, Júpiter y Saturno.

La creencia dominante en la teoría de las esferas celestes no sobrevivió a la Revolución científica . A principios del siglo XVII, Kepler siguió discutiendo las esferas celestes, aunque no consideraba que los planetas fueran transportados por las esferas, sino que sostenía que se movían en trayectorias elípticas descritas por las leyes de Kepler del movimiento planetario . A finales del siglo XVII, las teorías griegas y medievales sobre el movimiento de los objetos terrestres y celestes fueron reemplazadas por la ley de gravitación universal de Newton y la mecánica newtoniana , que explican cómo las leyes de Kepler surgen de la atracción gravitatoria entre los cuerpos.

Historia

Primeras ideas sobre esferas y círculos

En la antigüedad griega, las ideas de esferas y anillos celestes aparecieron por primera vez en la cosmología de Anaximandro a principios del siglo VI a. C. [7] En su cosmología, tanto el Sol como la Luna son aberturas circulares abiertas en anillos tubulares de fuego encerrados en tubos de aire condensado; estos anillos constituyen los bordes de las ruedas giratorias similares a carros que giran sobre la Tierra en su centro. Las estrellas fijas también son aberturas abiertas en tales bordes de ruedas, pero hay tantas ruedas de este tipo para las estrellas que sus bordes contiguos forman todos juntos una envoltura esférica continua que rodea la Tierra. Todos estos bordes de ruedas se habían formado originalmente a partir de una esfera original de fuego que rodeaba por completo la Tierra, que se había desintegrado en muchos anillos individuales. [8] Por lo tanto, en la cosmogonía de Anaximandro, en el principio era la esfera, a partir de la cual se formaron los anillos celestes, de algunos de los cuales se compuso a su vez la esfera estelar. Visto desde la Tierra, el anillo del Sol era el más alto, el de la Luna el más bajo y la esfera de las estrellas la más baja.

Siguiendo a Anaximandro, su discípulo Anaxímenes ( c.  585  – c.  528/4 ) sostuvo que las estrellas, el Sol, la Luna y los planetas están todos hechos de fuego. Pero mientras que las estrellas están fijadas en una esfera de cristal giratoria como clavos o tachuelas, el Sol, la Luna y los planetas, y también la Tierra, todos simplemente viajan en el aire como hojas debido a su anchura. [9] Y mientras que las estrellas fijas son transportadas en un círculo completo por la esfera estelar, el Sol, la Luna y los planetas no giran bajo la Tierra entre la puesta y la salida de nuevo como lo hacen las estrellas, sino que, al ponerse, giran lateralmente alrededor de la Tierra como un gorro que gira hasta la mitad de la cabeza hasta que vuelven a salir. Y a diferencia de Anaximandro, relegó las estrellas fijas a la región más distante de la Tierra. La característica más duradera del cosmos de Anaxímenes fue su concepción de las estrellas fijas en una esfera de cristal como en un marco rígido, que se convirtió en un principio fundamental de la cosmología hasta Copérnico y Kepler.

Después de Anaxímenes, Pitágoras , Jenófanes y Parménides sostuvieron que el universo era esférico. [10] Y mucho más tarde, en el siglo IV a. C., el Timeo de Platón propuso que el cuerpo del cosmos estaba hecho en la forma más perfecta y uniforme, la de una esfera que contenía las estrellas fijas. [11] Pero postuló que los planetas eran cuerpos esféricos dispuestos en bandas o anillos giratorios en lugar de llantas como en la cosmología de Anaximandro.

Surgimiento de las esferas planetarias

En lugar de bandas, Eudoxo, discípulo de Platón, desarrolló un modelo planetario utilizando esferas concéntricas para todos los planetas, con tres esferas para cada uno de sus modelos de la Luna y el Sol y cuatro para cada uno de los modelos de los otros cinco planetas, lo que hace un total de 26 esferas. [12] [13] Calipo modificó este sistema, utilizando cinco esferas para sus modelos del Sol, la Luna, Mercurio, Venus y Marte y conservando cuatro esferas para los modelos de Júpiter y Saturno, lo que hace un total de 33 esferas. [13] Cada planeta está unido a la más interna de su propio conjunto particular de esferas. Aunque los modelos de Eudoxo y Calipo describen cualitativamente las principales características del movimiento de los planetas, no logran dar cuenta exactamente de estos movimientos y, por lo tanto, no pueden proporcionar predicciones cuantitativas. [14] Aunque los historiadores de la ciencia griega han considerado tradicionalmente que estos modelos eran meras representaciones geométricas, [15] [16] estudios recientes han propuesto que también estaban destinados a ser físicamente reales [17] o han retenido su juicio, señalando la evidencia limitada para resolver la cuestión. [18]

En su Metafísica , Aristóteles desarrolló una cosmología física de esferas, basada en los modelos matemáticos de Eudoxo. En el modelo celestial completamente desarrollado de Aristóteles, la Tierra esférica está en el centro del universo y los planetas son movidos por 47 o 55 esferas interconectadas que forman un sistema planetario unificado, [19] mientras que en los modelos de Eudoxo y Calipo el conjunto individual de esferas de cada planeta no estaba conectado con el del planeta siguiente. Aristóteles dice que el número exacto de esferas, y por lo tanto el número de motores, debe determinarse mediante investigación astronómica, pero agregó esferas adicionales a las propuestas por Eudoxo y Calipo, para contrarrestar el movimiento de las esferas externas. Aristóteles considera que estas esferas están hechas de un quinto elemento inmutable, el éter . Cada una de estas esferas concéntricas es movida por su propio dios, un motor divino inmutable e inmóvil , y que mueve su esfera simplemente en virtud de ser amado por él. [20]

Modelo ptolemaico de las esferas de Venus, Marte, Júpiter y Saturno con epiciclo , deferente excéntrico y punto ecuante . Georg von Peuerbach , Theoricae novae planetarum , 1474.

En su Almagesto , el astrónomo Ptolomeo (fl. c. 150 d. C.) desarrolló modelos predictivos geométricos de los movimientos de las estrellas y los planetas y los extendió a un modelo físico unificado del cosmos en sus Hipótesis planetarias . [21] [22] [23] [24] Al usar excéntricos y epiciclos , su modelo geométrico logró un mayor detalle matemático y precisión predictiva que la que habían exhibido los modelos esféricos concéntricos anteriores del cosmos. [25] En el modelo físico de Ptolomeo, cada planeta está contenido en dos o más esferas, [26] pero en el Libro 2 de sus Hipótesis planetarias, Ptolomeo representó rebanadas circulares gruesas en lugar de esferas como en su Libro 1. Una esfera/rebanada es el deferente , con un centro desplazado algo de la Tierra; la otra esfera/rebanada es un epiciclo incrustado en el deferente, con el planeta incrustado en la esfera/rebanada epicíclica. [27] El modelo de esferas anidadas de Ptolomeo proporcionó las dimensiones generales del cosmos, siendo la distancia máxima de Saturno 19.865 veces el radio de la Tierra y la distancia de las estrellas fijas al menos 20.000 radios terrestres. [26]

Las esferas planetarias se dispusieron hacia afuera desde la Tierra esférica y estacionaria en el centro del universo en este orden: las esferas de la Luna , Mercurio , Venus , Sol , Marte , Júpiter y Saturno . En modelos más detallados, las siete esferas planetarias contenían otras esferas secundarias dentro de ellas. Las esferas planetarias fueron seguidas por la esfera estelar que contenía las estrellas fijas; otros eruditos agregaron una novena esfera para explicar la precesión de los equinoccios , una décima para explicar la supuesta trepidación de los equinoccios e incluso una undécima para explicar la oblicuidad cambiante de la eclíptica . [28] En la antigüedad, el orden de los planetas inferiores no fue aceptado universalmente. Platón y sus seguidores los ordenaron Luna, Sol, Mercurio, Venus y luego siguieron el modelo estándar para las esferas superiores. [29] [30] Otros no estaban de acuerdo sobre el lugar relativo de las esferas de Mercurio y Venus: Ptolomeo colocó a ambas debajo del Sol con Venus sobre Mercurio, pero señaló que otros las colocaron a ambas sobre el Sol; algunos pensadores medievales, como al-Bitruji , colocaron la esfera de Venus sobre el Sol y la de Mercurio debajo de él. [31]

Edad media

La Tierra dentro de siete esferas celestes, de Beda , De natura rerum , finales del siglo XI

Discusiones astronómicas

Una serie de astrónomos, comenzando con el astrónomo musulmán al-Farghānī , utilizaron el modelo ptolemaico de esferas anidadas para calcular distancias a las estrellas y esferas planetarias. La distancia de al-Farghānī a las estrellas era de 20.110 radios terrestres que, suponiendo que el radio de la Tierra fuera de 3.250 millas (5.230 kilómetros), ascendía a 65.357.500 millas (105.182.700 kilómetros). [32] Una introducción al Almagesto de Ptolomeo , el Tashil al-Majisti , que se cree que fue escrito por Thābit ibn Qurra , presentó variaciones menores de las distancias de Ptolomeo a las esferas celestes. [33] En su Zij , Al-Battānī presentó cálculos independientes de las distancias a los planetas sobre el modelo de esferas anidadas, que él creía que se debían a los eruditos que escribieron después de Ptolomeo. Sus cálculos arrojaron una distancia de 19.000 radios terrestres a las estrellas. [34]

A finales del milenio, el astrónomo y erudito árabe Ibn al-Haytham (Alhacen) presentó un desarrollo de los modelos geocéntricos de Ptolomeo en términos de esferas anidadas. A pesar de la similitud de este concepto con el de las Hipótesis planetarias de Ptolomeo , la presentación de al-Haytham difiere en suficiente detalle como para que se haya argumentado que refleja un desarrollo independiente del concepto. [35] En los capítulos 15-16 de su Libro de Óptica , Ibn al-Haytham también dijo que las esferas celestes no consisten en materia sólida . [36]

A finales del siglo XII, el astrónomo musulmán español Al-Bitrūjī (Alpetragius) intentó explicar los complejos movimientos de los planetas sin los epiciclos y excéntricos de Ptolomeo, utilizando un marco aristotélico de esferas puramente concéntricas que se movían a distintas velocidades de este a oeste. Este modelo era mucho menos preciso como modelo astronómico predictivo, [37] pero fue discutido por astrónomos y filósofos europeos posteriores. [38] [39]

En el siglo XIII, el astrónomo al-'Urḍi propuso un cambio radical en el sistema de esferas anidadas de Ptolomeo. En su Kitāb al-Hayáh , recalculó la distancia de los planetas utilizando parámetros que él mismo determinó de nuevo. Tomando la distancia del Sol como 1266 radios terrestres, se vio obligado a colocar la esfera de Venus por encima de la esfera del Sol; como un refinamiento adicional, agregó los diámetros de los planetas al grosor de sus esferas. Como consecuencia, su versión del modelo de esferas anidadas tenía la esfera de las estrellas a una distancia de 140.177 radios terrestres. [34]

Casi al mismo tiempo, los académicos de las universidades europeas comenzaron a abordar las implicaciones de la filosofía redescubierta de Aristóteles y la astronomía de Ptolomeo. Tanto los eruditos astronómicos como los escritores populares consideraron las implicaciones del modelo de esferas anidadas para las dimensiones del universo. [40] El texto astronómico introductorio de Campanus de Novara , Theorica planetarum , utilizó el modelo de esferas anidadas para calcular las distancias de los diversos planetas a la Tierra, que dio como 22.612 radios terrestres o 73.387.747+100 ⁄ 660 millas (118.106.130,55 km). [41] [42] En su Opus Majus , Roger Bacon citó la distancia de Al-Farghānī a las estrellas de 20.110 radios terrestres, o 65.357.700 millas (105.183.000 km), a partir de la cual calculó que la circunferencia del universo era de 410.818.517+3 ⁄ 7 millas (661,148,316.1 km). [43] Una evidencia clara de que se pensaba que este modelo representaba la realidad física son los relatos encontrados en el Opus Majus de Bacon sobre el tiempo necesario para caminar hasta la Luna [44] y en el popular Legendary del inglés medio del sur de Inglaterra , que tomaría 8,000 años para alcanzar el cielo estrellado más alto. [45] [46] La comprensión general de las dimensiones del universo derivadas del modelo de esfera anidada llegó a audiencias más amplias a través de las presentaciones en hebreo de Moisés Maimónides , en francés de Gossuin de Metz y en italiano de Dante Alighieri . [47]

Discusiones filosóficas y teológicas

Los filósofos estaban menos interesados ​​en esos cálculos matemáticos que en la naturaleza de las esferas celestes, su relación con los relatos revelados de la naturaleza creada y las causas de su movimiento.

Adi Setia describe el debate entre los eruditos islámicos en el siglo XII, basado en el comentario de Fakhr al-Din al-Razi sobre si las esferas celestes son cuerpos físicos reales y concretos o "simplemente los círculos abstractos en los cielos trazados... por las diversas estrellas y planetas". Setia señala que la mayoría de los eruditos y los astrónomos dijeron que eran esferas sólidas "sobre las que giran las estrellas... y esta opinión se acerca más al sentido aparente de los versículos coránicos sobre las órbitas celestes". Sin embargo, al-Razi menciona que algunos, como el erudito islámico Dahhak, las consideraban abstractas. Al-Razi mismo estaba indeciso, dijo: "En verdad, no hay manera de determinar las características de los cielos excepto por la autoridad [de la revelación divina o las tradiciones proféticas]". Setia concluye: "Así pues, parece que para al-Razi (y para otros antes y después de él), los modelos astronómicos, cualquiera que sea su utilidad o falta de ella para ordenar los cielos, no están fundados en pruebas racionales sólidas, y por tanto no se puede hacer ningún compromiso intelectual con ellos en lo que respecta a la descripción y explicación de las realidades celestiales". [48]

Los filósofos cristianos y musulmanes modificaron el sistema de Ptolomeo para incluir una región exterior inamovible, el cielo empíreo , que llegó a identificarse como la morada de Dios y todos los elegidos. [49] Los cristianos medievales identificaron la esfera de estrellas con el firmamento bíblico y, a veces, postularon una capa invisible de agua sobre el firmamento, para concordar con el Génesis . [50] Una esfera exterior, habitada por ángeles , apareció en algunos relatos. [51]

Edward Grant , un historiador de la ciencia, ha aportado pruebas de que los filósofos escolásticos medievales consideraban generalmente que las esferas celestes eran sólidas en el sentido de tridimensionales o continuas, pero la mayoría no las consideraba sólidas en el sentido de duras. El consenso era que las esferas celestes estaban hechas de algún tipo de fluido continuo. [52]

Más tarde en el siglo, el mutakallim Adud al-Din al-Iji (1281-1355) rechazó el principio del movimiento circular y uniforme, siguiendo la doctrina ash'ari del atomismo , que sostenía que todos los efectos físicos eran causados ​​directamente por la voluntad de Dios en lugar de por causas naturales. [53] Sostuvo que las esferas celestiales eran "cosas imaginarias" y "más tenues que una telaraña". [54] Sus puntos de vista fueron desafiados por al-Jurjani (1339-1413), quien sostuvo que incluso si las esferas celestiales "no tienen una realidad externa, sin embargo son cosas que se imaginan correctamente y corresponden a lo que [existe] en la actualidad". [54]

Los astrónomos y filósofos medievales desarrollaron diversas teorías sobre las causas de los movimientos de las esferas celestes. Intentaron explicar los movimientos de las esferas en términos de los materiales de los que se pensaba que estaban hechas, motores externos como las inteligencias celestiales y motores internos como las almas motrices o las fuerzas impresas. La mayoría de estos modelos eran cualitativos, aunque unos pocos incorporaron análisis cuantitativos que relacionaban la velocidad, la fuerza motriz y la resistencia. [55] A finales de la Edad Media, la opinión común en Europa era que los cuerpos celestes eran movidos por inteligencias externas, identificadas con los ángeles de la revelación . [56] La esfera móvil más externa , que se movía con el movimiento diario que afectaba a todas las esferas subordinadas, era movida por un motor inmóvil , el Primer Motor , que se identificaba con Dios. Cada una de las esferas inferiores era movida por un motor espiritual subordinado (un reemplazo de los múltiples motores divinos de Aristóteles), llamado inteligencia. [57]

Renacimiento

Modelo heliocéntrico copernicano de los orbes celestes de Thomas Digges de 1576

A principios del siglo XVI, Nicolás Copérnico reformó drásticamente el modelo de la astronomía desplazando a la Tierra de su lugar central en favor del Sol, aunque llamó a su gran obra De revolutionibus orbium coelestium ( Sobre las revoluciones de las esferas celestes ). Aunque Copérnico no trata la naturaleza física de las esferas en detalle, sus pocas alusiones dejan claro que, como muchos de sus predecesores, aceptó esferas celestes no sólidas. [58] Copérnico rechazó las esferas novena y décima, colocó el orbe de la Luna alrededor de la Tierra y movió al Sol desde su orbe al centro del universo . Los orbes planetarios giraban alrededor del centro del universo en el siguiente orden: Mercurio, Venus, el gran orbe que contiene la Tierra y el orbe de la Luna, luego los orbes de Marte, Júpiter y Saturno. Finalmente conservó la octava esfera de las estrellas , que sostuvo que era estacionaria. [59]

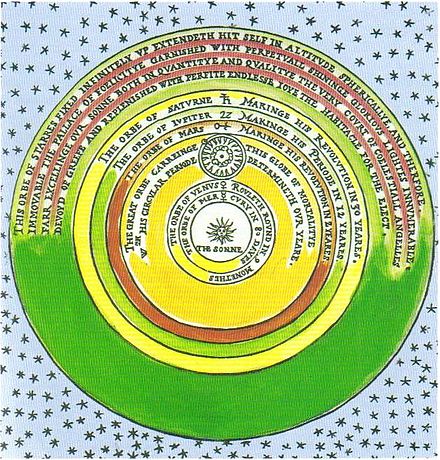
El creador de almanaques inglés, Thomas Digges , delineó las esferas del nuevo sistema cosmológico en su Descripción perfecta de los orbes celestiales... (1576). Allí dispuso los "orbes" en el nuevo orden copernicano, expandiendo una esfera para albergar "el globo de la mortalidad", la Tierra, los cuatro elementos clásicos y la Luna, y expandiendo la esfera de estrellas infinitamente para abarcar todas las estrellas y también para servir como "la corte del Gran Dios, la morada de los elegidos y de los ángeles celestiales". [60]

Diagrama de las esferas celestes y de los espacios entre ellas elaborado por Johannes Kepler, siguiendo la opinión de Copérnico ( Mysterium Cosmographicum , 2.ª ed., 1621)

En el siglo XVI, varios filósofos, teólogos y astrónomos, entre ellos Francesco Patrizi , Andrea Cisalpino, Peter Ramus , Robert Bellarmine , Giordano Bruno , Jerónimo Muñoz, Michael Neander , Jean Pena y Christoph Rothmann , abandonaron el concepto de esferas celestes. [61] Rothmann argumentó a partir de las observaciones del cometa de 1585 que la falta de paralaje observado indicaba que el cometa estaba más allá de Saturno, mientras que la ausencia de refracción observada indicaba que la región celeste era del mismo material que el aire, por lo tanto, no había esferas planetarias. [62]

Las investigaciones de Tycho Brahe sobre una serie de cometas entre 1577 y 1585, con la ayuda de la discusión de Rothmann sobre el cometa de 1585 y las distancias tabuladas de Michael Maestlin del cometa de 1577, que pasó por los orbes planetarios, llevaron a Tycho a concluir [63] que "la estructura de los cielos era muy fluida y simple". Tycho opuso su punto de vista al de "muchísimos filósofos modernos" que dividían los cielos en "varios orbes hechos de materia dura e impermeable". Edward Grant encontró relativamente pocos creyentes en esferas celestiales duras antes de Copérnico y concluyó que la idea se volvió común por primera vez en algún momento entre la publicación de De revolutionibus de Copérnico en 1542 y la publicación de Tycho Brahe de su investigación cometaria en 1588. [64] [65]

En su temprano Mysterium Cosmographicum , Johannes Kepler consideró las distancias de los planetas y los consiguientes huecos requeridos entre las esferas planetarias implicadas por el sistema copernicano, que había sido notado por su antiguo maestro, Michael Maestlin. [66] La cosmología platónica de Kepler llenó los grandes huecos con los cinco poliedros platónicos , que explicaban la distancia astronómica medida de las esferas. [67] [ página requerida ] En la física celestial madura de Kepler, las esferas eran consideradas como las regiones espaciales puramente geométricas que contenían cada órbita planetaria en lugar de como los orbes físicos giratorios de la física celestial aristotélica anterior. La excentricidad de la órbita de cada planeta definía así los radios de los límites interno y externo de su esfera celeste y, por lo tanto, su espesor. En la mecánica celestial de Kepler , la causa del movimiento planetario se convirtió en el Sol en rotación, a su vez girado por su propia alma motriz. [68] Sin embargo, una esfera estelar inmóvil era un remanente duradero de las esferas celestes físicas en la cosmología de Kepler.

Expresiones literarias y visuales

"Porque el universo medieval es finito, tiene una forma, la forma esférica perfecta, que contiene en sí una variedad ordenada...
"Las esferas... nos presentan un objeto en el que la mente puede descansar, abrumador en su grandeza pero satisfactorio en su armonía."

CS Lewis , La imagen descartada , pág. 99.

Dante y Beatriz contemplan el Cielo más alto; de las ilustraciones de Gustave Doré para la Divina Comedia , Paraíso, Canto 28, líneas 16-39.

En El sueño de Escipión de Cicerón , el anciano Escipión el Africano describe un ascenso a través de las esferas celestiales, en comparación con el cual la Tierra y el Imperio romano se reducen a la insignificancia. Un comentario sobre El sueño de Escipión del escritor romano Macrobio , que incluía un análisis de las diversas escuelas de pensamiento sobre el orden de las esferas, contribuyó en gran medida a difundir la idea de las esferas celestiales a lo largo de la Alta Edad Media . [69]

Nicole Oresme, Le livre du Ciel et du Monde, París, BnF, Manuscrits, P. 565, f. 69 (1377)

Algunas figuras de finales de la Edad Media observaron que el orden físico de las esferas celestiales era inverso a su orden en el plano espiritual, donde Dios estaba en el centro y la Tierra en la periferia. Cerca del comienzo del siglo XIV, Dante , en el Paraíso de su Divina Comedia , describió a Dios como una luz en el centro del cosmos. [70] Aquí el poeta asciende más allá de la existencia física al Cielo Empíreo , donde se encuentra cara a cara con Dios mismo y se le concede la comprensión de la naturaleza divina y humana. Más tarde en el siglo, el iluminador de Le livre du Ciel et du Monde de Nicole Oresme , una traducción y comentario sobre el De caelo de Aristóteles producido para el patrón de Oresme, el rey Carlos V , empleó el mismo motivo. Dibujó las esferas en el orden convencional, con la Luna más cercana a la Tierra y las estrellas más altas, pero las esferas eran cóncavas hacia arriba, centradas en Dios, en lugar de cóncavas hacia abajo, centradas en la Tierra. [71] Debajo de esta figura, Oresme cita los Salmos : "Los cielos declaran la gloria de Dios y el firmamento anuncia la obra de sus manos". [72]

La epopeya portuguesa de finales del siglo XVI, Los Lusíadas, describe vívidamente las esferas celestiales como una "gran máquina del universo" construida por Dios. [73] Al explorador Vasco da Gama se le muestran las esferas celestiales en forma de un modelo mecánico. Contrariamente a la representación de Cicerón, el recorrido de Da Gama por las esferas comienza con el Empíreo, luego desciende hacia el interior de la Tierra, culminando en un estudio de los dominios y divisiones de los reinos terrenales, magnificando así la importancia de las acciones humanas en el plan divino.

Véase también

Notas

  1. ^ Grant, Planetas, estrellas y orbes , pág. 440.
  2. ^ ab Lindberg, Comienzos de la ciencia occidental , pág. 251.
  3. ^ Van Helden, Midiendo el universo , págs.
  4. ^ Grant, Planetas, estrellas y orbes , págs. 437–8.
  5. ^ Van Helden, Midiendo el universo , p. 3.
  6. ^ Van Helden, Midiendo el universo , págs.37, 40.
  7. ^ Véase el capítulo 4 de Aristarco de Samos de Heath , 1913/97 Oxford University Press/Sandpiper Books Ltd; véase la pág. 11 de El mundo de Parménides de Popper , Routledge 1998
  8. ^ Heath ibíd. págs. 26-8
  9. ^ Véase el capítulo 5 de Aristarco de Samos de Heath de 1913.
  10. ^ Para las cosmologías esferistas de Jenófanes y Parménides, véase Heath ibid, capítulo 7 y capítulo 9 respectivamente, y Popper ibid, Ensayos 2 y 3.
  11. ^ FM Cornford, La cosmología de Platón: El Timeo de Platón , págs. 54-57
  12. ^ Neugebauer, Historia de la astronomía matemática antigua, vol. 2, págs. 677–85.
  13. ^ ab Lloyd, "Aberraciones celestiales", pág. 173.
  14. ^ Neugebauer, Historia de la astronomía matemática antigua, vol. 2, págs. 677–85.
  15. ^ Dreyer, Historia de los sistemas planetarios , págs. 90-1, 121-2
  16. ^ Lloyd, Aristóteles , pág. 150.
  17. ^ Larry Wright, "La astronomía de Eudoxo: geometría o física", Estudios en historia y filosofía de la ciencia , 4 (1973): 165–72.
  18. ^ GER Lloyd, "Salvando los fenómenos", Classical Quarterly, 28 (1978): 202–222, pág. 219.
  19. ^ Aristóteles, Metafísica 1073b1–1074a13, págs. 882–883 en Las obras básicas de Aristóteles Richard McKeon, ed., The Modern Library 2001
  20. ^ "La causa final, entonces, produce el movimiento al ser amada, pero todas las demás cosas se mueven al ser movidas" Aristóteles, Metafísica 1072b4.
  21. ^ Neugebauer, Historia de la astronomía matemática antigua, págs. 111-12, 148
  22. ^ Pedersen, Física y astronomía tempranas, pág. 87
  23. ^ Crowe, Teorías del mundo , págs. 45, 49-50, 72,
  24. ^ Linton, De Eudoxo a Einstein , págs. 63-64, 81.
  25. ^ Taliaferro , Introducción del traductor al Almagesto , pág. 1; Dreyer, Historia de los sistemas planetarios , págs. 160, 167.
  26. ^ ab Neugebauer, Historia de la astronomía matemática antigua , vol. 2, págs. 917–926.
  27. ^ Andrea Murschel, "La estructura y función de las hipótesis físicas de Ptolomeo sobre el movimiento planetario", Revista de Historia de la Astronomía, 26(1995): 33–61.
  28. ^ Francis R. Johnson, "El cielo imperial de Marlowe", ELH , 12 (1945): 35–44, pág. 39
  29. ^ Bruce S. Eastwood, Ordenando los cielos: astronomía y cosmología romana en el Renacimiento carolingio, (Leiden: Brill) 2007, págs. 36-45
  30. ^ En su De Revolutionibus Bk1.10 Copérnico afirmó que la razón empírica por la que los seguidores de Platón situaban las órbitas de Mercurio y Venus por encima de la del Sol era que, si fueran subsolares, entonces, por la luz reflejada del Sol, sólo aparecerían como hemisferios a lo sumo y también eclipsarían a veces al Sol, pero no hacen ninguna de las dos cosas. (Véase p521 Grandes libros del mundo occidental 16 Ptolomeo–Copérnico–Kepler )
  31. ^ al-Biţrūjī. (1971) Sobre los principios de la astronomía , 7.159–65, trad. Bernard R. Goldstein, vol. 1, págs. 123–5. New Haven: Universidad de Yale. ISBN  0-300-01387-6
  32. ^ Van Helden, Midiendo el universo , págs.
  33. ^ Van Helden, Midiendo el universo , p. 31.
  34. ^ ab Van Helden, Midiendo el universo , págs.
  35. ^ Langermann, Y. Tzvi (1990). Ibn al Haytham's on the Configuration of the World . Nueva York: Garland Publishing. págs. 11-25.
  36. ^ Rosen, Edward (1985). "La disolución de las esferas celestes sólidas". Revista de la historia de las ideas . 46 (1): 13–31 [19–20, 21]. doi :10.2307/2709773. JSTOR  2709773..
  37. ^ Goldstein, Bernard R. (1971). Al-Bitrūjī: Sobre los principios de la astronomía . Vol. 1. New Haven: Yale University Press. págs. 40–5.
  38. ^ Goldstein, Al-Bitrūjī , pág. 6.
  39. ^ Grant, Planetas, estrellas y orbes, págs. 563–6.
  40. ^ Grant, Planetas, estrellas y orbes , págs. 433–43.
  41. ^ Grant, Planetas, estrellas y orbes , págs. 434–8.
  42. ^ Van Helden, Midiendo el universo , págs.
  43. ^ Van Helden, Midiendo el universo , p. 36.
  44. ^ Van Helden, Midiendo el universo , p. 35.
  45. ^ Lewis, La imagen descartada , págs. 97–8.
  46. ^ Van Helden, Midiendo el universo , p. 38.
  47. ^ Van Helden, Midiendo el universo , págs.
  48. ^ Adi Setia (2004), "Fakhr Al-Din Al-Razi sobre la física y la naturaleza del mundo físico: un estudio preliminar", Islam & Science , 2 , consultado el 2 de marzo de 2010
  49. ^ Grant, Planetas, estrellas y orbes, págs. 382–3.
  50. ^ Lindberg, Comienzos de la ciencia occidental , págs. 249–50.
  51. ^ Lindberg, Comienzos de la ciencia occidental , pág. 250.
  52. ^ Grant, Planetas, estrellas y orbes, págs. 328–30.
  53. ^ Huff, Toby (2003). El auge de la ciencia moderna temprana: el Islam, China y Occidente . Cambridge University Press . pág. 175. ISBN. 978-0-521-52994-5.
  54. ^ ab Ragep, F. Jamil; Al-Qushji, Ali (2001). "Liberar la astronomía de la filosofía: un aspecto de la influencia islámica en la ciencia". Osiris . 2.ª serie. 16 (La ciencia en contextos teístas: dimensiones cognitivas): 55–57. Bibcode :2001Osir...16...49R. doi :10.1086/649338. ISSN  0369-7827. JSTOR  301979. S2CID  142586786.
  55. ^ Grant, Planetas, estrellas y orbes, pág. 541.
  56. ^ Grant, Planetas, estrellas y orbes, pág. 527.
  57. ^ Grant, Planetas, estrellas y orbes, págs. 526–45.
  58. ^ Nicholas Jardine, "El significado de los orbes copernicanos", Journal for the History of Astronomy, 13 (1982): 168–94, págs. 177–78.
  59. ↑ Hilderich von Varel (Edo Hildericus), Propositiones Cosmographicae de Globi Terreni Dimensione, (Frankfurt ad Oder, 1576), citado en Peter Barker y Bernard R. Goldstein, "Realismo e instrumentalismo en la astronomía del siglo XVI: una reevaluación", Perspectivas sobre la ciencia 6.3 (1998): 232–58, págs. 242–23.
  60. ^ Koyre, Desde el mundo cerrado , págs. 28-30.
  61. ^ Michael A. Granada, "¿Eliminó Tycho las esferas celestes antes de 1586?", Journal for the History of Astronomy, 37 (2006): 126–45, págs. 127–29.
  62. ^ Bernard R. Goldstein y Peter Barker, "El papel de Rothmann en la disolución de las esferas celestes", The British Journal for the History of Science , 28 (1995): 385–403, págs. 390–91.
  63. ^ Michael A. Granada, "¿Eliminó Tycho las esferas celestes antes de 1586?", Journal for the History of Astronomy, 37 (2006): 126–45, págs. 132–38.
  64. ^ Grant, "Orbes celestiales", págs. 185-86.
  65. ^ Grant, Planetas, estrellas y orbes, págs. 345–48.
  66. ^ Grasshoff, "El misterio de Michael Maestlin".
  67. ^ Campo, Cosmología geométrica de Kepler .
  68. ↑ Johannes Kepler, Epítome de la astronomía copernicana , vol. 1, libro 4.2.3, págs. 514-15 (1630).
  69. ↑ Macrobio, Comentario sobre el sueño de Escipión, traducido por William Harris Stahl, Nueva York: Columbia Univ. Pr., 1952; sobre el orden de las esferas, véanse las págs. 162-165.
  70. ^ CS Lewis, La imagen descartada: Una introducción a la literatura medieval y renacentista, Cambridge: Cambridge Univ. Pr., 1964, pág. 116. ISBN 0-521-09450-X . 
  71. ^ Nicole Oreseme, "Le livre du Ciel et du Monde", 1377, consultado el 2 de junio de 2007.[1]
  72. ^ Sal. 18: 2; citado en Nicole Oresme, Le livre du ciel et du monde, editado y traducido por A, D. Menut y AJ Denomy, Madison: Univ. of Wisconsin Pr., 1968, págs. 282–283.
  73. ↑ Luiz Vaz de Camões, Las Lusiadas , traducido por Landeg White. Prensa de la Universidad de Oxford, 2010.

Bibliografía

  • Metafísica de Aristóteles , en 'Las obras básicas de Aristóteles' Richard McKeon (Ed) The Modern Library, 2001
  • Clagett, Marshall La ciencia de la mecánica en la Edad Media University of Wisconsin Press 1959
  • Cohen, IB y Whitman, A. Principia, University of California Press, 1999
  • Cohen y Smith (eds.) El compañero de Cambridge para Newton CUP 2002
  • Copérnico, Nicolás Sobre las revoluciones de las esferas celestes , en Grandes libros del mundo occidental: 16 Ptolomeo Copérnico Kepler Encyclopædia Britannica Inc 1952
  • Crowe, Michael J. (1990). Teorías del mundo desde la Antigüedad hasta la revolución copernicana. Mineola, NY: Dover Publications, Inc. ISBN 978-0-486-26173-7.
  • Duhem, Pierre. "Historia de la física". The Catholic Encyclopedia. Vol. 12. Nueva York: Robert Appleton Company, 1911. 18 de junio de 2008. <http://www.newadvent.org/cathen/12047a.htm>.
  • Duhem, Pierre. Le Système du Monde: Historia de las doctrinas cosmológicas de Platon à Copernic, 10 vols., París: Hermann, 1959.
  • Duhem, Pierre. Cosmología medieval: teorías del infinito, el lugar, el tiempo, el vacío y la pluralidad de mundos , extractos de Le Système du Monde , traducido y editado por Roger Ariew, Chicago: University of Chicago Press, 1987 ISBN 0-226-16923-5 
  • Dreyer, John Louis Emil (2007) [1905]. Historia de los sistemas planetarios desde Tales hasta Kepler. Nueva York, NY: Cosimo. ISBN 978-1-60206-441-6.
  • Eastwood, Bruce, "Astronomía en la Europa latina cristiana c. 500 – c. 1150", Journal for the History of Astronomy, 28(1997): 235–258.
  • Eastwood, Bruce, Ordenando los cielos: astronomía y cosmología romana en el renacimiento carolingio, Leiden: Brill, 2007. ISBN 978-90-04-16186-3 . 
  • Eastwood, Bruce y Gerd Graßhoff, Diagramas planetarios para la astronomía romana en la Europa medieval, ca. 800-1500, Transactions of the American Philosophical Society, vol. 94, pt. 3, Filadelfia, 2004. ISBN 0-87169-943-5 
  • Field, JV , La cosmología geométrica de Kepler . Chicago: Chicago University Press, 1988 ISBN 0-226-24823-2 
  • Golino, Carlo (ed.), Galileo reevaluado , University of California Press 1966
  • Grant, Edward, "Orbes celestiales en la Edad Media latina", Isis, 78(1987): 153–73; reimpreso en Michael H. Shank, ed., The Scientific Enterprise in Antiquity and the Middle Ages, Chicago: Univ. of Chicago Pr., 2000. ISBN 0-226-74951-7 
  • Grant, Edward, Planetas, estrellas y orbes: el cosmos medieval, 1200-1687, Cambridge: Cambridge Univ. Pr., 1994. ISBN 0-521-56509-X 
  • Grant, Edward, Los fundamentos de la ciencia moderna en la Edad Media , Cambridge: Cambridge Univ. Pr., 1996. ISBN 0-521-56762-9 
  • Grasshoff, Gerd (2012). "El misterio de Michael Maestlin: construcción de teorías con diagramas". Revista de Historia de la Astronomía . 43 (1): 57–73. Bibcode :2012JHA....43...57G. doi :10.1177/002182861204300104. S2CID  117056401.
  • Gingerich, Owen El ojo del cielo , Instituto Americano de Física 1993
  • Hutchins, Robert Maynard; Adler, Mortimer J., eds. (1952). Ptolomeo, Copérnico, Kepler . Grandes libros del mundo occidental. Vol. 16. Chicago, Ill: William Benton.
  • Heath, Thomas, Aristarco de Samos Oxford University Press/Sandpiper Books Ltd. 1913/97
  • Jarrell, RA, Los contemporáneos de Tycho Brahe en Taton & Wilson (eds)1989
  • Koyré, Alexandre, Estudios de Galileo (traductor Mepham) Harvester Press 1977 ISBN 0-85527-354-2 
  • Koyré, Alexandre (1957). Del mundo cerrado al universo infinito. Libros olvidados. ISBN 978-1-60620-143-5.
  • Kepler, Johannes, Epítome de la astronomía copernicana (libros 4 y 5), publicado en Grandes libros del mundo occidental: 16 Ptolomeo Copérnico Kepler , Encyclopædia Britannica Inc. 1952
  • Lewis, CS, La imagen descartada: Una introducción a la literatura medieval y renacentista , Cambridge: Cambridge University Press 1964 ISBN 0-521-09450-X 
  • Lindberg, David C. (1992). Los orígenes de la ciencia occidental. Chicago: University of Chicago Press. ISBN 978-0-226-48231-6.
  • Lindberg, David C. (ed.), La ciencia en la Edad Media , Chicago: Univ. of Chicago Pr., 1978. ISBN 0-226-48233-2 
  • Linton, Christopher M. (2004). De Eudoxo a Einstein: una historia de la astronomía matemática. Cambridge: Cambridge University Press. ISBN 978-0-521-82750-8.[ enlace muerto permanente ]
  • Lloyd, GER , Aristóteles: El crecimiento y la estructura de su pensamiento, págs. 133–153, Cambridge: Cambridge Univ. Pr., 1968. ISBN 0-521-09456-9 . 
  • Lloyd, GER, "Aberraciones celestiales: Aristóteles, el astrónomo aficionado", págs. 160-183 en sus Exploraciones aristotélicas, Cambridge: Cambridge Univ. Pr., 1996. ISBN 0-521-55619-8 . 
  • Mach, Ernst, La ciencia de la mecánica. Tribunal abierto 1960.
  • Maier, Annaliese, En el umbral de la ciencia exacta: escritos seleccionados de Annaliese Maier sobre la filosofía natural medieval tardía , editado por Steven Sargent, Filadelfia: University of Pennsylvania Press, 1982.
  • McCluskey, Stephen C., Astronomías y culturas en la Europa medieval temprana, Cambridge: Cambridge Univ. Pr., 1998. ISBN 0-521-77852-2 
  • Neugebauer, Otto , Una historia de la astronomía matemática antigua, 3 vols., Nueva York: Springer, 1975. ISBN 0-387-06995-X 
  • Pederson, Olaf (1993) [1974]. Física y astronomía tempranas: una introducción histórica. Cambridge: Cambridge University Press. ISBN 978-0-521-40340-5.
  • Popper, Karl, El mundo de Parménides Routledge 1996
  • Rosen, Edward, Tres tratados copernicanos, Dover 1939/59.
  • Sambursky, S., El mundo físico de la Antigüedad tardía Routledge & Kegan Paul, 1962
  • Schofield, C., Los sistemas mundiales ticónicos y semiticónicos en Taton & Wilson (eds) 1989
  • Sorabji, Richard, Materia, espacio y movimiento. Londres: Duckworth, 1988. ISBN 0-7156-2205-6. 
  • Sorabji, Richard, (ed.) Philoponus y el rechazo de la ciencia aristotélica Londres e Ithaca, Nueva York, 1987
  • Sorabji, Richard, La filosofía de los comentaristas, 200-600 d. C.: Volumen 2 Física Duckworth 2004
  • Taliaferro, R. Catesby (1946). Introducción del traductor al Almagesto . En Hutchins (1952, págs. 1–4).
  • R. Taton y C. Wilson (eds.), Historia general de la astronomía: Volumen 2 Astronomía planetaria desde el Renacimiento hasta el surgimiento de la astrofísica Parte A De Tycho Brahe a Newton Cambridge: Cambridge Univ. Pr., 1989
  • Thoren, Victor E., "El cometa de 1577 y el sistema del mundo de Tycho Brahe", Archives Internationales d'Histoire des Sciences, 29 (1979): 53–67.
  • Thoren, Victor E., Tycho Brahe en Taton & Wilson 1989
  • Van Helden, Albert (1985). Midiendo el universo: dimensiones cósmicas desde Aristarco hasta Halley . Chicago y Londres: University of Chicago Press. ISBN 978-0-226-84882-2.
Wikimedia Commons alberga una categoría multimedia sobre Esferas celestes (modelo cosmológico) .
  • Modelo de trabajo y explicación completa de las Esferas de Eudoxo
  • Dennis Duke, Modelo ptolemaico animado de las esferas anidadas Archivado el 8 de septiembre de 2006 en Wayback Machine.
  • Henry Mendell, Viñetas de matemáticas antiguas: Eudoxo de Cnido Ptolomeo, Almagesto
  • M. Blundevile sus ejercicios, pág. 282 – Representación de esferas celestes en un libro de 1613

Obtenido de "https://es.wikipedia.org/w/index.php?title=Esferas_celestiales&oldid=1224863599"