Magnitud aparente

La magnitud aparente ( m ) es una medida del brillo de una estrella , un objeto astronómico u otros objetos celestes como los satélites artificiales . Su valor depende de su luminosidad intrínseca , su distancia y cualquier extinción de la luz del objeto causada por el polvo interestelar a lo largo de la línea de visión del observador.
A menos que se indique lo contrario, la palabra magnitud en astronomía generalmente se refiere a la magnitud aparente de un objeto celeste. La escala de magnitud probablemente data de antes del astrónomo romano Claudio Ptolomeo , cuyo catálogo de estrellas popularizó el sistema al enumerar las estrellas desde la primera magnitud (más brillante) hasta la sexta magnitud (más tenue). [1] La escala moderna fue definida matemáticamente para que coincidiera estrechamente con este sistema histórico por Norman Pogson en 1856.
La escala es logarítmica inversa : cuanto más brillante es un objeto, menor es su número de magnitud . Una diferencia de 1,0 en magnitud corresponde a una relación de brillo de , o aproximadamente 2,512. Por ejemplo, una estrella de magnitud 2,0 es 2,512 veces más brillante que una estrella de magnitud 3,0, 6,31 veces más brillante que una de magnitud 4,0 y 100 veces más brillante que una de magnitud 7,0.
Los objetos astronómicos más brillantes tienen magnitudes aparentes negativas: por ejemplo, Venus con -4,2 o Sirio con -1,46. Las estrellas más débiles visibles a simple vista en la noche más oscura tienen magnitudes aparentes de alrededor de +6,5, aunque esto varía según la vista de una persona y con la altitud y las condiciones atmosféricas. [2] Las magnitudes aparentes de los objetos conocidos varían desde el Sol con -26,832 hasta los objetos en imágenes profundas del Telescopio Espacial Hubble con magnitud +31,5. [3]
La medida de la magnitud aparente se denomina fotometría . Las mediciones fotométricas se realizan en las bandas de longitud de onda ultravioleta , visible o infrarroja utilizando filtros de banda de paso estándar que pertenecen a sistemas fotométricos como el sistema UBV o el sistema Strömgren uvbyβ . La medición en la banda V puede denominarse magnitud visual aparente .
La magnitud absoluta es una cantidad relacionada que mide la luminosidad que emite un objeto celeste, en lugar de su brillo aparente cuando se observa, y se expresa en la misma escala logarítmica inversa. La magnitud absoluta se define como la magnitud aparente que tendría una estrella u objeto si se observara desde una distancia de 10 parsecs (33 años luz; 3,1 × 10 14 kilómetros; 1,9 × 10 14 millas). Por lo tanto, es de mayor utilidad en astrofísica estelar , ya que se refiere a una propiedad de una estrella independientemente de lo cerca que esté de la Tierra. Pero en la astronomía observacional y la observación popular de estrellas , las referencias a "magnitud" se entienden como magnitud aparente.
Los astrónomos aficionados suelen expresar la oscuridad del cielo en términos de magnitud límite , es decir, la magnitud aparente de la estrella más débil que pueden ver a simple vista. Esto puede resultar útil como forma de controlar la propagación de la contaminación lumínica .
La magnitud aparente es técnicamente una medida de iluminancia , que también puede medirse en unidades fotométricas como el lux . [4]
Historia
Esta sección necesita citas adicionales para su verificación . ( Mayo de 2019 ) |
| Visible para el ojo humano típico [5] | Magnitud aparente | Brillo relativo a Vega | Número de estrellas (aparte del Sol ) más brillantes que la magnitud aparente [6] en el cielo nocturno |
|---|---|---|---|
| Sí | -1.0 | 251% | 1 ( Sirio ) |
| 0 0.0 | 100% | 4 (Vega, Canopus , Alfa Centauri , Arcturus ) | |
| 0 1.0 | 40% | 15 | |
| 0 2.0 | 16% | 48 | |
| 0 3.0 | 6,3% | 171 | |
| 0 4.0 | 2,5% | 513 | |
| 0 5.0 | 1.0% | 1602 | |
| 0 6.0 | 0,4% | 4800 | |
| 0 6.5 | 0,25% | 9100 [7] | |
| No | 0 7.0 | 0,16% | 14 000 |
| 0 8.0 | 0,063% | 42 000 | |
| 0 9.0 | 0,025% | 121 000 | |
| 10.0 | 0,010% | 340 000 |
La escala utilizada para indicar la magnitud tiene su origen en la práctica helenística de dividir las estrellas visibles a simple vista en seis magnitudes . Se decía que las estrellas más brillantes del cielo nocturno eran de primera magnitud ( m = 1), mientras que las más débiles eran de sexta magnitud ( m = 6), que es el límite de la percepción visual humana (sin la ayuda de un telescopio ). Cada grado de magnitud se consideraba el doble del brillo del grado siguiente (una escala logarítmica ), aunque esa relación era subjetiva ya que no existían fotodetectores . Esta escala bastante cruda para el brillo de las estrellas fue popularizada por Ptolomeo en su Almagesto y generalmente se cree que se originó con Hiparco . Esto no se puede probar ni refutar porque el catálogo de estrellas original de Hiparco se ha perdido. El único texto conservado del propio Hiparco (un comentario a Arato) documenta claramente que no tenía un sistema para describir el brillo con números: siempre usa términos como "grande" o "pequeño", "brillante" o "débil" o incluso descripciones como "visible en luna llena". [8]
En 1856, Norman Robert Pogson formalizó el sistema definiendo una estrella de primera magnitud como una estrella que es 100 veces más brillante que una estrella de sexta magnitud, estableciendo así la escala logarítmica que todavía se utiliza en la actualidad. Esto implica que una estrella de magnitud m es aproximadamente 2,512 veces más brillante que una estrella de magnitud m + 1. Esta cifra, la quinta raíz de 100 , se conoció como el coeficiente de Pogson. [9] Los catálogos de estrellas Harvard Photometry de 1884 y Potsdamer Duchmusterung de 1886 popularizaron el coeficiente de Pogson, y finalmente se convirtió en un estándar de facto en la astronomía moderna para describir las diferencias de brillo. [10]
Definir y calibrar lo que significa la magnitud 0,0 es difícil, y los diferentes tipos de mediciones que detectan diferentes tipos de luz (posiblemente mediante el uso de filtros) tienen diferentes puntos cero. El artículo original de Pogson de 1856 definió la magnitud 6,0 como la estrella más débil que el ojo humano puede ver sin ayuda, [11] pero el verdadero límite para la estrella visible más débil posible varía dependiendo de la atmósfera y de qué tan alta se encuentre una estrella en el cielo. La fotometría de Harvard utilizó un promedio de 100 estrellas cercanas a Polaris para definir la magnitud 5,0. [12] Más tarde, el sistema fotométrico Johnson UVB definió múltiples tipos de mediciones fotométricas con diferentes filtros, donde la magnitud 0,0 para cada filtro se define como el promedio de seis estrellas con el mismo tipo espectral que Vega. Esto se hizo para que el índice de color de estas estrellas fuera 0. [13] Aunque este sistema a menudo se denomina "normalizado de Vega", Vega es ligeramente más tenue que el promedio de seis estrellas utilizado para definir la magnitud 0,0, lo que significa que la magnitud de Vega está normalizada a 0,03 por definición.
Apertura del telescopio (mm) | Magnitud límite |
|---|---|
| 35 | 11.3 |
| 60 | 12.3 |
| 102 | 13.3 |
| 152 | 14.1 |
| 203 | 14.7 |
| 305 | 15.4 |
| 406 | 15.7 |
| 508 | 16.4 |
En los sistemas de magnitud modernos, el brillo se describe utilizando el coeficiente de Pogson. En la práctica, los números de magnitud rara vez superan 30 antes de que las estrellas se vuelvan demasiado débiles para detectarlas. Si bien Vega está cerca de la magnitud 0, hay cuatro estrellas más brillantes en el cielo nocturno en longitudes de onda visibles (y más en longitudes de onda infrarrojas), así como los planetas brillantes Venus, Marte y Júpiter, y como más brillante significa magnitud menor, estos deben describirse mediante magnitudes negativas . Por ejemplo, Sirio , la estrella más brillante de la esfera celeste , tiene una magnitud de −1,4 en el visible. Las magnitudes negativas para otros objetos astronómicos muy brillantes se pueden encontrar en la siguiente tabla.
Los astrónomos han desarrollado otros sistemas de punto cero fotométrico como alternativas a los sistemas normalizados de Vega. El más utilizado es el sistema de magnitud AB , [15] en el que los puntos cero fotométricos se basan en un espectro de referencia hipotético que tiene un flujo constante por intervalo de frecuencia unitario , en lugar de utilizar un espectro estelar o una curva de cuerpo negro como referencia. El punto cero de magnitud AB se define de modo que las magnitudes AB y Vega de un objeto sean aproximadamente iguales en la banda del filtro V. Sin embargo, el sistema de magnitud AB se define asumiendo un detector idealizado que mide solo una longitud de onda de luz, mientras que los detectores reales aceptan energía de un rango de longitudes de onda.
Medición
La medición precisa de la magnitud (fotometría) requiere la calibración del aparato de detección fotográfica o (normalmente) electrónica. Esto generalmente implica la observación contemporánea, en condiciones idénticas, de estrellas estándar cuya magnitud utilizando ese filtro espectral se conoce con precisión. Además, como la cantidad de luz que recibe realmente un telescopio se reduce debido a la transmisión a través de la atmósfera terrestre , deben tenerse en cuenta las masas de aire de las estrellas objetivo y de calibración . Normalmente, se observarían unas pocas estrellas diferentes de magnitud conocida que sean suficientemente similares. Se prefieren las estrellas calibradoras cercanas en el cielo al objetivo (para evitar grandes diferencias en las trayectorias atmosféricas). Si esas estrellas tienen ángulos cenitales ( altitudes ) algo diferentes, se puede derivar un factor de corrección en función de la masa de aire y aplicarlo a la masa de aire en la posición del objetivo. Dicha calibración obtiene el brillo que se observaría desde arriba de la atmósfera, donde se define la magnitud aparente. [ cita requerida ]
La escala de magnitud aparente en astronomía refleja la potencia recibida de las estrellas y no su amplitud. Los principiantes deberían considerar el uso de la medida de brillo relativo en astrofotografía para ajustar los tiempos de exposición entre estrellas. La magnitud aparente también se integra sobre todo el objeto, independientemente de su enfoque, y esto debe tenerse en cuenta al escalar los tiempos de exposición para objetos con un tamaño aparente significativo, como el Sol, la Luna y los planetas. Por ejemplo, escalar directamente el tiempo de exposición de la Luna al Sol funciona porque tienen aproximadamente el mismo tamaño en el cielo. Sin embargo, escalar la exposición de la Luna a Saturno daría como resultado una sobreexposición si la imagen de Saturno ocupa un área más pequeña en su sensor que la Luna (con el mismo aumento o, de manera más general, f/#).
Cálculos

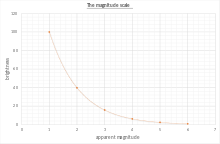
Cuanto más oscuro parezca un objeto, mayor será el valor numérico dado a su magnitud, correspondiendo una diferencia de 5 magnitudes a un factor de luminosidad de exactamente 100. Por lo tanto, la magnitud m , en la banda espectral x , vendría dada por que se expresa más comúnmente en términos de logaritmos comunes (base 10) como donde F x es la irradiancia observada utilizando el filtro espectral x , y F x ,0 es el flujo de referencia (punto cero) para ese filtro fotométrico . Dado que un aumento de 5 magnitudes corresponde a una disminución de la luminosidad por un factor de exactamente 100, cada aumento de magnitud implica una disminución de la luminosidad por el factor (coeficiente de Pogson). Invirtiendo la fórmula anterior, una diferencia de magnitud m 1 − m 2 = Δ m implica un factor de luminosidad de
Ejemplo: Sol y Luna
¿Cuál es la relación entre el brillo del Sol y la Luna llena ?
La magnitud aparente del Sol es −26,832 [16] (más brillante), y la magnitud media de la luna llena es −12,74 [17] (más oscura).
Diferencia de magnitud:
Factor de luminosidad:
El Sol parece estar aproximadamente400.000 veces más brillante que la Luna llena.
Adición de magnitudes
En ocasiones, es posible que se desee sumar el brillo. Por ejemplo, la fotometría en estrellas dobles muy separadas puede producir solo una medición de su emisión de luz combinada. Para encontrar la magnitud combinada de esa estrella doble conociendo solo las magnitudes de los componentes individuales, esto se puede hacer sumando el brillo (en unidades lineales) correspondiente a cada magnitud. [18]
Resolviendo para obtenemos donde m f es la magnitud resultante después de sumar los brillos a los que se refieren m 1 y m 2 .
Magnitud bolométrica aparente
Mientras que la magnitud generalmente se refiere a una medición en una banda de filtro particular correspondiente a un rango de longitudes de onda, la magnitud bolométrica aparente o absoluta (m bol ) es una medida del brillo aparente o absoluto de un objeto integrado en todas las longitudes de onda del espectro electromagnético (también conocido como la irradiancia o potencia del objeto, respectivamente). El punto cero de la escala de magnitud bolométrica aparente se basa en la definición de que una magnitud bolométrica aparente de 0 mag es equivalente a una irradiancia recibida de 2,518×10 −8 vatios por metro cuadrado (W·m −2 ). [16]
Magnitud absoluta
Mientras que la magnitud aparente es una medida del brillo de un objeto visto por un observador particular, la magnitud absoluta es una medida del brillo intrínseco de un objeto. El flujo disminuye con la distancia según una ley del cuadrado inverso , por lo que la magnitud aparente de una estrella depende tanto de su brillo absoluto como de su distancia (y de cualquier extinción). Por ejemplo, una estrella a una distancia tendrá la misma magnitud aparente que una estrella cuatro veces más brillante al doble de esa distancia. Por el contrario, el brillo intrínseco de un objeto astronómico no depende de la distancia del observador ni de ninguna extinción . [ cita requerida ]
La magnitud absoluta M de una estrella o un objeto astronómico se define como la magnitud aparente que tendría visto desde una distancia de 10 parsecs (33 años luz ). La magnitud absoluta del Sol es 4,83 en la banda V (visual), 4,68 en la banda G del satélite Gaia (verde) y 5,48 en la banda B (azul). [19] [20] [21]
En el caso de un planeta o asteroide, la magnitud absoluta H significa más bien la magnitud aparente que tendría si estuviera a 1 unidad astronómica (150.000.000 km) tanto del observador como del Sol, y totalmente iluminado en la oposición máxima (una configuración que sólo es alcanzable teóricamente, con el observador situado en la superficie del Sol). [22]
Valores de referencia estándar
| Banda | Lambda (μm) | Δλ/la ( FWHM ) | Flujo en m = 0 , F x ,0 | |
|---|---|---|---|---|
| Yo | 10 −20 erg/(s·cm2 · Hz) | |||
| tú | 0,36 | 0,15 | 1810 | 1.81 |
| B | 0,44 | 0,22 | 4260 | 4.26 |
| V | 0,55 | 0,16 | 3640 | 3.64 |
| R | 0,64 | 0,23 | 3080 | 3.08 |
| I | 0,79 | 0,19 | 2550 | 2,55 |
| Yo | 1.26 | 0,16 | 1600 | 1.60 |
| yo | 1.60 | 0,23 | 1080 | 1.08 |
| K | 2.22 | 0,23 | 0 670 | 0,67 |
| yo | 3,50 | |||
| gramo | 0,52 | 0,14 | 3730 | 3.73 |
| a | 0,67 | 0,14 | 4490 | 4.49 |
| i | 0,79 | 0,16 | 4760 | 4,76 |
| el | 0,91 | 0,13 | 4810 | 4.81 |
La escala de magnitud es una escala logarítmica inversa. Un error común es creer que la naturaleza logarítmica de la escala se debe a que el ojo humano tiene una respuesta logarítmica. En la época de Pogson se creía que esto era cierto (véase la ley de Weber-Fechner ), pero ahora se cree que la respuesta es una ley de potencia . [24]
La magnitud se complica por el hecho de que la luz no es monocromática . La sensibilidad de un detector de luz varía según la longitud de onda de la luz, y la forma en que varía depende del tipo de detector de luz. Por esta razón, es necesario especificar cómo se mide la magnitud para que el valor sea significativo. Para este propósito, se utiliza ampliamente el sistema UBV , en el que la magnitud se mide en tres bandas de longitud de onda diferentes: U (centrada en aproximadamente 350 nm, en el ultravioleta cercano ), B (aproximadamente 435 nm, en la región azul) y V (aproximadamente 555 nm, en la mitad del rango visual humano a la luz del día). La banda V se eligió para fines espectrales y proporciona magnitudes que se corresponden estrechamente con las vistas por el ojo humano. Cuando se analiza una magnitud aparente sin más calificación, generalmente se entiende la magnitud V. [25]
Debido a que las estrellas más frías, como las gigantes rojas y las enanas rojas , emiten poca energía en las regiones azul y ultravioleta del espectro, su potencia a menudo está subrepresentada por la escala UBV. De hecho, algunas estrellas de clase L y T tienen una magnitud estimada de más de 100, porque emiten muy poca luz visible, pero son más fuertes en el infrarrojo . [26]
Las medidas de magnitud requieren un tratamiento cauteloso y es extremadamente importante medir cosas iguales. En las películas fotográficas ortocromáticas (sensibles al azul) de principios del siglo XX y anteriores , los brillos relativos de la supergigante azul Rigel y la estrella variable irregular supergigante roja Betelgeuse (en su máximo) están invertidos en comparación con lo que perciben los ojos humanos, porque esta película arcaica es más sensible a la luz azul que a la luz roja. Las magnitudes obtenidas con este método se conocen como magnitudes fotográficas y ahora se consideran obsoletas. [27]
En el caso de los objetos dentro de la Vía Láctea con una magnitud absoluta dada, se suma 5 a la magnitud aparente por cada aumento de diez veces en la distancia al objeto. En el caso de objetos a distancias muy grandes (mucho más allá de la Vía Láctea), esta relación debe ajustarse para los desplazamientos al rojo y para las medidas de distancia no euclidianas debido a la relatividad general . [28] [29]
Para los planetas y otros cuerpos del Sistema Solar, la magnitud aparente se deriva de su curva de fase y de las distancias al Sol y al observador. [30]
Lista de magnitudes aparentes
This section needs additional citations for verification. (September 2019) |
Algunas de las magnitudes mencionadas son aproximadas. La sensibilidad del telescopio depende del tiempo de observación, del paso de banda óptico y de la luz interferente proveniente de la dispersión y la luminiscencia atmosférica .
Magnitud aparente (V) | Objeto | Visto desde... | Notas |
|---|---|---|---|
| −67,57 | explosión de rayos gamma GRB 080319B | Visto desde 1 UA de distancia | Se acabaría2 × 10 16 (20 cuatrillones) de veces más brillante que el Sol visto desde la Tierra |
| −43,27 | estrella NGC 2403 V14 | Visto desde 1 UA de distancia | |
| −41,82 | estrella NGC 2363-V1 | Visto desde 1 UA de distancia | |
| −41,39 | Estrella Cygnus OB2-12 | Visto desde 1 UA de distancia | |
| −40,67 | estrella M33-013406.63 | Visto desde 1 UA de distancia | |
| −40,17 | estrella η Carinae A | Visto desde 1 UA de distancia | |
| −40,07 | Estrella Zeta 1 Escorpio | Visto desde 1 UA de distancia | |
| −39,66 | estrella R136a1 | Visto desde 1 UA de distancia | |
| −39,47 | estrella P Cygni | Visto desde 1 UA de distancia | |
| −38,00 | estrella Rigel | Visto desde 1 UA de distancia | Se vería como un gran disco azulado muy brillante de 35° de diámetro aparente. |
| −37,42 | estrella Betelgeuse | Visto desde 1 UA de distancia | |
| -30,30 | estrella Sirio A | Visto desde 1 UA de distancia | |
| -29,30 | estrella sol | Visto desde Mercurio en el perihelio | |
| −27,40 | estrella sol | Visto desde Venus en el perihelio | |
| −26.832 | estrella sol | Visto desde la Tierra [16] | Aproximadamente 400.000 veces más brillante que la Luna llena promedio |
| -25,60 | estrella sol | Visto desde Marte en el afelio | |
| −25,00 | Brillo mínimo que provoca el típico dolor ocular leve al mirar | ||
| −23,00 | estrella sol | Visto desde Júpiter en el afelio | |
| -21,70 | estrella sol | Visto desde Saturno en el afelio | |
| −21,00 | estrella sol | Visto desde la Tierra en un mediodía nublado | midiendo aproximadamente 1000 lux |
| -20,20 | estrella sol | Visto desde Urano en el afelio | |
| -19.30 | estrella sol | Visto desde Neptuno | |
| −19,00 | estrella sol | Visto desde la Tierra en un mediodía muy nublado | midiendo aproximadamente 100 lux |
| -18,20 | estrella sol | Visto desde Plutón en el afelio | |
| -17,70 | planeta Tierra | Visto completamente iluminado como la luz de la Tierra desde la Luna [31] | |
| -16,70 | estrella sol | Visto desde Eris en el afelio | |
| −16,00 | estrella sol | como el crepúsculo en la Tierra | midiendo aproximadamente 10 lux [32] |
| -14,20 | Un nivel de iluminación de 1 lux [33] [34] | ||
| -12,60 | luna llena | Visto desde la Tierra en el perihelio | brillo máximo de perigeo + perihelio + Luna llena (~0,267 lux; el valor medio de la distancia es −12,74, [17] aunque los valores son aproximadamente 0,18 magnitudes más brillantes cuando se incluye el efecto de oposición ) |
| -12,40 | Betelgeuse (cuando era supernova) | Visto desde la Tierra cuando se convierte en supernova [35] | |
| -11,20 | estrella sol | Visto desde Sedna en el afelio | |
| −10,00 | Cometa Ikeya-Seki (1965) | Visto desde la Tierra | que fue el Kreutz Sungrazer más brillante de los tiempos modernos [36] |
| -9,50 | Destello de iridio (satélite) | Visto desde la Tierra | brillo máximo |
| −9 a −10 | Fobos (luna) | Visto desde Marte | brillo máximo |
| -7,50 | supernova de 1006 | Visto desde la Tierra | El evento estelar más brillante registrado en la historia (a 7200 años luz de distancia) [37] |
| -6,80 | Alfa Centauri A | Visto desde Próxima Centauri b | [38] |
| -6,00 | La magnitud total integrada del cielo nocturno (incluido el resplandor atmosférico ) | Visto desde la Tierra | midiendo aproximadamente 0,002 lux |
| -6,00 | Supernova del cangrejo de 1054 | Visto desde la Tierra | (A 6500 años luz de distancia) [39] |
| -5,90 | Estación Espacial Internacional | Visto desde la Tierra | cuando la ISS está en su perigeo y completamente iluminada por el Sol [40] |
| −4,92 | planeta venus | Visto desde la Tierra | brillo máximo [41] cuando se ilumina como una media luna |
| -4,14 | planeta venus | Visto desde la Tierra | brillo medio [41] |
| -4 | Los objetos más débiles que se pueden observar durante el día a simple vista cuando el Sol está alto . Un objeto astronómico proyecta sombras visibles para el ser humano cuando su magnitud aparente es igual o inferior a −4 [42] | ||
| −3,99 | estrella Epsilon Canis Majoris | Visto desde la Tierra | brillo máximo de hace 4,7 millones de años, la estrella históricamente más brillante de los últimos y próximos cinco millones de años . [43] |
| -3,69 | Luna | Iluminado por la luz de la Tierra, reflejando la luz de la Tierra vista desde la Tierra (máximo) [31] | |
| -2,98 | planeta venus | Visto desde la Tierra | brillo mínimo cuando está en el lado opuesto del Sol [41] |
| -2,94 | planeta Júpiter | Visto desde la Tierra | brillo máximo [41] |
| -2,94 | planeta Marte | Visto desde la Tierra | brillo máximo [41] |
| -2,5 | Los objetos más tenues son visibles durante el día a simple vista cuando el Sol está a menos de 10° sobre el horizonte. | ||
| -2,50 | luna nueva | Visto desde la Tierra | brillo mínimo |
| -2,50 | planeta Tierra | Visto desde Marte | brillo máximo |
| -2,48 | planeta Mercurio | Visto desde la Tierra | brillo máximo en la conjunción superior (a diferencia de Venus, Mercurio es más brillante cuando está en el lado opuesto del Sol, debido a sus diferentes curvas de fase) [41] |
| -2,20 | planeta Júpiter | Visto desde la Tierra | brillo medio [41] |
| -1,66 | planeta Júpiter | Visto desde la Tierra | brillo mínimo [41] |
| -1,47 | sistema estelar Sirio | Visto desde la Tierra | La estrella más brillante, excepto el Sol, en longitudes de onda visibles [44] |
| -0,83 | estrella Eta Carinae | Visto desde la Tierra | Brillo aparente como impostora de una supernova en abril de 1843 |
| -0,72 | estrella Canopus | Visto desde la Tierra | La segunda estrella más brillante del cielo nocturno [45] |
| -0,55 | planeta Saturno | Visto desde la Tierra | brillo máximo cerca de la oposición y el perihelio cuando los anillos están en ángulo hacia la Tierra [41] |
| -0,3 | El cometa Halley | Visto desde la Tierra | Magnitud aparente esperada al pasar en 2061 |
| -0,27 | Sistema estelar Alfa Centauri AB | Visto desde la Tierra | Magnitud combinada (tercera estrella más brillante en el cielo nocturno) |
| -0,04 | estrella Arcturus | Visto desde la Tierra | Cuarta estrella más brillante a simple vista [46] |
| -0,01 | Estrella Alfa Centauri A | Visto desde la Tierra | La cuarta estrella individual más brillante visible telescópicamente en el cielo nocturno |
| +0,03 | estrella vega | Visto desde la Tierra | originalmente elegido como definición del punto cero [47] |
| +0,23 | planeta Mercurio | Visto desde la Tierra | brillo medio [41] |
| +0,46 | estrella sol | Visto desde Alfa Centauri | |
| +0,46 | planeta Saturno | Visto desde la Tierra | brillo medio [41] |
| +0,71 | planeta Marte | Visto desde la Tierra | brillo medio [41] |
| +0,90 | Luna | Visto desde Marte | brillo máximo |
| +1,17 | planeta Saturno | Visto desde la Tierra | brillo mínimo [41] |
| +1,33 | Estrella Alfa Centauri B | Visto desde la Tierra | |
| +1,86 | planeta Marte | Visto desde la Tierra | brillo mínimo [41] |
| +1,98 | estrella Polaris | Visto desde la Tierra | brillo medio [48] |
| +3,03 | Supernova SN 1987A | Visto desde la Tierra | en la Gran Nube de Magallanes (a 160.000 años luz de distancia) |
| +3 a +4 | Las estrellas más débiles visibles en un barrio urbano a simple vista | ||
| +3,44 | Galaxia de Andrómeda | Visto desde la Tierra | M31 [49] |
| +4 | Nebulosa de Orión | Visto desde la Tierra | M42 |
| +4,38 | Luna Ganimedes | Visto desde la Tierra | brillo máximo [50] (luna de Júpiter y la luna más grande del Sistema Solar) |
| +4,50 | Cúmulo abierto M41 | Visto desde la Tierra | Un cúmulo abierto que pudo haber sido visto por Aristóteles [51] |
| +4.5 | Galaxia enana esferoidal de Sagitario | Visto desde la Tierra | |
| +5,20 | asteroide Vesta | Visto desde la Tierra | brillo máximo |
| +5,38 [52] | planeta Urano | Visto desde la Tierra | brillo máximo [41] (Urano llega al perihelio en 2050) |
| +5,68 | planeta Urano | Visto desde la Tierra | brillo medio [41] |
| +5,72 | Galaxia espiral M33 | Visto desde la Tierra | que se utiliza como prueba para ver a simple vista en cielos oscuros [53] [54] |
| +5.8 | explosión de rayos gamma GRB 080319B | Visto desde la Tierra | Magnitud visual máxima (el "evento Clarke") observada en la Tierra el 19 de marzo de 2008 desde una distancia de 7.500 millones de años luz. |
| +6.03 | planeta Urano | Visto desde la Tierra | brillo mínimo [41] |
| +6,49 | asteroide Palas | Visto desde la Tierra | brillo máximo |
| +6.5 | Límite aproximado de estrellas observables a simple vista en condiciones muy favorables. Hay alrededor de 9.500 estrellas visibles hasta magnitud 6,5. [5] | ||
| +6,64 | planeta enano Ceres | Visto desde la Tierra | brillo máximo |
| +6,75 | asteroide iris | Visto desde la Tierra | brillo máximo |
| +6,90 | Galaxia espiral M81 | Visto desde la Tierra | Se trata de un objetivo extremo a simple vista que lleva la vista humana y la escala Bortle al límite [55] |
| +7,25 | planeta Mercurio | Visto desde la Tierra | brillo mínimo [41] |
| +7,67 [56] | planeta Neptuno | Visto desde la Tierra | brillo máximo [41] (Neptuno llega al perihelio en 2042) |
| +7,78 | planeta Neptuno | Visto desde la Tierra | brillo medio [41] |
| +8.00 | planeta Neptuno | Visto desde la Tierra | brillo mínimo [41] |
| +8 | Límite extremo a simple vista, clase 1 en la escala de Bortle , los cielos más oscuros disponibles en la Tierra. [57] | ||
| +8,10 | Luna Titán | Visto desde la Tierra | brillo máximo; luna más grande de Saturno; [58] [59] magnitud de oposición media 8,4 [60] |
| +8,29 | estrella UY Scuti | Visto desde la Tierra | Máximo brillo; una de las estrellas más grandes conocidas por radio. |
| +8,94 | asteroide 10 Hygiea | Visto desde la Tierra | brillo máximo [61] |
| +9,50 | Objetos más débiles visibles utilizando binoculares comunes de 7x50 en condiciones típicas [62] | ||
| +10 | El CSM del Apolo 8 en órbita alrededor de la Luna | Visto desde la Tierra | calculado (Liemohn) [63] |
| +10,20 | Luna Japeto | Visto desde la Tierra | brillo máximo, [59] más brillante cuando está al oeste de Saturno y tarda 40 días en cambiar de lado |
| +11.05 | Estrella Próxima Centauri | Visto desde la Tierra | estrella más cercana |
| +11.8 | Luna Fobos | Visto desde la Tierra | Máximo brillo; luna más brillante de Marte |
| +12,23 | estrella R136a1 | Visto desde la Tierra | La estrella más luminosa y masiva conocida [64] |
| +12,89 | Luna Deimos | Visto desde la Tierra | Brillo máximo |
| +12,91 | Cuásar 3C 273 | Visto desde la Tierra | más brillante ( distancia de luminosidad de 2.400 millones de años luz ) |
| +13,42 | Luna Tritón | Visto desde la Tierra | Brillo máximo [60] |
| +13,65 | planeta enano Plutón | Visto desde la Tierra | brillo máximo, [65] 725 veces más débil que una magnitud 6,5 visible a simple vista |
| +13,9 | Luna Titania | Visto desde la Tierra | Máximo brillo; la luna más brillante de Urano |
| +14.1 | estrella WR 102 | Visto desde la Tierra | La estrella más caliente conocida |
| +15,4 | Centauro Quirón | Visto desde la Tierra | brillo máximo [66] |
| +15,55 | Luna Caronte | Visto desde la Tierra | brillo máximo (la luna más grande de Plutón) |
| +16,8 | planeta enano Makemake | Visto desde la Tierra | Brillo de la oposición actual [67] |
| +17,27 | planeta enano Haumea | Visto desde la Tierra | Brillo de la oposición actual [68] |
| +18,7 | planeta enano Eris | Visto desde la Tierra | Brillo de la oposición actual |
| +19,5 | Los objetos más débiles observables con el telescopio Catalina Sky Survey de 0,7 metros utilizando una exposición de 30 segundos [69] y también la magnitud límite aproximada del Sistema de Última Alerta de Impacto Terrestre de Asteroides (ATLAS) | ||
| +20,7 | Luna Callirrhoe | Visto desde la Tierra | (pequeño satélite de Júpiter de unos 8 km) [60] |
| +22 | Los objetos más débiles observables en luz visible con un telescopio Ritchey-Chrétien de 600 mm (24″) con 30 minutos de imágenes apiladas (6 subfotogramas de 5 minutos cada uno) utilizando un detector CCD [70] | ||
| +22,8 | Luhman 16 | Visto desde la Tierra | Enanas marrones más cercanas (Luhman 16A=23,25, Luhman 16B=24,07) [71] |
| +22,91 | Luna Hidra | Visto desde la Tierra | brillo máximo de la luna de Plutón |
| +23,38 | Luna Nix | Visto desde la Tierra | brillo máximo de la luna de Plutón |
| +24 | Los objetos más débiles observables con el telescopio Pan-STARRS de 1,8 metros usando una exposición de 60 segundos [72] Esta es actualmente la magnitud límite de los estudios astronómicos automatizados de todo el cielo . | ||
| +25.0 | Luna Fenrir | Visto desde la Tierra | (pequeño satélite de Saturno de unos 4 km) [73] |
| +25.3 | Objeto transneptuniano 2018 AG 37 | Visto desde la Tierra | El objeto observable más lejano conocido en el Sistema Solar, a unas 132 UA (19.700 millones de kilómetros) del Sol. |
| +26,2 | Objeto transneptuniano 2015 TH 367 | Visto desde la Tierra | Objeto de 200 km de tamaño, a unas 90 UA (13 mil millones de km) del Sol y aproximadamente 75 millones de veces más débil que lo que se puede ver a simple vista. |
| +27,7 | Los objetos más débiles observables con un solo telescopio terrestre de 8 metros, como el telescopio Subaru, en una imagen de 10 horas [74] | ||
| +28,2 | El cometa Halley | Visto desde la Tierra (2003) | en 2003, cuando se encontraba a 28 UA (4.200 millones de kilómetros) del Sol, fotografiada utilizando 3 de los 4 telescopios individuales sincronizados del conjunto Very Large Telescope del ESO, utilizando un tiempo de exposición total de aproximadamente 9 horas [75] |
| +28,4 | asteroide 2003 BH91 | Visto desde la órbita terrestre | magnitud observada de un objeto del cinturón de Kuiper de unos 15 kilómetros visto por el Telescopio Espacial Hubble (HST) en 2003, el asteroide más tenue conocido observado directamente. |
| +29,4 | Jades-GS-z13-0 | Visto desde la Tierra | Descubierto por el telescopio espacial James Webb . Uno de los objetos más lejanos descubiertos. [76] |
| +31,5 | Los objetos más débiles observables en luz visible con el telescopio espacial Hubble a través del Campo Profundo Extremo con un tiempo de exposición de aproximadamente 23 días recopilado durante 10 años [77] | ||
| +34 | Los objetos más débiles observables en luz visible con el telescopio espacial James Webb [78] | ||
| +35 | asteroide sin nombre | Visto desde la órbita terrestre | magnitud esperada del asteroide más tenue conocido, un objeto del cinturón de Kuiper de 950 metros descubierto (por el HST) que pasó frente a una estrella en 2009. [79] |
| +35 | estrella LBV 1806−20 | Visto desde la Tierra | Una estrella variable azul luminosa, de magnitud esperada en longitudes de onda visibles debido a la extinción interestelar. |
Véase también
- Diámetro angular
- Módulo de distancia
- Lista de estrellas brillantes más cercanas
- Lista de estrellas más cercanas
- Luminosidad
- Brillo de la superficie
Referencias
- ^ Toomer, GJ (1984). Almagesto de Ptolomeo. Nueva York: Springer-Verlag. pag. 16.ISBN 0-387-91220-7.
- ^ Curtis, Heber Doust (1903) [1901-03-27]. "Sobre los límites de la visión sin ayuda". Boletín del Observatorio Lick . 2 (38). Universidad de California : 67–69. Código Bibliográfico :1903LicOB...2...67C. doi :10.5479/ADS/bib/1903LicOB.2.67C.
- ^ Matthew, Templeton (21 de octubre de 2011). «Magnitudes: medición del brillo de las estrellas». Asociación Estadounidense de Estrellas Variables (AAVSO). Archivado desde el original el 18 de mayo de 2019. Consultado el 19 de mayo de 2019 .
- ^ Crumey, A. (octubre de 2006). "Umbral de contraste humano y visibilidad astronómica". Monthly Notices of the Royal Astronomical Society . 442 (3): 2600–2619. arXiv : 1405.4209 . Código Bibliográfico :2014MNRAS.442.2600C. doi : 10.1093/mnras/stu992 .
- ^ ab "Vmag<6.5". Base de datos astronómica SIMBAD. Archivado desde el original el 22 de febrero de 2015. Consultado el 25 de junio de 2010 .
- ^ "Magnitud". Observatorio Solar Nacional—Sacramento Peak. Archivado desde el original el 6 de febrero de 2008. Consultado el 23 de agosto de 2006 .
- ^ Catálogo Bright Star
- ^ Hoffmann, S., Hipparchs Himmelsglobus, Springer, Wiesbaden/Nueva York, 2017
- ^ Pogson, N. (1856). "Magnitudes de treinta y seis de los planetas menores para el primer día de cada mes del año 1857". MNRAS . 17 : 12. Bibcode :1856MNRAS..17...12P. doi : 10.1093/mnras/17.1.12 .
- ^ Hearnshaw, John B. (1996). La medición de la luz de las estrellas: dos siglos de fotometría astronómica (1.ª edición). Cambridge: Cambridge Univ. Press. ISBN 978-0-521-40393-1.
- ^ Pogson, N. (14 de noviembre de 1856). "Magnitudes de treinta y seis de los planetas menores para el primer día de cada mes del año 1857". Monthly Notices of the Royal Astronomical Society . 17 (1): 12–15. Bibcode :1856MNRAS..17...12P. doi : 10.1093/mnras/17.1.12 . ISSN 0035-8711.
- ^ Hearnshaw, JB (1996). La medición de la luz de las estrellas: dos siglos de fotometría astronómica . Cambridge [Inglaterra]; Nueva York, NY, EE. UU.: Cambridge University Press. ISBN 978-0-521-40393-1.
- ^ Johnson, HL; Morgan, WW (mayo de 1953). "Fotometría estelar fundamental para estándares de tipo espectral en el sistema revisado del atlas espectral de Yerkes". The Astrophysical Journal . 117 : 313. Bibcode :1953ApJ...117..313J. doi :10.1086/145697. ISSN 0004-637X.
- ^ North, Gerald; James, Nick (2014). Observación de estrellas variables, novas y supernovas. Cambridge University Press. pág. 24. ISBN 978-1-107-63612-5.
- ^ Oke, JB; Gunn, JE (15 de marzo de 1983). "Estrellas estándar secundarias para espectrofotometría absoluta". The Astrophysical Journal . 266 : 713–717. Bibcode :1983ApJ...266..713O. doi :10.1086/160817.
- ^ abc IAU Inter-Division AG Working Group on Nominal Units for Stellar & Planetary Astronomy (13 de agosto de 2015). «IAU 2015 Resolution B2 on Recommended Zero Points for the Absolute and Apparent Bolometric Magnitude Scales» (PDF) . Resoluciones adoptadas en las Asambleas Generales . arXiv : 1510.06262 . Bibcode :2015arXiv151006262M. Archivado (PDF) del original el 28 de enero de 2016 . Consultado el 19 de mayo de 2019 .
- ^ ab Williams, David R. (2 de febrero de 2010). «Hoja informativa sobre la Luna». NASA (Centro Nacional de Datos de Ciencia Espacial). Archivado desde el original el 23 de marzo de 2010. Consultado el 9 de abril de 2010 .
- ^ "Aritmética de magnitudes". Tema semanal . Caglow. Archivado desde el original el 1 de febrero de 2012 . Consultado el 30 de enero de 2012 .
- ^ Evans, Aaron. "Algunas definiciones astronómicas útiles" (PDF) . Programa de astronomía de Stony Brook. Archivado (PDF) desde el original el 20 de julio de 2011. Consultado el 12 de julio de 2009 .
- ^ Čotar, Klemen; Zwitter, Tomaž; et al. (21 de mayo de 2019). "El sondeo GALAH: estrellas triples similares al Sol no resueltas descubiertas por la misión Gaia". Monthly Notices of the Royal Astronomical Society . 487 (2). Oxford University Press (OUP): 2474–2490. arXiv : 1904.04841 . doi : 10.1093/mnras/stz1397 . ISSN 0035-8711.
- ^ Bessell, Michael S. (septiembre de 2005). «Sistemas fotométricos estándar» (PDF) . Revista anual de astronomía y astrofísica . 43 (1): 293–336. Código bibliográfico :2005ARA&A..43..293B. doi :10.1146/annurev.astro.41.082801.100251. ISSN 0066-4146. Archivado (PDF) desde el original el 9 de octubre de 2022.
- ^ Luciuk, M. "Magnitudes astronómicas" (PDF) . pág. 8. Consultado el 11 de enero de 2019 .
- ^ Huchra, John. «Sistemas de magnitud astronómica». Centro Harvard-Smithsoniano de Astrofísica. Archivado desde el original el 21 de julio de 2018. Consultado el 18 de julio de 2017 .
- ^ Schulman, E. ; Cox, CV (1997). "Conceptos erróneos sobre magnitudes astronómicas". American Journal of Physics . 65 (10): 1003. Bibcode :1997AmJPh..65.1003S. doi :10.1119/1.18714.
- ^ "Magnitud | Brillo, magnitud aparente y magnitud absoluta | Britannica". www.britannica.com . Consultado el 19 de octubre de 2023 .
- ^ "Introducción a las galaxias activas: Ver como una sola página". www.open.edu . Consultado el 19 de octubre de 2023 .
- ^ Pickering, Edward C. (1910). «1910HarCi.160....1P Página 1». Circular del Observatorio de Harvard College . 160 : 1. Código Bibliográfico :1910HarCi.160....1P . Consultado el 19 de octubre de 2023 .
- ^ Umeh, Obinna; Clarkson, Chris; Maartens, Roy (2014). "Correcciones relativistas no lineales a distancias cosmológicas, corrimiento al rojo y aumento de lente gravitacional: II. Derivación". Gravedad clásica y cuántica . 31 (20): 205001. arXiv : 1402.1933 . Código Bibliográfico :2014CQGra..31t5001U. doi :10.1088/0264-9381/31/20/205001. S2CID 54527784.
- ^ Hogg, David W.; Baldry, Ivan K.; Blanton, Michael R.; Eisenstein, Daniel J. (2002). "La corrección K". arXiv : astro-ph/0210394 .
- ^ Wing, RF (1967). "1967lts..conf..205W Página 205". Estrellas de tipo tardío : 205. Código Bibliográfico :1967lts..conf..205W . Consultado el 19 de octubre de 2023 .
- ^ ab Agrawal, Dulli Chandra (30 de marzo de 2016). "Magnitud aparente del brillo ceniciento: un cálculo sencillo". Revista Europea de Física . 37 (3). IOP Publishing: 035601. Bibcode :2016EJPh...37c5601A. doi :10.1088/0143-0807/37/3/035601. ISSN 0143-0807. S2CID 124231299.
- ^ Polakis, Tom (10 de septiembre de 1997). «Radiometría y fotometría en astronomía». Página de inicio de Paul Schlyter . Consultado el 25 de abril de 2024 .
- ^ Dufay, Jean (17 de octubre de 2012). Introducción a la astrofísica: las estrellas. Courier Corporation. p. 3. ISBN 978-0-486-60771-9Archivado desde el original el 24 de marzo de 2017 . Consultado el 28 de febrero de 2016 .
- ^ McLean, Ian S. (2008). Imágenes electrónicas en astronomía: detectores e instrumentación . Springer. pág. 529. ISBN. 978-3-540-76582-0.
- ^ Dolan, Michelle M.; Mathews, Grant J.; Lam, Doan Duc; Lan, Nguyen Quynh; Herczeg, Gregory J.; Dearborn, David SP (2017). "Trayectorias evolutivas de Betelgeuse". The Astrophysical Journal . 819 (1): 7. arXiv : 1406.3143 . Código Bibliográfico :2016ApJ...819....7D. doi : 10.3847/0004-637X/819/1/7 . S2CID 37913442.
- ^ "Los cometas más brillantes vistos desde 1935". International Comet Quarterly. Archivado desde el original el 28 de diciembre de 2011. Consultado el 18 de diciembre de 2011 .
- ^ Winkler, P. Frank; Gupta, Gaurav; Long, Knox S. (2003). "El remanente de SN 1006: movimientos ópticos propios, imágenes profundas, distancia y brillo al máximo". The Astrophysical Journal . 585 (1): 324–335. arXiv : astro-ph/0208415 . Código Bibliográfico :2003ApJ...585..324W. doi :10.1086/345985. S2CID 1626564.
- ^ Siegel, Ethan (6 de septiembre de 2016). «Diez formas en las que Proxima b es diferente de la Tierra». Forbes . Consultado el 19 de febrero de 2023 .
- ^ "Supernova 1054 – Creación de la Nebulosa del Cangrejo". SEDS . Archivado desde el original el 28 de mayo de 2014 . Consultado el 29 de julio de 2014 .
- ^ "Heavens-above.com". Heavens-above. Archivado desde el original el 5 de julio de 2009. Consultado el 22 de diciembre de 2007 .
- ^ abcdefghijklmnopqrstu Mallama, A.; Hilton, JL (2018). "Cálculo de magnitudes planetarias aparentes para el Almanaque Astronómico". Astronomía y Computación . 25 : 10–24. arXiv : 1808.01973 . Código Bibliográfico :2018A&C....25...10M. doi :10.1016/j.ascom.2018.08.002. S2CID 69912809.
- ^ Pregunta científica de la semana de la NASA. Gsfc.nasa.gov (7 de abril de 2006). Recuperado el 26 de abril de 2013.
- ^ Tomkin, Jocelyn (abril de 1998). "Reyes celestiales pasados y futuros". Sky and Telescope . 95 (4): 59–63. Código Bibliográfico :1998S&T....95d..59T.– basado en cálculos a partir de datos de HIPPARCOS . (Los cálculos excluyen estrellas cuya distancia o movimiento propio son inciertos).
- ^ "Sirius". Base de datos astronómica SIMBAD. Archivado desde el original el 11 de enero de 2014. Consultado el 26 de junio de 2010 .
- ^ "Canopus". Base de datos astronómica SIMBAD. Archivado desde el original el 14 de julio de 2014. Consultado el 26 de junio de 2010 .
- ^ "Arcturus". Base de datos astronómica SIMBAD. Archivado desde el original el 14 de enero de 2014. Consultado el 26 de junio de 2010 .
- ^ "Vega". Base de datos astronómica SIMBAD. Archivado desde el original el 7 de julio de 2015. Consultado el 14 de abril de 2010 .
- ^ Evans, NR; Schaefer, GH; Bond, HE; Bono, G.; Karovska, M.; Nelan, E.; Sasselov, D.; Mason, BD (2008). "Detección directa de la compañera cercana de Polaris con el telescopio espacial Hubble". The Astronomical Journal . 136 (3): 1137. arXiv : 0806.4904 . Bibcode :2008AJ....136.1137E. doi :10.1088/0004-6256/136/3/1137. S2CID 16966094.
- ^ "SIMBAD-M31". Base de datos astronómica SIMBAD. Archivado desde el original el 19 de mayo de 2014. Consultado el 29 de noviembre de 2009 .
- ^ Yeomans; Chamberlin. "Sistema de efemérides de Horizon Online para Ganimedes (cuerpo principal 503)". Instituto Tecnológico de California, Laboratorio de Propulsión a Chorro. Archivado desde el original el 2 de febrero de 2014. Consultado el 14 de abril de 2010 .(4.38 el 3 de octubre de 1951)
- ^ "M41 posiblemente registrado por Aristóteles". SEDS (Estudiantes para la Exploración y el Desarrollo del Espacio). 28 de julio de 2006. Archivado desde el original el 18 de abril de 2017. Consultado el 29 de noviembre de 2009 .
- ^ "Hoja informativa sobre Urano". nssdc.gsfc.nasa.gov . Archivado desde el original el 22 de enero de 2019. Consultado el 8 de noviembre de 2018 .
- ^ "SIMBAD-M33". Base de datos astronómica SIMBAD. Archivado desde el original el 13 de septiembre de 2014. Consultado el 28 de noviembre de 2009 .
- ^ Lodriguss, Jerry (1993). «M33 (Galaxia del Triángulo)». Archivado desde el original el 15 de enero de 2010. Consultado el 27 de noviembre de 2009 .(Muestra magnitud bolométrica, no magnitud visual).
- ^ "Messier 81". SEDS (Estudiantes para la Exploración y el Desarrollo del Espacio). 2 de septiembre de 2007. Archivado desde el original el 14 de julio de 2017. Consultado el 28 de noviembre de 2009 .
- ^ "Hoja informativa sobre Neptuno". nssdc.gsfc.nasa.gov . Archivado desde el original el 10 de enero de 2019. Consultado el 8 de noviembre de 2018 .
- ^ John E. Bortle (febrero de 2001). "La escala de cielo oscuro de Bortle". Sky & Telescope. Archivado desde el original el 23 de marzo de 2009. Consultado el 18 de noviembre de 2009 .
- ^ Yeomans; Chamberlin. "Sistema de efemérides de Horizon Online para Titán (cuerpo principal 606)". Instituto Tecnológico de California, Laboratorio de Propulsión a Chorro. Archivado desde el original el 13 de noviembre de 2012. Consultado el 28 de junio de 2010 .(8.10 del 30 de diciembre de 2003) Archivado el 13 de noviembre de 2012 en Wayback Machine.
- ^ ab «Satélites clásicos del Sistema Solar». Observatorio ARVAL. Archivado desde el original el 31 de julio de 2010. Consultado el 25 de junio de 2010 .
- ^ abc «Planetary Satellite Physical Parameters». JPL (Solar System Dynamics). 3 de abril de 2009. Archivado desde el original el 23 de julio de 2009. Consultado el 25 de julio de 2009 .
- ^ "AstDys (10) Hygiea Ephemerides". Departamento de Matemáticas, Universidad de Pisa, Italia. Archivado desde el original el 12 de mayo de 2014. Consultado el 26 de junio de 2010 .
- ^ Zarenski, Ed (2004). "Limiting Magnitude in Binoculars" (PDF) . Noches nubladas. Archivado (PDF) desde el original el 21 de julio de 2011. Consultado el 6 de mayo de 2011 .
- ^ "Seguimiento de los vuelos del Apolo". Páginas web estáticas de física y astronomía . 21 de diciembre de 1968. Consultado el 20 de marzo de 2024 .
- ^ "¿Cuál es la estrella más masiva?". Space.com . Archivado desde el original el 11 de enero de 2019. Consultado el 5 de noviembre de 2018 .
- ^ Williams, David R. (7 de septiembre de 2006). «Hoja informativa sobre Plutón». Centro Nacional de Datos de Ciencia Espacial . NASA. Archivado desde el original el 1 de julio de 2010. Consultado el 26 de junio de 2010 .
- ^ "AstDys (2060) Chiron Ephemerides". Departamento de Matemáticas, Universidad de Pisa, Italia. Archivado desde el original el 29 de junio de 2011 . Consultado el 26 de junio de 2010 .
- ^ "AstDys (136472) Efemérides de Makemake". Departamento de Matemáticas, Universidad de Pisa, Italia. Archivado desde el original el 29 de junio de 2011. Consultado el 26 de junio de 2010 .
- ^ "AstDys (136108) Efemérides de Haumea". Departamento de Matemáticas, Universidad de Pisa, Italia. Archivado desde el original el 29 de junio de 2011. Consultado el 26 de junio de 2010 .
- ^ "Instalaciones del Catalina Sky Survey (CSS)". Archivado desde el original el 3 de noviembre de 2019 . Consultado el 3 de noviembre de 2019 .
- ^ Steve Cullen (sgcullen) (5 de octubre de 2009). «17 nuevos asteroides descubiertos por LightBuckets». LightBuckets. Archivado desde el original el 31 de enero de 2010. Consultado el 15 de noviembre de 2009 .
- ^ Boffin, HMJ; Pourbaix, D. (2014). "Posible descubrimiento astrométrico de un compañero subestelar del sistema binario enano marrón más cercano WISE J104915.57–531906.1". Astronomía y Astrofísica . 561 : 5. arXiv : 1312.1303 . Bibcode :2014A&A...561L...4B. doi :10.1051/0004-6361/201322975. S2CID 33043358.
- ^ "Magnitud límite de Pan-STARRS". Archivado desde el original el 24 de noviembre de 2020. Consultado el 12 de agosto de 2019 .
- ^ Sheppard, Scott S. "Saturno's Known Satellites". Carnegie Institution (Departamento de Magnetismo Terrestre). Archivado desde el original el 15 de mayo de 2011. Consultado el 28 de junio de 2010 .
- ^ ¿ Cuál es el objeto más débil captado por telescopios terrestres? Archivado el 2 de febrero de 2016 en Wayback Machine , por: Los editores de Sky Telescope, 24 de julio de 2006
- ^ "Nueva imagen del cometa Halley en el frío". ESO . 1 de septiembre de 2003. Archivado desde el original el 1 de marzo de 2009 . Consultado el 22 de febrero de 2009 .
- ^ Robertson, BE; et al. (2023). "Identificación y propiedades de galaxias con intensa formación estelar en corrimientos al rojo z > 10". Nature Astronomy . 7 (5): 611–621. arXiv : 2212.04480 . Código Bibliográfico :2023NatAs...7..611R. doi :10.1038/s41550-023-01921-1. S2CID 257968812.
- ^ Illingworth, GD; Magee, D.; Oesch, PA; Bouwens, RJ; Labbé, I.; Stiavelli, M.; van Dokkum, PG; Franx, M.; Trenti, M.; Carollo, CM; Gonzalez, V. (21 de octubre de 2013). "El XDF de campo profundo extremo del HST: Combinando todos los datos ACS y WFC3/IR en la región HUDF en el campo más profundo jamás creado". The Astrophysical Journal Supplement Series . 209 (1): 6. arXiv : 1305.1931 . Código Bibliográfico :2013ApJS..209....6I. doi :10.1088/0067-0049/209/1/6. S2CID 55052332.
- ^ "Telescopios". www.jaymaron.com . Archivado desde el original el 1 de agosto de 2017 . Consultado el 14 de septiembre de 2017 .(consultado el 14 de septiembre de 2017)
- ^ "Hubble encuentra el objeto más pequeño jamás visto en el cinturón de Kuiper". NASA . Archivado desde el original el 9 de junio de 2017 . Consultado el 16 de marzo de 2018 .
Enlaces externos
- "La escala de magnitud astronómica". International Comet Quarterly .
![{\displaystyle {\sqrt[{5}]{100}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d26eff2c044a521107db3cf827e04c2b8415691d)



![{\displaystyle {\sqrt[{5}]{100}}\aproximadamente 2,512}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed184113e02b2f8b9edcedca0920c0d14661ead)








