Función de ventana
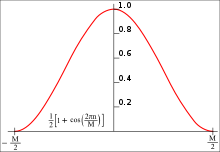
En el procesamiento de señales y las estadísticas , una función de ventana (también conocida como función de apodización o función de estrechamiento [1] ) es una función matemática que tiene un valor cero fuera de un intervalo elegido . Normalmente, las funciones de ventana son simétricas alrededor de la mitad del intervalo, se acercan a un máximo en la mitad y se estrechan a partir de la mitad. Matemáticamente, cuando otra función o forma de onda/secuencia de datos se "multiplica" por una función de ventana, el producto también tiene un valor cero fuera del intervalo: todo lo que queda es la parte donde se superponen, la "vista a través de la ventana". De manera equivalente, y en la práctica real, primero se aísla el segmento de datos dentro de la ventana y luego solo esos datos se multiplican por los valores de la función de ventana. Por lo tanto, el estrechamiento, no la segmentación, es el propósito principal de las funciones de ventana.
Las razones para examinar segmentos de una función más larga incluyen la detección de eventos transitorios y el promedio temporal de los espectros de frecuencia. La duración de los segmentos se determina en cada aplicación según requisitos como la resolución temporal y de frecuencia. Pero ese método también cambia el contenido de frecuencia de la señal mediante un efecto llamado fuga espectral . Las funciones de ventana nos permiten distribuir la fuga espectral de diferentes maneras, según las necesidades de la aplicación particular. Hay muchas opciones detalladas en este artículo, pero muchas de las diferencias son tan sutiles que resultan insignificantes en la práctica.
En aplicaciones típicas, las funciones de ventana utilizadas son curvas no negativas, suaves y "con forma de campana". [2] También se pueden utilizar funciones rectangulares, triangulares y de otro tipo. Una definición más general de las funciones de ventana no exige que sean idénticamente cero fuera de un intervalo, siempre que el producto de la ventana multiplicado por su argumento sea integrable al cuadrado y, más específicamente, que la función tienda a cero con la suficiente rapidez. [3]
Aplicaciones
Las funciones de ventana se utilizan en el análisis /modificación/ resíntesis espectral , [4] el diseño de filtros de respuesta de impulso finito , la fusión de conjuntos de datos multidimensionales y de múltiples escalas, [5] [6] así como en la formación de haces y el diseño de antenas .

Análisis espectral
La transformada de Fourier de la función cos( ωt ) es cero, excepto en la frecuencia ± ω . Sin embargo, muchas otras funciones y formas de onda no tienen transformadas de forma cerrada convenientes. Alternativamente, uno podría estar interesado en su contenido espectral solo durante un cierto período de tiempo.
En cualquier caso, la transformada de Fourier (o una transformada similar) se puede aplicar a uno o más intervalos finitos de la forma de onda. En general, la transformada se aplica al producto de la forma de onda y una función de ventana. Cualquier ventana (incluidas las rectangulares) afecta la estimación espectral calculada mediante este método.
Diseño de filtros
Las ventanas se utilizan a veces en el diseño de filtros digitales , en particular para convertir una respuesta de impulso "ideal" de duración infinita, como una función sinc , en un diseño de filtro de respuesta de impulso finito (FIR). Esto se denomina método de ventana . [7] [8] [9]
Estadísticas y ajuste de curvas
Las funciones de ventana se utilizan a veces en el campo del análisis estadístico para restringir el conjunto de datos que se analizan a un rango cercano a un punto determinado, con un factor de ponderación que disminuye el efecto de los puntos más alejados de la parte de la curva que se está ajustando. En el campo del análisis bayesiano y el ajuste de curvas , esto se suele denominar kernel .
Aplicaciones de ventanas rectangulares
Análisis de transitorios
Al analizar una señal transitoria en el análisis modal , como un impulso, una respuesta a un choque, una ráfaga sinusoidal, una ráfaga de chirrido o una ráfaga de ruido, donde la distribución de energía en función del tiempo es extremadamente desigual, la ventana rectangular puede ser la más apropiada. Por ejemplo, cuando la mayor parte de la energía se encuentra al principio de la grabación, una ventana no rectangular atenúa la mayor parte de la energía, degradando la relación señal-ruido. [10]
Análisis armónico
Se podría desear medir el contenido armónico de una nota musical de un instrumento en particular o la distorsión armónica de un amplificador a una frecuencia dada. Volviendo a la Figura 2 , podemos observar que no hay fugas en un conjunto discreto de frecuencias relacionadas armónicamente muestreadas por la transformada de Fourier discreta (DFT). (Los nulos espectrales son en realidad cruces por cero, que no se pueden mostrar en una escala logarítmica como esta). Esta propiedad es exclusiva de la ventana rectangular y debe configurarse adecuadamente para la frecuencia de la señal, como se describió anteriormente.
Ventanas superpuestas
Cuando la longitud de un conjunto de datos que se va a transformar es mayor que la necesaria para proporcionar la resolución de frecuencia deseada, una práctica común es subdividirlo en conjuntos más pequeños y dividirlos en ventanas individuales. Para mitigar la "pérdida" en los bordes de la ventana, los conjuntos individuales pueden superponerse en el tiempo. Consulte el método de Welch de análisis espectral de potencia y la transformada de coseno discreta modificada .
Ventanas bidimensionales
Las ventanas bidimensionales se utilizan comúnmente en el procesamiento de imágenes para reducir las altas frecuencias no deseadas en la transformada de Fourier de la imagen. [11] Se pueden construir a partir de ventanas unidimensionales en cualquiera de dos formas. [12] La forma separable, es trivial de calcular. La forma radial , , que involucra el radio , es isótropa , independiente de la orientación de los ejes de coordenadas. Solo la función gaussiana es separable e isótropa. [13] Las formas separables de todas las demás funciones de ventana tienen esquinas que dependen de la elección de los ejes de coordenadas. La isotropía/ anisotropía de una función de ventana bidimensional es compartida por su transformada de Fourier bidimensional. La diferencia entre las formas separables y radiales es similar al resultado de la difracción de aperturas rectangulares versus circulares, que se pueden visualizar en términos del producto de dos funciones sinc versus una función de Airy , respectivamente.
Ejemplos de funciones de ventana
Convenciones :
- es una función de fase cero (simétrica respecto a ), [14] continua para donde es un entero positivo (par o impar). [15]
- La secuencia es simétrica , de longitud
- es DFT-simétrico , de longitud [A]
- El parámetro B que se muestra en cada gráfico espectral es la métrica del ancho de banda equivalente de ruido de la función , en unidades de contenedores DFT . [16] : p.56 eq.(16)
- Consulte Fuga espectral §§ Señales de tiempo discreto y Algunas métricas de ventana y Frecuencia normalizada para comprender el uso de "contenedores" para el eje x en estos gráficos.
El muestreo disperso de una transformada de Fourier de tiempo discreto (DTFT), como las DFT de la figura 2, solo revela la fuga hacia los compartimentos de la DFT desde una sinusoide cuya frecuencia también es un compartimento entero de la DFT. Los lóbulos laterales no visibles revelan la fuga que se espera de las sinusoides en otras frecuencias. [a] Por lo tanto, al elegir una función de ventana, suele ser importante muestrear la DTFT de forma más densa (como hacemos a lo largo de esta sección) y elegir una ventana que suprima los lóbulos laterales a un nivel aceptable.
Ventana rectangular

La ventana rectangular (a veces conocida como ventana de vagón de carga , ventana uniforme o ventana de Dirichlet o, de manera engañosa, como "sin ventana" en algunos programas [18] ) es la ventana más simple, equivalente a reemplazar todos los valores consecutivos de una secuencia de datos excepto N por ceros, lo que hace que la forma de onda se encienda y apague repentinamente:
Otras ventanas están diseñadas para moderar estos cambios repentinos, reducir la pérdida por festoneado y mejorar el rango dinámico (descrito en § Análisis espectral).
La ventana rectangular es la ventana B -spline de primer orden , así como la ventana de potencia de seno de potencia 0 .
La ventana rectangular proporciona la estimación del error cuadrático medio mínimo de la transformada de Fourier de tiempo discreto , a costa de otras cuestiones analizadas.
B-ventanas spline
Las ventanas B -spline se pueden obtener como convoluciones k -fold de la ventana rectangular. Incluyen la ventana rectangular en sí ( k = 1), la ventana § triangular ( k = 2) y la ventana § Parzen ( k = 4). [19] Las definiciones alternativas muestrean las funciones base B -spline normalizadas apropiadas en lugar de convolucionar ventanas de tiempo discreto. Una función base B -spline de k - ésimo orden es una función polinómica por partes de grado k −1 que se obtiene por autoconvolución k-fold de la función rectangular .
Ventana triangular
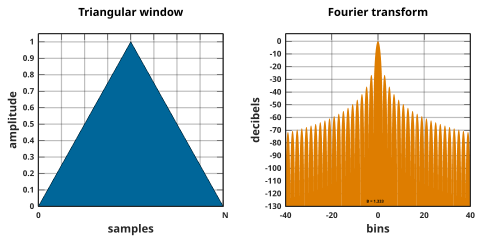
Las ventanas triangulares están dadas por:
donde L puede ser N , [20] N + 1, [16] [21] [22] o N + 2. [23] La primera también se conoce como ventana de Bartlett o ventana de Fejér . Las tres definiciones convergen en N grande .
La ventana triangular es la ventana B -spline de segundo orden . La forma L = N puede verse como la convolución de dos ventanas rectangulares de ancho N / 2 . La transformada de Fourier del resultado son los valores al cuadrado de la transformada de la ventana rectangular de ancho medio.
Ventana de Parzen

Definiendo L ≜ N + 1 , la ventana Parzen, también conocida como ventana de la Vallée Poussin , [16] es la ventana B -spline de cuarto orden dada por:

Otras ventanas polinómicas
Ventana de Welch
La ventana de Welch consta de una única sección parabólica :
- [23]
El polinomio cuadrático definitorio alcanza un valor de cero en las muestras justo fuera del alcance de la ventana.
Ventana sinusoidal

La función correspondiente es un coseno sin el desfase π /2. Por lo tanto, la ventana seno [24] a veces también se denomina ventana coseno . [16] Como representa la mitad de un ciclo de una función sinusoidal, también se la conoce como ventana seno-medio [25] o ventana senoseno-medio [26] .
La autocorrelación de una ventana seno produce una función conocida como ventana de Bohman. [27]
Ventanas de potencias de seno y coseno
Estas funciones de ventana tienen la forma: [28]
La ventana rectangular ( α = 0 ), la ventana senoidal ( α = 1 ) y la ventana de Hann ( α = 2 ) son miembros de esta familia.
Para valores enteros pares de α, estas funciones también se pueden expresar en forma de suma de cosenos:
Ventanas de suma de cosenos
Esta familia también se conoce como ventanas de coseno generalizadas .
| ( Ec.1 ) |
En la mayoría de los casos, incluidos los ejemplos siguientes, todos los coeficientes a k ≥ 0. Estas ventanas tienen solo 2 K + 1 coeficientes DFT de N puntos distintos de cero .
Ventanas de Hann y Hamming


Las ventanas de suma de cosenos habituales para el caso K = 1 tienen la forma:
que se confunde fácilmente (y a menudo) con su versión de fase cero:
La configuración produce una ventana de Hann:
- [29]
Se le llama así por Julius von Hann y, a veces, se le denomina erróneamente Hanning , probablemente debido a sus similitudes lingüísticas y formulaicas con la ventana de Hamming. También se la conoce como coseno elevado , porque la versión de fase cero es un lóbulo de una función de coseno elevado.
Esta función pertenece a las familias de suma de cosenos y potencia de senos. A diferencia de la ventana de Hamming, los puntos finales de la ventana de Hann apenas tocan el cero. Los lóbulos laterales resultantes disminuyen a unos 18 dB por octava. [30]
Si se establece en aproximadamente 0,54, o más precisamente 25/46, se produce la ventana de Hamming , propuesta por Richard W. Hamming . Esa elección coloca un cruce por cero en la frecuencia 5 π /( N − 1), que cancela el primer lóbulo lateral de la ventana de Hann, lo que le da una altura de aproximadamente una quinta parte de la de la ventana de Hann. [16] [31] [32] La ventana de Hamming a menudo se denomina blip de Hamming cuando se utiliza para dar forma a los pulsos . [33] [34] [35]
La aproximación de los coeficientes a dos decimales reduce sustancialmente el nivel de lóbulos laterales, [16] a una condición casi de ondulación equitativa. [32] En el sentido de ondulación equitativa, los valores óptimos para los coeficientes son a 0 = 0,53836 y a 1 = 0,46164. [32] [36]
Ventana de Blackman
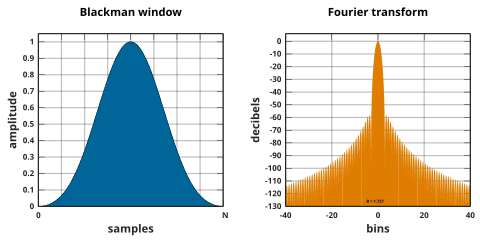
Las ventanas de Blackman se definen como:
Por convención común, el término no calificado ventana de Blackman se refiere a la "propuesta no muy seria" de Blackman de α = 0,16 ( a 0 = 0,42, a 1 = 0,5, a 2 = 0,08), que se aproxima mucho al Blackman exacto , [37] con a 0 = 7938/18608 ≈ 0,42659, a 1 = 9240/18608 ≈ 0,49656 y a 2 = 1430/18608 ≈ 0,076849. [38] Estos valores exactos colocan ceros en el tercer y cuarto lóbulos laterales, [16] pero dan como resultado una discontinuidad en los bordes y una caída de 6 dB/oct. Los coeficientes truncados no anulan también los lóbulos laterales, pero tienen una caída mejorada de 18 dB/oct. [16] [39]
Ventana de Nuttall, derivada primera continua

La forma continua de la ventana de Nuttall y su primera derivada son continuas en todas partes, como la función de Hann . Es decir, la función tiende a 0 en x = ± N /2, a diferencia de las ventanas de Blackman–Nuttall, Blackman–Harris y Hamming. La ventana de Blackman ( α = 0,16 ) también es continua con derivada continua en el borde, pero la "ventana de Blackman exacta" no lo es.
Ventana de Blackman-Nuttall

Ventana de Blackman-Harris

Una generalización de la familia Hamming, producida mediante la adición de más funciones sinc desplazadas, destinadas a minimizar los niveles de lóbulos laterales [40] [41]
Ventana de parte superior plana
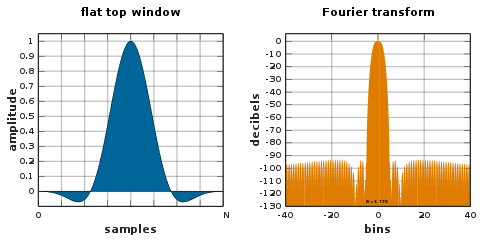
Una ventana de parte superior plana es una ventana con valores parcialmente negativos que tiene una pérdida mínima de festoneado en el dominio de frecuencia. Esa propiedad es deseable para la medición de amplitudes de componentes de frecuencia sinusoidal. [17] [42] Sin embargo, su amplio ancho de banda da como resultado un ancho de banda de ruido alto y una selección de frecuencia más amplia, lo que, según la aplicación, podría ser un inconveniente.
Las ventanas de parte superior plana se pueden diseñar utilizando métodos de diseño de filtro de paso bajo, [42] o pueden ser de la variedad habitual de suma de coseno:
La variante de Matlab tiene estos coeficientes:
Existen otras variaciones, como lóbulos laterales que disminuyen a costa de valores más altos cerca del lóbulo principal. [17]
Ventanas de Rife-Vincent
Las ventanas de Rife-Vincent [43] se escalan habitualmente para un valor promedio unitario, en lugar de un valor pico unitario. Los valores de coeficientes a continuación, aplicados a la ecuación 1 , reflejan esa costumbre.
Clase I, Orden 1 ( K = 1): Funcionalmente equivalente a la ventana de Hann.
Clase I, Orden 2 ( K = 2):
La clase I se define minimizando la amplitud del lóbulo lateral de orden superior. Se presentan en tablas los coeficientes para órdenes de hasta K=4. [44]
La clase II minimiza el ancho del lóbulo principal para un lóbulo lateral máximo dado.
La clase III es un compromiso para el cual el orden K = 2 se asemeja a la ventana de Blackman §. [44] [45]
Ventanas ajustables
Ventana gaussiana
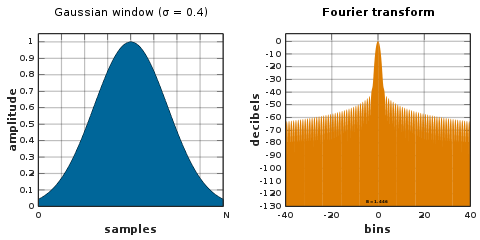
La transformada de Fourier de una función gaussiana también es una función gaussiana. Dado que el soporte de una función gaussiana se extiende hasta el infinito, debe truncarse en los extremos de la ventana o bien enventanarse con otra ventana de extremo cero. [46]
Dado que el logaritmo de una gaussiana produce una parábola , esto se puede utilizar para una interpolación cuadrática casi exacta en la estimación de frecuencia . [47] [46] [48]
La desviación estándar de la función gaussiana es σ · N /2 períodos de muestreo.
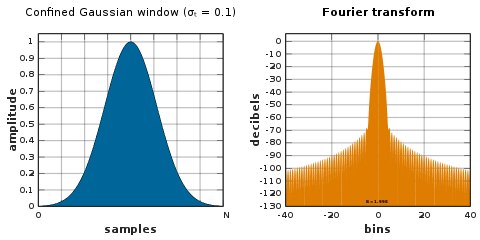
Ventana gaussiana confinada
La ventana gaussiana confinada produce el ancho de frecuencia cuadrático medio más pequeño posible σ ω para un ancho temporal dado ( N + 1) σ t . [49] Estas ventanas optimizan los productos de ancho de banda de tiempo-frecuencia RMS. Se calculan como los vectores propios mínimos de una matriz dependiente de parámetros. La familia de ventanas gaussianas confinadas contiene la ventana § Sinus y la ventana § Gaussiana en los casos límite de σ t grande y pequeño , respectivamente.

Ventana gaussiana confinada aproximada
Definiendo L ≜ N + 1 , una ventana gaussiana confinada de ancho temporal L × σ t se aproxima bien mediante: [49]
donde es una función gaussiana:
La desviación estándar de la ventana aproximada es asintóticamente igual (es decir, valores grandes de N ) a L × σ t para σ t < 0,14 . [49]
Ventana normal generalizada
Una versión más generalizada de la ventana gaussiana es la ventana normal generalizada. [50] Manteniendo la notación de la ventana gaussiana anterior, podemos representar esta ventana como
para cualquier par . En , esta es una ventana gaussiana y como se acerca a , esto se aproxima a una ventana rectangular. La transformada de Fourier de esta ventana no existe en una forma cerrada para un general . Sin embargo, demuestra los otros beneficios de ser suave, ancho de banda ajustable. Al igual que la ventana de Tukey §, esta ventana ofrece naturalmente una "parte superior plana" para controlar la atenuación de amplitud de una serie de tiempo (en la que no tenemos un control con la ventana gaussiana). En esencia, ofrece un buen compromiso (controlable), en términos de fuga espectral, resolución de frecuencia y atenuación de amplitud, entre la ventana gaussiana y la ventana rectangular. Véase también [51] para un estudio sobre la representación tiempo-frecuencia de esta ventana (o función).
Ventana de Tukey

La ventana de Tukey, también conocida como ventana cónica de coseno , puede considerarse como un lóbulo coseno de ancho Nα /2 (que abarca Nα /2 + 1 observaciones) que está convolucionado con una ventana rectangular de ancho N (1 − α /2) .
- [52] [B] [C]
En α = 0 se vuelve rectangular, y en α = 1 se convierte en una ventana de Hann.
Ventana cónica de Planck

La llamada ventana de "conicidad de Planck" es una función de protuberancia que se ha utilizado ampliamente [53] en la teoría de particiones de la unidad en variedades . Es suave (una función) en todas partes, pero es exactamente cero fuera de una región compacta, exactamente uno en un intervalo dentro de esa región y varía de manera suave y monótona entre esos límites. Su uso como función de ventana en el procesamiento de señales se sugirió por primera vez en el contexto de la astronomía de ondas gravitacionales , inspirada en la distribución de Planck . [54] Se define como una función por partes :
La cantidad de estrechamiento está controlada por el parámetro ε , y los valores más pequeños producen transiciones más nítidas.
Ventana DPSS o Slepian
La DPSS (secuencia esferoidal prolada discreta) o ventana de Slepian maximiza la concentración de energía en el lóbulo principal , [55] y se utiliza en el análisis espectral multiconicidad , que promedia el ruido en el espectro y reduce la pérdida de información en los bordes de la ventana.
El lóbulo principal termina en un intervalo de frecuencia dado por el parámetro α . [56]
 |  |
Las ventanas Kaiser que aparecen a continuación se crean mediante una aproximación simple a las ventanas DPSS:
 |  |
Ventana del Kaiser
La ventana de Kaiser, o Kaiser-Bessel, es una aproximación simple de la ventana DPSS utilizando funciones de Bessel , descubierta por James Kaiser . [57] [58]
- [D] [16] : pág. 73
donde es la función de Bessel modificada de orden 0 del primer tipo. El parámetro variable determina el equilibrio entre el ancho del lóbulo principal y los niveles del lóbulo lateral del patrón de fuga espectral. El ancho del lóbulo principal, entre los nulos, se da en unidades de contenedores DFT, [65] y un valor típico de es 3.
Ventana de Dolph-Chebyshev

Minimiza la norma de Chebyshev de los lóbulos laterales para un ancho de lóbulo principal dado. [66]
La función de ventana de Dolph-Chebyshev de fase cero se define generalmente en términos de su transformada de Fourier discreta de valor real , : [67]
T n ( x ) es el n - ésimo polinomio de Chebyshev de primer tipo evaluado en x , que se puede calcular utilizando
y
es la única solución real positiva para , donde el parámetro α establece la norma de Chebyshev de los lóbulos laterales en −20 α decibeles. [66]
La función de ventana se puede calcular a partir de W 0 ( k ) mediante una transformada de Fourier discreta inversa (DFT): [66]
La versión retrasada de la ventana se puede obtener mediante:
que para valores pares de N debe calcularse de la siguiente manera:
que es una DFT inversa de
Variaciones:
- Debido a la condición de equirruga, la ventana del dominio del tiempo tiene discontinuidades en los bordes. Una aproximación que las evita, al permitir que las equirrugas desaparezcan en los bordes, es una ventana de Taylor.
- También está disponible una alternativa a la definición DFT inversa.[1].
Ventana ultraesférica

La ventana ultraesférica fue introducida en 1984 por Roy Streit [68] y tiene aplicación en el diseño de matrices de antenas, [69] diseño de filtros no recursivos, [68] y análisis de espectro. [70]
Al igual que otras ventanas ajustables, la ventana Ultraspherical tiene parámetros que se pueden utilizar para controlar el ancho del lóbulo principal de la transformada de Fourier y la amplitud relativa del lóbulo lateral. A diferencia de otras ventanas, tiene un parámetro adicional que se puede utilizar para establecer la velocidad a la que los lóbulos laterales disminuyen (o aumentan) en amplitud. [70] [71] [72]
La ventana se puede expresar en el dominio del tiempo de la siguiente manera: [70]
donde es el polinomio ultrasférico de grado N, y y controlan los patrones de lóbulos laterales. [70]
Ciertos valores específicos de producen otras ventanas bien conocidas: y dan las ventanas de Dolph-Chebyshev y Saramäki respectivamente. [68] Véase aquí una ilustración de ventanas ultraesféricas con parametrización variada.
Ventana exponencial o de Poisson


La ventana de Poisson, o más genéricamente la ventana exponencial, aumenta exponencialmente hacia el centro de la ventana y disminuye exponencialmente en la segunda mitad. Dado que la función exponencial nunca llega a cero, los valores de la ventana en sus límites no son cero (puede verse como la multiplicación de una función exponencial por una ventana rectangular [73] ). Se define por
donde τ es la constante de tiempo de la función. La función exponencial decae cuando e ≃ 2,71828 o aproximadamente 8,69 dB por constante de tiempo. [74] Esto significa que para una caída objetivo de D dB sobre la mitad de la longitud de la ventana, la constante de tiempo τ está dada por
Ventanas híbridas
También se han construido funciones de ventana como combinaciones multiplicativas o aditivas de otras ventanas.
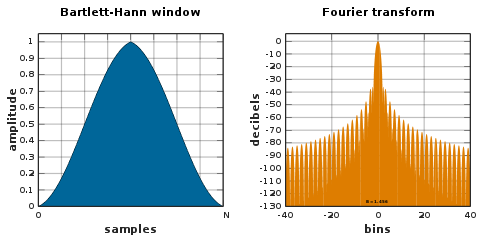
Ventana de Bartlett-Hann
Ventana de Planck-Bessel

Una ventana de conicidad de Planck multiplicada por una ventana de Kaiser que se define en términos de una función de Bessel modificada . Esta función de ventana híbrida se introdujo para disminuir el nivel máximo del lóbulo lateral de la ventana de conicidad de Planck y, al mismo tiempo, aprovechar su buena descomposición asintótica. [75] Tiene dos parámetros ajustables, ε de la conicidad de Planck y α de la ventana de Kaiser, por lo que se puede ajustar para adaptarse a los requisitos de una señal determinada.
Ventana de Hann-Poisson

Una ventana de Hann multiplicada por una ventana de Poisson. No tiene lóbulos laterales, ya que su transformada de Fourier cae para siempre alejándose del lóbulo principal sin mínimos locales. Por lo tanto, se puede utilizar en algoritmos de escalada de colinas como el método de Newton . [76] La ventana de Hann-Poisson se define por:
donde α es un parámetro que controla la pendiente de la exponencial.
Otras ventanas

Ventana polinómica adaptativa generalizada (GAP)
La ventana GAP es una familia de funciones de ventana ajustables que se basan en una expansión polinómica simétrica de orden . Es continua con derivada continua en todas partes. Con el conjunto adecuado de coeficientes de expansión y orden de expansión, la ventana GAP puede imitar todas las funciones de ventana conocidas, reproduciendo con precisión sus propiedades espectrales.
- [77]
donde es la desviación estándar de la secuencia.
Además, a partir de un conjunto de coeficientes de expansión que imita una determinada función de ventana conocida, la ventana GAP se puede optimizar mediante procedimientos de minimización para obtener un nuevo conjunto de coeficientes que mejoran una o más propiedades espectrales, como el ancho del lóbulo principal, la atenuación del lóbulo lateral y la tasa de caída del lóbulo lateral. [78] Por lo tanto, se puede desarrollar una función de ventana GAP con propiedades espectrales diseñadas dependiendo de la aplicación específica.

Ventana de Lanczos
- utilizado en el remuestreo de Lanczos
- Para la ventana de Lanczos, se define como
- También conocida como ventana sinc , porque: es el lóbulo principal de una función sinc normalizada
Funciones de ventana asimétricas
La forma, según la convención anterior, es simétrica en torno a . Sin embargo, existen funciones de ventana que son asimétricas, como la distribución Gamma utilizada en las implementaciones FIR de filtros Gammatone . Estas asimetrías se utilizan para reducir el retraso cuando se utilizan tamaños de ventana grandes o para enfatizar el transitorio inicial de un pulso en decaimiento. [ cita requerida ]
Cualquier función acotada con soporte compacto , incluidas las asimétricas, se puede utilizar fácilmente como función de ventana. Además, existen formas de transformar ventanas simétricas en asimétricas transformando la coordenada temporal, como con la siguiente fórmula
donde la ventana pondera más las muestras más antiguas cuando , y, a la inversa, pondera más las muestras más recientes cuando . [79]
Véase también
- Apodización
- Filtro Kolmogorov-Zurbenko
- Multicono
- Transformada de Fourier de corta duración
- Fuga espectral
- Método Welch
- Función de peso
- Método de diseño de ventanas
Notas
- ^ Algunos autores limitan su atención a este importante subconjunto e incluso a valores de N. [16] [17] Pero las fórmulas de coeficientes de ventana siguen siendo las que se presentan aquí.
- ^ Esta fórmula se puede confirmar simplificando la función coseno en MATLAB tukeywin y sustituyendo r = α y x = n / N .
- ^ Harris 1978 (p 67, ecuación 38) parece tener dos errores: (1) El operador de resta en el numerador de la función coseno debería ser una suma. (2) El denominador contiene un factor espurio de 2. Además, la figura 30 corresponde a α=0,25 utilizando la fórmula de Wikipedia, pero a 0,75 utilizando la fórmula de Harris. La figura 32 está mal etiquetada de manera similar.
- ^ La ventana de Kaiser a menudo se parametriza mediante β , donde β = π α . [59] [60] [61] [62] [56] [63] [7] : p. 474 El uso alternativo de solo α facilita las comparaciones con las ventanas DPSS. [64]
Citas de páginas
- ^ Harris 1978, pág. 57, figura 10.
Referencias
- ^ Weisstein, Eric W. (2003). Enciclopedia concisa de matemáticas del CRC. CRC Press. ISBN 978-1-58488-347-0.
- ^ Roads, Curtis (2002). Microsonido . MIT Press. ISBN 978-0-262-18215-7.
- ^ Cattani, Carlo; Rushchitsky, Jeremiah (2007). Análisis de ondas y wavelets aplicado a materiales con micro o nanoestructura. World Scientific. ISBN 978-981-270-784-0.
- ^ "Procesamiento STFT por superposición-adición (OLA) | Procesamiento de señales de audio espectrales". www.dsprelated.com . Consultado el 7 de agosto de 2016 .
La ventana se aplica dos veces: una antes de la FFT (la "ventana de análisis") y la segunda después de la FFT inversa antes de la reconstrucción por superposición-adición (la denominada "ventana de síntesis"). ... En términos más generales, cualquier ventana COLA positiva se puede dividir en un par de ventanas de análisis y síntesis tomando su raíz cuadrada.
- ^ Ajala, R.; Persaud, P. (2022). "Evaluación del movimiento del suelo de modelos híbridos de velocidad sísmica". El registro sísmico . 2 (3): 186–196. Código Bibliográfico :2022SeisR...2..186A. doi : 10.1785/0320220022 . S2CID 251504921.
- ^ Ajala, R.; Persaud, P. (2021). "Efecto de la fusión de modelos multiescala en las predicciones de campos de ondas sísmicas cerca de la falla de San Andrés del Sur". Revista de investigación geofísica: Tierra sólida . 126 (10). Código Bibliográfico :2021JGRB..12621915A. doi :10.1029/2021JB021915. ISSN 2169-9313. S2CID 239654900.
- ^ ab Oppenheim, Alan V. ; Schafer, Ronald W. ; Buck, John R. (1999). "7.2". Procesamiento de señales en tiempo discreto (2.ª ed.). Upper Saddle River, NJ: Prentice Hall. págs. 465–478. ISBN 0-13-754920-2.
- ^ "Filtros FIR mediante ventanas: páginas de libros de laboratorio". www.labbookpages.co.uk . Consultado el 13 de abril de 2016 .
- ^ "Mastering Windows" (PDF) . www.cg.tuwien.ac.at . Consultado el 12 de febrero de 2020 .
- ^ "Fundamentos del análisis de señales, nota de aplicación 243" (PDF) . hpmemoryproject.org . Consultado el 10 de abril de 2018 .
- ^ R. Hovden, Y. Jiang, H. Xin, LF Kourkoutis (2015). "Reducción periódica de artefactos en transformadas de Fourier de imágenes de resolución atómica de campo completo". Microscopía y microanálisis . 21 (2): 436–441. arXiv : 2210.09024 . Código Bibliográfico :2015MiMic..21..436H. doi :10.1017/S1431927614014639. PMID 25597865. S2CID 22435248.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Bernstein, Matt A.; King, Kevin Franklin; Zhou, Xiaohong Joe (2004). Manual de secuencias de pulsos de resonancia magnética. Londres: Elsevier Academic Press. págs. 495–499. ISBN 0-12-092861-2.
- ^ Awad, AI; Baba, K. (2011). "Una aplicación para la localización de puntos singulares en la clasificación de huellas dactilares". Procesamiento de información digital y comunicaciones . Comunicaciones en informática y ciencias de la información. Vol. 188. pág. 262. doi :10.1007/978-3-642-22389-1_24. ISBN 978-3-642-22388-4.
- ^ "Filtros de fase cero". ccrma.stanford.edu . Consultado el 12 de febrero de 2020 .
- ^ Rorabaugh, C. Britton (octubre de 1998). DSP Primer . Serie Primer. McGraw-Hill Professional. pág. 196. ISBN 978-0-07-054004-0.
- ^ abcdefghij Harris, Fredric J. (enero de 1978). "Sobre el uso de Windows para el análisis armónico con la transformada discreta de Fourier" (PDF) . Actas del IEEE . 66 (1): 51–83. Bibcode :1978IEEEP..66...51H. CiteSeerX 10.1.1.649.9880 . doi :10.1109/PROC.1978.10837. S2CID 426548. El artículo fundamental de 1978 sobre las ventanas FFT de Harris, que especificó muchas ventanas e introdujo métricas clave utilizadas para compararlas.
- ^ abc Heinzel, G.; Rüdiger, A.; Schilling, R. (2002). Estimación del espectro y la densidad espectral mediante la transformada discreta de Fourier (DFT), que incluye una lista completa de funciones de ventana y algunas nuevas ventanas de superficie plana (informe técnico). Instituto Max Planck (MPI) für Gravitationsphysik / Interferometría láser y astronomía de ondas gravitacionales. 395068.0 . Consultado el 10 de febrero de 2013 .También disponible en https://pure.mpg.de/rest/items/item_152164_1/component/file_152163/content
- ^ "Comprensión de las FFT y el uso de ventanas" (PDF) . National Instruments . Archivado (PDF) desde el original el 5 de enero de 2024 . Consultado el 13 de febrero de 2024 .
- ^ Toraichi, K.; Kamada, M.; Itahashi, S.; Mori, R. (1989). "Funciones de ventana representadas por funciones B-spline". IEEE Transactions on Acoustics, Speech, and Signal Processing . 37 : 145–147. doi :10.1109/29.17517.
- ^ "Ventana de Bartlett". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ Tukey, JW (1967). "Introducción a los cálculos del análisis numérico del espectro". Análisis espectral de series temporales : 25–46.
- ^ "Ventana triangular - triángulo MATLAB". www.mathworks.com . Consultado el 13 de abril de 2016 .
- ^ ab Welch, P. (1967). "El uso de la transformada rápida de Fourier para la estimación de espectros de potencia: un método basado en el promedio temporal sobre periodogramas cortos modificados". IEEE Transactions on Audio and Electroacoustics . 15 (2): 70–73. Bibcode :1967ITAE...15...70W. doi :10.1109/TAU.1967.1161901. S2CID 13900622.
- ^ Bosi, Marina; Goldberg, Richard E. (2003). "Mapeo de tiempo a frecuencia, parte II: MDCT". Introducción a la codificación y estándares de audio digital . Serie internacional Springer en ingeniería y ciencias de la computación. Vol. 721. Boston, MA: Springer US. p. 106. doi :10.1007/978-1-4615-0327-9. ISBN . 978-1-4615-0327-9.
- ^ Kido, Ken'iti; Suzuki, Hideo; Ono, Takahiko; Fukushima, Manabu (1998). "Deformación de las estimaciones de respuesta al impulso por ventana de tiempo en la técnica espectral cruzada". Revista de la Sociedad Acústica de Japón (E) . 19 (5): 349–361. doi : 10.1250/ast.19.349 .
- ^ Landisman, M.; Dziewonski, A.; Satô, Y. (1 de mayo de 1969). "Mejoras recientes en el análisis de observaciones de ondas superficiales". Geophysical Journal International . 17 (4): 369–403. Bibcode :1969GeoJ...17..369L. doi : 10.1111/j.1365-246X.1969.tb00246.x .
- ^ "Ventana de Bohman – R2019B". www.mathworks.com . Consultado el 12 de febrero de 2020 .
- ^ "Familia de ventanas de potencia de coseno". ccrma.stanford.edu . Consultado el 10 de abril de 2018 .
- ^ "Ventana Hann (Hanning) - MATLAB hann". www.mathworks.com . Consultado el 12 de febrero de 2020 .
- ^ "Hann o Hanning o coseno elevado". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ Enochson, Loren D.; Otnes, Robert K. (1968). Programación y análisis de datos de series temporales digitales. Departamento de Defensa de los EE. UU., Centro de información sobre vibraciones y choques. pág. 142.
- ^ abc "Ventana de Hamming". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ "Una radio digital con modulación de amplitud en cuadratura (QAM): construyendo una mejor radio" (PDF) . users.wpi.edu . p. 28 . Consultado el 12 de febrero de 2020 .
- ^ "De bits a símbolos, a señales y viceversa" (PDF) . users.wpi.edu . p. 7 . Consultado el 12 de febrero de 2020 .
- ^ Johnson, C. Richard Jr; Sethares, William A.; Klein, Andrew G. (18 de agosto de 2011). "11". Diseño de receptor de software . Cambridge University Press. ISBN 978-1-139-50145-3.También https://cnx.org/contents/[email protected]:6R_ztzDY@4/Conformación de pulsos y filtrado de recepción
- ^ Nuttall, Albert H. (febrero de 1981). "Algunas ventanas con muy buen comportamiento de lóbulos laterales". IEEE Transactions on Acoustics, Speech, and Signal Processing . 29 (1): 84–91. doi :10.1109/TASSP.1981.1163506. Amplía el artículo de Harris, cubriendo todas las funciones de ventana conocidas en ese momento, junto con comparaciones métricas clave.
- ^ Weisstein, Eric W. "Función Blackman". mathworld.wolfram.com . Consultado el 13 de abril de 2016 .
- ^ "Características de diferentes ventanas de suavizado - Ayuda de NI LabVIEW 8.6". zone.ni.com . Consultado el 13 de febrero de 2020 .
- ^ Blackman, RB ; Tukey, JW (1 de enero de 1959). La medición de espectros de potencia desde el punto de vista de la ingeniería de comunicaciones. Publicaciones de Dover. pág. 99. ISBN 978-0-486-60507-4.
- ^ "Familia de ventanas Blackman-Harris". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ "Ventana Blackman-Harris de tres períodos". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ ab Smith, Steven W. (2011). Guía para científicos e ingenieros sobre procesamiento de señales digitales. San Diego, California, EE. UU.: California Technical Publishing . Consultado el 14 de febrero de 2013 .
- ^ Rife, David C.; Vincent, GA (1970), "Uso de la transformada discreta de Fourier en la medición de frecuencias y niveles de tonos", Bell Syst. Tech. J. , 49 (2): 197–228, doi :10.1002/j.1538-7305.1970.tb01766.x
- ^ ab Andria, Gregorio; Savino, Mario; Trotta, Amerigo (1989), "Ventanas y algoritmos de interpolación para mejorar la precisión de las mediciones eléctricas", IEEE Transactions on Instrumentation and Measurement , 38 (4): 856–863, Bibcode :1989ITIM...38..856A, doi :10.1109/19.31004
- ^ Schoukens, Joannes; Pintelon, Rik; Van Hamme, Hugo (1992), "La transformada rápida de Fourier interpolada: un estudio comparativo", IEEE Transactions on Instrumentation and Measurement , 41 (2): 226–232, Bibcode :1992ITIM...41..226S, doi :10.1109/19.137352
- ^ ab "Matlab para la ventana gaussiana". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
Nótese que, en una escala de dB, las gaussianas son cuadráticas. Esto significa que la interpolación parabólica de una transformada gaussiana muestreada es exacta. ... la interpolación cuadrática de picos espectrales puede ser más precisa en una escala de magnitud logarítmica (por ejemplo, dB) que en una escala de magnitud lineal
- ^ "Ventana gaussiana y transformación". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ "Interpolación cuadrática de picos espectrales". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ abc Starosielec, S.; Hägele, D. (2014). "Ventanas de tiempo discreto con ancho de banda RMS mínimo para un ancho temporal RMS dado". Procesamiento de señales . 102 : 240–246. Código Bibliográfico :2014SigPr.102..240S. doi :10.1016/j.sigpro.2014.03.033.
- ^ Chakraborty, Debejyo; Kovvali, Narayan (2013). "Ventana normal generalizada para el procesamiento de señales digitales". Conferencia internacional IEEE de 2013 sobre acústica, habla y procesamiento de señales . págs. 6083–6087. doi :10.1109/ICASSP.2013.6638833. ISBN 978-1-4799-0356-6. Número de identificación del sujeto 11779529.
- ^ Diethorn, EJ (1994). "La distribución exponencial generalizada de tiempo-frecuencia". IEEE Transactions on Signal Processing . 42 (5): 1028–1037. Bibcode :1994ITSP...42.1028D. doi :10.1109/78.295214.
- ^ Bloomfield, P. (2000). Análisis de Fourier de series temporales: una introducción . Nueva York: Wiley-Interscience.
- ^ Tu, Loring W. (2008). "Bump Functions and Partitions of Unity". Introducción a las variedades . Universitext. Nueva York: Springer. págs. 127-134. doi :10.1007/978-0-387-48101-2_13. ISBN . 978-0-387-48098-5.
- ^ McKechan, DJA; Robinson, C.; Sathyaprakash, BS (21 de abril de 2010). "Una ventana de estrechamiento para plantillas de dominio temporal y señales simuladas en la detección de ondas gravitacionales a partir de sistemas binarios compactos coalescentes". Gravedad clásica y cuántica . 27 (8): 084020. arXiv : 1003.2939 . Bibcode :2010CQGra..27h4020M. doi :10.1088/0264-9381/27/8/084020. S2CID 21488253.
- ^ "Ventana Slepian o DPSS". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ ab Smith, JO (2011). "Comparación de Windows Kaiser y DPSS". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ Kaiser, James F.; Kuo, Franklin F. (1966). Análisis de sistemas por computadora digital . John Wiley and Sons. pp. 232–235.
Esta familia de funciones de ventana fue "descubierta" por Kaiser en 1962 después de una discusión con BF Logan de Bell Telephone Laboratories. ... Otra propiedad valiosa de esta familia... es que también se aproximan estrechamente a las funciones de onda esferoidales alargadas de orden cero.
- ^ Kaiser, James F. (noviembre de 1964). "Una familia de funciones de ventana con propiedades casi ideales". Memorándum inédito .
- ^ Rabiner, Lawrence R.; Gold, Bernard (1975). "3.11" . Teoría y aplicación del procesamiento de señales digitales . Englewood Cliffs, NJ: Prentice-Hall. pág. 94. ISBN. 0-13-914101-4.
- ^ Crochiere, RE; Rabiner, LR (1983). "4.3.1". Procesamiento de señales digitales de múltiples frecuencias. Englewood Cliffs, NJ: Prentice-Hall. p. 144. ISBN 0-13-605162-6.
- ^ Lin, Yuan-Pei; Vaidyanathan, PP (junio de 1998). "Un enfoque de ventana de Kaiser para el diseño de prototipos de filtros de bancos de filtros modulados por coseno" (PDF) . IEEE Signal Processing Letters . 5 (6): 132–134. Bibcode :1998ISPL....5..132L. doi :10.1109/97.681427. S2CID 18159105 . Consultado el 16 de marzo de 2017 .
- ^ Smith, JO (2011). "Ventana de Kaiser". ccrma.stanford.edu . Consultado el 20 de marzo de 2019 .
A veces, la ventana de Kaiser está parametrizada por
α
, donde
β
=
π
α
.
- ^ "Ventana Kaiser, R2020a". www.mathworks.com . Mathworks . Consultado el 9 de abril de 2020 .
- ^ "Ventana Kaiser". www.dsprelated.com . Consultado el 8 de abril de 2020 .
La siguiente comparación de Matlab de las ventanas DPSS y Kaiser ilustra la interpretación de
α
como el número de bin del borde del lóbulo principal de la ventana muestreada críticamente.
- ^ Kaiser, James F.; Schafer, Ronald W. (1980). "Sobre el uso de la ventana I 0 -sinh para el análisis espectral". IEEE Transactions on Acoustics, Speech, and Signal Processing . 28 : 105–107. doi :10.1109/TASSP.1980.1163349.
- ^ abc "Ventana de Dolph-Chebyshev". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ "Definición de la ventana de Dolph-Chebyshev". ccrma.stanford.edu . Consultado el 5 de marzo de 2019 .
- ^ abc Kabal, Peter (2009). "Time Windows for Linear Prediction of Speech" (PDF) . Informe técnico, Departamento de Ingeniería Eléctrica y Computación, Universidad McGill (2a): 31. Consultado el 2 de febrero de 2014 .
- ^ Streit, Roy (1984). "Una familia de pesos de dos parámetros para filtros digitales no recursivos y antenas". Transacciones de ASSP . 32 : 108–118. doi :10.1109/tassp.1984.1164275.
- ^ abcd Deczky, Andrew (2001). "Ventanas unisféricas". ISCAS 2001. Simposio internacional IEEE sobre circuitos y sistemas de 2001 (n.º de cat. 01CH37196) . Vol. 2. págs. 85–88. doi :10.1109/iscas.2001.921012. ISBN. 978-0-7803-6685-5. Número de identificación del sujeto 38275201.
- ^ Bergen, SWA; Antoniou, A. (2004). "Diseño de funciones de ventana ultraesféricas con características espectrales prescritas". Revista EURASIP sobre procesamiento de señales aplicado . 2004 (13): 2053–2065. Bibcode :2004EJASP2004...63B. doi : 10.1155/S1110865704403114 .
- ^ Bergen, Stuart WA (2005). "Diseño de la función de ventana ultraesférica y sus aplicaciones" (PDF) .Tesis, Universidad de Victoria.
- ^ Smith, Julius O. III (23 de abril de 2011). "Ventana de Poisson". ccrma.stanford.edu . Consultado el 12 de febrero de 2020 .
- ^ Gade, Svend; Herlufsen, Henrik (1987). "Revisión técnica n.º 3-1987: análisis de Windows a FFT (Parte I)" (PDF) . Brüel & Kjær . Consultado el 22 de noviembre de 2011 .
- ^ Berry, CPL; Gair, JR (12 de diciembre de 2012). "Observando el agujero negro masivo de la Galaxia con explosiones de ondas gravitacionales". Monthly Notices of the Royal Astronomical Society . 429 (1): 589–612. arXiv : 1210.2778 . Bibcode :2013MNRAS.429..589B. doi : 10.1093/mnras/sts360 . S2CID 118944979.
- ^ "Ventana de Hann-Poisson". ccrma.stanford.edu . Consultado el 13 de abril de 2016 .
- ^ Wesley Beccaro (31 de octubre de 2020), "Función de ventana polinomial adaptativa generalizada", mathworks.com , consultado el 2 de noviembre de 2020
- ^ "Función de ventana polinómica adaptativa generalizada". www.mathworks.com . Consultado el 12 de diciembre de 2020 .
- ^ Luo, Jiufel; Xie, Zhijiang; Li, Xinyi (2 de marzo de 2015). "Ventanas asimétricas y su aplicación en la estimación de frecuencia". Universidad de Chongqing . 9 (Algoritmos y tecnología computacional): 389–412. doi : 10.1260/1748-3018.9.4.389 . S2CID 124464194.
Lectura adicional
- Harris, Frederic J. (septiembre de 1976). "Windows, Harmonic Analysis, and the Discrete Fourier Transform" (PDF) . apps.dtic.mil . Naval Undersea Center, San Diego. Archivado (PDF) del original el 8 de abril de 2019 . Consultado el 8 de abril de 2019 .
- Albrecht, Hans-Helge (2012). Ventanas de suma de coseno de lóbulo lateral mínimo y de lóbulo lateral mínimo adaptadas. Versión 1.0 . vol. ISBN 978-3-86918-281-0). editor: Physikalisch-Technische Bundesanstalt. Physikalisch-Technische Bundesanstalt. doi :10.7795/110.20121022aa. ISBN 978-3-86918-281-0.
- Bergen, SWA; Antoniou, A. (2005). "Diseño de filtros digitales no recursivos utilizando la función de ventana ultraesférica". Revista EURASIP sobre procesamiento de señales aplicado . 2005 (12): 1910–1922. Bibcode :2005EJASP2005...44B. doi : 10.1155/ASP.2005.1910 .
- Prabhu, KMM (2014). Funciones de ventana y sus aplicaciones en el procesamiento de señales . Boca Raton, FL: CRC Press. ISBN 978-1-4665-1583-3.
- Patente estadounidense 7065150, Park, Young-Seo, "Sistema y método para generar una modulación de multiplexación por división de frecuencia ortogonal de coseno elevado (RRC OFDM)", publicada en 2003, expedida en 2006
Enlaces externos
 Medios relacionados con la función Ventana en Wikimedia Commons
Medios relacionados con la función Ventana en Wikimedia Commons- Ayuda de LabView, Características de los filtros de suavizado, http://zone.ni.com/reference/en-XX/help/371361B-01/lvanlsconcepts/char_smoothing_windows/
- Creación y propiedades de funciones de ventana de suma de coseno, http://electronicsart.weebly.com/fftwindows.html
- Simulación interactiva en línea de FFT, ventanas, resolución y fugas | RITEC | Biblioteca y herramientas





![{\displaystyle x\en [-N/2,N/2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0377d29e5715ebdd13819c1cc07c4638a0156afd)

![{\displaystyle \{w[n]=w_{0}(nN/2),\cuadrado 0\leq n\leq N\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f28eb10c2426fe0deb507ce933eb6b5df2c020e)

![{\displaystyle \{w[n],\cuadrado 0\leq n\leq N-1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f506d61ded38a4f9d8ecd59004fbf34e793d81f3)

![{\displaystyle w[n]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f071fdd6a0a02d6d9dc3c1325d88a6dda6a92781)
![{\displaystyle w[n]=1-\left|{\frac {n-{\frac {N}{2}}}{\frac {L}{2}}}\right|,\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884ef77423e593a74ebf40ec3eaa0c8f00ca5102)

![{\displaystyle w[n]=\w_{0}\left(n-{\tfrac {N}{2}}\right),\0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfa5797bd28cc542de9f224e4b9c7c0c37bff91a)
![{\displaystyle w[n]=1-\left({\frac {n-{\frac {N}{2}}}{\frac {N}{2}}}\right)^{2},\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3a944c6a5c2051217a53dd60a9693dd76c98a9)
![{\displaystyle w[n]=\sin({\frac {\pi n}{N}}\right)=\cos({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2af9f7febc105f1184bd114a1484bf16cf7325)

![{\displaystyle w[n]=\sin ^{\alpha}({\frac {\pi n}{N}}\right)=\cos ^{\alpha}({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b81af4c85e4b5e6909b3dfb7fef170a42a02f7e)
![{\displaystyle w[n]=a_{0}-a_{1}cos({\frac {2\pi n}{N}})+a_{2}cos({\frac {4\pi n}{N}})-a_{3}cos({\frac {6\pi n}{N}})+a_{4}cos({\frac {8\pi n}{N}})-...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3449e818cb0c7c261fe536655c3b5145fd4eda9d)

![{\displaystyle w[n]=\sum _{k=0}^{K}(-1)^{k}a_{k}\;\cos \left({\frac {2\pi kn}{N}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e597f0587d0c29feaf791fef475cf419be2987c9)
![{\displaystyle w[n]=a_{0}-\underbrace {(1-a_{0})} _{a_{1}}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b8f8c3192b06191db2bb7ad9247eeba6a6cb70)
![{\displaystyle {\begin{aligned}w_{0}(n)\ &=w\left[n+{\tfrac {N}{2}}\right]\\&=a_{0}+a_{1}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad -{\tfrac {N}{2}}\leq n\leq {\tfrac {N}{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a04d79e8c4de591b5badfd2864ebe7522c17b1ad)

![{\displaystyle w[n]=0.5\;[1-\cos \left({\frac {2\pi n}{N}}\right)\right]=\sin ^{2}\left({\frac {\pi n}{N}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd8d3e844a1443d7bedd57240588cf19fcd28af1)


![{\displaystyle w[n]=a_{0}-a_{1}cos({\frac {2\pi n}{N}})+a_{2}cos({\frac {4\pi n}{N}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1a6c47fc77da0b81229c3234068706a6ca8e6a)


![{\displaystyle w[n]=a_{0}-a_{1}cos({\frac {2\pi n}{N}})+a_{2}cos({\frac {4\pi n}{N}})-a_{3}cos({\frac {6\pi n}{N}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55aa618bd5010d83e5df4ae06fbb3abd509f12fd)



![{\displaystyle {\begin{aligned}w[n]=a_{0}&{}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)\\&{}-a_{3}\cos \left({\frac {6\pi n}{N}}\right)+a_{4}\cos \left({\frac {8\pi n}{N}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e117d087bf8d6345fb6ea8ffc7b5aa7f6faae4a)



![{\displaystyle w[n]=\exp \left(-{\frac {1}{2}}\left({\frac {nN/2}{\sigma N/2}}\right)^{2}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e201c829f6aabf4339fc0a1929367d5613dfe290)

![{\displaystyle w[n]=G(n)-{\frac {G(-{\frac {1}{2}})[G(n+L)+G(nL)]}{G(-{\frac {1}{2}}+L)+G(-{\frac {1}{2}}-L)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3094fa9469d1e65bfdb6a4e31cdafd037a8822ec)


![{\displaystyle w[n,p]=\exp \left(-\left({\frac {nN/2}{\sigma N/2}}\right)^{p}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/704a7de7c2a67fc8a24a140a151491bd7362698c)



![{\displaystyle \left.{\begin{array}{lll}w[n]={\frac {1}{2}}\left[1-\cos \left({\frac {2\pi n}{\alpha N}}\right)\right],\quad &0\leq n<{\frac {\alpha N}{2}}\\w[n]=1,\quad &{\frac {\alpha N}{2}}\leq n\leq {\frac {N}{2}}\\w[Nn]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab34271ac62f34c531c4d6cc0b8ffd2e9793623a)

![{\displaystyle \left.{\begin{array}{lll}w[0]=0,\\w[n]=\left(1+\exp \left({\frac {\varepsilon N}{n}}-{\frac {\varepsilon N}{\varepsilon Nn}}\right)\right)^{-1},\quad &1\leq n<\varepsilon N\\w[n]=1,\quad &\varepsilon N\leq n\leq {\frac {N}{2}}\\w[Nn]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f50bb4690593ab87a47ed71fec1945a3f95b9d0d)
![{\displaystyle w[n]={\frac {I_{0}(\pi \alpha {\sqrt {1-\left({\frac {2n}{N}}-1\right)^{2}}}\right)}{I_{0}(\pi \alpha )}},\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337ca65bf1465649348a8eb22356662c4188b092)




![estilo de visualización w_{0}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0d68356ad0cc45bf520fbe5be3266aa7c431cd8)
![Estilo de visualización W_{0}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1b9baa4526ac8ec5f39c3cd63782248015037f)





![{\displaystyle w[n]=w_{0}\left(n-{\frac {N}{2}}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3af173b60d19716e14882dabdec080868fa3e0ae)
![{\displaystyle {\begin{aligned}w_{0}\left(n-{\frac {N}{2}}\right)={\frac {1}{N+1}}\sum _{k=0}^{N}W_{0}(k)\cdot e^{\frac {i2\pi k(nN/2)}{N+1}}={\frac {1}{N+1}}\sum _{k=0}^{N}\left[\left(-e^{\frac {i\pi }{N+1}}\right)^{k}\cdot W_{0}(k)\right]e^{\frac {i2\pi kn}{N+1}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f3590133d3da32b13aa211153542e96d14a46e)

![{\displaystyle w[n]={\frac {1}{N+1}}[C_{N}^{\mu }(x_{0})+\sum _{k=1}^{\frac {N}{2}}C_{N}^{\mu }(x_{0}\cos {\frac {k\pi }{N+1}})\cos {\frac {2n\pi k}{N+1}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe5e8dc43d2c5edbe601e3abf542a177689f4276)





![{\displaystyle w[n]=e^{-\left|n-{\frac {N}{2}}\right|{\frac {1}{\tau }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/141d1630d759c1ebf5120671e36f86a6117f259c)

![{\displaystyle w[n]=a_{0}-a_{1}\left|{\frac {n}{N}}-{\frac {1}{2}}\right|-a_{2}\cos \left({\frac {2\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e64d33f0c717a2b40af2ed16c9fff5f58d95b937)


![{\displaystyle w[n]={\frac {1}{2}}(1-\cos \left({\frac {2\pi n}{N}})\right)e^{\frac {-\alpha \left|N-2n|}{N}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e7d44df8e90604b099629079cb1ed07faa045a3)

![{\displaystyle w_{0}[n]=a_{0}+\sum _{k=1}^{K}a_{2k}\left({\frac {n}{\sigma }}\right)^{2k},\quad -{\frac {N}{2}}\leq n\leq {\frac {N}{2}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0985efd235d3dcfbd7c9a2631aa173cd5c2d4cdf)



![{\displaystyle w[n]=\nombre del operador {sinc} \left({\frac {2n}{N}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380ec565d5a93c55eb9d1109065556115b5c0f99)






