Multicono

En el procesamiento de señales , el análisis multitaper es una técnica de estimación de densidad espectral desarrollada por David J. Thomson . [1] [2] Puede estimar el espectro de potencia S X de un proceso aleatorio estacionario de varianza finita ergódico X , dada una realización contigua finita de X como datos.
Motivación
El método multitaper supera algunas de las limitaciones del análisis de Fourier no paramétrico . Al aplicar la transformada de Fourier para extraer información espectral de una señal, asumimos que cada coeficiente de Fourier es una representación confiable de la amplitud y la fase relativa de la frecuencia del componente correspondiente. Sin embargo, esta suposición no es generalmente válida para los datos empíricos. Por ejemplo, un solo ensayo representa solo una realización ruidosa del proceso subyacente de interés. Una situación comparable surge en estadística cuando se estiman medidas de tendencia central , es decir, es una mala práctica estimar las cualidades de una población utilizando individuos o muestras muy pequeñas. Del mismo modo, una sola muestra de un proceso no necesariamente proporciona una estimación confiable de sus propiedades espectrales. Además, la densidad espectral de potencia ingenua obtenida de la transformada de Fourier bruta de la señal es una estimación sesgada del contenido espectral real.

Estos problemas suelen superarse haciendo un promedio de muchas realizaciones del mismo evento después de aplicar una reducción gradual a cada prueba. Sin embargo, este método no es confiable con conjuntos de datos pequeños y no es recomendable cuando no se desea atenuar los componentes de la señal que varían entre las pruebas. Además, incluso cuando se dispone de muchas pruebas, el periodograma sin reducción gradual generalmente está sesgado (con la excepción del ruido blanco) y el sesgo depende de la duración de cada realización, no del número de realizaciones registradas. La aplicación de una única reducción gradual reduce el sesgo, pero a costa de una mayor varianza del estimador debido a la atenuación de la actividad al inicio y al final de cada segmento registrado de la señal.
El método de reducción de la señal multicono evita parcialmente estos problemas al obtener múltiples estimaciones independientes a partir de la misma muestra. Cada reducción de la señal se multiplica elemento por elemento por la señal para proporcionar una prueba con ventana a partir de la cual se estima la potencia en cada frecuencia componente. Como cada reducción es ortogonal a todos los demás, las funciones de ventana no están correlacionadas entre sí. El espectro final se obtiene promediando todos los espectros con reducción de la señal, recuperando así parte de la información que se pierde debido a la atenuación parcial de la señal que resulta de la aplicación de las reducciones individuales.
Este método es especialmente útil cuando se dispone de un pequeño número de ensayos, ya que reduce la varianza del estimador más allá de lo que es posible con los métodos de reducción gradual única. Además, incluso cuando se dispone de muchos ensayos, el enfoque de reducción gradual múltiple es útil, ya que permite un control más riguroso del equilibrio entre sesgo y varianza que lo que es posible en el caso de reducción gradual única.
Thomson eligió las funciones de Slepian [4] o secuencias esferoidales alargadas discretas como conicidades, ya que estos vectores son mutuamente ortogonales y poseen propiedades de concentración espectral deseables (véase la sección sobre secuencias de Slepian). En la práctica, a menudo se utiliza un promedio ponderado para compensar la mayor pérdida de energía en conicidades de orden superior. [5]
Formulación
Considere un proceso estocástico estacionario de media cero de dimensión p
Aquí T denota la transposición de la matriz. En neurofisiología , por ejemplo, p se refiere al número total de canales y, por lo tanto, puede representar la medición simultánea de la actividad eléctrica de esos p canales. Sea , el intervalo de muestreo entre observaciones , de modo que la frecuencia de Nyquist sea .
El estimador espectral multiconicidad utiliza varios conos de datos diferentes que son ortogonales entre sí. El estimador multiconicidad cruzada entre los canales l y m es el promedio de K estimadores directos cruzados entre el mismo par de canales ( l y m ) y, por lo tanto, toma la forma
Aquí, (para ) es el k -ésimo estimador espectral cruzado directo entre el canal l y m y se da por
dónde
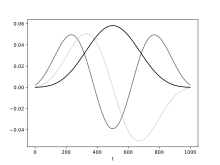
Las secuencias de Slepian
La secuencia es la conicidad de los datos para el estimador cruzado espectral directo k - ésimo y se elige de la siguiente manera:
Elegimos un conjunto de K conos de datos ortogonales de manera que cada uno proporcione una buena protección contra fugas. Estos están dados por las secuencias de Slepian, [6] después de David Slepian (también conocidas en la literatura como secuencias esferoidales prolatas discretas o DPSS para abreviar) con parámetro W y órdenes k = 0 a K − 1. El orden máximo K se elige para que sea menor que el número de Shannon . La cantidad 2 W define el ancho de banda de resolución para el problema de concentración espectral y . Cuando l = m , obtenemos el estimador de conos múltiples para el espectro automático del l ésimo canal. En los últimos años, se propuso un diccionario basado en DPSS modulado como una alternativa sobrecompleta a DPSS. [7]
Véase también Función de ventana: DPSS o ventana de Slepian
Aplicaciones
El método multitaper no se limita a series temporales, sino que se puede extender fácilmente a múltiples dimensiones cartesianas mediante funciones Slepianas personalizadas [8] y se puede reformular para la estimación espectral en la esfera mediante funciones Slepianas construidas a partir de armónicos esféricos [9] para aplicaciones en geofísica y cosmología [10] [11] , entre otras. Se puede encontrar aquí un tratamiento extenso sobre la aplicación de este método para analizar datos multiensayo y multicanal generados en neurociencia , ingeniería biomédica y otros campos. Esta técnica se utiliza actualmente en el kit de herramientas de análisis espectral de Chronux .
Véase también
Referencias
- ^ Thomson, DJ (1982) Estimación del espectro y análisis armónico . Actas del IEEE , 70, 1055–1096
- ^ * Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Sección 13.4.3. Métodos multicono y funciones de Slepian ", Recetas numéricas: el arte de la computación científica (3.ª ed.), Nueva York: Cambridge University Press, ISBN 978-0-85-0-31-2 978-0-521-88068-8
- ^ Simons, FJ; Korenaga, J.; Zuber, MT (2000). "Respuesta isostática de la litosfera australiana: estimación del espesor elástico efectivo y la anisotropía mediante análisis de conicidad múltiple". 105 (B8): 19163-19184.
{{cite journal}}: Requiere citar revista|journal=( ayuda ) - ^ Simons, FJ; Plattner, A. (2015). "Funciones escalares y vectoriales de Slep, estimación de señales esféricas y análisis espectral". Manual de geomatemáticas . págs. 2563–2608. doi :10.1007/978-3-642-54551-1_30. ISBN 978-3-642-54550-4.
- ^ Percival, DB y AT Walden. Análisis espectral para aplicaciones físicas: técnicas univariadas convencionales y multicono . Cambridge: Cambridge University Press, 1993.
- ^ Slepian, D. (1978) "Funciones de onda esferoidales alargadas, análisis de Fourier e incertidumbre – V: El caso discreto". Bell System Technical Journal , 57, 1371–1430
- ^ E. Sejdić, M. Luccini, S. Primak, K. Baddour, T. Willink, “Estimación de canal utilizando marcos basados en secuencias esferoidales prolatas discretas moduladas”, en Proc. de la Conferencia Internacional IEEE sobre Acústica, Habla y Procesamiento de Señales (ICASSP 2008) , Las Vegas, Nevada, EE. UU., 31 de marzo-4 de abril de 2008, págs. 2849-2852.
- ^ Simons, FJ; Wang, DV (2011). "Concentración espacioespectral en el plano cartesiano". GEM: Revista internacional de geomatemáticas . 2 : 1–36. doi :10.1007/s13137-011-0016-z..
- ^ Simons, FJ; Dahlen, FA; Wieczorek, MA (2006). "Concentración espacioespectral en una esfera". SIAM Review . 48 (3): 504–536. arXiv : math/0408424 . Código Bibliográfico :2006SIAMR..48..504S. doi :10.1137/S0036144504445765.
- ^ Wieczorek, MA; Simons, FJ (2007). "Estimación espectral multiconicidad de mínima varianza en la esfera". Revista de análisis y aplicaciones de Fourier . 13 (6): 665. doi :10.1007/s00041-006-6904-1.
- ^ Dahlen, FA; Simons, FJ (2008). "Estimación espectral en una esfera en geofísica y cosmología". Geophysical Journal International . 174 (3): 774. arXiv : 0705.3083 . Bibcode :2008GeoJI.174..774D. doi : 10.1111/j.1365-246X.2008.03854.x .
Enlaces externos
- [1] Bibliotecas C++/Octave para el método multitaper, incluida la ponderación adaptativa (alojadas en GitHub)
- [2] Documentación sobre el método multitaper de la implementación del kit de herramientas SSA-MTM
- [3] Biblioteca Fortran 90 con aplicaciones multivariadas adicionales
- [4] Base de código MATLAB para generar funciones escalares esféricas de Slepian
- [5] Base de código MATLAB para realizar análisis multiconicidad esférico
- [6] Base de código MATLAB para generar funciones cartesianas de Slepian
- [7] Base de código MATLAB para generar funciones Slepian vectoriales esféricas
- [8] Módulo Python
- [9] Paquete multitaper de lenguaje de programación R
- [10] Script S-Plus para generar secuencias Slepian (dpss)












