Cubo truncado
Sólido arquimediano con 14 caras regulares
Cubo truncado

(Haga clic aquí para ver el modelo rotatorio)
TipoSólido arquimediano
Poliedro uniforme
ElementosF = 14, E = 36, V = 24 (χ = 2)
Caras por lados8{3}+6{8}
Notación de Conwayt.c.
Símbolos de Schläflit{4,3}
t0,1 { 4,3}
Símbolo de Wythoff2 3 | 4
Diagrama de Coxeter
Grupo de simetríaOh , B 3 , [4,3], ( * 432), orden 48
Grupo de rotaciónO , [4,3] + , (432), orden 24
Ángulo diedro3-8: 125°15′51″
8-8: 90°
ReferenciasU 09 , C 21 , W 8
PropiedadesConvexo semirregular

Caras de colores
3.8.8
( Figura de vértice )

Triakis octaedro
( poliedro dual )
Neto
Modelo 3D de un cubo truncado

En geometría , el cubo truncado , o hexaedro truncado , es un sólido arquimediano . Tiene 14 caras regulares (6 octogonales y 8 triangulares ), 36 aristas y 24 vértices.

Si el cubo truncado tiene una longitud de arista unidad, su triakis octaedro dual tiene aristas de longitudes 2 y 2 +  √ 2 .

Área y volumen

El área A y el volumen V de un cubo truncado de longitud de arista a son:

A = 2 ( 6 + 6 2 + 3 ) a 2 ≈ 32.434 6644 a 2 V = 21 + 14 2 3 a 3 ≈ 13.599 6633 a 3 . {\displaystyle {\begin{aligned}A&=2\left(6+6{\sqrt {2}}+{\sqrt {3}}\right)a^{2}&&\aproximadamente 32,434\,6644a^{2}\\V&={\frac {21+14{\sqrt {2}}}{3}}a^{3}&&\aproximadamente 13,599\,6633a^{3}.\end{aligned}}}

Proyecciones ortogonales

El cubo truncado tiene cinco proyecciones ortogonales especiales , centradas en un vértice, sobre dos tipos de aristas y dos tipos de caras: triángulos y octógonos. Las dos últimas corresponden a los planos de Coxeter B2 y A2 .

Proyecciones ortogonales
Centrado porVérticeBorde
3-8		Filo
8-8
Octágono facial
Triángulo facial
Sólido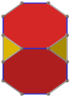
Estructura alámbrica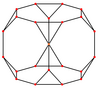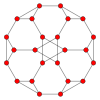
Dual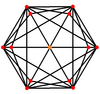

Simetría proyectiva		[2][2][2][4][6]

Azulejo esférico

El cubo truncado también puede representarse como un mosaico esférico y proyectarse sobre el plano mediante una proyección estereográfica . Esta proyección es conforme y conserva los ángulos, pero no las áreas ni las longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.


centrado en el octágono
centrado en un triangulo
Proyección ortográficaProyecciones estereográficas

Coordenadas cartesianas

Un cubo truncado con sus caras octogonales disecadas piritoédricamente con un vértice central en triángulos y pentágonos, creando un icosidodecaedro topológico

Las coordenadas cartesianas de los vértices de un hexaedro truncado centrado en el origen con una longitud de arista de 2 ξ son todas las permutaciones de

(± ξ , ±1, ±1),

donde ξ  =  √ 2  − 1.

El parámetro ξ puede variar entre ±1. Un valor de 1 produce un cubo , 0 produce un cuboctaedro y valores negativos producen caras octagrámicas autointersecantes .

Si se eliminan las partes autointersectadas de los octagramas, dejando cuadrados, y se truncan los triángulos en hexágonos, se producen octaedros truncados , y la secuencia termina con los cuadrados centrales reducidos a un punto, y creando un octaedro .

Disección

Cubo truncado diseccionado, con elementos expandidos

El cubo truncado se puede diseccionar en un cubo central , con seis cúpulas cuadradas alrededor de cada una de las caras del cubo y ocho tetraedros regulares en las esquinas. Esta disección también se puede ver dentro del panal cúbico rúnico , con celdas de cubo , tetraedro y rombicuboctaedro .

Esta disección se puede utilizar para crear un toroide de Stewart con todas las caras regulares eliminando dos cúpulas cuadradas y el cubo central. Este cubo excavado tiene 16 triángulos , 12 cuadrados y 4 octógonos . [1] [2]

Disposición de vértices

Comparte la disposición de vértices con tres poliedros uniformes no convexos :


Cubo truncado
Gran rombicuboctaedro no convexo
Gran cuboctaedro cúbico
Gran rombihexaedro

El cubo truncado se relaciona con otros poliedros y teselas en simetría.

El cubo truncado pertenece a una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.

Poliedros octaédricos uniformes
Simetría : [4,3], (*432)[4,3] +
(432)		[1 + ,4,3] = [3,3]
(*332)		[3 + ,4]
(3*2)
{4,3}t{4,3}r{4,3}
r{3 1,1 }		t{3,4}
t{3 1,1 }		{3,4}
{3 1,1 }		rr { 4,3}
s2 {3,4}		tr{4,3}sr{4,3}h{4,3}
{3,3}		h2 {4,3} t {
3,3}		s{3,4}
s{3 1,1 }

=
=
=		=
o		=
o		=





De poliedros duales a uniformes
V4 3Versión 3.8 2V(3.4) 2Versión 4.6 2Versión 3 4Versión 3.4 3V4.6.8Versión 3 4 .4Versión 3 3Versión 3.6 2V3 5

Mutaciones de simetría

Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros truncados uniformes con configuraciones de vértice (3,2 n .2 n ), y simetría de grupo de Coxeter [ n ,3] , y una serie de poliedros y teselaciones n .8.8.

* n 32 mutación de simetría de teselaciones esféricas truncadas: t{ n ,3}
Simetría
* n 32
[n,3]		EsféricoEuclides.Hiperb. compacta.Paraíso.
*232
[2,3]		*332
[3,3]		*432
[4,3]		*532
[5,3]		*632
[6,3]		*732
[7,3]		*832
[8,3]...		*∞32
[∞,3]

Cifras truncadas
Símbolot{2,3}t{3,3}t{4,3}t{5,3}t{6,3}t{7,3}t{8,3}t{∞,3}

Figuras de Triakis
Configuración.V3.4.4V3.6.6Versión 3.8.8V3.10.10V3.12.12V3.14.14V3.16.16V3.∞.∞
* n 42 mutación de simetría de teselaciones truncadas: n.8.8
Simetría
* n 42
[n,4]		EsféricoEuclidianoHiperbólica compactaParacompacto
*242
[2,4]		*342
[3,4]		*442
[4,4]		*542
[5,4]		*642
[6,4]		*742
[7,4]		*842
[8,4]...		*∞42
[∞,4]

Cifras truncadas
Configuración.2.8.83.8.84.8.85.8.86.8.87.8.88.8.8∞.8.8

figuras n-kis
Configuración.Versión 2.8.8Versión 3.8.8Versión 4.8.8V5.8.8V6.8.8V7.8.8V8.8.8V∞.8.8

Truncamiento alterno

Tetraedro, truncamiento de sus aristas y cubo truncado

Truncando vértices alternos del cubo se obtiene el tetraedro achaflanado , es decir, el truncamiento de la arista del tetraedro.

El trapezoedro triangular truncado es otro poliedro que puede formarse a partir del truncamiento de las aristas del cubo.

El cubo truncado es el segundo de una secuencia de hipercubos truncados :

Hipercubos truncados
Imagen...
NombreOctágonoCubo truncadoTeseracto truncadoCubo truncado de 5Cubo truncado de 6Cubo 7 truncadoCubo 8 truncado
Diagrama de Coxeter
Figura de vértice( )v( )
( )v{ }
( )v{3}
( )v{3,3}		( )v{3,3,3}( )v{3,3,3,3}( )v{3,3,3,3,3}

Gráfico cúbico truncado

Gráfico cúbico truncado
Diagrama de Schlegel de simetría cuádruple
Vértices24
Bordes36
Automorfismos48
Número cromático3
PropiedadesCúbico , hamiltoniano , regular , cero-simétrico
Tabla de gráficos y parámetros

En el campo matemático de la teoría de grafos , un grafo cúbico truncado es el grafo de vértices y aristas del cubo truncado , uno de los sólidos arquimedianos . Tiene 24 vértices y 36 aristas, y es un grafo arquimediano cúbico . [3]


Ortográfico

Véase también

Referencias

  1. ^ BM Stewart, Aventuras entre los toroides (1970) ISBN  978-0-686-11936-4
  2. ^ "Aventuras entre los toroides - Capítulo 5 - Toroides (R)(A)(Q)(T) más simples del género p=1".
  3. ^ Read, RC; Wilson, RJ (1998), Un atlas de gráficos , Oxford University Press , pág. 269
  • Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño . Dover Publications, Inc. ISBN 0-486-23729-X.(Sección 3-9)
  • Cromwell, P. Polyhedra , CUP hbk (1997), pbk. (1999). Cap. 2 págs. 79-86 Sólidos arquimedianos
  • Weisstein, Eric W. , "Cubo truncado" ("Sólido arquimediano") en MathWorld .
  • Klitzing, Richard. "Poliedros uniformes convexos 3D o3x4x - tic".
  • Red editable e imprimible de un cubo truncado con vista 3D interactiva
  • Los poliedros uniformes
  • Poliedros de realidad virtual www.georgehart.com: La enciclopedia de poliedros
    • Modelo VRML
    • Notación de Conway para poliedros Pruebe: "tC"
Obtenido de "https://es.wikipedia.org/w/index.php?title=Cubo_truncado&oldid=1175306638"