Onda triangular

Onda triangular
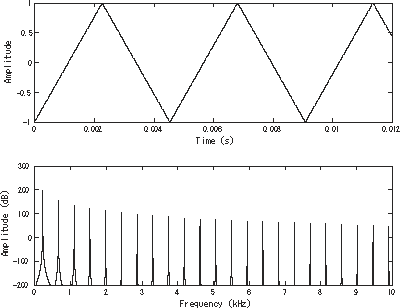Onda triangular de banda limitada [1] representada en el dominio del tiempo (arriba) y en el dominio de la frecuencia (abajo). La frecuencia fundamental está a 220 Hz (A 3 ).
información general
Definición general	${\displaystyle x(t)=4\left\vert t-\left\lfloor t+3/4\right\rfloor +1/4\right\vert -1}$
Campos de aplicación	Electrónica, sintetizadores
Dominio, codominio e imagen
Dominio	${\displaystyle \mathbb {R}}$
Codominio	${\displaystyle \izquierda[-1,1\derecha]}$
Características básicas
Paridad	Extraño
Período	1
Características específicas
Raíz	${\displaystyle \left\{{\tfrac {n}{2}}\right\},n\in \mathbb {Z} }$
Derivado	Onda cuadrada
Serie de Fourier	${\displaystyle x(t)=-{\frac {8}{{\pi }^{2}}}\sum _{k=1}^{\infty }{\frac {{\left(-1\right)}^{k}}{\left(2k-1\right)^{2}}}\sin \left(2\pi \left(2k-1\right)t\right)}$

Muestra de sonido de onda triangular

5 segundos de onda triangular a 220 Hz

---

¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .

Muestra de sonido de onda triangular aditiva

Después de cada segundo, se agrega un armónico a una onda sinusoidal creando una onda triangular de 220 Hz.

---

¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .

Una onda triangular es una forma de onda no sinusoidal llamada así por su forma triangular . Es una función real continua , lineal por partes y periódica .

Al igual que una onda cuadrada , la onda triangular contiene solo armónicos impares . Sin embargo, los armónicos más altos desaparecen mucho más rápido que en una onda cuadrada (proporcional al cuadrado inverso del número armónico, en lugar de solo al inverso).

Una onda triangular de período p que abarca el rango [0, 1] se define como donde es la función de suelo . Puede verse que es el valor absoluto de una onda de diente de sierra desplazada .$${\displaystyle x(t)=2\left|{\frac {t}{p}}-\left\lfloor {\frac {t}{p}}+{\frac {1}{2}}\right\rfloor \right|,}$$${\displaystyle \lpiso \ \rpiso }$

Para una onda triangular que abarca el rango [−1, 1] la expresión se convierte en$${\displaystyle x(t)=2\left|2\left({\frac {t}{p}}-\left\lfloor {\frac {t}{p}}+{\frac {1}{2}}\right\rfloor \right)\right|-1.}$$

Una ecuación más general para una onda triangular con amplitud y período utilizando la operación módulo y valor absoluto es${\estilo de visualización a}$${\estilo de visualización p}$$${\displaystyle y(x)={\frac {4a}{p}}\left|\left(\left(x-{\frac {p}{4}}\right){\bmod {p}}\right)-{\frac {p}{2}}\right|-a.}$$

Por ejemplo, para una onda triangular con amplitud 5 y período 4:$${\displaystyle y(x)=5\left|{\bigl (}(x-1){\bmod {4}}{\bigr )}-2\right|-5.}$$

Se puede obtener un cambio de fase alterando el valor del término, y el desplazamiento vertical se puede ajustar alterando el valor del término.${\estilo de visualización -p/4}$${\estilo de visualización -a}$

Como solo utiliza la operación de módulo y valor absoluto, se puede utilizar para implementar simplemente una onda triangular en la electrónica de hardware.

Tenga en cuenta que en muchos lenguajes de programación, el %operador es un operador de resto (cuyo resultado es el mismo signo que el dividendo), no un operador de módulo ; la operación de módulo se puede obtener utilizando ((x % p) + p) % pen lugar de x % p. En JavaScript, por ejemplo, esto da como resultado una ecuación de la forma 4*a/p * Math.abs((((x - p/4) % p) + p) % p - p/2) - a.

La onda triangular también se puede expresar como la integral de la onda cuadrada :$${\displaystyle x(t)=\int _{0}^{t}\operatorname {sgn} \left(\sin {\frac {u}{p}}\right)\,du.}$$

Una onda triangular con período p y amplitud a se puede expresar en términos de seno y arcoseno (cuyo valor varía de − π /2 a π /2): La identidad se puede utilizar para convertir una onda "seno" triangular en una onda "coseno" triangular. Esta onda triangular desfasada también se puede expresar con coseno y arcocoseno :$${\displaystyle y(x)={\frac {2a}{\pi }}\arcsin \left(\sin \left({\frac {2\pi }{p}}x\right)\right).}$$${\textstyle \cos {x}=\sin \left({\frac {p}{4}}-x\right)}$$${\displaystyle y(x)=a-{\frac {2a}{\pi }}\arccos \left(\cos \left({\frac {2\pi }{p}}x\right)\right).}$$

Otra definición de la onda triangular, con rango de −1 a 1 y período p , es$${\displaystyle x(t)={\frac {4}{p}}(t-{\frac {p}{2}}{\frac {2t}{p}}+{\frac {1}{2}}{\rfloor})(-1)^{\frac {2t}{p}}+{\frac {1}{2}}{\rfloor}.}$$

Es posible aproximar una onda triangular con síntesis aditiva sumando los armónicos impares de la fundamental mientras se multiplica cada otro armónico impar por −1 (o, equivalentemente, cambiando su fase por π ) y multiplicando la amplitud de los armónicos por uno sobre el cuadrado de su número de modo, n (que es equivalente a uno sobre el cuadrado de su frecuencia relativa a la fundamental ).

Lo anterior se puede resumir matemáticamente de la siguiente manera: donde N es el número de armónicos a incluir en la aproximación, t es la variable independiente (por ejemplo, el tiempo para las ondas sonoras), es la frecuencia fundamental e i es la etiqueta armónica que está relacionada con su número de modo por .$${\displaystyle x_{\text{triángulo}}(t)={\frac {8}{\pi ^{2}}}\sum _{i=0}^{N-1}(-1)^{i}n^{-2}\sin(2\pi f_{0}nt),}$$$estilo de visualización f_{0}}$${\estilo de visualización n=2i+1}$

Esta serie de Fourier infinita converge rápidamente a la onda triangular a medida que N tiende al infinito, como se muestra en la animación.

La longitud de arco por período de una onda triangular, denotada por s , se da en términos de la amplitud a y la longitud del período p por$${\displaystyle s={\sqrt {(4a)^{2}+p^{2}}}.}$$

• Lista de funciones periódicas
• Onda sinusoidal
• Onda cuadrada
• Onda de diente de sierra
• Onda de pulso
• Sonido
• Función triangular
• Ola
• Zigzag

• Weisstein, Eric W. "Serie de Fourier - Onda triangular". MathWorld .