Síntesis aditiva
La síntesis aditiva es una técnica de síntesis de sonido que crea un timbre sumando ondas sinusoidales . [1] [2]
A la luz de la teoría de Fourier, se puede considerar que el timbre de los instrumentos musicales está formado por múltiples armónicos o inarmónicos parciales o sobretonos . Cada parcial es una onda sinusoidal de diferente frecuencia y amplitud que aumenta y disminuye con el tiempo debido a la modulación de una envolvente ADSR o un oscilador de baja frecuencia .
La síntesis aditiva genera el sonido de forma más directa al sumar la salida de múltiples generadores de ondas sinusoidales. Las implementaciones alternativas pueden utilizar tablas de ondas precalculadas o la transformada rápida de Fourier inversa .
Explicación
Los sonidos que escuchamos en la vida cotidiana no se caracterizan por una única frecuencia , sino que consisten en una suma de frecuencias sinusoidales puras, cada una de ellas con una amplitud diferente . Cuando los humanos escuchamos estas frecuencias simultáneamente, podemos reconocer el sonido. Esto es cierto tanto para sonidos "no musicales" (por ejemplo, el chapoteo del agua, el crujido de las hojas, etc.) como para sonidos "musicales" (por ejemplo, una nota de piano, el trino de un pájaro, etc.). Este conjunto de parámetros (frecuencias, sus amplitudes relativas y cómo cambian las amplitudes relativas con el tiempo) están encapsulados por el timbre del sonido. El análisis de Fourier es la técnica que se utiliza para determinar estos parámetros de timbre exactos a partir de una señal de sonido global; a la inversa, el conjunto resultante de frecuencias y amplitudes se denomina serie de Fourier de la señal de sonido original.
En el caso de una nota musical, la frecuencia más baja de su timbre se designa como la frecuencia fundamental del sonido . Para simplificar, a menudo decimos que la nota se toca en esa frecuencia fundamental (por ejemplo, " el do central es 261,6 Hz"), [3] aunque el sonido de esa nota también consta de muchas otras frecuencias. El conjunto de las frecuencias restantes se denomina sobretonos (o armónicos , si sus frecuencias son múltiplos enteros de la frecuencia fundamental) del sonido. [4] En otras palabras, la frecuencia fundamental por sí sola es responsable del tono de la nota, mientras que los sobretonos definen el timbre del sonido. Los sobretonos de un piano que toca el do central serán bastante diferentes de los sobretonos de un violín que toca la misma nota; eso es lo que nos permite diferenciar los sonidos de los dos instrumentos. Incluso hay diferencias sutiles en el timbre entre diferentes versiones del mismo instrumento (por ejemplo, un piano vertical frente a un piano de cola ).
La síntesis aditiva pretende explotar esta propiedad del sonido para construir el timbre desde cero. Sumando frecuencias puras ( ondas sinusoidales ) de distintas frecuencias y amplitudes, podemos definir con precisión el timbre del sonido que queremos crear.
Definiciones

La síntesis aditiva armónica está estrechamente relacionada con el concepto de serie de Fourier , que es una forma de expresar una función periódica como la suma de funciones sinusoidales con frecuencias iguales a múltiplos enteros de una frecuencia fundamental común . Estas sinusoides se denominan armónicos , sobretonos o, en general, parciales . En general, una serie de Fourier contiene un número infinito de componentes sinusoidales, sin límite superior para la frecuencia de las funciones sinusoidales e incluye un componente de CC (uno con frecuencia de 0 Hz ). Las frecuencias fuera del rango audible humano se pueden omitir en la síntesis aditiva. Como resultado, solo se modela un número finito de términos sinusoidales con frecuencias que se encuentran dentro del rango audible en la síntesis aditiva.
Se dice que una forma de onda o función es periódica si
para todos y por algún tiempo .
La serie de Fourier de una función periódica se expresa matemáticamente como:
dónde
- es la frecuencia fundamental de la forma de onda y es igual al recíproco del período,
- es la amplitud del armónico n.º,
- es el desfase de fase del armónico n.º. atan2 es la función arcotangente de cuatro cuadrantes ,
Al ser inaudibles, el componente DC , , y todos los componentes con frecuencias superiores a un límite finito, , se omiten en las siguientes expresiones de síntesis aditiva.
Forma armónica
La síntesis aditiva armónica más simple se puede expresar matemáticamente como:
| ( 1 ) |
donde es la salida de síntesis, , , y son la amplitud, la frecuencia y el desfase de fase, respectivamente, del parcial armónico n de un total de parciales armónicos, y es la frecuencia fundamental de la forma de onda y la frecuencia de la nota musical .
Amplitudes dependientes del tiempo
 | Ejemplo de síntesis aditiva armónica en la que cada armónico tiene una amplitud dependiente del tiempo. La frecuencia fundamental es de 440 Hz. ¿Tiene problemas para escuchar este archivo? Consulte la ayuda de medios |
De manera más general, la amplitud de cada armónico se puede prescribir como una función del tiempo, en cuyo caso la salida de síntesis es
| . | ( 2 ) |
Cada envolvente debe variar lentamente en relación con el espaciamiento de frecuencia entre sinusoides adyacentes. El ancho de banda de debe ser significativamente menor que .
Forma inarmónica
La síntesis aditiva también puede producir sonidos inarmónicos (que son formas de onda aperiódicas ) en las que los armónicos individuales no necesitan tener frecuencias que sean múltiplos enteros de alguna frecuencia fundamental común. [5] [6] Si bien muchos instrumentos musicales convencionales tienen parciales armónicos (por ejemplo, un oboe ), algunos tienen parciales inarmónicos (por ejemplo, campanas ). La síntesis aditiva inarmónica se puede describir como
donde es la frecuencia constante del parcial.
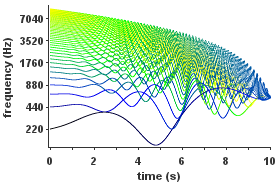 | Ejemplo de síntesis aditiva inarmónica en la que tanto la amplitud como la frecuencia de cada parcial dependen del tiempo. ¿Tiene problemas para escuchar este archivo? Consulte la ayuda de medios |
Frecuencias dependientes del tiempo
En el caso general, la frecuencia instantánea de una senoide es la derivada (con respecto al tiempo) del argumento de la función seno o coseno. Si esta frecuencia se representa en hercios , en lugar de en forma de frecuencia angular , entonces esta derivada se divide por . Esto es así tanto si la parcial es armónica como inarmónica y tanto si su frecuencia es constante o varía con el tiempo.
En la forma más general, la frecuencia de cada parcial no armónico es una función no negativa del tiempo, , lo que da como resultado
| ( 3 ) |
Definiciones más amplias
La síntesis aditiva en un sentido más amplio puede significar técnicas de síntesis de sonido que suman elementos simples para crear timbres más complejos, incluso cuando los elementos no son ondas sinusoidales. [7] [8] Por ejemplo, F. Richard Moore incluyó la síntesis aditiva como una de las "cuatro categorías básicas" de síntesis de sonido junto con la síntesis sustractiva , la síntesis no lineal y el modelado físico . [8] En este sentido amplio, los órganos de tubos , que también tienen tubos que producen formas de onda no sinusoidales, pueden considerarse como una forma variante de sintetizadores aditivos. La suma de componentes principales y las funciones de Walsh también se han clasificado como síntesis aditiva. [9]
Métodos de implementación
Las implementaciones modernas de la síntesis aditiva son principalmente digitales. (Consulte la sección Ecuaciones de tiempo discreto para conocer la teoría de tiempo discreto subyacente)
Síntesis de banco de osciladores
La síntesis aditiva se puede implementar utilizando un banco de osciladores sinusoidales, uno para cada parcial. [1]
Síntesis de tabla de ondas
En el caso de tonos musicales armónicos y cuasi periódicos, la síntesis de tabla de ondas puede ser tan general como la síntesis aditiva variable en el tiempo, pero requiere menos cálculos durante la síntesis. [10] [11] Como resultado, se puede lograr una implementación eficiente de la síntesis aditiva variable en el tiempo de tonos armónicos mediante el uso de la síntesis de tabla de ondas .
Síntesis aditiva grupal
La síntesis aditiva grupal [12] [13] [14] es un método para agrupar parciales en grupos armónicos (que tienen diferentes frecuencias fundamentales) y sintetizar cada grupo por separado con síntesis de tabla de ondas antes de mezclar los resultados.
Síntesis de FFT inversa
Se puede utilizar una transformada rápida de Fourier inversa para sintetizar de manera eficiente frecuencias que dividan de manera uniforme el período de la transformada o "marco". Si se considera detenidamente la representación en el dominio de la frecuencia de la DFT, también es posible sintetizar de manera eficiente sinusoides de frecuencias arbitrarias utilizando una serie de marcos superpuestos y la transformada rápida de Fourier inversa . [15]
Análisis aditivo/resíntesis

Es posible analizar los componentes de frecuencia de un sonido grabado dando una representación de "suma de sinusoides". Esta representación se puede volver a sintetizar mediante síntesis aditiva. Un método para descomponer un sonido en parciales sinusoidales que varían en el tiempo es el análisis de McAulay- Quatieri basado en la transformada de Fourier de tiempo corto (STFT) . [17] [18]
Modificando la representación de la suma de las sinusoides, se pueden realizar alteraciones tímbricas antes de la resíntesis. Por ejemplo, un sonido armónico podría reestructurarse para que suene inarmónico, y viceversa. La hibridación o "transformación" de sonidos se ha implementado mediante la resíntesis aditiva. [19]
El análisis aditivo/resíntesis se ha empleado en varias técnicas, incluidas la modelización sinusoidal, [20] la síntesis de modelización espectral (SMS), [19] y el modelo de sonido aditivo mejorado con ancho de banda reasignado. [21] El software que implementa el análisis aditivo/resíntesis incluye: SPEAR, [22] LEMUR, LORIS, [23] SMSTools, [24] ARSS. [25]
Productos
New England Digital Synclavier tenía una función de resíntesis donde las muestras podían analizarse y convertirse en "marcos de timbre" que formaban parte de su motor de síntesis aditiva. Technos acxel , lanzado en 1987, utilizó el modelo de análisis aditivo/resíntesis en una implementación de FFT.
También un sintetizador vocal, Vocaloid se ha implementado sobre la base del análisis aditivo/resíntesis: su modelo espectral de voz llamado modelo Excitation plus Resonances (EpR) [26] [27] se extiende sobre la base de Spectral Modeling Synthesis (SMS), y su síntesis concatenativa de difonos se procesa utilizando la técnica de procesamiento de pico espectral (SPP) [28] similar al vocoder de fase bloqueada modificado [29] (un vocoder de fase mejorado para el procesamiento de formantes). [30] Usando estas técnicas, los componentes espectrales ( formantes ) que consisten en parciales puramente armónicos se pueden transformar apropiadamente en la forma deseada para el modelado de sonido, y la secuencia de muestras cortas ( difonos o fonemas ) que constituyen la frase deseada, se pueden conectar suavemente interpolando parciales coincidentes y picos de formantes, respectivamente, en la región de transición insertada entre diferentes muestras. (Véase también Timbres dinámicos )
Aplicaciones
Instrumentos musicales
La síntesis aditiva se utiliza en instrumentos musicales electrónicos. Es la principal técnica de generación de sonido que utilizan los órganos Eminent .
Síntesis de voz
En la investigación lingüística , la síntesis aditiva armónica se utilizó en la década de 1950 para reproducir espectrogramas de habla modificados y sintéticos. [31]
Más tarde, a principios de los años 1980, se llevaron a cabo pruebas de escucha en el habla sintética despojada de señales acústicas para evaluar su importancia. Las frecuencias y amplitudes de formantes variables en el tiempo derivadas por codificación predictiva lineal se sintetizaron de forma aditiva como silbidos de tono puro. Este método se llama síntesis de ondas sinusoidales . [32] [33] También se sabe que el modelado sinusoidal compuesto (CSM) [34] [35] utilizado en una función de síntesis de voz cantada en Yamaha CX5M (1984), utiliza un enfoque similar que se desarrolló de forma independiente durante 1966-1979. [36] [37] Estos métodos se caracterizan por la extracción y recomposición de un conjunto de picos espectrales significativos correspondientes a los diversos modos de resonancia ocurridos en la cavidad oral y la cavidad nasal, desde un punto de vista acústico . Este principio también se utilizó en un método de síntesis de modelado físico , llamado síntesis modal . [38] [39] [40] [41]
Historia
El análisis armónico fue descubierto por Joseph Fourier , [42] quien publicó un extenso tratado de su investigación en el contexto de la transferencia de calor en 1822. [43] La teoría encontró una aplicación temprana en la predicción de mareas . Alrededor de 1876, [44] William Thomson (más tarde ennoblecido como Lord Kelvin ) construyó un predictor mecánico de mareas . Consistía en un analizador armónico y un sintetizador armónico , como se los llamaba ya en el siglo XIX. [45] [46] El análisis de las mediciones de mareas se realizó utilizando la máquina integradora de James Thomson . Los coeficientes de Fourier resultantes se introdujeron en el sintetizador, que luego utilizó un sistema de cuerdas y poleas para generar y sumar parciales sinusoidales armónicos para la predicción de mareas futuras. En 1910, se construyó una máquina similar para el análisis de formas de onda periódicas del sonido. [47] El sintetizador dibujó un gráfico de la forma de onda combinada, que se utilizó principalmente para la validación visual del análisis. [47]
Georg Ohm aplicó la teoría de Fourier al sonido en 1843. La línea de trabajo fue muy avanzada por Hermann von Helmholtz , quien publicó sus ocho años de investigación en 1863. [48] Helmholtz creía que la percepción psicológica del color del tono está sujeta al aprendizaje, mientras que la audición en el sentido sensorial es puramente fisiológica. [49] Apoyó la idea de que la percepción del sonido deriva de señales de las células nerviosas de la membrana basilar y que los apéndices elásticos de estas células vibran simpáticamente por tonos sinusoidales puros de frecuencias apropiadas. [47] Helmholtz estuvo de acuerdo con el hallazgo de Ernst Chladni de 1787 de que ciertas fuentes de sonido tienen modos de vibración inarmónicos. [49]
En la época de Helmholtz, la amplificación electrónica no estaba disponible. Para la síntesis de tonos con parciales armónicos, Helmholtz construyó un conjunto de diapasones excitados eléctricamente y cámaras de resonancia acústica que permitían el ajuste de las amplitudes de los parciales. [50] Construidos al menos en 1862, [50] estos fueron a su vez refinados por Rudolph Koenig , quien demostró su propia configuración en 1872. [50] Para la síntesis armónica, Koenig también construyó un gran aparato basado en su sirena de ondas . Era neumático y utilizaba ruedas fónicas recortadas , y fue criticado por la baja pureza de sus tonos parciales. [44] Además, los tubos tibiales de los órganos de tubos tienen formas de onda casi sinusoidales y se pueden combinar a la manera de la síntesis aditiva. [44]
En 1938, con nuevas evidencias significativas de apoyo, [51] se informó en las páginas de Popular Science Monthly que las cuerdas vocales humanas funcionan como una sirena de incendios para producir un tono rico en armónicos, que luego es filtrado por el tracto vocal para producir diferentes tonos vocálicos. [52] En ese momento, el órgano aditivo Hammond ya estaba en el mercado. La mayoría de los primeros fabricantes de órganos electrónicos pensaron que era demasiado caro fabricar la pluralidad de osciladores requeridos por los órganos aditivos, y comenzaron en cambio a construir órganos sustractivos . [53] En una reunión del Institute of Radio Engineers de 1940 , el ingeniero de campo jefe de Hammond explicó que el nuevo Novachord de la compañía tenía un "sistema sustractivo" en contraste con el órgano Hammond original en el que "los tonos finales se construían combinando ondas sonoras" . [54] Alan Douglas usó los calificadores aditivo y sustractivo para describir diferentes tipos de órganos electrónicos en un documento de 1948 presentado a la Royal Musical Association . [55] La redacción contemporánea de síntesis aditiva y síntesis sustractiva se puede encontrar en su libro de 1957 La producción eléctrica de la música , en el que enumera categóricamente tres métodos de formación de colores tonales musicales, en secciones tituladas Síntesis aditiva , Síntesis sustractiva y Otras formas de combinaciones . [56]
Un sintetizador aditivo moderno típico produce su salida como una señal eléctrica analógica o como audio digital , como en el caso de los sintetizadores de software , que se hicieron populares alrededor del año 2000. [57]
Cronología
A continuación se presenta una cronología de sintetizadores y dispositivos analógicos y digitales histórica y tecnológicamente notables que implementan síntesis aditiva.
| Implementación o publicación de la investigación | Disponible comercialmente | Empresa o institución | Sintetizador o dispositivo de síntesis | Descripción | Muestras de audio |
|---|---|---|---|---|---|
| 1900 [58] | 1906 [58] | Compañía de música eléctrica de Nueva Inglaterra | Telarmonio | El primer sintetizador musical polifónico sensible al tacto. [59] Implementó la síntesis aditiva sinusoidal utilizando ruedas fónicas y alternadores . Inventado por Thaddeus Cahill . | No se conocen grabaciones [58] |
| 1933 [60] | 1935 [60] | Compañía de órganos Hammond | Órgano Hammond | Un sintetizador aditivo electrónico que tuvo más éxito comercial que el Telharmonium. [59] Implementó la síntesis aditiva sinusoidal utilizando ruedas fónicas y pastillas magnéticas . Inventado por Laurens Hammond . | |
| 1950 o antes [31] | Laboratorios Haskins | Reproducción de patrones | Un sistema de síntesis de voz que controlaba las amplitudes de los armónicos parciales mediante un espectrograma dibujado a mano o el resultado de un análisis. Los armónicos parciales se generaban mediante una rueda fónica óptica multipista . [31] | muestras | |
| 1958 [61] | Respuesta | Un sintetizador aditivo [62] que reproducía partituras similares a espectrogramas microtonales utilizando múltiples ruedas tonales ópticas multipista . Inventado por Evgeny Murzin . Un instrumento similar que utilizaba osciladores electrónicos, el Oscillator Bank , y su dispositivo de entrada Spectrogram fueron creados por Hugh Le Caine en 1959. [63] [64] | |||
| 1963 [65] | Instituto Tecnológico de Massachusetts (MIT) | Un sistema fuera de línea para el análisis espectral digital y la resíntesis de las partes de ataque y estado estable de los timbres de instrumentos musicales por David Luce. [65] | |||
| 1964 [66] | Universidad de Illinois | Generador de tonos armónicos | Un sistema de síntesis aditiva armónica electrónica inventado por James Beauchamp. [66] [67] | muestras (info) | |
| 1974 o antes [68] [69] | 1974 [68] [69] | RMI | Sintetizador armónico | El primer producto sintetizador que implementó síntesis aditiva [70] usando osciladores digitales. [68] [69] El sintetizador también tenía un filtro analógico variable en el tiempo. [68] RMI era una subsidiaria de Allen Organ Company , que había lanzado el primer órgano de iglesia digital comercial , el Allen Computer Organ , en 1971, usando tecnología digital desarrollada por North American Rockwell . [71] | 1 2 3 4 |
| 1974 [72] | EMS (Londres) | Banco de osciladores digitales | Un banco de osciladores digitales con formas de onda arbitrarias, controles individuales de frecuencia y amplitud, [73] destinado a ser utilizado en análisis-resíntesis con el banco de filtros analizadores digitales (AFB) también construido en EMS. [72] [73] También conocido como: DOB . | en El nuevo sonido de la música [74] | |
| 1976 [75] | 1976 [76] | Luz justa | Qasar M8 | Un sintetizador totalmente digital que utiliza la transformada rápida de Fourier [77] para crear muestras a partir de envolventes de amplitud de armónicos dibujados de forma interactiva. [78] | muestras |
| 1977 [79] | Laboratorios Bell | Sintetizador digital | Un sintetizador aditivo digital en tiempo real [79] que ha sido llamado el primer sintetizador digital verdadero. [80] También conocido como: Alles Machine , Alice . | muestra (info) | |
| 1979 [80] | 1979 [80] | Nueva Inglaterra Digital | Sinclavier II | Un sintetizador digital comercial que permitió el desarrollo del timbre a lo largo del tiempo mediante suaves fundidos cruzados entre formas de onda generadas por síntesis aditiva. | |
| 1996 [81] | Kawaii | K5000 | Una estación de trabajo de sintetizador digital comercial capaz de realizar síntesis aditiva digital polifónica de hasta 128 ondas sinusoidales, así como peinar ondas PCM. [82] |
Ecuaciones de tiempo discreto
En las implementaciones digitales de síntesis aditiva, se utilizan ecuaciones de tiempo discreto en lugar de ecuaciones de síntesis de tiempo continuo. Una convención de notación para señales de tiempo discreto utiliza corchetes, es decir , y el argumento solo puede ser valores enteros. Si se espera que la salida de síntesis de tiempo continuo esté suficientemente limitada en banda ; por debajo de la mitad de la frecuencia de muestreo o , basta con muestrear directamente la expresión de tiempo continuo para obtener la ecuación de síntesis discreta. La salida de síntesis continua se puede reconstruir posteriormente a partir de las muestras utilizando un convertidor digital a analógico . El período de muestreo es .
Comenzando con ( 3 ),
y el muestreo en tiempos discretos da como resultado
dónde
- es la envolvente de amplitud variable en el tiempo discreto
- es la frecuencia instantánea de diferencia hacia atrás en tiempo discreto .
Esto es equivalente a
dónde
- para todos [15]
y
Véase también
Referencias
- ^ ab Julius O. Smith III. "Síntesis aditiva (modelado sinusoidal temprano)" . Consultado el 14 de enero de 2012.
El término "síntesis aditiva" se refiere al sonido que se forma sumando muchos componentes sinusoidales
. - ^ Gordon Reid. "Secretos de sintetizador, parte 14: Introducción a la síntesis aditiva". Sound on Sound (enero de 2000) . Consultado el 14 de enero de 2012 .
- ^ Mottola, Liutaio (31 de mayo de 2017). "Tabla de notas musicales y sus frecuencias y longitudes de onda".
- ^ "Frecuencia fundamental y armónicos".
- ^ Smith III, Julius O.; Serra, Xavier (2005). "Síntesis aditiva". PARSHL: un programa de análisis/síntesis para sonidos no armónicos basado en una representación sinusoidal. Actas de la Conferencia Internacional de Música por Computadora (ICMC-87, Tokio), Computer Music Association, 1987. CCRMA , Departamento de Música, Universidad de Stanford . Consultado el 11 de enero de 2015 .(reimpresión en línea)
- ^ Smith III, Julius O. (2011). "Síntesis aditiva (modelado sinusoidal temprano)". Procesamiento de señales de audio espectrales. CCRMA , Departamento de Música, Universidad de Stanford. ISBN 978-0-9745607-3-1. Recuperado el 9 de enero de 2012 .
- ^ Roads, Curtis (1995). El tutorial de música por computadora . MIT Press . pág. 134. ISBN 978-0-262-68082-0.
- ^ ab Moore, F. Richard (1995). Fundamentos de la música por computadora . Prentice Hall . pág. 16. ISBN 978-0-262-68082-0.
- ^ Roads, Curtis (1995). El tutorial de música por computadora . MIT Press . Págs. 150-153. ISBN. 978-0-262-68082-0.
- ^ Robert Bristow-Johnson (noviembre de 1996). «Wavetable Synthesis 101, A Fundamental Perspective» (PDF) . Archivado desde el original (PDF) el 15 de junio de 2013. Consultado el 21 de mayo de 2005 .
- ^ Andrew Horner (noviembre de 1995). "Síntesis de instrumentos dinámicos mediante emparejamiento de tabla de ondas con algoritmos genéticos". Revista de la Sociedad de Ingeniería de Audio . 43 (11): 916–931.
- ^ Julius O. Smith III. "Group Additive Synthesis". CCRMA , Universidad de Stanford. Archivado desde el original el 6 de junio de 2011. Consultado el 12 de mayo de 2011 .
- ^ P. Kleczkowski (1989). "Síntesis aditiva de grupos". Computer Music Journal . 13 (1): 12–20. doi :10.2307/3679851. JSTOR 3679851.
- ^ B. Eaglestone y S. Oates (1990). "Herramientas analíticas para la síntesis aditiva de grupos". Actas de la Conferencia Internacional de Música por Computadora de 1990, Glasgow . Asociación de Música por Computadora.
- ^ ab Rodet, X.; Depalle, P. (1992). "Sintesis de FFT inversa y envolventes espectrales". Actas de la 93.ª Convención de la Sociedad de Ingeniería de Audio . CiteSeerX 10.1.1.43.4818 .
- ^ McAulay, RJ; Quatieri, TF (1988). "Procesamiento del habla basado en un modelo sinusoidal" (PDF) . The Lincoln Laboratory Journal . 1 (2): 153–167. Archivado desde el original (PDF) el 21 de mayo de 2012 . Consultado el 9 de diciembre de 2013 .
- ^ McAulay, RJ; Quatieri, TF (agosto de 1986). "Análisis/síntesis del habla basada en una representación sinusoidal". IEEE Transactions on Acoustics, Speech, and Signal Processing . 34 (4): 744–754. doi :10.1109/TASSP.1986.1164910.
- ^ "Método McAulay-Quatieri".
- ^ ab Serra, Xavier (1989). Un sistema para el análisis/transformación/síntesis del sonido basado en una descomposición determinista más estocástica (tesis doctoral). Universidad de Stanford . Consultado el 13 de enero de 2012 .
- ^ Smith III, Julius O.; Serra, Xavier. "PARSHL: Un programa de análisis/síntesis para sonidos no armónicos basado en una representación sinusoidal" . Consultado el 9 de enero de 2012 .
- ^ Fitz, Kelly (1999). El método de síntesis aditiva mejorado con ancho de banda reasignado (tesis doctoral). Departamento de Ingeniería Eléctrica y Computacional, Universidad de Illinois Urbana-Champaign. CiteSeerX 10.1.1.10.1130 .
- ^ Análisis y resíntesis de edición parcial sinusoidal SPEAR para Mac OS X, MacOS 9 y Windows
- ^ "Software Loris para modelado, transformación y manipulación de sonido". Archivado desde el original el 30 de julio de 2012 . Consultado el 13 de enero de 2012 .
- ^ Aplicación SMSTools para Windows
- ^ ARSS: El espectrógrafo de análisis y resíntesis de sonido
- ^ Bonada, J.; Celma, O.; Loscos, A.; Órtola, J.; Serra, X.; Yoshioka, Y.; Kayama, H.; Hisaminato, Y.; Kenmochi, H. (2001). "Síntesis de voz cantada combinando excitación más resonancia y modelos sinusoidales más residuales". Proc. De la CCIM . CiteSeerX 10.1.1.18.6258 . (PDF)
- ^ Loscos, A. (2007). Procesamiento espectral de la voz cantada (tesis doctoral). Barcelona, España: Universidad Pompeu Fabra. hdl :10803/7542.(PDF).
Véase " Modelo de voz de excitación más resonancias " (p. 51) - ^ Loscos 2007, p. 44, " Procesamiento de picos espectrales"
- ^ Loscos 2007, p. 44, " Vocoder bloqueado por fase "
- ^ Bonada, Jordi; Loscos, Alex (2003). "Sintetizador de voz cantada basado en samples mediante concatenación espectral: 6. Concatenación de samples". Proc. of SMAC 03 : 439–442.
- ^ abc Cooper, FS; Liberman, AM; Borst, JM (mayo de 1951). "La interconversión de patrones audibles y visibles como base para la investigación en la percepción del habla". Proc. Natl. Sci. USA . 37 (5): 318–25. Bibcode :1951PNAS...37..318C. doi : 10.1073/pnas.37.5.318 . PMC 1063363 . PMID 14834156.
- ^ Remez, RE; Rubin, PE; Pisoni, DB; Carrell, TD (1981). "Percepción del habla sin claves tradicionales del habla". Science . 212 (4497): 947–950. Bibcode :1981Sci...212..947R. doi :10.1126/science.7233191. PMID 7233191. S2CID 13039853.
- ^ Rubin, PE (1980). "Sinewave Synthesis Instruction Manual (VAX)" (PDF) . Memorándum interno . Haskins Laboratories, New Haven, CT. Archivado desde el original (PDF) el 29 de agosto de 2021 . Consultado el 27 de diciembre de 2011 .
- ^ Sagayama, S. [en japonés] ; Itakura, F. (1979), 複合正弦波による音声合成[Síntesis de voz mediante ondas sinusoidales compuestas], Comité de voz de la Sociedad acústica de Japón (publicado en octubre de 1979), S79-39
- ^ Sagayama, S.; Itakura, F. (octubre de 1979). 複合正弦波による簡易な音声合成法[Método de síntesis de voz simple mediante ondas sinusoidales compuestas]. Actas de la Sociedad Acústica de Japón, Reunión de otoño . Vol. 3-2-3. págs. 557–558.
- ^ Sagayama, S.; Itakura, F. (1986). "Teoría de la dualidad del modelado sinusoidal compuesto y predicción lineal". ICASSP '86. IEEE International Conference on Acoustics, Speech, and Signal Processing . Vol. 11. Acústica, habla y procesamiento de señales, IEEE International Conference on ICASSP '86. (publicado en abril de 1986). págs. 1261–1264. doi :10.1109/ICASSP.1986.1168815. S2CID 122814777.
- ^ Itakura, F. (2004). "Modelado estadístico lineal del habla y sus aplicaciones: más de 36 años de historia de LPC" (PDF) . Actas del 18.º Congreso Internacional de Acústica (ICA 2004), We3.D, Kioto, Japón, abril de 2004. 3 ( publicado en abril de 2004): III–2077–2082.
6. Modelado sinusoidal compuesto (CSM) En 1975, Itakura propuso el concepto de representación de espectro de línea (LSR) y su algoritmo para obtener un conjunto de parámetros para la nueva representación del espectro del habla. Independientemente de esto, Sagayama desarrolló un concepto de modelado sinusoidal compuesto (CSM) que es equivalente a LSR pero que ofrece una formulación, un algoritmo de resolución y un esquema de síntesis bastante diferentes. Sagayama aclaró la dualidad de LPC y CSM y proporcionó una visión unificada que abarca LPC, PARCOR, LSR, LSP y CSM. CSM no es solo un nuevo concepto de análisis del espectro del habla sino también una idea clave para comprender la predicción lineal desde un punto de vista unificado.
- ^ Adrien, Jean-Marie (1991). "El eslabón perdido: la síntesis modal". En Giovanni de Poli; Aldo Piccialli; Curtis Roads (eds.). Representaciones de señales musicales . Cambridge, MA: MIT Press . pp. 269–298. ISBN 978-0-262-04113-3.
- ^ Morrison, Joseph Derek (IRCAM); Adrien, Jean-Marie (1993). "MOSAIC: Un marco para la síntesis modal". Revista de música informática . 17 (1): 45–56. doi :10.2307/3680569. JSTOR 3680569.
- ^ Bilbao, Stefan (octubre de 2009), "Síntesis modal", Síntesis numérica del sonido: esquemas de diferencias finitas y simulación en acústica musical , Chichester, Reino Unido: John Wiley and Sons, ISBN 978-0-470-51046-9Un enfoque diferente ,
con una larga historia de uso en la síntesis de sonido para modelado físico, se basa en una descripción modal o de dominio de frecuencia de la vibración de objetos de geometría potencialmente compleja. La síntesis modal [1,148], como se la denomina, es atractiva, ya que el comportamiento dinámico complejo de un objeto vibrante se puede descomponer en contribuciones de un conjunto de modos (cuyas formas espaciales son funciones propias del problema particular en cuestión y dependen de las condiciones de contorno), cada uno de los cuales oscila a una única frecuencia compleja. ...
(Ver también la página complementaria) - ^ Doel, Kees van den; Pai, Dinesh K. (2003). Greenebaum, K. (ed.). "Síntesis modal para objetos vibrantes" (PDF) . Anécdotas en audio . Natick, MA: AK Peter.
Cuando un objeto sólido se golpea, se raspa o se involucra en otras interacciones externas, las fuerzas en el punto de contacto provocan deformaciones que se propagan a través del cuerpo, lo que hace que sus superficies externas vibren y emitan ondas sonoras. ... Un buen modelo de síntesis motivado físicamente para objetos como este es la síntesis modal ... donde un objeto vibrante es modelado por un banco de osciladores armónicos amortiguados que son excitados por un estímulo externo.
- ^ Prestini, Elena (2004) [Ed. rev. de: Applicazioni dell'analisi armonica. Milán: Ulrico Hoepli, 1996]. La evolución del análisis armónico aplicado: modelos del mundo real. trad. Nueva York, EE. UU.: Birkhäuser Boston. págs. 114-115. ISBN 978-0-8176-4125-2. Recuperado el 6 de febrero de 2012 .
- ^ Fourier, Jean Baptiste José (1822). Théorie analytique de la chaleur [ La teoría analítica del calor ] (en francés). París, Francia: Chez Firmin Didot, père et fils. ISBN 9782876470460.
- ^ abc Miller, Dayton Clarence (1926) [1916]. La ciencia de los sonidos musicales. Nueva York: The Macmillan Company. págs. 110, 244–248.
- ^ Revista filosófica y revista científica de Londres, Edimburgo y Dublín . 49. Taylor & Francis: 490. 1875.
{{cite journal}}: Falta o está vacío|title=( ayuda ) [ verificación fallida ] - ^ Thomson, Sir W. (1878). "Analizador armónico". Actas de la Royal Society de Londres . 27 (185–189). Taylor y Francis: 371–373. doi : 10.1098/rspl.1878.0062 . JSTOR 113690.
- ^ abc Cahan, David (1993). Cahan, David (ed.). Hermann von Helmholtz y los fundamentos de la ciencia del siglo XIX. Berkeley y Los Ángeles, EE. UU.: University of California Press. pp. 110–114, 285–286. ISBN 978-0-520-08334-9.
- ^ Helmholtz, von, Hermann (1863). Die Lehre von den Tonempfindungen als psychologische Grundlage für die Theorie der Musik [Sobre las sensaciones del tono como base fisiológica de la teoría de la música ] (en alemán) (1ª ed.). Leipzig: Leopold Voss. págs.v.
- ^ ab Christensen, Thomas Street (2002). La historia de la música occidental en Cambridge. Cambridge, Reino Unido: Cambridge University Press. pp. 251, 258. ISBN 978-0-521-62371-1.
- ^ abc von Helmholtz, Hermann (1875). Sobre las sensaciones del tono como base fisiológica de la teoría de la música. Londres, Reino Unido: Longmans, Green y compañía, págs. xii, 175–179.
- ^ Russell, George Oscar (1936). Anuario - Carnegie Institution of Washington (1936). Carnegie Institution of Washington: Anuario. Vol. 35. Washington: Carnegie Institution of Washington. págs. 359–363.
- ^ Lodge, John E. (abril de 1938). Brown, Raymond J. (ed.). "Extrañas pruebas de laboratorio nos muestran cómo hablamos: utilizando rayos X, cámaras de cine rápidas y tubos de rayos catódicos, los científicos están descubriendo nuevos hechos sobre la voz humana y desarrollando métodos de enseñanza para hacernos mejores hablantes". Popular Science Monthly . 132 (4). Nueva York, EE. UU.: Popular Science Publishing: 32–33.
- ^ Comerford, P. (1993). "Simulación de un órgano con síntesis aditiva". Computer Music Journal . 17 (2): 55–65. doi :10.2307/3680869. JSTOR 3680869.
- ^ "Noticias del Instituto y Notas de Radio". Actas del IRE . 28 (10): 487–494. 1940. doi :10.1109/JRPROC.1940.228904.
- ^ Douglas, A. (1948). "Música electrotónica". Actas de la Royal Musical Association . 75 : 1–12. doi :10.1093/jrma/75.1.1.
- ^ Douglas, Alan Lockhart Monteith (1957). La producción eléctrica de la música . Londres, Reino Unido: Macdonald. pp. 140, 142.
- ^ Pejrolo, Andrea; DeRosa, Rich (2007). Orquestación acústica y MIDI para el compositor contemporáneo . Oxford, Reino Unido: Elsevier. pp. 53–54.
- ^ abc Weidenaar, Reynold (1995). Música mágica del telarmonio. Lanham, Maryland: Scarecrow Press. ISBN 978-0-8108-2692-2.
- ^ ab Moog, Robert A. (octubre-noviembre de 1977). "Música electrónica". Revista de la Sociedad de Ingeniería de Audio . 25 (11/10): 856.
- ^ ab Olsen, Harvey (14 de diciembre de 2011). Brown, Darren T. (ed.). "Altavoces Leslie y órganos Hammond: rumores, mitos, hechos y tradiciones". The Hammond Zone . Órgano Hammond en el Reino Unido Archivado desde el original el 1 de septiembre de 2012. Consultado el 20 de enero de 2012 .
- ^ Holzer, Derek (22 de febrero de 2010). «Una breve historia de la síntesis óptica» . Consultado el 13 de enero de 2012 .
- ^ Vail, Mark (1 de noviembre de 2002). "ANS de Eugeniy Murzin: sintetizador ruso aditivo". Revista Keyboard , pág. 120.
- ^ Young, Gayle. "Banco de osciladores (1959)".
- ^ Young, Gayle. "Espectrograma (1959)".
- ^ ab Luce, David Alan (1963). Correlatos físicos de los tonos de instrumentos musicales no percusivos (Tesis de tesis). Cambridge, Massachusetts, EE. UU.: Instituto Tecnológico de Massachusetts. hdl :1721.1/27450.
- ^ ab Beauchamp, James (17 de noviembre de 2009). "El generador de tonos armónicos: uno de los primeros sintetizadores analógicos controlados por voltaje". Página de inicio del profesor James W. Beauchamp .
- ^ Beauchamp, James W. (octubre de 1966). "Síntesis aditiva de tonos musicales armónicos". Revista de la Sociedad de Ingeniería de Audio . 14 (4): 332–342.
- ^ abcd «Sintetizador armónico RMI». Synthmuseum.com. Archivado desde el original el 9 de junio de 2011. Consultado el 12 de mayo de 2011 .
- ^ abc Reid, Gordon. «PROG SPAWN! The Rise And Fall of Rocky Mount Instruments (Retro)». Sound on Sound (diciembre de 2001). Archivado desde el original el 25 de diciembre de 2011. Consultado el 22 de enero de 2012 .
- ^ Flint, Tom. "Jean Michel Jarre: 30 Years of Oxygene". Sound on Sound (febrero de 2008) . Consultado el 22 de enero de 2012 .
- ^ "Compañía de órganos Allen". fundinguniverse.com .
- ^ ab Cosimi, Enrico (20 de mayo de 2009). "EMS Story - Prima Parte" [EMS Story - Primera parte]. Audio Accordo.it (en italiano). Archivado desde el original el 22 de mayo de 2009. Consultado el 21 de enero de 2012 .
- ^ ab Hinton, Graham (2002). "EMS: The Inside Story". Electronic Music Studios (Cornualles). Archivado desde el original el 21 de mayo de 2013.
- ^ El nuevo sonido de la música (TV). Reino Unido: BBC. 1979.Incluye una demostración de DOB y AFB.
- ^ Leete, norma. "Computadora Fairlight - Instrumento musical (retro)". Sonido sobre Sonido (abril de 1999) . Consultado el 29 de enero de 2012 .
- ^ Twyman, John (1 de noviembre de 2004). (Inter)facing the music: The history of the Fairlight Computer Musical Instrument (PDF) (Tesis de licenciatura en Ciencias (con honores)). Unidad de Historia y Filosofía de la Ciencia, Universidad de Sydney . Consultado el 29 de enero de 2012 .
- ^ Street, Rita (8 de noviembre de 2000). "Fairlight: A 25-year long fairytale". Revista Audio Media . IMAS Publishing UK. Archivado desde el original el 8 de octubre de 2003. Consultado el 29 de enero de 2012 .
- ^ "Computer Music Journal" (JPG) . 1978. Consultado el 29 de enero de 2012 .
- ^ ab Leider, Colby (2004). "El desarrollo de la DAW moderna". Estación de trabajo de audio digital . McGraw-Hill . pág. 58.
- ^ abc Joel, Chadabe (1997). Sonido eléctrico. Upper Saddle River, Nueva Jersey, EE. UU.: Prentice Hall. págs. 177-178, 186. ISBN 978-0-13-303231-4.
- ^ "Kawai K5000 | Vintage Synth Explorer" www.vintagesynth.com . Consultado el 21 de enero de 2024 .
- ^ "Kawai K5000R y K5000S". www.soundonsound.com . Consultado el 21 de enero de 2024 .
Enlaces externos
- Sinergia de teclados digitales






![{\displaystyle {\begin{aligned}y(t)&={\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }\left[a_{k}\cos(2\pi kf_{0}t)-b_{k}\sin(2\pi kf_{0}t)\right]\\&={\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }r_{k}\cos \left(2\pi kf_{0}t+\phi _{k}\right)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/522ace082a6d8990934113a639987f09a885cf02)





















![{\displaystyle y[n]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e73a8042c0d1a4c5d264982972d2ef33eda55e34)






![{\displaystyle {\begin{aligned}y[n]&=y(nT)=\sum _{k=1}^{K}r_{k}(nT)\cos \left(2\pi \int _{0}^{nT}f_{k}(u)\ du+\phi _{k}\right)\\&=\sum _{k=1}^{K}r_{k}(nT)\cos \left(2\pi \sum _{i=1}^{n}\int _{(i-1)T}^{iT}f_{k}(u)\ du+\phi _{k}\right)\\&=\sum _{k=1}^{K}r_{k}(nT)\cos \left(2\pi \sum _{i=1}^{n}(Tf_{k}[i])+\phi _{k}\right)\\&=\sum _{k=1}^{K}r_{k}[n]\cos \left({\frac {2\pi }{f_{\mathrm {s} }}}\sum _{i=1}^{n}f_{k}[i]+\phi _{k}\right)\\\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/235e423ed6dcd7564ba02d91eee3b6a012e84ce4)
![{\displaystyle r_{k}[n]=r_{k}(nT)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a91ccc3b0935394fad361cdc119c27a51b0c278)
![{\displaystyle f_{k}[n]={\frac {1}{T}}\int _{(n-1)T}^{nT}f_{k}(t)\ dt\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1043b3eaee212fedc8c9c8d408aad44dce3c4af1)
![{\displaystyle y[n]=\sum _{k=1}^{K}r_{k}[n]\cos \left(\theta _{k}[n]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbce88acb5e1e6a4ef32dd0be9bd49b78325a7de)
![{\displaystyle {\begin{alineado}\theta _ {k}[n]&={\frac {2\pi }{f_{\mathrm {s} }}}\sum _ {i=1}^{n }f_{k}[i]+\phi _{k}\\&=\theta _{k}[n-1]+{\frac {2\pi }{f_{\mathrm {s} }}} f_{k}[n]\\\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9b7b0acccac5e1f4c4d5739654caf234277411e)

![{\displaystyle \theta _ {k}[0]=\phi _ {k}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea1d7745c11e8890b24efb6c72f8c5a320d8b27e)