Símbolo de Schläfli

En geometría , el símbolo de Schläfli es una notación de la forma que define politopos y teselaciones regulares .${\displaystyle \{p,q,r,...\}}$

El símbolo de Schläfli debe su nombre al matemático suizo del siglo XIX Ludwig Schläfli , ^{[1] : 143} quien generalizó la geometría euclidiana a más de tres dimensiones y descubrió todos sus politopos regulares convexos, incluidos los seis que existen en cuatro dimensiones.

El símbolo de Schläfli es una descripción recursiva , ^{[1] : 129} que comienza con { p } para un polígono regular de p lados que es convexo . Por ejemplo, {3} es un triángulo equilátero , {4} es un cuadrado , {5} un pentágono regular convexo , etc.

Los polígonos regulares estrellados no son convexos, y sus símbolos de Schläfli { ^p / _q } contienen fracciones irreducibles ^p / _q , donde p es el número de vértices, y q es su número de giro . De manera equivalente, { ^p / _q } se crea a partir de los vértices de { p }, conectados cada q . Por ejemplo, { 5 ⁄ 2 } es un pentagrama ; { 5 ⁄ 1 } es un pentágono .

Un poliedro regular que tiene q caras poligonales regulares de p lados alrededor de cada vértice se representa mediante { p , q }. Por ejemplo, el cubo tiene 3 cuadrados alrededor de cada vértice y se representa mediante { 4,3}.

Un politopo regular de 4 dimensiones , con r { p , q } celdas poliédricas regulares alrededor de cada arista, se representa mediante { p , q , r }. Por ejemplo, un teseracto , {4,3,3}, tiene 3 cubos , {4,3}, alrededor de una arista.

En general, un politopo regular { p , q , r ,..., y , z } tiene z { p , q , r ,..., y } facetas alrededor de cada pico , donde un pico es un vértice en un poliedro, una arista en un 4-politopo, una cara en un 5-politopo y una ( n -3)-cara en un n -politopo.

Un politopo regular tiene una figura de vértice regular . La figura de vértice de un politopo regular { p , q , r ,..., y , z } es { q , r ,..., y , z }.

Los politopos regulares pueden tener elementos poligonales en forma de estrella , como el pentagrama , con símbolo { 5 ⁄ 2 }, representado por los vértices de un pentágono pero conectados alternativamente.

El símbolo de Schläfli puede representar un poliedro convexo finito , una teselación infinita del espacio euclidiano o una teselación infinita del espacio hiperbólico , dependiendo del defecto angular de la construcción. Un defecto angular positivo permite que la figura del vértice se pliegue en una dimensión superior y se enrolle sobre sí misma como un politopo. Un defecto angular cero tesela el espacio de la misma dimensión que las facetas. Un defecto angular negativo no puede existir en el espacio ordinario, pero puede construirse en el espacio hiperbólico.

Generalmente se supone que una faceta o una figura de vértice es un politopo finito, pero a veces puede considerarse en sí misma una teselación.

Un politopo regular también tiene un politopo dual, representado por los elementos del símbolo de Schläfli en orden inverso. Un politopo regular autodual tendrá un símbolo de Schläfli simétrico.

Además de describir politopos euclidianos, los símbolos de Schläfli se pueden utilizar para describir politopos esféricos o panales esféricos. ^{[1] : 138}

El trabajo de Schläfli era casi desconocido durante su vida, y su notación para describir politopos fue redescubierta independientemente por varios otros. En particular, Thorold Gosset redescubrió el símbolo de Schläfli, que escribió como | p | q | r | ... | z | en lugar de con corchetes y comas como lo hizo Schläfli. ^{[1] : 144}          

La forma de Gosset tiene mayor simetría, por lo que el número de dimensiones es el número de barras verticales y el símbolo incluye exactamente los subsímbolos de la figura de la faceta y del vértice. Gosset consideró a | p como un operador, que se puede aplicar a | q | ... | z | para producir un politopo con caras p -gonales cuya figura del vértice es | q | ... | z |.             

Los símbolos de Schläfli están estrechamente relacionados con los grupos de simetría de reflexión (finitos) , que corresponden precisamente a los grupos de Coxeter finitos y se especifican con los mismos índices, pero entre corchetes [ p , q , r ,...]. Dichos grupos suelen nombrarse por los politopos regulares que generan. Por ejemplo, [3,3] es el grupo de Coxeter para la simetría tetraédrica reflexiva , [3,4] es la simetría octaédrica reflexiva y [3,5] es la simetría icosaédrica reflexiva .

El símbolo de Schläfli de un polígono regular convexo con p aristas es { p }. Por ejemplo, un pentágono regular se representa con {5}.

Para polígonos estelares no convexos, se utiliza la notación constructiva { p ⁄ q }, donde p es el número de vértices y q −1 es el número de vértices que se omiten al dibujar cada arista de la estrella. Por ejemplo, { 5 ⁄ 2 } representa el pentagrama .

El símbolo de Schläfli de un poliedro regular es { p , q } si sus caras son p -gonos y cada vértice está rodeado por q caras (la figura del vértice es un q -gono).

Por ejemplo, {5,3} es el dodecaedro regular . Tiene caras pentagonales (5 aristas) y 3 pentágonos alrededor de cada vértice.

Vea los cinco sólidos platónicos convexos y los cuatro poliedros de Kepler-Poinsot no convexos .

Topológicamente, una teselación regular bidimensional puede considerarse similar a un poliedro (tridimensional), pero tal que el defecto angular es cero. Por lo tanto, los símbolos de Schläfli también pueden definirse para teselaciones regulares del espacio euclidiano o hiperbólico de manera similar a como se hace para los poliedros. La analogía es válida para dimensiones superiores.

Por ejemplo, el mosaico hexagonal está representado por {6,3}.

El símbolo de Schläfli de un 4-politopo regular tiene la forma { p , q , r }. Sus caras (bidimensionales) son p -gonos regulares ({ p }), las celdas son poliedros regulares de tipo { p , q }, las figuras de vértice son poliedros regulares de tipo { q , r } y las figuras de arista son r -gonos regulares (tipo { r }).

Vea los seis politopos convexos regulares y los diez politopos estelares regulares .

Por ejemplo, el modelo de 120 celdas está representado por {5,3,3}. Está formado por celdas dodecaédricas {5,3} y tiene 3 celdas alrededor de cada borde.

Hay una teselación regular del espacio tridimensional euclidiano: el panal cúbico , con un símbolo de Schläfli de {4,3,4}, hecho de celdas cúbicas y 4 cubos alrededor de cada borde.

También hay cuatro teselaciones hiperbólicas compactas regulares, entre ellas {5,3,4}, el pequeño panal dodecaédrico hiperbólico , que llena el espacio con celdas dodecaédricas .

Si el símbolo de un 4-politopo es palindrómico (por ejemplo, {3,3,3} o {3,4,3}), su truncamiento de bits solo tendrá formas truncadas de la figura del vértice como celdas.

Para politopos regulares de dimensiones superiores , el símbolo de Schläfli se define recursivamente como { p ₁ , p ₂ , ..., p _{n − 1} } si las facetas tienen el símbolo de Schläfli { p ₁ , p ₂ , ..., p _{n − 2} } y las figuras de vértice tienen el símbolo de Schläfli { p ₂ , p ₃ , ..., p _{n − 1} } .

Una figura de vértice de una faceta de un politopo y una faceta de una figura de vértice del mismo politopo son iguales: { p ₂ , p ₃ , ..., p _{n − 2} } .

Solo hay 3 politopos regulares de 5 dimensiones o más: el símplex , {3, 3, 3, ..., 3}; el politopo cruzado , {3, 3, ..., 3, 4}; y el hipercubo , {4, 3, 3, ..., 3}. No hay politopos regulares no convexos de más de 4 dimensiones.

Si un politopo de dimensión n  ≥  2 tiene símbolo de Schläfli { p ₁ , p ₂ , ..., p _{n − 1} } entonces su dual tiene símbolo de Schläfli { p _{n − 1} , ..., p ₂ , p ₁ }.  

Si la sucesión es palindrómica , es decir, la misma hacia delante y hacia atrás, el politopo es autodual . Todo politopo regular en 2 dimensiones (polígono) es autodual.

Los politopos prismáticos uniformes pueden definirse y nombrarse como un producto cartesiano (con el operador "×") de politopos regulares de menor dimensión.

• En 0D, un punto se representa mediante ( ). Su diagrama de Coxeter está vacío. Su simetría en notación de Coxeter es ][.
• En 1D, un segmento de línea se representa mediante { }. Su diagrama de Coxeter esSu simetría es [ ].
• En 2D, un rectángulo se representa como { } × { }. Su diagrama de Coxeter esSu simetría es [2].
• En 3D, un prisma p -gonal se representa como { } × { p }. Su diagrama de Coxeter esSu simetría es [2, p ].
• En 4D, un prisma édrico uniforme { p , q } se representa como { } × { p , q }. Su diagrama de Coxeter esSu simetría es [2, p , q ].
• En 4D, un duoprisma uniforme p - q se representa como { p } × { q }. Su diagrama de Coxeter esSu simetría es [ p ,2, q ].

Los duales prismáticos, o bipirámides, pueden representarse como símbolos compuestos, pero con el operador de adición , "+".

• En 2D, un rombo se representa como { } + { }. Su diagrama de Coxeter esSu simetría es [2].
• En 3D, una bipirámide p -gonal se representa como { } + { p }. Su diagrama de Coxeter esSu simetría es [2, p ].
• En 4D, una bipirámide { p , q } -édrica se representa como { } + { p , q }. Su diagrama de Coxeter esSu simetría es [ p , q ].
• En 4D, una duopirámide p - q se representa como { p } + { q }. Su diagrama de Coxeter esSu simetría es [ p ,2, q ].

Los politopos piramidales que contienen vértices desplazados ortogonalmente se pueden representar mediante un operador de unión, "∨". Cada par de vértices entre figuras unidas está conectado por aristas.

En 2D, un triángulo isósceles se puede representar como ( ) ∨ { } = ( ) ∨ [( ) ∨ ( )].

En 3D:

• Un disfenoide digonal se puede representar como { } ∨ { } = [( ) ∨ ( )] ∨ [( ) ∨ ( )].
• Una pirámide p-gonal se representa como ( ) ∨ { p }.

En 4D:

• Una pirámide pq-édrica se representa como ( ) ∨ { p , q }.
• Una celda de 5 se representa como ( ) ∨ [( ) ∨ {3}] o [( ) ∨ ( )] ∨ {3} = { } ∨ {3}.
• Una pirámide cuadrada se representa como ( ) ∨ [( ) ∨ {4}] o [( ) ∨ ( )] ∨ {4} = { } ∨ {4}.

Al mezclar operadores, el orden de las operaciones de mayor a menor es ×, +, ∨.

Los politopos axiales que contienen vértices en hiperplanos paralelos desplazados se pueden representar mediante el operador ‖. Un prisma uniforme es { n }‖{ n } y un antiprisma { n }‖ r { n }.

Un polígono regular truncado duplica sus lados. Un polígono regular con lados pares se puede dividir en dos. Un polígono regular 2n modificado con lados pares genera un compuesto de figura de estrella , 2{n}.

Forma	Símbolo de Schläfli	Simetría	Diagrama de Coxeter		Ejemplo, {6}
Regular	{pags}	[pag]				Hexágono
Truncado	t{p} = {2p}	[[p]] = [2p]	=			Hexágono truncado (dodecágono)	=
Alterado y holodesnudado	a{2p} = β{p}	[2pág.]	=			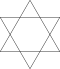Hexágono alterado (Hexagrama)	=
Mitad y desairado	h{2p} = s{p} = {p}	[1 + ,2p] = [p]	==			Medio hexágono (triángulo)	==

Coxeter amplió su uso del símbolo de Schläfli a los poliedros cuasirregulares añadiendo una dimensión vertical al símbolo. Fue un punto de partida hacia el diagrama de Coxeter más general . Norman Johnson simplificó la notación para los símbolos verticales con un prefijo r . La notación t es la más general y corresponde directamente a los anillos del diagrama de Coxeter. Los símbolos tienen una alternancia correspondiente , que reemplaza los anillos con agujeros en un diagrama de Coxeter y el prefijo h que representa la mitad , construcción limitada por el requisito de que las ramas vecinas deben ser de orden par y corta el orden de simetría a la mitad. Un operador relacionado, a para alterado , se muestra con dos agujeros anidados, representa un poliedro compuesto con ambas mitades alternadas, conservando la simetría completa original. Un snub es una forma de la mitad de un truncamiento, y un holosnub son ambas mitades de un truncamiento alternado.

Forma	Símbolos de Schläfli			Simetría	Diagrama de Coxeter		Ejemplo, {4,3}
Regular	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	{p,q}	t 0 {p,q}	[p,q] o [(p,q,2)]				Cubo
Truncado	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$	t{p,q}	t 0,1 {p,q}					Cubo truncado
Bittruncamiento (dual truncado)	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	2t{p,q}	t1,2 { p,q}					Octaedro truncado
Rectificado ( cuasirregular )	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	r{p,q}	t1 {p , q}					Cuboctaedro
Birectificación (Dual regular)	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	2r{p,q}	t2 {p , q}					Octaedro
Cantellado ( rectificado rectificado )	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	rr{p,q}	t 0,2 {p,q}					Rombicuboctaedro
Cantitruncado (Truncado rectificado)	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	tr{p,q}	t 0,1,2 {p,q}					Cuboctaedro truncado

Las alternancias tienen la mitad de simetría que los grupos de Coxeter y se representan mediante anillos vacíos. Hay dos opciones posibles en las que se toman la mitad de los vértices, pero el símbolo no indica cuál de ellas. Las formas de cuarto se muestran aquí con un + dentro de un anillo vacío para indicar que son dos alternancias independientes.

Alternancias

Forma	Símbolos de Schläfli			Simetría	Diagrama de Coxeter		Ejemplo, {4,3}
Regular alternado (medio)	${\displaystyle h{\begin{Bmatrix}2p,q\end{Bmatrix}}}$	h{2p,q}	alto 0 {2p,q}	[1 + ,2p,q]	=			Demicubo ( tetraedro )
Desaire regular	${\displaystyle s{\begin{Bmatrix}p,2q\end{Bmatrix}}}$	s{p,2q}	alto 0,1 {p,2q}	[p + ,2q]
Doble snub regular	${\displaystyle s{\begin{Bmatrix}q,2p\end{Bmatrix}}}$	s{q,2p}	alto 1,2 {2p,q}	[2p,q + ]				Octaedro romo ( icosaedro )
Rectificado alternado (p y q son pares)	${\displaystyle h{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	hr{p,q}	alto 1 {p,q}	[p,1 + ,q]
Rectificado alternado rectificado (p y q son pares)	${\displaystyle hr{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	hrr{p,q}	alto 0,2 {p,q}	[(p,q,2 + )]
Cuarteado (p y q son pares)	${\displaystyle q{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	q{p,q}	alto 0 alto 2 {p,q}	[1 + ,p,q,1 + ]
Desviado rectificado Desviado cuasirregular	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	sr{p,q}	alto 0,1,2 {p,q}	[p,q] +				Cuboctaedro romo (cubo romo)

Las formas alteradas y holocromadas tienen la simetría completa del grupo de Coxeter y están representadas por anillos dobles sin relleno, pero pueden representarse como compuestos.

Alterado y holodesnudado

Forma	Símbolos de Schläfli			Simetría	Diagrama de Coxeter		Ejemplo, {4,3}
Regular alterado	${\displaystyle a{\begin{Bmatrix}p,q\end{Bmatrix}}}$	a{p,q}	a las 0 {p,q}	[p,q]	=∪	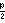		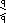Octaedro estrellado
Holosnub doble regular	ß{ q , p }	ß{q,p}	a las 0,1 {q,p}	[p,q]				Compuesto de dos icosaedros

ß , similar a la letra griega beta (β), es la letra eszett del alfabeto alemán .

Familias lineales

Forma	Símbolo de Schläfli			Diagrama de Coxeter		Ejemplo, {4,3,3}
Regular	${\displaystyle {\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	{p,q,r}	t 0 {p, q, r}				Teseracto
Truncado	${\displaystyle t{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	t{p,q,r}	t 0,1 {p,q,r}				Teseracto truncado
Rectificado	${\displaystyle \left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	r{p,q,r}	t1 {p,q,r }				Teseracto rectificado	=
Bittruncado		2t{p,q,r}	t 1,2 {p,q,r}				Teseracto bitruncado
Birectificado (Rectificado dual)	${\displaystyle \left\{{\begin{array}{l}q,p\\r\end{array}}\right\}}$	2r{p,q,r} = r{r,q,p}	t2 {p, q ,r}				Rectificado de 16 celdas	=
Tritruncado (dual truncado)	${\displaystyle t{\begin{Bmatrix}r,q,p\end{Bmatrix}}}$	3t{p,q,r} = t{r,q,p}	t2,3 {p, q ,r}				Teseracto bitruncado
Trirectificado (doble)	${\displaystyle {\begin{Bmatrix}r,q,p\end{Bmatrix}}}$	3r{p,q,r} = {r,q,p}	t 3 {p, q, r} = {r, q, p}				16 celdas
Cantelado	${\displaystyle r\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	rr{p,q,r}	t 0,2 {p,q,r}				Teseracto cantelado	=
Cantitruncado	${\displaystyle t\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	tr{p,q,r}	t 0,1,2 {p,q,r}				Teseracto cantitruncado	=
Runcinated ( Expandido )	${\displaystyle e_{3}{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	y 3 {p,q,r}	t 0,3 {p,q,r}				Teseracto runcinado
Runcitruncado			t 0,1,3 {p,q,r}				Teseracto runcitruncado
Omnitruncado			t 0,1,2,3 {p,q,r}				Teseracto omnitruncado

Alternancias

Forma	Símbolo de Schläfli			Diagrama de Coxeter		Ejemplo, {4,3,3}
Alternancias
La mitad de p par	${\displaystyle h{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	h{p,q,r}	alto 0 {p,q,r}				16 celdas
Cuarto p y r par	${\displaystyle q{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	q{p,q,r}	alto 0 alto 3 {p,q,r}
Desaire q incluso	${\displaystyle s{\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	s{p,q,r}	alto 0,1 {p,q,r}				Batería de 24 celdas de tamaño pequeño
Snub rectificado r incluso	${\displaystyle s\left\{{\begin{array}{l}p\\q,r\end{array}}\right\}}$	sr{p,q,r}	alto 0,1,2 {p,q,r}				Batería de 24 celdas de tamaño pequeño	=
Duoprisma alternado		s{p}s{q}	alto 0,1,2,3 {p,2,q}				Gran duoantiprisma

Familias bifurcadas

Forma	Símbolo Schläfli extendido			Diagrama de Coxeter		Ejemplos
Cuasiregular	${\displaystyle \left\{p,{q \atop q}\right\}}$	{p,q 1,1 }	t 0 {p,q 1,1 }				Demitesseract ( 16 celdas )
Truncado	${\displaystyle t\left\{p,{q \atop q}\right\}}$	t{p,q 1,1 }	t 0,1 {p,q 1,1 }				Demitesseract truncado ( 16 celdas truncadas )
Rectificado	${\displaystyle \left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	r{p,q 1,1 }	t 1 {p, q 1,1 }				Demitesseract rectificado ( 24 celdas )
Cantelado	${\displaystyle r\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	rr{p,q 1,1 }	t 0,2,3 {p,q 1,1 }				Demitesseract cantelado ( cantelado de 16 celdas )
Cantitruncado	${\displaystyle t\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	tr{p,q 1,1 }	t 0,1,2,3 {p,q 1,1 }				Demitesseract cantitruncado ( cantitruncado de 16 células )
Snub rectificado	${\displaystyle s\left\{{\begin{array}{l}p\\q\\q\end{array}}\right\}}$	sr{p,q 1,1 }	alto 0,1,2,3 {p,q 1,1 }				Cañón demitesseract de 24 celdas ( de 24 celdas )
Cuasiregular	${\displaystyle \left\{r,{p \atop q}\right\}}$	{r,/q\,p}	t 0 {r,/q\,p}				Panal tetraédrico-octaédrico
Truncado	${\displaystyle t\left\{r,{p \atop q}\right\}}$	t{r,/q\,p}	t 0,1 {r,/q\,p}				Panal tetraédrico-octaédrico truncado
Rectificado	${\displaystyle \left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}}$	r{r,/q\,p}	t 1 {r,/q\,p}				Panal tetraédrico-octaédrico rectificado (panal cúbico rectificado)
Cantelado	${\displaystyle r\left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}}$	rr{r,/q\,p}	t 0,2,3 {r,/q\,p}				Panal cúbico cantelado
Cantitruncado	${\displaystyle t\left\{{\begin{array}{l}r\\p\\q\end{array}}\right\}}$	tr{r,/q\,p}	t 0,1,2,3 {r,/q\,p}				Panal cúbico truncado cantimplora
Snub rectificado	${\displaystyle s\left\{{\begin{array}{l}p\\q\\r\end{array}}\right\}}$	sr{p,/q,\r}	alto 0,1,2,3 {p,/q\,r}				Panal cúbico rectificado de snub (no uniforme, pero casi fallido)

Esférico

Regular

Semi-regular

Hiperbólico

• Coxeter, Harold Scott MacDonald (1973) [1948]. Politopos regulares (3.ª ed.). Dover Publications. págs. 14, 69, 149. ISBN 0-486-61480-8. OCLC  798003. Politopos regulares.
• Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Caleidoscopios: escritos selectos de HSM Coxeter . Wiley. ISBN 978-0-471-01003-6.
  • (Artículo 22) págs. 251–278 Coxeter, HSM (1940). "Polítopos regulares y semirregulares I". Math. Zeit . 46 : 380–407. doi :10.1007/BF01181449. S2CID  186237114. Zbl  0022.38305.Sr. 2,10
  • (Artículo 23) págs. 279–312 — (1985). "Polítopos regulares y semirregulares II". Math. Zeit . 188 (4): 559–591. doi :10.1007/BF01161657. S2CID  120429557. Zbl  0547.52005.
  • (Artículo 24) págs. 313–358 — (1988). "Polítopos regulares y semirregulares III". Math. Zeit . 200 (1): 3–45. doi :10.1007/BF01161745. S2CID  186237142. Zbl  0633.52006.

• Weisstein, Eric W. "Símbolo de Schläfli". MundoMatemático . Consultado el 28 de diciembre de 2019 .
• Starck, Maurice (13 de abril de 2012). "Nombres y notaciones de poliedros". Un paseo por el mundo de los poliedros . Consultado el 28 de diciembre de 2019 .