Tetracordio
Series of four notes separated by three intervals

En teoría musical , un tetracordio ( griego : τετράχορδoν ; latín : tetrachordum ) es una serie de cuatro notas separadas por tres intervalos . En la teoría musical tradicional, un tetracordio siempre abarcaba el intervalo de una cuarta perfecta , una proporción de frecuencia de 4:3 (aproximadamente 498 centésimas ), pero en el uso moderno significa cualquier segmento de cuatro notas de una escala o fila de tonos , no necesariamente relacionado con un sistema de afinación en particular.

Historia

El nombre proviene de tetra (del griego, "cuatro de algo") y acorde (del griego chordon , "cuerda" o "nota"). En la teoría musical griega antigua, tetracordio significaba un segmento de los sistemas mayor y menor perfectos delimitados por notas inamovibles ( griego : ἑστῶτες ); las notas entre estos eran móviles ( griego : κινούμενοι ). Literalmente significa cuatro cuerdas , originalmente en referencia a instrumentos similares al arpa como la lira o la cítara, con el entendimiento implícito de que las cuatro cuerdas producían notas adyacentes (es decir, conjuntas).

La teoría musical moderna utiliza la octava como unidad básica para determinar la afinación, mientras que los antiguos griegos utilizaban el tetracordio. Los teóricos de la antigua Grecia reconocían que la octava es un intervalo fundamental, pero la consideraban formada por dos tetracordios y un tono entero . [1]

Teoría musical de la antigua Grecia

La teoría musical griega antigua distingue tres géneros (singular: género ) de tetracordios. Estos géneros se caracterizan por el mayor de los tres intervalos del tetracordio:

Diatónico
Un tetracordio diatónico tiene un intervalo característico que es menor o igual a la mitad del intervalo total del tetracordio (o aproximadamente 249  centésimas ). Este intervalo característico suele ser ligeramente menor (aproximadamente 200 centésimas), convirtiéndose en un tono entero . Clásicamente, el tetracordio diatónico consta de dos intervalos de un tono y uno de un semitono , p. ej. A–G–F–E.
Cromático
Un tetracordio cromático tiene un intervalo característico que es mayor que aproximadamente la mitad del intervalo total del tetracordio, pero no tan grande como cuatro quintos del intervalo (entre aproximadamente 249 y 398 centésimas). Clásicamente, el intervalo característico es una tercera menor (aproximadamente 300 centésimas), y los dos intervalos más pequeños son semitonos iguales, por ejemplo, A–G ♭ –F–E.
Enarmónico
Dos tetracordios griegos en el género enarmónico, formando una escala dórica enarmónica
Un tetracordio enarmónico tiene un intervalo característico que es mayor que aproximadamente cuatro quintas partes del intervalo total del tetracordio. Clásicamente, el intervalo característico es un ditono o una tercera mayor , [2] y los dos intervalos más pequeños son cuartos de tono , p. ej. A–Gdoble piso-Fmedio plano-MI.

Cuando la composición de los dos intervalos más pequeños es menor que el intervalo restante ( incompuesto ), el grupo de tres notas se denomina pyknón (de pyknós , que significa "comprimido"). Este es el caso de los tetracordios cromáticos y enarmónicos, pero no del tetracordio diatónico (que significa "estirado").

Cualquiera que sea la afinación del tetracordio, sus cuatro grados se denominan, en orden ascendente, hipato , parhipato , lichanos (o hipermesa ) y mese y, para el segundo tetracordio en la construcción del sistema, paramesa , trita , paraneta y neta . El hipato y la mese , y el paramesa y la neta son fijos, y separados por una cuarta perfecta, mientras que la posición del parhipato y el lichanos , o trita y paraneta , son móviles.

Como los tres géneros simplemente representan rangos de intervalos posibles dentro del tetracordio, se especificaron varios tonos ( chroai ) con afinaciones específicas. Una vez que se especifican el género y el tono del tetracordio, su disposición puede producir tres tipos principales de escalas, dependiendo de qué nota del tetracordio se tome como la primera nota de la escala. Los tetracordios en sí mismos permanecen independientes de las escalas que producen, y los teóricos griegos nunca los nombraron en base a estas escalas. [3]

Escala dórica
La primera nota del tetracordio es también la primera nota de la escala.
Diatónica: Mi–Re–Do–Si | La–Sol–Fa–Mi
Cromática: Mi–Re ♭ –Do–Si | La–Sol ♭ –Fa–Mi
Enarmónico: E–Ddoble piso-DOmedio plano–B │ A–Gdoble piso-Fmedio plano-MI
Escala frigia
La segunda nota del tetracordio (en orden descendente) es la primera de la escala.
Diatónica: D–C–B | A–G–F–E | D
Cromática: Re ♭ –Do–Si | La–Sol ♭ –Fa–Mi | Re ♭
Enarmónico: Ddoble piso-DOmedio plano–B | A–Gdoble piso-Fmedio plano–Mi | Redoble piso
Escala lidia
La tercera nota del tetracordio (en orden descendente) es la primera de la escala.
Diatónica: C–B | A–G–F–E | D–C
Cromática: C–B | A–G ♭ –F–E | D ♭ –C
Enarmónico: Cmedio plano–B | A–Gdoble piso-Fmedio plano–Mi | Redoble piso-DOmedio plano

En todos los casos, las notas extremas de los tetracordios, Mi – Si y La – Mi, permanecen fijas, mientras que las notas intermedias son diferentes según el género.

Afinaciones pitagóricas

Aquí están las afinaciones pitagóricas tradicionales de los tetracordios diatónicos y cromáticos:

Diatónico
Hipar   parhipar         licanos         mes
⁠4/3⁠⁠81/64⁠⁠9/8⁠⁠1/1⁠
│⁠256/243⁠│⁠9/8⁠│⁠9/8⁠│
−498 ¢−408 ¢−204 ¢0 ¢
Afinación pitagórica del tetracordio diatónico
¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .
Cromático
Hipar   parhipar   licanos             mes
⁠4/3⁠⁠81/64⁠⁠32/27⁠⁠1/1⁠
│⁠256/243⁠│⁠2187/2048⁠│⁠32/27⁠│
−498 ¢−408 ¢−294 ¢0 ¢
Afinación pitagórica del tetracordio cromático

He aquí una afinación pitagórica representativa del género enarmónico atribuido a Arquitas :

Enarmónico
Hiparparhiparlicanos                 mes
⁠4/3⁠⁠9/7⁠⁠5/4⁠⁠1/1⁠
│⁠28/27⁠│⁠36/35⁠│⁠5/4⁠│
−498 ¢−435 ¢−386 ¢0 ¢
Afinación pitagórica del tetracordio enarmónico

El número de cuerdas de la lira clásica variaba en diferentes épocas y posiblemente en diferentes localidades: cuatro, siete y diez eran los números favoritos. Las escalas más grandes se construyen a partir de tetracordios conjuntos o disyuntos. Los tetracordios conjuntos comparten una nota, mientras que los tetracordios disyuntos están separados por un tono disyuntivo de 9/8 (una segunda mayor pitagórica). La alternancia de tetracordios conjuntos y disyuntos forma una escala que se repite en octavas (como en la conocida escala diatónica , creada de esa manera a partir del género diatónico), pero este no era el único arreglo.

Los griegos analizaban los géneros utilizando diversos términos, entre ellos, diatónico, enarmónico y cromático. Las escalas se construyen a partir de tetracordios conjuntos o disjuntos.

Tetracordio cromático de Dídimo4:3(6:5)10:9(25:24)16:15(16:15)1:1
El tetracordio cromático de Eratóstenes4:3(6:5)10:9(19:18)20:19(20:19)1:1
El suave cromatismo de Ptolomeo4:3(6:5)10:9(15:14)28:27(28:27)1:1
El intenso cromatismo de Ptolomeo4:3(7:6)8:7(12:11)22:21(22:21)1:1
El enarmónico de Arquitas4:3(5:4)9:7(36:35)28:27(28:27)1:1

Esta es una tabla parcial de las divisiones superparticulares de Chalmers según Hofmann. [ ¿quién? ] [4]

Variaciones

Era romántica

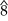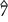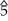Tetracordio descendente en el locrio si moderno (también conocido como tetracordio menor superior):grado de escala 8– ♭Grado de escala 7– ♭grado de escala 6– ♭grado de escala 5(b–a–g–f). Este tetracordio abarca un tritono en lugar de una cuarta perfecta.
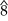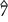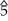La progresión frigia crea un tetracordio descendente [5] [¿ fuente poco confiable? ] línea de bajo : grado de escala 8– ♭Grado de escala 7– ♭grado de escala 6–grado de escala 5. Media cadencia frigia : i–v6–iv6–V en do menor (línea de bajo: do–si ♭ –la ♭ –sol)

Los tetracordios basados ​​en la afinación de temperamento igual se utilizaron para explicar las escalas heptatónicas comunes . Dado el siguiente vocabulario de tetracordios (los dígitos indican el número de semitonos en intervalos consecutivos del tetracordio, sumando cinco):

TetracordioCuerda de medio paso
Importante2 2 1
Menor2 1 2
Armónico1 3 1
Menor superior1 2 2

Las siguientes escalas podrían derivarse uniendo dos tetracordios con un tono entero (2) entre ellos: [6] [7]

Tetracordios componentesCuerda de medio pasoEscala resultante
Mayor + mayor2 2 1 : 2 : 2 2 1Diatónica mayor
Menor + menor superior2 1 2 : 2 : 1 2 2Menor natural
Mayor + armónico2 2 1 : 2 : 1 3 1Armónica mayor
Menor + armónico2 1 2 : 2 : 1 3 1Menor armónico
Armónico + armónico1 3 1 : 2 : 1 3 1Escala armónica doble [8] [9] o gitana mayor [10]
Mayor + menor superior2 2 1 : 2 : 1 2 2Mayor melódico
Menor + mayor2 1 2 : 2 : 2 2 1Menor melódica
Menor superior + armónico1 2 2 : 2 : 1 3 1Menor napolitano

Todas estas escalas están formadas por dos tetracordios completamente disjuntos: contrariamente a la teoría griega y medieval, los tetracordios cambian aquí de escala a escala (es decir, el tetracordio de do mayor sería do-re-mi-fa, el de re mayor re-mi-fa ♯ -sol, el de do menor do-re-mi ♭ -fa, etc.). Los teóricos de la música griega antigua del siglo XIX creían que esto también había sido así en la Antigüedad, e imaginaban que habían existido tetracordios dóricos, frigios o lidios. Esta idea errónea fue denunciada en la tesis de Otto Gombosi (1939). [11]

Análisis del siglo XX

Los teóricos de finales del siglo XX suelen utilizar el término "tetracordio" para describir cualquier conjunto de cuatro notas al analizar música de una variedad de estilos y períodos históricos. [12] La expresión "tetracordio cromático" puede utilizarse en dos sentidos diferentes: para describir el caso especial que consiste en un segmento de cuatro notas de la escala cromática, [13] o, en un contexto más orientado históricamente, para referirse a las seis notas cromáticas utilizadas para llenar el intervalo de una cuarta perfecta, que se encuentra normalmente en líneas de bajo descendentes. [14] También puede utilizarse para describir conjuntos de menos de cuatro notas, cuando se utilizan en forma de escala para abarcar el intervalo de una cuarta perfecta. [15]

Uso atonal

Allen Forte utiliza ocasionalmente el término tetracordio para referirse a lo que en otros lugares llama una tétrada o simplemente un "conjunto de 4 elementos": un conjunto de cuatro tonos o clases de tonos . [16] En la teoría de doce tonos , el término puede tener el sentido especial de cuatro notas consecutivas de una fila de doce tonos. [17]

Escalas no occidentales

Los tetracordios basados ​​en la afinación de temperamento igual también se utilizaron para aproximarse a las escalas heptatónicas comunes que se utilizan en la música india, húngara, árabe y griega. Los teóricos occidentales de los siglos XIX y XX, convencidos de que cualquier escala debería constar de dos tetracordios y un tono, describieron varias combinaciones que se suponía que correspondían a una variedad de escalas exóticas. Por ejemplo, los siguientes intervalos diatónicos de uno, dos o tres semitonos, que siempre suman cinco semitonos, producen 36 combinaciones cuando se unen mediante un tono entero : [18]

Tetracordios inferioresTetracordios superiores
3 1 13 1 1
2 2 12 2 1
1 3 11 3 1
2 1 22 1 2
1 2 21 2 2
1 1 31 1 3

Sistema de tetracordios específico de la India

También se dice que los tetracordios separados por un semitono aparecen particularmente en la música india. En este caso, el "tetracordio" más bajo suma un total de seis semitonos (un tritono). Los siguientes elementos producen 36 combinaciones cuando se unen por semitonos. [18] Estas 36 combinaciones, junto con las 36 combinaciones descritas anteriormente, producen los llamados "72 modos karnáticos". [19]

Tetracordios inferioresTetracordios superiores
3 2 13 1 1
3 1 22 2 1
2 2 21 3 1
1 3 22 1 2
2 1 31 2 2
1 2 31 1 3

persa

La música persa divide el intervalo de cuarta de forma diferente a la griega. Por ejemplo, Al-Farabi describe cuatro géneros de división de cuarta: [20]

  • El primer género, correspondiente al diatónico griego, está compuesto de un tono, un tono y un semitono, como G–A–B–C.
  • El segundo género se compone de un tono, tres cuartos de tono y tres cuartos de tono, como G–A–Bmedio plano-DO.
  • El tercer género tiene un tono y un cuarto, tres cuartos de tono y un semitono, como G–Amedio afilado-ANTES DE CRISTO.
  • El cuarto género, correspondiente al cromático griego, tiene un tono y medio, un semitono y un semitono, como G–A ♯ –B–C.

Continúa con otros cuatro géneros posibles “dividiendo el tono en cuartos, octavos, tercios, medios tercios, cuartos de tercio, y combinándolos de diversas maneras”. [21] Más adelante, presenta posibles posiciones de los trastes en el laúd, produciendo diez intervalos que dividen el intervalo de una cuarta entre las cuerdas: [22]

Relación:⁠1/1⁠⁠256/243⁠⁠18/17⁠⁠162/149⁠⁠54/49⁠⁠9/8⁠⁠32/27⁠⁠81/68⁠⁠27/22⁠⁠81/64⁠⁠4/3⁠
Nombre de la nota:doC ♯C ♯dotres cuartos en puntodotres cuartos en puntoDmi ♭mi ♭mimedio planomiF
Centavos :09099145168204294303355408498

Si se considera que el intervalo de una cuarta entre las cuerdas del laúd ( Oud ) corresponde a un tetracordio, y que hay dos tetracordios y un tono mayor en una octava, esto crearía una escala de 25 tonos. Una descripción más inclusiva (donde se superponen los otomanos, persas y árabes), de las divisiones de la escala es la de 24 cuartos de tono (véase también maqam árabe ). Cabe mencionar que Al-Farabi, entre otros tratados islámicos, también contenía esquemas de división adicionales, además de proporcionar una glosa del sistema griego, ya que las doctrinas aristoxénicas a menudo se incluían. [23]

Formas compositivas

El tetracordio, un fragmento fundamentalmente incompleto, es la base de dos formas compositivas construidas a partir de la repetición de ese fragmento: la queja y la letanía.

El tetracordio descendente de tónica a dominante, típicamente en menor (p. ej. A–G–F–E en la menor), se ha utilizado desde el Renacimiento para denotar una lamentación. Algunos casos bien conocidos incluyen el bajo ostinato del aria de Dido Cuando soy puesto en la tierra en Dido y Eneas de Henry Purcell , el Crucifixus en la Misa en si menor de Johann Sebastian Bach , BWV 232, o el Qui tollis en la Misa en do menor de Mozart , KV 427, etc. [24] Este tetracordio, conocido como lamento ("queja", "lamentación"), se ha utilizado hasta hoy. Una forma variante, el descenso cromático completo (p. ej. A–G ♯ –G–F ♯ –F–E en la menor), se ha conocido como Passus duriusculus en la Figurenlehre barroca . [ cita completa requerida ]

Existe una forma musical breve y libre de la era romántica , llamada queja o complainte (fr.) o lamento . [25] Se trata típicamente de un conjunto de variaciones armónicas en textura homofónica , en donde el bajo desciende a través de algún tetracordio, posiblemente el del párrafo anterior, pero generalmente uno que sugiere un modo menor . Este tetracordio, tratado como un bajo de fondo muy corto , se repite una y otra vez a lo largo de la composición.

Otra forma musical, del mismo período de tiempo, es la letanía o litanie (Fr.), o lytanie (OE spur). [26] También es un conjunto de variaciones armónicas en textura homofónica , pero en contraste con el lamento, aquí el fragmento tetracordal -ascendente o descendente y posiblemente reordenado- se establece en la voz superior a la manera de un preludio coral . Debido a la extrema brevedad del tema y el número de repeticiones requeridas, y libre de la vinculación de la progresión de acordes al tetracordio en el lamento, la amplitud de la excursión armónica en la letanía suele ser notable.

Véase también

Referencias

  1. ^ Mathiesen, Thomas J. (2001). "Grecia §I: Antigua". En Sadie, S. ; Tyrrell, J. (eds.). The New Grove Dictionary of Music and Musicians (segunda ed.). Londres, Reino Unido: Macmillan. 6 Teoría musical, (iii) Tradición aristoxeniana, (d) Escalas.
  2. ^ Chalmers 1993, pág. 8.
  3. ^ Chalmers 1993, pág. 103.
  4. ^ Chalmers 1993, pág. 11.
  5. ^ "Progresión frigia", Blog de música clásica . Archivado el 6 de octubre de 2011 en Wayback Machine.
  6. ^ Marcel Dupré, Cours Complet d'Improvisation a l'Orgue , 2 vols., traducido por John Fenstermaker. París: Alphonse Leduc, 1962, 2:35. ASIN: B0006CNH8E.
  7. ^ Joseph Schillinger , El sistema Schillinger de composición musical , 2 vols. (Nueva York: Carl Fischer, 1941), 1:112–114. ISBN 978-0306775215 . 
  8. ^ Joshua Craig Podolsky, Conceptos avanzados de guitarra líder (Pacific, Missouri: Mel Bay, 2010): 111. ISBN 978-0-7866-8236-2 . 
  9. ^ "Escala armónica doble y sus modos". docs.solfege.org . Archivado desde el original el 2015-06-18 . Consultado el 2015-04-12 .
  10. ^ Jonathan Bellman , El "estilo hongrois" en la música de Europa occidental (Boston: Northeastern University Press, 1993): 120. ISBN 1-55553-169-5 . 
  11. ^ Otto Johannes Gombosi, Tonarten und Stimmungen der Antiken Musik , Copenhague, Ejnar Munksgaard, 1939.
  12. ^ Benedict Taylor, "Modal Four-Note Pitch Collections in the Music of Dvořák 's American Period", Music Theory Spectrum 32, no. 1 (primavera de 2010): 44-59; Steven Block y Jack Douthett, " Vector Products and Intervallic Weighting", Journal of Music Theory 38, no. 1 (primavera de 1994): 21-41; Ian Quinn, "Listening to Similarity Relations", Perspectives of New Music 39, no. 2 (verano de 2001): 108-158; Joseph N. Straus, " Stravinsky 'Construction of Twelve Verticals': An Aspect of Harmony in the Serial Music", Music Theory Spectrum 21, no. 1 (primavera de 1999): 43-73; Tuire Kuusi, "Relación de clase de subconjunto, tonos comunes y estructura de intervalo común que guían las estimaciones de similitud", Music Perception 25, no. 1 (septiembre de 2007): 1–11; Joshua B. Mailman , "Un drama imaginado de oposición competitiva en Scrivo in Vento de Carter , con notas sobre narrativa, simetría, flujo cuantitativo y Heráclito", Music Analysis 28, no. 2/3 (julio–octubre de 2009): 373–422; John Harbison y Eleanor Cory , " Martin Boykan : Cuarteto de cuerdas (1967): dos puntos de vista", Perspectives of New Music 11, no. 2 (primavera–verano de 1973): 204–209; Milton Babbitt , " Edgard Varèse : Algunas observaciones sobre su música", Perspectivas de la nueva música 4, n.º 2 (primavera-verano de 1966): 14-22; Annie K. Yih, "Análisis de Debussy : tonalidad, conjuntos motívicos y la colección específica de la clase de tono referencial", Análisis musical 19, n.º 2 (julio de 2000): 203-229; J. K. Randall , " Composición para orquesta de Godfrey Winham ", Perspectivas de la nueva música 2, n.º 1 (otoño-invierno de 1963): 102-113.
  13. ^ Brent Auerbach, "Polifonía escalonada y su papel determinante en la música para piano de Johannes Brahms ", Journal of Music Theory 52, no. 2 (otoño de 2008): 273–320.
  14. ^ Robert Gauldin , "El tetracordio interrumpido de Beethoven y la Séptima sinfonía ", Integral 5 (1991): 77–100.
  15. ^ Nors S. Josephson, "Sobre algunos bocetos aparentes de la Octava Sinfonía de Sibelius ", Archiv für Musikwissenschaft 61, no. 1 (2004): 54–67.
  16. ^ Allen Forte (1973). The Structure of Atonal Music , págs. 1, 18, 68, 70, 73, 87, 88, 21, 119, 123, 124, 125, 138, 143, 171, 174 y 223. New Haven y Londres: Yale University Press. ISBN 0-300-01610-7 (en tela) ISBN 0-300-02120-8 (en papel). Allen Forte (1985). "Pitch-Class Set Analysis Today". Music Analysis 4, núms. 1 y 2 (marzo-julio: número especial: King's College London Music Analysis Conference 1984): 29-58, citas en 48-51, 53.  
  17. ^ Reynold Simpson, "Nuevos bocetos, viejos fragmentos y el Tercer Cuarteto de Cuerdas de Schoenberg, Op. 30", Teoría y Práctica 17, En Celebración de Arnold Schoenberg (1) (1992): 85–101.
  18. ^ ab Marcel Dupré, Cours Complet d'Improvisation a l'Orgue , 2 vols., traducido por John Fenstermaker (París: Alphonse Leduc, 1962): 2:35. ASIN: B0006CNH8E.
  19. ^ Joanny Grosset, "Inde. Histoire de la musique depuis l'origine jusqu'à nos jours", Encyclopédie de la musique et Dictionnaire du Conservatoire , vol. 1, París, Delagrave, 1914, pág. 325.
  20. ^ Al-Farabi 2001, págs. 56–57.
  21. ^ Al-Farabi 2001, pág. 58.
  22. ^ Al-Farabi 2001, págs. 165-179; Liberty Manik, Das Arabische Tonsystem im Mittelalter (Leiden, EJ Brill, 1969): 42; Habib Hassan Touma , La música de los árabes , traducida por Laurie Schwartz. (Portland, Oregón: Amadeus Press, 1996): 19. ISBN 0-931340-88-8 . 
  23. ^ Chalmers 1993, pág. 20.
  24. ^ Ellen Rosand, "El tetracordio descendente: un emblema del lamento", The Musical Quarterly 65, no. 3 (1979): 346–59.
  25. ^ Marcel Dupré, Cours complet d'improvisation a l'orgue: Exercices preparées , 2 vols., traducido por John Fenstermaker. París: Alphonse Leduc, 1937): 1:14.
  26. ^ Marcel Dupré, (1962). Cours complet d'improvisation a l'orgue , 2 vols., traducido por John Fenstermaker (París: Alphonse Leduc, 1962): 2:110.

Fuentes

  • Al-Farabi (2001) [1930]. Kitābu l-mūsīqī al-kabīr [ La musique arabe ] (reimpresión) (en francés). Traducido por Rodolphe d'Erlanger. París: Geuthner.
  • Chalmers, John H. Jr (1993). Larry Polansky ; Carter Scholz (eds.). Divisiones del tetracordio: un prolegómeno [introducción] a la construcción de escalas musicales. Prólogo de Lou Harrison . Hanover, New Hampshire: Frog Peak Music. ISBN 0-945996-04-7.

Lectura adicional

Retrieved from "https://en.wikipedia.org/w/index.php?title=Tetrachord&oldid=1252803039"