Teselación euclidiana mediante polígonos regulares convexos
 Un mosaico regular tiene un tipo de cara regular. |  Un mosaico semirregular o uniforme tiene un tipo de vértice , pero dos o más tipos de caras. |
 Un mosaico k-uniforme tiene k tipos de vértices y dos o más tipos de caras regulares. |  Un mosaico que no es de borde a borde puede tener caras regulares de diferentes tamaños. |
Las teselas euclidianas de polígonos regulares convexos se han utilizado ampliamente desde la antigüedad. El primer tratamiento matemático sistemático fue el de Kepler en su Harmonices Mundi ( en latín : La armonía del mundo , 1619).
Notación de teselas euclidianas
Los mosaicos euclidianos suelen recibir su nombre de acuerdo con la notación de Cundy y Rollett. [1] Esta notación representa (i) el número de vértices, (ii) el número de polígonos alrededor de cada vértice (ordenados en el sentido de las agujas del reloj) y (iii) el número de lados de cada uno de esos polígonos. Por ejemplo: 3 6 ; 3 6 ; 3 4 .6, nos dice que hay 3 vértices con 2 tipos de vértices diferentes, por lo que este mosaico se clasificaría como un mosaico "3-uniforme (2-tipos de vértices)". Desglosado, 3 6 ; 3 6 (ambos de diferente clase de transitividad), o (3 6 ) 2 , nos dice que hay 2 vértices (denotados por el superíndice 2), cada uno con 6 polígonos equiláteros de 3 lados (triángulos). Con un vértice final 3 4 .6, 4 triángulos equiláteros contiguos más y un único hexágono regular.
Sin embargo, esta notación tiene dos problemas principales relacionados con la conformación ambigua y la unicidad [2] En primer lugar, cuando se trata de teselaciones k-uniformes, la notación no explica las relaciones entre los vértices. Esto hace imposible generar un plano cubierto dada solo la notación. Y segundo, algunas teselaciones tienen la misma nomenclatura, son muy similares pero se puede notar que las posiciones relativas de los hexágonos son diferentes. Por lo tanto, el segundo problema es que esta nomenclatura no es única para cada teselación.
Para resolver estos problemas, la notación de GomJau-Hogg [3] es una versión ligeramente modificada de la investigación y notación presentada en 2012 [2] sobre la generación y nomenclatura de teselaciones y cuadrículas de doble capa. Antwerp v3.0 [4] , una aplicación en línea gratuita, permite la generación infinita de teselados de polígonos regulares a través de un conjunto de etapas de colocación de formas y operaciones iterativas de rotación y reflexión, obtenidas directamente de la notación de GomJau-Hogg.
Azulejos regulares
Siguiendo a Grünbaum y Shephard (sección 1.3), se dice que un mosaico es regular si el grupo de simetría del mosaico actúa transitivamente sobre las banderas del mosaico, donde una bandera es una terna que consiste en un vértice , una arista y una baldosa del mosaico mutuamente incidentes. Esto significa que, para cada par de banderas, hay una operación de simetría que mapea la primera bandera a la segunda. Esto es equivalente a que el mosaico sea un mosaico de arista con arista por polígonos regulares congruentes . Debe haber seis triángulos equiláteros , cuatro cuadrados o tres hexágonos regulares en un vértice, lo que produce las tres teselaciones regulares .
| p6m, *632 | p4m, *442 | |
|---|---|---|
 |  |  |
 C&R: 3 6 GJ-H: 3/m30/r(h2) ( t = 1, e = 1) |  C&R: 6 3 GJ-H: 6/m30/r(h1) ( t = 1, e = 1) |  C&R: 4 4 GJ-H: 4/m45/r(h1) ( t = 1, e = 1) |
C&R: Notación de Cundy y Rollet
GJ-H: Notación de GomJau-Hogg
Teselación arquimediana, uniforme o semirregular
La transitividad de vértices significa que para cada par de vértices hay una operación de simetría que asigna el primer vértice al segundo. [5]
Si el requisito de transitividad de banderas se relaja a uno de transitividad de vértices, mientras que la condición de que el teselado sea de borde a borde se mantiene, hay ocho teselados adicionales posibles, conocidos como teselados arquimedianos , uniformes o semirregulares . Tenga en cuenta que hay dos formas de imagen especular (enantiomórficas o quirales ) del teselado 3 4 .6 (hexagonal romo), solo una de las cuales se muestra en la siguiente tabla. Todos los demás teselados regulares y semirregulares son aquirales.
| p6m, *632 | |||||
|---|---|---|---|---|---|
  C&R: 3,12 2 GJ-H: 12-3/m30/r(h3) ( t = 2, e = 2) t {6,3} |   C&R: 3.4.6.4 GJ-H: 6-4-3/m30/r(c2) ( t = 3, e = 2) rr {3,6} |   C&R: 4.6.12 GJ-H: 12-6,4/m30/r(c2) ( t = 3, e = 3) tr {3,6} |   C&R: (3.6) 2 GJ-H: 6-3-6/m30/r(v4) ( t = 2, e = 1) r {6,3} | ||
  C&R: 4,8 2 GJ-H: 8-4/m90/r(h4) ( t = 2, e = 2) t {4,4} |   C&R: 3 2 .4.3.4 GJ-H: 4-3-3,4/r90/r(h2) ( t = 2, e = 2) s {4,4} |   C&R: 3 3 .4 2 GJ-H: 4-3/m90/r(h2) ( t = 2, e = 3) {3,6}: e |   C&R: 3 4 .6 GJ-H: 6-3-3/r60/r(h5) ( t = 3, e = 3) sr {3,6} | ||
C&R: Notación de Cundy y Rollet
GJ-H: Notación de GomJau-Hogg
Grünbaum y Shephard distinguen la descripción de estos teselados como arquimedianos como referencia únicamente a la propiedad local de que la disposición de los teselas alrededor de cada vértice es la misma, y la de que son uniformes como referencia a la propiedad global de transitividad de vértices. Aunque estos dan como resultado el mismo conjunto de teselados en el plano, en otros espacios hay teselados arquimedianos que no son uniformes.
Teselación plano-vértice
Existen 17 combinaciones de polígonos convexos regulares que forman 21 tipos de teselación de vértices y planos . [6] [7] Los polígonos en estos se encuentran en un punto sin espacio ni superposición. Si los enumeramos por sus figuras de vértices , uno tiene 6 polígonos, tres tienen 5 polígonos, siete tienen 4 polígonos y diez tienen 3 polígonos. [8]
Tres de ellos pueden realizar teselaciones regulares (6 3 , 4 4 , 3 6 ), y ocho más pueden realizar teselaciones semirregulares o arquimedianas (3.12.12, 4.6.12, 4.8.8, (3.6) 2 , 3.4.6.4, 3.3.4.3.4, 3.3.3.4.4, 3.3.3.3.6). Cuatro de ellos pueden existir en teselados k-uniformes superiores (3.3.4.12, 3.4.3.12, 3.3.6.6, 3.4.4.6), mientras que seis no pueden usarse para teselar completamente el plano con polígonos regulares sin espacios ni superposiciones; solo teselan el espacio por completo cuando se incluyen polígonos irregulares (3.7.42, 3.8.24, 3.9.18, 3.10.15, 4.5.20, 5.5.10). [9]
| 6 |  3 6 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 |  3.3.4.3.4 |  3.3.3.4.4 |  3.3.3.3.6 | |||||||
| 4 |  3.3.4.12 |  3.4.3.12 |  3.3.6.6 |  (3.6) 2 |  3.4.4.6 |  3.4.6.4 |  4 4 | |||
| 3 |  3.7.42 |  3.8.24 |  3.9.18 |  3.10.15 |  3.12.12 |  4.5.20 |  4.6.12 |  4.8.8 |  5.5.10 |  6 3 |
a-azulejos uniformes
Estos mosaicos periódicos pueden clasificarse por el número de órbitas de vértices, aristas y teselas. Si hay k órbitas de vértices, un mosaico se conoce como k -uniforme o k -isogonal; si hay t órbitas de teselas, como t -isoédrico; si hay e órbitas de aristas, como e -isotoxal.
Los mosaicos k -uniformes con las mismas figuras de vértice se pueden identificar además por su simetría de grupo de papel tapiz .
Los mosaicos 1-uniformes incluyen 3 mosaicos regulares y 8 semirregulares, con 2 o más tipos de caras de polígonos regulares. Hay 20 mosaicos 2-uniformes, 61 mosaicos 3-uniformes, 151 mosaicos 4-uniformes, 332 mosaicos 5-uniformes y 673 mosaicos 6-uniformes. Cada uno puede agruparse por el número m de figuras de vértices distintas, que también se denominan mosaicos m -arquimedianos. [10]
Finalmente, si el número de tipos de vértices es el mismo que la uniformidad ( m = k a continuación), entonces se dice que el teselado es Krotenheerdt . En general, la uniformidad es mayor o igual que el número de tipos de vértices ( m ≥ k ), ya que diferentes tipos de vértices necesariamente tienen diferentes órbitas, pero no al revés. Si m = n = k , hay 11 teselados de este tipo para n = 1; 20 teselados de este tipo para n = 2; 39 teselados de este tipo para n = 3; 33 teselados de este tipo para n = 4; 15 teselados de este tipo para n = 5; 10 teselados de este tipo para n = 6; y 7 teselados de este tipo para n = 7.
A continuación se muestra un ejemplo de mosaico de 3 uniformes:
| m -Arquímedes | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ≥ 15 | Total | ||
| k -uniforme | 1 | 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 |
| 2 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | |
| 3 | 0 | 22 | 39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 61 | |
| 4 | 0 | 33 | 85 | 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 151 | |
| 5 | 0 | 74 | 149 | 94 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 332 | |
| 6 | 0 | 100 | 284 | 187 | 92 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 673 | |
| 7 | 0 | 175 | 572 | 426 | 218 | 74 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1472 | |
| 8 | 0 | 298 | 1037 | 795 | 537 | 203 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2850 | |
| 9 | 0 | 424 | 1992 | 1608 | 1278 | 570 | 80 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5960 | |
| 10 | 0 | 663 | 3772 | 2979 | 2745 | 1468 | 212 | 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11866 | |
| 11 | 0 | 1086 | 7171 | 5798 | 5993 | 3711 | 647 | 52 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 24459 | |
| 12 | 0 | 1607 | 13762 | 11006 | 12309 | 9230 | 1736 | 129 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 49794 | |
| 13 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | ? | 0 | 0 | 0 | 0 | 0 | 103082 | |
| 14 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | ? | 0 | 0 | 0 | 0 | 0 | ? | |
| ≥ 15 | 0 | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | 0 | ? | |
| Total | 11 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | ∞ | |
2-azulejos uniformes
Hay veinte (20) teselaciónes 2-uniformes del plano euclidiano. (también llamadas teselaciónes 2- isogonales o teselaciónes demirregulares ) [5] : 62-67 [14] [15] Se enumeran los tipos de vértice para cada una. Si dos teselaciónes comparten los mismos dos tipos de vértice, se les asignan los subíndices 1,2.
| p6m, *632 | p4m, *442 | |||||
|---|---|---|---|---|---|---|
 [3 6 ; 3 2 .4.3.4] 3-4-3/m30/r(c3) ( t = 3, e = 3) |  [3.4.6.4; 3 2 .4.3.4] 6-4-3,3/m30/r(h1) ( t = 4, e = 4) |  [3.4.6.4; 3 3 .4 2 ] 6-4-3-3/m30/r(h5) ( t = 4, e = 4) |  [3.4.6.4; 3,4 2 , 6] 6-4-3,4-6/m30/r(c4) ( t = 5, e = 5) |  [4.6.12; 3.4.6.4] 12-4,6-3/m30/r(c3) ( t = 4, e = 4) |  [3 6 ; 3 2 .4.12] 12-3,4-3/m30/r(c3) ( t = 4, e = 4) |  [3.12.12; 3.4.3.12] 12-0,3,3-0,4/m45/m(h1) ( t = 3, e = 3) |
| p6m, *632 | pág. 6, 632 | pág. 6, 632 | cmm, 2*22 | Por favor, *2222 | cmm, 2*22 | Por favor, *2222 |
 [3 6 ; 3 2 .6 2 ] 3-6/m30/r(c2) ( t = 2, e = 3) |  [3 6 ; 3 4 .6] 1 6-3,3-3/m30/r(h1) ( t = 3, e = 3) |  [3 6 ; 3 4 .6] 2 6-3-3,3-3/r60/r(h8) ( t = 5, e = 7) |  [3 2 .6 2 ; 3 4 .6] 6-3/m90/r(h1) ( t = 2, e = 4) |  [3.6.3.6; 3 2 .6 2 ] 6-3,6/m90/r(h3) ( t = 2, e = 3) |  [3.4 2 .6; 3.6.3.6] 2 6-3,4-6-3,4-6,4/m90/r(c6) ( t = 3, e = 4) |  [3.4 2 .6; 3.6.3.6] 1 6-3,4/m90/r(h4) ( t = 4, e = 4) |
| p4g, 4*2 | pág., 22× | cmm, 2*22 | cmm, 2*22 | Por favor, *2222 | cmm, 2*22 | |
 [3 3 .4 2 ; 3 2 .4.3.4] 1 4-3,3-4,3/r90/m(h3) ( t = 4, e = 5) |  [3 3 .4 2 ; 3 2 .4.3.4] 2 4-3,3,3-4,3/r(c2)/r(h13)/r(h45) ( t = 3, e = 6) |  [4 4 ; 3 3 .4 2 ] 1 4-3/m(h4)/m(h3)/r(h2) ( t = 2, e = 4) |  [4 4 ; 3 3 .4 2 ] 2 4-4-3-3/m90/r(h3) ( t = 3, e = 5) |  [3 6 ; 3 3 .4 2 ] 1 4-3,4-3,3/m90/r(h3) ( t = 3, e = 4) |  [3 6 ; 3 3 .4 2 ] 2 4-3-3-3/m90/r(h7)/r(h5) ( t = 4, e = 5) | |
Más altoa-azulejos uniformes
Se han enumerado hasta 6 teselas k -uniformes. Existen 673 teselas 6-uniformes del plano euclidiano. La búsqueda de Brian Galebach reprodujo la lista de Krotenheerdt de 10 teselas 6-uniformes con 6 tipos de vértices distintos, y encontró 92 de ellas con 5 tipos de vértices, 187 con 4 tipos de vértices, 284 con 3 tipos de vértices y 100 con 2 tipos de vértices.
Fractalizacióna-azulejos uniformes
Existen muchas maneras de generar nuevos mosaicos k -uniformes a partir de mosaicos k -uniformes antiguos. Por ejemplo, observe que el mosaico 2-uniforme [3.12.12; 3.4.3.12] tiene una red cuadrada, el mosaico 4(3-1)-uniforme [343.12; (3.12 2 )3] tiene una red cuadrada chata y el mosaico 5(3-1-1)-uniforme [334.12; 343.12; (3.12.12)3] tiene una red triangular alargada. Estos mosaicos uniformes de orden superior utilizan la misma red pero poseen una mayor complejidad. La base fractalizadora para estos mosaicos es la siguiente: [16]
| Triángulo | Cuadrado | Hexágono | Dodecágono diseccionado | |
|---|---|---|---|---|
| Forma |  |  |  |  |
| Fractalización |  |  |  |  |
Las longitudes de los lados se dilatan por un factor de .
Esto se puede hacer de manera similar con el mosaico trihexagonal truncado como base, con la dilatación correspondiente de .
| Triángulo | Cuadrado | Hexágono | Dodecágono diseccionado | |
|---|---|---|---|---|
| Forma |  |  |  |  |
| Fractalización |  |  | 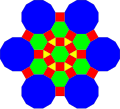 | 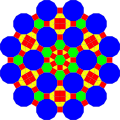 |
Ejemplos de fractalización
| Teselación hexagonal truncada | Teselación triangular truncada | |
|---|---|---|
| Fractalización |  |  |
Azulejos que no están borde a borde
Los polígonos regulares convexos también pueden formar mosaicos planos que no estén unidos por sus bordes. Dichos mosaicos pueden considerarse como polígonos irregulares con bordes adyacentes colineales.
Existen siete familias de teselas isogonales, cada una de las cuales tiene un parámetro de valor real que determina la superposición entre los lados de las teselas adyacentes o la relación entre las longitudes de las aristas de las diferentes teselas. Dos de las familias se generan a partir de posiciones cuadradas desplazadas, ya sea progresivas o en zigzag. Grünbaum y Shephard denominan a estas teselas uniformes , aunque esto contradice la definición de uniformidad de Coxeter, que requiere polígonos regulares de arista con arista. [17] Estas teselas isogonales son en realidad topológicamente idénticas a las teselas uniformes, con diferentes proporciones geométricas.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
 Filas de cuadrados con desplazamientos horizontales |  Filas de triángulos con desplazamientos horizontales |  Un mosaico por cuadrados |  Tres hexágonos rodean cada triángulo. |  Seis triángulos rodean cada hexágono. |  Triángulos de tres tamaños | |
| cmm (2*22) | pág. 2 (2222) | cmm (2*22) | p4m (*442) | pág. 6 (632) | pág. 3 (333) | |
| Azulejos hexagonales | Azulejos cuadrados | Teselación cuadrada truncada | Teselación hexagonal truncada | Azulejos hexagonales | Azulejos trihexagonales | |
Véase también
- Cuadrícula (índice espacial)
- Teselación uniforme en el plano hiperbólico
- Lista de teselados uniformes
- Símbolo de Wythoff
- Mosaico
- Grupo de fondos de pantalla
- Poliedro regular (los sólidos platónicos )
- Poliedro semirregular (incluidos los sólidos de Arquímedes )
- Geometría hiperbólica
- Mosaico de Penrose
- Azulejos con rectángulos
- Enrejado (grupo)
Referencias
- ^ Cundy, HM; Rollett, AP (1981). Modelos matemáticos; . Stradbroke (Reino Unido): Tarquin Publications.
- ^ ab Gomez-Jauregui, Valentin al.; Otero, Cesar; et al. (2012). "Generación y nomenclatura de teselaciones y cuadrículas de doble capa". Journal of Structural Engineering . 138 (7): 843–852. doi :10.1061/(ASCE)ST.1943-541X.0000532. hdl : 10902/5869 .
- ^ Gomez-Jauregui, Valentin; Hogg, Harrison; et al. (2021). "Notación de GomJau-Hogg para la generación automática de teselaciones k-uniformes con ANTWERP v3.0". Simetría . 13 (12): 2376. Bibcode :2021Symm...13.2376G. doi : 10.3390/sym13122376 . hdl : 10902/23907 .
- ^ Hogg, Harrison; Gómez-Jáuregui, Valentín. < "Amberes 3.0".
- ^ ab Critchlow, K. (1969). Orden en el espacio: un libro de referencia sobre diseño . Londres: Thames and Hudson. págs. 60–61.
- ^ Dallas, Elmslie William (1855), Los elementos de la geometría práctica plana, etc., John W. Parker & Son, pág. 134
- ^ Mosaicos y patrones , Figura 2.1.1, p.60
- ^ Azulejos y patrones , pág. 58-69
- ^ "Empaquetamiento pentágono-decágono". Sociedad Matemática Estadounidense . AMS . Consultado el 7 de marzo de 2022 .
- ^ Teselación k-uniforme mediante polígonos regulares Archivado el 30 de junio de 2015 en Wayback Machine Nils Lenngren, 2009
- ^ "N-Uniform Tilings". probabilitysports.com . Consultado el 21 de junio de 2019 .
- ^ Sloane, N. J. A. (ed.). "Secuencia A068599 (Número de teselas n-uniformes)". La enciclopedia en línea de secuencias de enteros . Fundación OEIS . Consultado el 7 de enero de 2023 .
- ^ "Enumeración de teselaciones k-arquímedianas n-uniformes". zenorogue.github.io/tes-catalog/?c= . Consultado el 24 de agosto de 2024 .
- ^ Mosaicos y patrones , Grünbaum y Shephard 1986, págs. 65-67
- ^ "En busca de teselaciones demiregulares" (PDF) . Archivado desde el original (PDF) el 7 de mayo de 2016. Consultado el 4 de junio de 2015 .
- ^ Chavey, Darrah (2014). "TEJIDOS POR POLÍGONOS REGULARES III: TEJIDOS DENSOS EN DODECÁGONOS". Simetría-Cultura y Ciencia . 25 (3): 193–210. S2CID 33928615.
- ^ Teselación de polígonos regulares p.236
- Grünbaum, Branko; Shephard, Geoffrey C. (1977). "Teselación mediante polígonos regulares". Math. Mag . 50 (5): 227–247. doi :10.2307/2689529. JSTOR 2689529.
- Grünbaum, Branko; Shephard, GC (1978). "Los noventa y un tipos de teselación isogonal en el plano". Trans. Am. Math. Soc . 252 : 335–353. doi : 10.1090/S0002-9947-1978-0496813-3 . MR 0496813.
- Debroey, I.; Landuyt, F. (1981). "Mosaicos equitransitivos de borde a borde". Geometriae Dedicata . 11 (1): 47–60. doi :10.1007/BF00183189. S2CID 122636363.
- Grünbaum, Branko ; Shephard, GC (1987). Mosaicos y patrones . WH Freeman and Company. ISBN 0-7167-1193-1.
- Ren, Ding; Reay, John R. (1987). "La característica de contorno y el teorema de Pick en los teselados planos de Arquímedes". J. Comb. Theory A . 44 (1): 110–119. doi :10.1016/0097-3165(87)90063-X.
- Chavey, D. (1989). "Teselas mediante polígonos regulares—II: Un catálogo de teselas" . Computers & Mathematics with Applications . 17 : 147–165. doi :10.1016/0898-1221(89)90156-9.
- Orden en el espacio: un libro de referencia sobre diseño, Keith Critchlow, 1970 ISBN 978-0-670-52830-1
- Sommerville, Duncan MacLaren Young (1958). Introducción a la geometría de n dimensiones . Publicaciones de Dover.Capítulo X: Los politopos regulares
- Préa, P. (1997). "Secuencias de distancias y umbrales de percolación en teselados arquimedianos". Mathl. Comput. Modelling . 26 (8–10): 317–320. doi :10.1016/S0895-7177(97)00216-1.
- Kovic, Jurij (2011). "Gráficos de tipo simétrico de sólidos platónicos y arquimedianos". Math. Commun . 16 (2): 491–507.
- Pellicer, Daniel; Williams, Gordon (2012). "Recubrimientos mínimos de los teselados de Arquímedes, parte 1". Revista Electrónica de Combinatoria . 19 (3): #P6. doi : 10.37236/2512 .
- Dale Seymour y Jill Britton , Introducción a las teselaciones , 1989, ISBN 978-0866514613 , págs. 50–57
Enlaces externos
Enlaces euclidianos y de teselación general:
- mosaicos n-uniformes, Brian Galebach
- Dutch, Steve. "Uniform Tilings". Archivado desde el original el 2006-09-09 . Consultado el 2006-09-09 .
- Mitchell, K. "Semi-Regular Tilings" (Milímetros semirregulares) . Consultado el 9 de septiembre de 2006 .
- Weisstein, Eric W. "Teselación". MathWorld .
- Weisstein, Eric W. "Teselación semirregular". MathWorld .
- Weisstein, Eric W. "Teselación demirregular". MathWorld .



