Par solitario

En ciencia, un par solitario se refiere a un par de electrones de valencia que no se comparten con otro átomo en un enlace covalente ^[1] y a veces se lo llama par no compartido o par no enlazante . Los pares solitarios se encuentran en la capa electrónica más externa de los átomos. Se pueden identificar utilizando una estructura de Lewis . Por lo tanto, los pares de electrones se consideran pares solitarios si dos electrones están emparejados pero no se utilizan en un enlace químico . Por lo tanto, la cantidad de electrones en pares solitarios más la cantidad de electrones en enlaces es igual a la cantidad de electrones de valencia alrededor de un átomo.

El concepto de par solitario se utiliza en la teoría de repulsión de pares electrónicos de la capa de valencia (teoría VSEPR), que explica las formas de las moléculas . También se hace referencia a ellos en la química de los ácidos y bases de Lewis . Sin embargo, los químicos no consideran que todos los pares de electrones no enlazantes sean pares solitarios. Algunos ejemplos son los metales de transición, donde los pares no enlazantes no influyen en la geometría molecular y se dice que son estereoquímicamente inactivos. En la teoría de orbitales moleculares ( orbitales canónicos completamente deslocalizados o localizados de alguna forma), el concepto de par solitario es menos claro, ya que la correspondencia entre un orbital y los componentes de una estructura de Lewis a menudo no es sencilla. Sin embargo, los orbitales no enlazantes ocupados (u orbitales de carácter mayoritariamente no enlazante) se identifican con frecuencia como pares solitarios.

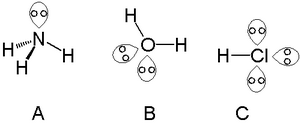
Se puede encontrar un solo par solitario con átomos del grupo del nitrógeno , como el nitrógeno en el amoniaco . Se pueden encontrar dos pares solitarios con átomos del grupo del calcógeno , como el oxígeno en el agua. Los halógenos pueden tener tres pares solitarios, como el cloruro de hidrógeno .

En la teoría VSEPR, los pares de electrones en el átomo de oxígeno en el agua forman los vértices de un tetraedro con los pares solitarios en dos de los cuatro vértices. El ángulo de enlace H–O–H es de 104,5°, menor que los 109° predichos para un ángulo tetraédrico , y esto puede explicarse por una interacción repulsiva entre los pares solitarios. ^{[2] [3] [4]}

Se han propuesto varios criterios computacionales para la presencia de pares solitarios. Si bien la densidad electrónica ρ( r ) en sí misma generalmente no proporciona una guía útil a este respecto, el laplaciano de la densidad electrónica es revelador, y un criterio para la ubicación del par solitario es donde L ( r ) = – ∇ ² ρ( r ) es un máximo local. Los mínimos del potencial electrostático V ( r ) es otro criterio propuesto. Otro más considera la función de localización electrónica (ELF). ^[5]

Los pares suelen exhibir un carácter polar negativo con su alta densidad de carga y se ubican más cerca del núcleo atómico en promedio en comparación con el par de electrones enlazantes. La presencia de un par solitario disminuye el ángulo de enlace entre el par de electrones enlazantes, debido a su alta carga eléctrica, lo que provoca una gran repulsión entre los electrones. También están involucrados en la formación de un enlace dativo . Por ejemplo, la creación del ion hidronio (H ₃ O ⁺ ) ocurre cuando los ácidos se disuelven en agua y se debe a que el átomo de oxígeno dona un par solitario al ion hidrógeno .

Esto se puede ver más claramente cuando se observa en dos moléculas más comunes . Por ejemplo, en el dióxido de carbono (CO2 ₎ , que no tiene un par solitario, los átomos de oxígeno están en lados opuestos del átomo de carbono ( geometría molecular lineal ), mientras que en el agua ( _H2O ), que tiene dos pares solitarios, el ángulo entre los átomos de hidrógeno es de 104,5° ( geometría molecular doblada ). Esto es causado por la fuerza repulsiva de los dos pares solitarios del átomo de oxígeno que empuja a los átomos de hidrógeno a separarse aún más, hasta que las fuerzas de todos los electrones sobre el átomo de hidrógeno están en equilibrio . Esta es una ilustración de la teoría VSEPR .

Los pares solitarios pueden contribuir al momento dipolar de una molécula . El NH ₃ tiene un momento dipolar de 1,42 D. Como la electronegatividad del nitrógeno (3,04) es mayor que la del hidrógeno (2,2), el resultado es que los enlaces NH son polares con una carga neta negativa en el átomo de nitrógeno y una carga neta positiva más pequeña en los átomos de hidrógeno. También hay un dipolo asociado con el par solitario y esto refuerza la contribución hecha por los enlaces covalentes polares NH al momento dipolar del amoníaco . En contraste con el NH ₃ , el NF ₃ tiene un momento dipolar mucho menor de 0,234 D. El flúor es más electronegativo que el nitrógeno y la polaridad de los enlaces NF es opuesta a la de los enlaces NH en el amoníaco, de modo que el dipolo debido al par solitario se opone a los dipolos del enlace NF, lo que resulta en un momento dipolar molecular bajo. ^[6]

	⇌
Inversión de una molécula genérica de amina orgánica en nitrógeno

Un par solitario puede contribuir a la existencia de quiralidad en una molécula, cuando otros tres grupos unidos a un átomo son todos diferentes. El efecto se observa en ciertas aminas , fosfinas , ^{[7] iones} sulfonio y oxonio , sulfóxidos e incluso carbaniones .

La resolución de enantiómeros cuyo centro estereogénico es una amina suele verse impedida porque la barrera energética para la inversión del nitrógeno en el centro estereogénico es baja, lo que permite que los dos estereoisómeros se interconviertan rápidamente a temperatura ambiente. Como resultado, dichas aminas quirales no pueden resolverse, a menos que los grupos de la amina estén restringidos en una estructura cíclica (como en la base de Tröger ).

También se espera un par solitario estereoquímicamente activo para los iones de plomo y estaño divalentes debido a su configuración electrónica formal de n s ² . En el estado sólido, esto da como resultado la coordinación metálica distorsionada observada en la estructura de litargirio tetragonal adoptada tanto por PbO como por SnO. La formación de estos pares solitarios n s ^{2 de metales pesados, que anteriormente se atribuía a} la hibridación intraatómica de los estados s y p del metal ^[8], ha demostrado recientemente tener una fuerte dependencia del anión. ^[9] Esta dependencia de los estados electrónicos del anión puede explicar por qué algunos materiales divalentes de plomo y estaño, como PbS y SnTe, no muestran evidencia estereoquímica del par solitario y adoptan la estructura cristalina simétrica de la sal de roca. ^{[10] [11]}

En los sistemas moleculares, el par solitario también puede producir una distorsión en la coordinación de los ligandos alrededor del ion metálico. El efecto de par solitario del plomo se puede observar en complejos supramoleculares de nitrato de plomo (II) , y en 2007 un estudio relacionó el par solitario con el envenenamiento por plomo . ^[12] Los iones de plomo pueden reemplazar a los iones metálicos nativos en varias enzimas clave, como los cationes de zinc en la enzima ALAD , que también se conoce como porfobilinógeno sintasa , y es importante en la síntesis de hemo , un componente clave de la molécula transportadora de oxígeno hemoglobina . Esta inhibición de la síntesis de hemo parece ser la base molecular del envenenamiento por plomo (también llamado "saturnismo" o "plumbismo"). ^{[13] [14] [15]}

Los experimentos computacionales revelan que, aunque el número de coordinación no cambia tras la sustitución en las proteínas que se unen al calcio, la introducción de plomo distorsiona la forma en que los ligandos se organizan para adaptarse a la aparición de un par solitario de este tipo: en consecuencia, estas proteínas se ven perturbadas. Este efecto de par solitario se vuelve dramático para las proteínas que se unen al zinc, como la porfobilinógeno sintasa mencionada anteriormente, ya que el sustrato natural ya no puede unirse; en esos casos, la proteína se inhibe .

En los elementos del Grupo 14 (el grupo del carbono ), los pares solitarios pueden manifestarse acortando o alargando las longitudes de los enlaces simples ( orden de enlace 1), ^[16] así como también en el orden efectivo de los enlaces triples . ^{[17] [18]} Los familiares alquinos tienen un triple enlace carbono-carbono ( orden de enlace 3) y una geometría lineal de ángulos de enlace de 180° (figura A en la referencia ^[19] ). Sin embargo, más abajo en el grupo ( silicio , germanio y estaño ), los enlaces triples formales tienen un orden de enlace efectivo 2 con un par solitario (figura B ^[19] ) y geometrías trans -dobladas. En el plomo , el orden de enlace efectivo se reduce aún más a un enlace simple, con dos pares solitarios para cada átomo de plomo (figura C ^[19] ). En el compuesto de organogermanio ( Esquema 1 en la referencia), el orden de enlace efectivo también es 1, con la complejación de los grupos CN ácidos de isonitrilo (o isocianuro ), basada en la interacción con el orbital 4p vacío del germanio. ^{[19] [20]}

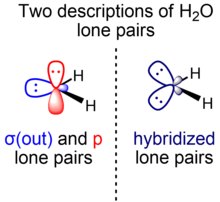
En los cursos de química elemental, los pares solitarios del agua se describen como "orejas de conejo": dos pares de electrones equivalentes de hibridación aproximadamente sp ³ , mientras que el ángulo de enlace HOH es de 104,5°, ligeramente menor que el ángulo tetraédrico ideal de arccos(–1/3) ≈ 109,47°. El ángulo de enlace más pequeño se racionaliza mediante la teoría VSEPR al atribuir un requisito de espacio mayor para los dos pares solitarios idénticos en comparación con los dos pares de enlace. En cursos más avanzados, una explicación alternativa para este fenómeno considera la mayor estabilidad de los orbitales con exceso de carácter s utilizando la teoría de la hibridación isovalente , en la que los enlaces y los pares solitarios se pueden construir con híbridos sp ^x en los que se permiten valores no enteros de x , siempre que se conserve la cantidad total de carácter s y p (un orbital s y tres orbitales p en el caso de elementos del bloque p de la segunda fila).

Para determinar la hibridación de los orbitales de oxígeno utilizados para formar los pares de enlace y pares solitarios del agua en esta imagen, utilizamos la fórmula 1 + x cos θ = 0, que relaciona el ángulo de enlace θ con el índice de hibridación x . Según esta fórmula, se considera que los enlaces O–H se construyen a partir de orbitales de enlace O de hibridación ~sp ^4.0 (~80% carácter p, ~20% carácter s), lo que deja atrás orbitales de pares solitarios O de hibridación ~sp ^{2.3 (~70% carácter p, ~30% carácter s). Estas desviaciones de la hibridación sp 3} idealizada (75% carácter p, 25% carácter s) para la geometría tetraédrica son consistentes con la regla de Bent : los pares solitarios localizan más densidad electrónica más cerca del átomo central en comparación con los pares de enlace; Por lo tanto, el uso de orbitales con exceso de carácter s para formar pares solitarios (y, en consecuencia, aquellos con exceso de carácter p para formar pares de enlace) es energéticamente favorable.

Sin embargo, los teóricos a menudo prefieren una descripción alternativa del agua que separa los pares solitarios de agua según la simetría con respecto al plano molecular. En este modelo, hay dos pares solitarios de agua energéticamente y geométricamente distintos que poseen diferente simetría: uno (σ) en el plano y simétrico con respecto al plano molecular y el otro (π) perpendicular y antisimétrico con respecto al plano molecular. El par solitario de simetría σ (σ(out)) se forma a partir de un orbital híbrido que mezcla el carácter 2s y 2p, mientras que el par solitario de simetría π (p) es de origen orbital 2p exclusivo. El orbital de par solitario O σ(out) rico en caracteres s (también denominado n _O ^(σ) ) es un híbrido ~sp ^0,7 (~40 % carácter p, 60 % carácter s), mientras que el orbital de par solitario p (también denominado n _O ^(π) ) consta de un 100 % de caracteres p.

Ambos modelos son valiosos y representan la misma densidad electrónica total, con los orbitales relacionados por una transformación unitaria . En este caso, podemos construir los dos orbitales híbridos de pares solitarios equivalentes h y h ' tomando combinaciones lineales h = c ₁ σ(out) + c ₂ p y h ' = c ₁ σ(out) – c ₂ p para una elección apropiada de coeficientes c ₁ y c ₂ . Para las propiedades químicas y físicas del agua que dependen de la distribución electrónica general de la molécula, el uso de h y h ' es tan válido como el uso de σ(out) y p. En algunos casos, tal punto de vista es intuitivamente útil. Por ejemplo, el requisito estereoelectrónico para el efecto anomérico se puede racionalizar utilizando pares solitarios equivalentes, ya que es la donación general de densidad electrónica en el orbital antienlazante lo que importa. Un tratamiento alternativo que utiliza pares solitarios separados σ/π también es válido, pero requiere lograr un equilibrio entre maximizar la superposición n _O ^(π) -σ* (máximo en un ángulo diedro de 90°) y la superposición n _O ^(σ) -σ* (máximo en un ángulo diedro de 0°), un compromiso que lleva a la conclusión de que una conformación gauche (ángulo diedro de 60°) es la más favorable, la misma conclusión que el modelo de pares solitarios equivalente racionaliza de una manera mucho más directa. ^[21] De manera similar, los enlaces de hidrógeno del agua se forman a lo largo de las direcciones de los pares solitarios en "orejas de conejo", como un reflejo de la mayor disponibilidad de electrones en estas regiones. Esta visión está respaldada computacionalmente. ^[5] Sin embargo, debido a que sólo los orbitales canónicos adaptados a la simetría tienen energías físicamente significativas, los fenómenos que tienen que ver con las energías de los orbitales individuales , como la reactividad fotoquímica o la espectroscopia fotoelectrónica , se explican más fácilmente utilizando pares solitarios σ y π que respetan la simetría molecular. ^{[21] [22]}

Debido a la popularidad de la teoría VSEPR , el tratamiento de los pares solitarios de agua como equivalentes prevalece en los cursos introductorios de química, y muchos químicos en ejercicio continúan considerándolo como un modelo útil. Una situación similar surge cuando se describen los dos pares solitarios en el átomo de oxígeno carbonílico de una cetona. ^[23] Sin embargo, la cuestión de si es conceptualmente útil derivar orbitales equivalentes a partir de los adaptados a la simetría, desde el punto de vista de la teoría del enlace y la pedagogía, sigue siendo controvertida, con artículos recientes (2014 y 2015) que se oponen ^[24] y apoyan ^[25] la práctica.

Busque par solitario en Wikcionario, el diccionario libre.

Wikimedia Commons alberga una categoría multimedia sobre Par solitario .

• Complejo de coordinación
• HOMO y LUMO (orbital molecular ocupado más alto y orbital molecular desocupado más bajo)
• Efecto de par inerte
• Ligando
• Par compartido