Semitono
| Inverso | séptima mayor (para segunda menor); octava disminuida (para unísono aumentado); octava aumentada (para unísono disminuido) |
|---|---|
| Nombre | |
| Otros nombres | segunda menor, semitono diatónico, unísono aumentado, unísono disminuido, semitono cromático |
| Abreviatura | m2;A1 |
| Tamaño | |
| Semitonos | 1 |
| Clase de intervalo | 1 |
| Sólo intervalo | 16:15, [1] 17:16, [2] 27:25, 135:128, [1] 25:24, [1] 256:243 |
| Centavos | |
| Temperamento igual de 12 tonos | 100 [1] |
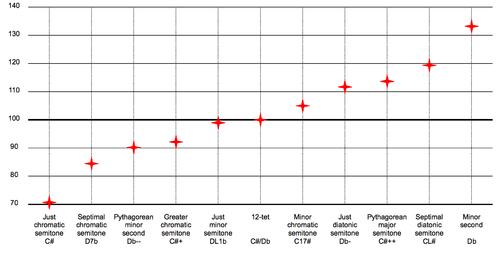
| Solo entonación | 112, [1] 105, 133, 92, [1] 71, [1] 90 |

Un semitono , también llamado segunda menor , semitono o semitono , [3] es el intervalo musical más pequeño que se utiliza habitualmente en la música tonal occidental, [4] y se considera el más disonante [5] cuando suena armónicamente. Se define como el intervalo entre dos notas adyacentes en una escala de 12 tonos (o la mitad de un tono entero ), que se ve visualmente en un teclado como la distancia entre dos teclas adyacentes entre sí. Por ejemplo, C es adyacente a C ♯ ; el intervalo entre ellas es un semitono. [6]
En una escala de 12 notas dividida aproximadamente de manera uniforme, cualquier intervalo se puede definir en términos de un número apropiado de semitonos (por ejemplo, un tono entero o una segunda mayor tiene 2 semitonos de ancho, una tercera mayor 4 semitonos y una quinta perfecta 7 semitonos).
En teoría musical , se hace una distinción [7] entre un semitono diatónico , o segunda menor (un intervalo que abarca dos posiciones diferentes del pentagrama , por ejemplo, de do a re ♭ ) y un semitono cromático o unísono aumentado (un intervalo entre dos notas en la misma posición del pentagrama, por ejemplo, de do a do ♯ ). Estos son enarmónicamente equivalentes si y solo si se usa el temperamento igual de doce tonos ; por ejemplo, no son lo mismo en el temperamento de medio tono , donde el semitono diatónico se distingue y es más grande que el semitono cromático (unísono aumentado), o en la afinación pitagórica , donde el semitono diatónico es más pequeño en su lugar. Consulte Intervalo (música) § Número para obtener más detalles sobre esta terminología.
En el temperamento igual de doce tonos, todos los semitonos tienen el mismo tamaño (100 centésimas). En otros sistemas de afinación, "semitono" se refiere a una familia de intervalos que pueden variar tanto en tamaño como en nombre. En la afinación pitagórica , siete semitonos de doce son diatónicos, con una proporción de 256:243 o 90,2 centésimas (limma pitagórica), y los otros cinco son cromáticos, con una proporción de 2187:2048 o 113,7 centésimas (apótoma pitagórica); se diferencian por la coma pitagórica de proporción 531441:524288 o 23,5 centésimas. En el mediotono de un cuarto de coma , siete de ellos son diatónicos y tienen una amplitud de 117,1 centésimas, mientras que los otros cinco son cromáticos y tienen una amplitud de 76,0 centésimas; Se diferencian por la menor proporción de 128:125 o 41,1 centésimas. Las escalas de 12 tonos afinadas en entonación justa suelen definir tres o cuatro tipos de semitonos. Por ejemplo, la afinación asimétrica de cinco límites produce semitonos cromáticos con proporciones de 25:24 (70,7 centésimas) y 135:128 (92,2 centésimas), y semitonos diatónicos con proporciones de 16:15 (111,7 centésimas) y 27:25 (133,2 centésimas). Para más detalles, consulte a continuación.
La condición de tener semitonos se llama hemitonia; la de no tener semitonos es anhemitonia . Una escala musical o acorde que contiene semitonos se llama hemitónica; una que no tiene semitonos es anhemitónica.
Segunda menor

| Inverso | séptima mayor |
|---|---|
| Nombre | |
| Otros nombres | semitono, medio paso |
| Abreviatura | metros cuadrados |
| Tamaño | |
| Semitonos | 1 |
| Clase de intervalo | 1 |
| Centavos | |
| Temperamento igual de 12 tonos | 100.0 |
La segunda menor se da en la escala mayor , entre el tercer y cuarto grado, ( mi (E) y fa (F) en Do mayor), y entre el séptimo y octavo grado ( ti (B) y do (C) en Do mayor). También se llama semitono diatónico porque se da entre pasos en la escala diatónica . La segunda menor se abrevia m2 (o −2 ). Su inversión es la séptima mayor ( M7 o Ma7 ).
. Aquí,el do centrales seguido por re ♭ , que es un tono 100centésimasmás agudo que el do, y luego por ambos tonos juntos.
Melódicamente , este intervalo se utiliza con mucha frecuencia y tiene una importancia particular en las cadencias . En las cadencias perfectas y engañosas aparece como una resolución de la nota principal a la tónica . En la cadencia plagal , aparece como la caída de la subdominante a la medianera . También aparece en muchas formas de la cadencia imperfecta , donde la tónica cae a la nota principal.
Armónicamente , el intervalo suele aparecer como una forma de disonancia o un tono que no forma parte de la armonía funcional . También puede aparecer en inversiones de un acorde de séptima mayor y en muchos acordes de tono añadido .

En situaciones inusuales, la segunda menor puede añadir mucho carácter a la música. Por ejemplo, el Estudio Op. 25, n.º 5 de Frédéric Chopin comienza con una melodía acompañada de una línea que toca fugaces segundas menores. Estas se utilizan con un efecto humorístico y caprichoso, que contrasta con su sección central más lírica. Esta disonancia excéntrica le ha valido a la pieza su apodo: el estudio de la "nota equivocada". Este tipo de uso de la segunda menor aparece en muchas otras obras del período romántico , como el Ballet de los polluelos no nacidos de Modest Mussorgsky . Más recientemente, la música de la película Tiburón ejemplifica la segunda menor.
En otros temperamentos
En la entonación justa, surge una segunda menor de 16:15 en la escala de Do mayor entre Si y Do y Mi y Fa, y es "la disonancia más aguda que se encuentra en la escala [mayor] ". [8]
Unísono aumentado


El unísono aumentado , el intervalo producido por el aumento , o ensanchamiento en un semitono, del unísono perfecto, [9] no ocurre entre pasos de la escala diatónica, sino entre un paso de la escala y una alteración cromática del mismo paso. También se llama semitono cromático . El unísono aumentado se abrevia A1 , o aug 1. Su inversión es la octava disminuida ( d8 , o dim 8 ). El unísono aumentado es también la inversión de la octava aumentada , porque el intervalo del unísono disminuido no existe. [10] Esto se debe a que un unísono siempre se hace más grande cuando una nota del intervalo se cambia con una alteración. [11] [12]
Melódicamente , un unísono aumentado ocurre muy frecuentemente cuando se procede a un acorde cromático, como una dominante secundaria , un acorde de séptima disminuida o un acorde de sexta aumentada . Su uso también es a menudo la consecuencia de una melodía que procede en semitonos, independientemente del soporte armónico, p. ej. , D , D♯ , E , F , F♯ . (Restringir la notación a solo segundas menores es poco práctico, ya que el mismo ejemplo tendría un número rápidamente creciente de alteraciones accidentales, escritas enarmónicamente como D , E ♭ , F ♭ , G , A
, A ).
).

Armónicamente , los unísonos aumentados son bastante raros en el repertorio tonal. En el ejemplo de la derecha, Liszt había escrito un Mi ♭ contra un Mi ♮ en el bajo. Aquí se prefirió Mi ♭ a un Re ♯ para dejar clara la función del tono como parte de un acorde de séptima dominante de Fa , y el unísono aumentado es el resultado de superponer esta armonía sobre un punto de pedal de Mi.
Además de este tipo de uso, los unísonos aumentados armónicos se escriben con frecuencia en obras modernas que involucran grupos de tonos , como Evryali de Iannis Xenakis para piano solo.
Historia
El semitono apareció en la teoría musical de la antigüedad griega como parte de un tetracordio diatónico o cromático y siempre ha tenido un lugar en las escalas diatónicas de la música occidental desde entonces. Las diversas escalas modales de la teoría musical medieval se basaban en este patrón diatónico de tonos y semitonos.
Aunque más tarde se convertiría en una parte integral de la cadencia musical , en la polifonía temprana del siglo XI no era así. Guido de Arezzo sugirió en su Micrologus otras alternativas: o bien proceder por tonos enteros desde una segunda mayor hasta un unísono, o bien un happensus en el que dos notas en una tercera mayor se mueven por movimiento contrario hacia un unísono, habiéndose movido cada una un tono entero.
"Hasta el siglo XIII el semitono se percibía como un intervalo problemático y difícil de comprender, como el resto irracional [ sic ] entre la cuarta perfecta y el dítono ". En un semitono melódico, no se percibía ninguna "tendencia del tono más bajo hacia el más alto, ni del más alto hacia el más bajo. El segundo tono no se consideraba el 'objetivo' del primero. En cambio, el semitono se evitaba en las cláusulas porque carecía de claridad como intervalo". [13]

Sin embargo, a partir del siglo XIII las cadencias comienzan a requerir movimiento en una voz por semitono y en la otra un tono entero en movimiento contrario. [13] Estas cadencias se convertirían en una parte fundamental del lenguaje musical, incluso hasta el punto en que el accidental habitual que acompaña a la segunda menor en una cadencia a menudo se omitía de la partitura escrita (una práctica conocida como musica ficta ). Para el siglo XVI, el semitono se había convertido en un intervalo más versátil, a veces incluso apareciendo como un unísono aumentado en pasajes muy cromáticos . Semánticamente , en el siglo XVI el semitono melódico repetido se asoció con el llanto, véase: passus duriusculus , lament bass y pianto .
En la época barroca (1600 a 1750), el marco armónico tonal ya estaba plenamente formado y se comprendían rigurosamente las diversas funciones musicales del semitono. Más adelante en este período, la adopción de temperamentos adecuados para la afinación instrumental y el uso más frecuente de equivalencias enarmónicas aumentaron la facilidad con la que se podía aplicar un semitono. Su función se mantuvo similar durante el período clásico y, aunque se utilizó con más frecuencia a medida que el lenguaje de la tonalidad se volvía más cromático en el período romántico , la función musical del semitono no cambió.
En el siglo XX, sin embargo, compositores como Arnold Schoenberg , Béla Bartók e Ígor Stravinski buscaron alternativas o extensiones de la armonía tonal y encontraron otros usos para el semitono. A menudo, el semitono se explotaba armónicamente como una disonancia cáustica, sin resolución. Algunos compositores incluso utilizaban grandes colecciones de semitonos armónicos ( grupos de tonos ) como fuente de cacofonía en su música (por ejemplo, las primeras obras para piano de Henry Cowell ). Para entonces, la equivalencia enarmónica era una propiedad común del temperamento igual y el uso instrumental del semitono no era en absoluto problemático para el intérprete. El compositor era libre de escribir semitonos donde quisiera.
Semitonos en diferentes afinaciones
El tamaño exacto de un semitono depende del sistema de afinación utilizado. Los temperamentos de medio tono tienen dos tipos distintos de semitonos, pero en el caso excepcional del temperamento igual , solo hay uno. Los temperamentos bien distribuidos de forma desigual contienen muchos semitonos diferentes. La afinación pitagórica , similar a la afinación de medio tono, tiene dos, pero en otros sistemas de entonación justa hay muchas más posibilidades.
Temperamento meítono
En los sistemas de medias tintas , hay dos semitonos diferentes. Esto se debe a la ruptura del círculo de quintas que se produce en el sistema de afinación: los semitonos diatónicos se derivan de una cadena de cinco quintas que no cruza la ruptura, y los semitonos cromáticos provienen de una que sí lo hace.
El semitono cromático suele ser más pequeño que el diatónico. En el semitono común de cuarto de coma , afinado como un ciclo de quintas temperadas desde Mi ♭ hasta Sol ♯ , los semitonos cromático y diatónico tienen una amplitud de 76,0 y 117,1 centésimas respectivamente.
| Semitono cromático | 76.0 | 76.0 | 76.0 | 76.0 | 76.0 | |||||||||||||||||||||
| Paso | do | C ♯ | D | mi ♭ | mi | F | F ♯ | GRAMO | Sol ♯ | A | B ♭ | B | do | |||||||||||||
| Centavos | 0.0 | 76.0 | 193.2 | 310.3 | 386.3 | 503.4 | 579,5 | 696.6 | 772.6 | 889.7 | 1006.8 | 1082.9 | 1200.0 | |||||||||||||
| Semitono diatónico | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 | 117.1 | |||||||||||||||||||
Los temperamentos medios extendidos con más de 12 notas aún conservan los mismos tamaños de dos semitonos, pero hay más flexibilidad para el músico sobre si usar un unísono aumentado o una segunda menor. El temperamento igual de 31 tonos es el más flexible de estos, que forma un círculo ininterrumpido de 31 quintas notas, lo que permite elegir el semitono para cualquier tono.
Temperamento igual
El temperamento igual de doce tonos es una forma de afinación de tono medio en la que los semitonos diatónicos y cromáticos son exactamente iguales, porque su círculo de quintas no tiene interrupción. Cada semitono es igual a un doceavo de una octava. Esta es una relación de 2 1/12 (aproximadamente 1,05946), o 100 centésimas, y es 11,7 centésimas más estrecha que la relación 16:15 (su forma más común en entonación justa , que se analiza a continuación).
Todos los intervalos diatónicos pueden expresarse como un número equivalente de semitonos. Por ejemplo, una sexta mayor equivale a nueve semitonos.
Existen muchas aproximaciones, racionales o no, al semitono de temperamento igual. Por citar algunas:
Sugerido por Vincenzo Galilei y utilizado por los luthiers del Renacimiento ,
sugerido por Marin Mersenne como una alternativa construible y más precisa,
utilizado por Julián Carrillo como parte de un sistema de dieciseisavos de tono.
Para ver más ejemplos, consulte los sistemas de afinación pitagórico y justo a continuación.
Buen temperamento
Existen muchas formas de buen temperamento , pero la característica que todas ellas comparten es que sus semitonos son de un tamaño desigual. Cada semitono en un buen temperamento tiene su propio intervalo (normalmente cercano a la versión de temperamento igual de 100 centésimas), y no hay una distinción clara entre un semitono diatónico y uno cromático en la afinación. El buen temperamento se construyó de modo que se pudiera asumir una equivalencia enarmónica entre todos estos semitonos, y que el hecho de que se escribieran como segunda menor o unísono aumentado no afectara a un sonido diferente. En cambio, en estos sistemas, cada clave tenía un color o carácter sonoro ligeramente diferente, más allá de las limitaciones de la notación convencional.
Afinación pitagórica
Al igual que el temperamento de tono medio, la afinación pitagórica es un círculo de quintas quebrado . Esto crea dos semitonos distintos, pero como la afinación pitagórica también es una forma de entonación justa de 3 límites , estos semitonos son racionales. Además, a diferencia de la mayoría de los temperamentos de tono medio, el semitono cromático es más grande que el diatónico.
El semitono diatónico pitagórico tiene una proporción de 256/243 ( ), y a menudo se lo llama limma pitagórico . También se lo llama a veces semitono menor pitagórico . Tiene aproximadamente 90,2 centésimas.
Se puede considerar como la diferencia entre tres octavas y cinco quintas partes , y funciona como un semitono diatónico en una afinación pitagórica .
El semitono cromático pitagórico tiene una proporción de 2187/2048 ( ). Es de aproximadamente 113,7 centésimas . También se lo puede llamar apótoma pitagórica [14] [15] [16] o semitono mayor pitagórico . ( Véase intervalo pitagórico .)
Se puede considerar como la diferencia entre cuatro octavas perfectas y siete quintas partes , y funciona como un semitono cromático en una afinación pitagórica .
La limma pitagórica y la apótoma pitagórica son equivalentes enarmónicos (semitonos cromáticos) y están separados solo por una coma pitagórica , en contraste con los semitonos diatónicos y cromáticos en el temperamento medio y la entonación justa de 5 límites .
Sólo entonación de 5 límites




Una segunda menor en entonación justa corresponde típicamente a una relación de tono de 16:15 ( ) o 1.0666... (aproximadamente 111.7 cents ), llamado semitono diatónico justo . [17] Este es un semitono justo práctico, ya que es el intervalo que ocurre dos veces dentro de la escala diatónica entre:
- tercera mayor (5:4) y cuarta perfecta (4:3) y una
- séptima mayor (15:8) y octava perfecta (2:1)
La segunda menor de 16:15 surge en la escala de Do mayor entre Si y Do y Mi y Fa, y es "la disonancia más aguda que se encuentra en la escala". [8]
Un "unísono aumentado" (sostenido) en entonación justa es un semitono diferente, más pequeño, con una relación de frecuencia de 25:24 ( ) o 1.0416... (aproximadamente 70.7 cents). Es el intervalo entre una tercera mayor (5:4) y una tercera menor (6:5). De hecho, es el espacio entre las terceras menores y mayores, sextas y séptimas (pero no necesariamente entre la segunda mayor y menor). El compositor Ben Johnston usó un sostenido ( ♯ ) para indicar que una nota se eleva 70.7 cents, o un bemol ( ♭ ) para indicar que una nota se baja 70.7 cents. [18] (Esta es la práctica estándar para la entonación justa, pero no para todas las demás microafinaciones).
La afinación de límite 5 produce otros dos tipos de semitonos. Una escala cromática define 12 semitonos como los 12 intervalos entre las 13 notas adyacentes, que abarcan una octava completa (por ejemplo, de C 4 a C 5 ). Los 12 semitonos producidos por una versión de afinación de límite 5 de uso común tienen cuatro tamaños diferentes y se pueden clasificar de la siguiente manera:
- Sólo semitono cromático
- semitono cromático , o más pequeño , o semitono cromático menor entre bemoles y sostenidos relacionados armónicamente, por ejemplo entre Mi bemol y Mi (6:5 y 5:4):
- Semitono cromático más grande
- o semitono cromático mayor , o limma mayor , o croma mayor , [18] p. ej. entre C y un C ♯ agudo (C ♯ elevado por una coma sintónica ) (1:1 y 135:128):
- Sólo semitono diatónico
- o más pequeño , o semitono diatónico menor , por ejemplo entre E y F (5:4 a 4:3):
- Semitono diatónico más grande
- o semitono diatónico mayor o mayor , por ejemplo entre A y B ♭ (5:3 a 9:5), o C y D ♭ cromático (27:25), o F ♯ y G (25:18 y 3:2):
Los semitonos que aparecen con mayor frecuencia son los justos ( S 3 , 16:15, y S 1 , 25:24): S 3 aparece en 6 intervalos cortos de 12, S 1 3 veces, S 2 dos veces y S 4 solo en un intervalo (si el Re ♭ diatónico reemplaza al Re ♭ cromático y no se usan notas sostenidas).
Los semitonos cromáticos y diatónicos más pequeños se diferencian de los más grandes por la coma sintónica (81:80 o 21,5 cents). Los semitonos cromáticos más pequeños y más grandes se diferencian de los semitonos diatónicos respectivos por la misma diesis de 128:125 que los semitonos medios anteriores. Finalmente, mientras que los semitonos internos se diferencian por el diasquisma (2048:2025 o 19,6 cents), los externos se diferencian por la diesis mayor (648:625 o 62,6 cents).
Entonaciones justas extendidas
En la afinación límite 7 existe el semitono diatónico séptimal de 15:14 ( ) disponible entre la séptima mayor límite 5 (15:8) y la séptima menor / séptima armónica límite 7 (7:4). También hay un semitono cromático séptimal más pequeño de 21:20 ( ) entre una séptima menor séptima y una quinta (21:8) y una octava y una tercera mayor (5:2). Ambos se usan con menos frecuencia que sus vecinos de límite 5, aunque el primero fue implementado a menudo por el teórico Cowell , mientras que Partch usó el último como parte de su escala de 43 tonos .
En la afinación límite 11, hay una segunda neutra indecimal bastante común (12:11) ( ), pero se encuentra en el límite entre la segunda menor y la mayor (150,6 centésimas). En la entonación justa hay infinitas posibilidades de intervalos que caen dentro del rango del semitono (por ejemplo, los semitonos pitagóricos mencionados anteriormente), pero la mayoría de ellos son poco prácticos.
En la afinación de límite 13, hay un tridecimal 2/3 tono (13:12 o 138,57 centésimas) y tridecimal 1/3 tono (27:26 o 65,34 cents).
En la entonación límite justa de 17, el semitono diatónico mayor es 15:14 o 119,4 cents ( ), y el semitono diatónico menor es 17:16 o 105,0 cents, [19] y el semitono septendecimal es 18:17 o 98,95 cents.
Aunque los nombres diatónico y cromático se utilizan a menudo para estos intervalos, su función musical no es la misma que la de los semitonos medios. Por ejemplo, 15:14 se escribiría normalmente como un unísono aumentado, que funcionaría como la contraparte cromática de un 16:15 diatónico . Estas distinciones dependen en gran medida del contexto musical, y la entonación justa no es particularmente adecuada para el uso cromático (la función de semitono diatónico es más frecuente).
Otros temperamentos iguales
El temperamento igual de 19 tonos distingue entre los semitonos cromáticos y diatónicos; en esta afinación, el semitono cromático es un paso de la escala ( ), y el semitono diatónico es dos ( ). El temperamento igual de 31 tonos también distingue entre estos dos intervalos, que se convierten en 2 y 3 pasos de la escala, respectivamente. 53-ET tiene una coincidencia aún más cercana con los dos semitonos con 3 y 5 pasos de su escala, mientras que 72-ET usa 4 ( ) y 7 ( ) pasos de su escala.
En general, debido a que el semitono más pequeño puede verse como la diferencia entre una tercera menor y una tercera mayor, y el más grande como la diferencia entre una tercera mayor y una cuarta perfecta, los sistemas de afinación que coinciden estrechamente con esos intervalos justos (6/5, 5/4 y 4/3) también distinguirán entre los dos tipos de semitonos y coincidirán estrechamente con sus intervalos justos (25/24 y 16/15).
Véase también
- Temperamento igual de 12 tonos
- Lista de intervalos de medias tintas
- Lista de intervalos musicales
- Lista de intervalos de tono
- Acorde de aproximación
- Segunda mayor
- Segundo punto muerto
- Intervalo pitagórico
- Temperamento regular
Referencias
- ^ abcdefg Duffin, Ross W. (2008). Cómo el temperamento igual arruinó la armonía: (y por qué debería importarte) (Publicado por primera vez como edición de bolsillo de Norton). Nueva York: WW Norton. p. 163. ISBN 978-0-393-33420-3. Recuperado el 28 de junio de 2017 .
- ^ Haluska, enero (2003). La teoría matemática de los sistemas tonales , p. xiv. ISBN 0-8247-4714-3 . Semitono armónico.
- ^ Semitono , medio paso , medio tono , semitono y semitono se utilizan de diversas formas en las fuentes.[1][2][3][4][5]
Aaron Copland , Leonard Bernstein y otros usan "medio tono".[6] [7][8][9]
Una fuente dice que el paso es "principalmente estadounidense",[10] y que el medio tono es "principalmente norteamericano".[11] - ^ Miller, Michael. Guía completa para idiotas sobre teoría musical, 2.ª ed. [Indianápolis, Indiana]: Alpha, 2005. ISBN 1-59257-437-8 . pág. 19.
- ^ Capstick, John Walton (1913). Sonido: un libro de texto elemental para escuelas y universidades. Cambridge University Press.
- ^ "musictheory.net". www.musictheory.net . Consultado el 4 de enero de 2024 .
- ^ Wharram, Barbara (2010). Rudimentos elementales de música (2.ª ed.). Mississauga, Ontario: Frederick Harris Music. pág. 17. ISBN 978-1-55440-283-0.
- ^ ab Paul, Oscar (1885). Un manual de armonía para uso en escuelas de música y seminarios y para autoinstrucción , pág. 165. Theodore Baker , trad. G. Schirmer.
- ^ Benward y Saker (2003). Música: en teoría y práctica, vol. I , pág. 54. ISBN 978-0-07-294262-0 . No se proporciona un ejemplo específico de un A1, pero se describe un ejemplo general de intervalos perfectos.
- ^ Kostka y Payne (2003). Tonal Harmony , pág. 21. ISBN 0-07-285260-7 . "No existe tal cosa como un unísono disminuido".
- ^ Day y Pilhofer (2007). Teoría musical para tontos , pág. 113. ISBN 0-7645-7838-3 . "No existe tal cosa como unísono disminuido, porque no importa cómo cambies los unísonos con alteraciones, estás agregando semitonos al intervalo total".
- ^ Surmani, Andrew ; Karen Farnum Surmani; Morton Manus (2009). Fundamentos de teoría musical de Alfred: un curso completo de autoaprendizaje para todos los músicos . Alfred Music Publishing. pág. 135. ISBN 978-0-7390-3635-8. Dado que disminuir cualquiera de las notas de un unísono perfecto en realidad aumentaría su tamaño, el unísono perfecto no se puede disminuir, solo aumentar.
- ^ ab Dahlhaus, Carl , trad. Gjerdingen, Robert O. Estudios sobre el origen de la tonalidad armónica . Princeton University Press: Princeton, 1990. ISBN 0-691-09135-8 .
- ^ Rashed, Roshdi (ed.) (1996). Enciclopedia de la historia de la ciencia árabe, volumen 2 , págs. 588, 608. Routledge. ISBN 0-415-12411-5 .
- ^ Hermann von Helmholtz (1885). Sobre las sensaciones del sonido como base fisiológica de la teoría de la música , pág. 454.
- ^ Benson, Dave (2006). Música: una propuesta matemática , pág. 369. ISBN 0-521-85387-7 .
- ^ " [sin título citado] ". Actas de la Royal Society de Londres . 30. Gran Bretaña: Royal Society: 531. 1880.
Digitalizado el 26 de febrero de 2008; Universidad de Harvard
- ^ ab Fonville, J. (verano de 1991). " La entonación justa extendida de Ben Johnston : una guía para intérpretes". Perspectivas de la nueva música . 29 (2): 106–137. doi :10.2307/833435. JSTOR 833435.
... el
25/24La relación es la relación sostenida ( ♯ ) ... esto eleva una nota aproximadamente 70,6 centavos. (p109)
- ^ Prout, E. (2004). Armonía . Prensa Universitaria del Pacífico. pág. 325. ISBN 1-4102-1920-8.
Lectura adicional
- Grout, Donald Jay y Claude V. Palisca . Una historia de la música occidental, 6ª ed . Nueva York: Norton, 2001. ISBN 0-393-97527-4 .
- Hoppin, Richard H. Música medieval . Nueva York: WW Norton, 1978. ISBN 0-393-09090-6 .




![{\displaystyle {\sqrt[{4}]{\frac {2}{3-{\sqrt {2}}}}}\approx 100,4{\text{ centavos,}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/237847316a3aea533ae093273132eda8e4d25250)








