Protuberancia ecuatorial
Este artículo necesita citas adicionales para su verificación . ( abril de 2023 ) |
Un abultamiento ecuatorial es una diferencia entre los diámetros ecuatorial y polar de un planeta , debido a la fuerza centrífuga ejercida por la rotación sobre el eje del cuerpo. Un cuerpo en rotación tiende a formar un esferoide achatado en lugar de una esfera .

En la Tierra
El planeta Tierra tiene una protuberancia ecuatorial bastante leve; su diámetro ecuatorial es aproximadamente 43 km (27 mi) mayor que su diámetro polar, con una diferencia de aproximadamente 1 ⁄ 298 del diámetro ecuatorial. Si la Tierra se redujera a un globo con un diámetro ecuatorial de 1 metro (3,3 pies), esa diferencia sería de solo 3 mm (0,12 pulgadas). Si bien es demasiado pequeña para notarla visualmente, esa diferencia sigue siendo más del doble de las mayores desviaciones de la superficie real con respecto al elipsoide, incluidas las montañas más altas y las fosas oceánicas más profundas .
La rotación de la Tierra también afecta al nivel del mar , la superficie imaginaria que se utiliza como marco de referencia para medir las altitudes . Esta superficie coincide con el nivel medio de las aguas superficiales de los océanos y se extrapola a la tierra teniendo en cuenta el potencial gravitatorio local y la fuerza centrífuga.
La diferencia de los radios es, por tanto, de unos 21 km (13 mi). Por tanto, un observador situado a nivel del mar en cualquiera de los polos está 21 km (13 mi) más cerca del centro de la Tierra que si se encuentra a nivel del mar en el Ecuador. Como resultado, el punto más alto de la Tierra, medido desde el centro hacia fuera, es el pico del monte Chimborazo en Ecuador en lugar del monte Everest . Pero como el océano también se abulta, como la Tierra y su atmósfera , el Chimborazo no está tan alto sobre el nivel del mar como el Everest. Del mismo modo, el punto más bajo de la Tierra, medido desde el centro hacia fuera, es el abismo de Litke en el océano Ártico en lugar del abismo de Challenger en el océano Pacífico . Pero como el océano también se aplana, como la Tierra y su atmósfera, el abismo de Litke no está tan bajo por debajo del nivel del mar como el abismo de Challenger.
Más precisamente, la superficie de la Tierra suele aproximarse mediante un elipsoide oblato ideal , a los efectos de definir con precisión la cuadrícula de latitud y longitud para la cartografía , así como el "centro de la Tierra". En el elipsoide terrestre estándar WGS-84 , ampliamente utilizado para la elaboración de mapas y el sistema GPS , se supone que el radio de la Tierra es de 6 378,137 km ( 3 963,191 mi) hasta el Ecuador y de 6 356,752 3142 km ( 3 949,902 7642 mi) hasta cada polo, lo que significa una diferencia de 21,384 6858 km ( 13,287 8277 mi) entre los radios o 42,769 3716 km ( 26,575 6554 mi) entre los diámetros, y un aplanamiento relativo de 1/298,257223563. La superficie del océano está mucho más cerca de este elipsoide estándar que la superficie sólida de la Tierra.
El equilibrio como balance de energías
La gravedad tiende a contraer un cuerpo celeste hasta formar una esfera , la forma en la que toda la masa está lo más cerca posible del centro de gravedad. La rotación provoca una distorsión de esta forma esférica; una medida común de la distorsión es el aplanamiento (a veces llamado elipticidad u oblato), que puede depender de una variedad de factores, incluidos el tamaño, la velocidad angular , la densidad y la elasticidad .
Una forma de hacerse una idea del tipo de equilibrio que se produce es imaginar a una persona sentada en una silla giratoria y sosteniendo una pesa en cada mano; si la persona tira de las pesas hacia adentro, se realiza un trabajo y aumenta su energía cinética rotacional. El aumento de la velocidad de rotación es tan fuerte que, a una velocidad de rotación más rápida, la fuerza centrípeta requerida es mayor que con la velocidad de rotación inicial.
Algo similar ocurre en la formación de planetas: primero la materia se fusiona formando una distribución en forma de disco que gira lentamente y las colisiones y la fricción convierten la energía cinética en calor, lo que permite que el disco gravite por sí mismo y se convierta en un esferoide muy achatado.
Mientras el protoplaneta sea demasiado achatado para estar en equilibrio, la liberación de energía potencial gravitatoria durante la contracción seguirá impulsando el aumento de la energía cinética rotacional. A medida que avanza la contracción, la velocidad de rotación seguirá aumentando, por lo que la fuerza necesaria para una mayor contracción seguirá aumentando. Hay un punto en el que el aumento de la energía cinética rotacional durante una mayor contracción sería mayor que la liberación de energía potencial gravitatoria. El proceso de contracción solo puede continuar hasta ese punto, por lo que se detiene allí.
Mientras no haya equilibrio, puede haber convección violenta, y mientras haya convección violenta, la fricción puede convertir la energía cinética en calor, drenando energía cinética rotacional del sistema. Cuando se alcanza el estado de equilibrio, cesa la conversión a gran escala de energía cinética en calor. En ese sentido, el estado de equilibrio es el estado de energía más bajo que se puede alcanzar.
La velocidad de rotación de la Tierra sigue disminuyendo, aunque de forma gradual, a razón de unas dos milésimas de segundo por rotación cada 100 años. [1] Las estimaciones sobre la velocidad de rotación de la Tierra en el pasado varían, porque no se sabe exactamente cómo se formó la Luna. Las estimaciones de la rotación de la Tierra hace 500 millones de años son de unas 20 horas modernas por "día".
La velocidad de rotación de la Tierra se está desacelerando principalmente debido a las interacciones de las mareas con la Luna y el Sol. Dado que las partes sólidas de la Tierra son dúctiles , el abultamiento ecuatorial de la Tierra ha estado disminuyendo al mismo ritmo que la disminución de la velocidad de rotación.
Efecto sobre la aceleración gravitacional
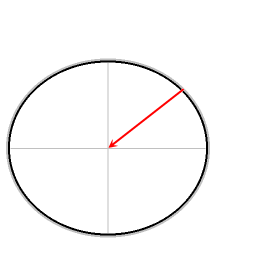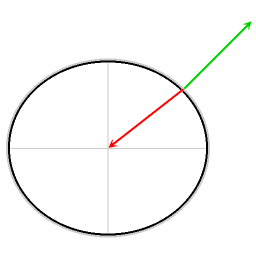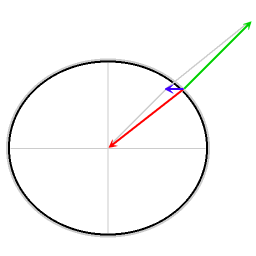
Flecha roja: gravedad
Flecha verde: fuerza normal
Flecha azul: fuerza resultante
La fuerza resultante proporciona la fuerza centrípeta requerida. Sin esta fuerza centrípeta, los objetos sin fricción se deslizarían hacia el ecuador.
En los cálculos, cuando se utiliza un sistema de coordenadas que gira conjuntamente con la Tierra, el vector de la fuerza centrífuga teórica apunta hacia afuera y es tan grande como el vector que representa la fuerza centrípeta.
Debido a la rotación de un planeta sobre su propio eje, la aceleración gravitacional es menor en el ecuador que en los polos . En el siglo XVII, tras la invención del reloj de péndulo , los científicos franceses descubrieron que los relojes enviados a la Guayana Francesa , en la costa norte de América del Sur , funcionaban más lentamente que sus homólogos exactos en París. Las mediciones de la aceleración debida a la gravedad en el ecuador también deben tener en cuenta la rotación del planeta. Cualquier objeto que esté estacionario con respecto a la superficie de la Tierra sigue en realidad una trayectoria circular, circunnavegando el eje de la Tierra. Para atraer un objeto hacia una trayectoria circular de este tipo se necesita una fuerza. La aceleración que se requiere para circunnavegar el eje de la Tierra a lo largo del ecuador a una revolución por día sideral es de 0,0339 m/s2 . Al proporcionar esta aceleración se reduce la aceleración gravitacional efectiva. En el ecuador, la aceleración gravitacional efectiva es de 9,7805 m/ s2 . Esto significa que la verdadera aceleración gravitacional en el Ecuador debe ser 9,8144 m/s2 ( 9,7805 + 0,0339 = 9,8144).
En los polos, la aceleración gravitacional es de 9,8322 m/s 2 . La diferencia de 0,0178 m/s 2 entre la aceleración gravitacional en los polos y la aceleración gravitacional real en el Ecuador se debe a que los objetos ubicados en el Ecuador están aproximadamente 21 km (13 mi) más lejos del centro de masa de la Tierra que en los polos, lo que corresponde a una aceleración gravitacional menor.
En resumen, hay dos factores que contribuyen a que la aceleración gravitatoria efectiva sea menor en el ecuador que en los polos: aproximadamente el 70% de la diferencia se debe al hecho de que los objetos giran alrededor del eje de la Tierra y aproximadamente el 30% se debe a la forma no esférica de la Tierra.
El diagrama ilustra que en todas las latitudes la aceleración gravitacional efectiva disminuye por la necesidad de proporcionar una fuerza centrípeta; el efecto decreciente es más fuerte en el ecuador.
Efecto sobre las órbitas de los satélites
El hecho de que el campo gravitatorio de la Tierra se desvíe ligeramente de ser esféricamente simétrico también afecta a las órbitas de los satélites a través de precesiones orbitales seculares . [2] [3] [4] Dependen de la orientación del eje de simetría de la Tierra en el espacio inercial y, en el caso general, afectan a todos los elementos orbitales keplerianos con la excepción del semieje mayor . Si el eje de referencia z del sistema de coordenadas adoptado está alineado a lo largo del eje de simetría de la Tierra, entonces solo la longitud del nodo ascendente Ω, el argumento del pericentro ω y la anomalía media M experimentan precesiones seculares. [5]
Estas perturbaciones, que antes se utilizaban para mapear el campo gravitacional de la Tierra desde el espacio, [6] pueden jugar un papel perturbador relevante cuando se utilizan satélites para realizar pruebas de relatividad general [7] porque los efectos relativistas mucho más pequeños son cualitativamente indistinguibles de las perturbaciones impulsadas por la achatamiento.
Formulación
El aplanamiento para la configuración de equilibrio de un esferoide autogravitante, compuesto de fluido incompresible de densidad uniforme, que gira de manera constante alrededor de un eje fijo, para una pequeña cantidad de aplanamiento, se aproxima mediante: [8]
dónde
- es la constante gravitacional universal ,
- es el radio medio,
- y son respectivamente el radio ecuatorial y polar, [ dudoso – discutir ]
- es el período de rotación y es la velocidad angular ,
- es la densidad corporal y es la masa corporal total.
Una cantidad relacionada es el segundo factor de forma dinámico del cuerpo , J 2 : [9]
con J 2 = − √ 5 C 20 =1.082 626 68 × 10 −3 para la Tierra, [10] donde
- ε E es la oblatividad del cuerpo central,
- R E es el radio ecuatorial del cuerpo central (6 378 137 m para la Tierra),
- ω E es la velocidad de rotación del cuerpo central (7,292 115 × 10 −5 rad/s para la Tierra),
- GM E es el producto de la constante universal de gravitación y la masa del cuerpo central (3,986 004 418 × 10 14 m 3 /s 2 para la Tierra).
Valores típicos
El aplanamiento real es menor debido a la concentración de masa en el centro de los cuerpos celestes.
| una y [km] | una p [km] | f de verdad | Yo [yo] | M [10,26 kg ] | fórmula f | |
|---|---|---|---|---|---|---|
| Júpiter | 71,492 | 66.854 | 0,066 | 9.9 | 18,98 | 0,104 |
| Saturno | 60,268 | 54.364 | 0,108 | 10.6 | 5.68 | 0,178 |
| Urano | 25,559 | 24.973 | 0,023 | 17.2 | 0,87 | 0,036 |
| Neptuno | 24.764 | 24.341 | 0,017 | 16.1 | 1.02 | 0,032 |
Véase también
- Objeto astronómico § Forma
- Teorema de Clairaut (gravedad)
- La gravedad de la Tierra
- Aplanamiento planetario
Referencias
- ^ Hadhazy, Adam. "Realidad o ficción: los días (y las noches) se están haciendo más largos". Scientific American . Consultado el 5 de diciembre de 2011 .
- ^ Iorio, L. (2011). "Movimientos estelares perturbados alrededor del agujero negro giratorio en Sgr A* para una orientación genérica de su eje de giro". Physical Review D . 84 (12): 124001. arXiv : 1107.2916 . Bibcode :2011PhRvD..84l4001I. doi :10.1103/PhysRevD.84.124001. S2CID 118305813.
- ^ Renzetti, G. (2013). "Precesiones orbitales de satélites causadas por el momento de masa octupolar de un cuerpo no esférico arbitrariamente orientado en el espacio". Revista de Astrofísica y Astronomía . 34 (4): 341–348. Bibcode :2013JApA...34..341R. doi :10.1007/s12036-013-9186-4. S2CID 120030309.
- ^ Renzetti, G. (2014). "Precesiones orbitales de satélites causadas por el primer multipolo zonal J3 impar de un cuerpo no esférico orientado arbitrariamente en el espacio". Astrofísica y ciencia espacial . 352 (2): 493–496. Bibcode :2014Ap&SS.352..493R. doi :10.1007/s10509-014-1915-x. S2CID 119537102.
- ^ King-Hele, DG (1961). "El potencial gravitatorio de la Tierra, deducido de las órbitas de satélites artificiales". Revista Geofísica . 4 (1): 3–16. Código Bibliográfico :1961GeoJ....4....3K. doi : 10.1111/j.1365-246X.1961.tb06801.x .
- ^ King-Hele, DG (1983). "Investigaciones geofísicas con las órbitas de los primeros satélites". Revista Geofísica . 74 (1): 7–23. Código Bibliográfico :1983GeoJ...74....7K. doi : 10.1111/j.1365-246X.1983.tb01868.x .
- ^ Renzetti, G. (2012). "¿Son los zonales de grado superior realmente perjudiciales para el experimento de arrastre de marco LARES/LAGEOS?". Revista Canadiense de Física . 90 (9): 883–888. Bibcode :2012CaJPh..90..883R. doi :10.1139/p2012-081.
- ^ "Aplanamiento rotacional". utexas.edu .
- ^ UCSD David T.Sandwell – Campo de gravedad (2002) (PDF) .
- ^ IERS - Modelo geopotencial (2010) (PDF) .











