Velocidad del sonido
_-_filtered.jpg/440px-FA-18_Hornet_breaking_sound_barrier_(7_July_1999)_-_filtered.jpg)
| Mediciones de sonido | |
|---|---|
Característica | Símbolos |
| Presión sonora | p , SPL , LPA |
| Velocidad de la partícula | v , LLV |
| Desplazamiento de partículas | del |
| Intensidad del sonido | Yo , SIL |
| Potencia del sonido | P , SWL, LWA |
| Energía sonora | Yo |
| Densidad de energía del sonido | el |
| Exposición al sonido | Yo , SEL |
| Impedancia acústica | O |
| Audiofrecuencia | A.C. |
| Pérdida de transmisión | ES |
La velocidad del sonido es la distancia recorrida por unidad de tiempo por una onda sonora a medida que se propaga a través de un medio elástico . En términos más simples, la velocidad del sonido es la velocidad a la que viajan las vibraciones. A 20 °C (68 °F), la velocidad del sonido en el aire es de aproximadamente 343 m/s (1125 ft/s ; 1235 km/h ; 767 mph ; 667 kn ), o1 km en2,91 s o una milla en4,69 s . Depende en gran medida de la temperatura, así como del medio a través del cual se propaga la onda sonora . A 0 °C (32 °F), la velocidad del sonido en el aire es de aproximadamente 331 m/s (1086 ft/s; 1192 km/h; 740 mph; 643 kn). [1]
La velocidad del sonido en un gas ideal depende únicamente de su temperatura y composición. La velocidad tiene una dependencia débil de la frecuencia y la presión en el aire ordinario, desviándose ligeramente del comportamiento ideal. En el lenguaje coloquial, la velocidad del sonido se refiere a la velocidad de las ondas sonoras en el aire . Sin embargo, la velocidad del sonido varía de una sustancia a otra: por lo general, el sonido viaja más lentamente en los gases , más rápido en los líquidos y más rápido en los sólidos . Por ejemplo, mientras que el sonido viaja a343 m/s en el aire, viaja a1481 m/s en el agua (casi 4,3 veces más rápido) y a5120 m/s en hierro (casi 15 veces más rápido). En un material excepcionalmente rígido como el diamante, el sonido viaja a 12 000 m/s (39 370 pies/s), [2] – alrededor de 35 veces su velocidad en el aire y aproximadamente la más rápida que puede viajar en condiciones normales. En teoría, la velocidad del sonido es en realidad la velocidad de las vibraciones. Las ondas sonoras en sólidos se componen de ondas de compresión (al igual que en gases y líquidos) y un tipo diferente de onda sonora llamada onda transversal , que se produce solo en sólidos. Las ondas transversales en sólidos generalmente viajan a velocidades diferentes a las ondas de compresión, como se muestra en la sismología . La velocidad de las ondas de compresión en sólidos está determinada por la compresibilidad , el módulo de corte y la densidad del medio. La velocidad de las ondas transversales está determinada solo por el módulo de corte y la densidad del material sólido.
En dinámica de fluidos , la velocidad del sonido en un medio fluido (gas o líquido) se utiliza como medida relativa de la velocidad de un objeto que se mueve a través del medio. La relación entre la velocidad de un objeto y la velocidad del sonido (en el mismo medio) se denomina número de Mach del objeto . Se dice que los objetos que se mueven a velocidades superiores a la velocidad del sonido ( Mach 1 ) viajan a velocidades supersónicas .
Tierra
En la atmósfera de la Tierra, la velocidad del sonido varía enormemente, desde unos 295 m/s (1.060 km/h; 660 mph) a grandes altitudes hasta unos 355 m/s (1.280 km/h; 790 mph) a altas temperaturas.
Historia
Los Principia de Sir Isaac Newton de 1687 incluyen un cálculo de la velocidad del sonido en el aire de 979 pies por segundo (298 m/s). Esta cifra es aproximadamente un 15 % inferior a la real. [3] La discrepancia se debe principalmente a que se descuida el efecto (entonces desconocido) de la temperatura rápidamente fluctuante en una onda sonora (en términos modernos, la compresión y expansión de la onda sonora en el aire es un proceso adiabático , no un proceso isotérmico ). Este error fue rectificado posteriormente por Laplace . [4]
Durante el siglo XVII hubo varios intentos de medir la velocidad del sonido con precisión, incluidos los intentos de Marin Mersenne en 1630 (1.380 pies parisinos por segundo), Pierre Gassendi en 1635 (1.473 pies parisinos por segundo) y Robert Boyle (1.125 pies parisinos por segundo). [5] En 1709, el reverendo William Derham , rector de Upminster, publicó una medida más precisa de la velocidad del sonido, en 1.072 pies parisinos por segundo. [5] (El pie parisino era325 mm . Es más largo que el "pie internacional" estándar de uso común en la actualidad, que se definió oficialmente en 1959 como304,8 mm , lo que hace que la velocidad del sonido a 20 °C (68 °F) sea de 1.055 pies parisinos por segundo).
Derham utilizó un telescopio desde la torre de la iglesia de St. Laurence, Upminster , para observar el destello de un disparo de escopeta distante y luego midió el tiempo hasta que escuchó el disparo con un péndulo de medio segundo. Se realizaron mediciones de disparos desde varios puntos de referencia locales, incluida la iglesia de North Ockendon . La distancia se conoció por triangulación y, por lo tanto, se calculó la velocidad a la que había viajado el sonido. [6]
Conceptos básicos
La transmisión del sonido se puede ilustrar utilizando un modelo que consiste en un conjunto de objetos esféricos interconectados por resortes.
En términos materiales reales, las esferas representan las moléculas del material y los resortes representan los enlaces entre ellas. El sonido pasa a través del sistema comprimiendo y expandiendo los resortes, transmitiendo la energía acústica a las esferas vecinas. Esto ayuda a transmitir la energía a su vez a los resortes de las esferas vecinas (enlaces), y así sucesivamente.
La velocidad del sonido a través del modelo depende de la rigidez de los resortes y de la masa de las esferas. Mientras el espaciamiento de las esferas permanezca constante, los resortes o enlaces más rígidos transmiten energía más rápidamente, mientras que las esferas más masivas transmiten energía más lentamente.
En un material real, la rigidez de los resortes se conoce como " módulo elástico ", y la masa corresponde a la densidad del material . El sonido se propagará más lentamente en materiales esponjosos y más rápido en los más rígidos. Efectos como la dispersión y la reflexión también se pueden entender utilizando este modelo. [ cita requerida ]
Algunos libros de texto afirman erróneamente que la velocidad del sonido aumenta con la densidad. Esta idea se ilustra presentando datos de tres materiales, como el aire, el agua y el acero, y observando que la velocidad del sonido es mayor en los materiales más densos. Pero el ejemplo no tiene en cuenta que los materiales tienen una compresibilidad muy diferente, lo que compensa con creces las diferencias de densidad, que reducirían la velocidad de las ondas en los materiales más densos. Un ejemplo ilustrativo de los dos efectos es que el sonido viaja solo 4,3 veces más rápido en el agua que en el aire, a pesar de las enormes diferencias de compresibilidad entre los dos medios. La razón es que la mayor densidad del agua, que actúa para reducir la velocidad del sonido en el agua en relación con el aire, casi compensa las diferencias de compresibilidad entre los dos medios.
Por ejemplo, el sonido se propaga 1,59 veces más rápido en el níquel que en el bronce, debido a la mayor rigidez del níquel a una densidad similar. De manera similar, el sonido se propaga aproximadamente 1,41 veces más rápido en el gas de hidrógeno ligero ( protio ) que en el gas de hidrógeno pesado ( deuterio ), ya que el deuterio tiene propiedades similares pero el doble de densidad. Al mismo tiempo, el sonido de "tipo compresión" se propaga más rápido en los sólidos que en los líquidos, y más rápido en los líquidos que en los gases, porque los sólidos son más difíciles de comprimir que los líquidos, mientras que los líquidos, a su vez, son más difíciles de comprimir que los gases.
Un ejemplo práctico se puede observar en Edimburgo, cuando se dispara el "cañón de la una" en el extremo oriental del Castillo de Edimburgo. Desde la base del extremo occidental de Castle Rock, el sonido del cañón se puede escuchar a través de la roca, un poco antes de que llegue por vía aérea, parcialmente retrasado por la ruta ligeramente más larga. Es especialmente eficaz si se dispara un saludo con varios cañones, como por ejemplo para el "Cumpleaños de la Reina".
Ondas de compresión y de corte


En un gas o líquido, el sonido consiste en ondas de compresión. En los sólidos, las ondas se propagan como dos tipos diferentes. Una onda longitudinal está asociada con la compresión y descompresión en la dirección de propagación, y es el mismo proceso en gases y líquidos, con una onda de tipo compresión análoga en sólidos. Solo las ondas de compresión se admiten en gases y líquidos. Un tipo adicional de onda, la onda transversal , también llamada onda de corte , ocurre solo en sólidos porque solo los sólidos admiten deformaciones elásticas. Se debe a la deformación elástica del medio perpendicular a la dirección de propagación de la onda; la dirección de la deformación de corte se llama " polarización " de este tipo de onda. En general, las ondas transversales ocurren como un par de polarizaciones ortogonales .
Estas diferentes ondas (ondas de compresión y las diferentes polarizaciones de las ondas transversales) pueden tener distintas velocidades a la misma frecuencia, por lo que llegan al observador en momentos diferentes. Un ejemplo extremo es un terremoto , donde las ondas de compresión agudas llegan primero y las ondas transversales oscilantes segundos después.
La velocidad de una onda de compresión en un fluido está determinada por la compresibilidad y la densidad del medio . En los sólidos, las ondas de compresión son análogas a las de los fluidos, dependiendo de la compresibilidad y la densidad, pero con el factor adicional del módulo de corte que afecta a las ondas de compresión debido a las energías elásticas fuera del eje que pueden influir en la tensión y la relajación efectivas en una compresión. La velocidad de las ondas de corte, que solo pueden ocurrir en sólidos, está determinada simplemente por el módulo de corte y la densidad del material sólido.
Ecuaciones
La velocidad del sonido en notación matemática se representa convencionalmente por c , del latín celeritas, que significa "rapidez".
Para los fluidos en general, la velocidad del sonido c viene dada por la ecuación de Newton-Laplace: donde
- es un coeficiente de rigidez, el módulo volumétrico isentrópico (o el módulo de elasticidad volumétrica para gases);
- es la densidad .
, donde es la presión y la derivada se toma isentrópicamente, es decir, con entropía constante s . Esto se debe a que una onda de sonido viaja tan rápido que su propagación puede aproximarse como un proceso adiabático , lo que significa que no hay tiempo suficiente, durante un ciclo de presión del sonido, para que se produzca una conducción y radiación de calor significativas.
Por lo tanto, la velocidad del sonido aumenta con la rigidez (la resistencia de un cuerpo elástico a la deformación por una fuerza aplicada) del material y disminuye con un aumento de la densidad. Para los gases ideales, el módulo volumétrico K es simplemente la presión del gas multiplicada por el índice adiabático adimensional , que es aproximadamente 1,4 para el aire en condiciones normales de presión y temperatura.
Para las ecuaciones de estado generales , si se utiliza la mecánica clásica , la velocidad del sonido c se puede derivar [7] de la siguiente manera:
Consideremos la onda sonora propagándose a velocidad a través de un tubo alineado con el eje y con un área de sección transversal de . En el intervalo de tiempo se mueve una longitud de . En estado estacionario , el caudal másico debe ser el mismo en los dos extremos del tubo, por lo tanto, el flujo másico es constante y . Según la segunda ley de Newton , la fuerza del gradiente de presión proporciona la aceleración:
Y por lo tanto:
Si los efectos relativistas son importantes, la velocidad del sonido se calcula a partir de las ecuaciones relativistas de Euler .
En un medio no dispersivo , la velocidad del sonido es independiente de la frecuencia del sonido , por lo que las velocidades de transporte de energía y propagación del sonido son las mismas para todas las frecuencias. El aire, una mezcla de oxígeno y nitrógeno, constituye un medio no dispersivo. Sin embargo, el aire contiene una pequeña cantidad de CO 2 que es un medio dispersivo y causa dispersión en el aire a frecuencias ultrasónicas (superiores a28 kHz ). [8]
En un medio dispersivo , la velocidad del sonido es una función de la frecuencia del sonido, a través de la relación de dispersión . Cada componente de frecuencia se propaga a su propia velocidad, llamada velocidad de fase , mientras que la energía de la perturbación se propaga a la velocidad de grupo . El mismo fenómeno ocurre con las ondas de luz; consulte la dispersión óptica para obtener una descripción.
Dependencia de las propiedades del medio
La velocidad del sonido es variable y depende de las propiedades de la sustancia a través de la cual viaja la onda. En los sólidos, la velocidad de las ondas transversales (o de corte) depende de la deformación de corte bajo tensión de corte (llamada módulo de corte ) y de la densidad del medio. Las ondas longitudinales (o de compresión) en los sólidos dependen de los mismos dos factores con el añadido de una dependencia de la compresibilidad .
En los fluidos, sólo la compresibilidad y la densidad del medio son factores importantes, ya que los fluidos no transmiten tensiones de corte. En fluidos heterogéneos, como un líquido lleno de burbujas de gas, la densidad del líquido y la compresibilidad del gas afectan a la velocidad del sonido de manera aditiva, como se demuestra en el efecto del chocolate caliente .
En los gases, la compresibilidad adiabática está directamente relacionada con la presión a través de la relación de capacidad térmica (índice adiabático), mientras que la presión y la densidad están inversamente relacionadas con la temperatura y el peso molecular, lo que hace que solo las propiedades completamente independientes de la temperatura y la estructura molecular sean importantes (la relación de capacidad térmica puede determinarse por la temperatura y la estructura molecular, pero el simple peso molecular no es suficiente para determinarla).
El sonido se propaga más rápido en gases de bajo peso molecular , como el helio, que en gases más pesados, como el xenón . En el caso de los gases monoatómicos, la velocidad del sonido es aproximadamente el 75 % de la velocidad media a la que se mueven los átomos en ese gas.
Para un gas ideal dado, la composición molecular es fija y, por lo tanto, la velocidad del sonido depende solo de su temperatura . A una temperatura constante, la presión del gas no tiene efecto sobre la velocidad del sonido, ya que la densidad aumentará y, dado que la presión y la densidad (también proporcionales a la presión) tienen efectos iguales pero opuestos sobre la velocidad del sonido, y las dos contribuciones se cancelan exactamente. De manera similar, las ondas de compresión en los sólidos dependen tanto de la compresibilidad como de la densidad (al igual que en los líquidos), pero en los gases la densidad contribuye a la compresibilidad de tal manera que una parte de cada atributo se excluye, dejando solo una dependencia de la temperatura, el peso molecular y la relación de capacidad térmica que se puede derivar independientemente de la temperatura y la composición molecular (ver las derivaciones a continuación). Por lo tanto, para un solo gas dado (suponiendo que el peso molecular no cambia) y en un pequeño rango de temperatura (para el cual la capacidad térmica es relativamente constante), la velocidad del sonido depende solo de la temperatura del gas.
En el régimen de comportamiento de gas no ideal, para el cual se utilizaría la ecuación de gas de Van der Waals , la proporcionalidad no es exacta y existe una ligera dependencia de la velocidad del sonido con respecto a la presión del gas.
La humedad tiene un efecto pequeño pero medible en la velocidad del sonido (hace que aumente entre un 0,1% y un 0,6%), porque las moléculas de oxígeno y nitrógeno del aire son reemplazadas por moléculas más ligeras de agua . Se trata de un simple efecto de mezcla.
Variación de altitud e implicaciones para la acústica atmosférica

En la atmósfera terrestre , el factor principal que afecta la velocidad del sonido es la temperatura . Para un gas ideal dado con capacidad calorífica y composición constantes, la velocidad del sonido depende únicamente de la temperatura; véase el apartado Detalles más abajo. En un caso ideal de este tipo, los efectos de la disminución de la densidad y de la presión de la altitud se anulan entre sí, salvo por el efecto residual de la temperatura.
Dado que la temperatura (y por tanto la velocidad del sonido) disminuye con el aumento de la altitud hastaA 11 km , el sonido se refracta hacia arriba, lejos de los oyentes en el suelo, creando una sombra acústica a cierta distancia de la fuente. [9] La disminución de la velocidad del sonido con la altura se conoce como gradiente negativo de la velocidad del sonido .
Sin embargo, existen variaciones en esta tendencia anterior.11 km . En particular, en la estratosfera por encima de aproximadamenteA 20 km , la velocidad del sonido aumenta con la altura, debido a un aumento de temperatura por el calentamiento dentro de la capa de ozono . Esto produce un gradiente positivo de velocidad del sonido en esta región. Otra región de gradiente positivo se produce a altitudes muy elevadas, en la termosfera por encima de90 kilometros .
Detalles
Velocidad del sonido en gases ideales y aire.
Para un gas ideal, K (el módulo volumétrico en las ecuaciones anteriores, equivalente a C , el coeficiente de rigidez en sólidos) está dado por Por lo tanto, a partir de la ecuación de Newton-Laplace anterior, la velocidad del sonido en un gas ideal está dada por donde
- γ es el índice adiabático también conocido como factor de expansión isentrópica . Es la relación entre el calor específico de un gas a presión constante y el de un gas a volumen constante ( ) y surge porque una onda de sonido clásica induce una compresión adiabática, en la que el calor de la compresión no tiene tiempo suficiente para escapar del pulso de presión y, por lo tanto, contribuye a la presión inducida por la compresión;
- p es la presión ;
- ρ es la densidad .
Usando la ley de los gases ideales para reemplazar p con nRT / V , y reemplazando ρ con nM / V , la ecuación para un gas ideal se convierte en donde
- c ideal es la velocidad del sonido en un gas ideal ;
- R es la constante molar del gas ;
- k es la constante de Boltzmann ;
- γ (gamma) es el índice adiabático . A temperatura ambiente, donde la energía térmica se reparte completamente en rotación (las rotaciones están completamente excitadas) pero los efectos cuánticos impiden la excitación de los modos vibracionales, el valor es 7/5 = 1,400 para gases diatómicos (como el oxígeno y el nitrógeno ), según la teoría cinética. En realidad, el índice gamma se mide experimentalmente en un rango de 1,3991 a 1,403 a0 °C , para el aire. Gamma es exactamente 5/3 = 1,667 para gases monoatómicos (como el argón ) y es 4/3 = 1,333 para gases de moléculas triatómicas que, como el H
2O , no son colineales (un gas triatómico colineal como el CO
2es equivalente a un gas diatómico para nuestros propósitos aquí); - T es la temperatura absoluta;
- M es la masa molar del gas. La masa molar media del aire seco es de aproximadamente 0,02897 kg/mol (28,97 g/mol);
- n es el número de moles;
- m es la masa de una sola molécula.
Esta ecuación se aplica únicamente cuando la onda sonora es una pequeña perturbación de las condiciones ambientales y se cumplen las otras condiciones señaladas, como se indica a continuación. Se ha descubierto que los valores calculados para c aire varían ligeramente de los valores determinados experimentalmente. [10]
Newton consideró la velocidad del sonido antes de la mayor parte del desarrollo de la termodinámica y, por lo tanto, utilizó incorrectamente cálculos isotérmicos en lugar de adiabáticos . Su resultado no tenía en cuenta el factor γ, pero por lo demás era correcto.
La sustitución numérica de los valores anteriores proporciona la aproximación de la velocidad del sonido para los gases, que es precisa a presiones y densidades de gas relativamente bajas (para el aire, esto incluye las condiciones estándar del nivel del mar en la Tierra). Además, para los gases diatómicos, el uso de γ = 1,4000 requiere que el gas exista en un rango de temperatura lo suficientemente alto como para que la capacidad calorífica rotacional se excite por completo (es decir, la rotación molecular se utiliza por completo como una "partición" o depósito de energía térmica); pero al mismo tiempo, la temperatura debe ser lo suficientemente baja como para que los modos vibracionales moleculares no contribuyan a la capacidad calorífica (es decir, entra en vibración un calor insignificante, ya que todos los modos cuánticos vibracionales por encima del modo de energía mínima tienen energías que son demasiado altas para ser pobladas por un número significativo de moléculas a esta temperatura). Para el aire, estas condiciones se cumplen a temperatura ambiente y también a temperaturas considerablemente inferiores a la temperatura ambiente (ver las tablas a continuación). Ver la sección sobre gases en capacidad calorífica específica para una discusión más completa de este fenómeno.
Para el aire, introducimos la taquigrafía
Además, pasamos a la temperatura Celsius θ = T −273,15 K , lo que resulta útil para calcular la velocidad del aire en la región cercana0 °C (273 K ). Luego, para aire seco,
Sustituyendo valores numéricos y utilizando el valor del gas diatómico ideal de γ = 1,4000 , tenemos
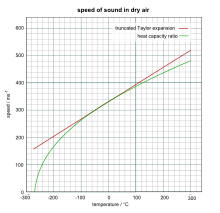
Finalmente, la expansión de Taylor de la raíz cuadrada restante en produce
A la derecha se muestra un gráfico que compara los resultados de las dos ecuaciones, utilizando el valor ligeramente más preciso de 331,5 m/s (1088 ft/s) para la velocidad del sonido.0 °C . [11] : 120-121
Efectos debidos a la cizalladura del viento
La velocidad del sonido varía con la temperatura. Dado que la temperatura y la velocidad del sonido normalmente disminuyen con el aumento de la altitud, el sonido se refracta hacia arriba, lejos de los oyentes en el suelo, creando una sombra acústica a cierta distancia de la fuente. [9] Una cizalladura del viento de 4 m/(s · km) puede producir una refracción igual a una tasa de gradiente de temperatura típica de7,5 °C/km . [12] Valores más altos de gradiente de viento refractarán el sonido hacia abajo, en dirección a la superficie, en la dirección de sotavento, [13] eliminando la sombra acústica en el lado de sotavento. Esto aumentará la audibilidad de los sonidos en la dirección de sotavento. Este efecto de refracción en la dirección de sotavento ocurre porque hay un gradiente de viento; el hecho de que el sonido sea transportado por el viento no es importante. [14]
Para la propagación del sonido, la variación exponencial de la velocidad del viento con la altura se puede definir de la siguiente manera: [15] donde
- U ( h ) es la velocidad del viento a la altura h ;
- ζ es el coeficiente exponencial basado en la rugosidad de la superficie del suelo, normalmente entre 0,08 y 0,52;
- dU / dH ( h ) es el gradiente de viento esperado a la altura h .
En la Batalla de Iuka de la Guerra Civil estadounidense de 1862 , una sombra acústica, que se cree que fue intensificada por un viento del noreste, mantuvo a dos divisiones de soldados de la Unión fuera de la batalla, [16] porque no podían escuchar los sonidos de la batalla solo10 km (seis millas) a favor del viento. [17]
Tablas
En la atmósfera estándar :
- T 0 es273,15 K (=0 °C =32 °F ), dando un valor teórico de331,3 m/s (=1 086 .9 pies/s =1193 kilómetros por hora =741,1 mph = 644,0 nudos ). Valores que van desde 331,3 aSin embargo, en la literatura de referencia se puede encontrar 331,6 m/s ;
- T 20 es293,15 K (=20 °C =68 °F ), dando un valor de343,2 m/s (=1 126 .0 pies/s =1236 kilómetros por hora =767,8 mph = 667,2 nudos );
- T 25 es298,15 K (=25 °C =77 °F ), dando un valor de346,1 m/s (=1 135 .6 pies/s =1246 kilómetros por hora =774,3 mph = 672,8 nudos ).
De hecho, suponiendo que se trata de un gas ideal , la velocidad del sonido c depende únicamente de la temperatura y la composición, no de la presión o la densidad (ya que estas cambian al unísono para una temperatura dada y se cancelan). El aire es casi un gas ideal. La temperatura del aire varía con la altitud, lo que da las siguientes variaciones en la velocidad del sonido utilizando la atmósfera estándar; las condiciones reales pueden variar . [ cita requerida ]
Temperatura Celsius θ [ °C ] | Velocidad del sonido c [ m / s ] | Densidad del aire ρ [ kg / m 3 ] | Impedancia acústica específica característica z 0 [ Pa ⋅ s / m ] |
|---|---|---|---|
| 35 | 351,88 | 1.1455 | 403.2 |
| 30 | 349.02 | 1.1644 | 406,5 |
| 25 | 346.13 | 1.1839 | 409.4 |
| 20 | 343.21 | 1.2041 | 413.3 |
| 15 | 340.27 | 1.2250 | 416.9 |
| 10 | 337.31 | 1.2466 | 420.5 |
| 5 | 334.32 | 1.2690 | 424.3 |
| 0 | 331.30 | 1.2922 | 428.0 |
| -5 | 328,25 | 1.3163 | 432.1 |
| -10 | 325,18 | 1.3413 | 436.1 |
| -15 | 322.07 | 1.3673 | 440.3 |
| -20 | 318,94 | 1.3943 | 444.6 |
| -25 | 315,77 | 1.4224 | 449.1 |
Dadas condiciones atmosféricas normales, la temperatura, y por tanto la velocidad del sonido, varía con la altitud:
| Altitud | Temperatura | EM | kilómetros por hora | millas por hora | saber |
|---|---|---|---|---|---|
| Nivel del mar | 15 °C (59 °F ) | 340 | 1.225 | 761 | 661 |
| 11.000 m a 20.000 m (altitud de crucero de aviones comerciales y primer vuelo supersónico ) | -57 °C (-70 °F ) | 295 | 1.062 | 660 | 573 |
| 29.000 m (vuelo del X-43A ) | -48 °C (−53 °F ) | 301 | 1.083 | 673 | 585 |
Efecto de la frecuencia y la composición del gas.
Consideraciones físicas generales
El medio en el que viaja una onda sonora no siempre responde adiabáticamente y, como resultado, la velocidad del sonido puede variar con la frecuencia. [18]
Las limitaciones del concepto de velocidad del sonido debido a la atenuación extrema también son motivo de preocupación. La atenuación que existe a nivel del mar para las frecuencias altas se aplica a frecuencias sucesivamente más bajas a medida que disminuye la presión atmosférica o a medida que aumenta el recorrido libre medio . Por esta razón, el concepto de velocidad del sonido (excepto para frecuencias que se aproximan a cero) pierde progresivamente su rango de aplicabilidad a grandes altitudes. [10] Las ecuaciones estándar para la velocidad del sonido se aplican con una precisión razonable solo a situaciones en las que la longitud de onda de la onda sonora es considerablemente más larga que el recorrido libre medio de las moléculas en un gas.
La composición molecular del gas influye tanto en la masa (M) de las moléculas como en sus capacidades térmicas, por lo que ambas influyen en la velocidad del sonido. En general, a la misma masa molecular, los gases monoatómicos tienen una velocidad del sonido ligeramente superior (más del 9 % superior) porque tienen un γ más alto ( 5/3 = 1,66 ...) que los diatómicos ( 7/5 = 1,4 ). Por lo tanto, a la misma masa molecular, la velocidad del sonido de un gas monoatómico aumenta en un factor de
Esto da una diferencia del 9%, y sería una relación típica para las velocidades del sonido a temperatura ambiente en helio vs. deuterio , cada uno con un peso molecular de 4. El sonido viaja más rápido en helio que en deuterio porque la compresión adiabática calienta más al helio, ya que las moléculas de helio pueden almacenar energía térmica de la compresión solo en traslación, pero no en rotación. Por lo tanto, las moléculas de helio (moléculas monoatómicas) viajan más rápido en una onda de sonido y transmiten el sonido más rápido. (El sonido viaja a aproximadamente el 70% de la velocidad molecular media en los gases; la cifra es del 75% en los gases monoatómicos y del 68% en los gases diatómicos).
En este ejemplo, hemos asumido que la temperatura es lo suficientemente baja como para que las capacidades térmicas no se vean influenciadas por la vibración molecular (ver capacidad térmica ). Sin embargo, los modos vibracionales simplemente causan gammas que disminuyen hacia 1, ya que los modos de vibración en un gas poliatómico le dan al gas formas adicionales de almacenar calor que no afectan la temperatura y, por lo tanto, no afectan la velocidad molecular ni la velocidad del sonido. Por lo tanto, el efecto de temperaturas más altas y la capacidad térmica vibracional actúa para aumentar la diferencia entre la velocidad del sonido en moléculas monoatómicas y poliatómicas, y la velocidad sigue siendo mayor en las moléculas monoatómicas.
Aplicación práctica al aire
Sin duda, el factor más importante que influye en la velocidad del sonido en el aire es la temperatura. La velocidad es proporcional a la raíz cuadrada de la temperatura absoluta, lo que da un aumento de aproximadamente0,6 m/s por grado Celsius. Por este motivo, el tono de un instrumento musical de viento aumenta a medida que aumenta su temperatura.
La velocidad del sonido aumenta con la humedad. La diferencia entre el 0% y el 100% de humedad es de aproximadamente1,5 m/s a presión y temperatura estándar, pero el tamaño del efecto de la humedad aumenta drásticamente con la temperatura.
La dependencia de la frecuencia y la presión normalmente es insignificante en aplicaciones prácticas. En aire seco, la velocidad del sonido aumenta aproximadamente0,1 m/s a medida que la frecuencia aumenta desde10 Hz a100 Hz . Para frecuencias audibles superiores100 Hz es relativamente constante. Los valores estándar de la velocidad del sonido se dan en el límite de las frecuencias bajas, donde la longitud de onda es grande en comparación con el recorrido libre medio. [19]
Como se muestra arriba, el valor aproximado 1000/3 = 333,33... m/s es exacto un poco por debajo5 °C y es una buena aproximación para todas las temperaturas exteriores "habituales" (en climas templados, al menos), de ahí la regla general para determinar a qué distancia ha caído un rayo: contar los segundos desde el inicio del destello del rayo hasta el inicio del trueno correspondiente y dividir por 3: el resultado es la distancia en kilómetros hasta el punto más cercano del rayo.
Número de Mach
El número de Mach, una cantidad útil en aerodinámica, es la relación entre la velocidad del aire y la velocidad local del sonido. En altitud, por las razones explicadas, el número de Mach es una función de la temperatura. Sin embargo, los instrumentos de vuelo de las aeronaves funcionan utilizando el diferencial de presión para calcular el número de Mach, no la temperatura. Se supone que una presión particular representa una altitud particular y, por lo tanto, una temperatura estándar. Los instrumentos de vuelo de las aeronaves deben funcionar de esta manera porque la presión de estancamiento detectada por un tubo de Pitot depende de la altitud y de la velocidad.
Métodos experimentales
Existe una variedad de métodos diferentes para medir el sonido en el aire.
La primera estimación razonablemente precisa de la velocidad del sonido en el aire fue realizada por William Derham y reconocida por Isaac Newton . Derham tenía un telescopio en lo alto de la torre de la Iglesia de San Lorenzo en Upminster , Inglaterra. En un día tranquilo, se le daba un reloj de bolsillo sincronizado a un asistente que disparaba una escopeta a una hora predeterminada desde un punto visible a algunas millas de distancia, al otro lado del campo. Esto podía confirmarse con un telescopio. Luego midió el intervalo entre ver el humo de la pistola y la llegada del sonido usando un péndulo de medio segundo. La distancia desde donde se disparó el arma se encontró por triangulación, y la simple división (distancia/tiempo) proporcionó la velocidad. Por último, al hacer muchas observaciones, utilizando un rango de distancias diferentes, la inexactitud del péndulo de medio segundo podía promediarse, dando su estimación final de la velocidad del sonido. Los cronómetros modernos permiten utilizar hoy este método en distancias tan cortas como 200-400 metros, sin necesidad de algo tan ruidoso como una escopeta.
Métodos de cronometraje de un solo disparo
El concepto más simple es la medición realizada con dos micrófonos y un dispositivo de grabación rápido, como un osciloscopio de almacenamiento digital . Este método utiliza la siguiente idea.
Si se colocan en línea recta una fuente de sonido y dos micrófonos, con la fuente de sonido en un extremo, se puede medir lo siguiente:
- La distancia entre los micrófonos ( x ), llamada base del micrófono.
- El tiempo de llegada entre las señales (retardo) que llegan a los diferentes micrófonos ( t ).
Entonces v = x / t .
Otros métodos
En estos métodos, la medición del tiempo ha sido sustituida por una medición del inverso del tiempo ( frecuencia ).
El tubo de Kundt es un ejemplo de experimento que permite medir la velocidad del sonido en un volumen pequeño. Tiene la ventaja de poder medir la velocidad del sonido en cualquier gas. Este método utiliza un polvo para hacer visibles los nodos y antinodos al ojo humano. Este es un ejemplo de un montaje experimental compacto.
Se puede colocar un diapasón cerca de la boca de un tubo largo que se está sumergiendo en un barril de agua . En este sistema, se puede hacer que el tubo entre en resonancia si la longitud de la columna de aire en el tubo es igual a (1 + 2 n ) λ /4 donde n es un número entero. Como el punto antinodal del tubo en el extremo abierto está ligeramente fuera de la boca del tubo, es mejor encontrar dos o más puntos de resonancia y luego medir la mitad de una longitud de onda entre ellos.
Aquí se da el caso de que v = fλ .
Mediciones de alta precisión en el aire
El efecto de las impurezas puede ser significativo cuando se realizan mediciones de alta precisión. Se pueden utilizar desecantes químicos para secar el aire, pero, a su vez, contaminarán la muestra. El aire se puede secar criogénicamente, pero esto tiene el efecto de eliminar también el dióxido de carbono; por lo tanto, muchas mediciones de alta precisión se realizan con aire libre de dióxido de carbono en lugar de con aire natural. Una revisión de 2002 [20] encontró que una medición de 1963 realizada por Smith y Harlow utilizando un resonador cilíndrico dio "el valor más probable de la velocidad estándar del sonido hasta la fecha". El experimento se realizó con aire del que se había eliminado el dióxido de carbono, pero el resultado se corrigió luego para este efecto de modo que fuera aplicable al aire real. Los experimentos se realizaron en30 °C pero corregidos por temperatura para poder reportarlos en0 °C . El resultado fue 331,45 ± 0,01 m/s para aire seco a STP, para frecuencias de93 Hz a 1.500 Hz .
Medios no gaseosos
Velocidad del sonido en sólidos
Sólidos tridimensionales
En un sólido, existe una rigidez distinta de cero tanto para las deformaciones volumétricas como para las deformaciones cortantes. Por lo tanto, es posible generar ondas sonoras con diferentes velocidades dependiendo del modo de deformación. Las ondas sonoras que generan deformaciones volumétricas (compresión) y deformaciones cortantes (cortante) se denominan ondas de presión (ondas longitudinales) y ondas cortantes (ondas transversales), respectivamente. En los terremotos , las ondas sísmicas correspondientes se denominan ondas P (ondas primarias) y ondas S (ondas secundarias), respectivamente. Las velocidades del sonido de estos dos tipos de ondas que se propagan en un sólido tridimensional homogéneo se dan respectivamente por [11] donde
- K es el módulo volumétrico de los materiales elásticos;
- G es el módulo de corte de los materiales elásticos;
- E es el módulo de Young ;
- ρ es la densidad;
- ν es el coeficiente de Poisson .
La última cantidad no es independiente, ya que E = 3K(1 − 2ν) . La velocidad de las ondas de presión depende tanto de las propiedades de presión como de resistencia al corte del material, mientras que la velocidad de las ondas de corte depende únicamente de las propiedades de corte.
Por lo general, las ondas de presión se propagan más rápido en los materiales que las ondas transversales y, en el caso de los terremotos, esta es la razón por la que el inicio de un terremoto suele estar precedido por un rápido choque ascendente y descendente, antes de la llegada de ondas que producen un movimiento de lado a lado. Por ejemplo, para una aleación de acero típica, K = 170 GPa , G = 80 GPa y p =7700 kg/m 3 , lo que produce una velocidad de compresión c sólido,p de 6000 m/s . [11] Esto concuerda razonablemente con c sólido,p medido experimentalmente a 5930 m/s para un tipo de acero (posiblemente diferente). [21] La velocidad de corte c sólido,s se estima en 3200 m/s utilizando los mismos números.
La velocidad del sonido en los sólidos semiconductores puede ser muy sensible a la cantidad de dopante electrónico que contienen. [22]
Sólidos unidimensionales
La velocidad del sonido para ondas de presión en materiales rígidos como los metales se da a veces para "barras largas" del material en cuestión, en las que la velocidad es más fácil de medir. En las barras donde su diámetro es más corto que una longitud de onda, la velocidad de las ondas de presión puras se puede simplificar y se da por: [11] : 70 donde E es el módulo de Young . Esto es similar a la expresión para ondas transversales, excepto que el módulo de Young reemplaza al módulo de corte . Esta velocidad del sonido para ondas de presión en barras largas siempre será ligeramente menor que la misma velocidad en sólidos tridimensionales homogéneos, y la relación de las velocidades en los dos tipos diferentes de objetos depende del coeficiente de Poisson para el material.
Velocidad del sonido en líquidos
En un fluido, la única rigidez distinta de cero es la de la deformación volumétrica (un fluido no soporta fuerzas de corte).
Por lo tanto, la velocidad del sonido en un fluido viene dada por donde K es el módulo volumétrico del fluido.
Agua
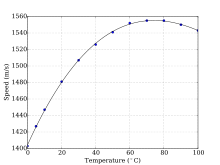
En agua dulce, el sonido viaja a una velocidad de aproximadamente1481 m/s a20 °C (consulte la sección Enlaces externos a continuación para obtener calculadoras en línea). [23] Se pueden encontrar aplicaciones del sonido submarino en el sonar , la comunicación acústica y la oceanografía acústica .
Agua de mar

En agua salada libre de burbujas de aire o sedimentos suspendidos, el sonido viaja a aproximadamente1500 m/s (1 500 .235 m/s a1000 kilopascales ,10 °C y 3% de salinidad por un método). [24] La velocidad del sonido en el agua de mar depende de la presión (por lo tanto, la profundidad), la temperatura (un cambio de1 °C ~4 m/s ) y salinidad (un cambio de 1 ‰ ~1 m/s ), y se han derivado ecuaciones empíricas para calcular con precisión la velocidad del sonido a partir de estas variables. [25] [26] Otros factores que afectan a la velocidad del sonido son menores. Dado que en la mayoría de las regiones oceánicas la temperatura disminuye con la profundidad, el perfil de la velocidad del sonido con la profundidad disminuye hasta un mínimo a una profundidad de varios cientos de metros. Por debajo del mínimo, la velocidad del sonido aumenta de nuevo, ya que el efecto del aumento de la presión supera el efecto de la disminución de la temperatura (derecha). [27] Para obtener más información, consulte Dushaw et al. [28]
Mackenzie proporciona una ecuación empírica para la velocidad del sonido en el agua del mar: [29] donde
- T es la temperatura en grados Celsius;
- S es la salinidad en partes por mil;
- z es la profundidad en metros.
Las constantes a 1 , a 2 , ..., a 9 son con valor de verificación1 550 .744 m/s para T =25 °C , S = 35 partes por mil , z = 1000 m . Esta ecuación tiene un error estándar de0,070 m/s para una salinidad entre 25 y 40 ppt . Consulte [1] para obtener una calculadora en línea.
(El gráfico de velocidad del sonido frente a profundidad no se correlaciona directamente con la fórmula de MacKenzie. Esto se debe al hecho de que la temperatura y la salinidad varían a diferentes profundidades. Cuando T y S se mantienen constantes, la fórmula en sí siempre aumenta con la profundidad).
Otras ecuaciones para la velocidad del sonido en el agua de mar son precisas en un amplio rango de condiciones, pero son mucho más complicadas, por ejemplo, la de VA Del Grosso [30] y la ecuación de Chen-Millero-Li. [28] [31]
Velocidad del sonido en el plasma
La velocidad del sonido en un plasma para el caso común de que los electrones estén más calientes que los iones (pero no demasiado más calientes) viene dada por la fórmula (ver aquí ) donde
- m i es la masa del ion ;
- μ es la relación entre la masa del ion y la masa del protón μ = m i / m p ;
- T e es la temperatura del electrón ;
- Z es el estado de carga;
- k es la constante de Boltzmann ;
- γ es el índice adiabático .
A diferencia de un gas, la presión y la densidad las proporcionan especies distintas: la presión, los electrones, y la densidad, los iones. Ambas están acopladas a través de un campo eléctrico fluctuante.
Marte
La velocidad del sonido en Marte varía en función de la frecuencia. Las frecuencias más altas viajan más rápido que las frecuencias más bajas. El sonido de frecuencia más alta de los láseres viaja a 250 m/s (820 pies/s), mientras que el sonido de baja frecuencia alcanza un máximo de 240 m/s (790 pies/s). [32]
Gradientes
Cuando el sonido se propaga uniformemente en todas las direcciones en tres dimensiones, la intensidad disminuye en proporción al cuadrado inverso de la distancia. Sin embargo, en el océano existe una capa llamada "canal de sonido profundo" o canal SOFAR que puede confinar las ondas sonoras a una profundidad determinada.
En el canal SOFAR, la velocidad del sonido es menor que en las capas superiores e inferiores. Así como las ondas de luz se refractan hacia una región de mayor índice de refracción , las ondas sonoras se refractan hacia una región donde su velocidad es menor. El resultado es que el sonido queda confinado en la capa, de forma muy similar a como la luz puede quedar confinada en una lámina de vidrio o fibra óptica . Por lo tanto, el sonido queda confinado esencialmente en dos dimensiones. En dos dimensiones, la intensidad cae en proporción únicamente a la inversa de la distancia. Esto permite que las ondas viajen mucho más lejos antes de volverse indetectablemente débiles.
En la atmósfera se produce un efecto similar. El proyecto Mogul aprovechó con éxito este efecto para detectar una explosión nuclear a una distancia considerable.
Véase también
- Efecto acústico elástico
- Onda elástica
- Segundo sonido
- Estampido sónico
- Barrera del sonido
- Velocidades del sonido de los elementos
- Acústica subacuática
- Vibraciones
- Campana X-1
Referencias
- ^ "Calculadora de la velocidad del sonido". Servicio Meteorológico Nacional . Consultado el 23 de julio de 2021 .
- ^ "Velocidad del sonido". hyperphysics.phy-astr.gsu.edu . Consultado el 24 de octubre de 2022 .
- ^ "La velocidad del sonido". mathpages.com . Consultado el 3 de mayo de 2015 .
- ^ Bannon, Mike; Kaputa, Frank (12 de diciembre de 2014). «La ecuación de Newton-Laplace y la velocidad del sonido». Chaquetas térmicas . Consultado el 3 de mayo de 2015 .
- ^ ab Murdin, Paul (25 de diciembre de 2008). Meridiano de gloria: peligrosas aventuras en la competencia para medir la Tierra . Springer Science & Business Media. págs. 35-36. ISBN 9780387755342.
- ^ Fox, Tony (2003). Essex Journal . Essex Arch & Hist Soc. págs. 12–16.
- ^ "17.2 Velocidad del sonido | Física universitaria, volumen 1". courses.lumenlearning.com . Consultado el 24 de enero de 2020 .
- ^ Dean, EA (agosto de 1979). Efectos atmosféricos sobre la velocidad del sonido, informe técnico del Centro de Información Técnica de Defensa
- ^ ab Everest, F. (2001). Manual maestro de acústica . Nueva York: McGraw-Hill. págs. 262-263. ISBN 978-0-07-136097-5.
- ^ ab Atmósfera estándar de EE. UU., 1976, Oficina de Imprenta del Gobierno de EE. UU., Washington, DC, 1976.
- ^ abcd Kinsler, LE; Frey, AR; Coppens, AB; Sanders, JV (2000). Fundamentos de acústica (4.ª ed.). Nueva York: John Wiley & Sons. ISBN 0-471-84789-5.
- ^ Uman, Martin (1984). Lightning . Nueva York: Dover Publications. ISBN 978-0-486-64575-9.
- ^ Volland, Hans (1995). Manual de electrodinámica atmosférica . Boca Raton: CRC Press. pág. 22. ISBN 978-0-8493-8647-3.
- ^ Singal, S. (2005). Contaminación acústica y estrategia de control . Oxford: Alpha Science International. pág. 7. ISBN 978-1-84265-237-4Se puede observar
que los efectos de refracción ocurren solo porque hay un gradiente de viento y no se deben al resultado de la convección del sonido a través del viento.
- ^ Bies, David (2009). Control de ruido en ingeniería, teoría y práctica . Londres: CRC Press. p. 249. ISBN 978-0-415-26713-7
Como la velocidad del viento generalmente aumenta con la altitud, el viento que sopla hacia el oyente desde la fuente refractará las ondas sonoras hacia abajo, lo que dará como resultado mayores niveles de ruido
. - ^ Cornwall, Sir (1996). Grant como comandante militar . Nueva York: Barnes & Noble. pág. 92. ISBN. 978-1-56619-913-1.
- ^ Cozens, Peter (2006). Los días más oscuros de la guerra: las batallas de Iuka y Corinto . Chapel Hill: The University of North Carolina Press. ISBN 978-0-8078-5783-0.
- ^ AB Wood , Un libro de texto sobre el sonido (Bell, Londres, 1946)
- ^ "Velocidad del sonido en el aire". Phy.mtu.edu . Consultado el 13 de junio de 2014 .
- ^ Zuckerwar, Manual de la velocidad del sonido en gases reales, pág. 52
- ^ J. Krautkrämer y H. Krautkrämer (1990), Pruebas ultrasónicas de materiales , 4.ª edición completamente revisada, Springer-Verlag, Berlín, Alemania, pág. 497
- ^ Slade, Tyler; Anand, Shashwat; Wood, Max; Male, James; Imasato, Kazuki; Cheikh, Dean; Al Malki, Muath; Agne, Matthias; Griffith, Kent; Bux, Sabah; Wolverton, Chris; Kanatzidis, Mercouri; Snyder, Jeff (2021). "El ablandamiento reticular mediado por portadores de carga contribuye a un zT alto en semiconductores termoeléctricos". Joule . 5 (5): 1168-1182. Bibcode :2021Joule...5.1168S. doi : 10.1016/j.joule.2021.03.009 . S2CID 233598665.
- ^ "Velocidad del sonido en el agua a temperaturas entre 32 y 212 °F (0 y 100 °C) — unidades imperiales y del SI". The Engineering Toolbox .
- ^ Wong, George SK; Zhu, Shi-ming (1995). "Velocidad del sonido en el agua de mar en función de la salinidad, la temperatura y la presión". Revista de la Sociedad Acústica de América . 97 (3): 1732. Bibcode :1995ASAJ...97.1732W. doi :10.1121/1.413048.
- ^ APL-UW TR 9407 Manual de modelos acústicos ambientales oceánicos de alta frecuencia, págs. I1-I2.
- ^ Robinson, Stephen (22 de septiembre de 2005). «Guías técnicas: velocidad del sonido en el agua de mar». Laboratorio Nacional de Física . Archivado desde el original el 29 de abril de 2017. Consultado el 7 de diciembre de 2016 .
- ^ "¿Qué tan rápido viaja el sonido?". Descubrimiento del sonido en el mar . Universidad de Rhode Island. Archivado desde el original el 20 de mayo de 2017. Consultado el 30 de noviembre de 2010 .
- ^ ab Dushaw, Brian D.; Worcester, PF; Cornuelle, BD; Howe, BM (1993). "Sobre ecuaciones para la velocidad del sonido en agua de mar". Revista de la Sociedad Acústica de América . 93 (1): 255–275. Bibcode :1993ASAJ...93..255D. doi :10.1121/1.405660.
- ^ Kenneth V., Mackenzie (1981). "Discusión sobre las determinaciones de la velocidad del sonido en agua de mar". Revista de la Sociedad Acústica de América . 70 (3): 801–806. Bibcode :1981ASAJ...70..801M. doi :10.1121/1.386919.
- ^ Del Grosso, VA (1974). "Nueva ecuación para la velocidad del sonido en aguas naturales (con comparaciones con otras ecuaciones)". Journal of the Acoustical Society of America . 56 (4): 1084–1091. Bibcode :1974ASAJ...56.1084D. doi : 10.1121/1.1903388 .
- ^ Meinen, Christopher S.; Watts, D. Randolph (1997). "Más pruebas de que el algoritmo de velocidad del sonido de Del Grosso es más preciso que el de Chen y Millero". Revista de la Sociedad Acústica de América . 102 (4): 2058–2062. Bibcode :1997ASAJ..102.2058M. doi :10.1121/1.419655. S2CID 38144335.
- ^ Maurice, S.; Chide, B.; Murdoch, N.; Lorenz, RD; Mimoun, D.; Wiens, RC; Stott, A.; Jacob, X.; Bertrand, T.; Montmessin, F.; Lanza, NL; Alvarez-Llamas, C.; Angel, SM; Aung, M.; Balaram, J. (1 de abril de 2022). "Grabación in situ del paisaje sonoro de Marte". Nature . 605 (7911): 653–658. Bibcode :2022Natur.605..653M. doi : 10.1038/s41586-022-04679-0 . ISSN 1476-4687. PMC 9132769 . PMID 35364602.
Enlaces externos
- Calculadora de la velocidad del sonido
- Cálculo: Velocidad del sonido en el aire y la temperatura
- Velocidad del sonido: lo que importa es la temperatura, no la presión del aire
- Propiedades de la atmósfera estándar de Estados Unidos, 1976
- La velocidad del sonido
- Cómo medir la velocidad del sonido en un laboratorio
- ¿El sonido alguna vez viajó a la velocidad de la luz?
- Propiedades acústicas de diversos materiales, incluida la velocidad del sonido Archivado el 16 de febrero de 2014 en Wayback Machine
- Descubrimiento del sonido en el mar (usos del sonido por los humanos y otros animales)













![{\displaystyle {\begin{aligned}{\frac {dv}{dt}}&=-{\frac {1}{\rho }}{\frac {dP}{dx}}\\[1ex]\rightarrow dP&=(-\rho \,dv){\frac {dx}{dt}}=(v\,d\rho )v\\[1ex]\rightarrow v^{2}&\equiv c^{2}={\frac {dP}{d\rho }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d00b195aeca690b20dd277cf48ac3cc893505d37)




















