Dispersión (óptica)


La dispersión es el fenómeno en el que la velocidad de fase de una onda depende de su frecuencia. [1] A veces, el término dispersión cromática se utiliza para referirse a la óptica específicamente, en contraposición a la propagación de ondas en general. Un medio que tiene esta propiedad común puede denominarse medio dispersivo .
Aunque el término se utiliza en el campo de la óptica para describir la luz y otras ondas electromagnéticas , la dispersión en el mismo sentido puede aplicarse a cualquier tipo de movimiento ondulatorio, como la dispersión acústica en el caso de las ondas sonoras y sísmicas, y en las ondas gravitacionales (ondas oceánicas). En el campo de la óptica, la dispersión es una propiedad de las señales de telecomunicaciones a lo largo de las líneas de transmisión (como las microondas en un cable coaxial ) o los pulsos de luz en la fibra óptica .
En óptica, una consecuencia importante y conocida de la dispersión es el cambio en el ángulo de refracción de diferentes colores de luz, [2] como se ve en el espectro producido por un prisma dispersivo y en la aberración cromática de las lentes. El diseño de lentes acromáticas compuestas , en las que la aberración cromática se cancela en gran medida, utiliza una cuantificación de la dispersión de un vidrio dada por su número de Abbe V , donde los números de Abbe más bajos corresponden a una mayor dispersión en el espectro visible . En algunas aplicaciones como las telecomunicaciones, la fase absoluta de una onda a menudo no es importante sino solo la propagación de paquetes de ondas o "pulsos"; en ese caso, uno solo está interesado en las variaciones de la velocidad de grupo con la frecuencia, la llamada dispersión de velocidad de grupo.
Todos los medios de transmisión comunes también varían en atenuación (normalizada a la longitud de transmisión) en función de la frecuencia, lo que genera distorsión de atenuación ; esto no es dispersión, aunque a veces las reflexiones en límites de impedancia muy espaciados (por ejemplo, segmentos engarzados en un cable) pueden producir distorsión de la señal, lo que agrava aún más el tiempo de tránsito inconsistente que se observa en todo el ancho de banda de la señal.
Ejemplos
El ejemplo más conocido de dispersión es probablemente el arcoíris , en el que la dispersión provoca la separación espacial de una luz blanca en componentes de diferentes longitudes de onda (diferentes colores ). Sin embargo, la dispersión también tiene un efecto en muchas otras circunstancias: por ejemplo, la dispersión por velocidad de grupo hace que los pulsos se dispersen en las fibras ópticas , degradando las señales a grandes distancias; también, una cancelación entre la dispersión por velocidad de grupo y los efectos no lineales conduce a ondas solitones .
Dispersión de materiales y guías de ondas
En la mayoría de los casos, la dispersión cromática se refiere a la dispersión de material a granel, es decir, el cambio en el índice de refracción con la frecuencia óptica. Sin embargo, en una guía de ondas también existe el fenómeno de dispersión de guía de ondas , en cuyo caso la velocidad de fase de una onda en una estructura depende de su frecuencia simplemente debido a la geometría de la estructura. De manera más general, la dispersión de "guía de ondas" puede ocurrir para ondas que se propagan a través de cualquier estructura no homogénea (por ejemplo, un cristal fotónico ), ya sea que las ondas estén confinadas o no a alguna región. [ dudoso – discutir ] En una guía de ondas, ambos tipos de dispersión generalmente estarán presentes, aunque no sean estrictamente aditivos. [ cita requerida ] Por ejemplo, en la fibra óptica, la dispersión del material y la guía de ondas pueden cancelarse efectivamente entre sí para producir una longitud de onda de dispersión cero , importante para la comunicación rápida por fibra óptica .
Dispersión de materiales en óptica
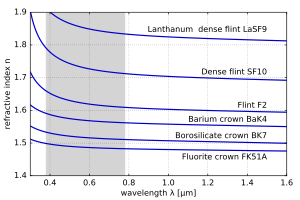

La dispersión de material puede ser un efecto deseable o indeseable en aplicaciones ópticas. La dispersión de la luz por prismas de vidrio se utiliza para construir espectrómetros y espectrorradiómetros . Sin embargo, en lentes, la dispersión causa aberración cromática , un efecto indeseado que puede degradar las imágenes en microscopios, telescopios y objetivos fotográficos.
La velocidad de fase v de una onda en un medio uniforme dado está dada por
donde c es la velocidad de la luz en el vacío y n es el índice de refracción del medio.
En general, el índice de refracción es una función de la frecuencia f de la luz, por lo tanto n = n ( f ), o alternativamente, con respecto a la longitud de onda de la onda n = n ( λ ). La dependencia de la longitud de onda del índice de refracción de un material suele cuantificarse mediante su número de Abbe o sus coeficientes en una fórmula empírica como las ecuaciones de Cauchy o Sellmeier .
Debido a las relaciones de Kramers–Kronig , la dependencia de la longitud de onda de la parte real del índice de refracción está relacionada con la absorción del material , descrita por la parte imaginaria del índice de refracción (también llamada coeficiente de extinción ). En particular, para materiales no magnéticos ( μ = μ 0 ), la susceptibilidad χ que aparece en las relaciones de Kramers–Kronig es la susceptibilidad eléctrica χ e = n 2 − 1.
La consecuencia más común de la dispersión en óptica es la separación de la luz blanca en un espectro de color por un prisma . De la ley de Snell se desprende que el ángulo de refracción de la luz en un prisma depende del índice de refracción del material del prisma. Como el índice de refracción varía con la longitud de onda, se deduce que el ángulo con el que se refracta la luz también variará con la longitud de onda, lo que provoca una separación angular de los colores conocida como dispersión angular .
Para la luz visible, los índices de refracción n de la mayoría de los materiales transparentes (por ejemplo, aire, vidrios) disminuyen al aumentar la longitud de onda λ :
o en general,
En este caso, se dice que el medio tiene dispersión normal , mientras que si el índice aumenta con el aumento de la longitud de onda (que es típicamente el caso en el ultravioleta [4] ), se dice que el medio tiene dispersión anómala .
En la interfaz de dicho material con el aire o el vacío (índice de ~1), la ley de Snell predice que la luz incidente en un ángulo θ con respecto a la normal se refractará en un ángulo arcsin (pecado θ/norte ). Así, la luz azul, con un índice de refracción más alto, se desviará más fuertemente que la luz roja, dando lugar al conocido patrón del arco iris .
Dispersión de velocidad de grupo

Más allá de describir simplemente un cambio en la velocidad de fase a lo largo de la longitud de onda, una consecuencia más grave de la dispersión en muchas aplicaciones se denomina dispersión de velocidad de grupo (GVD). Si bien la velocidad de fase v se define como v = c / n , esto describe solo un componente de frecuencia. Cuando se combinan diferentes componentes de frecuencia, como cuando se considera una señal o un pulso, a menudo uno está más interesado en la velocidad de grupo , que describe la velocidad a la que se propaga un pulso o información superpuesta a una onda (modulación). En la animación que acompaña, se puede ver que la onda en sí (naranja-marrón) viaja a una velocidad de fase mucho más rápida que la velocidad de la envolvente (negra), que corresponde a la velocidad de grupo. Este pulso podría ser una señal de comunicaciones, por ejemplo, y su información solo viaja a la velocidad de grupo, aunque consiste en frentes de onda que avanzan a una velocidad más rápida (la velocidad de fase).
Es posible calcular la velocidad de grupo a partir de la curva de índice de refracción n ( ω ) o más directamente a partir del número de onda k = ωn / c , donde ω es la frecuencia en radianes ω = 2 πf . Mientras que una expresión para la velocidad de fase es v p = ω / k , la velocidad de grupo se puede expresar utilizando la derivada : v g = dω / dk . O en términos de la velocidad de fase v p ,
Cuando hay dispersión, no solo la velocidad de grupo no es igual a la velocidad de fase, sino que generalmente varía con la longitud de onda. Esto se conoce como dispersión de velocidad de grupo y hace que un pulso corto de luz se ensanche, ya que los componentes de diferente frecuencia dentro del pulso viajan a diferentes velocidades. La dispersión de velocidad de grupo se cuantifica como la derivada del recíproco de la velocidad de grupo con respecto a la frecuencia angular , lo que da como resultado dispersión de velocidad de grupo = d 2 k / dω 2 .
Si un pulso de luz se propaga a través de un material con dispersión de velocidad de grupo positiva, entonces los componentes de longitud de onda más corta viajan más lento que los componentes de longitud de onda más larga. Por lo tanto, el pulso se vuelve positivo o ascendente , aumentando en frecuencia con el tiempo. Por otro lado, si un pulso viaja a través de un material con dispersión de velocidad de grupo negativa, los componentes de longitud de onda más corta viajan más rápido que los más largos, y el pulso se vuelve negativo o descendente , disminuyendo en frecuencia con el tiempo.
Un ejemplo cotidiano de una señal de chirrido negativo en el ámbito acústico es el de un tren que se aproxima y choca contra deformidades en una vía soldada. El sonido causado por el propio tren es impulsivo y viaja mucho más rápido en las vías metálicas que en el aire, de modo que el tren puede escucharse mucho antes de su llegada. Sin embargo, desde lejos no se oye como causante de impulsos, sino que produce un chirrido descendente característico, en medio de la reverberación causada por la complejidad de los modos vibratorios de la vía. La dispersión de velocidad de grupo se puede escuchar en el sentido de que el volumen de los sonidos se mantiene audible durante un tiempo sorprendentemente largo, hasta varios segundos.
Control de dispersión
El resultado de la GVD, ya sea negativa o positiva, es en última instancia la propagación temporal del pulso. Esto hace que la gestión de la dispersión sea extremadamente importante en los sistemas de comunicaciones ópticas basados en fibra óptica, ya que si la dispersión es demasiado alta, un grupo de pulsos que representan un flujo de bits se propagará en el tiempo y se fusionará, haciendo que el flujo de bits sea ininteligible. Esto limita la longitud de fibra por la que se puede enviar una señal sin regeneración. Una posible respuesta a este problema es enviar señales por la fibra óptica a una longitud de onda donde la GVD sea cero (por ejemplo, alrededor de 1,3–1,5 μm en fibras de sílice ), por lo que los pulsos en esta longitud de onda sufren una propagación mínima por dispersión. En la práctica, sin embargo, este enfoque causa más problemas de los que resuelve porque la GVD cero amplifica de manera inaceptable otros efectos no lineales (como la mezcla de cuatro ondas ). Otra opción posible es utilizar pulsos de solitones en el régimen de dispersión negativa, una forma de pulso óptico que utiliza un efecto óptico no lineal para automantener su forma. Sin embargo, los solitones tienen el problema práctico de que requieren que se mantenga un cierto nivel de potencia en el pulso para que el efecto no lineal tenga la intensidad correcta. En cambio, la solución que se utiliza actualmente en la práctica es realizar una compensación de dispersión, normalmente haciendo coincidir la fibra con otra fibra de dispersión de signo opuesto para que los efectos de dispersión se cancelen; dicha compensación está limitada en última instancia por efectos no lineales como la modulación de fase propia , que interactúan con la dispersión para hacer que sea muy difícil de deshacer.
El control de la dispersión también es importante en los láseres que producen pulsos cortos . La dispersión general del resonador óptico es un factor importante para determinar la duración de los pulsos emitidos por el láser. Se puede disponer un par de prismas para producir una dispersión neta negativa, que se puede utilizar para equilibrar la dispersión normalmente positiva del medio láser. Las rejillas de difracción también se pueden utilizar para producir efectos dispersivos; estas se utilizan a menudo en sistemas de amplificadores láser de alta potencia. Recientemente, se ha desarrollado una alternativa a los prismas y rejillas: los espejos chirped . Estos espejos dieléctricos están recubiertos de modo que las diferentes longitudes de onda tienen diferentes longitudes de penetración y, por lo tanto, diferentes retardos de grupo. Las capas de recubrimiento se pueden adaptar para lograr una dispersión neta negativa.
En guías de ondas
Las guías de ondas son altamente dispersivas debido a su geometría (en lugar de solo a su composición material). Las fibras ópticas son un tipo de guía de ondas para frecuencias ópticas (luz) ampliamente utilizadas en los sistemas de telecomunicaciones modernos. La velocidad a la que se pueden transportar datos en una sola fibra está limitada por el ensanchamiento de pulsos debido a la dispersión cromática, entre otros fenómenos.
En general, para un modo de guía de ondas con una frecuencia angular ω ( β ) a una constante de propagación β (de modo que los campos electromagnéticos en la dirección de propagación z oscilan proporcionalmente a e i ( βz − ωt ) ), el parámetro de dispersión de velocidad de grupo D se define como [5]
donde λ = 2 π c / ω es la longitud de onda del vacío, y v g = dω / dβ es la velocidad de grupo. Esta fórmula generaliza la de la sección anterior para medios homogéneos e incluye tanto la dispersión de la guía de ondas como la dispersión del material. La razón para definir la dispersión de esta manera es que | D | es la dispersión temporal (asintótica) del pulso Δ t por unidad de ancho de banda Δ λ por unidad de distancia recorrida, comúnmente reportada en ps /( nm ⋅ km ) para fibras ópticas.
En el caso de las fibras ópticas multimodo , la denominada dispersión modal también provocará un ensanchamiento de los pulsos. Incluso en las fibras monomodo , el ensanchamiento de los pulsos puede producirse como resultado de la dispersión del modo de polarización (ya que todavía hay dos modos de polarización). Estos no son ejemplos de dispersión cromática, ya que no dependen de la longitud de onda o del ancho de banda de los pulsos propagados.
Dispersión de orden superior en anchos de banda amplios
Cuando hay una amplia gama de frecuencias (un ancho de banda amplio) en un solo paquete de ondas, como en un pulso ultracorto o un pulso con chirrido u otras formas de transmisión de espectro ensanchado , puede que no sea preciso aproximar la dispersión mediante una constante en todo el ancho de banda, y se requieren cálculos más complejos para calcular efectos como la expansión del pulso.
En particular, el parámetro de dispersión D definido anteriormente se obtiene a partir de una sola derivada de la velocidad del grupo. Las derivadas superiores se conocen como dispersión de orden superior . [6] [7] Estos términos son simplemente una expansión de la serie de Taylor de la relación de dispersión β ( ω ) del medio o guía de ondas alrededor de alguna frecuencia particular. Sus efectos se pueden calcular mediante la evaluación numérica de las transformadas de Fourier de la forma de onda, mediante la integración de aproximaciones de envolvente de orden superior que varían lentamente , mediante un método de paso dividido (que puede utilizar la relación de dispersión exacta en lugar de una serie de Taylor), o mediante la simulación directa de las ecuaciones de Maxwell completas en lugar de una ecuación de envolvente aproximada.
Dispersión espacial
En electromagnetismo y óptica, el término dispersión se refiere generalmente a la dispersión temporal o de frecuencia antes mencionada. La dispersión espacial se refiere a la respuesta no local del medio al espacio; esto se puede reformular como la dependencia del vector de onda de la permitividad. Para un medio anisotrópico ejemplar , la relación espacial entre el campo eléctrico y el campo de desplazamiento eléctrico se puede expresar como una convolución : [8]
donde el núcleo es la respuesta dieléctrica (susceptibilidad); sus índices lo convierten en general en un tensor para dar cuenta de la anisotropía del medio. La dispersión espacial es despreciable en la mayoría de los casos macroscópicos, donde la escala de variación de es mucho mayor que las dimensiones atómicas, porque el núcleo dieléctrico se extingue a distancias macroscópicas. Sin embargo, puede dar lugar a efectos macroscópicos no despreciables, en particular en medios conductores como metales , electrolitos y plasmas . La dispersión espacial también desempeña un papel en la actividad óptica y el ensanchamiento Doppler , [8] así como en la teoría de los metamateriales . [9]
En gemología
| Nombre del mineral | nB - nG | nC − nF |
|---|---|---|
| Hematites | 0,500 | — |
| Cinabrio (HgS) | 0,40 | — |
| Sintetizador Rutilo | 0.330 | 0,190 |
| Rutilo (TiO 2 ) | 0,280 | 0,120–0,180 |
| Anatasa (TiO 2 ) | 0,213–0,259 | — |
| Wulfenita | 0,203 | 0,133 |
| Vanadinita | 0,202 | — |
| Fabulita | 0,190 | 0,109 |
| Esfalrita (ZnS) | 0,156 | 0,088 |
| Azufre (S) | 0,155 | — |
| Estibiotantalita | 0,146 | — |
| Goethita (FeO(OH)) | 0,14 | — |
| Brookita (TiO 2 ) | 0,131 | 0,12–1,80 |
| Linobato | 0,13 | 0,075 |
| Zincita (ZnO) | 0,127 | — |
| Moissanita sintética (SiC) | 0,104 | — |
| Casiterita (SnO 2 ) | 0,071 | 0,035 |
| Zirconia ( ZrO2 ) | 0,060 | 0,035 |
| Powellita (CaMoO 4 ) | 0,058 | — |
| Andradita | 0,057 | — |
| Demantoide | 0,057 | 0,034 |
| Cerusita | 0,055 | 0,033–0,050 |
| Titanita | 0,051 | 0,019–0,038 |
| Benitoíta | 0,046 | 0,026 |
| Anglesita | 0,044 | 0,025 |
| Diamante (C) | 0,044 | 0,025 |
| Sintetizador Casiterita (SnO 2 ) | 0,041 | — |
| Vidrio de pedernal | 0,041 | — |
| Jacinto | 0,039 | — |
| Jerga | 0,039 | — |
| Estrella lite | 0,039 | — |
| Scheelita | 0,038 | 0,026 |
| Circón (ZrSiO 4 ) | 0,039 | 0,022 |
| GGG | 0,038 | 0,022 |
| Dioptasa | 0,036 | 0,021 |
| Cuando Vinay Wellite | 0,034 | — |
| Yeso | 0,033 | 0,008 |
| Alabastro | 0,033 | — |
| Epidota | 0,03 | 0,012–0,027 |
| Tanzanita | 0,030 | 0,011 |
| Tulita | 0,03 | 0,011 |
| Zoisita | 0,03 | — |
| YAG | 0,028 | 0,015 |
| Espesartina | 0,027 | 0,015 |
| Uvarovita | 0,027 | 0,014–0,021 |
| Almandina | 0,027 | 0,013–0,016 |
| Hessonita | 0,027 | 0,013–0,015 |
| Willemita | 0,027 | — |
| Pleonaste | 0,026 | — |
| Rodolita | 0,026 | — |
| Boracita | 0,024 | 0,012 |
| Criolita | 0,024 | — |
| Estaurolita | 0,023 | 0,012–0,013 |
| Piropo | 0,022 | 0,013–0,016 |
| Diáspora | 0,02 | — |
| Grosularia | 0,020 | 0,012 |
| Hemimorfita | 0,020 | 0,013 |
| Cianita | 0,020 | 0,011 |
| Peridoto | 0,020 | 0,012–0,013 |
| Espinela | 0,020 | 0,011 |
| Vesuvianita | 0,019–0,025 | 0,014 |
| Gahnita | 0,019–0,021 | — |
| Clinozoisita | 0,019 | 0,011–0,014 |
| Labradorita | 0,019 | 0,010 |
| Axinita | 0,018–0,020 | 0,011 |
| Diópsido | 0,018–0,020 | 0,01 |
| Ekanita | 0,018 | 0,012 |
| Corindón ( Al2O3 ) | 0,018 | 0,011 |
| Sintetizador Corindón | 0,018 | 0,011 |
| Rubí ( Al2O3 ) | 0,018 | 0,011 |
| Zafiro ( Al2O3 ) | 0,018 | 0,011 |
| Cornerupina | 0,018 | 0,010 |
| Cingalita | 0,018 | 0,010 |
| Sodalita | 0,018 | 0,009 |
| rodizita | 0,018 | — |
| Ocultita | 0,017 | 0,010 |
| Kunzita | 0,017 | 0,010 |
| Espodumena | 0,017 | 0,010 |
| Turmalina | 0,017 | 0,009–0,011 |
| Cordierita | 0,017 | 0,009 |
| Danburita | 0,017 | 0,009 |
| Herderita | 0,017 | 0,008–0,009 |
| Rubelita | 0,017 | 0,008–0,009 |
| Acroíta | 0,017 | — |
| Dravita | 0,017 | — |
| Elbaíta | 0,017 | — |
| Indicolita | 0,017 | — |
| Liddicoatita | 0,017 | — |
| Escapolita | 0,017 | — |
| Turmalina negra | 0,017 | — |
| Verdelita | 0,017 | — |
| Andalucita | 0,016 | 0,009 |
| Barita (BaSO 4 ) | 0,016 | 0,009 |
| Euclasa | 0,016 | 0,009 |
| Datolita | 0,016 | — |
| Alejandrita | 0,015 | 0,011 |
| Crisoberilo | 0,015 | 0,011 |
| Rodocrosita | 0,015 | 0,010–0,020 |
| Sillimanita | 0,015 | 0,009–0,012 |
| Hambergita | 0,015 | 0,009–0,010 |
| Piroxmangita | 0,015 | — |
| sintetizador scheelite | 0,015 | — |
| Smithsonita | 0,014–0,031 | 0,008–0,017 |
| Ambligonita | 0,014–0,015 | 0,008 |
| Aguamarina | 0,014 | 0,009–0,013 |
| Berilo | 0,014 | 0,009–0,013 |
| Esmeralda | 0,014 | 0,009–0,013 |
| Heliodor | 0,014 | 0,009–0,013 |
| Morganita | 0,014 | 0,009–0,013 |
| Brasileña | 0,014 | 0,008 |
| Celestina | 0,014 | 0,008 |
| Topacio | 0,014 | 0,008 |
| Goshenita | 0,014 | — |
| Apatito | 0,013 | 0,008–0,010 |
| Venturina | 0,013 | 0,008 |
| Amatista (SiO 2 ) | 0,013 | 0,008 |
| Cuarzo citrino | 0,013 | 0,008 |
| Prasiolita | 0,013 | 0,008 |
| Cuarzo (SiO 2 ) | 0,013 | 0,008 |
| Cuarzo rosa (SiO 2 ) | 0,013 | 0,008 |
| Cuarzo ahumado (SiO 2 ) | 0,013 | 0,008 |
| Anhidrita | 0,013 | — |
| Dolomita | 0,013 | — |
| Morión | 0,013 | — |
| Feldespato | 0,012 | 0,008 |
| Piedra de la luna | 0,012 | 0,008 |
| Ortoclasa | 0,012 | 0,008 |
| polucita | 0,012 | 0,007 |
| Albita | 0,012 | — |
| Habitante de Bytown | 0,012 | — |
| sintetizador esmeralda | 0,012 | — |
| Magnesita ( MgCO3 ) | 0,012 | — |
| Sanidina | 0,012 | — |
| Piedra solar | 0,012 | — |
| Sintetizador Alejandrita | 0,011 | — |
| Sintetizador Zafiro ( Al2O3 ) | 0,011 | — |
| Fosfofilita | 0,010–0,011 | — |
| Fenakita | 0,01 | 0,009 |
| Cancrinita | 0,010 | 0,008–0,009 |
| Leucita | 0,010 | 0,008 |
| Enstatita | 0,010 | — |
| Obsidiana | 0,010 | — |
| Anortita | 0,009–0,010 | — |
| Actinolita | 0,009 | — |
| Jeremejevita | 0,009 | — |
| Nefelina | 0,008–0,009 | — |
| Apofilita | 0,008 | — |
| Hauyne | 0,008 | — |
| Natrolita | 0,008 | — |
| Cuarzo sintético ( SiO2 ) | 0,008 | — |
| Aragonito | 0,007–0,012 | — |
| Augelita | 0,007 | — |
| Berilonita | 0,010 | 0,007 |
| Estroncianita | 0,008–0,028 | — |
| Calcita ( CaCO3 ) | 0,008–0,017 | 0,013–0,014 |
| Fluorita (CaF 2 ) | 0,007 | 0,004 |
| Tremolita | 0,006–0,007 | — |
En la terminología técnica de la gemología , la dispersión es la diferencia en el índice de refracción de un material en las longitudes de onda de Fraunhofer B y G (686,7 nm y 430,8 nm) o C y F (656,3 nm y 486,1 nm) , y está destinada a expresar el grado en el que un prisma cortado de la piedra preciosa demuestra "fuego". Fuego es un término coloquial utilizado por los gemólogos para describir la naturaleza dispersiva de una piedra preciosa o la falta de ella. La dispersión es una propiedad del material. La cantidad de fuego demostrado por una piedra preciosa dada es una función de los ángulos de las facetas de la piedra preciosa, la calidad del pulido, el entorno de iluminación, el índice de refracción del material, la saturación del color y la orientación del observador en relación con la piedra preciosa. [10] [11]
En imágenes
En las lentes fotográficas y microscópicas, la dispersión provoca aberración cromática , lo que hace que los diferentes colores de la imagen no se superpongan correctamente. Se han desarrollado diversas técnicas para contrarrestar esto, como el uso de acromáticos , lentes multielementos con cristales de distinta dispersión. Están construidas de tal forma que las aberraciones cromáticas de las diferentes partes se anulen.
Emisiones de pulsares
Los púlsares son estrellas de neutrones giratorias que emiten pulsos a intervalos muy regulares que van desde milisegundos hasta segundos. Los astrónomos creen que los pulsos se emiten simultáneamente en un amplio rango de frecuencias. Sin embargo, como se observa en la Tierra, los componentes de cada pulso emitidos a frecuencias de radio más altas llegan antes que los emitidos a frecuencias más bajas. Esta dispersión se produce debido al componente ionizado del medio interestelar , principalmente los electrones libres, que hacen que la velocidad de grupo dependa de la frecuencia. El retraso adicional agregado a una frecuencia ν es
donde la constante de dispersión k DM viene dada por [12]
y la medida de dispersión (DM) es la densidad de columna de electrones libres ( contenido total de electrones ), es decir, la densidad numérica de electrones n e integrados a lo largo del camino recorrido por el fotón desde el púlsar hasta la Tierra, y se da por
con unidades de parsecs por centímetro cúbico (1 pc/cm 3 = 30,857 × 1021 m −2 ). [13]
Por lo general, en las observaciones astronómicas, este retraso no se puede medir directamente, ya que se desconoce el tiempo de emisión. Lo que sí se puede medir es la diferencia en los tiempos de llegada a dos frecuencias diferentes. El retraso Δ t entre un componente de alta frecuencia ν hi y un componente de baja frecuencia ν lo de un pulso será
Reescribir la ecuación anterior en términos de Δ t permite determinar la densidad de masas midiendo los tiempos de llegada de los pulsos a múltiples frecuencias. Esto, a su vez, puede utilizarse para estudiar el medio interestelar, así como para combinar observaciones de púlsares a diferentes frecuencias.
Véase también
- Número de Abbe
- Cálculo de propiedades del vidrio, incluida la dispersión.
- Ecuación de Cauchy
- Relación de dispersión
- Ráfaga rápida de ondas de radio (astronomía)
- Teorema de fluctuación
- Relaciones entre Green y Kubo
- Retraso de grupo
- Dispersión intramodal
- Relaciones Kramers-Kronig
- Función de respuesta lineal
- Teoría de dispersión de prismas múltiples
- Ecuación de Sellmeier
- Pulso ultracorto
- Matriz en fase con imágenes virtuales
Referencias
- ^ Born, Max ; Wolf, Emil (octubre de 1999). Principios de óptica . Cambridge: Cambridge University Press . pp. 14-24. ISBN. 0-521-64222-1.
- ^ Compensación de dispersión. Consultado el 25-08-2015.
- ^ Cálculo de la dispersión media de vidrios.
- ^ Born, M. y Wolf, E. (1980) " Principios de Óptica ", 6ª ed., pág. 93. Pergamon Press.
- ^ Ramaswami, Rajiv y Sivarajan, Kumar N. (1998) Redes ópticas: una perspectiva práctica . Academic Press: Londres.
- ^ Dispersión cromática, Enciclopedia de física y tecnología láser (Wiley, 2008).
- ^ Mai, Wending; Campbell, Sawyer D.; Whiting, Eric B.; Kang, Lei; Werner, Pingjuan L.; Chen, Yifan; Werner, Douglas H. (1 de octubre de 2020). "Método prismático discontinuo de dominio temporal de Galerkin con un modelo de dispersión generalizado integrado para un análisis eficiente de la metasuperficie óptica". Materiales ópticos Express . 10 (10): 2542–2559. Código Bibliográfico :2020OMExp..10.2542M. doi : 10.1364/OME.399414 . ISSN 2159-3930.
- ^ ab Landau, LD ; Lifshitz, EM ; Pitaevskii, LP (1984). Electrodinámica de medios continuos . Vol. 8 (2.ª ed.). Butterworth-Heinemann . ISBN 978-0-7506-2634-7.
- ^ Demetriadou, A.; Pendry, JB (1 de julio de 2008). "Dominando la dispersión espacial en metamaterial de alambre". Journal of Physics: Condensed Matter . 20 (29): 295222. Bibcode :2008JPCM...20C5222D. doi :10.1088/0953-8984/20/29/295222. S2CID 120249447.
- ^ ab Schumann, Walter (2009). Gemstones of the World (cuarta edición revisada y ampliada). Sterling Publishing Company. págs. 41–42. ISBN 978-1-4027-6829-3. Recuperado el 31 de diciembre de 2011 .
- ^ "¿Qué es la dispersión de piedras preciosas?". International Gem Society (GemSociety.org) . Consultado el 9 de marzo de 2015 .
- ^ "Radioastronomía de plato único: técnicas y aplicaciones", Actas de la conferencia de la ASP, vol. 278. Editado por Snezana Stanimirovic, Daniel Altschuler , Paul Goldsmith y Chris Salter. ISBN 1-58381-120-6 . San Francisco: Astronomical Society of the Pacific, 2002, págs. 251–269.
- ^ Lorimer, DR, y Kramer, M., Handbook of Pulsar Astronomy , vol. 4 de Cambridge Observing Handbooks for Research Astronomers ( Cambridge University Press , Cambridge, Reino Unido; Nueva York, EE. UU., 2005), 1.ª edición.
Enlaces externos
- Wiki dispersiva Archivado el 23 de julio de 2017 en Wayback Machine : análisis de los aspectos matemáticos de la dispersión.
- Dispersión – Enciclopedia de física y tecnología láser
- Animaciones que demuestran la dispersión óptica mediante QED
- Demostración web interactiva de dispersión cromática Instituto de Telecomunicaciones, Universidad de Stuttgart













