Ruido blanco

En el procesamiento de señales , el ruido blanco es una señal aleatoria que tiene la misma intensidad en diferentes frecuencias , lo que le da una densidad espectral de potencia constante . ^[1] El término se utiliza con este o similares significados en muchas disciplinas científicas y técnicas, incluidas la física , la ingeniería acústica , las telecomunicaciones y la previsión estadística . El ruido blanco se refiere a un modelo estadístico para señales y fuentes de señales, no a ninguna señal específica. El ruido blanco toma su nombre de la luz blanca , ^[2] aunque la luz que parece blanca generalmente no tiene una densidad espectral de potencia plana en la banda visible .

En tiempo discreto , el ruido blanco es una señal discreta cuyas muestras se consideran una secuencia de variables aleatorias serialmente no correlacionadas con media cero y varianza finita ; una sola realización de ruido blanco es un choque aleatorio . En algunos contextos, también se requiere que las muestras sean independientes y tengan una distribución de probabilidad idéntica (en otras palabras, las variables aleatorias independientes e idénticamente distribuidas son la representación más simple del ruido blanco). ^[3] En particular, si cada muestra tiene una distribución normal con media cero, se dice que la señal es ruido blanco gaussiano aditivo . ^[4]

Las muestras de una señal de ruido blanco pueden ser secuenciales en el tiempo o estar dispuestas a lo largo de una o más dimensiones espaciales. En el procesamiento de imágenes digitales , los píxeles de una imagen de ruido blanco suelen estar dispuestos en una cuadrícula rectangular y se supone que son variables aleatorias independientes con una distribución de probabilidad uniforme a lo largo de un intervalo. El concepto también se puede definir para señales distribuidas en dominios más complejos, como una esfera o un toro .

UnLa señal de ruido blanco de ancho de banda infinito es una construcción puramente teórica. El ancho de banda del ruido blanco está limitado en la práctica por el mecanismo de generación del ruido, por el medio de transmisión y por las capacidades finitas de observación. Por lo tanto, las señales aleatorias se consideran ruido blanco si se observa que tienen un espectro plano en el rango de frecuencias que son relevantes para el contexto. Para unaseñal de audio, el rango relevante es la banda de frecuencias de sonido audibles (entre 20 y 20.000Hz). El oído humano escucha una señal de este tipo como un sonido silbante, parecido al sonido /h/ en una aspiración sostenida. Por otro lado, elsonidosh/ʃ/enashes un ruido coloreado porque tiene unade formantes. Enmúsicayacústica, el términoruido blancopuede usarse para cualquier señal que tenga un sonido silbante similar.

En el contexto de los métodos estadísticos basados ​​en la filogenia , el término ruido blanco puede referirse a la falta de un patrón filogenético en los datos comparativos. ^[5] En contextos no técnicos, a veces se utiliza para referirse a una "conversación aleatoria sin contenido significativo". ^{[6] [7]}

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (January 2022) (Learn how and when to remove this message)

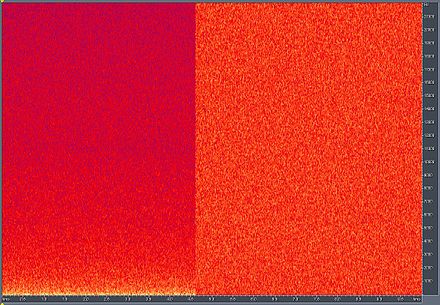
Es posible cualquier distribución de valores (aunque debe tener un componente de CC cero ). Incluso una señal binaria que solo puede tomar los valores 1 o -1 será blanca si la secuencia no está correlacionada estadísticamente. El ruido que tiene una distribución continua, como una distribución normal , por supuesto puede ser blanco.

A menudo se supone incorrectamente que el ruido gaussiano (es decir, el ruido con una distribución de amplitud gaussiana; consulte la distribución normal ) se refiere necesariamente al ruido blanco, pero ninguna propiedad implica la otra. La gaussianidad se refiere a la distribución de probabilidad con respecto al valor, en este contexto, la probabilidad de que la señal se encuentre dentro de un rango particular de amplitudes, mientras que el término "blanco" se refiere a la forma en que se distribuye la potencia de la señal (es decir, de forma independiente) a lo largo del tiempo o entre frecuencias.

Una forma de ruido blanco es la derivada cuadrática media generalizada del proceso de Wiener o movimiento browniano .

Una generalización a elementos aleatorios en espacios de dimensión infinita, como los campos aleatorios , es la medida de ruido blanco .

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (January 2022) (Learn how and when to remove this message)

El ruido blanco se utiliza habitualmente en la producción de música electrónica , normalmente de forma directa o como entrada para un filtro para crear otros tipos de señales de ruido. Se utiliza ampliamente en la síntesis de audio , normalmente para recrear instrumentos de percusión como platillos o cajas que tienen un alto contenido de ruido en su dominio de frecuencia. ^[8] Un ejemplo sencillo de ruido blanco es una estación de radio inexistente (estática).

El ruido blanco también se utiliza para obtener la respuesta al impulso de un circuito eléctrico, en particular de amplificadores y otros equipos de audio. No se utiliza para probar altavoces, ya que su espectro contiene una cantidad demasiado grande de contenido de alta frecuencia. El ruido rosa , que se diferencia del ruido blanco en que tiene la misma energía en cada octava, se utiliza para probar transductores como altavoces y micrófonos.

El ruido blanco se utiliza como base de algunos generadores de números aleatorios . Por ejemplo, Random.org utiliza un sistema de antenas atmosféricas para generar patrones de dígitos aleatorios a partir de fuentes que pueden ser bien modeladas por el ruido blanco. ^[9]

El ruido blanco es una fuente de ruido sintético común que se utiliza para enmascarar el sonido mediante un enmascarador de tinnitus . ^[10] Las máquinas de ruido blanco y otras fuentes de ruido blanco se venden como potenciadores de la privacidad y ayudas para dormir (ver música y sueño ) y para enmascarar el tinnitus . ^[11] El Marpac Sleep-Mate fue la primera máquina de ruido blanco de uso doméstico construida en 1962 por el vendedor ambulante Jim Buckwalter. ^[12] Alternativamente, el uso de una radio AM sintonizada en frecuencias no utilizadas ("estática") es una fuente de ruido blanco más simple y rentable. ^[13] Sin embargo, el ruido blanco generado a partir de un receptor de radio comercial común sintonizado en una frecuencia no utilizada es extremadamente vulnerable a estar contaminado con señales espurias, como estaciones de radio adyacentes, armónicos de estaciones de radio no adyacentes, equipo eléctrico en las proximidades de la antena receptora que causa interferencias, o incluso eventos atmosféricos como erupciones solares y especialmente relámpagos.

Los efectos del ruido blanco sobre la función cognitiva son variados. Recientemente, un pequeño estudio descubrió que la estimulación de fondo con ruido blanco mejora el funcionamiento cognitivo entre los estudiantes de secundaria con trastorno por déficit de atención e hiperactividad (TDAH), mientras que disminuye el rendimiento de los estudiantes sin TDAH. ^{[14] [15]} Otros trabajos indican que es eficaz para mejorar el estado de ánimo y el rendimiento de los trabajadores al enmascarar el ruido de fondo de la oficina, ^[16] pero disminuye el rendimiento cognitivo en tareas complejas de clasificación de tarjetas. ^[17]

De manera similar, se llevó a cabo un experimento con sesenta y seis participantes sanos para observar los beneficios de utilizar ruido blanco en un entorno de aprendizaje. El experimento consistió en que los participantes identificaran diferentes imágenes mientras escuchaban diferentes sonidos de fondo. En general, el experimento demostró que el ruido blanco, de hecho, tiene beneficios en relación con el aprendizaje. Los experimentos mostraron que el ruido blanco mejoraba ligeramente las habilidades de aprendizaje de los participantes y su memoria de reconocimiento. ^[18]

Se dice que un vector aleatorio (es decir, una variable aleatoria con valores en R ⁿ ) es un vector de ruido blanco o un vector aleatorio blanco si sus componentes tienen cada uno una distribución de probabilidad con media cero y varianza finita , ^{[ aclaración necesaria ]} y son estadísticamente independientes : es decir, su distribución de probabilidad conjunta debe ser el producto de las distribuciones de los componentes individuales. ^[19]

Una condición necesaria (pero, en general, no suficiente ) para la independencia estadística de dos variables es que no estén estadísticamente correlacionadas ; es decir, su covarianza es cero. Por lo tanto, la matriz de covarianza R de los componentes de un vector de ruido blanco w con n elementos debe ser una matriz diagonal n por n , donde cada elemento diagonal R _ii es la varianza del componente w _i ; y la matriz de correlación debe ser la matriz identidad n por n .

Si, además de ser independientes, cada variable en w también tiene una distribución normal con media cero y la misma varianza , se dice que w es un vector de ruido blanco gaussiano. En ese caso, la distribución conjunta de w es una distribución normal multivariante ; la independencia entre las variables implica entonces que la distribución tiene simetría esférica en un espacio n -dimensional. Por lo tanto, cualquier transformación ortogonal del vector dará como resultado un vector aleatorio blanco gaussiano. En particular, bajo la mayoría de los tipos de transformada de Fourier discreta , como FFT y Hartley , la transformada W de w también será un vector de ruido blanco gaussiano; es decir, los n coeficientes de Fourier de w serán variables gaussianas independientes con media cero y la misma varianza .${\displaystyle \sigma ^{2}}$${\displaystyle \sigma ^{2}}$

El espectro de potencia P de un vector aleatorio w se puede definir como el valor esperado del módulo al cuadrado de cada coeficiente de su transformada de Fourier W , es decir, P _i = E(| W _i | ² ). Según esa definición, un vector de ruido blanco gaussiano tendrá un espectro de potencia perfectamente plano, con P _i  =  σ ² para todo  i .

Si w es un vector aleatorio blanco, pero no gaussiano, sus coeficientes de Fourier W _i no serán completamente independientes entre sí; aunque para n grandes y distribuciones de probabilidad comunes las dependencias son muy sutiles y se puede suponer que sus correlaciones por pares son cero.

A menudo, en la definición de ruido blanco se utiliza la condición más débil estadísticamente no correlacionada, en lugar de estadísticamente independiente. Sin embargo, algunas de las propiedades comúnmente esperadas del ruido blanco (como el espectro de potencia plano) pueden no ser válidas para esta versión más débil. Bajo este supuesto, la versión más estricta puede denominarse explícitamente vector de ruido blanco independiente. ^{[20] : p.60} Otros autores utilizan fuertemente blanco y débilmente blanco en su lugar. ^[21]

Un ejemplo de un vector aleatorio que es ruido blanco gaussiano en el sentido débil pero no en el fuerte es donde es una variable aleatoria normal con media cero, y es igual a o a , con igual probabilidad. Estas dos variables no están correlacionadas y se distribuyen normalmente individualmente, pero no se distribuyen normalmente en conjunto y no son independientes. Si se gira 45 grados, sus dos componentes seguirán sin estar correlacionados, pero su distribución ya no será normal.${\displaystyle x=[x_{1},x_{2}]}$${\displaystyle x_{1}}$${\displaystyle x_{2}}$${\displaystyle +x_{1}}$${\displaystyle -x_{1}}$${\displaystyle x}$

En algunas situaciones, se puede relajar la definición permitiendo que cada componente de un vector aleatorio blanco tenga un valor esperado distinto de cero . En el procesamiento de imágenes en particular, donde las muestras suelen estar restringidas a valores positivos, a menudo se toma como la mitad del valor máximo de la muestra. En ese caso, el coeficiente de Fourier correspondiente al componente de frecuencia cero (esencialmente, el promedio de ) también tendrá un valor esperado distinto de cero ; y el espectro de potencia será plano solo sobre las frecuencias distintas de cero.${\displaystyle w}$${\displaystyle \mu }$${\displaystyle \mu }$${\displaystyle W_{0}}$${\displaystyle w_{i}}$${\displaystyle \mu {\sqrt {n}}}$${\displaystyle P}$

Un proceso estocástico de tiempo discreto es una generalización de un vector aleatorio con un número finito de componentes a un número infinito de componentes. Un proceso estocástico de tiempo discreto se denomina ruido blanco si su media es igual a cero para todos los , es decir, y si la función de autocorrelación tiene un valor distinto de cero solo para , es decir , . ^{[ cita requerida ] [ aclaración necesaria ]}${\displaystyle W(n)}$${\displaystyle W(n)}$${\displaystyle n}$${\displaystyle \operatorname {E} [W(n)]=0}$${\displaystyle R_{W}(n)=\operatorname {E} [W(k+n)W(k)]}$${\displaystyle n=0}$${\displaystyle R_{W}(n)=\sigma ^{2}\delta (n)}$

Para definir la noción de ruido blanco en la teoría de señales de tiempo continuo , se debe reemplazar el concepto de vector aleatorio por el de señal aleatoria de tiempo continuo; es decir, un proceso aleatorio que genera una función de un parámetro de valor real .${\displaystyle w}$${\displaystyle t}$

Se dice que un proceso de este tipo es ruido blanco en el sentido más fuerte si el valor para cualquier tiempo es una variable aleatoria que es estadísticamente independiente de toda su historia antes de . Una definición más débil requiere independencia solo entre los valores y en cada par de tiempos distintos y . Una definición aún más débil requiere solo que dichos pares y no estén correlacionados. ^[22] Como en el caso discreto, algunos autores adoptan la definición más débil para ruido blanco y usan el calificador independiente para referirse a cualquiera de las definiciones más fuertes. Otros usan débilmente blanco y fuertemente blanco para distinguirlos.${\displaystyle w(t)}$${\displaystyle t}$${\displaystyle t}$${\displaystyle w(t_{1})}$${\displaystyle w(t_{2})}$${\displaystyle t_{1}}$${\displaystyle t_{2}}$${\displaystyle w(t_{1})}$${\displaystyle w(t_{2})}$

Sin embargo, una definición precisa de estos conceptos no es trivial, porque algunas cantidades que son sumas finitas en el caso discreto finito deben ser reemplazadas por integrales que pueden no converger. De hecho, el conjunto de todas las instancias posibles de una señal ya no es un espacio de dimensión finita , sino un espacio de función de dimensión infinita . Además, según cualquier definición, una señal de ruido blanco tendría que ser esencialmente discontinua en cada punto; por lo tanto, incluso las operaciones más simples sobre , como la integración sobre un intervalo finito, requieren maquinaria matemática avanzada.${\displaystyle w}$${\displaystyle \mathbb {R} ^{n}}$${\displaystyle w}$${\displaystyle w}$

Algunos autores ^{[ cita requerida ] [ aclaración necesaria ]} requieren que cada valor sea una variable aleatoria de valor real con expectativa y cierta varianza finita . Entonces, la covarianza entre los valores en dos momentos y está bien definida: es cero si los momentos son distintos y si son iguales. Sin embargo, según esta definición, la integral${\displaystyle w(t)}$${\displaystyle \mu }$${\displaystyle \sigma ^{2}}$${\displaystyle \mathrm {E} (w(t_{1})\cdot w(t_{2}))}$${\displaystyle t_{1}}$${\displaystyle t_{2}}$${\displaystyle \sigma ^{2}}$

${\displaystyle W_{[a,a+r]}=\int _{a}^{a+r}w(t)\,dt}$

sobre cualquier intervalo con ancho positivo sería simplemente el ancho multiplicado por la expectativa: . ^{[ aclaración necesaria ]} Esta propiedad hace que el concepto sea inadecuado como modelo de señales de ruido blanco, ya sea en un sentido físico o matemático. ^{[ aclaración necesaria ]}${\displaystyle r}$${\displaystyle r\mu }$

Por lo tanto, la mayoría de los autores definen la señal indirectamente especificando valores aleatorios para las integrales de y en cada intervalo . Sin embargo, en este enfoque, el valor de en un tiempo aislado no se puede definir como una variable aleatoria de valor real ^{[ cita requerida ]} . Además, la covarianza se vuelve infinita cuando ; y la función de autocorrelación debe definirse como , donde es una constante real y es la función delta de Dirac . ^{[ aclaración necesaria ]}${\displaystyle w}$${\displaystyle w(t)}$${\displaystyle |w(t)|^{2}}$${\displaystyle [a,a+r]}$${\displaystyle w(t)}$${\displaystyle \mathrm {E} (w(t_{1})\cdot w(t_{2}))}$${\displaystyle t_{1}=t_{2}}$${\displaystyle \mathrm {R} (t_{1},t_{2})}$${\displaystyle N\delta (t_{1}-t_{2})}$${\displaystyle N}$${\displaystyle \delta }$

En este enfoque, se suele especificar que la integral de sobre un intervalo es una variable aleatoria real con distribución normal, media cero y varianza ; y también que la covarianza de las integrales , es , donde es el ancho de la intersección de los dos intervalos . Este modelo se denomina señal (o proceso) de ruido blanco gaussiano.${\displaystyle W_{I}}$${\displaystyle w(t)}$${\displaystyle I=[a,b]}$${\displaystyle (b-a)\sigma ^{2}}$${\displaystyle \mathrm {E} (W_{I}\cdot W_{J})}$${\displaystyle W_{I}}$${\displaystyle W_{J}}$${\displaystyle r\sigma ^{2}}$${\displaystyle r}$${\displaystyle I\cap J}$${\displaystyle I,J}$

En el campo matemático conocido como análisis de ruido blanco , un ruido blanco gaussiano se define como una distribución templada estocástica, es decir, una variable aleatoria con valores en el espacio de distribuciones templadas . De manera análoga al caso de los vectores aleatorios de dimensión finita, una ley de probabilidad en el espacio de dimensión infinita se puede definir a través de su función característica (la existencia y unicidad están garantizadas por una extensión del teorema de Bochner-Minlos, que se conoce con el nombre de teorema de Bochner-Minlos-Sazanov); de manera análoga al caso de la distribución normal multivariante , que tiene una función característica${\displaystyle w}$${\displaystyle {\mathcal {S}}'(\mathbb {R} )}$${\displaystyle {\mathcal {S}}'(\mathbb {R} )}$${\displaystyle X\sim {\mathcal {N}}_{n}(\mu ,\Sigma )}$

${\displaystyle \forall k\in \mathbb {R} ^{n}:\quad \mathrm {E} (\mathrm {e} ^{\mathrm {i} \langle k,X\rangle })=\mathrm {e} ^{\mathrm {i} \langle k,\mu \rangle -{\frac {1}{2}}\langle k,\Sigma k\rangle },}$

El ruido blanco debe satisfacer${\displaystyle w:\Omega \to {\mathcal {S}}'(\mathbb {R} )}$

${\displaystyle \forall \varphi \in {\mathcal {S}}(\mathbb {R} ):\quad \mathrm {E} (\mathrm {e} ^{\mathrm {i} \langle w,\varphi \rangle })=\mathrm {e} ^{-{\frac {1}{2}}\|\varphi \|_{2}^{2}},}$

donde es el emparejamiento natural de la distribución templada con la función de Schwartz , tomada en cada escenario para , y .${\displaystyle \langle w,\varphi \rangle }$${\displaystyle w(\omega )}$${\displaystyle \varphi }$${\displaystyle \omega \in \Omega }$${\displaystyle \|\varphi \|_{2}^{2}=\int _{\mathbb {R} }\vert \varphi (x)\vert ^{2}\,\mathrm {d} x}$

En estadística y econometría, a menudo se supone que una serie observada de valores de datos es la suma de los valores generados por un proceso lineal determinista , que depende de ciertas variables independientes (explicativas) y de una serie de valores de ruido aleatorio. Luego, se utiliza el análisis de regresión para inferir los parámetros del proceso del modelo a partir de los datos observados, por ejemplo, mediante mínimos cuadrados ordinarios , y para probar la hipótesis nula de que cada uno de los parámetros es cero frente a la hipótesis alternativa de que no es cero. Las pruebas de hipótesis generalmente suponen que los valores de ruido no están mutuamente correlacionados con media cero y tienen la misma distribución de probabilidad gaussiana; en otras palabras, que el ruido es blanco gaussiano (no solo blanco). Si existe una correlación distinta de cero entre los valores de ruido subyacentes a diferentes observaciones, entonces los parámetros estimados del modelo siguen siendo imparciales , pero las estimaciones de sus incertidumbres (como los intervalos de confianza ) estarán sesgadas (no serán precisas en promedio). Esto también es cierto si el ruido es heterocedástico  , es decir, si tiene diferentes varianzas para diferentes puntos de datos.

Alternativamente, en el subconjunto del análisis de regresión conocido como análisis de series temporales, a menudo no hay variables explicativas distintas de los valores pasados ​​de la variable que se está modelando (la variable dependiente ). En este caso, el proceso de ruido se modela a menudo como un proceso de promedio móvil , en el que el valor actual de la variable dependiente depende de los valores actuales y pasados ​​de un proceso de ruido blanco secuencial.

Estas dos ideas son fundamentales en aplicaciones como la estimación de canal y la ecualización de canal en comunicaciones y audio . Estos conceptos también se utilizan en la compresión de datos .

En particular, mediante una transformación lineal adecuada (una transformación de coloración), un vector aleatorio blanco puede utilizarse para producir un vector aleatorio no blanco (es decir, una lista de variables aleatorias) cuyos elementos tienen una matriz de covarianza prescrita . A la inversa, un vector aleatorio con una matriz de covarianza conocida puede transformarse en un vector aleatorio blanco mediante una transformación de blanqueamiento adecuada .

El ruido blanco se puede generar digitalmente con un procesador de señal digital , un microprocesador o un microcontrolador . La generación de ruido blanco generalmente implica introducir un flujo apropiado de números aleatorios en un convertidor digital-analógico . La calidad del ruido blanco dependerá de la calidad del algoritmo utilizado. ^[23]

El término se utiliza a veces como coloquialismo para describir un fondo de sonido ambiental que crea una conmoción indistinta o uniforme. A continuación se muestran algunos ejemplos:

• Parloteo de múltiples conversaciones dentro de la acústica de un espacio confinado.
• La jerga pleonástica utilizada por los políticos para enmascarar un punto que no quieren que se note. ^[24]
• Música desagradable, áspera, disonante o discordante sin melodía .

El término también puede usarse metafóricamente, como en la novela White Noise (1985) de Don DeLillo , que explora los síntomas de la cultura moderna que se unieron para dificultar que un individuo actualice sus ideas y personalidad.

Wikimedia Commons tiene medios relacionados con Ruido blanco .