Ruido rosa

El ruido rosa , ruido 1 ⁄ f , ruido fraccional o ruido fractal es una señal o proceso con un espectro de frecuencia tal que la densidad espectral de potencia (potencia por intervalo de frecuencia) es inversamente proporcional a la frecuencia de la señal. En el ruido rosa, cada intervalo de octava (reduciendo a la mitad o duplicando la frecuencia) transporta una cantidad igual de energía de ruido.

El ruido rosa suena como una cascada . ^[2] Se utiliza a menudo para sintonizar sistemas de altavoces en audio profesional . ^[3] El ruido rosa es una de las señales más comúnmente observadas en los sistemas biológicos. ^[4]

El nombre surge de la apariencia rosada de la luz visible con este espectro de potencia. ^[5] Esto contrasta con el ruido blanco que tiene la misma intensidad por intervalo de frecuencia.

Ruido rosa

10 segundos de ruido rosa, normalizado a una amplitud máxima de −1 dBFS

---

¿Tiene problemas para reproducir este archivo? Consulte la ayuda multimedia .

En la literatura científica, el término ruido 1/f se utiliza a veces de forma imprecisa para referirse a cualquier ruido con una densidad espectral de potencia de la forma

$${\displaystyle S(f)\propto {\frac {1}{f^{\alpha }}},}$$

donde f es la frecuencia y 0 < α < 2, con un exponente α generalmente cercano a 1. Las señales unidimensionales con α = 1 generalmente se denominan ruido rosa. ^[6]

La siguiente función describe una señal de ruido rosa unidimensional de longitud (es decir, una señal de ruido blanco gaussiano con media y desviación estándar cero , que ha sido filtrada adecuadamente), como una suma de ondas sinusoidales con diferentes frecuencias, cuyas amplitudes caen inversamente con la raíz cuadrada de la frecuencia (de modo que la potencia, que es el cuadrado de la amplitud, cae inversamente con la frecuencia), y las fases son aleatorias: ^[7]${\estilo de visualización N}$${\estilo de visualización \sigma}$${\estilo de visualización u}$

$${\displaystyle h(x)=\sigma {\sqrt {\frac {N}{2}}}\sum _{u}{\frac {\chi _{u}}{u}}\sin({\ frac {2\pi ux}{N}}+\phi _{u}),\quad \chi _{u}\sim \chi (2),\quad \phi _{u}\sim U(0, 2\pi ).}$$

${\displaystyle \chi_{u}}$son variables distribuidas mediante chi iid y son aleatorias uniformes.${\displaystyle \phi _{u}}$

En una señal de ruido rosa bidimensional, la amplitud en cualquier orientación disminuye inversamente con la frecuencia. El cuadrado de longitud del ruido rosa se puede escribir como: ^[7]${\estilo de visualización N}$$${\displaystyle h(x,y)={\frac {\sigma N}{\sqrt {2}}}\sum _{u,v}{\frac {\chi _{uv}}{\sqrt {u^{2}+v^{2}}}}\sin \left({\frac {2\pi }{N}}(ux+vy)+\phi _{uv}\right),\quad \chi _{uv}\sim \chi (2),\quad \phi _{uv}\sim U(0,2\pi ).}$$

Los ruidos generales de tipo 1/ f  ^α se producen ampliamente en la naturaleza y son una fuente de considerable interés en muchos campos. Los ruidos con α cerca de 1 generalmente provienen de sistemas de materia condensada en cuasi-equilibrio , como se analiza a continuación. ^[8] Los ruidos con un amplio rango de α generalmente corresponden a una amplia gama de sistemas dinámicos impulsados ​​por no equilibrio .

Las fuentes de ruido rosa incluyen el ruido de parpadeo en los dispositivos electrónicos. En su estudio del movimiento browniano fraccional , ^[9] Mandelbrot y Van Ness propusieron el nombre de ruido fraccional (a veces llamado desde entonces ruido fractal ) para describir los ruidos 1/ f  ^α para los cuales el exponente α no es un número entero par, ^[10] o que son derivados fraccionarios del ruido browniano (1/ f  ² ).

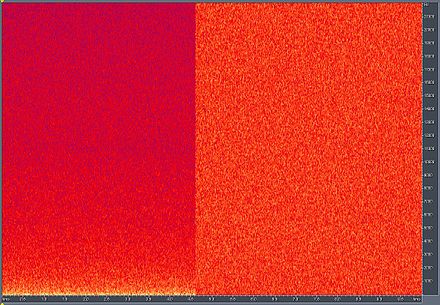
En el ruido rosa, la energía es igual por octava de frecuencia. Sin embargo, la energía del ruido rosa en cada nivel de frecuencia disminuye aproximadamente 3  dB por octava. Esto contrasta con el ruido blanco , que tiene la misma energía en todos los niveles de frecuencia. ^[11]

El sistema auditivo humano , que procesa las frecuencias de una manera aproximadamente logarítmica, aproximada por la escala Bark , no percibe frecuencias diferentes con la misma sensibilidad; las señales de alrededor de 1 a 4 kHz suenan más fuertes para una intensidad dada. Sin embargo, los humanos aún diferencian entre ruido blanco y ruido rosa con facilidad.

Los ecualizadores gráficos también dividen las señales en bandas de forma logarítmica y reportan la potencia por octavas; los ingenieros de audio hacen pasar ruido rosa por un sistema para probar si tiene una respuesta de frecuencia plana en el espectro de interés. Los sistemas que no tienen una respuesta plana se pueden ecualizar creando un filtro inverso utilizando un ecualizador gráfico. Debido a que el ruido rosa tiende a ocurrir en sistemas físicos naturales, a menudo es útil en la producción de audio. El ruido rosa se puede procesar, filtrar y/o se pueden agregar efectos para producir los sonidos deseados. Los generadores de ruido rosa están disponibles comercialmente.

Un parámetro del ruido, el contenido de energía pico versus promedio, o factor de cresta , es importante para fines de prueba, como por ejemplo para amplificadores de potencia de audio y capacidades de altavoces , porque la potencia de la señal es una función directa del factor de cresta. Se pueden utilizar varios factores de cresta de ruido rosa en simulaciones de varios niveles de compresión de rango dinámico en señales musicales. En algunos generadores digitales de ruido rosa se puede especificar el factor de cresta.

El ruido rosa se puede generar por computadora generando primero una señal de ruido blanco, transformándola por Fourier y luego dividiendo las amplitudes de los diferentes componentes de frecuencia por la raíz cuadrada de la frecuencia (en una dimensión) o por la frecuencia (en dos dimensiones), etc. ^[7] Esto es equivalente a filtrar espacialmente (convolucionar) la señal de ruido blanco con un filtro blanco-rosa. Para una señal de longitud en una dimensión, el filtro tiene la siguiente forma: ^[7]${\estilo de visualización N}$

$${\displaystyle a(x)={\frac {1}{N}}\left[1+{\frac {1}{\sqrt {N/2}}}\cos \pi (x-1)+2\sum _{k=1}^{N/2-1}{\frac {1}{\sqrt {k}}}\cos {{\frac {2\pi k}{N}}(x-1)}\right].}$$

Hay programas de Matlab disponibles para generar ruido rosa y otros ruidos de color de ley de potencia en una o cualquier número de dimensiones.

El espectro de potencia del ruido rosa es solo para señales unidimensionales. Para señales bidimensionales (por ejemplo, imágenes), el espectro de potencia promedio en cualquier orientación cae como , y en dimensiones, cae como . En cada caso, cada octava lleva una cantidad igual de potencia de ruido. ${\displaystyle {\frac {1}{f}}}$${\displaystyle {\frac {1}{f^{2}}}}$${\estilo de visualización d}$${\displaystyle {\frac {1}{f^{d}}}}$

La amplitud y potencia promedio de una señal de ruido rosa en cualquier orientación y la potencia total en todas las orientaciones disminuyen como una potencia de la frecuencia. La siguiente tabla enumera estas dependencias de frecuencia de ley de potencia para la señal de ruido rosa en diferentes dimensiones y también para el ruido coloreado de ley de potencia general con potencia (por ejemplo: el ruido marrón tiene ): ^[7]${\displaystyle a_{\theta}}$${\displaystyle p_{\theta}}$${\estilo de visualización \theta}$${\estilo de visualización \alpha}$${\displaystyle \alpha =2}$

Espectros de ley de potencia del ruido rosa

dimensiones	amperaje promedio${\displaystyle a_{\theta}(f)}$	potencia media${\displaystyle p_{\theta}(f)}$	potencia total${\displaystyle p(f)}$
1	${\displaystyle 1/{\sqrt {f}}}$	${\estilo de visualización 1/f}$	${\estilo de visualización 1/f}$
2	${\estilo de visualización 1/f}$	$Estilo de visualización 1/f^{2}}$	${\estilo de visualización 1/f}$
3	$Estilo de visualización 1/f^{3/2}}$	${\estilo de visualización 1/f^{3}}$	${\estilo de visualización 1/f}$
${\estilo de visualización d}$	$Estilo de visualización 1/f^{d/2}}$	${\displaystyle 1/f^{d}}$	${\estilo de visualización 1/f}$
${\estilo de visualización d}$, fuerza${\estilo de visualización \alpha}$	${\displaystyle 1/f^{\alpha d/2}}$	${\displaystyle 1/f^{\alpha d}}$	${\displaystyle 1/f^{1+(\alpha -1)d}}$

Consideremos el ruido rosa de cualquier dimensión que se produce generando una señal de ruido blanco gaussiano con media y desviación estándar y luego multiplicando su espectro con un filtro (equivalente a filtrarlo espacialmente con un filtro ). Entonces, los valores puntuales de la señal de ruido rosa también se distribuirán normalmente, con media y desviación estándar . ^[7]${\estilo de visualización \mu}$${\estilo de visualización \sigma}$${\displaystyle {\boldsymbol {a}}}$${\estilo de visualización \mu}$${\displaystyle \lVert {\boldsymbol {a}}\rVert \sigma }$

A diferencia del ruido blanco, que no tiene correlaciones a través de la señal, una señal de ruido rosa está correlacionada consigo misma, de la siguiente manera.

El coeficiente de correlación de Pearson de una señal de ruido rosa unidimensional (que comprende frecuencias discretas ) consigo misma a través de una distancia en el dominio de configuración (espacio o tiempo) es: ^[7] Si en lugar de frecuencias discretas, el ruido rosa comprende una superposición de frecuencias continuas de a , el coeficiente de autocorrelación es: ^[7] donde es la función integral del coseno .${\estilo de visualización k}$${\estilo de visualización d}$$${\displaystyle r(d)={\frac {\suma _{k}{\frac {\cos {\frac {2\pi kd}{N}}}{k}}}{\suma _{k}{\frac {1}{k}}}}.}$$${\displaystyle k_{\textrm {min}}}$${\displaystyle k_{\textrm {máximo}}}$$${\displaystyle r(d)={\frac {{\textrm {Ci}}({\frac {2\pi k_{\textrm {max}}d}{N}})-{\textrm {Ci}}({\frac {2\pi k_{\textrm {min}}d}{N}})}{\log {\frac {k_{\textrm {max}}}{k_{\textrm {min}}}}}},}$$${\displaystyle {\textrm {Ci}}(x)}$

El coeficiente de autocorrelación de Pearson de una señal de ruido rosa bidimensional que comprende frecuencias discretas se aproxima teóricamente como: ^[7] donde es la función de Bessel del primer tipo .$${\displaystyle r(d)={\frac {\sum _{k}{\frac {J_{0}({\frac {2\pi kd}{N}})}{k}}}{\sum _{k}{\frac {1}{k}}}},}$$${\displaystyle J_{0}}$

El ruido rosa se ha descubierto en las fluctuaciones estadísticas de un número extraordinariamente diverso de sistemas físicos y biológicos (Press, 1978; ^[12] véanse los artículos en Handel & Chung, 1993, ^[13] y las referencias allí citadas). Entre los ejemplos de su aparición se incluyen las fluctuaciones en las alturas de las mareas y los ríos, las emisiones de luz de los cuásares , los latidos del corazón, las activaciones de neuronas individuales , la resistividad en la electrónica de estado sólido y las señales de conductancia de moléculas individuales ^[14] que dan lugar al ruido parpadeante . El ruido rosa describe la estructura estadística de muchas imágenes naturales . ^[1]

 ^{Los ruidos α} generales 1/ f se producen en muchos sistemas físicos, biológicos y económicos, y algunos investigadores los describen como ubicuos. ^[15] En los sistemas físicos, están presentes en algunas series de datos meteorológicos , la emisión de radiación electromagnética de algunos cuerpos astronómicos. En los sistemas biológicos, están presentes, por ejemplo, en los ritmos de los latidos del corazón , la actividad neuronal y las estadísticas de las secuencias de ADN , como un patrón generalizado. ^[16]

Una introducción accesible a la importancia del ruido rosa es la que da Martin Gardner (1978) en su columna de Scientific American "Mathematical Games". ^[17] En esta columna, Gardner preguntaba en qué sentido la música imita a la naturaleza. Los sonidos de la naturaleza no son musicales en el sentido de que tienden a ser demasiado repetitivos (el canto de los pájaros, los ruidos de los insectos) o demasiado caóticos (las olas del océano, el viento en los árboles, etc.). La respuesta a esta pregunta la dieron en un sentido estadístico Voss y Clarke (1975, 1978), quienes demostraron que las fluctuaciones de tono y volumen en el habla y la música son ruidos rosas. ^{[18] [19]} Por lo tanto, la música es como las mareas no en términos de cómo suenan las mareas, sino en cómo varía su altura.

El ruido omnipresente 1/f supone un "piso de ruido" para el cronometraje de precisión. ^[12] La derivación se basa en. ^[20]

Supongamos que tenemos un dispositivo para medir el tiempo (puede ser cualquier cosa, desde osciladores de cuarzo , relojes atómicos y relojes de arena ^[21] ). Sea su lectura un número real que cambia con el tiempo real . Para ser más concretos, consideremos un oscilador de cuarzo. En un oscilador de cuarzo, es el número de oscilaciones y es la tasa de oscilación. La tasa de oscilación tiene un componente constante y un componente fluctuante , por lo que . Al seleccionar las unidades correctas para , podemos tener , lo que significa que, en promedio, pasa un segundo de tiempo de reloj por cada segundo de tiempo real.${\displaystyle x(t)}$${\displaystyle t}$${\displaystyle x(t)}$${\displaystyle {\dot {x}}(t)}$${\displaystyle {\dot {x}}_{0}}$${\displaystyle {\dot {x}}_{f}}$${\textstyle {\dot {x}}(t)={\dot {x}}_{0}+{\dot {x}}_{f}(t)}$${\displaystyle x}$${\displaystyle {\dot {x}}_{0}=1}$

La estabilidad del reloj se mide por la cantidad de "ticks" que hace en un intervalo fijo. Cuanto más estable sea el número de tics, mejor será la estabilidad del reloj. Por lo tanto, defina la frecuencia de reloj promedio en el intervalo como Nótese que no tiene unidades: es la relación numérica entre los tics del reloj físico y los tics de un reloj ideal ^{[nota 1]} .${\displaystyle [k\tau ,(k+1)\tau ]}$$${\displaystyle y_{k}={\frac {1}{\tau }}\int _{k\tau }^{(k+1)\tau }{\dot {x}}(t)dt={\frac {x((k+1)\tau )-x(k\tau )}{\tau }}}$$${\displaystyle y_{k}}$

La varianza de Allan de la frecuencia del reloj es la mitad del cuadrado medio del cambio en la frecuencia promedio del reloj: donde es un entero lo suficientemente grande para que el promedio converja a un valor definido. Por ejemplo, un reloj atómico de 2013 ^[22] logró , lo que significa que si el reloj se usa para medir repetidamente intervalos de 7 horas, la desviación estándar del tiempo realmente medido sería de alrededor de 40 femtosegundos .$${\displaystyle \sigma ^{2}(\tau )={\frac {1}{2}}{\overline {(y_{k}-y_{k-1})^{2}}}={\frac {1}{K}}\sum _{k=1}^{K}{\frac {1}{2}}(y_{k}-y_{k-1})^{2}}$$${\displaystyle K}$${\displaystyle \sigma (25000{\text{ seconds}})=1.6\times 10^{-18}}$

Ahora tenemos donde es un paquete de una onda cuadrada con altura y longitud de onda . Sea un paquete de una onda cuadrada con altura 1 y longitud de onda 2, entonces , y su transformada de Fourier satisface .$${\displaystyle y_{k}-y_{k-1}=\int _{\mathbb {R} }g(k\tau -t){\dot {x}}_{f}(t)dt=(g\ast {\dot {x}}_{f})(k\tau )}$$${\displaystyle g(t)={\frac {-1_{[0,\tau ]}(t)+1_{[-\tau ,0]}(t)}{\tau }}}$${\displaystyle 1/\tau }$${\displaystyle 2\tau }$${\displaystyle h(t)}$${\displaystyle g(t)=h(t/\tau )/\tau }$${\displaystyle {\mathcal {F}}[g](\omega )={\mathcal {F}}[h](\tau \omega )}$

La varianza de Allan es entonces , y el promedio discreto se puede aproximar mediante un promedio continuo: , que es la potencia total de la señal , o la integral de su espectro de potencia :${\displaystyle \sigma ^{2}(\tau )={\frac {1}{2}}{\overline {(y_{k}-y_{k-1})^{2}}}={\frac {1}{2}}{\overline {(g\ast {\dot {x}}_{f})(k\tau )^{2}}}}$${\displaystyle {\frac {1}{K}}\sum _{k=1}^{K}{\frac {1}{2}}(y_{k}-y_{k-1})^{2}\approx {\frac {1}{K\tau }}\int _{0}^{K\tau }{\frac {1}{2}}(g\ast {\dot {x}}_{f})(t)^{2}dt}$${\displaystyle (g\ast {\dot {x}}_{f})}$

$${\displaystyle \sigma ^{2}(\tau )\approx \int _{0}^{\infty }S[g\ast {\dot {x}}_{f}](\omega )d\omega =\int _{0}^{\infty }S[g](\omega )\cdot S[{\dot {x}}_{f}](\omega )d\omega =\int _{0}^{\infty }S[h](\tau \omega )\cdot S[{\dot {x}}_{f}](\omega )d\omega }$$En palabras, la varianza de Allan es aproximadamente la potencia de la fluctuación después del filtrado de paso de banda con un ancho de banda .${\displaystyle \omega \sim 1/\tau }$${\displaystyle \Delta \omega \sim 1/\tau }$

Para la fluctuación, tenemos para alguna constante , por lo que . En particular, cuando el componente fluctuante es un ruido 1/f, entonces es independiente del tiempo de promediado , lo que significa que la frecuencia de reloj no se vuelve más estable simplemente promediando durante más tiempo. Esto contrasta con una fluctuación de ruido blanco, en cuyo caso , lo que significa que duplicar el tiempo de promediado mejoraría la estabilidad de la frecuencia en . ^[12]${\displaystyle 1/f^{\alpha }}$${\displaystyle S[{\dot {x}}_{f}](\omega )=C/\omega ^{\alpha }}$${\displaystyle C}$${\displaystyle \sigma ^{2}(\tau )\approx \tau ^{\alpha -1}\sigma ^{2}(1)\propto \tau ^{\alpha -1}}$${\displaystyle {\dot {x}}_{f}}$${\displaystyle \sigma ^{2}(\tau )}$${\displaystyle \tau }$${\displaystyle \sigma ^{2}(\tau )\propto \tau ^{-1}}$${\displaystyle {\sqrt {2}}}$

La causa del nivel de ruido a menudo se remonta a componentes electrónicos particulares (como transistores, resistencias y condensadores) dentro de la retroalimentación del oscilador. ^[23]

En los cerebros , el ruido rosa se ha observado ampliamente en muchas escalas temporales y físicas, desde la activación de canales iónicos hasta registros de EEG , MEG y LFP en humanos. ^[24] En el EEG clínico, las desviaciones de este ruido rosa 1/f se pueden utilizar para identificar la epilepsia , incluso en ausencia de una convulsión , o durante el estado interictal. ^[25] Los modelos clásicos de generadores de EEG sugirieron que las entradas dendríticas en la materia gris eran las principales responsables de generar el espectro de potencia 1/f observado en las señales de EEG/MEG. Sin embargo, modelos computacionales recientes que utilizan la teoría del cable han demostrado que la transducción del potencial de acción a lo largo de los tractos de materia blanca en el cerebro también genera una densidad espectral 1/f. Por lo tanto, la transducción de señales de la materia blanca también puede contribuir al ruido rosa medido en los registros de EEG del cuero cabelludo, ^[26] particularmente si se tienen en cuenta los efectos del acoplamiento efáptico. ^[27]

También se ha aplicado con éxito al modelado de estados mentales en psicología , ^[28] y se ha utilizado para explicar variaciones estilísticas en la música de diferentes culturas y períodos históricos. ^[29] Richard F. Voss y J. Clarke afirman que casi todas las melodías musicales, cuando cada nota sucesiva se traza en una escala de tonos , tenderán hacia un espectro de ruido rosa. ^[30] De manera similar, el investigador James E. Cutting de la Universidad de Cornell ha observado un patrón de distribución generalmente rosa en la duración de las tomas de películas en el estudio de 150 películas populares estrenadas entre 1935 y 2005. ^[31]

También se ha descubierto que el ruido rosa es endémico en la respuesta humana. Gilden et al. (1995) encontraron ejemplos extremadamente puros de este ruido en las series temporales formadas a partir de la producción iterada de intervalos temporales y espaciales. ^[32] Más tarde, Gilden (1997) y Gilden (2001) descubrieron que las series temporales formadas a partir de la medición del tiempo de reacción y de la elección forzada iterada de dos alternativas también producían ruido rosa. ^{[33] [34]}

Las principales fuentes de ruido rosa en los dispositivos electrónicos son casi invariablemente las fluctuaciones lentas de las propiedades de los materiales de materia condensada de los dispositivos. En muchos casos, se conocen las fuentes específicas de las fluctuaciones. Estas incluyen configuraciones fluctuantes de defectos en metales, ocupaciones fluctuantes de trampas en semiconductores y estructuras de dominio fluctuantes en materiales magnéticos. ^{[8] [35]} La explicación de la forma espectral aproximadamente rosada resulta ser relativamente trivial, y generalmente proviene de una distribución de energías de activación cinética de los procesos fluctuantes. ^[36] Dado que el rango de frecuencia del experimento de ruido típico (por ejemplo, 1 Hz – 1 kHz) es bajo en comparación con las "frecuencias de intento" microscópicas típicas (por ejemplo, 10 ¹⁴  Hz), los factores exponenciales en la ecuación de Arrhenius para las tasas son grandes. Las distribuciones relativamente pequeñas en las energías de activación que aparecen en estos exponentes dan como resultado grandes distribuciones de tasas características. En el caso del juguete más simple, una distribución plana de energías de activación da exactamente un espectro rosa, porque${\displaystyle \textstyle {\frac {d}{df}}\ln f={\frac {1}{f}}.}$

No se conoce un límite inferior para el ruido rosa de fondo en electrónica. Las mediciones realizadas hasta 10 ⁻⁶  Hz (que llevan varias semanas) no han demostrado que el comportamiento del ruido rosa desaparezca. ^[37] (Kleinpenning, de Kuijper, 1988) ^[38] midieron la resistencia en una resistencia de lámina de carbono ruidosa y encontraron un comportamiento de ruido 1/f en el rango de , un rango de 9,5 décadas.${\displaystyle [10^{-5.5}\mathrm {Hz} ,10^{4}\mathrm {Hz} ]}$

Un investigador pionero en este campo fue Aldert van der Ziel . ^[39]

El ruido de parpadeo se utiliza comúnmente para la caracterización de la confiabilidad de los dispositivos electrónicos. ^[40] También se utiliza para la detección de gases en sensores quimiorresistivos ^[41] mediante configuraciones de medición dedicadas. ^[42]

1/ f Los ruidos  ^α con α cerca de 1 son un factor en la astronomía de ondas gravitacionales . La curva de ruido a frecuencias muy bajas afecta a los conjuntos de sincronización de pulsares , el Conjunto Europeo de Sincronización de Pulsares (EPTA) y el futuro Conjunto Internacional de Sincronización de Pulsares (IPTA); a frecuencias bajas se encuentran los detectores espaciales, la Antena Espacial de Interferómetro Láser (LISA) propuesta anteriormente y la Antena Espacial de Interferómetro Láser evolucionada (eLISA) propuesta actualmente, y a frecuencias altas se encuentran los detectores terrestres, el Observatorio de Ondas Gravitacionales de Interferómetro Láser (LIGO) inicial y su configuración avanzada (aLIGO). También se muestra la tensión característica de las fuentes astrofísicas potenciales. Para ser detectable, la tensión característica de una señal debe estar por encima de la curva de ruido. ^[43]

Se ha encontrado ruido rosa en escalas de tiempo de décadas en datos proxy climáticos, lo que puede indicar amplificación y acoplamiento de procesos en el sistema climático . ^{[44] [45]}

Se sabe que muchos procesos estocásticos dependientes del tiempo exhiben ruidos 1/ f  ^α con α entre 0 y 2. En particular, el movimiento browniano tiene una densidad espectral de potencia que es igual a 4 D / f  ² , ^[46] donde D es el coeficiente de difusión . Este tipo de espectro a veces se conoce como ruido browniano . Curiosamente, el análisis de trayectorias de movimiento browniano individual también muestra un espectro 1/ f  ² , aunque con amplitudes aleatorias. ^[47] El movimiento browniano fraccional con exponente de Hurst H también muestra una densidad espectral de potencia 1/ f  ^α con α = 2 H +1 para procesos subdifusivos ( H < 0,5) y α = 2 para procesos superdifusivos (0,5 < H < 1). ^[48]

Existen muchas teorías sobre el origen del ruido rosa. Algunas teorías intentan ser universales, mientras que otras se aplican solo a un tipo determinado de material, como los semiconductores . Las teorías universales del ruido rosa siguen siendo un tema de interés para la investigación actual.

Se ha propuesto una hipótesis (conocida como la hipótesis de Tweedie) para explicar la génesis del ruido rosa sobre la base de un teorema de convergencia matemática relacionado con el teorema del límite central de las estadísticas. ^[49] El teorema de convergencia de Tweedie ^[50] describe la convergencia de ciertos procesos estadísticos hacia una familia de modelos estadísticos conocidos como las distribuciones de Tweedie . Estas distribuciones se caracterizan por una ley de potencia de varianza a media , que se ha identificado de diversas formas en la literatura ecológica como la ley de Taylor ^[51] y en la literatura de física como escala de fluctuación . ^[52] Cuando esta ley de potencia de varianza a media se demuestra mediante el método de expansión de contenedores enumerativos, esto implica la presencia de ruido rosa, y viceversa. ^[49] Se puede demostrar que ambos efectos son consecuencia de la convergencia matemática , como la forma en que ciertos tipos de datos convergerán hacia la distribución normal bajo el teorema del límite central. Esta hipótesis también proporciona un paradigma alternativo para explicar las manifestaciones de la ley de potencia que se han atribuido a la criticidad autoorganizada . ^[53]

Existen varios modelos matemáticos para crear ruido rosa. Aunque la criticidad autoorganizada ha sido capaz de reproducir el ruido rosa en modelos de pila de arena , estos no tienen una distribución gaussiana ni otras cualidades estadísticas esperadas. ^{[54] [55]} Se puede generar en la computadora, por ejemplo, filtrando el ruido blanco, ^{[56] [57] [58]} transformada inversa de Fourier , ^[59] o mediante variantes de múltiples frecuencias en la generación de ruido blanco estándar. ^{[19] [17]}

En la teoría supersimétrica de la estocástica , ^[60] una teoría libre de aproximación de ecuaciones diferenciales estocásticas , el ruido 1/ f es una de las manifestaciones de la ruptura espontánea de la supersimetría topológica . Esta supersimetría es una propiedad intrínseca de todas las ecuaciones diferenciales estocásticas y su significado es la preservación de la continuidad del espacio de fase por la dinámica temporal continua. La ruptura espontánea de esta supersimetría es la generalización estocástica del concepto de caos determinista , ^[61] mientras que la aparición asociada de la memoria dinámica de largo plazo u orden, es decir, 1/ f y ruidos crepitantes , el efecto mariposa , etc., es la consecuencia del teorema de Goldstone en la aplicación a la supersimetría topológica rota espontáneamente.

El ruido rosa se utiliza habitualmente para probar los altavoces en los sistemas de refuerzo de sonido , y el sonido resultante se mide con un micrófono de prueba en el espacio de escucha conectado a un analizador de espectro ^{[3] o a una computadora que ejecuta un programa analizador} de transformada rápida de Fourier (FFT) en tiempo real como Smaart . El sistema de sonido reproduce ruido rosa mientras el ingeniero de audio realiza ajustes en un ecualizador de audio para obtener los resultados deseados. El ruido rosa es predecible y repetible, pero resulta molesto para el público de un concierto. Desde finales de la década de 1990, el análisis basado en FFT permitió al ingeniero realizar ajustes utilizando música pregrabada como señal de prueba, o incluso la música que provenía de los intérpretes en tiempo real. ^[62] El ruido rosa todavía lo utilizan los contratistas de sistemas de audio ^[63] y los sistemas de sonido computarizados que incorporan una función de ecualización automática. ^[64]

En la industria manufacturera, el ruido rosa se utiliza a menudo como señal de quemado para amplificadores de audio y otros componentes, para determinar si el componente mantendrá la integridad del rendimiento durante un uso sostenido. ^[65] El proceso de los usuarios finales de quemar sus auriculares con ruido rosa para lograr una mayor fidelidad se ha denominado un "mito" audiófilo . ^[66]

• Bak, P.; Tang, C.; Wiesenfeld, K. (1987). "Criticidad autoorganizada: una explicación del ruido 1/ ƒ ". Physical Review Letters . 59 (4): 381–384. Bibcode :1987PhRvL..59..381B. doi :10.1103/PhysRevLett.59.381. PMID  10035754. S2CID  7674321.
• Dutta, P.; Horn, PM (1981). "Fluctuaciones de baja frecuencia en sólidos: ruido 1/ ƒ ". Reseñas de Física Moderna . 53 (3): 497–516. Bibcode :1981RvMP...53..497D. doi :10.1103/RevModPhys.53.497.
• Field, DJ (1987). "Relaciones entre las estadísticas de imágenes naturales y los perfiles de respuesta de las células corticales" (PDF) . Journal of the Optical Society of America A . 4 (12): 2379–2394. Bibcode :1987JOSAA...4.2379F. CiteSeerX  10.1.1.136.1345 . doi :10.1364/JOSAA.4.002379. PMID  3430225.
• Gisiger, T. (2001). "Invariancia de escala en biología: ¿coincidencia o huella de un mecanismo universal?". Biological Reviews . 76 (2): 161–209. CiteSeerX  10.1.1.24.4883 . doi :10.1017/S1464793101005607. PMID  11396846. S2CID  14973015.
• Johnson, JB (1925). "El efecto Schottky en circuitos de baja frecuencia". Physical Review . 26 (1): 71–85. Bibcode :1925PhRv...26...71J. doi :10.1103/PhysRev.26.71.
• Kogan, Shulim (1996). Ruido electrónico y fluctuaciones en sólidos . Cambridge University Press . ISBN 978-0-521-46034-7.
• Press, WH (1978). "Ruidos de parpadeo en astronomía y en otros ámbitos" (PDF) . Comentarios sobre Astrofísica . 7 (4): 103–119. Código Bibliográfico :1978ComAp...7..103P. Archivado (PDF) desde el original el 27 de septiembre de 2007.
• Schottky, W. (1918). "Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern". Annalen der Physik . 362 (23): 541–567. Código bibliográfico : 1918AnP...362..541S. doi : 10.1002/andp.19183622304.
• Schottky, W. (1922). "Zur Berechnung und Beurteilung des Schroteffektes". Annalen der Physik . 373 (10): 157-176. Código bibliográfico : 1922AnP...373..157S. doi : 10.1002/andp.19223731007.
• Keshner, MS (1982). "1/ ƒ noise". Actas del IEEE . 70 (3): 212–218. doi :10.1109/PROC.1982.12282. S2CID  921772.
• Chorti, A.; Brookes, M. (2007). "Resolución de infinitos espectrales de portadora cercana debido al ruido de fase 1/ f en osciladores". Conferencia internacional IEEE 2007 sobre acústica, habla y procesamiento de señales - ICASSP '07 . Vol. 3. págs. III–1005–III–1008. doi :10.1109/ICASSP.2007.366852. ISBN 978-1-4244-0727-9.S2CID14339595  .​

• Ruido coloreado: caja de herramientas de Matlab para generar señales de ruido coloreado de ley de potencia de cualquier dimensión.
• Powernoise: software de Matlab para generar ruido 1/f, o más generalmente, ruido 1/fα
• 1/f ruido en Scholarpedia
• Definición de ruido blanco vs ruido rosa