Regla de fase

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Regla de fase» – noticias  · periódicos  · libros  · académico  · JSTOR ( octubre de 2022 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En termodinámica , la regla de las fases es un principio general que rige los sistemas "pVT", cuyos estados termodinámicos están completamente descritos por las variables presión ( p ), volumen ( V ) y temperatura ( T ), en equilibrio termodinámico . Si F es el número de grados de libertad , C es el número de componentes y P es el número de fases , entonces

${\displaystyle F=C-P+2}$^{[1] [2] : 123–125}

Fue derivada por el físico estadounidense Josiah Willard Gibbs en su artículo histórico titulado Sobre el equilibrio de sustancias heterogéneas , publicado en partes entre 1875 y 1878. ^[3] La regla supone que los componentes no reaccionan entre sí.

El número de grados de libertad es el número de variables intensivas independientes , es decir, el mayor número de parámetros termodinámicos como la temperatura o la presión que pueden variarse simultáneamente y de forma arbitraria sin determinarse entre sí. Un ejemplo de sistema de un componente es un sistema que involucra una sustancia química pura, mientras que los sistemas de dos componentes, como las mezclas de agua y etanol, tienen dos componentes químicamente independientes, y así sucesivamente. Las fases típicas son los sólidos , los líquidos y los gases .

• Una fase es una forma de materia que es homogénea en composición química y estado físico . Las fases típicas son sólido, líquido y gas. Dos líquidos inmiscibles (o mezclas de líquidos con composiciones diferentes) separados por un límite definido se cuentan como dos fases diferentes, al igual que dos sólidos inmiscibles.
• El número de componentes ( C ) es el número de constituyentes químicamente independientes del sistema, es decir, el número mínimo de especies independientes necesarias para definir la composición de todas las fases del sistema. ^[2]
• El número de grados de libertad ( F ) en este contexto es el número de variables intensivas que son independientes entre sí.

La base de la regla ^{[2] : 122–126} es que el equilibrio entre fases impone una restricción a las variables intensivas. Más rigurosamente, puesto que las fases están en equilibrio termodinámico entre sí, los potenciales químicos de las fases deben ser iguales. El número de relaciones de igualdad determina el número de grados de libertad. Por ejemplo, si los potenciales químicos de un líquido y de su vapor dependen de la temperatura ( T ) y la presión ( p ), la igualdad de potenciales químicos significará que cada una de esas variables dependerá de la otra. Matemáticamente, la ecuación μ _liq ( T , p ) = μ _vap ( T , p ) , donde μ , el potencial químico, define la temperatura como una función de la presión o viceversa. (Precaución: no confunda p como presión con P , número de fases).

Para ser más específicos, la composición de cada fase está determinada por C − 1 variables intensivas (como fracciones molares) en cada fase. El número total de variables es ( C − 1) P + 2 , donde las dos adicionales son temperatura T y presión p . El número de restricciones es C ( P − 1) , ya que el potencial químico de cada componente debe ser igual en todas las fases. Reste el número de restricciones del número de variables para obtener el número de grados de libertad como F = ( C − 1) P + 2 − C ( P − 1) = C − P + 2 .

La regla es válida siempre que el equilibrio entre fases no esté influenciado por fuerzas gravitacionales, eléctricas o magnéticas, ni por el área de superficie, y solo por la temperatura, la presión y la concentración.

Para sustancias puras C = 1 de modo que F = 3 − P . En una condición de fase única ( P = 1 ) de un sistema de componentes puros, dos variables ( F = 2 ), como la temperatura y la presión, pueden elegirse independientemente para que sean cualquier par de valores consistentes con la fase. Sin embargo, si la combinación de temperatura y presión varía hasta un punto en el que el componente puro experimenta una separación en dos fases ( P = 2 ), F disminuye de 2 a 1. Cuando el sistema entra en la región de dos fases, ya no es posible controlar de forma independiente la temperatura y la presión.

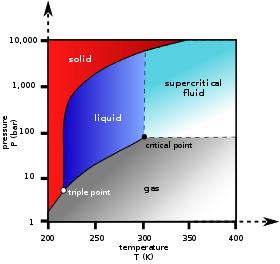
En el diagrama de fases de la derecha, la curva límite entre las regiones de líquido y gas representa la restricción entre la temperatura y la presión cuando el sistema de un solo componente se ha separado en fases líquida y gaseosa en equilibrio. La única forma de aumentar la presión en la línea de dos fases es aumentando la temperatura. Si la temperatura disminuye mediante enfriamiento, parte del gas se condensa, lo que disminuye la presión. A lo largo de ambos procesos, la temperatura y la presión se mantienen en la relación que muestra esta curva límite a menos que una fase se consuma por completo por evaporación o condensación, o a menos que se alcance el punto crítico . Mientras haya dos fases, solo hay un grado de libertad, que corresponde a la posición a lo largo de la curva límite de fases.

El punto crítico es el punto negro al final del límite líquido-gas. A medida que se acerca a este punto, las fases líquida y gaseosa se vuelven progresivamente más similares hasta que, en el punto crítico, ya no hay separación en dos fases. Por encima del punto crítico y lejos de la curva del límite de fases, F = 2 y la temperatura y la presión se pueden controlar de forma independiente. Por lo tanto, solo hay una fase y tiene las propiedades físicas de un gas denso, pero también se lo conoce como fluido supercrítico .

De las otras dos curvas límite, una es la curva límite sólido-líquido o curva de punto de fusión , que indica las condiciones de equilibrio entre estas dos fases, y la otra, a menor temperatura y presión, es la curva límite sólido-gas.

Incluso para una sustancia pura, es posible que tres fases, como sólido, líquido y vapor, puedan existir juntas en equilibrio ( P = 3 ). Si solo hay un componente, no hay grados de libertad ( F = 0 ) cuando hay tres fases. Por lo tanto, en un sistema de un solo componente, esta mezcla trifásica solo puede existir a una única temperatura y presión, lo que se conoce como punto triple . Aquí hay dos ecuaciones μ _sol ( T , p ) = μ _liq ( T , p ) = μ _vap ( T , p ) , que son suficientes para determinar las dos variables T y p. En el diagrama para CO ₂ el punto triple es el punto en el que las fases sólida, líquida y gaseosa se unen, a 5,2 bar y 217 K. También es posible que otros conjuntos de fases formen un punto triple, por ejemplo en el sistema de agua hay un punto triple donde pueden coexistir hielo I , hielo III y líquido.

Si cuatro fases de una sustancia pura estuvieran en equilibrio ( P = 4 ), la regla de fases daría F = −1 , lo cual no tiene sentido, ya que no puede haber −1 variables independientes. Esto explica el hecho de que cuatro fases de una sustancia pura (como hielo I, hielo III, agua líquida y vapor de agua) no se encuentren en equilibrio a ninguna temperatura y presión. En términos de potenciales químicos hay ahora tres ecuaciones, que en general no pueden ser satisfechas por ningún valor de las dos variables T y p , aunque en principio podrían ser resueltas en un caso especial donde una ecuación es matemáticamente dependiente de las otras dos. En la práctica, sin embargo, la coexistencia de más fases de las permitidas por la regla de fases normalmente significa que las fases no están todas en verdadero equilibrio.

Para mezclas binarias de dos componentes químicamente independientes, C = 2, de modo que F = 4 − P. Además de la temperatura y la presión, el otro grado de libertad es la composición de cada fase, a menudo expresada como fracción molar o fracción de masa de un componente.

Como ejemplo, considere el sistema de dos líquidos completamente miscibles, como el tolueno y el benceno , en equilibrio con sus vapores. Este sistema puede describirse mediante un diagrama de punto de ebullición que muestra la composición (fracción molar) de las dos fases en equilibrio en función de la temperatura (a una presión fija).

Cuatro variables termodinámicas que pueden describir el sistema incluyen temperatura ( T ), presión ( p ), fracción molar del componente 1 (tolueno) en la fase líquida ( x _1L ), y fracción molar del componente 1 en la fase vapor ( x _1V ). Sin embargo, dado que hay dos fases presentes ( P = 2 ) en equilibrio, solo dos de estas variables pueden ser independientes ( F = 2 ). Esto se debe a que las cuatro variables están restringidas por dos relaciones: la igualdad de los potenciales químicos del tolueno líquido y el vapor de tolueno, y la igualdad correspondiente para el benceno.

Para T y p dadas , habrá dos fases en equilibrio cuando la composición general del sistema ( punto del sistema ) se encuentre entre las dos curvas. Se puede trazar una línea horizontal ( isoterma o línea de unión) a través de cualquiera de esos puntos del sistema, y ​​que intersecta la curva para cada fase en su composición de equilibrio. La cantidad de cada fase está dada por la regla de la palanca (expresada en la variable correspondiente al eje x , aquí fracción molar).

Para el análisis de la destilación fraccionada , se consideran las dos variables independientes la composición de la fase líquida (x _1L ) y la presión. En ese caso, la regla de las fases implica que se determinan la temperatura de equilibrio ( punto de ebullición ) y la composición de la fase de vapor.

Los diagramas de fases líquido-vapor de otros sistemas pueden tener azeótropos (máximos o mínimos) en las curvas de composición, pero la aplicación de la regla de fases no varía. La única diferencia es que las composiciones de las dos fases son exactamente iguales en la composición azeotrópica.

Consideremos una solución acuosa que contiene cloruro de sodio (NaCl), cloruro de potasio (KCl), bromuro de sodio (NaBr) y bromuro de potasio (KBr), en equilibrio con sus respectivas fases sólidas. Cada sal, en forma sólida, es una fase diferente, porque cada una posee una estructura y composición cristalina distintas. La solución acuosa en sí es otra fase, porque forma una fase líquida homogénea separada de las sales sólidas, con su propia composición y propiedades físicas distintas. Por lo tanto, tenemos P = 5 fases.

Hay 6 elementos presentes (H, O, Na, K, Cl, Br), pero tenemos 2 restricciones:

• La estequiometría del agua: n(H) = 2n(O).
• Balance de carga en la solución: n(Na) + n(K) = n(Cl) + n(Br).

dando C = 6 - 2 = 4 componentes. La regla de fases de Gibbs establece que F = 1. Por lo tanto, por ejemplo, si trazamos el diagrama de fases PT del sistema, solo hay una línea en la que coexisten todas las fases. Cualquier desviación de la línea provocaría que una de las sales se disolviera por completo o que uno de los iones se precipitara por completo de la solución.

Para aplicaciones en ciencia de materiales que tratan cambios de fase entre diferentes estructuras sólidas, a menudo se imagina que la presión es constante (por ejemplo, a una atmósfera) y se ignora como un grado de libertad, por lo que la fórmula se convierte en: ^[4]

${\displaystyle F=C-P+1}$

Esto a veces se denomina incorrectamente "regla de la fase condensada", pero no es aplicable a sistemas condensados ​​que están sujetos a altas presiones (por ejemplo, en geología), ya que los efectos de estas presiones son importantes. ^[5]

En mezclas coloidales se han descrito puntos quíntuples ^{[6] [7] y séxtuples [8] [9]} en violación de la regla de fases de Gibbs, pero se argumenta que en estos sistemas la regla se puede generalizar a donde tenga en cuenta parámetros adicionales de interacción entre los componentes, como el diámetro de un tipo de partícula en relación con el diámetro de las otras partículas en la solución.${\displaystyle F=M+C-P+1}$${\estilo de visualización M}$

• Predel, Bruno; Hoch, Michael JR; Pool, Monte (14 de septiembre de 2004). Diagramas de fases y equilibrios heterogéneos: una introducción práctica . Springer. ISBN 3-540-14011-5.
• White, Mary Anne (1999). Propiedades de los materiales . Oxford University Press (1999). ISBN 0-19-511331-4.Capítulo 9. Aspectos termodinámicos de la estabilidad