Moda (estadística)
En estadística , la moda es el valor que aparece con mayor frecuencia en un conjunto de valores de datos. [1] Si X es una variable aleatoria discreta, la moda es el valor x en el que la función de masa de probabilidad toma su valor máximo (es decir, x = argmax x i P( X = x i ) ). En otras palabras, es el valor que tiene más probabilidades de ser muestreado.
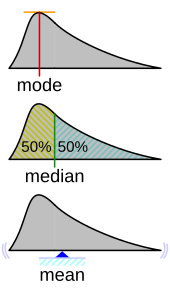
Al igual que la media y la mediana estadísticas , la moda es una forma de expresar, en un número (normalmente) único, información importante sobre una variable aleatoria o una población . El valor numérico de la moda es el mismo que el de la media y la mediana en una distribución normal , y puede ser muy diferente en distribuciones muy sesgadas .
La moda no es necesariamente única en una distribución discreta dada ya que la función de masa de probabilidad puede tomar el mismo valor máximo en varios puntos x 1 , x 2 , etc. El caso más extremo ocurre en distribuciones uniformes , donde todos los valores ocurren con la misma frecuencia.
A menudo se considera que una moda de una distribución de probabilidad continua es cualquier valor x en el que su función de densidad de probabilidad tiene un valor máximo local. [2] Cuando la función de densidad de probabilidad de una distribución continua tiene múltiples máximos locales, es común referirse a todos los máximos locales como modas de la distribución, por lo que cualquier pico es una moda. Una distribución continua de este tipo se denomina multimodal (a diferencia de unimodal ).
En distribuciones unimodales simétricas , como la distribución normal , la media (si está definida), la mediana y la moda coinciden. En el caso de las muestras, si se sabe que se extraen de una distribución unimodal simétrica, la media de la muestra se puede utilizar como estimación de la moda de la población.
Moda de una muestra
La moda de una muestra es el elemento que aparece con mayor frecuencia en la colección. Por ejemplo, la moda de la muestra [1, 3, 6, 6, 6, 6, 7, 7, 12, 12, 17] es 6. Dada la lista de datos [1, 1, 2, 4, 4] su moda no es única. En tal caso, se dice que un conjunto de datos es bimodal , mientras que un conjunto con más de dos modas puede describirse como multimodal .
Para una muestra de una distribución continua, como [0,935..., 1,211..., 2,430..., 3,668..., 3,874...], el concepto es inutilizable en su forma bruta, ya que no habrá dos valores exactamente iguales, por lo que cada valor aparecerá precisamente una vez. Para estimar la moda de la distribución subyacente, la práctica habitual es discretizar los datos asignando valores de frecuencia a intervalos de igual distancia, como para hacer un histograma , reemplazando efectivamente los valores por los puntos medios de los intervalos a los que están asignados. La moda es entonces el valor donde el histograma alcanza su pico. Para muestras pequeñas o medianas, el resultado de este procedimiento es sensible a la elección del ancho del intervalo si se elige demasiado estrecho o demasiado ancho; normalmente, uno debería tener una fracción considerable de los datos concentrados en un número relativamente pequeño de intervalos (5 a 10), mientras que la fracción de los datos que caen fuera de estos intervalos también es considerable. Un enfoque alternativo es la estimación de la densidad del kernel , que esencialmente difumina las muestras puntuales para producir una estimación continua de la función de densidad de probabilidad que puede proporcionar una estimación de la moda.
El siguiente ejemplo de código MATLAB (o Octave ) calcula la moda de una muestra:
X = sort ( x ); % x es un conjunto de datos de vector de columna indices = find ( diff ([ X ; realmax ]) > 0 ); % índices donde cambian los valores repetidos [ modeL , i ] = max ( diff ([ 0 ; indices ])); % longitud de persistencia más larga de valores repetidos mode = X ( indices ( i )); El algoritmo requiere, como primer paso, ordenar la muestra en orden ascendente. A continuación, calcula la derivada discreta de la lista ordenada y encuentra los índices donde esta derivada es positiva. A continuación, calcula la derivada discreta de este conjunto de índices, localizando el máximo de esta derivada de índices y, finalmente, evalúa la muestra ordenada en el punto donde se produce ese máximo, que corresponde al último miembro del tramo de valores repetidos.
Comparación de media, mediana y moda
| Tipo | Descripción | Ejemplo | Resultado |
|---|---|---|---|
| Media aritmética | Suma de valores de un conjunto de datos dividida por el número de valores | (1+2+2+3+4+7+9) / 7 | 4 |
| Mediana | Valor medio que separa las mitades mayor y menor de un conjunto de datos | 1, 2, 2, 3 , 4, 7, 9 | 3 |
| Modo | Valor más frecuente en un conjunto de datos | 1, 2 , 2 , 3, 4, 7, 9 | 2 |
Usar
A diferencia de la media y la mediana, el concepto de moda también tiene sentido para los " datos nominales " (es decir, que no consisten en valores numéricos en el caso de la media, o incluso en valores ordenados en el caso de la mediana). Por ejemplo, tomando una muestra de apellidos coreanos , se podría encontrar que " Kim " aparece con más frecuencia que cualquier otro nombre. Entonces "Kim" sería la moda de la muestra. En cualquier sistema de votación donde una pluralidad determina la victoria, un único valor modal determina al vencedor, mientras que un resultado multimodal requeriría que se llevara a cabo algún procedimiento de desempate.
A diferencia de la mediana, el concepto de moda tiene sentido para cualquier variable aleatoria que suponga valores de un espacio vectorial , incluidos los números reales (un espacio vectorial unidimensional) y los enteros ( que pueden considerarse incluidos en los reales). Por ejemplo, una distribución de puntos en el plano normalmente tendrá una media y una moda, pero el concepto de mediana no se aplica. La mediana tiene sentido cuando hay un orden lineal en los valores posibles. Las generalizaciones del concepto de mediana a espacios de dimensiones superiores son la mediana geométrica y el punto central .
Unicidad y definición
Para algunas distribuciones de probabilidad , el valor esperado puede ser infinito o indefinido, pero si está definido, es único. La media de una muestra (finita) siempre está definida. La mediana es el valor tal que las fracciones que no lo superan ni lo bajan son cada una al menos 1/2. No es necesariamente única, pero nunca infinita o totalmente indefinida. Para una muestra de datos es el valor "a mitad de camino" cuando la lista de valores está ordenada en valor creciente, donde generalmente para una lista de longitud par se toma el promedio numérico de los dos valores más cercanos a "la mitad". Finalmente, como se dijo antes, la moda no es necesariamente única. Ciertas distribuciones patológicas (por ejemplo, la distribución de Cantor ) no tienen moda definida en absoluto. [ cita requerida ] [4] Para una muestra de datos finitos, la moda es uno (o más) de los valores en la muestra.
Propiedades
Suponiendo definición y, para simplificar, unicidad, las siguientes son algunas de las propiedades más interesantes.
- Las tres medidas tienen la siguiente propiedad: si la variable aleatoria (o cada valor de la muestra) se somete a la transformación lineal o afín , que reemplaza X por aX + b , también lo son la media, la mediana y la moda.
- Salvo en el caso de muestras extremadamente pequeñas, la moda es insensible a los " valores atípicos " (como lecturas experimentales falsas, ocasionales y poco frecuentes). La mediana también es muy robusta en presencia de valores atípicos, mientras que la media es bastante sensible.
- En distribuciones unimodales continuas, la mediana a menudo se encuentra entre la media y la moda, aproximadamente un tercio del camino que va de la media a la moda. En una fórmula, la mediana ≈ (2 × media + moda)/3. Esta regla, debida a Karl Pearson , a menudo se aplica a distribuciones ligeramente no simétricas que se parecen a una distribución normal, pero no siempre es cierta y, en general, las tres estadísticas pueden aparecer en cualquier orden. [5] [6]
- En el caso de distribuciones unimodales, la moda está dentro de √ 3 desviaciones estándar de la media, y la desviación cuadrática media sobre la moda está entre la desviación estándar y el doble de la desviación estándar. [7]
Ejemplo de una distribución sesgada
Un ejemplo de distribución asimétrica es la riqueza personal : pocas personas son muy ricas, pero entre ellas algunas son extremadamente ricas, pero muchas son bastante pobres.

Una clase bien conocida de distribuciones que pueden estar sesgadas arbitrariamente es la distribución log-normal . Se obtiene transformando una variable aleatoria X que tiene una distribución normal en la variable aleatoria Y = e X . Entonces el logaritmo de la variable aleatoria Y se distribuye normalmente, de ahí el nombre.
Si tomamos la media μ de X como 0, la mediana de Y será 1, independientemente de la desviación estándar σ de X. Esto es así porque X tiene una distribución simétrica, por lo que su mediana también es 0. La transformación de X a Y es monótona, por lo que encontramos la mediana e 0 = 1 para Y.
Cuando X tiene una desviación estándar σ = 0,25, la distribución de Y está ligeramente sesgada. Utilizando fórmulas para la distribución log-normal , encontramos:
De hecho, la mediana se encuentra aproximadamente un tercio del camino entre la media y la moda.
Cuando X tiene una desviación estándar mayor, σ = 1 , la distribución de Y está fuertemente sesgada.
En este caso, la regla general de Pearson falla.
Condición de Van Zwet
Van Zwet derivó una desigualdad que proporciona condiciones suficientes para que esta desigualdad se cumpla. [8] La desigualdad
- Moda ≤ Mediana ≤ Media
se sostiene si
- F(Mediana - x ) + F(Mediana + x ) ≥ 1
para todo x donde F() es la función de distribución acumulativa de la distribución.
Distribuciones unimodales
Se puede demostrar para una distribución unimodal que la mediana y la media se encuentran dentro de (3/5) 1/2 ≈ 0,7746 desviaciones estándar una de la otra. [9] En símbolos,
¿Dónde está el valor absoluto?
Una relación similar existe entre la mediana y la moda: se encuentran dentro de 3 1/2 ≈ 1,732 desviaciones estándar una de otra:
Historia
El término modo se origina con Karl Pearson en 1895. [10]
Pearson utiliza el término moda de manera intercambiable con el término ordenada máxima . En una nota al pie, dice: "He encontrado conveniente utilizar el término moda para la abscisa correspondiente a la ordenada de frecuencia máxima".
Véase también
- Arg máx.
- Tendencia central
- Estadísticas descriptivas
- Momento (matemáticas)
- Resumen de estadísticas
- Función unimodal
Referencias
- ^ Damodar N. Gujarati . Fundamentos de econometría . McGraw-Hill Irwin. Tercera edición, 2006: pág. 110.
- ^ Zhang, C; Mapes, BE; Soden, BJ (2003). "Bimodalidad en vapor de agua tropical". QJR Meteorol. Soc . 129 (594): 2847–2866. Código Bibliográfico : 2003QJRMS.129.2847Z. doi : 10.1256/qj.02.166. S2CID 17153773.
- ^ "AP Statistics Review - Curvas de densidad y distribuciones normales". Archivado desde el original el 2 de abril de 2015 . Consultado el 16 de marzo de 2015 .
- ^ Morrison, Kent (23 de julio de 1998). "Paseos aleatorios con pasos decrecientes" (PDF) . Departamento de Matemáticas, Universidad Politécnica Estatal de California . Archivado desde el original (PDF) el 2 de diciembre de 2015. Consultado el 16 de febrero de 2007 .
- ^ "Relación entre la media, la mediana, la moda y la desviación estándar en una distribución unimodal".
- ^ Hippel, Paul T. von (2005). "Media, mediana y asimetría: corrección de una regla de libro de texto". Revista de educación estadística . 13 (2). doi : 10.1080/10691898.2005.11910556 .
- ^ Bottomley, H. (2004). "Distancia máxima entre la moda y la media de una distribución unimodal" (PDF) . Preimpresión no publicada .
- ^ van Zwet, WR (1979). "Media, mediana, modo II". Statistica Neerlandica . 33 (1): 1–5. doi :10.1111/j.1467-9574.1979.tb00657.x.
- ^ Basu, Sanjib; Dasgupta, Anirban (1997). "La media, la mediana y la moda de distribuciones unimodales: una caracterización". Teoría de la probabilidad y sus aplicaciones . 41 (2): 210–223. doi :10.1137/S0040585X97975447.
- ^ Pearson, Karl (1895). "Contribuciones a la teoría matemática de la evolución. II. Variación sesgada en material homogéneo". Philosophical Transactions of the Royal Society of London A . 186 : 343–414. Bibcode :1895RSPTA.186..343P. doi : 10.1098/rsta.1895.0010 .
Enlaces externos
- "Modo", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- Una guía para comprender y calcular la moda
- Weisstein, Eric W. "Modo". MundoMatemático .
- Vídeo breve para principiantes sobre media, mediana y moda de Khan Academy







